Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantifying the hygroscopic properties of cyclodextrin containing aerosol for drug delivery to the lungs†
C. P. F.
Day
 ,
A.
Miloserdov
,
K.
Wildish-Jones
,
E.
Pearson
and
A. E.
Carruthers
,
A.
Miloserdov
,
K.
Wildish-Jones
,
E.
Pearson
and
A. E.
Carruthers
 *
*
Chemistry, School of Natural and Environmental Sciences, Bedson Building, Newcastle University, Newcastle Upon Tyne, NE1 7RU, UK. E-mail: toni.carruthers@ncl.ac.uk
First published on 6th May 2020
Abstract
Aerosol dynamics is important to quantify in drug delivery to the lungs with the aim of delivering therapeutics to a target location and optimising drug efficacy. The macrocycle (2-hydroxypropyl)-β-cyclodextrin (2-HP-β-CD) is thought to alleviate symptoms associated with neurodegenerative diseases when inhaled but the hygroscopic response is not well understood. Here we measure the hygroscopic growth of individual aqueous aerosol containing 2-HP-β-CD in optical tweezers through analysis of morphology-dependent resonances arising in Raman spectra. Droplets are analysed in the size range of 3–5 μm in radius. The evolving radius and refractive index of each droplet are measured in response to change in relative humidity from 98–20% to determine mass and radius based hygroscopic growth factors, and compared with dynamic vapour sorption measurements. Bulk solution refractive index and density measurements were used in accordance with the self-consistent Lorenz–Lorentz rule to determine melt solute and droplet properties. The refractive index of 2-HP-β-CD was determined to be 1.520 ± 0.002 with a density of 1.389 ± 0.005 g cm−3. To our knowledge, we show the first aerosol measurements of 2-HP-β-CD and determine hygroscopicity. By quantifying the hygroscopic growth and physicochemical properties of 2-HP-β-CD, the impact of aerosol dynamics can be accounted for in tailoring drug formulations and informing models used to predict drug deposition patterns within the respiratory system.
1. Introduction
Determining and controlling aerosol properties is important for targeted and effective drug deposition patterns where the environment of the drug path towards and into the respiratory tract or through the olfactory system is known to influence pharmaceuticals.1 A poor understanding of the relationship between the physicochemical characteristics of aerosol formulation and the medicinal efficacy in the humid environment of the respiratory tract has been identified as the key barrier in optimising inhalation therapies.2 Recent studies have shown characterisation of the physiochemical properties of aerosolised medicinal agents used in drug delivery to the lung, e.g. salbutamol sulphate,3 where the aging of the droplet as it responds to rapid changes in RH and temperature during inhalation is known to significantly impact aerosol properties. Such studies demonstrate the importance of quantifying the hygroscopic response to predict particle deposition patterns within the pulmonary system. On inhalation, aerosol radii of ≥5 μm are more likely to deposit in the mouth and throat, <5 μm will travel to the lung, and particles <1 μm are thought to be predominantly exhaled.3,4For a drug molecule to be pharmacologically active it may be designed to have lipophilic properties to allow absorption and diffusion through biological membranes, and be hydrophilic to improve water solubility. Cyclodextrins (CD) have been identified as medicinal agents for use in drug inhalation formulations and can enable the controlled release of drugs.5 They are useful excipients because their physiochemical properties can be tuned through molecular modification to improve hydrophilicity and bioavailability. CDs are macrocycles that consist of a hydrophilic exterior and lipophilic interior that can selectively complex with inorganic and organic molecules in aqueous solution. These properties enable cyclodextrins to carry drug molecules in solution, delivering them to the surface of biological membranes.6 Naturally occurring CDs are cyclic oligomers of glucopyranose, containing six (α-CD), seven (β-CD) and eight (γ-CD) glucopyranose units connected by glucosidic bonds. The smaller inner cavity size of α-CD can be a limiting factor for complexation with large drug molecules and the larger cavity of γ-CD typically does not offer enough complexation stability.7 Studies have therefore focussed on β-CD, and in particular modifying β-CD to improve its unwanted tendency to aggregate and unusually low water solubility.8,9 Molecular modelling suggests that low hydrophilicity stems from intermolecular bonding in the natural β-CD crystal state that affects the rigidity of the molecule and induces strong ordering on the surrounding water molecules.10 In comparison, the position of hydroxyl groups in the modification site of the parent CD in (2-hydroxypropyl)-β-cyclodextrin (2-HP-β-CD) have been shown through molecular docking models7 to slightly reduce the size of the cavity and allow hydrogen bonding with external neighbouring water molecules in aqueous solution. 2-HP-β-CD therefore has improved water solubility over the parent compound and is well suited to pharmaceutical and environmental applications. Furthermore, the porous nature of CD molecules and their amphiphilicity makes them a highly interesting structure to investigate hygroscopic response. Potential formation of amorphous phases observed in CDs may reveal interesting water kinetics that can impact droplet concentration and drug uptake in the lungs. Studying hygroscopicity of aerosol in femtolitre to picolitre volumes, where the droplet surface area to volume ratio is favourable, can provide insight into chemistry occurring at the surface and on a molecular level.
Aerosol consist of microscopic and sub-microscopic particles and droplets dispersed in a gas medium that evolve dynamically to equilibrate with the surrounding environment. They are thermodynamically unstable due to their large surface area but can be kinetically stabilised with respect to relative humidity (RH), where RH is the partial pressure of water vapour in the gas phase compared to the vapour pressure of pure water. The behaviour of aerosol can deviate from that expected in a bulk solution, offering higher concentrations, metastable states and extreme pH values that help drive chemical reactions.11 Aerosol respond to an increase or decrease in RH inducing a change in the number of water molecules in the atmosphere and vapour pressure of the droplet. This RH change drives the droplet towards reaching equilibrium in terms of size, concentration and phase (e.g. liquid, glass, gel). A dry and hygroscopic aerosol particle held at low RH, close to RH = 0%, will respond immediately to a driven and controlled atmosphere. As RH increases, the water vapour around the aerosol particle also increases and creates a net flux of water molecules towards the aerosol surface. The continual increase in RH brings the aerosol towards the saturation point of the bulk solution where water molecules adsorb onto the particle surface and are accommodated, known as deliquescence. This uptake of water induces a phase change of the aerosol from solid to liquid. The droplet will continue to take up water with a further increase in RH that increases the droplet size as the mass fraction of water (MFW) in the droplet increases. Correspondingly, the mass fraction of solute (MFS) in the droplet decreases, i.e. MFS + MFW = 1, and droplet refractive index (RI) tends towards that of water as RH approaches 100%. On responding to a decrease in RH, the droplet can exist in a liquid state beyond the deliquescence point (i.e. at lower RHs) because there is no site on which nucleation can take place, and the MFS of the droplet can exceed that of a bulk solution. The aerosol is then said to exist in a highly-concentrated super-saturated state and is the region where meta-stable phases can form that exhibit interesting water uptake kinetics.12,13 The hygroscopic evolution of an aerosol droplet therefore ranges from the dilute limit to that of a pure liquid solute or melt,14 which we refer to here as melt solute. Hygroscopic growth curves, also referred to as humidity isotherms for bulk sample measurements, are characteristic of aerosol composition. Here we measure the hygroscopic growth of (2-hydroxypropyl)-β-cyclodextrin (2-HP-β-CD) which, as a medicinal agent, is thought to alleviate symptoms associated with neurodegenerative diseases for use in drug inhalation formulations.1,15,16 The hygroscopicity of microscopic sized aerosol droplets is determined on a single droplet basis using Raman tweezers17,18 and compared with dynamic vapour sorption (DVS) humidity isotherm measurements.19,20
As an excipient, 2-HP-β-CD is used in developing environment-friendly formulations removing polycyclic aromatic hydrocarbons (PAHs) from soil21 and has shown to complex with heavy metals,6 small organic guest molecules22 and acetanilides.23 In ref. 24 the concentration of HP-β-CD was found to increase linearly when complexed with PAHs, and is thought to have no critical micelle concentration. In the form of nanofibers, HP-β-CD has shown to improve the molecular entrapment of VOCs, potentially serving as a filtering material in air filtration applications.25 In drug delivery applications 2-HP-β-CD is thought to have significant medicinal benefits in alleviating symptoms of neurodegenerative disorders, e.g. Alzheimer's, Neimann Pick's, Parkinson's and Huntington's diseases, when inhaled.15,16 The commercially available Kleptose® 10 (β-CD) has been developed as an attractive excipient for nasal and pulmonary drug administration, and Kleptose® HPB (HP-β-CD) for alternative delivery routes.26 Erickson et al.27 used a mouse model where a 20% HP-β-CD in saline solution was used to assess the inhaled therapeutic potential in Neimann-Pick type C1 disease and drug impact on the lungs. Further studies have shown complexation of pulmonary delivered HP-β-CD with salbutamol in rabbits,28 where the use of HP-β-CD provides tuneability of active drug hydrophilicity. Aerosolised CDs used in this way can help alleviate site toxicity issues associated with dry powder inhaler formulations. Determining aerosol response to change in RH is crucial in qualifying and quantifying hygroscopicity and understanding how this influences physiochemical properties such as size, concentration and phase (e.g. liquid, solid, glass, gel).
Despite the interest in CDs as medicinal agents and excipients, the physiochemical properties of CDs and CD derivatives, for example hygroscopicity, RI and density are ill-defined or unknown, and there is a need to understand the underlying aerosol science impacting inhaled formulation.2,3 Qualifying and quantifying aerosol hygroscopic response is key to improving drug formulations and informing models used to predict drug deposition patterns within the lung or taken up through the olfactory system. The use of optical tweezers is a well-established technique often coupled with Raman spectroscopy to quantify physiochemical properties of microscopic droplets and particles.17,29–31 By studying droplets on an individual basis, detailed information can be retrieved that is often over-looked from aerosol ensemble measurements due to averaging effects. Optical tweezers are well suited to enable characterisation of microscopic droplets of a size relevant to inhalation into the lung. The aerosol droplets measured with optical tweezers and discussed here range between 3–5 μm in radius. The position of morphology dependent resonances (MDRs), also known as whispering gallery modes, arising over the chemical OH and CH stretches observed in Raman spectra can be measured and used to determine droplet radius, RI and dispersion in RI. A least squares fit to minimise the error is used matching experimentally obtained MDRs to Mie theory calculations and described in detail by Preston and Reid.32,33 The hygroscopicity of the aerosol can then be determined through knowledge of the MFS of the droplet at a given RH. Bulk solution measurements are used to infer aerosol properties at high concentrations, and for that of the melt solute, and it is important that there is a physical basis to inform measurement. In the measurements presented here, the RI and density of aqueous 2-HP-β-CD were measured with varying MFS in bulk solution to infer concentrations relevant to aerosol. The solution density measurements allowed determination of melt solute density using the two-component mixing rule. The RI of solute was then retrieved using the self-consistent Lorenz–Lorentz medium approximation, derived from the Clausius–Mossotti relation.34
2. Methods and materials
2.1 Determining growth factors and the mass based hygroscopicity parameter
The hygroscopic response of aerosol is often described in terms of mass (GFm) and radius (GFr) based growth factors that can be converted between where density or RI are known.18,35 Through control of the RH around a droplet MFS can be tuned by initiating a change in the droplet water activity. This drives the droplet dynamically to equilibrate with the surrounding RH resulting in a change in size, RI, density and MFS. Equilibrium is reached once the vapour pressure at the droplet surface reaches that of the partial vapour pressure an infinite distance away from the droplet. Eqn (1) is valid for particle sizes >1 μm where the surface curvature of droplets do not play a significant role and water activity can be approximated as aw ≈ RH/100.35 | (1) |
 | (2) |
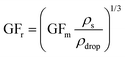 | (3) |
2.2 AIOMFAC modelling and hygroscopicity order
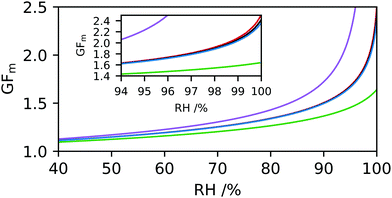
Hygroscopicity can be modelled using AIOMFAC (Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients), a thermodynamic model based on UNIFAC calculations.36,37 The AIOMFAC model allows properties such as the mass fraction of water (MFW) and solute (MFS) of the droplet to be predicted at each RH value based on the assignment of functional groups. The AIOMFAC curves predict the evaporative hygroscopic response of aerosol, i.e. as RH is decreased. The hygroscopicity of the aerosol composition can then be determined in terms of GFm, κm and GFr at a defined temperature. It is worth noting that structural information is not included in AIOMFAC and predicted hygroscopicities are thought to deviate from experimental measurements for large and complex molecules.38 For purposes of AIOMFAC modelling, we have restricted discussion of CDs to the three parent compounds (α-CD, β-CD and γ-CD), the derivative HP-β-CD and glucopyranose (as representative of one repeat unit of the cyclic sugars). The hygroscopicity of all molecules discussed here have been predicted at T = 25 °C to coincide with DVS measurements.The HP-β-CD ring contains seven repeat units, with a chemical formula of (C9H16O6)7. For purposes of AIOMFAC modelling the functional groups within the HP-β-CD molecule are assigned according to ref. 36, as are a single glucopyranose unit, α-CD, β-CD and γ-CD (see ESI† for functional group assignments). AIOMFAC modelling of the parent compounds α-CD, β-CD and γ-CD show similar trends in terms of MFS, κm and GFm with respect to RH, Fig. 1. An insert of the GFm values obtained at higher RHs is shown to clarify the predicted order of hygroscopicity. It can be seen that AIOMFAC predicts HP-β-CD to be less hygroscopic than β-CD and suggests a hygroscopicity order of HP-β-CD ≪ γ-CD ∼ β-CD ∼ α-CD ≪ glucopyranose. These results indicate that strong ordering of β-CD on neighbouring water molecules cannot be accounted for using AIOMFAC, which is unsurprising given that the linear structure of glucopyranose and cyclic CD structural information are not included. The amphiphilic nature of CDs arises due to the inside of the torus being relatively hydrophobic and the outside hydrophilic. Neighbouring water molecules on the outside of the torus are therefore in a distinct environment compared to the high-energy bound water molecules on the inside of the structure and likely to impact hygroscopicity. Here we are not determining the chemical complexity of hygroscopicity order, but it serves to illustrate the limitations of current understanding and the need to support aerosol measurements with alternative experimental techniques, for example in ref. 39 and 40.
In interpreting predicted hygroscopicity of CDs from AIOMFAC it is useful to consider the compounds in terms of solubility, elemental O/C ratio and molecular mass, thought to influence order,17,41–44 see Table 1. The properties of modified β-CDs are not well defined in the literature and the solubility of HP-β-CD is indicated as ≥600 mg mL−1 in Loftsson41 and Gidwani and Vyas,42 where the position of the hydroxypropylation has not been assigned. Blanford22 assigns HP-β-CD a much higher solubility value of >800 mg mL−1, and Saokham et al.7 reports solubility to be >1200 mg mL−1. It should be noted here that the degree of substitution of CD in formulating HP-β-CD is thought to be important and each variant may be chemically distinct due to differences found arising in mass spectrometry.45 Commercially available functionalised CDs tend to be heterogeneous in nature, and there is likely to be batch-to-batch variation. In our experiments, we did not set out to determine the solubility limit of 2-HP-β-CD. However, we observed complete solvation of 2-HP-β-CD in deionised water at a concentration of 600 mg mL−1 for temperatures between 22–25 °C, and by simply warming the solution in our hands concentrations of up to 800 mg mL−1 could be achieved.
| Cyclodextrin | Chemical formula | Solubility (mg mL−1) | Molecular mass (g mol−1) | O/C |
|---|---|---|---|---|
| α-CD | (C6H10O5)6 | 145 | 972.8 | 0.83 |
| β-CD | (C6H10O5)7 | 18.5 | 1135 | 0.83 |
| γ-CD | (C6H10O5)8 | 232 | 1297.1 | 0.83 |
| HP-β-CD | (C9H16O6)7 | ≥600 | 1541.6 | 0.67 |
| Glucopyranose | C6H10O5 | 1200 | 180.16 | 0.83 |
2.3 Dynamic vapour sorption
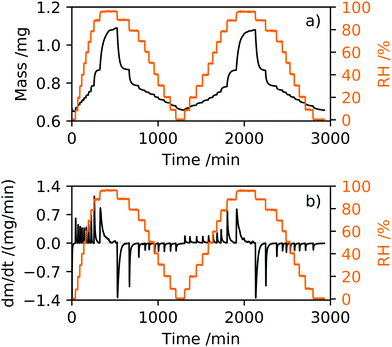
DVS is an analytical tool used to determine humidity isotherms and the moisture content of inorganic and organic compounds19 under controlled environmental conditions of RH and temperature. It is a technique commonly used to determine the stability of pharmaceutical and food products in different atmospheres to optimise storage conditions,20 and ideally suited for comparison with aerosol measurements. The DVS instrument (SMS DVS-1) is configured such that two balances are held in a climate chamber of controllable RH and temperature. The DVS relies on placing a pan containing the sample to be measured on one balance and an empty reference pan is placed on the second balance. Prior to each measurement, an empty pan was placed on the sample balance, the RH increased to 90% to remove static and the balance was tared. A sample of dry white 2-HP-β-CD powder (CAS 128446-35-5, Cambridge Bioscience, purity ≥95%) was placed into the pan and allowed to equilibrate in the balance to a dry N2 gas environment, ∼RH = 0.4%. Fig. 2 shows the mass and rate of change of mass with respect to time in response to relative humidity for a sample mass of mo = 0.6498 mg. The dm/dt response of 2-HP-β-CD, shown in Fig. 2(b), provides a useful indication of phase change in the humidity isotherm, where positive and negative peaks are indicative of adsorption and desorption processes, respectively.For the experiments described here, the RH was varied and monitored using a Rotronic A/H hygrometer with a ±1% accuracy, and the sample maintained at a constant temperature of 25 ± 1 °C. The DVS was used in dm/dt mode that allows the RH to step increase or decrease in RH after the sample mass had stabilised to within a tolerance level of ±0.001% over a time period of five minutes. Each RH step was set to a maximum time of tmax = 360 min such that if the sample had not stabilised in mass within this time the RH would continue to step. Where stabilisation in mass was not fully achieved at each set RH within time tmax, the response of sample mass with time at each RH step was fitted to an exponential growth (adsorption) or decay (desorption) function to determine equilibration mass. All DVS measurements discussed here consisted of two adsorption and desorption cycles. The adsorption section of the humidity isotherm was recorded using 10% RH steps from 0–90% followed by a step from 90–98% RH, and the desorption followed the reverse RH stepping. Typical sample masses were prepared to be less than 1 mg to reduce the potential for skin formation on the surface of the sample during measurement that might inhibit water uptake into the bulk of the sample.
2.4 Optical tweezers coupled with cavity enhanced Raman spectroscopy
Raman spectroscopy was integrated with optical tweezers to allow measurement of aerosol on a single particle basis. The laser used for optically tweezing droplets and Raman excitation was a diode-pumped solid-state laser (3W Opus, Laser Quantum) at a wavelength of 532 nm. An LED of wavelength 447.5 nm allowed bright-field illumination of the droplet to observe the position stability of the droplet. Individual optically tweezed droplets were held in an environment chamber under controlled RH and at room temperatures ranging from 18–23 °C. The spontaneous Raman signature collected provided information on the chemical properties of the aqueous droplet, and MDRs superimposed over the chemical bond vibrations were used to determine size, RI and dispersion in RI.32,33 Raman spectra were measured using an iHR550 Raman spectrometer (Horiba Scientific) and the droplet imaged onto a Peltier-cooled Syncerity CCD (Horiba Scientific). Spectra of aerosol droplets were recorded using an acquisition time of 10 s, a diffraction grating of 600 grooves per mm and a slit width of 20 μm. The broad OH stretch arises in the Stokes shifted Raman spectra at λOH ≈ 650 nm, and the CH stretch at λCH ≈ 630 nm. A sample of dry powder 2-HP-β-CD was recorded in the Raman spectrum placed on a coverslip to observe the underlying CH and OH stretches without the presence of MDRs, Fig. 3(a), and relative intensities of the vibration bands. A spectrum of an aqueous droplet held in optical tweezers and equilibrated to an RH of 80% is shown for comparison where MDRs are visible over the chemical stretches. The RI of the droplet is taken to be at reference wavelength of λOH = 650 nm because this wavelength is close to the centre of the OH band where the majority of the MDRs lie and are used for sizing the droplet. Fig. 3(b) illustrates the MDR positions shifting to a lower wavelength in response to a change in RH from 98–90% and 70–60%, and is indicative of size suppression caused by water evaporation away from the droplet. A least squares fit error analysis of experimental Raman spectra with Mie theory allows droplet radius and RI to be accurately determined, see Fig. 4. The uncertainty in radius and RI is estimated from minimising the error arising from matching MDR positions in each spectrum to a library of Mie theory calculations. The dispersion in RI, μ, can be also be determined through analysis of MDR positions using Mie theory calculations32,33 and can be expressed in terms of wavelength in eqn (4), where μ is measured in cm−1.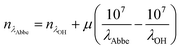 | (4) |
2.5 Determining MFS of aerosol droplets
Direct measurement of the density and RI of a powdered solute is not straightforward in aerosol, and techniques rely on indirect measurements and extrapolation to determine melt solute and highly viscous states. Methods used to retrieve RI, density and MFS need to be underpinned with a physical basis and with a well-defined relationship to determine aerosol characteristics in under-saturated and super-saturated regions of the hygroscopic growth curve. Knowledge of the melt solute properties can then be used to determine the MFS of the droplet where RI is known and can be written as a mixing rule, ndroplet = nsMFS + nwMFW. Such mixing rules assume that the melt solute RI and density values are used (rather than a stable crystalline form) and therefore valid for liquid and metastable glassy states of relevance to aerosol.14 The method chosen for extrapolating data to determine ρs and ns (i.e. when MFS = 1) has previously, to some extent depended on the fit of the data using linear and polynomial extrapolations.17,46,47 However, predicting aerosol properties of RI (optical density) and density (mass density) can be achieved using the Lorenz–Lorentz medium approximation.34 Written in eqn (5) in the form of molar refraction, R, the Lorenz–Lorentz rule can be used to determine RI and density where one of the properties is known.46,48 | (5) |
 | (6) |
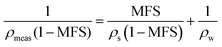 | (7) |
3. Results
3.1 Refractive index and density measurements
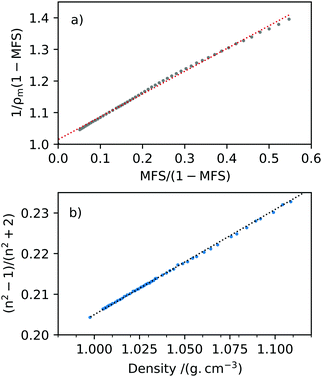
The density measurements with change in MFS were plotted such that the gradient of the line was equal to the reciprocal of the melt solute density, 1/ρs, with a y-intercept of 1/ρw, see Fig. 5(a). The pure solute melt density of 2-HP-β-CD was determined for MFS = 1 to be ρs = 1.389 ± 0.005 g cm−3 in Fig. 5(a) and the square of the correlation coefficient R2 = 0.9973. These density measurements for bulk aqueous 2-HP-β-CD are in reasonable agreement with ref. 49 where aqueous solutions of HP-β-CD were measured at ambient room temperature up to a concentration of 800 mg mL−1. For comparison, Girolami,50 used in aerosol model e-AIM51 where solute density is unknown, estimates a pure melt density for 2-HP-β-CD of 1.245 ± 0.200 g cm−3 at T = 25 °C.The densitometer and Abbe refractometer measurements were then used in accordance with the Lorenz–Lorentz rule in eqn (6), shown in Fig. 5(b). The data was fitted to a linear trendline and using the pure melt solute density obtained from the two-component mixing rule. The RI of pure solute was determined to be ns = 1.520 ± 0.002 (T = 25 °C, λ = 589.3 nm), where R2 = 0.9995. To our knowledge, there is no solute RI literature value for 2-HP-β-CD for comparison.
3.2 Dynamic vapor sorption hygroscopic growth measurements
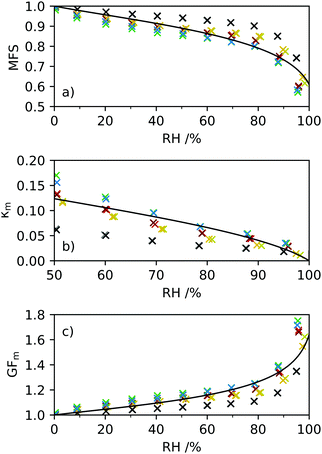
The extrapolated equilibrium mass values were obtained from the DVS measurement of mo_1 = 0.6498 mg for first and second adsorption and desorption profiles at each RH value. The growth factors at each RH value were calculated using eqn (1). Three further DVS measurements were recorded for samples of mo_2 = 0.6404 mg, mo_3 = 0.4219 mg and mo_4 = 0.1765 mg each consisting of two humidity isotherms and shown in Fig. 6. The sensitivity of the mass microbalance was 0.0001 mg and the precision associated with each individual mass measurement due to RH drift was less than ±0.001 mg. The error bars shown on Fig. 6 indicate the deviation of the extrapolated mass value from the recorded raw data mass value. The accuracy in the RH originates from the hygroclip humidity probe of ±1% that decreases to ±2% at extremes of RH, and we have conservatively assumed a ±2% accuracy across RH measurements. At 90% RH, average growth factors for each sample were GFm_1(mo_1 = 0.6498 mg) = 1.337 ± 0.004, GFm_2(mo_2 = 0.6404 mg) = 1.176 ± 0.0.001, GFm_3(mo_3 = 0.4219 mg) = 1.284 ± 0.008 and GFm_4(mo_4 = 0.1765 mg) = 1.388 ± 0.005. The DVS measurements allowed determination of MFS and κm of 2-HP-β-CD using eqn (1) and (2) and are shown in Fig. 6 with AIOMFAC modelling for comparison. In Fig. 3(b)κm can be seen to curve as RH decreases and the contribution of dry mass in the sample becomes more significant. The range of hygroscopic GFs determined between successive DVS measurements is slightly surprising and may be a result of the choice to use mass samples of <1 mg due to the likelihood of heterogeneous variations between each sample.3.3 Optical tweezers hygroscopic growth measurements
Raman spectra were recorded continuously over a time of 90 min, with a minimum of 4 hours stabilisation time following each change in RH. The radius and RI were determined from each spectrum, and a mean and standard deviation measurement obtained for each RH value. The relationships obtained between MFS, RI and density based on Abbe refractometer measurements were used to determine GFm of individual optically tweezed droplets. The RIs retrieved from optical tweezers measurements of five individual aerosol droplets are considered here, seen in Fig. 7. The RI and dispersion in RI fitting values for each droplet held at a given RH can be found in the ESI.† The RI values from each droplet were dispersion corrected to a wavelength of 589.3 nm using eqn (4). The growth factor measurements obtained through DVS are indicated with a grey area for clarity of optical tweezers data. AIOMFAC modelling is shown for comparison and in good agreement with the experimental data determined using optical tweezers and DVS techniques. The data was converted to GFr using eqn (3) for each data set. | ||
| Fig. 7 The mass growth factor (GFm) and radius growth factor (GFr) are shown for five aerosol droplets measured using optical tweezers and indicated as diamond markers. DVS measurements are shown as a grey shaded area representative of the maximum and minimum values from the data discussed in Fig. 6 and AIOMFAC predictions are indicated as a black line. | ||
3.4 Amorphous phase formation
During our optical tweezers and DVS measurements of 2-HP-β-CD we observed evidence of formation of a kinetically arrested state. The DVS samples were prepared using dry white solute powder, and observed post humidity isotherm measurement to be clear and highly viscous that hardened over time in ambient room atmosphere conditions. This observation was visually verified in the optical tweezers through a simplified poke-and-flow experiment.52 An aqueous 2-HP-β-CD drop sample of concentration 600 mg mL−1 was placed on a coverslip and held at 98% RH for three hours. The RH was then reduced to 30% RH to equilibrate over-night. The sample on the coverslip was removed from the optical tweezers RH environment chamber and observed to be clear and highly viscous. A pipette tip was used to poke the sample leaving an indentation, and left over-night in ambient room temperature and RH. The sample was observed to harden to a clear solid and exhibited cracking behaviour with the poke indentation no longer visible. The measured hygroscopic response in terms of GFm using optical tweezers and DVS are also indicative of highly viscous particle formation, similar to optical tweezers measurements of sucrose measured by Tong et al. indicating a glass transition at ∼24% RH.53 During our measurements no crystallisation was observed to occur at low RH values, and the long timescales for equilibration indicative of slow water transport and formation of a kinetically arrested state. These observations are in agreement with previous work using molecular docking models that indicate water molecules can remain in the porous cavity of 2-HP-β-CD on dehydration10 and in agreement with the amorphous complex formation of 2-HP-β-CD observed by Sonoda et al.54 Water molecules could therefore be constrained to the inner cavity of 2-HP-β-CD at low RH values, enabling amorphous transition and hydrated crystal formation as observed previously in α, β and γ cyclodextrins.554. Conclusions
Hygroscopic measurements on aqueous 2-HP-β-CD droplets have been reported using optical tweezers coupled with Raman spectroscopy. Aerosol properties are determined through analysis of the wavelength position of MDRs and compared with a library of Mie theory simulations to determine droplet radius, RI and dispersion in RI. Aerosol measurements have been compared with DVS humidity isotherm measurements and AIOMFAC modelling. Bulk RI and density measurements allowed determination of aerosol properties at high concentration using the Lorenz–Lorentz rule. The 2-HP-β-CD melt solute is self-consistent in RI and density with change in MFS in agreement with the Lorenz–Lorentz rule. Measurements indicate a solute melt density and RI of 1.389 ± 0.005 g cm−3 and 1.520 ± 0.002, respectively. The hygroscopic growth factor of 2-HP-β-CD has been determined in terms of mass and radius, and is of significance in optimising drug inhalation formulations and medicinal efficacy. By quantifying hygroscopicity, aerosol dynamics can be exploited and properties tuned to ensure droplets are appropriately sized to reach the intended location in the lung or through the olfactory system on inhalation. Growth factor DVS measurements at 90% RH indicate an average GFm(DVS) = 1.30 ± 0.08 and is in good agreement with AIOMFAC modelling indicating GFm(AIOMFAC) = 1.37. In comparison, optical tweezers measurements provided a slightly lower GFm(OT) = 1.22 ± 0.06 and GFr(OT) = 1.08 ± 0.05, within error of DVS measurements. Slight discrepancy of optical tweezers GFm values with DVS measurements may have arisen from the determination of melt solute properties from bulk solution measurements. It is also worth noting that successive DVS measurements indicate a range of GFm values that can occur when samples undergo skin layer formation. An amorphous transition and formation of ultra-viscous aerosol has been identified through optical tweezers measurements and is in agreement with observations made from DVS measurements. The slow water transfer observed in amorphous cyclodextrin molecules coupled with their porous nature could reveal interesting water uptake kinetics in aerosol. Furthermore, cyclodextrins and cyclodextrin derivatives may provide valuable insight into understanding the chemical complexities of hygroscopicity and help in determining hygroscopic order.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AEC acknowledges the Royal Society for early funding of the optical tweezers system through Research Grant RG130441. CPFD acknowledges Newcastle University for funding through a Research Excellence Award. We acknowledge Dr J. S. Walker and Prof. J. P. Reid in the School of Chemistry at the University of Bristol for the use of software used in aerosol analysis. Thank you to Prof. J. P. Reid for valuable comments on the manuscript. We thank Dr D. A. Fulton (Chemistry, School of Natural and Environmental Sciences, Newcastle University) for useful discussions on cyclodextrins and comments on the manuscript. We acknowledge the School of Pharmacy (Newcastle University) for use of the DVS and the School of Engineering (Newcastle University) for use of the refractometer and densitometer.References
- M. Vecsernyés, F. Fenyvesi, I. Bácskay, M. A. Deli, L. Szente and E. Fenyvesi, Arch. Med. Res., 2014, 45, 711–729 CrossRef PubMed.
- N. R. Labiris and M. B. Dolovich, Br. J. Clin. Pharmacol., 2003, 56, 600–612 CrossRef CAS PubMed.
- A. E. Haddrell, J. F. Davies, R. E. H. Miles, J. P. Reid, L. A. Dailey and D. Murnane, Int. J. Pharm., 2014, 463, 50–61 CrossRef CAS PubMed.
- C. Darquenne, J. Aerosol Med. Pulm. Drug Delivery, 2012, 25, 140–147 CrossRef CAS PubMed.
- C. Muankaew and T. Loftsson, Basic Clin. Pharmacol. Toxicol., 2018, 122, 46–55 CrossRef CAS PubMed.
- E. M. Del Valle, Process Biochem., 2004, 39, 1033–1046 CrossRef CAS.
- P. Saokham, C. Muankaew, P. Jansook and T. Loftsson, Molecules, 2018, 23, 1161 CrossRef PubMed.
- E. Sabadini, T. Cosgrove and F. do Carmo Egidio, Carbohydr. Res., 2006, 341, 270–274 CrossRef CAS PubMed.
- A. W. Coleman, I. Nicolis, N. Keller and J. P. Dalbiez, J. Incl. Phenom. Mol. Recognit. Chem., 1992, 13, 139–143 CrossRef CAS.
- K. J. Naidoo, J. Y. Chen, J. L. M. Jansson, G. Widmalm and A. Maliniak, J. Phys. Chem. B, 2004, 108, 4236–4238 CrossRef CAS.
- H. Wei, E. P. Vejerano, W. Leng, Q. Huang, M. R. Willner, L. C. Marr and P. J. Vikesland, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7272–7277 CrossRef CAS PubMed.
- C. Cai, S. Tan, H. Chen, J. Ma, Y. Wang, J. P. Reid and Y. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 29753–29763 RSC.
- J. W. Lu, A. M. J. Rickards, J. S. Walker, K. J. Knox, R. E. H. Miles, J. P. Reid and R. Signorell, Phys. Chem. Chem. Phys., 2014, 16, 9819–9830 RSC.
- S. L. Clegg and A. S. Wexler, J. Phys. Chem. A, 2011, 115, 3393–3460 CrossRef CAS PubMed.
- R. A. Rajewski and V. J. Stella, J. Pharm. Sci., 1996, 85, 1142–1169 CrossRef CAS PubMed.
- C. Coisne, S. Tilloy, E. Monflier, D. Wils, L. Fenart and F. Gosselet, Molecules, 2016, 21, 1748 CrossRef PubMed.
- A. M. J. Rickards, R. E. H. Miles, J. F. Davies, F. H. Marshall and J. P. Reid, J. Phys. Chem. A, 2013, 117, 14120–14131 CrossRef CAS PubMed.
- E. Mikhailov, S. Vlasenko, D. Rose and U. Pöschl, Atmos. Chem. Phys., 2013, 13, 717–740 CrossRef.
- I. Rörig-Dalgaard and S. Svensson, Rev. Sci. Instrum., 2016, 87, 054101 CrossRef PubMed.
- L. Červenka, J. Kubínová, L. Juszczak and M. Witczak, Food Sci. Technol. Int., 2012, 18, 81–91 CrossRef PubMed.
- E. Morillo, M. A. Sánchez-Trujillo, J. R. Moyano, J. Villaverde and M. E. Gómez-Pantoja, PLoS One, 2012, 7, e44137 CrossRef CAS PubMed.
- W. J. Blanford, J. Incl. Phenom. Macrocycl. Chem., 2013, 79, 57–64 CrossRef.
- Q. Geng, J. Xie, X. Wang, M. Cai, H. Ma and H. Ni, J. Agric. Food Chem., 2018, 66, 12198–12205 CrossRef CAS PubMed.
- X. Wang and M. L. Brusseau, Environ. Sci. Technol., 1993, 27, 2821–2825 CrossRef CAS.
- A. Celebioglu, H. S. Sen, E. Durgun and T. Uyar, Chemosphere, 2016, 144, 736–744 CrossRef CAS PubMed.
- M. Ghadiri, P. M. Young and D. Traini, Pharmaceutics, 2019, 11, 113 CrossRef CAS PubMed.
- R. P. Erickson, G. Deutsch and R. Patil, J. Appl. Genet., 2018, 59, 187–191 CrossRef CAS PubMed.
- H. M. Cabral Marques, J. Hadgraft, I. W. Kellaway and G. Taylor, Int. J. Pharm., 1991, 77, 303–307 CrossRef CAS.
- R. E. H. Miles, A. E. Carruthers and J. P. Reid, Laser Photonics Rev., 2011, 5, 534–552 CrossRef CAS.
- L. Collard, D. Perez-Guaita, B. H. A. Faraj, B. R. Wood, R. Wallis, P. W. Andrew and A. J. Hudson, Sci. Rep., 2017, 7, 8589 CrossRef PubMed.
- L. J. Moore, M. D. Summers and G. A. D. Ritchie, Phys. Chem. Chem. Phys., 2013, 15, 13489 RSC.
- T. C. Preston and J. P. Reid, J. Opt. Soc. Am. B, 2013, 30, 2113–2122 CrossRef CAS.
- T. C. Preston and J. P. Reid, J. Opt. Soc. Am. A, 2015, 32, 2210–2217 CrossRef PubMed.
- H. Kragh, Substantia, 2018, 2, 7–18 Search PubMed.
- M. D. Petters and S. M. Kreidenweis, Atmos. Chem. Phys., 2007, 7, 1961–1971 CrossRef CAS.
- A. Zuend, C. Marcolli, A. M. Booth, D. M. Lienhard, V. Soonsin, U. K. Krieger, D. O. Topping, G. McFiggans, T. Peter and J. H. Seinfeld, Atmos. Chem. Phys., 2011, 11, 9155–9206 CrossRef CAS.
- G. Ganbavale, A. Zuend, C. Marcolli and T. Peter, Atmos. Chem. Phys., 2015, 15, 447–493 CrossRef.
- A. Marsh, R. E. H. Miles, G. Rovelli, A. G. Cowling, L. Nandy, C. S. Dutcher and J. P. Reid, Atmos. Chem. Phys., 2017, 17, 5583–5599 CrossRef CAS.
- H. S. Morris, A. D. Estillore, O. Laskina, V. H. Grassian and A. V. Tivanski, Anal. Chem., 2016, 88, 3647–3654 CrossRef CAS PubMed.
- A. D. Estillore, H. S. Morris, V. W. Orr, H. D. Lee, M. R. Alves, M. A. Marciano, O. Laskina, Z. Qin, A. V. Tivanski and V. H. Grassian, Phys. Chem. Chem. Phys., 2017, 19, 21101 RSC.
- T. Loftsson, J. Incl. Phenom. Macrocycl. Chem., 2002, 44, 63–67 CrossRef CAS.
- B. Gidwani and A. Vyas, BioMed Res. Int., 2015, 2015, 198268 Search PubMed.
- M. Kuwata, S. R. Zorn and S. T. Martin, Environ. Sci. Technol., 2012, 46, 787–794 CrossRef CAS PubMed.
- J. Wang, J. E. Shilling, J. Liu, A. Zelenyuk, D. M. Bell, M. D. Petters, R. Thalman, F. Mei, R. A. Zaveri and G. Zheng, Atmos. Chem. Phys., 2019, 19, 941–954 CrossRef CAS.
- A. L. Yergey, P. S. Blank, S. M. Cologna, P. S. Backlund, F. D. Porter and A. J. Darling, PLoS One, 2017, 12, e0175478 CrossRef PubMed.
- C. Cai, R. E. H. Miles, M. I. Cotterell, A. Marsh, G. Rovelli, A. M. J. Rickards, Y. Zhang and J. P. Reid, J. Phys. Chem. A, 2016, 120, 6604–6617 CrossRef CAS PubMed.
- B. J. Dennis-Smither, F. H. Marshall, R. E. H. Miles, T. C. Preston and J. P. Reid, J. Phys. Chem. A, 2014, 118, 5680–5691 CrossRef CAS PubMed.
- Y. Liu and P. H. Daum, J. Aerosol Sci., 2008, 39, 974–986 CrossRef CAS.
- W. J. Blanford, M. L. Barackman, T. B. Boving, E. J. Klingel, G. R. Johnson and M. L. Brusseau, Groundwater Monit. Rem., 2001, 21, 58–66 CrossRef CAS.
- G. S. Girolami, J. Chem. Educ., 1994, 71, 962–964 CrossRef CAS.
- A. S. Wexler and S. L. Clegg, J. Geophys. Res., 2002, 107, 4207 CrossRef.
- J. W. Grayson, E. Evoy, M. Song, Y. Chu, A. Maclean, A. Nguyen, M. A. Upshur, M. Ebrahimi, C. K. Chan, F. M. Geiger, R. J. Thomson and A. K. Bertram, Atmos. Chem. Phys., 2017, 17, 8509–8524 CrossRef CAS.
- H.-J. Tong, J. P. Reid, D. L. Bones, B. P. Luo and U. K. Krieger, Atmos. Chem. Phys., 2011, 11, 4739–4754 CrossRef CAS.
- Y. Sonoda, F. Hirayama, H. Arima and K. Uekama, J. Incl. Phenom. Macrocycl. Chem., 2004, 50, 73–77 CrossRef CAS.
- E. Specogna, K. W. Li, M. Djabourov, F. Carn and K. Bouchemal, J. Phys. Chem. B, 2015, 119, 1433–1442 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01385d |
| This journal is © the Owner Societies 2020 |