Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
In situ XAFS of acid-resilient iridate pyrochlore oxygen evolution electrocatalysts under operating conditions†
David L.
Burnett
 a,
Enrico
Petrucco
b,
Andrea E.
Russell
a,
Enrico
Petrucco
b,
Andrea E.
Russell
 c,
Reza J.
Kashtiban
d,
Jonathan D. B
Sharman
b and
Richard I.
Walton
c,
Reza J.
Kashtiban
d,
Jonathan D. B
Sharman
b and
Richard I.
Walton
 *a
*a
aDepartment of Chemistry, University of Warwick, Gibbet Hill Road, Coventry CV4 7AL, UK. E-mail: r.i.walton@warwick.ac.uk
bJohnson Matthey Technology Centre, Blounts Court, Sonning Common, Reading, RG4 9NH, UK
cDepartment of Chemistry, University of Southampton, University Road, Southampton SO17 1BJ, UK
dDepartment of Physics, University of Warwick, Gibbet Hill Road, Coventry CV4 7AL, UK
First published on 18th May 2020
Abstract
Pyrochlore iridates (Na,Ca)2−xIr2O6·H2O are acid-stable electrocatalysts that are candidates for use in electrolysers and fuel cells. Ir LIII-edge X-ray absorption fine structure spectroscopy in 1 M H2SO4 at oxygen evolution conditions suggests the involvement of the electrons from the conduction band of the metallic particles, rather than just surface iridium reacting.
Acid-stable electrocatalysts are sought after for application in polymer electrolyte membrane (PEM) devices, such as electrolysers for water splitting1 and in fuel cells where they can provide a buffer to counter the corrosion of the carbon support at extremes of potential.2 The acid electrolyte in these PEM devices provides advantages over alkali systems, with high charge density and no detrimental effects of carbonate contamination.3 The dioxides of ruthenium and of iridium, both with the rutile structure, have been proven to be both active and robust catalysts for the oxygen evolution reaction (OER) in these situations.4 The combination of the two precious metals in a ternary mixed oxide has been used to temper the high reactivity of ruthenium, which can be dissolved under operating conditions, with the greater stability of iridium.5 In the past few years a number of other ruthenium and iridium oxides have been studied as acid resilient electrocatalysts with the purpose of discovering new more active catalysts as well including partner base metals to lower the concentration of the precious metals, making more economically viable materials. This includes mixed rutile phases, such as Cr0.6Ru0.4O2,6 perovskites, such as SrRuO3,7 Sr1−xNaxRuO3,8 Ba2MIrO6 (M = Y, La, Ce, Pr, Nd, Tb),9 and Sr2MIrO6 (M = Fe, Co),10 and pyrochlores such as Y2Ru2O7,11 Y1.85Zn0.15Ru2O7−δ,12 and A2Ru2O7 (A = Yb, Gd, Nd).13 In these materials the non-precious metal cation stabilises the crystal structures of the multinary compositions, allowing access to higher oxidation states of Ru and Ir than seen in binary oxides. In our own work we studied the pyrochlores Bi2Ir2O714 and (Na,Ce)2(Ru1−xIrx)O715 and showed them to be robust electrocatalysts, with the latter showing activity and stability modulated by the Ru
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ir ratio.
Ir ratio.
The mechanism of action of the precious-metal oxide electrocatalysts is still under consideration, with many of the conclusions indirectly inferred from electrochemical data,16 rather than from direct probes of atomic structure. Hillman et al. used X-ray absorption fine structure (XAFS) spectroscopy to study the local iridium environment on deposited iridium oxide films upon redox cycling in neutral and alkaline aqueous condition.17 That work, carried out over a rather limited potential range short of OER conditions, proposed a scenario by which the iridium atoms respond by a two-site reaction, where two types of active sites, which have distinct local structure and electrochemical response, have distinct redox potentials. For (Na,Ce)2(Ru1−xIrx)O7 we used in situ XAFS to monitor change of Ir and Ru oxidation state upon application of potential into the OER regime and used the X-ray absorption near edge structure (XANES) to track metal oxidation state, revealing a cooperative response of the two metals under electrocatalytic conditions.15 In this communication we report application of this methodology to the pyrochlore system (Na,Ca)2−xIr2O6·H2O18 and consider the extended X-ray absorption fine structure (EXAFS) to quantify local atomic structure in situ with electrocatalysis at potentials associated with OER. We were interested to study a pure iridate that may offer long-term stability, since the loss of ruthenium remains an issue even in these multinary oxides. In addition, with only a single precious metal to consider we aimed to obtain definitive structural information as a function of applied potential.
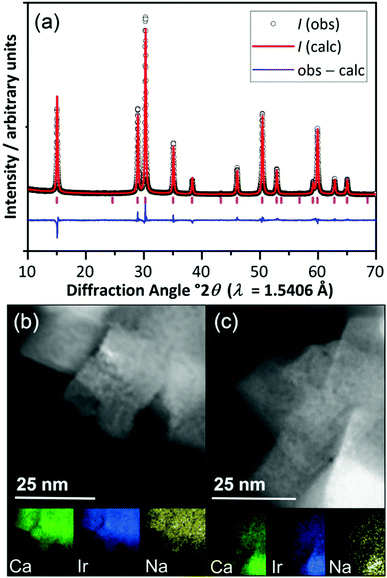
The pyrochlore material (Na,Ca)2−xIr2O6·H2O was prepared by a hydrothermal crystallisation directly from CaO2, Na2O2 and IrCl3·5H2O in 10 M NaOH solution at 240 °C (ESI†), and was characterised using powder X-ray diffraction (XRD) and scanning transmission electron microscopy (STEM), Fig. 1. Scherrer analysis of the diffraction profile gave an average crystallite domain size of 36.2 ± 2.4 nm, consistent with the STEM imaging, while lowering the synthesis temperature to 170 °C gave a second sample that consisted of smaller crystallite sizes (11.2 ± 1.9 nm by Scherrer analysis, ESI†). Surface areas, measured by nitrogen adsorption isotherms and the BET method for the two samples were 7.2 m2 g−1 and 62.7 m2 g−1, respectively, consistent with the relative dimensions of crystallites assuming no significant agglomeration (as confirmed by STEM images). The Rietveld method was used to refine chemical composition and this gave empirical formula (Ca0.70Na0.24)2Ir2O6·H2O, for the most crystalline sample with the crystal water content verified using thermogravimetric analysis (ESI†). Using the refined crystal structure model, the bond valence sum method gave an Ir oxidation state of +4.5, not inconsistent with the value expected by charge balance of +4.4.
Prior to in situ EXAFS measurements, ex situ XANES spectra were recorded at the Ir LIII-edge to determine the average oxidation state of Ir in the pyrochlore, by comparison to the reference materials IrCl3, IrO2 and BaNa0.5Ir0.5O3−δ, that contain iridium in oxidation state +3, +4 and 4.9, respectively, Fig. 2. This shows the iridium to be in average oxidation state of +4.5, consistent with the results from crystallography and also earlier work on a material with similar composition but prepared by a different method.18 The XANES measurements made in situ were similarly analysed (see below) and an important, immediate conclusion from these data is that there is negligible loss of iridium into solution with applied potential in 1 M H2SO4 solution, since the white line intensity of the raw data was not seen to diminish during the course of the experiment (see ESI†).
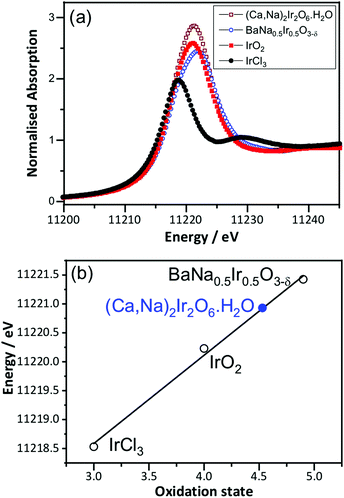 | ||
| Fig. 2 (a) Room temperature Ir LIII-edge XANES spectra of (Ca0.70Na0.24)2Ir2O6·H2O and reference materials and (b) oxidation state calibration graph, with the white line maximum used. | ||
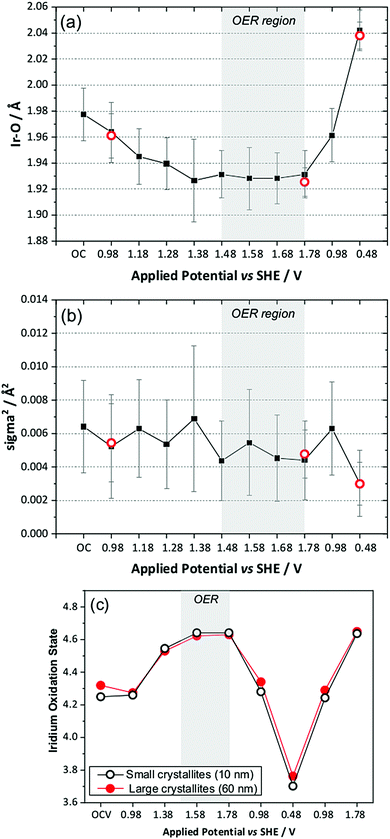
The in situ EXAFS data were analysed to obtain quantitative information about the Ir local environment. A single-shell fit was performed to focus on the Ir–O contribution to the spectrum, and typical fits to the spectra, and their associated Fourier transforms are shown in Fig. 3 for data measured prior to application of potential and at the highest potential, 1.78 V vs. standard hydrogen electrode (SHE). Fitted EXAFS parameters from these spectra are presented in ESI.† For the highly crystalline sample of the pyrochlore, EXAFS spectra were successfully recorded and analysed in a sequence of applied voltage steps, up to 1.78 V, and then upon reversal of potential to a lower than initial starting value. Fig. 4 summarises the structural information obtained from fitting the spectra and full details are provided in the ESI.† These results highlight the gradual shortening of Ir–O distance up to 1.48 V, the onset of OER, reaching constant value during OER and then lengthening upon reversal of potential, Fig. 4a. A shorter average Ir–O distance implies oxidation of the iridium. Meanwhile, the Debye–Waller factor essentially shows no change in magnitude over the whole process, Fig. 4b. The iridium oxidation state can be quantified by the shift in edge position, as shown in Fig. 4c, and this measurement was carried out in a separate experiment on materials of two different particle sizes. We can thus conclude that the iridium, on average, increases in oxidation state by 0.5 units under OER conditions and that this is independent of the particle size (and surface area) of the material, despite the greater proportion of available iridium expected for the higher surface area sample.
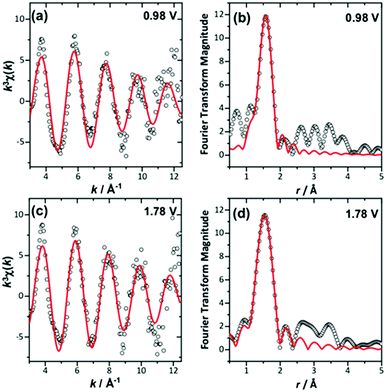 | ||
| Fig. 3 Single-shell fits of k3-weighted EXAFS (left), with Fourier transforms (right) from (Ca0.70Na0.24)2Ir2O6·H2O at (a) and (b) 0.98 V and (c) and (d) maximum applied potential. | ||
We also compared the oxidation state shift from XANES with that derived from the Ir–O bond distance using the bond valence sum method, and this showed essentially the same behaviour with applied potential, thus giving independent verification of the changes in average oxidation state seen in situ (ESI†).
To understand the changing local structure of iridium in the pyrochlore during operation as an electrocatalyst we consider the models proposed by Hillman et al. in their study of iridium oxide films.17 In that work it was observed that the Debye–Waller factor of the Ir–O shell showed an increase upon iridium oxidation (albeit below potentials needed to reach OER conditions), which was reconciled as due to a two-site bond model for redox, in which two iridium species responded differently to applied potential to give a greater static disorder contribution to the Debye–Waller factor. An alternative model is one in which all iridium atoms in the sample respond simultaneously to the applied potential such that the Ir–O bond distance of all are shortened by the same amount with no increase in static disorder. This can be explained by a single-site band model whereby electrons are removed not just from surface sites, but from the conduction band of the metallic particles. The observed behaviour of the pyrochlore is entirely consistent with this idea. Independent verification of this model comes from study of the sample with higher surface area, smaller crystallite domain size, which shows no greater extent of iridium oxidation, despite the ten-fold increase in specific surface area. Thus we propose that the iridate pyrochlores show redox behaviour different to the previously studied iridium oxide films: this could be due to the different local structure of the materials since the films were structurally disordered, being hydrated and low density forms of iridium oxide,17 rather than the well-defined, crystalline particles that we have studied.
Conclusions
We have shown that in situ XAFS (XANES and EXAFS) can be recorded from electrocatalysts operating under realistic conditions to extract quantitative structural information that can be used to probe mechanism of their operation. This method could be applied to other families of oxide materials currently emerging as acid-stable catalysts in important contemporary energy-related applications. For the pyrochlore studied here, we have shown how the bulk metallic character of the oxide particles plays an important role in their mode of operation, with electrons from the conduction band of the oxide being extracted to bring about OER. Complementary cyclic voltammetry (see Fig. S3, ESI†) shows only one redox feature in the potential window of the in situ XAFS experiment that would correspond to oxidation/reduction or Ir4+/Ir5+. The surface reactivity must clearly also hold the key to catalysis properties since this is where the water interacts with the catalyst surface, and where the splitting of water and release of oxygen takes place, but the transport of charge from the bulk particle is an important aspect of the overall mechanism. In multinary oxides, such as the pyrochlore studied here, the role of the partner non-precious-metal cations may also be important in providing charge balance at electrocatalysis conditions, which may explain their different mode of operation compared to binary precious-metal oxides. More mechanistic studies on other members of the pyrochlore family would give a greater insight into this idea. Further work is also needed to understand the long-term stability of the pyrochlores under operating conditions, and their application in real devices, which will be topic of forthcoming publications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Johnson Matthey and the EPSRC (University of Warwick Doctoral Training account EP/K503204/1) for providing funds for a PhD studentship for DLB. RIW thanks the Royal Society for the award of an industry fellowship with Johnson Matthey (2015–2019). We are grateful to Diamond Light Source for provision of beamtime at B18 (SP11646-2) and we thank Dr Diego Gianolio and Turgut Sonmez for their assistance with running the experiments there. Some of the equipment used in this work was provided by the University of Warwick's Research Technology Platforms. The in situ XAS cell was designed by Peter W. Richardson and constructed by Alan Glass (University of Southampton). The research data underpinning this article can be accessed at: http://wrap.warwick.ac.uk/135296/.Notes and references
- M. Carmo, D. L. Fritz, J. Merge and D. Stolten, Int. J. Hydrogen Energy, 2013, 38, 4901–4934 CrossRef CAS.
- W. Gu, R. N. Carter, P. T. Yu and H. A. Gasteiger, ECS Trans., 2007, 11, 963–973 CAS.
- A. Kraytsberg and Y. Ein-Eli, Energy Fuels, 2014, 28, 7303–7330 CrossRef CAS.
- J. Yu, Q. J. He, G. M. Yang, W. Zhou, Z. P. Shao and M. Ni, ACS Catal., 2019, 9, 9973–10011 CrossRef CAS.
- (a) I. M. Kodintsev and S. Trasatti, Electrochim. Acta, 1994, 39, 1803–1808 CrossRef CAS; (b) O. Kasian, S. Geiger, P. Stock, G. Polymeros, B. Breitbach, A. Savan, A. Ludwig, S. Cherevko and K. J. J. Mayrhofer, J. Electrochem. Soc., 2016, 163, F3099–F3104 CrossRef CAS.
- Y. C. Lin, Z. Q. Tian, L. J. Zhang, J. Y. Ma, Z. Jiang, B. J. Deibert, R. X. Ge and L. Chen, Nat. Commun., 2019, 10, 162 CrossRef PubMed.
- B. J. Kim, D. F. Abbott, X. Cheng, E. Fabbri, M. Nachtegaal, F. Bozza, I. E. Castelli, D. Lebedev, R. Schaublin, C. Coperet, T. Graule, N. Marzari and T. J. Schmidt, ACS Catal., 2017, 7, 3245–3256 CrossRef CAS.
- M. Retuerto, L. Pascual, F. Calle-Vallejo, P. Ferrer, D. Gianolio, A. G. Pereira, A. Garcia, J. Torrero, M. T. Fernandez-Diaz, P. Bencok, M. A. Pena, J. L. G. Fierro and S. Rojas, Nat. Commun., 2019, 10, 2041 CrossRef PubMed.
- O. Diaz-Morales, S. Raaijman, R. Kortlever, P. J. Kooyman, T. Wezendonk, J. Gascon, W. T. Fu and M. T. M. Koper, Nat. Commun., 2016, 7, 12363 CrossRef CAS PubMed.
- R. H. Zhang, N. Dubouis, M. Ben Osman, W. Yin, M. T. Sougrati, D. A. D. Corte, D. Giaume and A. Grimaud, Angew. Chem., Int. Ed., 2019, 58, 4571–4575 CrossRef CAS PubMed.
- J. Kim, P. C. Shih, K. C. Tsao, Y. T. Pan, X. Yin, C. J. Sun and H. Yang, J. Am. Chem. Soc., 2017, 139, 12076–12083 CrossRef CAS PubMed.
- Q. Feng, Q. Wang, Z. Zhang, Y. Y. H. Xiong, H. Y. Li, Y. Yao, X. Z. Yuan, M. C. Williams, M. Gu, H. Chen, H. Li and H. J. Wang, Appl. Catal., B, 2019, 244, 494–501 CrossRef CAS.
- D. F. Abbott, R. K. Pittkowski, K. Macounova, R. Nebel, E. Marelli, E. Fabbri, I. E. Castelli, P. Krtil and T. J. Schmidt, ACS Appl. Mater. Interfaces, 2019, 11, 37748–37760 CrossRef CAS PubMed.
- K. Sardar, S. C. Ball, J. D. B. Sharman, D. Thompsett, J. M. Fisher, R. A. P. Smith, P. K. Biswas, M. R. Lees, R. J. Kashtiban, J. Sloan and R. I. Walton, Chem. Mater., 2012, 24, 4192–4200 CrossRef CAS.
- K. Sardar, E. Petrucco, C. I. Hiley, J. D. B. Sharman, P. P. Wells, A. E. Russell, R. J. Kashtiban, J. Sloan and R. I. Walton, Angew. Chem., Int. Ed., 2014, 53, 10960–10964 CrossRef CAS PubMed.
- R. L. Doyle, I. J. Godwin, M. P. Brandon and M. E. G. Lyons, Phys. Chem. Chem. Phys., 2013, 15, 13737–13783 RSC.
- A. R. Hillman, M. A. Skopek and S. J. Gurman, Phys. Chem. Chem. Phys., 2011, 13, 5252–5263 RSC.
- K. Sardar, J. Fisher, D. Thompsett, M. R. Lees, G. J. Clarkson, J. Sloan, R. J. Kashtiban and R. I. Walton, Chem. Sci., 2011, 2, 1573–1578 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Further materials characterisation data. See DOI: 10.1039/d0cp01378a |
| This journal is © the Owner Societies 2020 |

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif)