 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Direct magnetic-field dependence of NMR chemical shift†
Anu M.
Kantola
 a,
Perttu
Lantto
a,
Perttu
Lantto
 a,
Ivo
Heinmaa
b,
Juha
Vaara
a,
Ivo
Heinmaa
b,
Juha
Vaara
 a and
Jukka
Jokisaari
a and
Jukka
Jokisaari
 *a
*a
aNMR Research Unit, University of Oulu, P.O. Box 3000, FI-90014, Finland. E-mail: Jukka.Jokisaari@oulu.fi
bNational Institute of Chemical Physics and Biophysics, Akadeemia tee 23, EE-12618 Tallinn, Estonia
First published on 6th April 2020
Abstract
Nuclear shielding and chemical shift are considered independent of the magnetic-field strength. Ramsey proposed on theoretical grounds in 1970 that this may not be valid for heavy nuclei. Here we present experimental evidence for the direct field dependence of shielding, using 59Co shielding in Co(acac)3 [tris(acetylacetonate)cobalt(III)] as an example. We carry out NMR experiments in four field strengths for this low-spin diamagnetic Co(III) complex, which features a very large and negative nuclear shielding constant of the central Co nucleus. This is due to a magnetically accessible, low-energy eg ← t2g orbital excitation of the d6 system. The experiments result in temperature-dependent magnetic-field dependence of −5.7 to −5.2 ppb T−2 of the 59Co shielding constant, arising from the direct modification of the electron cloud of the complex by the field. First-principles multiconfigurational non-linear response theory calculations verify the sign and order of magnitude of the experimental results.
Introduction
Nuclear magnetic resonance (NMR) parameters,1 nuclear shielding, its associated chemical shift, spin–spin coupling and quadrupole coupling, are normally considered independent of the applied magnetic field. Due to the increasing field strengths used in contemporary NMR instrumentation, currently reaching 1.2 GHz proton resonance frequency, the validity of this approximation should be investigated. In 1970, Ramsey2 published a theoretical study predicting a quadratic, O(B02), leading-order dependence on the field strength, B0. Ramsey concluded that “in some molecules, especially where the magnetic shielding is abnormally large, it is possible that the field dependence of the shielding could be large enough to be observable”. Inspired by this prediction, Bendall and Doddrell3 carried out 59Co NMR experiments of diamagnetic cobalt compounds. The authors claimed a field dependence of 59Co shielding constant in Co(15NH3)Cl3 and Co(acac)3, with values −70(30) and −80(50) ppb T−2, respectively. Such Co(III) complexes feature a broad chemical shift range and show a sensitivity of the NMR signal on temperature, pressure and solvent,4 which can be ascribed to the existence of low-lying, magnetically accessible d–d excitations5 at the metal centre and, correspondingly, a large tendency of the electron cloud to accommodate to changing interactions with surroundings.About 25 years later, Manninen and Vaara6 presented a theory and computed from first principles the field-dependence of 59Co shielding in the same compounds, with results that are by an order of magnitude smaller than the experimentally derived values in ref. 3. This effect can be termed direct field dependence, arising from the modification of the molecular electron cloud by the magnetic field. In contrast, the indirect effect results from a slight influence on the orientational distribution of molecules in liquid samples due to the interaction of magnetic field with the anisotropy of the molecular susceptibility, causing incomplete rotational averaging of NMR parameters.7
Further computational work on the direct field dependence of nuclear shielding has been reported at both semi-empirical8,9 and first-principles10–12 levels. The field dependence of spin–spin coupling has been elaborated in ref. 13 and 14. So far, the only both experimentally observed and theoretically confirmed case of direct field dependence of an NMR parameter is that of 131Xe quadrupole coupling in atomic xenon.15–18 The 131Xe NMR spectrum consists of a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 triplet when the nuclear electric quadrupole moment interacts with a non-vanishing electric field gradient (EFG) at the nuclear site. In this case, the non-zero EFG stems from the slight deformation of the atomic electron cloud induced by the magnetic field.16
3 triplet when the nuclear electric quadrupole moment interacts with a non-vanishing electric field gradient (EFG) at the nuclear site. In this case, the non-zero EFG stems from the slight deformation of the atomic electron cloud induced by the magnetic field.16
In the present work, we report experiments carried out at four magnetic fields, as well as improved first-principles nonlinear response theory computations on the direct field effect on the 59Co shielding in Co(acac)3. We eliminate the difficulty of precise temperature control of the experiments in different NMR instruments by using the gaseous and solution-state 129Xe NMR signal as a chemical shift and temperature reference, respectively.19 Our experiments demonstrate the existence of the direct field dependence of shielding and, hence, verify the prediction by Ramsey.
Results and discussion
Due to the requirement of time-reversal symmetry, terms in the molecular energy expression have to contain the nuclear spin IK and external magnetic field B0 appearing to even total power.2,6 The nuclear Zeeman term in the standard NMR spin Hamiltonian1 is O(I1KB10) (total power 2) and the next term in increasing powers of the magnetic field is O(I1KB03) (total power 4). Consequently, to the leading order, the B0-dependent NMR shielding tensor component σK,αβ for nucleus K can be expressed as2,6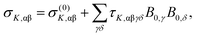 | (1) |
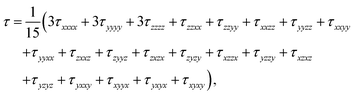 | (2) |
A sample consisting of saturated solution of tris(acetylacetonate)cobalt(III) [Co(acac)3] in CDCl3 and natural xenon gas of about 2 atm was prepared into a 5 mm (o.d.) NMR tube. Resonance frequency of natural abundance gaseous 129Xe (2 atm in a 5 mm tube) was used as an external chemical shift reference for both 59Co and 129Xe resonance frequencies in the solution. Experiments were carried out at four magnetic fields, 18.8, 14.1, 9.4 and 7.0 T, and five temperatures at each field strength, on Bruker Avance III instruments. Following Ramsey, 59Co resonance frequency can be presented in the form
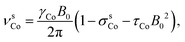 | (3) |
There is a strong temperature dependence of 59Co chemical shift in Co(acac)3, e.g., reported in ref. 20 at +2.79 ppm K−1 in CHCl3 solution. Therefore, one must guarantee that the 59Co frequencies in different magnetic-field instruments are obtained at the same temperature. To this end, we used the 129Xe chemical shift in solution, δsXe, as an internal temperature reference (see ESI†), and ensured that δsCo at each magnetic field corresponds to the same δsXe value. This procedure is based on the extreme sensitivity of δsXe upon temperature19 and is done to gain a precise value for τCo. The resonance frequencies of xenon in gas (g) and in solution (s) can be approximately written as
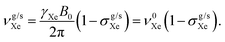 | (4) |
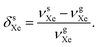 | (5) |
The 59Co resonance frequency relative to the chosen shift reference, xenon gas, is
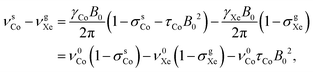 | (6) |
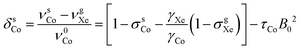 | (7) |
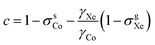 and τCo. The results, obtained at the 129Xe chemical shift values of 200, 202, 205, 206 and 208 ppm, are listed in Table 1 and illustrated in Fig. 1. Fig. 1(b) shows linear dependence of c on temperature. The slope of the line is 2.793 ± 0.007 ppm K−1, corresponding to the temperature coefficient of the 59Co chemical shift in chloroform/xenon solution, in excellent agreement with the value of 2.79 ± 0.02 ppm K−1 reported in ref. 20 for a sample without xenon gas.
and τCo. The results, obtained at the 129Xe chemical shift values of 200, 202, 205, 206 and 208 ppm, are listed in Table 1 and illustrated in Fig. 1. Fig. 1(b) shows linear dependence of c on temperature. The slope of the line is 2.793 ± 0.007 ppm K−1, corresponding to the temperature coefficient of the 59Co chemical shift in chloroform/xenon solution, in excellent agreement with the value of 2.79 ± 0.02 ppm K−1 reported in ref. 20 for a sample without xenon gas.
δ
sXe
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ppm)
(ppm) |
T (K) | c (ppm) | τ Co (ppb T−2) |
|---|---|---|---|
| a 129Xe chemical shift of xenon in the solution, δsXe, is used to approximately detect the temperature T. The given temperatures were determined from the equation given in ref. 19. In this case, the sample contained only D-chloroform and xenon gas. Therefore, the tabulated temperatures may not be correct. One should note that the knowledge of exact temperatures is not essential in this case, but that of the 129Xe chemical shift is. b Parameters c and τCo appearing in eqn (7) are listed for a fit of a series of measurements at different magnetic fields. Each series is performed at a constant value of δsXe. | |||
| 200 | 319.9 | −153932.2 ± 0.2 | −5.2 ± 1.0 |
| 202 | 314.7 | −153946.7 ± 0.2 | −5.4 ± 0.9 |
| 205 | 307.0 | −153968.4 ± 0.2 | −5.5 ± 1.1 |
| 206 | 304.4 | −153979.7 ± 0.2 | −5.6 ± 0.8 |
| 208 | 299.2 | −153990.1 ± 0.2 | −5.7 ± 0.8 |
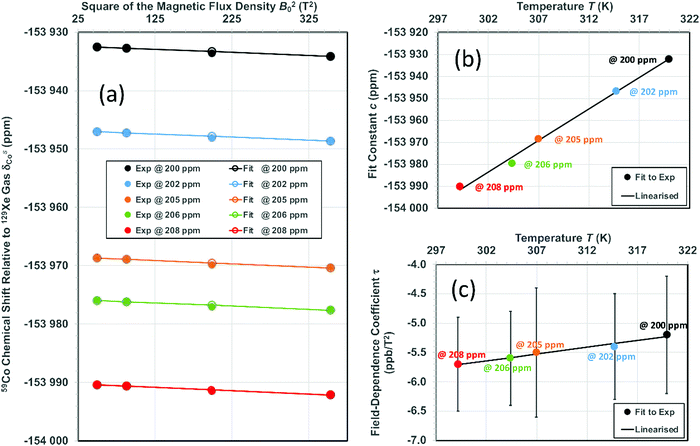 | ||
Fig. 1 (a) 59Co chemical shift relative to 129Xe gas, δsCo, when δsXe is (from top to bottom) 200, 202, 205, 206 and 208 ppm, corresponding to approximate temperatures 319.9, 314.7, 307.0, 304.4 and 299.2 K as given in Table 1. Fit parameters for (b) the field-independent part of the shift, 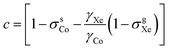 and (c) the leading field-dependence coefficient τCo [see eqn (7)] as functions of temperature. Colour coding is used to indicate corresponding data points in panel (a) and panels (b and c). The error margins resulting from the statistical uncertainty of the fit are in panel (b) smaller (circa ±0.2 ppm) than the used symbols and in (c) circa ±1 ppb T−2. and (c) the leading field-dependence coefficient τCo [see eqn (7)] as functions of temperature. Colour coding is used to indicate corresponding data points in panel (a) and panels (b and c). The error margins resulting from the statistical uncertainty of the fit are in panel (b) smaller (circa ±0.2 ppm) than the used symbols and in (c) circa ±1 ppb T−2. | ||
At this point we may assess the significance of the temperature dependence of σsXe, which we neglected in the above analysis. As this effect does not depend on the external magnetic field, it could be absorbed in the field-independent fitting parameter c in eqn (7). Using the ideal gas law to approximate the number density of a 2 atm Xe gas at room temperature and the temperature-dependent second virial coefficient, σXe,1, of 129Xe shielding constant reported in ref. 22, one can arrive at a (linearized) contribution to the temperature dependence of c amounting to just −0.0019 ppm K−1. This change would be inside the error margins of the present fit results for c and those of the previous experiment of ref. 20.
Another physical influence that should be considered is the correction due to the difference of the bulk magnetic susceptibilities of the chloroform solution, χs, and that of the external xenon gas reference, χr. At the limit of an infinitely long cylindrical sample oriented along B0, the associated chemical shift contribution (in SI units) to eqn (7) equals approximately
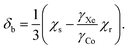 | (8) |
Using the molar susceptibilities χm listed in ref. 24, −58.9 × 10−6 × 4π and −45.5 × 10−6 × 4π cm3 mol−1 for chloroform and xenon, respectively, we obtain χs = −9.19 and χr = −0.02509 ppm, corresponding to δb = −3.07 ppm from eqn (8). This is an additional, magnetic field-independent contribution to the parameter c. We are not aware of data on the temperature dependence of the susceptibility of either chloroform or xenon, which hinders us from accurately evaluating the contribution of the δb term to the temperature dependence of c. Presumably the susceptibility of liquid CHCl3, which is bigger than that of gaseous Xe by three orders of magnitude, dominates also the temperature dependence of δb. Ref. 25 reported a close-to-linear temperature dependence of the relative mass susceptibility of water at temperatures in the liquid range as χ(T)/χ(20C) ≈ 1 + 1.39 × 10−4 (T – 20C). Using χm(H2O) = −12.96 × 10−6 × 4π cm3 mol−1,24 hence χ(H2O) = −9.01 ppm, corresponds to 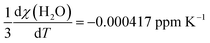 . Presumably the same property for chloroform does not deviate very much from this result for liquid water. Therefore, also the bulk susceptibility effect falls well within the error margins obtained in the present fit of the c parameter.
. Presumably the same property for chloroform does not deviate very much from this result for liquid water. Therefore, also the bulk susceptibility effect falls well within the error margins obtained in the present fit of the c parameter.
Fig. 1 shows the principal result of the paper: the field-dependence coefficient τ resulting from the slope of 59Co shift with respect to B02 [Fig. 1(a)]. The magnitude of the field dependence is around −5.5 ± 0. 9 ppb T−2, which is significant in view of the NMR instruments with 1.2 GHz proton frequency (28.2 T field strength) in production use soon. This result deviates clearly from the experimental data reported by Bendall and Doddrell,3 where a distinctly larger magnitude of the field dependence, at τ = −80 ± 50 ppb T−2, was found. The underlying reasons of the difference include the limitation of the 40-year-old experiment to the modest maximum field of 2.1 T in contrast to the 18.8 T field strength used in the present work. In a similar vein, the precise temperature control enabled by using 129Xe signal in solution is instrumental to the present success. Despite the sizable statistical error margins, τ from the present measurements shows evidence of temperature dependence: its magnitude decreases with temperature with a least-squares fitted slope of 2.29 × 10−2 ppb T−2 K−1.
Theoretical electronic-structure formulation of the field-dependence tensor τK was presented in the form of four distinct linear and nonlinear response functions26 in ref. 6:
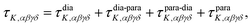 | (9) |
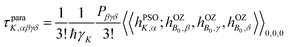 | (10) |
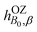 etc. the corresponding components of the Zeeman interaction of the orbital motion of the electrons with the external field,27 as static perturbations. The symbol Pβγδ denotes a sum over all six permutations of its three indices.
etc. the corresponding components of the Zeeman interaction of the orbital motion of the electrons with the external field,27 as static perturbations. The symbol Pβγδ denotes a sum over all six permutations of its three indices.
Computations of eqn (9) were carried out for Co(acac)3 in 2004 using Hartree–Fock (HF) and density-functional theory (DFT) levels.6 The result of HF calculation, τparaCo ∼ O(1) ppb T−2 agrees with the experiment carried out presently. In view of the importance of electron correlation effects on high-order valence-like response properties such as τ a question remains whether this agreement is coincidental. Since then, cubic response functions at electron-correlated ab initio levels have become feasible for systems of the present size in the DALTON software.28 We employ the multiconfigurational self-consistent field (MCSCF) level of theory29 to address this question here, on models of Co(acac)3 described in the ESI.†
All the tensorial components of the four terms in eqn (9) were computed using HF and MCSCF response theory. In the latter, restricted active-space (RASSCF)-type wave functions30 correlating 18, 32 or 38 electrons [denoted RASSCF (18/32/38 el.)] were used for a truncated molecular model. The ESI† is referred to for details of the used MCSCF wave functions (Table S7, ESI†) and basis sets. For calculating the magnetic properties of a low-gap Co(acac)3 complex, multireference-type wave functions are preferred over single configuration-based methods such as DFT, second-order many-body perturbation theory, or coupled-cluster theory at low excitation level.31 Even the present truncated model of Co(acac)3 is currently prohibitively large for beyond-singles and doubles (CCSD) coupled-cluster theory-based nonlinear response theory calculations.32
Table 2 lists the computational results for the dominating τpara contribution to the field-dependence coefficient, as well as the total τ (the latter using three of the methods: HF, RASSCF (32 el.) and DFT/BHandHLYP33,34). While the results depend on the method used, both HF and the different RASSCF wave functions lead to τ in an order-of-magnitude agreement with the experimental datum, with the largest result, −1.4 ppb T−2 obtained at the HF level. Increasing the number of correlated electrons tends to lower the final result as evidenced by the 10% decrease between RASSCF (18 el.) and RASSCF (32 el.), and further to RASSCF (38 el.), whereas increasing the virtual orbital space, e.g., from the RASSCF (32 el.) to the RASSCF’ (32 el.) wave function has the opposite effect. In contrast, the DFT result is at a much smaller value. The small difference between the τpara and τtotal results reassures us of the earlier finding that the 4th-order term dominates in the field dependence in Co(acac)3. The small contributions of the other terms are listed in Table S9 of the ESI.†
The present calculations of τ at optimised, static molecular geometries lead to negative field-dependence coefficient of 59Co nuclear shielding constant in agreement with the experimental findings, and at the ab initio level similar order of magnitude of the coefficient as in the experimental data. At the same time, the new calculations result also in smaller τpara than what was found earlier6 at the HF level. The well-known sensitivity of 59Co chemical shift on temperature in this complex suggests that both thermal rovibrational and solvation effects, which are neglected in the present computations, may significantly influence τ. To investigate this possibility, we repeated the HF calculations of τpara in modified models obtained by varying the Co–O bond distance from the value 1.885 Å of the optimised truncated model (for reference, 1.880 Å was obtained for the optimised full model). The results (Fig. 2 and Table S10 in the ESI†) indicate, expectedly, a strong dependence of τ on the Co–O bond lengths of the coordination shell of the Co ion. Indeed, coincidence with the range of present experimental data for τ is reached at the HF level by relatively modest modification of r(Co–O).
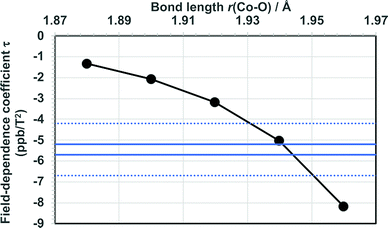 | ||
| Fig. 2 Calculated field-dependence coefficient τ as a function of the Co–O bond length in Co(acac)3. The bonds are symmetrically extended, maintaining the D3 point-group symmetry. The range of present experimental data is indicated by horizontal lines (error margins as dotted lines). The bond length in the results of Table 2 is 1.885 Å. | ||
In addition to the direct magnetic field effect, molecular properties may also depend upon the indirect magnetic-field effect.7 It arises from partial alignment of molecules because of the interaction of the anisotropy of the molecular susceptibility with the magnetic field. In partially aligned molecules, the NMR properties become dependent on the orientational order parameter.35 In the case of Co(acac)3, the 59Co chemical shift, when excluding the direct field effect, can be presented in the form36,37
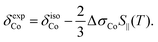 | (11) |
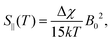 | (12) |
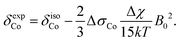 | (13) |
Conclusions
We have both experimentally and computationally verified the 50-year-old prediction of Ramsey of direct magnetic-field dependence of nuclear magnetic shielding and the associated NMR chemical shift. The present experiments on 59Co NMR in Co(acac)3 resulted in significant field-dependence coefficient by using a range of high-field instruments and both external and internal 129Xe reference in solution-state experiments. The external xenon gas, with its well-known and modest temperature and pressure dependence of the NMR frequency acted as the shift reference for 59Co. On the other hand, the xenon resonance in the liquid state is extremely sensitive to the experimental conditions, which was used to adjust the temperature to constant value in NMR instruments of different field strengths. This way, the effects due to the temperature dependence of the 59Co signal could be effectively eliminated. Similarly, the bulk magnetic susceptibility and field-induced molecular orientation (the indirect field dependence) were shown to be insignificant in the present results.Ab initio nonlinear response theory computations confirmed the order of magnitude of the field dependence and indicated its strong dependence on the coordination distance of the Co(III) ion, as expected based on the well-known temperature dependence of the 59Co chemical shift. The magnitude of the observed field dependence in Co(acac)3, circa −5.5 ppb T−2, corresponds to an experimentally significant frequency shift in, e.g., the 28.2 T field of a 1.2 GHz 1H frequency instrument, and the phenomenon is expected to gain importance in pursuit of even higher fields and resolution in contemporary NMR. The verification of the fundamental field dependence of shielding and chemical shift adds a new parameter to the panoply of NMR observables, for which one can envision applicability in future high-field experiments designed to specifically make use of the explicit field dependence. Questions for future work remain also in finding the specific molecular characteristics that predict a significant field dependence.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support has been obtained from the University of Oulu (Kvantum Institute), and the Academy of Finland (projects 285666 and 296292). Computational resources due to CSC (Espoo, Finland) and the Finnish Grid and Cloud Infrastructure project (persistent identifier urn:nbn:fi:research-infras-2016072533), were used. IH was supported by European Regional Development Fund (TK134).References
- M. H. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, Wiley, 2nd edn, 2008 Search PubMed.
- N. F. Ramsey, Phys. Rev. A: At., Mol., Opt. Phys., 1970, 1, 1320 CrossRef.
- M. R. Bendall and D. M. Doddrell, J. Magn. Reson., 1979, 33, 659 CAS.
- N. Juranic, Coord. Chem. Rev., 1989, 96, 253 CrossRef CAS.
- K. Kanda, H. Nakatsuji and T. Yonezawa, J. Am. Chem. Soc., 1984, 106, 5888 CrossRef CAS.
- P. Manninen and J. Vaara, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 69, 022503 CrossRef.
- J. Jokisaari, A. M. Kantola and J. Vaara, J. Magn. Reson., 2017, 281, 1 CrossRef CAS PubMed and references therein.
- D. M. Doddrell, D. T. Pegg and M. R. Bendall, Aust. J. Chem., 1979, 32, 1 CrossRef CAS.
- K. Endo and K. Yamamoto, J. Phys. Soc. Jpn., 1995, 64, 4053 CrossRef CAS.
- A. Boucekkine, G. Boucekkine-Yaker, M. Nait Achour and G. Berthier, THEOCHEM, 1988, 166, 109 CrossRef.
- J. Vaara, P. Manninen and J. Lounila, Chem. Phys. Lett., 2003, 372, 750 CrossRef CAS.
- J. Boyd, G. I. Pagola, M. C. Caputo, M. B. Ferraro and P. Lazzeretti, J. Chem. Theory Comput., 2009, 5, 1343 CrossRef CAS PubMed.
- W. T. Raynes and S. J. Stevens, Magn. Reson. Chem., 1992, 30, 124 CrossRef CAS.
- P. Manninen, PhD thesis, University of Oulu, Finland, 2004.
- T. Meersmann and M. Haake, Phys. Rev. Lett., 1998, 81, 1211 CrossRef CAS.
- J. Vaara and P. Pyykkö, Phys. Rev. Lett., 2001, 86, 3268 CrossRef CAS PubMed.
- P. Manninen, J. Vaara and P. Pyykkö, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 043401 CrossRef.
- N. Abuzaid, A. M. Kantola and J. Vaara, Mol. Phys., 2013, 111, 1390 CrossRef CAS.
- J. Saunavaara and J. Jokisaari, J. Magn. Reson., 2006, 180, 58 CrossRef CAS PubMed.
- M. Kanakubo, T. Uda, H. Ikeuchi and G. P. Satô, J. Solutions Chem., 1998, 27, 645 CrossRef CAS.
- C. J. Jameson, A. K. Jameson and S. M. Cohen, J. Chem. Phys., 1973, 59, 4540 CrossRef CAS.
- C. J. Jameson, A. K. Jameson and S. M. Cohen, J. Chem. Phys., 1975, 62, 4224 CrossRef CAS.
- J. Jokisaari, Prog. Nucl. Magn. Reson. Spectrosc., 1994, 26, 1 CrossRef CAS.
- Diamagnetic Susceptibility of Selected Organic Compounds and Magnetic Susceptibility of the Elements and Inorganic Compounds, in CRC Handbook of Chemistry and Physics, Internet Version 2006, ed. D. R. Lide, Taylor and Francis, Boca Raton, FL, 2006 Search PubMed.
- J. S. Philo and W. M. Fairbank, J. Chem. Phys., 1980, 72, 4429 CrossRef CAS.
- J. Olsen and P. Jørgensen, J. Chem. Phys., 1985, 82, 3235 CrossRef CAS.
- P. Atkins and R. Friedman, Molecular Quantum Mechanics, Oxford University Press, Oxford, 5th edn, 2011 Search PubMed.
- Dalton, a Molecular Electronic Structure Program, Release 2016.1, see http://daltonprogram.org; K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansik, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. Rybkin, P. Salek, C. C. M. Samson, A. Sánchez de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, The Dalton quantum chemistry program system, WIREs Comput. Mol. Sci., 2014, 4, 269 CrossRef CAS PubMed.
- D. Jonsson, P. Norman and H. Ågren, J. Chem. Phys., 1996, 105, 6331 Search PubMed.
- J. Olsen, B. O. Roos, P. Jørgensen and H. J. A. Jensen, J. Chem. Phys., 1988, 89, 2185 CrossRef CAS.
- T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic Structure Theory, John Wiley & Sons, Chichester, 2000 Search PubMed.
- C. Hättig, O. Christiansen and P. Jørgensen, Chem. Phys. Lett., 1998, 282, 139 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- J. W. Emsley and J. C. Lindon, NMR Spectroscopy Using Liquid Crystal Solvents, Pergamon Press, 1975 Search PubMed.
- J. Lounila and J. Jokisaari, Prog. Nucl. Magn. Reson. Spectrosc., 1982, 15, 249 CrossRef CAS.
- J. Jokisaari, Encyclopedia of NMR Spectroscopy, 1996, vol. 1, p. 83 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of experiments and computations. See DOI: 10.1039/d0cp01372b |
| This journal is © the Owner Societies 2020 |
