Solvation of coronene oligomers by para-H₂ molecules: the effects of size and shape

Abstract

The stepwise solvation of various cationic coronene oligomers by para-hydrogen (p-H₂) molecules was computationally investigated using a united-atom model for the p-H₂ molecules and the Silvera–Goldman potential, together with a polarizable description for the interaction with the hydrocarbon molecules. A survey of the energy landscape for oligomers containing between 1 and 4 coronene molecules and possible different conformers was carried out using standard global optimization, the hydrocarbon complex being kept as rigid. The most stable structures provided the starting configuration of systematic path-integral molecular dynamics simulations at 2 K. The variations of the geometric and energetic properties of the solvation shell were determined with increasing number of para-hydrogen molecules. The relative stability of the solvation shell is generally found to be more robustly determined by the energy increment (or dissociation energy) than by geometrical indicators, especially when the oligomers have less ordered structures. In agreement with recent mass spectrometry experiments, the size at which the first solvation shell is complete is found to vary approximately linearly with the oligomer size when the coronene molecules stack together, with a slope that is related to the offset between two successive molecules.

---

1 Introduction

Polycyclic aromatic hydrocarbons (PAHs) provide very efficient models for graphene-like structures. Adsorption of small molecules on aromatic surfaces is of fundamental importance for the interaction between gas molecules and carbon structures, e.g. in the intercalation between graphene layers¹ or in the adsorption into nanotubes^2–5 or fullerenes.^4,6 In this respect it is, in turn, also relevant for efficient energy storage problems, catalytic processes or for developing molecular sensors.

Another aspect of the interest in PAHs comes from their importance in combustion science as precursors of soot particles.^7,8 They are also notorious candidates in the astrophysical context to explain the possible formation of H₂ through surface recombination of atomic hydrogen^9–11 as well as some of the observed astronomical features in the interstellar medium known as diffuse interstellar bands¹² and aromatic infrared bands.^13,14

Except when they contain five- or seven-membered rings, PAH molecules are usually planar and do not assemble isotropically but tend to stack parallel to each other. However, and as in bulk graphite, there are different ways for the carbon flakes to assemble, either by rotating or by shifting, displacement parallel to the molecular planes being associated with only moderate energy barriers of a fraction of eV.¹⁵ In the case of the neutral coronene dimer, earlier theoretical studies generally suggested that the shifting pattern leads to the most stable structure (called ‘parallel displaced’), although the details of the horizontal displacement vary depending on the method.^16–24 In a computational study based on empirical potential modeling and rigid molecules, the opposite conclusion was reached for this system, which was predicted to be more stable as a rotated stack obtained by aligning the perpendicular axis of the two molecules.²⁵

Despite seemingly being chemically simple, the structure of PAH oligomers thus appears not entirely trivial, and this situation results from the interplay between delocalized dispersion forces and the multipolar distribution on rather large molecules. Already for benzene, the precise structure of the dimer has long remained a challenge for quantum chemical methods.²⁶ Beyond their fundamental interest, PAH oligomers can also exhibit the so-called singlet fission phenomenon in which a singlet electronic excited state decays into two triplet states localized on each monomer, thereby opening the way to efficient energy harvesting applications.²⁷ Singlet fission is highly sensitive to the oligomer conformation, hence it is important to characterize these structures as accurately as possible.

In the gas phase, only few experimental approaches are available to achieve such a characterization. Spectroscopic studies have been attempted under the cryogenic conditions of helium nanodroplets for the perylene dimer,²⁸ and although they support the parallel displaced motif they do not provide direct quantitative information about the structure. Femtosecond strong-field ionization measurements leading to Coulomb explosion monitored by angular map imaging could recently be achieved for the tetracene dimer, ruling out configurations in which the molecular planes are perpendicular to each other.²⁹ Very recently, electron diffraction was conducted for pyrene clusters under superfluid helium droplets, confirming the stacking between monomers at an interlayer distance of 3.5 Å in the dimer but indicating that molecules in the trimer were no longer completely parallel.³⁰

Alternatively, the structure of coronene oligomers was experimentally investigated in a more indirect way by Goulart and coworkers,³¹ who identified by mass spectrometry their propensity to attach para-hydrogen molecules. More precisely, variations in ion abundances were interpreted to infer the magnitude of the displacement between two coronene molecules, which was estimated to be about twice as large as the offset between graphene layers in conventional graphite.²² Similar measurements on fullerenes, using para-hydrogen³² or helium as solvents,^33,34 were found to be particularly insightful in unravelling the type of packing adopted by the solvation layer, and in particular its commensurate nature.

In earlier work, we computationally examined the solvation of various carbonaceous molecules by para-hydrogen and ortho-deuterium, including coronene and other PAHs ranging from benzene to circumcoronene,³⁵ as well as fullerenes.^36,37 The carbonaceous dopants were modeled at the atomistic level but treated as rigid, the hydrogen molecules being described as pointlike and interacting with each other through the long established Silvera–Goldman (SG) potential.³⁸ The interaction between the dopant and the hydrogen molecules was modeled from a pairwise additive contribution from repulsion and dispersion terms, plus a vectorial polarization term acting on the solvent molecules arising from the multipolar distribution on the dopant set as partial atomic charges. This potential was fitted to reproduce quantum chemistry (QC) results, and in a separate contribution the issue of the most appropriate QC method for such systems was discussed separately.³⁷ After identifying candidate structures using classical global optimization, quantum nuclear effects were subsequently included with path-integral molecular dynamics (PIMD) simulations.

In the present contribution we extend these efforts to the case where the solute system is a cationic coronene oligomer, and attempt to determine the size of the solvation shell and compare it with the experimental conclusions by Goulart and coworkers.³⁴ In doing so, we have found that the purely geometric criteria introduced in our earlier studies (prior to any available experimental data to compare with) were not close enough to the actual way ion abundances are obtained in mass spectrometry, which is more related to the binding energy and the propensity to not thermally dissociate. As was discussed more extensively in the case of the helium solvent coating fullerene³⁹ or PAH cations^40,41 the completion of the first shell is not necessarily accompanied with strong geometrical changes, additional solvent molecules only making the single shell larger, even more molecules being needed to actually start a second well-defined shell. Here we thus examine the notion of solvation shell in the light of both geometric and energetic criteria.

Our PIMD simulations confirm that the energy difference provides a more robust definition of the solvation shell, in that it is sensitive to the adhesion site of additional solvent molecules as well as the possibly already completed character of the first shell. In particular, for coronene molecules in a parallel displaced stacked form, we essentially recover the variations in the solvation shell experimentally determined in mass spectrometry experiments,³¹ despite the offset between molecules being closer to that in graphite.

The article is organized as follows. In Section 2, we summarize the computational methods used to model the solvation of coronene oligomers by para-hydrogen molecules. This includes some details about the potential energy surface already developed for studying the solvation of PAHs and fullerenes by para-H₂,³⁵ as well as the additional description of the structures and models chosen for the cationic coronene oligomers, the global optimization and path-integral molecular dynamics simulations. In Section 3 the results are presented and discussed and some concluding remarks are finally given in Section 4.

2 Methods

Our modeling of cationic coronene oligomers coated by para-hydrogen molecules was performed along the same lines as in our previous work with individual carbonaceous monomers,³⁵ with the notable difference that we now need to describe the detailed atomic structure of the oligomers themselves and their charge distributions.

2.1 Potential energy surface

The system of interest consists of a rigid dopant, here a cationic coronene oligomer containing up to m = 4 molecules and simply denoted as ‘HC’ for brevity, coated with a finite number N of para-hydrogen molecules. The dopant is assumed to be described by a set of atomic positions collectively denoted as R⁰ = {r⁰_j, j = 1,…,M}, the atom r⁰_j carrying a partial charge q_j. Here M = 36m denotes the number of atoms in the cationic coronene oligomers. The hydrogen molecules located at the positions R = {r_i, i = 1,…,N} interact between each other and with the dopant through short-range repulsion, long-range dispersion, and polarization forces.

As in our former investigations^35–37 we used a united-atom model for para-hydrogen for both structural and path-integral molecular dynamics computations. This is justified by the experimental situation we are referring to, in which the coronene cations coated by hydrogen are initially generated into the cryogenic medium of helium nanodroplets. At such low temperatures and pressures, the para-H₂ molecules experience free rotation and can be treated, in a first approximation, as point-like particles. The “isolated” form of the SG potential, preferred here over the “solid” form to describe the mutual interactions, has been used many times in the past to simulate para-H₂ clusters and bulk para-hydrogen.^42–48 Its expression reads

V_SG(r) = V^rep_SG(r) + V^att_SG(r)f^cut_SG(r)

V^rep_SG(r) = exp(α − βr − γr²) (1)

For the sake of consistency a similar form is employed for the interaction between the carbonaceous solute and individual H₂ molecules, with the extra complication of a vectorial polarization term, the total potential remaining additive over the hydrogen molecules. The interaction V_i between para-H₂ molecule numbered i and the dopant thus reads

where r̃_ij denotes the distance between atom j from the dopant and hydrogen molecule i. V_rep and V_disp represent the short-range repulsion and the long-range dispersion forces, respectively expressed as

V^(j)_rep(r̃_ij) = A_j exp(−b_jr̃_ij) (5)

with 2 × 4 parameters A_j, b_j, C_6,j and C_8,j for j = C and H. The polarization contribution V⁽ⁱ⁾_pol on hydrogen molecule i readsThe parameters of this potential were determined by fitting to the results of QC calculations on small molecules, they are unchanged since our earlier work.³⁵

2.2 Models for cationic coronene oligomers

It is not the purpose of the present work to determine the most stable structure of cationic coronene clusters, or even to compare the relative energetic stability of their various conformers. Instead we restrict ourselves to evaluating their propensity for adsorbing para-H₂ molecules, and for this purpose we look for conformations that are both structurally and chemically realistic in their interaction with the hydrogen solvent.

The structures of coronene clusters have been investigated mostly in neutral form,^19,22,24 and here we start by borrowing configurations from the empirical but seminal work by Rapacioli and coworkers,²⁵ in which the PAH molecules interacting through additive pair forces of the Lennard-Jones and Coulomb types were treated as rigid bodies. Since we are interested in the effects of oligomer structure on the solvation shell of coating para-hydrogen molecules, we have not only considered the putative global minima of the coronene oligomers predicted by this empirical potential, but higher lying structures as well, sometimes not even local minima.

Because we are dealing with cationic oligomers rather than neutrals, the presence of the extra charge must be taken into account as well. The effects of ionization on PAH clusters have been specifically scrutinized earlier⁴⁹ and as in rare-gas clusters removing an electron can lead to some resonance phenomena and charge delocalization. Here we assume for simplicity that the extra charge only moderately alters the structure of the oligomer, but its possible delocalization is accounted for by replacing the fixed charges by fluctuating ones, using the very same model as detailed in the work by Rapacioli et al.¹⁹ that was introduced to rationalize the DFT results used to set the fixed charges, only applying it now to the entire oligomer rather than to individual molecules.

Briefly, within the fluctuating charges model⁵⁰ the partial charges {q_j} on each atom of the hydrocarbon molecular dopant are treated as dependent on its geometry R, the global electrostatic energy being minimized under the constraint of total charge conservation:

where ε_j for j = H and C are the respective electronegativities of the two elements, U_j being their so-called hardness, and J_ij = (r_ij³ + U_ij)^−1/3 a screened Coulomb interaction. In the previous equation, Q₀ is the fixed total charge of the system (+1 for a cation) and λ a Lagrange multiplier. Taking the values for these different parameters from Rapacioli and coworkers,²⁵ the model can be applied to oligomers rather than monomers, and in the presence of a total charge other than zero the partial charges on atomic sites adjust to effectively spread over these sites, in a similar way as a density-functional calculation processed with a restrained electrostatic potential analysis.⁵¹ In particular, the partial charges on a given atom are now no longer the same for all molecules, even though the differences are not always significant. But these charges are more realistic than what would have been obtained by imposing that only one molecule carries the extra charge of +1, and the model captures a large part of delocalization effects.²⁵

In the present model, the geometries of the oligomers were generally taken as local minima of specific conformers for the neutral cluster, neglecting in a first approximation the variations in atomic charges caused by ionization. Additionally, geometries that are not local minima but higher-order stationary points for the empirical potential such as T-shape isomers were constructed by imposing the required symmetry and optimizing the distance between the molecules to minimize the potential, again keeping the partial charges as that of neutral coronene. Eventually the cationic state was imposed and partial charges were recalculated using the fluctuating charges model. While the final geometry for the neutral system is not fully consistent with the charges determined for the cation, minor structural changes are actually expected upon ionization for the relatively large coronene molecule, differences being essentially a shorter intermolecular distance near the cluster center but no significant intramolecular relaxation.⁴⁹

For the coronene dimer, we have thus considered three possible conformers, namely the rotated stack, the parallel displaced (of shifted stack) structure, and a metastable T-shape conformer. The rotated stack, which for the simple pairwise potential of ref. 25 was the most stable structure, shows the two molecules exactly above one another but rotated by 30°. The parallel displaced conformer was found by Bartolomei and coworkers to be slightly more stable for the neutral cluster.²⁴ Lastly, the T-shape conformer was proposed by Obolensky and coworkers¹⁹ to be a possibly competitive structure depending on how dispersion forces are accounted for. While not a local minimum for the present potential, we considered it as a quite different alternative to the stacked structures.

For the trimer, four conformers were considered, three of which are made of planar stacks with either the three molecules parallel displaced to each other in the same direction or in reverse directions (referred to as the zigzag conformer), or on top of each other with the central molecule being rotated by 30°. The fourth conformer denoted as 2 + 1 is a local minimum of the pairwise potential with two molecules parallel displaced and the third one on the side.

Among the many possible conformers for the tetramer, only two were considered in the present work with perfect stacked character, the four molecules being either parallel displaced along the same direction or alternatively rotating by ±30° and sharing a common axis perpendicular to the molecular planes.

2.3 Structure optimization and path-integral molecular dynamics simulations

Candidates for the most stable solvation pattern of para-H₂ molecules around the cationic coronene oligomers were first generated by performing basin-hopping Monte Carlo global optimization and classical molecular dynamics at the relatively high temperature of 25 K, followed by systematic quenching.

For each of the most stable structures thus obtained, PIMD trajectories were conducted to account for vibrational delocalization in the binding energies. Details about the PIMD methodology are similar as explained in our earlier related papers.³⁵ In short, we kept the temperature to be T = 2 K and a Trotter number of P = 128, shown to be sufficient for the present type of system.³⁵ The PIMD trajectories were 100 ps long and used a time step of 0.2 fs, averages being accumulated after an extra 20 ps thermalization period. Systematic quenching was also performed from the centroid positions. If a new putative global minimum was found, then the PIMD simulation was restarted from this structure.

From the PIMD trajectories we mostly examined the structural properties, including the solvent density around the cationic oligomer, and evaluated the size of the first solvation shell using different methods, as discussed below. The virial energies also determined turned out to provide valuable information as well as a way to actually compare the relative stability of neighboring sizes much more closely to mass spectrometry experiments.

3 Results and discussion

3.1 Solvation shell based on geometric criteria

In this study we notably aim at characterizing the size of the solvation shell of hydrogen molecules coating cationic coronene oligomers. Following our earlier investigations of hydrogen uptake on individual PAH molecules,^35–37 we first employ geometric criteria to achieve this characterization, by examining the distribution of the (minimum) distance between the para-H₂ molecules to the various atoms of the solute. The minimum distance is a more appropriate quantity than the distance to the center of the solute owing to the strongly aspherical character of polyaromatic molecules. While coronene clusters tend to be more spherical than their monomer unit, the situation remains problematic for several of their conformers and notably the T-shape structure.

From the present simulations, we thus determine the distribution of minimum distance between hydrogen molecules and the various atoms of the coronene oligomer, nuclear delocalization being accounted for by accumulating the results over all beads in the PIMD description.

Fig. 1 precisely depicts the distribution of minimum distance obtained for several numbers of hydrogen molecules coating the cationic coronene dimer in its T-shape conformation.⁵² The sizes were chosen near the completion of the shell, N = 54–56. The distributions at these sizes are either unimodal (N = 54 and 55) or bimodal (N = 56), which we tentatively interpret as the signatures of a single solvation shell and a single shell plus a floating molecule marking the onset of the second shell. For unimodal distributions that correspond to a single shell, the size of the shell (which is the prescribed number of hydrogen molecules) is also straightforwardly obtained by integrating the distribution. This procedure no longer applies for multimodal distributions, and we resort to two approximate schemes instead.

Fig. 1 Upper panel: Distributions of minimum distance between p-H₂ molecules and the (coronene₂)⁺ solute in its T-shape conformer, solvated by N = 54–56 hydrogen molecules, and best fit using a Gaussian form. The vertical dashed line marks the maximum distance where the shell size at size N = 56 is determined by limited numerical integration. Lower panel: Visual depiction of the hydrogen densities for N = 55 and 56, the solute being shown under two perpendicular views. The extra hydrogen molecule causing the additional peak in the distance distribution for N = 56 is highlighted by a red circle.

As in ref. 35, the first peak of the shortest distances can be represented by a Gaussian distribution, whose integration then provides an estimate of the size of the first solvation shell. For the present distributions, the Gaussian approximation appears to perform better on the short distances side, the long distance size being more prone to fluxional motion and much more stronger broadenings (see Fig. 1). Alternatively to Gaussian fitting, the multimodal distribution can be integrated only up to the distance where it reaches its first local minimum, preserving its anharmonic nature over a broader range.

Visual depiction of the 3D densities shown in Fig. 1 for N = 55 and 56 reveals possible difficulties associated with using the minimum distance as the main geometric criterion for quantifying the solvation shell. In particular, the side views of the densities clearly show a few atoms on the side, just above the plane of the horizontal coronene, that cannot be seen from the front views. These hydrogen molecules are considered to belong to the first shell because their distances to this horizontal coronene are compatible with those of the other hydrogens, although their binding energies are probably much lower due to their outside location. The additional H₂ molecule sitting next to them on the left side of the vertical coronene in Fig. 1 for N = 56, highlighted on the figure, is more distant from both hydrocarbons, hence causing the bimodal distribution, and furthermore it is expected to be energetically even less stable.

While the definition based on limited integration seems appropriate to discriminate between such situations, it also experiences difficulties in some cases where solvent molecules from the second shell significantly overlap with the first inner shell. As an example, we show in Fig. 2 the distribution of minimum distance in the case of N = 50–52 para-H₂ molecules around the cationic coronene dimer in the rotated stack configuration. For this system, the onset of the second shell appears above N = 50 hydrogen molecules, and this is manifested both on the 3D density (shown as an inset in Fig. 2) and on the one-dimensional distribution of minimum distance, but this time as a shoulder rather than a proper peak. To cope with such situations in a more automated way, the possible presence of a shoulder is detected from the numerical second derivative of the distribution, and integration is restricted up to this point.

Fig. 2 Distributions of minimum distance between p-H₂ molecules and the (coronene₂)⁺ solute in its rotated stack conformer, for N = 50–52 hydrogen molecules. In the inset, the hydrogen density obtained for N = 51 is depicted.

With these two geometric definitions at hand, we show in Fig. 3 the variations of the size of the first solvation shell with increasing number of para-H₂ molecules coating the cationic coronene monomer. Here we compare the results obtained by limited integration of the minimum distance distribution until it reaches a local minimum (or over the whole distance domain in case of unimodality) to our earlier results³⁵ in which the first peak was fitted by a Gaussian, as obtained here for the neutral coronene solute. The corresponding data for cationic coronene, virtually identical, are not represented, hence the variations between the two sets of data reflect differences in the geometric definitions rather than being due to charge differences.

Fig. 3 Size of the first solvation shell in (H₂)_Ncoronene⁺ as a function of N, as determined by integrating the minimum distance distribution and in comparison to earlier results obtained for the neutral coronene solute and using the Gaussian fit approximation (ref. 35). The vertical arrow points to the size above which the distribution is always multimodal or with a large distance shoulder.

As expected, the shell size varies essentially monotonically with increasing number of coating hydrogen molecules, minor deviations being due to finite size fluctuations.³⁶ At small coverage N < 40, limited integration of the minimum distance distribution yields a shell size that, by construction, is identical to the number of available molecules. In contrast, the Gaussian fit approximation predicts shell sizes that are actually lower, although the trends are similar. Such quantitative differences confirm the difficulties associated with the geometrical definitions of the first solvation shell. At large coverage, the shell size reaches a plateau but again with a significantly lower value when the first peak of the distribution is fitted by a Gaussian (shells of 42 molecules versus 46 approximately).

These results indicate that the Gaussian fit method is not quantitative, and for the remainder of this work we will only consider the integration method restricted up to the possible presence of a local minimum or a shoulder feature. The corresponding variations of Fig. 3 can be used to bracket the size at which the solvation shell is complete, namely in the range 42–46 where it saturates with increasing number of hydrogen molecules. More accurate definitions for the onset of the second shell are possible but require taking into account the finite size fluctuations, which can cause the occasional appearance of a second shell and its disappearance once another hydrogen molecule is added.³⁶ In particular, the first shell N^max can be defined as the maximum number of hydrogen molecules that can be sustained by the system to produce a unimodal minimum distance distribution with no shoulder on the large distance side, the distribution at size N^max + 1 showing a second peak or a shoulder on the large distance side.

Alternatively, it can be also defined as the upper size N^min above which all distributions are multimodal or exhibit a shoulder at large distances. For the present example of single coronene cation as the solute, N^max = 42 while N^min = 44. This narrower bracketing provides a slightly higher accuracy regarding the range of completion of the first solvation shell. It is also physically more sound as it conveys the very asymmetric nature of shell filling for these anisotropic hydrocarbon solutes. In the similar case of solvation by helium, it was notably shown that the first shell is completed between 38 and 44 atoms, the last 6 solvent atoms occupying peripheral sites with a much lower binding strength.^41,53 The present definition of the geometrical shell based on limited integration and N^min seems compatible with these other results and will thus be adopted to evaluate the shell size for any given isomer of the cationic coronene oligomers.

Fig. 4–6 show the variations of the size of the first solvation shell based on limited integration, but now for the different isomers considered for the 2-, 3-, and 4-molecule oligomers, respectively. In addition to the graphs with those size variations, the corresponding oligomers themselves are depicted. From these figures, the effects of the oligomer structure on the solvation shell size are quite striking. Concerning the dimer, the shell size essentially grows with the exposed area of the hydrocarbons, and is lowest for the (most compact) rotated stack while being highest for the (least compact) T-shape structure, the parallel displaced isomer providing the intermediate situation. At large numbers of coating hydrogen molecules, the T-shape structure accommodates a larger first solvation shell than both isomers with parallel hydrocarbons. For these systems, N^min is found to be 63, 60, and 50, respectively, the particularly low value of 50 for the rotated stack oligomer being visible in Fig. 2.

Fig. 4 Upper panel: Size of the first solvation shell in (H₂)_N(coronene₂)⁺ clusters as a function of N, for the three conformations of the cationic coronene dimer shown in the lower panel. The vertical arrows point to the sizes above which the distributions are always multimodal or with a large distance shoulder.

Fig. 5 Upper panel: Size of the first solvation shell in (H₂)_N(coronene₃)⁺ clusters as a function of N, for the four conformations of the cationic coronene trimer shown in the lower panel. The vertical arrows point to the sizes above which the distributions are always multimodal or with a large distance shoulder.

Fig. 6 Upper panel: Size of the first solvation shell in (H₂)_N(coronene₄)⁺ clusters as a function of N, for the two conformations of the cationic coronene tetramer shown in the lower panel. The vertical arrows point to the sizes above which the distributions are always multimodal or with a large distance shoulder.

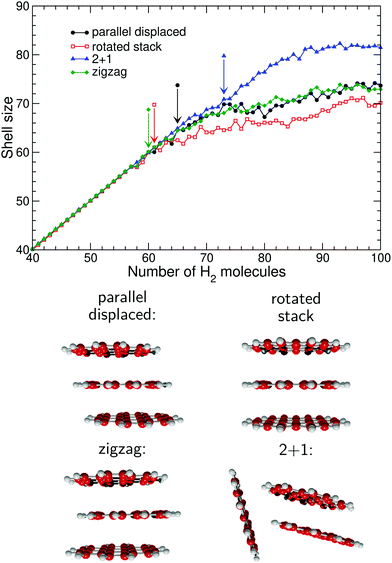
In Fig. 5 the dependence of the solvation shell on the structure of the PAH oligomer is also rather significant in the case of the coronene trimer. As was the case with the dimer, the rotated stack accommodates the smallest shell size while the 2 + 1 structure with its greater exposed area accommodates the largest number of hydrogen molecules. In contrast, the two remaining oligomers with parallel displaced and zigzag structures differ only in the relative location of one molecule and apparently exhibit very similar first solvation shell sizes. However, examination of the distributions themselves yields rather different onsets for the completion of first shell, with N^min taking values of 65, 61, 60, and 73 for the parallel displaced, rotated stack, zigzag and 2 + 1 oligomers, respectively. The particularly low value obtained for the zigzag oligomer seems to contradict the general trend obtained for the otherwise similar parallel displaced structure, however it contains a convex region which can accommodate fewer molecules, hence leading to floating atoms at much earlier sizes.

Only two four-molecule oligomers were considered, to highlight more specifically the role of the shift between successive molecules on the resulting size of the solvation shell. For this system, the differences between the results obtained for two structures, represented in Fig. 6, are also significant, with more hydrogen molecules filling the first shell in the parallel displaced structure relative to the more compact rotated stack. The sizes N^min above which the minimum distance distributions are no longer unimodal and without any shoulder are 80 and 72 for the shifted and rotated stacks, respectively.

Fig. 7 depicts the hydrogen densities at the size of 74 molecules intermediate between those of the shell completion for the two oligomer structures, as pinpointed by the values of N^min. At this size, the density of hydrogen molecules around the rotated stack cluster clearly exhibits two floating atoms belonging to the second shell, located on either side of the stack and along its symmetry axis where adsorption is energetically favored. In contrast, the slightly larger area exposed by the parallel displaced structure allows the same number of hydrogen molecules to fill a single shell (which furthermore is not fully complete yet).

Fig. 7 Visual depiction of the hydrogen densities obtained for (H₂)₇₄(coronene₄)⁺ and the two conformations of the cationic coronene tetramer. (a) Parallel displaced; (b) rotated stack.

3.2 Solvation shell based on energetic criteria

Given the difficulties in determining the size of the solvation shell only based on geometric arguments alone, we have looked for alternative definitions. In comparing with mass spectrometry experiments, where abundances are primarily related to the propensity to thermally dissociate (here, hydrogen molecules) over a fixed time, a more closely related quantity is the binding energy, or the energy difference between successive numbers of solvent molecules. From the virial energies E_N determined along the PIMD trajectories for the various clusters containing N para-H₂ molecules, the binding energy difference ΔE is thus defined as ΔE(N) = E_N+1 − E_N − E_H2, with E_H2 = 0 the intrinsic energy of the hydrogen molecule, neglected here since a coarse-grained model is employed for these pointlike molecules.

The variations of the binding energy difference ΔE with increasing number of hydrogen molecules are represented in Fig. 8–11 for cationic coronene oligomers with 1–4 molecules, in the various structures considered. For each system, we also included the corresponding quantity but obtained from the putative global minimum energies, that is in complete absence of zero-point energy contribution and at zero temperature.

Fig. 8 Difference in binding energy between coronene⁺(H₂)_N+1 and coronene⁺(H₂)_N, as obtained from the lowest-energy structures (black symbols) or from PIMD simulations at 2 K. The red arrow and dashed line locate the completion of the first solvation shell based on the geometric and energetic definitions, respectively (see text for details).

Fig. 9 Difference in binding energy between (coronene₂)⁺(H₂)_N+1 and (coronene₂)⁺(H₂)_N, as obtained from the lowest-energy structures (black symbols) or from PIMD simulations at 2 K and for three conformations of the coronene dimer, (a) parallel displaced; (b) rotated stack; (c) T-shape. The red arrow and dashed line locate the completion of the first solvation shell based on the geometric and energetic definitions, respectively (see text for details).

Fig. 10 Difference in binding energy between (coronene₃)⁺(H₂)_N+1 and (coronene₃)⁺(H₂)_N, as obtained from the lowest-energy structures (black symbols) or from PIMD simulations at 2 K and for four conformations of the coronene trimer. The red arrow and dashed line locate the completion of the first solvation shell based on the geometric and energetic definitions, respectively (see text for details).

Fig. 11 Difference in binding energy between (coronene₄)⁺(H₂)_N+1 and (coronene₄)⁺(H₂)_N, as obtained from the lowest-energy structures (black symbols) or from PIMD simulations at 2 K and for the two conformations of the coronene tetramer. The red arrow and dashed line locate the completion of the first solvation shell based on the geometric and energetic definitions, respectively (see text for details).

The main effect of including zero-point energies in the PIMD approach (and a minor fraction of thermal energy at 2 K) is to generally shift the binding energies by an approximately constant value of 150 K and to smoothen the finite-size fluctuations. Individual PAH molecules attract hydrogen solvent molecules on their outer flat faces before the peripheral regions are filled,³⁵ just as with helium as the solvent.^{40,41,54–57} This growth process also takes place for solutes made of coronene oligomers, and it can give rise to a marked increase in the binding energy difference around 14 hydrogen molecules, when two opposite facets of coronene are covered. Deviations from this behavior are found when the coronene molecules are not in stacked form, as in the T-shape and 2 + 1 isomers of the coronene dimer and trimer, respectively.

At higher coverage, it is usually difficult to distinguish marked variations in the classical energies based on the global minima due to the significant size variations. Such fluctuations are markedly washed away in the PIMD description, allowing us to identify a size interpreted as due to the closure of the solvation shell, although not based on geometric arguments but now on energetic grounds.

In the cationic monomer case (Fig. 8), the binding energy difference thus decreases by a few tens of Kelvin between N = 38 and N = 39, a size regime where the molecules can no longer accommodate adsorption sites on either side of the hydrocarbon but have to nest in the peripheral region.³⁵ We thus attribute a shell size of 38 hydrogen molecules for the coronene monomer, noticing that it is significantly lower than the value of 44 based on geometrical filling of the minimum distance distribution.

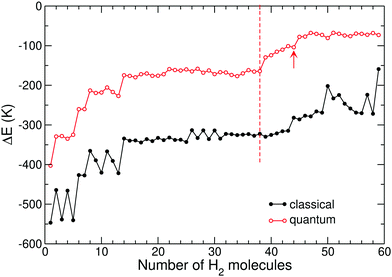
Following the same approach but now for the cationic coronene dimer (Fig. 9), the clearest jumps in the binding energy difference are found at sizes 50, 48, and 56 for the parallel displaced, rotated stack, and T-shape isomers, respectively, again providing lower values than those based on the geometric definitions. However we also note that for the three isomers of this system the jumps in binding energy are also not as sharp as they were for the coronene monomer, and such behavior will also convey to larger sizes.

Likewise, for the cationic coronene trimer we find in Fig. 10 marked jumps at 62, 58, 58, and 68 for the parallel displaced, zigzag, rotated stack, and 2 + 1 isomers.

Concerning the tetramer, jumps in the binding energy difference are found at 74 and 68 hydrogen molecules in Fig. 11 for the parallel displaced and rotated stack isomers, respectively.

3.3 Relation to stacking shift

The previous results indicate that the geometric definition for the size of the solvation shell is more ambiguous than the energetic definition, especially when the coronene cluster is not based on a single stack motif. Focusing now on the values of the shell size obtained from the jumps in the binding energy difference, we can now discuss the effect of solute size and shape on the solvation shell.

The various sizes of the solvation shells determined from the energetic definition are reported in Fig. 12 as a function of coronene cluster size in their various isomers. Obviously the shell size grows monotonically with the solute size, and it is also larger for isomers that have a greater apparent extension towards the solute molecules, the irregular T-shape and 2 + 1 isomers exhibiting the largest values while the single rotated stack isomers yield the lowest values.

Fig. 12 Size in the first solvation shell of para-hydrogen molecules around cationic coronene oligomers as a function of the number of coronene monomers and assuming different conformations.

Rather regular trends are found for the two regular stacked motifs of parallel displaced and rotated stack isomers. The approximate linear slopes that can be extracted in both cases are 11.3 and 10.0 per coronene molecule, respectively. In their mass spectrometry study, Goulart and coworkers³¹ reported a slightly higher slope of 11.4 per coronene, which remains in reasonable agreement with our own data for the parallel displaced motif while being at variance with the slope obtained for the rotated stack motif along a common axis.

The authors of this reference interpreted their measurements as the signature of a shift between successive coronene molecules, taken between hexagonal centers, of about 2.5 Å, which is significantly larger than the corresponding distance in our explicit models of cationic coronene oligomers that is about 1.5 Å, in agreement with essentially all available theoretical results within 0.1 Å (although for neutrals).^16–25 It is not fully clear what causes this possible discrepancy in the inferred geometry while the main observable (closure of the solvation shell) essentially agrees. However, we note that although the limitations of the geometric definition of shell size were made rather clear, the energetic definition is not flawless either and involves an accuracy not much greater than ±2 units of hydrogen molecules, especially in the case of the larger oligomers.

Another approximation of our modeling that could explain this difference in step size is the rigid nature of the hydrocarbon solute, which we justified by the very low temperature of the experiments in presence of a helium droplet embedding medium. However, while the individual coronene molecules are indeed expected to be fairly rigid, the intermolecular modes are comparatively softer and it could well be that even under cryogenic conditions the molecules experience some motion at least in the lateral direction, or even some effective expansion due to vibrational delocalization, that would both contribute to enlarging the effective step size. Treating the cationic coronene oligomer dynamically, even still within the rigid intramolecular approximation, would alter the interactions with the hydrogen molecules directly, through the relative motion of the PAH molecules themselves, but also indirectly through changes in the charges distribution.

4 Concluding remarks

Polycyclic aromatic hydrocarbons and their clusters can bind parahydrogen under the cryogenic conditions provided by the environment of helium nanodroplets. The uptake of hydrogen on such aromatic compounds follows a rather complicated pattern due to their strong anisotropy both in shape and in the strength of the interaction, adsorption being favored over carbon cycles relative to hydrogen extremities.³⁵ Besides interaction strength, the typical equilibrium distance between para-hydrogen molecules (3.4 Å) also significantly exceeds the size of aromatic cycles (2.5 Å), which in bulk systems gives rise to the commensurate phase of the hydrogen monolayer on graphite.⁵⁸ Although the curvature in other hydrocarbon solutes such as fullerenes is sufficient to allow adsorbed molecules to sit comfortably over the centre of hexagonal and pentagonal cycles, strain is more important for molecules lying in contact with flat PAHs, causing a lateral expansion of the finite layer.⁴² Yet, for the relatively small coronene, adsorption sites roughly respect the honeycomb symmetry leading to 19 molecules on each side and the magic number observed at 38.

The present article was concerned with the uptake of para-hydrogen on larger cationic assemblies of coronene molecules, aiming to determine from computational modeling the sizes at which the first solvation shell closes and the influence of both the size of the assembly and its specific shape on this limiting size. Our atomistic approach relies on a polarizable force field for the para-H₂ molecules whose interaction with the hydrocarbon atoms was calibrated on quantum chemical results,^35,37 combined with a chemically realistic model for the cationic assembly based on fluctuating charges.²⁵ Combining a classical survey of the low-energy structures by global optimization followed by path-integral molecular dynamics simulations to account for the main nuclear quantum effects, we have calculated the binding energy and the main structural features of cationic oligomers coated by increasing numbers of para-hydrogen molecules, also taking into account several isomers that the hydrocarbon assembly possibly exhibits. From the computational point of view this represents a total of 940 different systems for which global optimization and path-integral molecular dynamics were carried out.

Several definitions for the solvation shell based on either geometric or energetic properties were scrutinized and critically assessed. The geometric approach based on the distribution of minimum distance between the para-H₂ solvent molecules and the hydrocarbon assembly, which was used in our earlier and related investigations,³⁵ turned out not to be fully quantitative or even sometimes ambiguous for the more complicated solute shapes considered here due to the greater variety of adsorption sites they present and the more regular distance distributions they produce. A definition based on the binding energy difference between successive numbers of solvent molecules, much closer to the abundances determined in mass spectrometry experiments, was found as a possible alternative from which the approximate shell closing can be estimated. Whichever definition is used, a significant dependence of the shell closure was found on the size and shape of the cationic coronene oligomer, essentially increasing with the effective aromatic area exposed.

Using the energetic definition, the results obtained for the single stack motifs over assemblies containing between one and four coronene molecules show approximately linear variations that are consistent with those reported experimentally by Goulart and coworkers,³¹ providing further support for the stacking between successive molecules with an incremental shift. The magnitude of this shift inferred by these authors, which is of the order of the aromatic cycle, remains lower than the value in our model of coronene assembly by about 1 Å. We pointed out some limitations in our modeling that could explain this discrepancy, mostly the still approximate values of the shell closing size based on energetic criteria for larger oligomers and possibly the rigid assumption for the hydrocarbon assembly itself. Our treatment of electrostatics, which includes a fluctuating charges component for the solute and direct polarization effects for the para-hydrogen solvent, could also be improved by including some higher order multipoles and accounting for their feedback on the coronene assembly. Such an endeavour would be far more involved than the present study, although it could use as a starting point the putative global minima that were thoroughly searched here.

The puzzling value of the 2.5 Å shift could also be addressed by considering polycyclic aromatic hydrocarbons larger than coronene, and for which we would expect a gradual evolution towards the features in conventional graphite. Focusing on dimers only, larger molecules such as circumcoronene (C₅₄H₁₈) could shed light on various issues raised above, such as the reliability of the rigid approximation, the importance of charge delocalization, and the role of many-body multipolar electrostatics.

Finally, our modeling also considered the para-hydrogen molecules to be pointlike and chemically inert towards the cationic coronene assembly. This approximation is reasonable owing to very low temperatures involved in the experiment and to the significant spreading of the extra charge, but it would be interesting to evaluate the propensity for dissociative chemisorption of H₂ on such radical compounds due to vibrational delocalization. This might require more sophisticated reactive models that lie chemically beyond the semi-empirical potential used in the present work, and is left for future investigations.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Access to the computational resources of the Pôle Scientifique de Modélisation Numérique in Lyon, France, is gratefully acknowledged.

References

1. J. Lim and C.-S. Yoo, Appl. Phys. Lett., 2016, 109, 051905.
2. C. Liu, Y. Y. Fan, M. Liu, H. T. Cong, H. M. Cheng and M. S. Dresselhaus, Science, 1999, 286, 1127–1129.
3. H.-M. Cheng, Q.-H. Yang and C. Liu, Carbon, 2001, 39, 1447–1454.
4. G. E. Froudakis, Mater. Today, 2011, 14, 324–328.
5. S. Zhou, X. Liu and H. Zou, AIP Adv., 2013, 3, 082119.
6. D. J. Durbin, N. L. Allan and C. Malardier-Jugroot, Int. J. Hydrogen Energy, 2016, 41, 13116–13130.
7. J. Fetzer, Handbook of Combustion, Wiley-VCH Verlag, Berlin, 2010.
8. F. Zasada, W. Piskorz, P. Stelmachowski, P. Legutko, A. Kotarba and Z. Sojka, J. Phys. Chem. C, 2015, 119, 6568–6580.
9. S. Morisset, F. Aguillon, M. Sizun and V. Sidis, J. Chem. Phys., 2004, 121, 6493–6501.
10. S. Casolo, G. F. Tantardini and R. Martinazzo, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6674–6677.
11. M. Pasquini, M. Bonfanti and R. Martinazzo, Phys. Chem. Chem. Phys., 2016, 18, 6607–6617.
12. L. M. Hobbs, D. G. York, J. A. Thorburn, T. P. Snow, M. Bishof, S. D. Friedman, B. J. McCall, T. Oka, B. Rachford, P. Sonnentrucker and D. E. Welty, Astrophys. J., 2009, 705, 32–45.
13. A. Léger and J.-L. Puget, Astron. Astrophys., 1984, 137, L5–L8.
14. L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Astrophys. J., 1985, 290, L25–L28.
15. J. Hernández-Rojas, F. Calvo, S. Niblett and D. J. Wales, Phys. Chem. Chem. Phys., 2017, 19, 1884–1895.
16. J. Rodriguez, J. Sanchezmarin, F. Torrens and F. Ruette, J. Mol. Struct., 1992, 86, 429–441.
17. H. Ruuska and T. A. Pakkanen, J. Phys. Chem. B, 2001, 105, 9541–9547.
18. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
19. O. I. Obolensky, V. V. Semenikhina, A. V. Solov'yov and W. Greiner, Int. J. Quantum Chem., 2007, 107, 1335–1343.
20. I. D. Mackie and G. A. DiLabio, J. Phys. Chem. A, 2008, 112, 10968–10976.
21. Y. Zhao and D. G. Truhlar, J. Phys. Chem. C, 2008, 112, 4061–4067.
22. R. Podeszwa, J. Chem. Phys., 2010, 132, 044704.
23. A. J. Perez-Jimenez and J. C. Sancho-Garcia, Chem. Phys., 2015, 459, 112–124.
24. M. Bartolomei, F. Pirani and J. M. C. Marques, J. Phys. Chem. C, 2017, 121, 14330–14338.
25. M. Rapacioli, F. Calvo, F. Spiegelman, C. Joblin and D. J. Wales, J. Phys. Chem. A, 2005, 109, 2487–2497.
26. M. Pitoňák, P. Neogrády, J. Rezáč, P. Jurečka, M. Urban and P. Hobza, J. Chem. Theory Comput., 2008, 4, 1829–1834.
27. M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936.
28. Ö. Birer and E. Yurtsever, J. Mol. Struct., 2015, 1097, 29–36.
29. C. Schouder, A. S. Chatterley, F. Calvo, L. Christiansen and H. Stapelfeldt, Struct. Dyn., 2019, 6, 044301.
30. L. Lei, Y. Z. Yao, J. Zhang, D. Tronrud, W. Kong, C. Z. Zhang, L. Xue, L. Dontot and M. Rapacioli, J. Phys. Chem. Lett., 2020, 11, 724–729.
31. M. Goulart, M. Kuhn, B. Rasul, J. Postler, M. Gatchell, H. Zettergren, P. Scheier and O. Echt, Phys. Chem. Chem. Phys., 2017, 19, 27968–27973.
32. C. Leidlmair, P. Bartl, H. Schöbel, S. Denifl, M. Probst, P. Scheier and O. Echt, Astrophys. J., Lett., 2011, 738, L4–L8.
33. C. Leidlmair, Y. Wang, P. Bartl, H. Schöbel, S. Denifl, M. Probst, M. Alcamí, F. Martín, H. Zettergren, K. Hansen, O. Echt and P. Scheier, Phys. Rev. Lett., 2012, 108, 076101.
34. M. Harnish, N. Weinberger, S. Denifl, P. Scheier and O. Echt, Mol. Phys., 2015, 113, 2191–2196.
35. F. Calvo and E. Yurtsever, J. Chem. Phys., 2016, 144, 224302.
36. F. Calvo and E. Yurtsever, J. Chem. Phys., 2016, 145, 084304.
37. F. Calvo, E. Yurtsever and A. Tekin, J. Phys. Chem. A, 2018, 122, 2792–2800.
38. I. F. Silvera and V. V. Goldman, J. Chem. Phys., 1978, 69, 4209–4213.
39. F. Calvo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 060502(R).
40. F. Calvo, J. Phys. Chem. A, 2015, 119, 5959–5970.
41. F. Calvo, Comput. Theor. Chem., 2017, 1107, 2–6.
42. K. Nho and E. Manousakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 115409.
43. F. Mezzacapo and M. Boninsegni, Phys. Rev. Lett., 2008, 100, 145301.
44. M. C. Gordillo, C. Cazorla and J. Boronat, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 83, 121406(R).
45. F. Mezzacapo and M. Boninsegni, J. Phys. Chem. A, 2011, 115, 6831–6837.
46. J. Navarro and R. Guardiola, Int. J. Quantum Chem., 2011, 111, 463–471.
47. M. C. Gordillo, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 041406(R).
48. J. Turnbull and M. Boninsegni, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205421.
49. M. Rapacioli and F. Spiegelman, Eur. Phys. J. D, 2009, 52, 55–58.
50. A. K. Rappé and W. A. Goddard, J. Phys. Chem., 1991, 95, 3358–3363.
51. P. Istkowitz and M. L. Berkowitz, J. Phys. Chem., 1997, 101, 5687–5691.
52. The 3D density plots have been constructed using the Mayavi2 suite of Python scripts: P. Ramachandran and G. M. Varoquaux, IEEE Comput. Sci. Eng., 2011, 13, 40–51.
53. T. Kurzthaler, B. Rasul, M. Kuhn, A. Lindinger, P. Scheier and A. M. Ellis, J. Chem. Phys., 2016, 145, 064305.
54. A. Bach, S. Leutwyler, D. Sabo and Z. Bačić, J. Chem. Phys., 1997, 107, 8781–8793.
55. Y. Kwon and K. B. Whaley, J. Chem. Phys., 2000, 114, 3163–3169.
56. A. Heidenreich, U. Even and J. Jortner, J. Chem. Phys., 2001, 115, 10175–10185.
57. R. Rodríguez-Cantano, R. Pérez de Tudela, M. Bartolomei, M. I. Hernández, J. Campos-Martínez, T. González-Lezana, P. Villareal, J. Hernández-Rojas and J. Bretón, J. Chem. Phys., 2015, 143, 224306.
58. H. Wiechert, Phys. B, 1991, 169, 144–152.

---

Footnote

† Electronic supplementary information (ESI) available: We provide all configurations (positions and atomic charges) for the various coronene oligomers, as well as all putative global minima that served as initial conditions of the PIMD trajectories. See DOI: 10.1039/d0cp01357a

---