Open Access Article
Open Access ArticleCalculations of quantum tunnelling rates for muonium reactions with methane, ethane and propane
Gabriel
Laude
 a,
Danilo
Calderini
a,
Ralph
Welsch
a,
Danilo
Calderini
a,
Ralph
Welsch
 b and
Jeremy O.
Richardson
b and
Jeremy O.
Richardson
 *a
*a
aLaboratory of Physical Chemistry, ETH Zürich, Switzerland. E-mail: jeremy.richardson@phys.chem.ethz.ch
bCenter for Free-Electron Laser Science, Deutsches Elektronen-Synchrotron, Hamburg, Germany
First published on 6th July 2020
Abstract
Thermal rate constants for Mu + CH4, Mu + C2H6 and Mu + C3H8 and their equivalent reactions with H were evaluated with ab initio instanton rate theory. The potential-energy surfaces are fitted using Gaussian process regression to high-level electronic-structure calculations evaluated around the tunnelling pathway. This method was able to successfully reproduce various experimental measurements for the rate constant of these reactions. However, it was not able to reproduce the faster-than-expected rate of Mu + C3H8 at 300 K reported by Fleming et al. [Phys. Chem. Chem. Phys., 2015, 17, 19901 and Phys. Chem. Chem. Phys., 2020, 22, 6326]. Analysis of our results indicates that the kinetic isotope effect at this temperature is not significantly influenced by quantum tunnelling. We consider many possible factors for the discrepancy between theory and experiment but conclude that in each case, the instanton approximation is unlikely to be the cause of the error. This is in part based on the good agreement we find between the instanton predictions and new multiconfigurational time-dependent Hartree (MCTDH) calculations for Mu + CH4 using the same potential-energy surface. Further experiments will therefore be needed to resolve this issue.
1 Introduction
Kinetic isotope effects (KIEs) are a useful probe of the mechanism of chemical reactions. Comparing experimental results and theoretical predictions can also provide a stress-test for the accuracy of potential-energy surfaces (PESs) and various approximations to quantum dynamics.1–13 Muonium (Mu = μ+e−) is an exotic isotope of hydrogen, with a mass about 9 times smaller than H.14 Due to this very light mass, comparison of the rates of H + Y reactions with Mu + Y (where Y is a member of the family of alkanes: CH4, C2H6, C3H8, etc.) are expected to result in strong kinetic isotope effects.Experiments on Mu + CH4 and Mu + C2H6 show inverse kinetic isotope effects which become more pronounced with decreasing temperature.15,16 If Mu + C3H8 followed this same behaviour, one would expect the rate to be on the order of 1000 less than the reaction with H at 300 K. However, experimental investigations of the Mu + C3H8 reaction by Fleming et al.17 reveal an anomalous KIE at 300 K, wherein the rate is measured to be almost as fast as that of H + C3H8. The experiments were recently repeated using a more sensitive technique18 which confirmed the result at 300 K and provided further data at temperatures up to 435 K, which also demonstrated unexpected KIEs. Similar behaviour was also seen for Mu + n-C4H10, although data is less reliable for this reaction and we will thus concentrate on the Mu + C3H8 case. It was proposed that the rates of the reactions with muonium are considerably sped-up due to tunnelling effects, and it is one aim of this work to test this suggestion.
We first perform transition-state theory (TST) calculations using high-level electronic-structure calculations based on coupled-cluster theory with explicit correlation.19 We show that these reproduce the high-temperature (T ≳ 500 K) experimental rates (where available) for all H + Y reactions as well as Mu + CH4 and Mu + C2H6 and hence the observed KIEs for these two reactions. Analysis of the TST formula shows that these KIEs are mostly due to zero-point energy corrections of the effective barrier height and to a lesser extent due to minor changes in the translational and rotational partition functions.
In order to correctly predict the reaction rate constant for these reactions at low temperature (T ≲ 300 K), a rate theory is required which takes into account quantum tunnelling. We apply the ring-polymer instanton approach,20–24 which is a form of semiclassical transition-state theory.25,26 It has been successfully applied to study quantum tunnelling in a wide variety of chemical processes.5,8–10,23,27–39
The instanton is defined as the optimal tunnelling pathway which traverses the barrier region. This pathway is found using a discretisation into N ring-polymer beads and by locating a saddle-point on the resulting effective ring-polymer potential-energy surface.21 The optimisation is carried out in full-dimensionality and no a priori choice is made about the tunnelling pathway. Once the instanton has been located, the theory accounts for fluctuations up to second order, taking as input the Hessian of each ring-polymer bead.
The approach is much more efficient than full-dimensional quantum scattering theory40,41 as it only requires evaluations of the PES along the instanton pathway. However, it still remains far less efficient than transition-state theory, as it typically requires at least on the order of N/2 = 50 independent beads for a converged rate (although up to N/2 = 256 were used in this work to ensure full convergence). Therefore a typical optimisation of about 10 iterations necessitates calculating 500 ab initio potentials and gradients and 50 Hessians. The rate is highly dependent on the quality of the PES as is well known,1,2 and it is thus imperative that one utilises high-level electronic-structure methods. Gradients and Hessians are typically evaluated by finite differences and are thus particularly computationally expensive. Therefore, when combined with these high-level electronic-structure methods, an ab initio ring-polymer instanton approach can remain prohibitively expensive.
Fortunately, the ring-polymer instanton approach only requires a local representation of the PES. One can thus make the approach more efficient by using a machine-learning method, such as Gaussian process regression (GPR),42 to fit the PES around the tunnelling pathway using only a fraction of the number of electronic-structure evaluations.32,43 Similar approaches have been used in finding saddle points and minimum-energy paths.44–47 We have shown that the GPR-aided approach can be converged such that it has no impact on the accuracy of the result from ab initio instanton theory.32 We therefore use this approach in this work to compute ab initio instanton rates for the six bimolecular reactions of interest and hence the KIEs.
Instanton rate theory is an approximate method which does not account for the anharmonicity of fluctuations around the pathway.20,21 It also neglects recrossing effects, although it effectively uses an optimal dividing surface to minimize this error.22 For X + CH4 (where X is H or Mu), the small size of the system allows for the application of exact quantum dynamics methods in the evaluation of the rate. Thus in this work, we benchmark the results obtained with instanton rate theory to results obtained with the multiconfigurational time-dependent Hartree (MCTDH) method41,48 for X + CH4 using the same precalculated PES. In this way we show that no major errors are introduced by the instanton approximation.
2 Methods
In this section, we outline our approach to predicting reaction rates from first principles at both high and low temperatures. The results of the low-temperature rates are presented and discussed in Section 3.2.1 Description of the reactions
The bimolecular reactions to be studied are (where X is H or Mu):| X˙ + CH4 → XH + CH3˙ |
| X˙ + C2H6 → XH + C2H5˙ |
| X˙ + C3H8 → XH + C3H7˙. |
 | ||
| Fig. 1 A schematic representation of C3H8, where the three distinct channels for the hydrogen abstraction mechanism are identified. These are labelled n1, n2 and i. | ||
The H + CH4 reaction has been studied extensively and many excellent precalculated PESs exist.41,49–53 In previous work we have computed the rate for this reaction both “on the fly”31 and using the GPR approach32 in order to test our implementations. However, in this paper, we utilise the permutationally-invariant polynomial neural network (PIP-NN) PES fitted by Li et al.54 to UCCSD(T)-F12a/aug-cc-pVTZ calculations. We do this in order to be able to make a direct comparison with the MCTDH results, and we thus perform TST, ring-polymer instanton as well as MCTDH calculations using this same PES. It should be noted that the total rates which we present are calculated for one reaction channel and are then effectively multiplied by 4 to account for the other indistinguishable channels.
We have obtained ab initio instanton rates for the H + C2H6 reaction in a previous study32 using the GPR-aided instanton approach, wherein the training points were based on UCCSD(T)-F12b/cc-pVTZ-F12 calculations. In this work, we employ an equivalent ab initio approach to accurately evaluate rates for Mu + C2H6. A typical training dataset included 30–50 potentials and gradients, and 5–10 Hessians evaluated at the coupled-cluster level. Indistinguishability of the reaction channels is accounted for by multiplying the rate for one channel by 6.
The GPR-aided instanton method was again utilised to evaluate instanton rates for each of the three channel types in X + C3H8. The training data were obtained from UCCSD(T)-F12b/cc-pVDZ-F12 calculations, including no more than 80 potentials and gradients and 13 Hessians for each channel. All electronic-structure calculations were performed using MOLPRO.55 The choice of basis set for the electronic-structure calculations was based on the findings by the group of Clary,56 where it was shown that CCSD(T)-F12a/cc-pVTZ-F12 and CCSD(T)-F12a/cc-pVDZ-F12 methods both yield similar results. Indistinguishability is accounted for by multiplying the obtained rate by 2, 2 and 4 for the X + i-C3H8, X + n1-C3H8 and X + n2-C3H8 channels respectively. These are then summed to obtain the overall X + C3H8 rate.
To ensure that the coupled-cluster methods are reliable for calculating the transition-state energies, we checked the T1 and D1 diagnostics57–59 obtained from MOLPRO calculations to determine the extent of the electronic wavefunction's multireference character. The largest value of T1 was 0.012 (for H + C2H6) and all D1 values were approximately 0.03 or lower. We found similar values for geometries near the transition state which are used for the instanton calculations. According to standard interpretation, there is a strong indication of multireference character if T1 > 0.02 and D1 > 0.05.57,58,60 As we are below these limits, we can therefore assume that the coupled-cluster results are reliable, as will also be confirmed by a comparison of high-temperature TST results with experiment.
2.2 Stationary points of the potential-energy surfaces
The most important factor which determines the rate is the barrier height. However, the most important factor for the tunnelling effect is the barrier width, which can be approximately described by the magnitude of the imaginary frequency, ωb, associated with the transition state. The ring-polymer instanton approach is applicable below a certain crossover temperature Tc = ħωb/(2πkB).61 This defines the onset of the deep-tunnelling regime, where significant deviations from the TST results are expected.62The calculated barrier heights (with and without harmonic zero-point energy corrections) and the crossover temperatures for the reactions of interest are presented in Table 1. It can be seen that the effective barrier heights for the Mu + Y reactions are significantly larger than those of H + Y reactions. The difference arises purely from the increase in some of the frequencies of the transition state and is the main reason that Mu + Y rates are expected to be orders of magnitude smaller than H + Y rates.
| Y | PES | V ‡ | V ‡a(H) | V ‡a(Mu) | T c(H) | T c(Mu) |
|---|---|---|---|---|---|---|
| CH4 | PIP-NN | 61.41 | 54.79 | 82.46 | 331 | 331 |
| C2H6 | UCCSD(T)-F12b/cc-pVTZ-F12 | 50.03 | 42.31 | 68.75 | 335 | 337 |
| i-C3H8 | UCCSD(T)-F12b/cc-pVDZ-F12 | 42.22 | 34.42 | 59.17 | 321 | 325 |
| n1-C3H8 | UCCSD(T)-F12b/cc-pVDZ-F12 | 53.26 | 45.80 | 71.26 | 329 | 329 |
| n2-C3H8 | UCCSD(T)-F12b/cc-pVDZ-F12 | 51.89 | 44.47 | 72.56 | 327 | 328 |
It can be observed that all Tc values fall between 320 and 340 K, which suggests that instanton theory will be required for the low temperature regime in this study (i.e. 200 to 300 K), but that the high-temperature studies (T ≳ 500 K) are not in the deep-tunnelling regime such that the use of transition-state theory is justified. In each case the crossover temperature is only slightly higher for the Mu reactant because reducing the mass of this atom increases the magnitude of all the frequencies. The effect is very small because the imaginary mode is dominated by the abstracted H atom, not the incoming radical.
It is interesting to note here that the X + i-C3H8 channel has a significantly lower barrier than X + n1-C3H8 and X + n2-C3H8. This means that the X + i-C3H8 rate is expected to be the dominant contributor to the overall X + C3H8 rate. This is justified by the fact that the X + i-C3H8 product channel has a more stable radical than X + n-C3H8.63
An analysis of the symmetry point groups64 of the minima and transition state geometries shows that our simple approach for accounting for the degeneracy of the reactions leads to the correct symmetry factor in each case. We also find that each instanton has the same point group symmetry as the equivalent transition state geometry and thus the same symmetry factors are also valid under that theory.
2.3 MCTDH rate constant calculations
Rate constants for the X + CH4 reactions were calculated using the MCTDH approach obtained by employing the quantum transition-state concept65–74 closely following previous work,75–78 and thus only a short summary of the methods is given. Thermal rate constants are obtained from cumulative reaction probabilities and employing J-shifting79 as | (1) |
 | (2) |
The calculations of the thermal flux eigenstates as well as the subsequent imaginary and real time propagation employ the MCTDH approach48,83,84 and its multilayer85,86 and state-averaged69 extensions as well as the multilayer correlation discrete variable representation.86–88 For the H + CH4 reaction, modified transition-state normal-mode coordinates are employed.89 The dividing surface was located in the modified coordinate Q1′ = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αQ1 + cos
αQ1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αQ9, with α = 18, at Q1′ = 0 a.u. Converged results are found with 15 pairs of thermal flux eigenstates and a propagation time of 30 fs. The largest basis set employed in the calculations is given in Fig. 2a. For the Mu + CH4 reaction curvilinear coordinates,90 as used in state-selective descriptions of H + CH4,91–93 were employed. The dividing surface was located at r = 125.0 a.u. Converged results are found with 12 pairs of thermal flux eigenstates and a propagation time of 15 fs. The largest basis set employed in the calculations is given in Fig. 2b.
αQ9, with α = 18, at Q1′ = 0 a.u. Converged results are found with 15 pairs of thermal flux eigenstates and a propagation time of 30 fs. The largest basis set employed in the calculations is given in Fig. 2a. For the Mu + CH4 reaction curvilinear coordinates,90 as used in state-selective descriptions of H + CH4,91–93 were employed. The dividing surface was located at r = 125.0 a.u. Converged results are found with 12 pairs of thermal flux eigenstates and a propagation time of 15 fs. The largest basis set employed in the calculations is given in Fig. 2b.
 | ||
| Fig. 2 Tree representation of the ml-MCTDH wavefunction structure and basis set sizes for (a) H + CH4 (b) Mu + CH4. See ref. 86 for an explanation of the notation. | ||
The largest systems that could be treated with MCTDH simulations to date are six-atomic X + CH4 (X = Mu, H, D or O) reactions. Unfavourable scaling of the quantum dynamics simulations, the need for accurate and efficiently evaluated PES and, for many cases, the need for a dedicated curvilinear coordinate system with complicated kinetic energy operators are the biggest challenges to extend these simulations towards larger reactions. Thus, it is not yet possible to calculate benchmark rate constants for the larger systems employed in this work, i.e. for X + C2H6 or X + C3H8.
2.4 TST rates in the high-temperature regime
At high temperatures (T ≳ 500 K) well above the crossover temperature, tunnelling is not expected to be significant. Thus in this regime, rates were evaluated with Eyring transition-state theory94 for the six reactions of interest. The PESs used in each case were described in Section 2.1 and are summarised in Table 1.High temperature rates for the reactions of interest are presented in Table 2. Experimental results by Snooks et al.15,16 exhibit Arrhenius behaviour for Mu + CH4 and Mu + C2H6, which is indicative that tunnelling effects are insignificant at these temperatures. This is also clear from the fact that the TST results are in good agreement (i.e. the error is less than about a factor of 2) with the experimental rates for both X + CH4 and X + C2H6 sets of reactions.
| Y | T (K) | H + Y | Mu + Y | KIE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TST | MCTDH | Expt.100,101 | TST | MCTDH | Expt.15,16 | TST | MCTDH | Expt. | ||
| CH4 | 800 | 4.2 (−14) | 5.5 (−14) | 4.4 (−14) | 5.8 (−15) | 1.1 (−14) | 1.0 (−14) | 0.14 | 0.21 | 0.25 |
| 750 | 2.3 (−14) | 3.2 (−14) | 2.5 (−14) | 2.6 (−15) | 4.9 (−15) | 3.7 (−15) | 0.11 | 0.15 | 0.15 | |
| 700 | 1.1 (−14) | 1.7 (−14) | 1.3 (−14) | 7.0 (−16) | 1.9 (−15) | 1.1 (−15) | 0.064 | 0.11 | 0.085 | |
| 650 | 5.1 (−15) | 8.1 (−15) | 6.6 (−15) | 2.3 (−16) | 6.4 (−16) | 2.9 (−16) | 0.045 | 0.078 | 0.044 | |
| C2H6 | 700 | 1.4 (−13) | — | 2.2 (−13) | 1.1 (−14) | — | 1.6 (−14) | 0.079 | — | 0.073 |
| 650 | 7.6 (−14) | — | 1.3 (−13) | 4.5 (−15) | — | 6.9 (−15) | 0.059 | — | 0.053 | |
| 600 | 3.6 (−14) | — | 7.0 (−14) | 1.5 (−15) | — | 2.6 (−15) | 0.041 | — | 0.037 | |
| 550 | 1.6 (−14) | — | 3.5 (−14) | 4.2 (−16) | — | 7.9 (−16) | 0.026 | — | 0.023 | |
| C3H8 | 700 | 2.8 (−13) | — | 8.7 (−13) | 2.7 (−14) | — | — | 0.10 | — | — |
| 600 | 8.3 (−14) | — | 3.2 (−13) | 4.3 (−15) | — | — | 0.052 | — | — | |
| 500 | 1.6 (−14) | — | 9.0 (−14) | 3.6 (−16) | — | — | 0.022 | — | — | |
| 435 | 4.0 (−15) | — | 3.1 (−14) | 4.0 (−17) | — | 1.9 (−15) | 0.010 | — | 0.06 | |
| 397 | 1.5 (−15) | — | 1.5 (−14) | 8.1 (−18) | — | 1.6 (−15) | 0.006 | — | 0.11 | |
| 358 | 4.3 (−16) | — | 5.9 (−15) | 1.1 (−18) | — | 1.1 (−15) | 0.003 | — | 0.19 | |
The rates for the H + CH4 and Mu + CH4 reactions have been calculated many times with various methods and there are no major differences in our results compared to previous work involving TST, VTST, CVT/μOMT, RPMD and reduced-dimensionality quantum scattering.1,2,6,95,96 In fact, these small differences between our results and those reported previously typically fall within the errors of the various PESs used. For instance, the barrier height of the older CBE PES50 is approximately 1.4 kJ mol−1 higher than that of the newer PIP-NN PES54 we are using in this work, which at 500 K can cause discrepancies of about 40%. We will however, not discuss these subtle differences further, as the comparison between our TST calculations with the MCTDH benchmark on the same PES shows that there are no significant problems associated with the TST approximations which might lead to order-of-magnitude errors.
Less work has been carried out on the H + C2H6 reaction as only recently has an accurate potential been fitted.97 Canonical variational transition-state theory with the so-called “least-action tunnelling correction” (CVT/LAT)98 gives rate constants of 6.0 × 10−14 cm3 s−1 and 2.0 × 10−13 cm3 s−1 at T = 600 K and 700 K respectively.99 These are slightly higher than our TST predictions, which can be partly explained by the fact that the barrier height of their fitted PES is 1.4 kJ mol−1 lower than our ab initio value. That there is only a small remaining discrepancy implies that there are no significant corrections introduced by the CVT/LAT approach in this case, implying that the simple TST is adequate for our requirements. In particular, our predicted KIEs are in excellent agreement with experiment.
Therefore, for both X + CH4 and X + C2H6 sets of reactions, TST predicts a strong inverse KIE, which becomes weaker (i.e. closer to 1) at high temperatures and is in good agreement with the experimental data. A similar observation was also made about the X + H2 reaction3 and was also understood by considering the zero-point energy corrected barrier height, which is larger for the case X = Mu than X = H.
Considering the good agreement for X + CH4 and X + C2H6, one would expect that TST should also be valid for X + C3H8 at this temperature range, and a similar KIE trend is predicted. However, this is in stark contrast with experimental results,18 where the KIE is observed to be much weaker than our prediction and also to get stronger at higher temperatures. It is clear that the main discrepancy emanates from the prediction of the Mu + C3H8 rates, for which TST gives results 2–3 orders of magnitude lower than experiment. One possible explanation for this behaviour proposed in ref. 18 is that it is caused by tunnelling effects, which we have so far neglected in our TST treatment. Although we have shown that this approximation is justified for the high-temperature results of X + CH4 and X + C2H6, the Mu + C3H8 experiments were all performed at temperatures below 500 K, where tunnelling may play a larger role. In the following sections, we will therefore include tunnelling effects in our calculations to discover whether this can explain the experimental data.
2.5 Details of the instanton calculations
Instanton rate theory calculations were performed in the low temperature regime (in this work, 200 to 300 K), where the quantum tunnelling effect is expected to have a strong contribution to the rate.Whereas X + CH4 results were obtained directly using the PIP-NN PES,54 we employed the machine-learning method of Gaussian process regression42 to obtain ab initio instanton rates for X + C2H6 and X + C3H8. This was done in order to reduce the computational costs associated with on-the-fly calculations, which would be extreme in the case of the largest system, X + C3H8. The GPR-aided instanton approach has been shown to reduce the number of ab initio evaluations required by an order of magnitude without compromising on the accuracy of the instanton rate calculation.32 In this work, an equivalent protocol was employed as in ref. 32. To briefly summarise, this involved the generation of a GPR-based PES from an initial training dataset (i.e. consisting of ab initio potentials and gradients, with points based on an initial guess configuration of the instanton) which is continuously refined through the addition of more ab initio potentials, gradients and Hessians until one obtains a converged instanton rate. This process is carried out for each reaction and each temperature.
The instanton is expected to be more delocalised at low temperatures, and also slightly more so in the X = Mu case due to the lower mass. Due to this, it was thus necessary to include more ab initio evaluations into the GPR training set at low temperatures,32 and slightly more for X = Mu compared to X = H reactions. However, in all cases, we observed fast convergence, such that the largest dataset used only comprised of 80 potentials, gradients and 13 Hessians, which is a huge computational saving when compared with an on-the-fly implementation.
We note here that alternative machine-learning approaches have been employed in instanton calculations based on neural networks.43,102 However, we find the GPR approach simpler, especially seeing as we have a rather small dataset.
In our case, the availability of the GPR-based PES allows us to employ a large number of beads without excessive computational overhead. This allows us to eliminate the ring-polymer discretisation error such that all instanton rates are converged with respect to N to two significant figures. For all Mu + Y reactions studied in this work, the number of beads required for the discretisation was N = 256 at T ≥ 250 K and N = 512 at T = 200 K in order to obtain converged rates. For the H + Y reactions, N = 128 beads were enough to achieve converged rates for the entire low-temperature regime. More beads are required for the reactions involving Mu because the fluctuation terms in the instanton rate equation converge slower due to the increased vibrational frequencies.21 Nonetheless, we had no particular difficulties with running calculations with these large values of N, but note that for even larger calculations, alternative methods exist for reducing the computational cost of this procedure.103
3 Results for the low-temperature regime
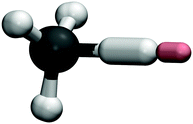
A representation of the instanton optimised for the Mu + CH4 reaction is shown in Fig. 3. Comparing this to the H + CH4 reaction, which was depicted in ref. 31, one can conclude that the mechanisms are similar despite the replacement of the incoming atom with muonium. It is worth noting here that it is the abstracted H atom which does most of the tunnelling, as is clear from the fact that it is the most delocalised, with relatively small contributions from the incoming Mu and the neighbouring hydrogens. This was expected from the fact that the crossover temperature was almost unchanged by the isotopic substitution, but could only be confirmed by performing an instanton optimisation to find the optimal tunnelling pathway.Low-temperature rate constants for X + CH4 evaluated with various quantum dynamics approaches are presented in Table 3. Instanton theory, MCTDH and reduced-dimensionality quantum scattering (RD-QS) are all seen to lie with about a factor of 2 of the experimental result at 300 K.
The results of our instanton calculations for H + CH4 using the PIP-NN surface presented here are slightly larger than those predicted using an ab initio PES in previous work.31,32 This is simply because the barrier height used here is lower by about 2 kJ mol−1. Likewise, instanton calculations8 on the CBE PESs50 are about a factor of 2 smaller than those we report here. However, these minor differences are not expected to significantly affect the KIE calculation, for which the barrier height does not directly contribute.
Instanton rates are in good agreement (better than a factor of 2) with MCTDH for both H + CH4 and Mu + CH4, and because these are computed using the same PES, this is a direct test of the approximations inherent in instanton theory. Our instanton results are also of a similar quality as those from RPMD6 calculated on the CBE PES.50 These two comparisons suggest that there are no obvious problems from neglecting anharmonicity and recrossing in the instanton calculation. There is a small discrepancy between RD-QS results, which were obtained using curvilinear coordinates,56,104 and MCTDH for the Mu + CH4 reaction, where the RD-QS rate is too low by an order of magnitude. This may be a consequence of the differences in the PESs used as well as small errors due to the reduced-dimensionality approximation and is thus difficult to disentangle further.
The similar tunnelling factors (defined by the instanton approach) for the H and Mu variant of the reaction confirms that the tunnelling effect is not strongly influenced by the isotopic substitution. It had been suggested that anharmonicity effects, which are neglected in instanton theory, may play a larger role in Mu + Y reactions.1,2,105 However, the MCTDH results provide a benchmark to test the instanton approximation and the good agreement of the rates shows that the instanton approximation does not in fact introduce significant errors. In fact, the results of the muonium reactions are not seen to be significantly less accurate than those with the incoming H atom. The KIE prediction is expected to be especially accurate as some cancellation of errors is expected to occur,8 which at least partly explains why the neglect anharmonicity is not a major problem. Instanton theory predicts a KIE at 300 K of 1.6 × 10−4, which is in good agreement with the prediction from MCTDH of 2.0 × 10−4.
We had already reported ab initio instanton results for H + C2H6 (but not Mu + C2H6) in ref. 32. These results were seen to be in good agreement with experiment as well as various other quantum rate theories such as semiclassical transition-state theory106 and RD-QS.56Table 4 reproduces some of these results alongside newly calculated rate constants for Mu + C2H6. Recently CVT/LAT99 calculations on the newly constructed PES by Espinosa-García et al.,97 gave rates of 4.60 × 10−17 cm3 s−1 and 2.09 × 10−19 cm3 s−1 at T = 300 K and 200 K respectively and are thus within the same order of magnitude as our instanton results. This good agreement implies that the simpler one-dimensional tunnelling correction provides a good approximation to the full-dimensional instanton analysis in this case.
Fig. 4 shows the instanton pathway for Mu + C2H6. Here, similar behaviour to X + CH4 and H + C2H6 (see ref. 32) can be observed, with the abstracted H atom again doing most of the tunnelling. This is reflected in the obtained rate constants for Mu + C2H6, which follow the same trends as Mu + CH4. The tunnelling factors increase as the temperature is lowered, although at each temperature studied the tunnelling factors for H and Mu reactions remain quite similar, such that tunnelling is not a major contributor to the KIE at any temperature. Unfortunately, at the time of writing, no other results, experimental or theoretical are available for comparison for Mu + C2H6 at these temperatures. If we take into account the arguments we have made for X + CH4, and the fact that we have shown that the tunnelling mechanism of X + C2H6 is similar to that of X + CH4, we expect that these calculations of Mu + C2H6 at the very least provide a good order-of-magnitude estimate of the rate constant and hence of the kinetic isotope effect, which we predict to be 2.6 × 10−4 at 300 K.
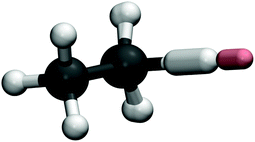 | ||
| Fig. 4 As Fig. 3 for Mu + C2H6. | ||
The X + C3H8 reaction has three distinct channels as illustrated in Fig. 1. We evaluated instanton rates for each of these individual channels at 300 K for the X + C3H8 reactions, with results presented in Table 5. From this, it can be observed that as expected the X + i-C3H8 channel gives the dominant contribution to the rate constant and the other two channels can effectively be neglected without affecting our rate prediction at this temperature by more than 5%. A similar conclusion was reached in ref. 104. To test this assertion at lower temperatures, we calculated instantons for X + n1-C3H8 and found that the ratio between X + i-C3H8 and X + n1-C3H8 increases even further. The instantons representing reactions in these two channels are shown in Fig. 5.
| Y | Degeneracy | H + Y | Mu + Y |
|---|---|---|---|
| i-C3H8 | 2 | 2.9 (−16) | 8.3 (−20) |
| n1-C3H8 | 2 | 2.3 (−18) | 7.5 (−22) |
| n2-C3H8 | 4 | 4.0 (−18) | 1.1 (−21) |
 | ||
| Fig. 5 As Fig. 3 for the two main abstraction channels of Mu + C3H8. | ||
Table 6 presents the calculated instanton rates for X + C3H8 at (T ≤ 300 K) alongside experimental and other theoretical values if available for comparison. In particular, it can be observed that the instanton rate calculations for the H variant of the reaction are in good agreement with the experimental measurement at 300 K by Tsang et al.101
| T (K) | H + C3H8 | Mu + C3H8 | KIE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| κ tun | This work | RD-QS56 | Expt.101 | κ tun | This work | Expt.18 | This work | Expt. | |
| a RD-QS values at 397 and 358 K are approximated by results reported at 400 K and 350 K respectively. | |||||||||
| 700 | 1.5 | 4.2 (−13) | 6.1 (−13) | 8.7 (−13) | 1.5 | 4.0 (−14) | — | 0.094 | — |
| 600 | 1.7 | 1.4 (−13) | 2.3 (−13) | 3.2 (−13) | 1.7 | 7.3 (−15) | — | 0.053 | — |
| 500 | 2.1 | 3.4 (−14) | 6.5 (−14) | 8.9 (−14) | 2.2 | 7.7 (−16) | — | 0.022 | — |
| 435 | 2.7 | 1.1 (−14) | — | 3.1 (−14) | 2.8 | 1.1 (−16) | 1.9 (−15) | 0.010 | 0.061 |
| 397 | 3.4 | 5.0 (−15) | 1.2 (−14)a | 1.5 (−14) | 3.5 | 2.8 (−17) | 1.6 (−15) | 0.0057 | 0.11 |
| 358 | 4.7 | 2.0 (−15) | 4.2 (−15)a | 5.9 (−15) | 4.8 | 5.4 (−18) | 1.1 (−15) | 0.0027 | 0.19 |
| 324 | 6.9 | 8.1 (−16) | — | 2.3 (−15) | 7.1 | 9.9 (−19) | 9.5 (−16) | 0.0012 | 0.41 |
| 300 | 14 | 5.9 (−16) | 1.1 (−15) | 1.1 (−15) | 14 | 3.3 (−19) | 8.9 (−16) | 5.6 (−4) | 0.81 |
| 250 | 27 | 6.6 (−17) | 2.3 (−16) | — | 35 | 7.4 (−21) | — | 1.1 (−4) | — |
| 200 | 180 | 6.8 (−18) | 3.3 (−17) | — | 1220 | 2.2 (−22) | — | 3.2 (−5) | — |
The instanton results differ from those of the RD-QS calculations56 by a factor of two at 300 K (increasing to a factor of four at 200 K). This relatively minor discrepancy is due to a number of differences between the approaches. On one hand instanton theory employs a semiclassical approximation to the full-dimensional problem, and on the other exact quantum scattering theory is applied to a reduced-dimensionality approximation of the system. In addition, slightly different electronic-structure methods were used in the calculations. The RD-QS builds a two-dimensional surface of CCSD(T)-F12 energies corrected by harmonic zero-point energies evaluated by MP2. The barrier height we obtain with a full UCCSD(T)-F12b/cc-pVDZ-F12 calculation is approximately 2 kJ mol−1 higher than that with the dual-level approach based on geometries optimised with MP2, which may explain why the RD-QS rates are about a factor of two larger than the instanton predictions at 300 K. It is expected that the almost perfect agreement between RD-QS and experiment at 300 K is partly due to a fortuitous cancellation of errors, and one should simply conclude that both instanton theory and RD-QS are reliable at predicting the correct order of magnitude of the rate at this temperature.
For the Mu + C3H8 reaction, no other theoretical predictions are available in the literature. However an experimental value has been measured at 300 K.17 The observed rate at 300 K is more than three orders of magnitude larger than our instanton prediction.
Very recently more experimental rates were reported in the range 300–435 K.18 Most of these new rates are close to or larger than the cross-over temperature (see Table 1), where semiclassical theory predicts that the deep-tunnelling mechanism via the instanton tunnelling pathway no longer exists and that a shallow-tunnelling mechanism becomes dominant. For this, simpler tunnelling-correction approaches are expected to become valid. We thus apply the Eckart tunnelling correction at temperatures greater than 300 K.107 The tunnelling factors κtun are thus given by
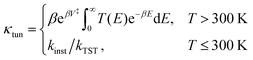 | (3) |
 | ||
| Fig. 6 Rates for H + C3H8 (top) and Mu + C3H8 (bottom) calculated using TST, Eckart-tunnelling corrected TST (T > 300 K) and instanton theory (T ≤ 300 K). These are compared with the experimental rates from ref. 18 and 101. | ||
The good agreement between the predictions for H + C3H8 and experimental results confirms that the ab initio PES is accurate and that the GPR fitting procedure is also applicable to this system, which is larger than those we have applied it to previously. The trends also confirm that the shallow-tunnelling correction gives an accurate description at temperatures above 300 K.
Based on our findings for H + C3H8, one would expect that the same approach would also be valid for Mu + C3H8. However, not only are the values of the rates different, our prediction for the slope of the Arrhenius plot is much steeper than the experimental observations, as shown in the bottom plot of Fig. 6. Even more surprising is that the trend in the experimental KIEs is opposite to that which we have calculated, i.e. the values of the experimental KIE increase with decreasing temperature whereas ours decrease. This results in a experimental KIE at 300 K which is reported17,18 to be more than three orders of magnitude larger than what our calculations predict. The unexpected KIE has been attributed to tunnelling effects in the Mu + C3H8 reactions.17,18 Our instanton calculations however refute this and predict that tunnelling plays a similar role as for the other two classes of reactions studied in this paper. Although the tunnelling factor at 200 K is larger for Mu + C3H8 than for H + C3H8, at 300 K and above the tunnelling factors are approximately the same.
As demonstrated previously, for the hydrogen abstraction reactions, the atom most involved in the tunnelling process is the abstracted H atom, and tunnelling is only weakly dependent on the mass of the incoming reactant atom. We can quantify this by computing the contributions of various atoms to the squared mass-weighted path length of the instanton (called BN in ref. 21), which is proportional to the ring-polymer spring energy. The contribution from the incoming atom (regardless of whether it is H or Mu) was found to be no more than 12% for all reactions studied. In contrast, the abstracted H atom contributes at least 70% of the squared mass-weighted path length, and thus dominates the tunnelling process. Overall we observed only a 15–45% increase in the squared mass-weighted path length for reactions with Mu compared to those with H. In contrast, it increases more than five-fold when the temperature is decreased from T = 300 K to T = 200 K. This explains why temperature is a much more important factor in our predicted KIEs than the mass of the incoming atom.
In order to explain the discrepancy between the experimental and theoretical results for Mu + C3H8, it will be necessary to find the source of error. If the instanton prediction at 300 K is incorrect, it must be shown why this error lowers the Mu + C3H8 reaction by three orders of magnitude, but not the other reactions considered here, which are in good agreement with experiment.
There are a number of approximations involved in the ab initio instanton approach which are potential sources of error in the predicted rate. As already stated, we can eliminate the discretisation error by using a large number of ring-polymer beads. However even in this limit, instanton theory neglects recrossing effects and uses semiclassical approximations which are equivalent to treating the fluctuations around the dominant tunnelling pathway harmonically. Due to the light mass of Mu, one might expect that the reaction path is strongly skewed leading to more recrossing. However, the neglect of recrossing typically overpredicts rates and thus this cannot explain why our predicted rate is too low. As mentioned in various studies,1,2,104,109 an accurate treatment of vibrational modes is necessary for these reactions, with the large vibrational frequencies introduced by replacement of the H atom with Mu indicating that it may be necessary to account for anharmonicity effects. The comparison for Mu + CH4 between instanton and MCTDH calculations gives us insight into the error associated with approximations made in instanton rate theory. In this case at least, they are rather minor and it is seen that anharmonicity does not strongly affect the rate. One might argue that there are more anharmonic modes in Mu + C3H8 than Mu + CH4, but the majority of these are not involved in the reaction and thus do not affect the rate. Also we observe that they apparently do not cause errors in instanton theory for the equivalent H + C3H8 reaction.
An alternative explanation for the discrepancy would be that the reaction observed in experiment does not proceed according to bimolecular kinetics but involves a more complicated process through the formation of clusters. The possibility of roaming dynamics110,111 influencing the rate constant was also considered and briefly investigated. We explored possible configurations in an attempt to find a minimum describing a bound X + C3H8 complex, from which a unimolecular dissociation into XH + C3H7 might occur. However, despite many attempts, we were not able to find such a configuration. In order to go beyond instanton theory to treat recrossing and anharmonicity more accurately and also allow for the possibility of roaming trajectories, a ring-polymer molecular dynamics simulation could be carried out.112,113 However, this would require the construction of a globally-accurate PES, which is not currently available.
The quality of the PES directly ties in to the accuracy of the rates calculated by various quantum dynamics approaches, including instanton theory. This has in fact been observed in the calculation of the H + CH4 rates at high temperatures using various quantum dynamics approaches, wherein the accuracy of the PES matters more than the quantum dynamics approach.1,2,8,109 In this work, we used coupled-cluster theory with F12 methodology, which is expected to give energies near the basis-set limit.19 This has been demonstrated in various work for similar systems,32,114 including the calculation by Horsten et al. for H + C3H8.56 That our high-temperature TST results match well with experiment suggests that at least the barrier heights and frequencies are accurately described by this method.
From the H + C3H8 results, we can infer that the PES is accurate as it should be identical to that of H + C3H8, within the Born–Oppenheimer approximation. Truhlar has suggested that due to the small mass of Mu, the validity of the Born–Oppenheimer approximation should be questioned.2 However, he does not suggest that it would be a major source of error and that it would perhaps change rates by a factor of two at most.
In this work, a local representation of the PES was generated with GPR. We find that this approach gives smooth surfaces which converge as the training set is increased. In previous work, we showed that this GPR-aided approach gives exactly the same rate for an on-the-fly instanton calculation for H + CH4.32 Considering that the approach has also been shown to be successful for H + C2H6 and now for H + C3H8 as well, we see little reason as to why it should not work for Mu + C3H8.
4 Conclusions
We have evaluated rate constants for Mu + CH4, Mu + C2H6 and Mu + C3H8 and their equivalent reactions with H. In the case of X + C2H6 and X + C3H8, we have employed GPR to reduce computational costs while retaining an accuracy similar to that of an ab initio instanton rate calculation. Our instanton calculations show that although tunnelling has a significant effect on the rate at 300 K for these reactions, it speeds up the Mu + Y reactions by the same factor as H + Y and it can therefore be ruled out as the major contributor to the KIE at 300 K and above.Our results for the H + X reactions agree well with experimental measurements and other theoretical predictions, which suggests that the potential-energy surfaces are of sufficient accuracy. Additionally, we have performed MCTDH calculations for Mu + CH4 on the same PES as a benchmark to ascertain how the approximations made by instanton rate theory affect the rate constant. For the Mu + CH4 reaction, we observe good agreement between the instanton rate theory results and MCTDH calculations, which suggest that the approximations made by instanton rate theory (such as the neglect of anharmonicity perpendicular to the path and recrossing) are not detrimental to the study of this reaction.
We argue that our instanton rate calculations are accurate for the Mu + C2H6 and Mu + C3H8 reactions as well, as the predicted mechanisms are similar to that of Mu + CH4. However, our Mu + C3H8 prediction did not reproduce the unexpected experimental result by Fleming et al.17,18 whereas no experimental or benchmark results were available for comparison for Mu + C2H6 at low temperatures. The cause of the discrepancy thus remains unidentified and further studies need to be conducted in order to understand and explain it. We do however provide evidence to argue that the experimental KIE is not caused by tunnelling effects. It is also unlikely that including recrossing effects would provide the explanation as this could only reduce the predicted rate further away from the experimental result. If an accurate full-dimensional fitted PES were available, one could use RPMD to check whether significant anharmonic effects are present which can explain the result. A simpler alternative may be the VPT2 approach of Clary and coworkers11,106,115 which treats tunnelling less accurately than instanton theory, but has a perturbative approach to anharmonicity in all modes, which may shed light on whether the anharmonic effects are important.
It would also be useful to confirm whether the Mu + C3H8 reaction is fundamentally different from Mu + CH4 and Mu + C2H6. Currently experiments have not been reported which measure the rates of both reactions within the same temperature range. Therefore, if new experimental results for Mu + CH4 and Mu + C2H6 at 300 K (even if it were simply to find an upper bound to the rate) or Mu + C3H8 at high temperatures were available, this would allow better benchmarking of the theoretical predictions and potentially help hunt down the source of the discrepancy.
Theoretical studies of H + n-C4H10 have shown that tunnelling effects enhance the rate by 1–2 orders of magnitude at 300 K.116 Although we have not tackled the X + n-C4H10 reaction in this work, we expect that when studied with instanton theory it will behave similarly to the other reactions, and that tunnelling effects of H + n-C4H10 will be similar to those of Mu + n-C4H10 such that making hard to explain the unexpected KIEs observed in ref. 18.
On a positive note, this study provides further evidence that the GPR-aided instanton approach32 can be employed efficiently to study polyatomic reactions. The calculations do not require reduced-dimensionality approximations or compromise on the electronic-structure method. We thus expect the approach to be widely applicable to a variety of large and complex systems.
For instance, while abstraction reactions result in an inverse KIE (i.e. the H variant of the reactions have a larger rate compared to the Mu variant), it is known that for addition reactions involving Mu (e.g. Mu + C2H4,117 Mu + C2H2118 and Mu + C6H6119) tunnelling makes much larger contributions. Other similar reactions of interest include Mu + F2 (for which a large KIE is observed)120 and reactions with muonic helium (Heμ = [4Heμ−]+e−) such as Heμ + CH4.105 The GPR-aided instanton approach would be an excellent candidate for the study of these reactions too.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Stephen Cottrell and Don Fleming for first introducing us to their work on muonium reactions and Martin Quack for useful comments after a presentation of our study at a MOLIM meeting. This research has been financially supported by the Swiss National Science Foundation (Project No. 175696).References
- J. Espinosa-García, Phys. Chem. Chem. Phys., 2008, 10, 1277–1284 RSC.
- J. Pu and D. G. Truhlar, J. Chem. Phys., 2002, 117, 10675–10687 CrossRef CAS.
- R. Pérez de Tudela, F. J. Aoiz, Y. V. Suleimanov and D. E. Manolopoulos, J. Phys. Chem. Lett., 2012, 3, 493–497 CrossRef PubMed.
- Y. V. Suleimanov, R. Pérez de Tudela, P. G. Jambrina, J. F. Castillo, V. Sáez-Rábanos, D. E. Manolopoulos and F. J. Aoiz, Phys. Chem. Chem. Phys., 2013, 15, 3655–3665 RSC.
- R. Pérez de Tudela, Y. V. Suleimanov, J. O. Richardson, V. Sáez Rábanos, W. H. Green and F. J. Aoiz, J. Phys. Chem. Lett., 2014, 5, 4219–4224 CrossRef PubMed.
- Y. Li, Y. V. Suleimanov, J. Li, W. H. Green and H. Guo, J. Chem. Phys., 2013, 138, 094307 CrossRef PubMed.
- Q. Meng, J. Chen and D. H. Zhang, J. Chem. Phys., 2016, 144, 154312 CrossRef PubMed.
- K. Karandashev, Z.-H. Xu, M. Meuwly, J. Vaníček and J. O. Richardson, Struct. Dyn., 2017, 4, 061501 CrossRef PubMed.
- J. Meisner, J. B. Rommel and J. Kästner, J. Comput. Chem., 2011, 32, 3456–3463 CrossRef CAS PubMed.
- M. Kryvohuz, J. Phys. Chem. A, 2014, 118, 535–544 CrossRef CAS PubMed.
- X. Shan, T. A. H. Burd and D. C. Clary, J. Phys. Chem. A, 2019, 123, 4639–4657 CrossRef CAS PubMed.
- T. A. Burd, X. Shan and D. C. Clary, Chem. Phys. Lett., 2019, 735, 136783 CrossRef.
- T. A. Burd, X. Shan and D. C. Clary, Chem. Phys. Lett., 2018, 693, 88–94 CrossRef CAS.
- E. Cohen, T. Cvitaš, J. Frey, B. Holmström, K. Kuchitsu, R. Marquardt, I. Mills, F. Pavese, M. Quack, J. Stohner, H. L. Strauss, M. Takami and A. J. Thor, IUPAC Physical and Biophysical Chemistry Division, Quantities, Units and Symbols in Physical Chemistry. (The IUPAC ‘Green Book’), RSC Publishing, Cambridge, 3rd edn, 2007 Search PubMed.
- R. Snooks, D. J. Arseneau, S. Baer, D. G. Fleming, M. Senba, J. J. Pan and M. Shelley, Hyperfine Interact., 1994, 87, 911–916 CrossRef CAS.
- R. Snooks, D. J. Arseneau, D. G. Fleming, M. Senba, J. J. Pan, M. Shelley and S. Baer, J. Chem. Phys., 1995, 102, 4860–4869 CrossRef CAS.
- D. G. Fleming, S. P. Cottrell, I. McKenzie and K. Ghandi, Phys. Chem. Chem. Phys., 2015, 17, 19901–19910 RSC.
- D. G. Fleming, D. J. Arseneau, S. P. Cottrell and J. N. T. Peck, Phys. Chem. Chem. Phys., 2020, 22, 6326–6334 RSC.
- D. P. Tew, W. Klopper, C. Neiss and C. Hättig, Phys. Chem. Chem. Phys., 2007, 9, 1921–1930 RSC.
- J. O. Richardson, J. Chem. Phys., 2018, 148, 200901 CrossRef PubMed.
- J. O. Richardson, Int. Rev. Phys. Chem., 2018, 37, 171–216 Search PubMed.
- J. O. Richardson and S. C. Althorpe, J. Chem. Phys., 2009, 131, 214106 CrossRef PubMed.
- S. Andersson, G. Nyman, A. Arnaldsson, U. Manthe and H. Jónsson, J. Phys. Chem. A, 2009, 113, 4468–4478 CrossRef CAS PubMed.
- J. B. Rommel, T. P. M. Goumans and J. Kästner, J. Chem. Theory Comput., 2011, 7, 690–698 CrossRef CAS PubMed.
- W. H. Miller, J. Chem. Phys., 1975, 62, 1899–1906 CrossRef CAS.
- J. O. Richardson, J. Chem. Phys., 2016, 144, 114106 CrossRef PubMed.
- J. B. Rommel, Y. Liu, H.-J. Werner and J. Kästner, J. Phys. Chem. B, 2012, 116, 13682–13689 CrossRef CAS PubMed.
- T. Lamberts, P. K. Samanta, A. Köhn and J. Kästner, Phys. Chem. Chem. Phys., 2016, 18, 33021–33030 RSC.
- J. Meisner and J. Kästner, Angew. Chem., Int. Ed., 2016, 55, 5400–5413 CrossRef CAS PubMed.
- V. Ásgeirsson, A. Arnaldsson and H. Jónsson, J. Chem. Phys., 2018, 148, 102334 CrossRef PubMed.
- A. N. Beyer, J. O. Richardson, P. J. Knowles, J. Rommel and S. C. Althorpe, J. Phys. Chem. Lett., 2016, 7, 4374–4379 CrossRef CAS PubMed.
- G. Laude, D. Calderini, D. P. Tew and J. O. Richardson, Faraday Discuss., 2018, 212, 237–258 RSC.
- J. O. Richardson, S. C. Althorpe and D. J. Wales, J. Chem. Phys., 2011, 135, 124109 CrossRef PubMed.
- M. T. Cvitaš and J. O. Richardson, Phys. Chem. Chem. Phys., 2020, 22, 1035 RSC.
- J. O. Richardson, C. Pérez, S. Lobsiger, A. A. Reid, B. Temelso, G. C. Shields, Z. Kisiel, D. J. Wales, B. H. Pate and S. C. Althorpe, Science, 2016, 351, 1310–1313 CrossRef CAS PubMed.
- J. O. Richardson, Phys. Chem. Chem. Phys., 2017, 19, 966–970 RSC.
- Y. Litman, J. O. Richardson, T. Kumagai and M. Rossi, J. Am. Chem. Soc., 2019, 141, 2526–2534 CrossRef CAS PubMed.
- P. Bajaj, J. O. Richardson and F. Paesani, Nat. Chem., 2019, 11, 367–374 CrossRef CAS PubMed.
- W. Fang, J. Chen, P. Pedevilla, X.-Z. Li, J. O. Richardson and A. Michaelides, Nat. Commun., 2020, 11, 1689 CrossRef CAS PubMed.
- S. C. Althorpe and D. C. Clary, Annu. Rev. Phys. Chem., 2003, 54, 493–529 CrossRef CAS PubMed.
- T. Wu, H.-J. Werner and U. Manthe, Science, 2004, 306, 2227–2229 CrossRef CAS PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, The MIT Press, Cambridge, Massachusetts, 2006 Search PubMed.
- A. M. Cooper, P. P. Hallmen and J. Kästner, J. Chem. Phys., 2018, 148, 094106 CrossRef.
- O.-P. Koistinen, E. Maras, A. Vehtari and H. Jónsson, Nanosyst.: Phys., Chem., Math., 2016, 7, 925 Search PubMed.
- O.-P. Koistinen, F. B. Dagbjartsdóttir, V. Ásgeirsson, A. Vehtari and H. Jónsson, J. Chem. Phys., 2017, 147, 152720 CrossRef PubMed.
- A. Denzel and J. Kästner, J. Chem. Theory Comput., 2018, 14, 5777–5786 CrossRef CAS PubMed.
- A. Denzel, B. Haasdonk and J. Kästner, J. Phys. Chem. A, 2019, 123, 9600–9611 CrossRef CAS PubMed.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef CAS.
- J. Espinosa-García, J. Chem. Phys., 2002, 116, 10664 CrossRef.
- J. C. Corchado, J. L. Bravo and J. Espinosa-García, J. Chem. Phys., 2009, 130, 184314 CrossRef PubMed.
- X. Xu, J. Chen and D. H. Zhang, Chin. J. Chem. Phys., 2014, 27, 373–379 CrossRef CAS.
- X. Zhang, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2006, 124, 021104 CrossRef PubMed.
- R. Welsch and U. Manthe, J. Chem. Phys., 2013, 138, 164118 CrossRef PubMed.
- J. Li, J. Chen, Z. Zhao, D. Xie, D. H. Zhang and H. Guo, J. Chem. Phys., 2015, 142, 204302 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS.
- H. F. von Horsten, S. T. Banks and D. C. Clary, J. Chem. Phys., 2011, 135, 094311 CrossRef CAS PubMed.
- T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199–207 CrossRef.
- C. L. Janssen and I. M. Nielsen, Chem. Phys. Lett., 1998, 290, 423–430 CrossRef CAS.
- T. J. Lee, Chem. Phys. Lett., 2003, 372, 362–367 CrossRef CAS.
- T. Husch, L. Freitag and M. Reiher, J. Chem. Theory Comput., 2018, 14, 2456–2468 CrossRef CAS PubMed.
- M. J. Gillan, J. Phys. C: Solid State Phys., 1987, 20, 3621–3641 CrossRef.
- V. A. Benderskii, D. E. Makarov and C. A. Wight, Chemical Dynamics at Low Temperatures, Wiley, New York, 1994 Search PubMed.
- H. Zipse, in Radical Stability-A Theoretical Perspective, ed. A. Gansäuer, Springer Berlin Heidelberg, Berlin, Heidelberg, 2006, pp. 163–189 Search PubMed.
- A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. C. Marques and D. G. Truhlar, Theor. Chem. Acc., 2007, 118, 813–826 Search PubMed.
- W. H. Miller, S. D. Schwartz and J. W. Tromp, J. Chem. Phys., 1983, 79, 4889 CrossRef CAS.
- D. H. Zhang and J. C. Light, J. Chem. Phys., 1996, 104, 6184 CrossRef CAS.
- F. Matzkies and U. Manthe, J. Chem. Phys., 1997, 106, 2646–2653 CrossRef CAS.
- F. Matzkies and U. Manthe, J. Chem. Phys., 1998, 108, 4828–4836 CrossRef CAS.
- U. Manthe, J. Chem. Phys., 2008, 128, 064108 CrossRef PubMed.
- F. Huarte-Larrañaga and U. Manthe, Z. Phys. Chem., 2007, 221, 171–213 CrossRef.
- U. Manthe, Mol. Phys., 2011, 109, 1415–1426 CrossRef CAS.
- R. Welsch, F. Huarte-Larranaga and U. Manthe, J. Chem. Phys., 2012, 136, 064117 CrossRef PubMed.
- R. Welsch and U. Manthe, Mol. Phys., 2012, 110, 703–715 CrossRef CAS.
- U. Manthe and R. Welsch, J. Chem. Phys., 2014, 140, 244113 CrossRef PubMed.
- R. Welsch, J. Chem. Phys., 2018, 148, 204304 CrossRef PubMed.
- R. Welsch, Angew. Chem., Int. Ed., 2018, 57, 13150 CrossRef CAS PubMed.
- R. Welsch, Phys. Chem. Chem. Phys., 2019, 21, 17054 RSC.
- R. Ellerbrock and U. Manthe, Chem. Phys., 2017, 482, 106–112 CrossRef CAS.
- J. M. Bowman, J. Phys. Chem., 1991, 95, 4960–4968 CrossRef CAS.
- R. Welsch and U. Manthe, J. Chem. Phys., 2012, 137, 244106 CrossRef PubMed.
- R. Welsch and U. Manthe, J. Chem. Phys., 2015, 142, 064309 CrossRef PubMed.
- J. M. Bowman, D. Wang, X. Huang, F. Huarte-Larrañaga and U. Manthe, J. Chem. Phys., 2001, 114, 9683–9684 CrossRef CAS.
- U. Manthe, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1992, 97, 3199–3213 CrossRef CAS.
- F. Gatti, B. Lasorne, H.-D. Meyer and A. Nauts, Applications of Quantum Dynamics in Chemistry, Springer, 2017 Search PubMed.
- H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS.
- U. Manthe, J. Chem. Phys., 2008, 128, 164116 CrossRef PubMed.
- U. Manthe, J. Chem. Phys., 1996, 105, 6989–6994 CrossRef CAS.
- U. Manthe, J. Chem. Phys., 2009, 130, 054109 CrossRef PubMed.
- F. Huarte-Larrañaga and U. Manthe, J. Chem. Phys., 2000, 113, 5115–5118 CrossRef.
- G. Schiffel and U. Manthe, J. Chem. Phys., 2010, 132, 084103 CrossRef PubMed.
- R. Welsch and U. Manthe, J. Chem. Phys., 2014, 141, 051102 CrossRef PubMed.
- R. Welsch and U. Manthe, J. Chem. Phys., 2014, 141, 174313 CrossRef PubMed.
- R. Welsch and U. Manthe, J. Phys. Chem. Lett., 2015, 6, 338–342 CrossRef CAS PubMed.
- H. Eyring, Trans. Faraday Soc., 1938, 34, 41–48 RSC.
- B. Kerkeni and D. C. Clary, Phys. Chem. Chem. Phys., 2006, 8, 917–925 RSC.
- S. T. Banks, C. S. Tautermann, S. M. Remmert and D. C. Clary, J. Chem. Phys., 2009, 131, 044111 CrossRef PubMed.
- J. Espinosa-García, M. García-Chamorro and J. C. Corchado, Phys. Chem. Chem. Phys., 2019, 21, 13347–13355 RSC.
- T. C. Allison and D. G. Truhlar, in Testing the Accuracy of Practical Semiclassical Methods: Variational Transition State Theory with Optimized Multidimensional Tunneling, ed. D. L. Thompson, World Scientific, 1998, pp. 618–712 Search PubMed.
- J. Espinosa-García and J. C. Corchado, Phys. Chem. Chem. Phys., 2019, 21, 13356–13367 RSC.
- D. L. Baulch, C. T. Bowman, C. J. Cobos, R. A. Cox, T. Just, J. A. Kerr, M. J. Pilling, D. Stocker, J. Troe, W. Tsang, R. W. Walker and J. Warnatz, J. Phys. Chem. Ref. Data, 2005, 34, 757–1397 CrossRef CAS.
- W. Tsang, J. Phys. Chem. Ref. Data, 1988, 17, 887–951 CrossRef CAS.
- S. R. McConnell and J. Kästner, J. Comput. Chem., 2019, 40, 866–874 CrossRef CAS PubMed.
- P. Winter and J. O. Richardson, J. Chem. Theory Comput., 2019, 15, 2816–2825 CrossRef CAS PubMed.
- S. T. Banks, C. S. Tautermann, S. M. Remmert and D. C. Clary, J. Chem. Phys., 2009, 131, 044111 CrossRef PubMed.
- D. J. Arseneau, D. G. Fleming, Y. Li, J. Li, Y. V. Suleimanov and H. Guo, J. Phys. Chem. B, 2016, 120, 1641–1648 CrossRef CAS PubMed.
- S. M. Greene, X. Shan and D. C. Clary, J. Chem. Phys., 2016, 144, 244116 CrossRef PubMed.
- H. S. Johnston and J. Heicklen, J. Phys. Chem., 1962, 66, 532–533 CrossRef.
- C. Eckart, Phys. Rev., 1930, 35, 1303 CrossRef CAS.
- Y. V. Suleimanov, R. Collepardo-Guevara and D. E. Manolopoulos, J. Chem. Phys., 2011, 134, 044131 CrossRef PubMed.
- J. M. Bowman and B. C. Shepler, Annu. Rev. Phys. Chem., 2011, 62, 531–553 CrossRef CAS PubMed.
- J. M. Bowman, Mol. Phys., 2014, 112, 2516–2528 CrossRef CAS.
- I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2005, 123, 034102 CrossRef PubMed.
- Y. V. Suleimanov, F. J. Aoiz and H. Guo, J. Phys. Chem. A, 2016, 120, 8488–8502 CrossRef CAS PubMed.
- P. R. Spackman, D. Jayatilaka and A. Karton, J. Chem. Phys., 2016, 145, 104101 CrossRef PubMed.
- S. M. Greene, X. Shan and D. C. Clary, J. Chem. Phys., 2016, 144, 084113 CrossRef PubMed.
- X. Shan and D. C. Clary, Phys. Chem. Chem. Phys., 2013, 15, 1222–1231 RSC.
- D. M. Garner, D. G. Fleming, D. J. Arseneau, M. Senba, I. D. Reid and R. J. Mikula, J. Chem. Phys., 1990, 93, 1732–1740 CrossRef CAS.
- D. J. Arseneau, D. M. Garner, I. D. Reid and D. G. Fleming, J. Phys. Chem. A, 2015, 119, 7247–7256 CrossRef CAS PubMed.
- E. Roduner, P. W. F. Louwrier, G. A. Brinkman, D. M. Garner, I. D. Reid, D. J. Arseneau, M. Senba and D. G. Fleming, Ber. Bunsen-Ges. Phys. Chem., 1990, 94, 1224–1230 CrossRef CAS.
- T. Tanaka and T. Takayanagi, Chem. Phys. Lett., 2010, 496, 248–253 CrossRef CAS.
| This journal is © the Owner Societies 2020 |