Disorder-driven doping activation in organic semiconductors

Abstract

Conductivity doping of organic semiconductors is an essential prerequisite for many organic devices, but the specifics of dopant activation are still not well understood. Using many-body simulations that include Coulomb interactions and dopant ionization/de-ionization events explicitly we here show significant doping efficiency even before the electron affinity of the dopant exceeds the ionization potential of the organic matrix (p-doping), similar to organic salts. We explicitly demonstrate that the ionization of weak molecular dopants in organic semiconductors is a disorder-, rather than thermally induced process. Practical implications of this finding are a weak dependence of the ionized dopant fraction on the electron affinity of the dopant, and an enhanced ionization of the weak dopants upon increasing dopant molar fraction. As a result, strategies towards dopant optimization should aim for presently neglected goals, such as the binding energy in host-dopant charge-transfer states being responsible for the number of mobile charge carriers. Insights into reported effects are provided from the analysis of the density of states, where two novel features appear upon partial dopant ionization. The findings in this work can be used in the rational design of dopant molecules and devices.

---

Molecular electrical doping of organic semiconductors has been studied for more than 20 years as a versatile methods to control the conductivity and position of the Fermi level of organic semiconductors.^1–12 It has been employed to improve the performance of organic light-emitting devices, organic solar cells and organic transistors.^3,4,13,14

However, many aspects governing doping in organic semiconductors remain elusive and controversial issues until now. In contrast to their inorganic counterparts, where the ionized dopant atom produces (typically) one charge carrier, free carrier generation in molecularly doped organic materials can be considered as a two-step process. In the first step, the dopant is ionized with donation of a hole to the host, in the second, this electron–hole pair is separated, creating a free hole.^3,7,10 At the same time, it has been reported that only a partial (as opposed to integer) charge transfer may occur in some host-dopant pairs,^5,15 but these processes are not considered here to be able to clearly explore the consequences of integer charge-transfer complexes (ICTCs). It has been shown that even if 100% of the dopants are ionized, only a small fraction of the resulting carriers are mobile, while a considerable fraction of the generated charges remain bonded in ICTCs.^10,16–19 In the ultralow doping regime, a rapid increase of the conductivity attributed to traps passivation is observed.^16,17,20 In the moderate and high doping regime, the binding energy of charge-transfer (CT) states seems to be a main obstacle to reach a high density of mobile carriers.^11,12 Due to a weak screening, ionized host and dopant molecules create electrostatic disorder, which broadens the density of states (DOS).^6,9,21 Finally, the activation energy of the conductivity, which is much lower than the energy of the CT states, drops as the dopant concentration increases.^10,17,22

Considering isolated molecular pairs one can expect that p-dopants are ionized if their electron affinity (EA_d) is higher than the ionization potential of the host (IP_h). The corresponding trend has been indeed experimentally observed: for example, the degree of charge transfer from zinc phthalocyanine (ZnPc) matrix (IP = 5.1 eV) to the dopant 2,3,5,6-tetrafluoro-7,7,8,8-tetracyano-quinodimethane, F₄TCNQ (EA = 5.2 eV) determined from Fourier transform infrared spectroscopy (FTIR) is 100%, while the weaker dopant 7,7′,8,8′-tetracyanoquinodimethane, TCNQ (EA = 4.5 eV) in the same matrix is only 20% ionized.³ However, the material space of the well-characterized dopants reported in the literature is narrow and for hole dopants is mainly restricted to TCNQ – derivatives (TCNQ, F₄TCNQ, F₆TCNNQ) and fluorinated fullerenes (such as C₆₀F₃₆).³ Moreover, these considerations may fall short to describe doping in a matrix, because the EA of dopant molecules embedded into an organic matrix may differ by an order of 1 eV from those measured in the gas phase.²³

Theoretical work on dopant ionization has been limited by the lack of a material-specific mesoscopic model to accurately describe the doping and the charge carrier generation process. In the work of Tietze et al., the dopant ionization has been considered in the context of inorganic doping theory.²⁴ On the basis of this model typical “classical” doping regimes have been rationalized, such as the dopant saturation and the dopant freeze-out (“reserve” regime).¹⁶ However, in organic semiconductors Coulomb interactions play a pivotal role,^6,11 and the particles are not delocalized, so that the statistics applied to inorganic materials cannot be readily applied to these systems. In the following, we present kinetic Monte-Carlo (kMC) simulations, where Coulomb interactions, disorder effects and three-dimensional morphology of the material are explicitly included;^9,25–27 the particular kMC implementation in this work is similar to our recent manuscript,²⁷ but here we analyze the ionization of weak dopants. Calculations were done using the Lightforge kmc package.²⁸ This results in a statistically accurate model that yields the ionized dopant fraction (Z) under equilibrium conditions depending on the strength of the dopant and other relevant parameters of the doped organic semiconductors. To sample the configurational space of the system of neutral and ionized molecules, we determine the time-averaged number of the ionized dopant molecules and the energy distribution of their frontier orbitals. This model explains the recently observed weak dependence of Z on the difference EA_d − IP_h,²⁹ and predicts a new phenomenon: ionization of the dopant due to intrinsic and doping-induced disorder. In addition we discuss two effects related to the configurational entropy of the doped material, which are manifestations of the fundamental difference between doping in inorganic and organic materials: while dopant ionization is a thermally activated process in inorganic materials, it is a disorder-activated process in organic semiconductors. We proved this by explicit simulations of the temperature dependence of Z.

The reported effects result in a drastic modification of the density of states of doped organic materials depending on the strength of the dopant and the energetic disorder of the material. For partly ionized dopants, the density of states modification is even more pronounced than in the case of a strong dopant.¹² We find that the DOS of such materials comprises two dense distributions of the orbital energies of host cations and neutral hosts, as well as two dense distributions of dopant anions and neutral dopants separated by a gap that results from the combination of Coulomb and disorder effects. This picture generalizes the previously discussed modification of the DOS in organic semiconductors with fully ionized dopants towards the case of partially ionized dopants.^6,9,11,12

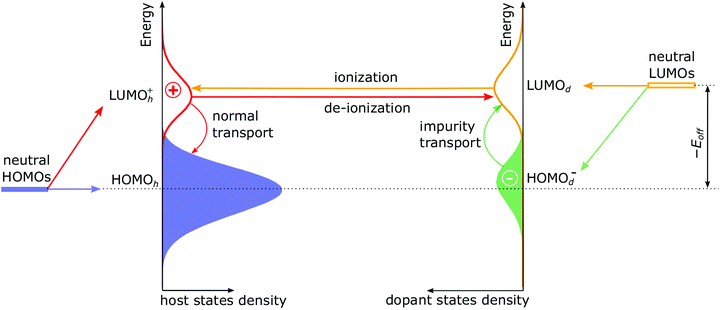
In doped organic semiconductors a typical dielectric permittivity ε of 3…4 is observed, while the distance between molecules is of the order of a = 1 nm. A hole generated by integer charge transfer from a dopant is strongly bound to the dopant due to Coulomb interaction V_C (for instance, assuming a = 1 nm and ε = 4, V_C = −e²/(4πεε₀a) = 0.36 eV (in classical approximation), where e and ε₀ are elementary charge and dielectric constant, respectively). This energy stabilizes the ionized state of the host-dopant pairs (also known as the integer charge-transfer complexes, ICTC)⁵ and favours the ionization of a dopant even if the host-dopant HOMO–LUMO offset defined as E_off = HOMO_h − LUMO_d is negative (normally such a dopant is called a “weak” dopant) but does not exceed V_C (where HOMO_h and LUMO_d are HOMO and LUMO of the host and dopant, respectively) by more than a few k_BT with k_B and T being the Boltzman constant and absolute temperature, respectively. We note that HOMO_h and LUMO_d have to be understood as the corresponding binding energies that is −IP_h and −EA_d, respectively.

The energy of the frontier orbitals in amorphous organic semiconductors is not the same, but distributed with a typical standard deviation σ_int up to 0.2 eV due to intrinsic morphological and electrostatic disorder effects.^30,31 Moreover, charges generated as a result of doping introduce an additional source of disorder, the doping-induced electrostatic disorder.^6,9,21 Finally, doping changes the configurational entropy of the doped organic semiconductor, especially at high doping molar ratios, mainly as a result of the decreased average number of host molecules in the vicinity of the dopant at a high dopant concentration. All these effects are addressed in the following, using Monte-Carlo simulations where we explicitly determine the fraction of the ionized dopants in the vicinity of the “turning point” E_off = V_C that formally splits “weak” (E_off < V_C) and “strong” (E_off > V_C) dopants (see ESI,† Section S1).

To fully describe doped organic semiconductors, we consider the following four microscopic processes: hopping of a hole from host to host molecule and from dopant to dopant molecule; ionization of the dopant (charge separation) and charge recombination (see ESI,† Section S2). In this work we intend to identify and quantify the main distinctive factors responsible for the ionization of molecular dopants in organic materials, which distinguish ionization of doped organic semiconductors from inorganic doped semiconductors and organic salts (two closets materials classes in the regard of the ionization). To this end, we consider a model of p-doped organic semiconductor at 300 K (if otherwise is not stated) with relative permittivity ε =  4, where molecular sites are mapped to a cubic lattice with a lattice spacing of 1 nm. Dopant molecules randomly substitute host molecules. The number of sites were chosen dependent on the dopant concentration: from 10⁶ sites in the case of the low dopant concentration to 8 × 10³ for high dopant concentration. Each point shown on the plots below is a time average taken over the last 1000 steps of the 10⁶ steps kMC trajectory and 100 replicas. More details are provided in ESI,† Section S3 We note that this model does not take into account such possible effects as dopant clustering or morphological changes due to doping, which may potentially influence ionization fraction of the dopants.

To gain insights into dopant ionization, we first analyse the modification of the DOS upon doping, which is shown in Fig. 1 at the example of a 50% ionized dopant. Extraction of the orbital-resolved DOS from the kMC simulations are given in ESI,† Section S4. It is known that for doped organic semiconductor with 100% ionized (“strong”) dopants, the formation of the host-dopant charge-transfer states modifies the DOS of the host material. This, in turn, yields a novel HOMO_h-derived LUMO_h⁺ level that is separated from the original HOMO_h by electron–hole binding energy in ICTCs.^10,11,27 The magnitude of this separation (sometimes referred to as the Coulomb gap) consists of the coulomb interaction of the adjacent host-dopant ions and additional contribution due to material disorder.²⁷ In the case of weak dopants (Fig. 1), LUMO_d has to be considered as well. Upon dopant ionization (as the dopant gets an electron from the host), LUMO_d gives rise to a HOMO_d⁻ level, which is shifted down with respect to (w.r.t.) the LUMO_d by the same mechanism as the LUMO_h⁺ is shifted down w.r.t. the HOMO_h. In addition, the doping-induced disorder broadens the DOS. Detailed reasoning on the appearance and positioning of HOMO_h, LUMO_d and derived LUMO_h⁺ and HOMO_d⁻ distributions are given in ESI,† Section S5.

Fig. 1 Density of states of an organic semiconductor doped with a weak (approximately 50% ionized) dopant extracted from kMC simulations (E_off = V_C − 0.15 eV, ε = 4, σ_int = 0.1 eV). Upon dopant ionization, generated hole tends to stay in proximity to dopant anion. The presence of an opposite charge next to the ionized molecules causes the HOMO_d⁻ and LUMO_h⁺ distributions to shift up and down, respectively. As a result, new dense LUMO_h⁺ and HOMO_d⁻ distributions (levels) appear. Charge carrier dynamics is comprised of four microscopic processes shown by arrows: normal and impurity transport and ionization and deionization of a dopant. The energy axis has been removed to enhance perception of the qualitative physical picture, but fully labelled figures of the DOS are presented below.

The four processes that occur in doped organic semiconductor with a weak dopant are shown in Fig. 1. Note that the dopant ionization can be considered either as a hop of the hole from the dopant LUMO to the LUMO_h⁺ (which is shown in Fig. 1), or as an electron hop from the host HOMO to the HOMO_d⁻. In both cases, an electron–hole pair is generated.

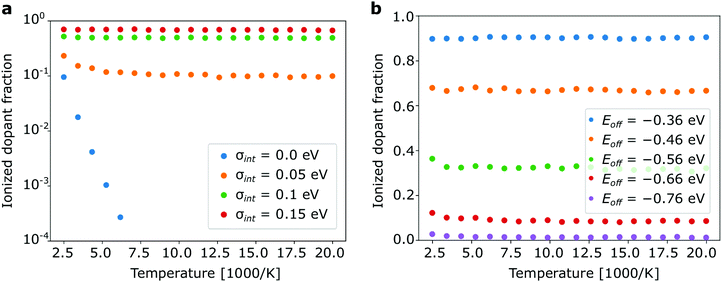
Fig. 2a and 3a show the ionized dopant fraction Z(n_d) = n_d−/n_d (where n_d− and n_d denote ionized and total dopant molar fraction, respectively) as a function of n_d for organic materials without energetic disorder doped with a weak dopant (the procedure of extraction of Z from kMC simulations is given in ESI,† Section S4). If the dopant activation would be governed exclusively by the mean values of HOMO_h and LUMO_d, charge transfer would be energetically unfavourable if E_off < V_C. As a result, the thermally activated ionized dopant fraction Z would be exponentially small. For example, at E_off = V_C − 0.15 eV, where 0.15 eV is approximately six times higher than the room-temperature k_BT, one would expect only Z = e⁻⁶ ≈ 0.2% ionized dopants. However, the kMC simulations for zero intrinsic disorder predict such a small dopant ionization rate only at very low dopant concentrations (Fig. 2a). Starting from 1 mol% doping, a sharp ionization enhancement is observed and the ionized dopant fraction exceeds 40%. On the other hand, for typical amorphous organic materials with intrinsic disorder 0.1 eV, Z is over 50% for essentially the entire attainable dopant concentration range (Fig. 3a). Below, we provide an explanation of these observations.

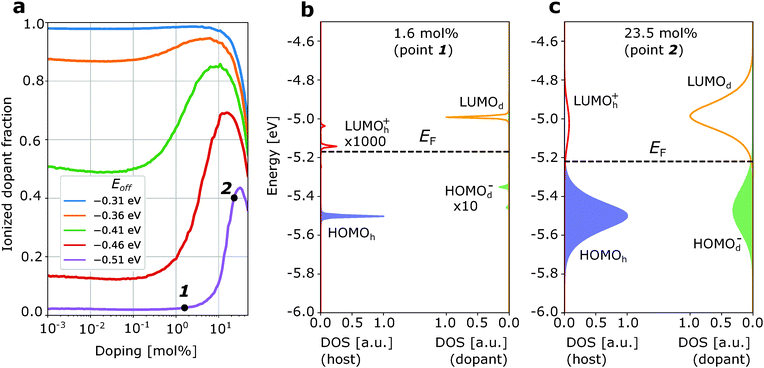Fig. 2 Enhancement of weak dopant ionization due to doping-induced disorder. (a) Dopant ionization rate as a function of dopant molar ratio for a material with zero intrinsic energetic disorder. The two visible peaks at LUMO_h⁺ and HOMO_d⁻ distributions correspond to the host-dopant pairs at a distance a and 2a with a being the lattice constant. (b) Density of frontier orbitals states at low dopant concentration (1.6 mol%). (c) The same as (b) at higher dopant concentration (23.5 mol%). Note: the scale of the DOS is different for host and dopant, but the same for HOMO and LUMO of the host/dopant. The increase of Z at very low (<10⁻² mol%) and very high (>10 mol%) dopant concentrations is the manifestation of high/low-configurational entropy effects. The Fermi level E_F (dashed line) is computed using charge neutrality equation.²⁷

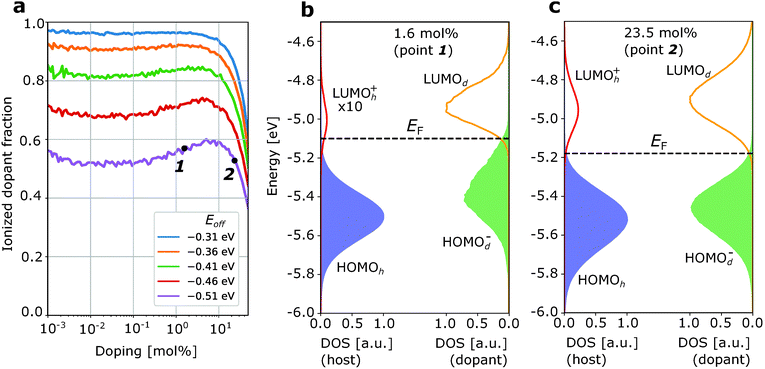Fig. 3 Ionization of the weak dopant in the organic matrix with typical intrinsic disorder σ_int = 0.1 eV. (a) Ionized dopant fraction Z as a function of doping concentration. (b) Density of frontier orbitals at low doping concentration (1.6 mol%). (c) The same as (b) at higher dopant concentration (23.5 mol%). Additional broadening of the DOS due to doping-induced disorder is not substantial (comparing the difference between (b) and (c) here and (b) and (c) in Fig. 2). As a result, dopant concentration dependence of Z is weak. The increase of Z at very low (<10⁻² mol%) and very high (>10 mol%) dopant concentrations is due to entropic effects (as in Fig. 2).

First, we discuss how intrinsic disorder impacts dopant ionization. Let us consider a small dopant concentration (1.6 mol%), where doping-induced disorder can be neglected due to low dopant concentration. For a weak dopant with E_off = V_C − 0.15 eV = −0.51 eV in a material without intrinsic disorder, this leads to a very small, 2% ionized dopant fraction (Fig. 2a). The density of states plotted in Fig. 2b, corresponding to the dopant molar fraction labelled by 1 in Fig. 2a, shows that the LUMO_h⁺ distribution remains below LUMO_d so that it is energetically favourable for holes to stay at LUMO_d rather than hopping to the LUMO_h⁺. Ionization events in this case would have to overcome a problematic 0.15 eV barrier. In contrast, for a material with intrinsic disorder σ_int = 0.1 eV (Fig. 3a) at the same dopant concentration, the ionized dopant fraction is as large as ≈50%. In order to explain this from a microscopic point of view, we can imagine a single dopant and the energetics of the several adjacent host molecules (six in a fictitious cubic lattice). For the material with zero disorder, the HOMO is the same for all hosts and separated by 6k_BT from the LUMO of the dopant and as a result, there is only a very small probability that the dopant is ionized (about 6e⁻⁶ ≈ 0.012). On the other hand, for a material with intrinsic disorder, the HOMO of the host fluctuates around the mean value with a standard deviation of σ_int = 0.1 eV. As a result, it often occurs that at least for one of the neighbouring hosts E_off − V_C > −0.15 eV (Fig. 3a), favouring charge transfer even without the necessity of thermal activation. In other words, the ionization of a very weak dopant can be facilitated by intrinsic disorder. Fig. 3b “macroscopically” shows the same phenomenon.

Now, we discuss the role of doping-induced (extrinsic) disorder, which is more pronounced in materials with low intrinsic disorder.²⁷ As reported earlier, dopant anions and host catios, which are mostly paired in CT complexes, generate electric field felt by other molecules. As dopants distribution in the host is random, this field creates an additional (doping-induced) electrostatic disorder that randomly shifts energy levels of molecules.^6,11,27 In the material with zero intrinsic disorder, this source of energy disorder is the only one. Its mean value increases upon doping and the standard deviation of HOMO_h, σ, reaches 0.12 eV at 20 mol% for material with a = 1 nm and ε = 4 (see ESI,† Section S6). For this reason, in Fig. 2a we observe a steep increase of the ionized dopant fraction with increasing dopant concentration (once doping-induced disorder becomes comparable to k_BT). In doped materials with non-zero intrinsic disorder, this effect is much weaker (see Fig. 3a where ionized dopant fraction is computed for materials with intrinsic disorder 0.1 eV) due to smaller excess disorder defined as σ_exc = σ_tot − σ_int. In the first approximation, intrinsic and doping-induced disorders are uncorrelated and thus the total disorder is equal to (σ_int² + σ_dop²)^1/2, which is smaller than σ_int + σ_dop. Moreover, in highly disordered organic semiconductors (σ_int = 0.2 eV), the intrinsic disorder is overcompensated by doping, that is the total disorder at high dopant molar fractions decreases in spite of progressively higher doping-induced disorder.²⁷ We note that this work does not include the possible effect of enhanced structural disorder due to doping.

The effect of the enhanced dopant ionization due to doping-induced disorder correlates with recent observations, where the conductivity of different organic host semiconductors, poly2,3-bis(3-octyloxyphenyl)-5,8-quinoxalinediyl-2,5-thiophenediyl (TQ1) and regioregular-poly(3-hexylthiophene-2,5-diyl) (P3HT) doped with F₄TCNQ was measured as a function of dopant concentration.³² For TQ1, F₄TCNQ is a weak dopant (E_off = −0.36 eV), while it is a very strong dopant (E_off = 0.76 eV) for P3HT (E_off is estimated taking experimental values of IP and EA, and is only a qualitatively measure of the real energy offset). For P3HT:F₄TCNQ, the conductivity increases monotonically (almost linearly as expected in the case of the full dopant ionization) over the whole doping range of the dopant molar fraction: from 10⁻⁵ to 10⁻¹. For TQ1:F₄TCNQ, however, conductivity is nearly the same at low dopant concentration, and then sharply increases starting from 0.1 mol% – which agrees with the behavior of Z in Fig. 2a. This sharp increase of the conductivity for TQ1:F₄TCNQ and the absence of this effect in the case of P3HT:F₄TCNQ is an indication of the disorder-induced ionization of the dopant according to the mechanism illustrated in Fig. 2b and c.

The effects of intrinsic and doping-induced material disorder do not explain our observation that the ionized dopant fraction slightly rises at a very low n_d (n_d < 10⁻⁴) and steeply drops at a very high n_d (n_d > 0.1) – see Fig. 2a and 3a. These two effects are high- and low-entropy effects as explained below.

If n_d is of the order of 1/n_nn (n_nn being the number of nearest neighbours) or larger, the number of statistically relevant microstates for the ionized dopant molecules decreases, yielding a sharp decrease of the ionization probability. Indeed, the smaller the number of the hosts next to the dopant, the smaller is the probability that one of the remaining neighbouring hosts has an IP that favours the ionization of the dopants. If the number of statistically relevant microstates is of the order of 1/n_nn, entropy effects are negligible and this “medium doping” regime can be treated solely by the effects of intrinsic and extrinsic disorder. Finally, if n_d is below 10⁻³, a slight increase of the ionized dopant fraction is observed. In this scenario the number of microstates that correspond to the ionized dopant state overcompensates the fact that they are all energetically unfavourable. The range of doping where it is observed being of a little practical relevance. We emphasize, however, that this small effect is not a numerical simulations artefact, but a physical feature. It can be referred to as a “high entropy effect”.

According to the recent experimental data, the ionized dopant fraction of a F₆-TCNNQ dopant in ZnPc matrix, drops at high dopant rates (starting from n_d = 10⁻²…10⁻¹) from 100% to 50%, indicating a small entropy effect.¹⁰ According to another experimental measurement of the F₄TCNQ-doped P3HT layer, the dependence of Z on the doping ratio is weak and qualitatively similar to our simulation results (Fig. 3a): at a low dopant concentration (doping ratio 1 : 200) Z first slowly drops (high-entropy effect) from 0.77 to 0.51 and then slowly increases from 0.64 to 0.67 at a doping ratio of 1 : 40 (doping-induced disorder effect).³³

Note that the drop of Z at high dopant concentrations (>10 mol%) is due to the small entropy effect, theoretically predicted here, and does not require dopant clustering or morphological changes of the material. In some doped materials (e.g. P3HT:F4TCNQ), material morphology can indeed be strikingly distinct at low and high dopant concentrations, including aggregation (clustering) of dopants in the latter case.^34–37 Based on this, the drop of Z has been explained solely by morphological changes at high doping concentrations (>10 mol%). In light of our results, this explanation has to be partly revised. We can claim that at high dopant concentration, Z would drop even if dopants are randomly distributed rather than clustered. If dopant molecules tend to form clusters as reported for P3HT:F4TCNQ,^34–37 this will probably lead to an even stronger drop of Z.

After considering how energetic disorder enhances ionization of weak dopants, we investigate how weak dopants can be ionized in a given matrix despite large negative (unfavorable) values of the offset energy: E_off = HOMO_h − LUMO_d ≤ V_C.

Fig. 4a shows the dependence of the ionized dopant fraction on the dopant strength, i.e. the offset energy E_off, for a material with intrinsic disorder σ_int = 0.15 eV. We observe that even for negative offset energies as low as −0.6 eV, the ionization rate exceeds 50%. For comparison, experimental data reported for N,N′-di(naphthalene-1-yl)-N,N′-diphenyl-benzidine (α-NPD), N,N′-(diphenyl-N,N′-bis)9,9,-dimethyl-fluorene-2-yl-benzidine (BF-DPB), 9,9-bis4-(N,N-bis-biphenyl-4-yl-amino)phenyl-9H-fluorene (BPAPF), and 4,4′,4′′-tris(carbazolyl-9-yl)-triphenylamine (TCTA) doped with highly fluorinated fullerene (C₆₀F₄₈) at a dopant molar ratio of 4% are plotted in the same figure.²⁹ The experimental offset energy E_off is extracted from the LUMO_d and HOMO_h reported in the same reference. The results of the kMC simulations are in good agreement with reported experimental data. The experimentally observed weak dependence of the ionized dopant fraction on the offset energy is due to the energetic disorder. Fig. 4b–d show the changes in the density of the dopant states as the “weakness” of the dopant, −E_off, increases: for E_off = −0.06 eV (Fig. 4b) 99.7% dopant molecules are ionized and only the ionization of the upper tail of LUMO_d distribution causes a small neutral dopant fraction. For weaker dopants (E_off = −0.56 eV, Fig. 4c) 56.4% dopants are ionized – mainly from the lower part of the LUMO distribution. Finally, for the offset of −1.06 eV (Fig. 4d), 99.5% of dopants are neutral, so that only host molecules of the upper part of HOMO_h distribution, that slightly overlap with LUMO_d, are ionized. HOMO⁽⁰⁾_h, LUMO⁽⁰⁾_d, and LUMO⁽⁰⁾_d − |V_C| marked with dashed lines are the mean energies of the HOMO_h and LUMO_d distributions and the expected position of the mean HOMO_d⁻ distribution, if it would be shifted w.r.t. the mean LUMO_d by exactly V_C. The offset energy −E_off is the difference between the black and green dashed line.

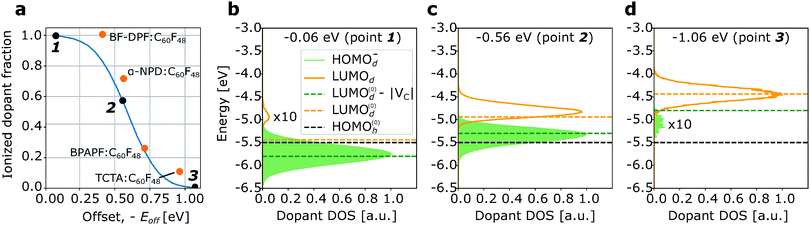Fig. 4 (a) Simulated ionized dopant fraction as a function of the negative offset energy −E_off between the HOMO_h and LUMO_d (solid line) and experimental data for different hosts doped by C₆₀F₄₈ (orange points).²⁹ (b and c) Density of states of dopant molecule for different E_off values (black points at (a)). Simulations has been done for material with σ_int = 0.15 eV, ε = 4, and σ_int = 0.1 eV and dopant molar ratio of 4%. The area filled in green is proportional to the ionized dopant fraction; the area under the orange line is proportional to the “inactive” (neutral) dopants. The offset energy −E_off is the distance between the black and orange dashed lines; the green dashed line denotes the expected mean value of the HOMO_d⁻ distribution, i.e. LUMO⁽⁰⁾_d − V_C.

Our simulations show that in case of strong dopants Z reaches 1 as the difference between HOMO_h and LUMO_d exceeds V_C with no noticeable temperature dependence at all (relevant temperature range). In contrast to inorganic semiconductor theory we observe only a very weak temperature dependence of the ionization ratio for weak dopants with E_off < V_C (Fig. 5). The only exception is a fictitious material with zero energetic disorder (Fig. 5a), where thermal activation is clearly seen. Already at σ_int = 0.05 eV, which can only be attained in nearly crystalline materials, the temperature dependence is very weak. Fig. 5a explicitly shows the fundamental difference between doping in organic and inorganic semiconductors: doping in weak organic semiconductors is a disorder-rather than temperature-activated process and rising disorder increases the ionized dopant fraction by orders of magnitude at room temperature. The reason for this is that the scale of the energetic disorder is almost one order of magnitude greater than the room temperature k_BT. The mentioned dopant freeze-out regime (exponential drop of the ionized dopant faction at low temperatures) is thus unlikely to be observed in organic semiconductors. Even in organic semiconductors with low disorder the temperature dependence of Z will be “masked” by the effect of disorder.

Fig. 5 Temperature dependence of the dopant ionization fraction: (a) for materials with various intrinsic energy disorder and offset energy E_off = −0.51 eV. Note that the intrinsic material disorder significantly enhances ionization of weak dopants while dopant ionization depends on the temperature only for materials with zero intrinsic disorder; (b) for materials with a typical disorder of 0.1 eV no temperature dependence of the dopant ionization is observed, regardless of the energy offset. The molar dopant fraction is 1 mol% for both plots.

If the offset energy increases (very weak dopants), the temperature dependence starts to slowly develop (Fig. 5b) but this only holds for noticeable unrealistic systems in which less than 1% of the dopant molecules are ionized.

All effects reported in this work can be qualitatively understood as a result of the interplay of various energy scales relevant for electronic processes in doped organic semiconductors. These are: (i) scale of the thermal fluctuations k_BT = 0.025 eV, (ii) scale of the intrinsic material disorder: <0.2 eV; (iii) scale of the total disorder (including doping-induced disorder): σ < 0.22 eV (for a typical organic material considered here). In contrast to inorganic semiconductor theory we find that thermal fluctuations play only a minor role (see Fig. 5) for all application relevant materials. The doping-induced disorder dominates all other energy scales if intrinsic disorder is lower than k_BT. Thus, we observe an enhanced ionization of weak dopants in non-disordered semiconductor if we add more dopants (Fig. 2). This effect corresponds to the transition of dominant energy scale from k_BT to the scale of doping induced disorder.

Intrinsic disorder typically dominates other energy scales at small doping concentration. Higher intrinsic disorder favours the ionization of weak dopants (cf.Fig. 2a and 3a), and Z does not depend on the dopant concentration.

Finally, the offset-dependence of the ionized dopant fraction demonstrated here (Fig. 4) and observed earlier in experiments is quite weak,²⁹ because it is defined by the energy scale of the intrinsic material disorder (typical value: 0.1 eV), not the room-temperature k_BT = 0.025 eV, as in the case of inorganic semiconductors. Considering a host-dopant material, where 90% of the dopants are ionized, one would need to decrease EA of the dopant by approximately 0.5 eV to reduce dopant ionization to 10%. This finding has important implications for material design. Rather than aiming at a shift of 100 meV of the EA of the dopant in a favorable direction, it may be much more promising to optimize other dopant properties, e.g. the energy of the ICTC states responsible for the number of mobile charge carriers.^11,12

Note that in this work we restrict ourselves to the case of the complete charge transfer from the dopant to the host molecule. This assumes a weak hybridization between the HOMO of the host and LUMO, in which the pair may be either neutral or the integer charge transfer complex (ICTC) is formed known also as IPA (ion pair association).⁵ If the host HOMO – dopant LUMO hybridization if strong, the hybrid host-dopant state (CTX) and incomplete charge transfer are observed.⁵ Incomplete charge transfer with a strong dopant-host orbital hybridization has been reported in pentacene doped with F₄TCNQ regioregular-poly(3-hexylthiophene-2,5-diyl) (rrP3HT) doped with F₄TCNQ.¹⁵ It has been reported that the as-prepared P3HT:F₄TCNQ features ICTCs, whereas upon aging ICTCs are steadily transforming into CTXs.⁴²

It is instructive to compare molecules ionization of doped organic materials with that of another organic materials class, organic or CT salts.³⁹ Similar to doped organic semiconductors, a full ionization in organic salts (a typical representative is TTF-TCNQ, where TTF and TCNQ stand for tetrathiafulvalene and tetracyanoquinodimethane, respectively) is experimentally and theoretically proven to be determined primarily by the negative of the offset energy −E_off (that favours the neutral state of molecules in the crystal) and the Madelung energy V_M (which, unlike V_C, includes not only the short-range donor–acceptor pair Coulomb interaction, but all short- and long-range interactions of a given ion with all other ions of the ionic crystal),^37,40 which favours the ionized state. As a result, for |V_M| ≫ −E_off the salt is expected to be fully ionized; for |V_M| ≪ −E_off the salt is expected to be neutral, which correlates well with experimental data.³⁹ As the molecules constituting π-stacks of organic salts are planar and are separated by only 3.5 Å, Coulomb interaction of the adjacent ions is about 4 eV, if one assumes these interactions to be unscreened. The Madelung energies, which include all short and long-range interactions are estimated to be 2…5 eV,^38,41 in particular for a prototypical organic salt TTF-TCNQ, V_M = 2.3 eV.³⁵ This means that the ionization of salts even with large negative E_off is possible.

We note that the estimation of the V_M and −E_off is made using gas-phase electron affinity/ionization potential and assuming unscreened Coulomb interactions. Both assumptions are relatively rough. Thus, recent IPES measurements report EA of TCNQ thin films of 4.23 eV as compared to EA = 2.8 eV in the gas-phase (the difference is 1.43 eV).^38,43 This is confirmed by the accurate quantum chemistry computation at GW level showing that the error in estimation of the offset energies in the solid state made with the use of vacuum binding energies of the host-dopant systems may exceed 1 eV (analyzed systems are pentacene and NPD (full name: N,N′-diphenyl-N,N′-bis(1-naphthyl)-1,1′-biphenyl-4,4′-diamine) doped with F₄TCNQ).²³ In addition, Coulomb interactions of the nearest host-dopant pair in a prototypical doped organic crystal (pentacene:F₄TCNQ) are shown to be strongly screened: the Coulomb interaction as a function of distance between host cation and dopant anion are well-fitted by that of the point charges interacting in the effective medium with the dielectric permittivity of 3.5, which is in strong contrast to assuming non-polarizable medium as it is done for Madelung energies in organic salts. A good predictive abilities of the estimations based on unscreened Coulomb interactions and the gas-phase offset energies may thus be ascribed to error compensation (that is, both Coulomb interaction and offsets are overestimated).

By assuming that the Coulomb interactions in CT complexes can be approximated classically that is by point-charges interaction in effective-medium with epsilon of an organic semiconductor, we have relied on the mentioned GW embedded computations,²³ which (to the best of our knowledge) represents the most reliable estimation of the CT energy in doped materials available so far.

In comparison to organic salts, small organic molecules in amorphous materials are normally larger, more bulky and do not form π–π stacks (these have amorphous morphologies) as opposed to those used in organic salts, which is expected to (1) increase the effective distances between charges and (2) provide additional screening, both reducing Coulomb interactions.

Comparing doped organic semiconductors to organic salts close to the point where the offset energy is almost compensated by coulomb interaction (−E_off ≈ V_C for organic salts and −E_off ≈ V_M for doped organic semiconductors) reveals principal difference between two materials classes. Organic salts in these conditions may demonstrate the incomplete charge transfer (only part of the molecules are ionized) and become metallic.³⁸ The metallicity has never been reported for doped small-molecule organic semiconductors perhaps because it requires a long-range order and bands transport. In contrast, the effect of the static energy disorder discussed here is a specific effect for amorphous organic materials and may not be observed in organic salts (static energy disorder in a perfect crystals is zero).

Conclusions

In this work we have presented a thorough analysis of a charge-resolved mesoscopic model for doped organic semiconductors. Our kMC simulations provided first insight into the modification of the density of states of an organic semiconductor doped by a weak dopant. In comparison to strong dopants, where doping efficiency is governed by the HOMO of the host and its derived LUMO⁺ polaron level, the energy landscape of OS doped with weak dopants has two additional relevant levels: LUMO of the neutral dopant and HOMO⁺ of the dopant cation. The effects described below can now be understood by shifts of these energy levels and their broadening. Performing kMC simulations, we have explicitly shown that the ionization of weak dopants is activated by disorder rather than temperature, in stark contrast to doped inorganic materials. We have shown that strong Coulomb interactions and charge localization highly affect the ionization ratio of organic dopants in an organic matrix and introduce unique features that cannot be accounted for in inorganic semiconductor models.

First of all, Coulomb interactions in the ionized host-dopant pair favour dopant ionization and the dopant ionization does not require HOMO_h − LUMO_d > 0, as naively expected, but the condition HOMO_h − LUMO_d > V_C is sufficient even in the absence of disorder. Secondly we find that in contrast to inorganic semiconductor models, the relevant energy scale that controls doping is not the temperature, but the disorder of the material. The disorder comprises not only the intrinsic morphological and electrostatic disorder of the material,³⁰ but also the doping-induced disorder.⁶

As a result, even nominally weak dopants according to the energy criterion above can be almost fully ionized for several reasons: charge localization and low screening induce electrostatic disorder and strongly affect the ionized dopant fraction. As far as doping-induced disorder depends on doping concentration, so does the ionized dopant fraction. This is accentuated strongly in dopants, for which HOMO_h − LUMO_d < V_C in host materials with low intrinsic disorder. For these systems the ionized dopant fraction at high doping levels (>10 mol%) exceeds that in low doping regime by a factor of 40.

In materials with high intrinsic disorder (0.1 eV and higher), ionization of the weak dopants is additionally enhanced because of random fluctuations of the value HOMO_h − LUMO_d, which favours ionization of some dopant-host pairs energetically. As an example, taking two materials with E_off = −0.51 eV, one with zero and one with 0.1 eV intrinsic disorder, the dopant ionization fractions are 2% and 55%, respectively.

One widely pursued strategy to make doping more efficient aims to increase the energy offset E_off = HOMO_h − LUMO_d. We demonstrate here that the ionized dopant fraction (particularly in the case of weak dopants) depends only weakly on this difference (Fig. 4). Our results therefore suggest alternative strategies to reach high doping efficiency, addressing other critical factors such as the energy of ICTCs.^11,12

Conflicts of interest

W. W. holds shares of a KIT spinoff, Nanomatch GmbH, which markets software developed by KIT. The other authors declare no competing interests.

Acknowledgements

A. F. and W. W. received funding from the European Union Horizon 2020 research and innovation programme under grant agreement no. 646176 (EXTMOS). This work was performed on the supercomputer ForHLR-II funded by the Ministry of Science, Research and the Arts Baden-Württemberg and by the Federal Ministry of Education and Research.

Notes and references

1. J. Blochwitz, M. Pfeiffer, T. Fritz and K. Leo, Appl. Phys. Lett., 1998, 73, 729.
2. A. Yamamori, C. Adachi, T. Koyama and Y. Taniguchi, Appl. Phys. Lett., 1998, 72, 2147.
3. B. Lüssem, M. Riede and K. Leo, Phys. Status Solidi A, 2013, 210, 9.
4. B. Lüssem, C.-M. Keum, D. Kasemann, B. Naab, Z. Bao and K. Leo, Chem. Rev., 2016, 116, 13714.
5. I. Salzmann, G. Heimel, M. Oehzelt, S. Winkler and N. Koch, Acc. Chem. Res., 2016, 49, 370.
6. V. I. Arkhipov, P. Heremans, E. V. Emelianova and H. Bässler, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(4), 45214,  DOI:10.1103/PhysRevB.71.045214.
7. A. Mityashin, Y. Olivier, T. Van Regemorter, C. Rolin, S. Verlaak, N. G. Martinelli, D. Beljonne, J. Cornil, J. Genoe and P. Heremans, Adv. Mater., 2012, 24, 1535.
8. S. Winkler, P. Amsalem, J. Frisch, M. Oehzelt, G. Heimel and N. Koch, Mater. Horiz., 2015, 2, 427.
9. G. Zuo, H. Abdalla and M. Kemerink, Phys. Rev. B, 2016, 93(23), 235203,  DOI:10.1103/PhysRevB.93.235203.
10. M. L. Tietze, J. Benduhn, P. Pahner, B. Nell, M. Schwarze, H. Kleemann, M. Krammer, K. Zojer, K. Vandewal and K. Leo, Nat. Commun., 2018, 9, 1182,  DOI:10.1038/s41467-018-03302-z.
11. C. Gaul, S. Hutsch, M. Schwarze, K. S. Schellhammer, F. Bussolotti, S. Kera, G. Cuniberti, K. Leo and F. Ortmann, Nat. Mater., 2018, 17, 439.
12. M. Schwarze, C. Gaul, R. Scholz, F. Bussolotti, A. Hofacker, K. S. Schellhammer, B. Nell, B. D. Naab, Z. Bao, D. Spoltore, K. Vandewal, J. Widmer, S. Kera, N. Ueno, F. Ortmann and K. Leo, Nat. Mater., 2019, 18, 242.
13. K. Walzer, B. Maennig, M. Pfeiffer and K. Leo, Chem. Rev., 2007, 107, 1233.
14. I. E. Jacobs and A. J. Moulé, Adv. Mater., 2017, 1703063.
15. I. Salzmann, G. Heimel, S. Duhm, M. Oehzelt, P. Pingel, B. M. George, A. Schnegg, K. Lips, R.-P. Blum, A. Vollmer and N. Koch, Phys. Rev. Lett., 2012, 108(3), 35502,  DOI:10.1103/PhysRevLett.108.035502.
16. M. L. Tietze, P. Pahner, K. Schmidt, K. Leo and B. Lüssem, Adv. Funct. Mater., 2015, 25, 2701.
17. S. Olthof, W. Tress, R. Meerheim, B. Lüssem and K. Leo, J. Appl. Phys., 2009, 106, 103711.
18. Y. Zhang, B. de Boer and P. W. M. Blom, Adv. Funct. Mater., 2009, 19, 1901.
19. Y. Zhang and P. W. M. Blom, Org. Electron., 2010, 11, 1261.
20. Y. Zhang, B. de Boer and P. W. M. Blom, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085201.
21. X. Lin, G. E. Purdum, Y. Zhang, S. Barlow, S. R. Marder, Y.-L. Loo and A. Kahn, Chem. Mater., 2016, 28, 2677.
22. F. Zhang and A. Kahn, Adv. Funct. Mater., 2018, 28, 1703780.
23. J. Li, I. Duchemin, O. M. Roscioni, P. Friederich, M. Anderson, E. Da Como, G. Kociok-Kohn, W. Wenzel, C. Zannoni, D. Beljonne, X. Blase and G. D’Avino, Mater. Horiz., 2019, 6, 107.
24. S. M. Sze and K. K. Ng, Physics of Semiconductor Devices, Wiley-Interscience, Hoboken, NJ, 2007.
25. V. Rühle, A. Lukyanov, F. May, M. Schrader, T. Vehoff, J. Kirkpatrick, B. Baumeier and D. Andrienko, J. Chem. Theory Comput., 2011, 7, 3335.
26. F. Symalla, P. Friederich, A. Massé, V. Meded, R. Coehoorn, P. Bobbert and W. Wenzel, Phys. Rev. Lett., 2016, 117(27), 276803,  DOI:10.1103/PhysRevLett.117.276803.
27. A. Fediai, F. Symalla, P. Friederich and W. Wenzel, Nat. Commun., 2019, 10, 4547.
28. F. Symalla, S. Heidrich, M. Kubillus, T. Strunk, T. Neumann and W. Wenzel, SID Symp. Dig. Tech. Pap., 2019, 50, 259.
29. B. Nell, K. Ortstein, O. V. Boltalina and K. Vandewal, J. Phys. Chem. C, 2018, 122, 11730.
30. P. Friederich, V. Meded, A. Poschlad, T. Neumann, V. Rodin, V. Stehr, F. Symalla, D. Danilov, G. Lüdemann, R. F. Fink, I. Kondov, F. von Wrochem and W. Wenzel, Adv. Funct. Mater., 2016, 26, 5757.
31. I. I. Fishchuk, A. Kadashchuk, S. T. Hoffmann, S. Athanasopoulos, J. Genoe, H. Bässler and A. Köhler, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 125202.
32. G. Zuo, Z. Li, O. Andersson, H. Abdalla, E. Wang and M. Kemerink, J. Phys. Chem. C, 2017, 121, 7767.
33. P. Pingel and D. Neher, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 115209.
34. E. F. Aziz, A. Vollmer, S. Eisebitt, W. Eberhardt, P. Pingel, D. Neher and N. Koch, Adv. Mater., 2007, 19, 3257.
35. D. T. Duong, C. Wang, E. Antono, M. F. Toney and A. Salleo, Org. Electron., 2013, 14, 1330.
36. E. Lim, K. A. Peterson, G. M. Su and M. L. Chabinyc, Chem. Mater., 2018, 30, 998.
37. D. T. Duong, H. Phan, D. Hanifi, P. S. Jo, T.-Q. Nguyen and A. Salleo, Adv. Mater., 2014, 26, 6069.
38. K. E. Watts, B. Neelamraju, E. L. Ratcliff and J. E. Pemberton, Chem. Mater., 2019, 31, 6986.
39. J. B. Torrance, Acc. Chem. Res., 1979, 12, 79.
40. E. Madelung, Phys. Z, 1918, 524.
41. L. Glasser, Inorg. Chem., 2012, 51, 2420.
42. J. B. Torrance and B. D. Silverman, Phys. Rev. B: Solid State, 1977, 15, 788.
43. B. Wegner, L. Grubert, C. Dennis, A. Opitz, A. Röttger, Y. Zhang, S. Barlow, S. R. Marder, S. Hecht, K. Müllen and N. Koch, J. Mater. Chem. C, 2019, 7, 13839.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01333a

---