Static field gradient NMR studies of water diffusion in mesoporous silica†
Abstract
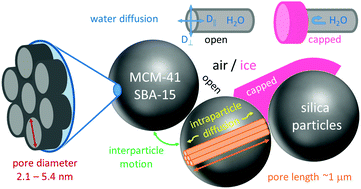
NMR diffusometry is used to ascertain the pore-size dependent water diffusion in MCM-41 and SBA-15 silica over broad temperature ranges. Detailed analysis of 1H and 2H NMR stimulated-echo decays reveals that fast water motion through voids between different silica particles impairs such studies in the general case. However, water diffusion inside single pores is probed in the present approach, which applies high static field gradients to enhance the spatial resolution of the experiment and uses excess water in combination with subzero temperatures to embed the silica particles in an ice matrix and, thus, to suppress interparticle water motion. It is found that the diffusion of confined water slows down by almost two orders of magnitude when the pore diameter is reduced from 5.4 nm to 2.1 nm at weak cooling. In the narrower silica pores, the temperature dependence of the self-diffusion coefficient of water is well described by an Arrhenius law with an activation energy of Ea = 0.40 eV. The Arrhenius behavior extends over a broad temperature range of at least 207–270 K, providing evidence against a fragile-to-strong crossover in response to a proposed liquid–liquid phase transition near 225 K. In the wider silica pores, partial crystallization results in a discontinuous temperature dependence. Explicitly, the diffusion coefficients drop when cooling through the pore-size dependent melting temperatures Tm of confined water. This finding can be rationalized by the fact that water can explore the whole pore volumes above Tm, but is restricted to narrow interfacial layers sandwiched between silica walls and ice crystallites below this temperature. Comparing our findings for water diffusion with previous results for water reorientation, we find significantly different temperature dependencies, indicating that the Stokes–Einstein–Debye relation is not obeyed.
- This article is part of the themed collection: 2020 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...