Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pyroelectrically-driven chemical reactions described by a novel thermodynamic cycle†
Mateo U.
de Vivanco‡
 *a,
Matthias
Zschornak‡
a,
Hartmut
Stöcker
a,
Sven
Jachalke
a,
Erik
Mehner
a,
Tilmann
Leisegang
*a,
Matthias
Zschornak‡
a,
Hartmut
Stöcker
a,
Sven
Jachalke
a,
Erik
Mehner
a,
Tilmann
Leisegang
 ab and
Dirk C.
Meyer
a
ab and
Dirk C.
Meyer
a
aTechnische Universität Bergakademie Freiberg, Institut für Experimentelle Physik, Leipziger Straße 23, 09596 Freiberg, Germany. E-mail: mateo.devivanco@physik.tu-freiberg.de; Fax: +49 3731 39 4314; Tel: +49 3731 39 3341
bSamara State Technical University, Samara Center for Theoretical Materials Science, Molodogvardeyskaya Str. 244, 443100 Samara, Russia
First published on 26th June 2020
Abstract
Pyroelectrocatalysis is the conversion of thermal energy directly into chemical energy. On the background of renewable energies and the need for efficient industrial processes, the conversion of waste heat into hydrogen is of special relevance. Since the reported thermodynamic cycles for pyroelectric energy harvesting do not fit the conditions encountered in a reactive medium such as water appropriately, we describe a new thermodynamic charge-voltage-cycle characterised by fixed upper and lower potentials. These threshold potentials comprise the redox potential of the reaction of interest – here the hydrogen evolution reaction – as well as an overpotential mainly dictated by the temperature-induced bending of electronic bands in the pyroelectric semiconductor. Because polarisation changes below the threshold are useless for chemical reactions, material properties as well as process conditions have to be chosen accordingly. In particular the particle size along with the temperature difference are shown to determine the conversion efficiency.
1 Introduction
Due to the tremendous ecological footprint of fossil fuels and industry, a meaningful measure to slow down environment degradation would be to improve our energy balance by increasing conversion efficiencies and tapping waste energy sources. The reason is that a considerable share of our primary energy (the energy contained in raw materials) is lost during conversion – an estimated 72% worldwide.1 The heat demand of the chemical, metallurgic and manufacturing industries tends to be very high, sometimes achieving process temperatures well above 1000 °C. High-temperature waste heat could be, disregarding some technical obstacles, directly employed to generate electricity e.g. with the aid of the Rankine cycle.2On the other hand, low-grade waste heat usually has temperatures below 100 °C and its usable extractable work tends to be modest. At the same time, it accounts for the bigger share on rejected energy with approx. 63%.1 Low-grade waste heat originates mainly from electricity generation, and to a lower extent from transport and industry branches such as the food and drink industry.3 Beside the Rankine cycle and the thermoelectric effect, the pyroelectric effect poses a suitable technology for its recovery. As will be described in this article, water splitting – which belongs to the 100 radical innovation breakthroughs for the future – is one possibility for waste heat recovery.4
1.1 The pyroelectric effect
In its natural state, the crystallographic unit cell of a pyroelectric substance possesses a net dipole moment. Individual dipole contributions sum up throughout the material5 resulting in an inner dielectric field![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) and (partial) electric charges at opposite surfaces of the pyroelectric. Under non-vacuum conditions the surface charges attract charges from the surroundings in order to screen the electric field.
and (partial) electric charges at opposite surfaces of the pyroelectric. Under non-vacuum conditions the surface charges attract charges from the surroundings in order to screen the electric field.
The spontaneous polarisation ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) s of pyroeletric materials is a function of temperature. Upon a temperature increase, either the atoms in the crystal are displaced or the concerted orientations of the dipoles are randomised, depending on the type of material. As a result the dipole moment shrinks and an induced charge imbalance results at the interface to the medium surrounding the pyroelectric.
s of pyroeletric materials is a function of temperature. Upon a temperature increase, either the atoms in the crystal are displaced or the concerted orientations of the dipoles are randomised, depending on the type of material. As a result the dipole moment shrinks and an induced charge imbalance results at the interface to the medium surrounding the pyroelectric.
The polarisation difference d![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) directly depends on the magnitude of the temperature change dT. The proportionality factor
directly depends on the magnitude of the temperature change dT. The proportionality factor ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) is named the pyroelectric coefficient (eqn (1)), and is a temperature-dependent material property which can be measured.6
is named the pyroelectric coefficient (eqn (1)), and is a temperature-dependent material property which can be measured.6
d![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) = = ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) (T)dT (T)dT | (1) |
![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) may be reduced to a – in most cases negative – scalar p.5,7–9 The amount of electric charge Q displaced due to dT is given by eqn (2), where A is the cross-sectional area of the particle perpendicular to the polarisation axis.
may be reduced to a – in most cases negative – scalar p.5,7–9 The amount of electric charge Q displaced due to dT is given by eqn (2), where A is the cross-sectional area of the particle perpendicular to the polarisation axis.| dQ = AdP = Ap(T)dT | (2) |
1.2 Pyroelectric energy harvesting
If the pyroelectric material is electrically connected through electrodes, compensation charges will be induced in these (shown in green in Fig. 1a). When the material is heated and its polarisation decreases (Fig. 1b), the excess charge will flow as an electric current (Fig. 1e). Charge neutrality at the new temperature is achieved and the electric flow ceases (Fig. 1c). If the temperature is then lowered, the original dipole moment is restored and current will flow in the opposite direction (Fig. 1d) until charge neutrality prevails again (Fig. 1a).The described process is the basis for a number of pyroelectric harvesting devices. They differ in the way in which the pyroelectric material is thermally contacted. Leng et al.10 switched a pyroelectric between a hot and a cold water stream. With the energy generated they were able to light up LEDs. Lee et al.11 pressed the pyroelectric element onto a hot and a cold plate successively. Other authors decided to save the energy required for switching by designing self-moving devices. Such is the example of a bimetal plate which bends to contact the hot or cold plate alternately due to the different thermal expansion coefficients of the two metals.12 In addition, a system converting solar and wind energy into temporal temperature differences, as required for pyroelectrics, by use of a light chopper was reported.13 The cited articles are examples and by no means a comprehensive list.§
1.3 Pyroelectrocatalysis
If the pyroelectric is in contact with a chemically labile medium, redox reactions can be carried out by the unmatched surface charges, as shown in Fig. 2. Starting from the thermally equilibrated material (Fig. 2a), heating diminishes the pyroelectric polarisation (Fig. 2b). The emerging potentials can be capacitively compensated by ions in solution at the beginning. When the potential reaches a certain value or threshold, excess free surface charges (Qf) can react with the medium or species therein. One end of the crystal becomes oxidising, the other end becomes reducing. Redox reactions can occur on both ends until charge equilibrium is achieved (Fig. 2c). Cooling increases polarisation, the pyroelectric must snatch free charges from its surroundings to balance the polarisation charges (black) caused by the polarisation increase to achieve charge neutrality (Fig. 2d). Redox reactions take place anew, though the reducing and oxidising surfaces reverse.Such pyroelectrocatalytic reactions have already been reported. The generation of reactive oxygen species was studied in the context of dye oxidation14–16 as well as bacteria inactivation.14,17 More recently, the feasibility of pyroelectrocatalytic hydrogen production was demonstrated. Kakekhani and Ismail-Beigi18 theoretically predicted the formation of hydrogen when cycling a ferroelectric across or underneath its critical temperature: a temperature – and thus potential – change affects the thermodynamic stability of the material surface. As a result, the surface undergoes stabilisation with its surrounding medium through chemisorption; hydrogen emerges as a result (eqn (3)).
 | (3) |
Several authors have confirmed the formation of hydrogen experimentally in two set-ups: externally positioned pyroelectrics, which collect pyroelectric current to drive an electrolyser19,20 (principle shown in Fig. 1) and internally positioned pyroelectrics, where chemical reactions take place directly on the pyroelectric surface (principle shown in Fig. 2).16
The existing theoretical background on pyroelectricity (based on eqn (2)) is straightforward and effective in describing energy harvesting. However, it has major boundaries when it comes to describing chemical reactions. According to eqn (2) even the smallest temperature stimulus would displace charge and enable chemical conversions. Kakekhani and Ismail-Beigi18 already pointed out the necessity of a minimum variation of chemical potential and thus critical temperature window in order to realise pyroelectrocatalysis.
1.4 Thermodynamic pyroelectric cycles
For the pyroelectric effect to occur, at least one heat source and one heat sink are required for temperature cycling. The pyroelectric process thus resembles a heat engine and is as such subject to the second law of thermodynamics.The thermodynamic cycle for pyroelectrics bearing the highest energy density was developed by Olsen et al.21 (also refer to Bowen et al.22). It is a four-step process which, in electric analogy to the heat engine, produces work from variations of polarisation (charge) in an external electric field (voltage). A schematic of the cycle can be found in Fig. S1a (ESI†). Lefeuvre et al.23 and Sebald et al.24 described the synchronised electric charge extraction, short SECE, consisting of four partial processes of varying the temperature to charge the pyroelectric and subsequently releasing the charge.
Although these cycles are veracious descriptions of the pyroelectric process, they do not represent the situation of chemical energy harvesting i.e. pyroelectrocatalysis well. When e.g. very small pyroelectric particles should harvest chemical energy, connecting the pyroelectric to a resistor is impossible or undesired. The reactive medium would close the circuit through ion migration. In the simplest setup, no external field would be applied, leaving us with the resistor cycle (Fig. S1b, ESI†). Since the work performed in a charge-voltage diagram depends on the actual path taken, a new cycle describing the exact path must be defined. Most recently, Schlechtweg et al.25 proposed a time-dependent model to predict hydrogen yields from pyroelectrocatalysis. They describe the dynamics of pyroelectrocatalysis by modelling the process electrically as an RC-circuit with faradaic processes. Up to now it appears to be the best model describing pyroelectrocatalysis, albeit it neither accounts for material specifics nor does it regard interface properties in detail. Thus, the accuracy of their predictions is limited.
The present paper deals with formal aspects of pyroelectrocatalytic energy harvesting. We develop a physical model to explain the occurrence of chemical reactions on pyroelectric surfaces. Furthermore we propose an appropriate thermodynamic cycle, i.e. one that does not require external electric fields and where work is a function of the real pyroelectric potential in a chemically labile medium. Estimations of the efficiency of the cycle are presented. In addition we study the influence of various operational and material parameters on the chemical output and compare simulation results to real experiments reported in literature.
2 The pyroelectrocatalytic threshold cycle (PTC)
2.1 General characteristics
The main discordance between existing thermodynamic cycles for electric energy harvesting and the process for the harvesting of chemical energy is that the potential of a pyroelectric particle in a reactive medium (e.g. water) can be raised only up to a certain limit or threshold. The varying temperature induces polarisation changes which again induce surface-bound charges. These charges increase the electrostatic potential and can become operative at the interface to the surrounding fluid after a certain energetic barrier – the activation energy – is overcome.Let us call the voltage difference required for chemical reactions to take place the threshold voltage, Vth. Charge build-up from zero to this threshold reaction potential is not available for chemical reactions (high electric resistance of the medium, capacitive regime). Once Vth has been reached, the next unit charge activated by an infinitesimal temperature increase (Tn−1 < Tn) will not increment the surface potential further, because it will have the appropriate energy for becoming operative within the fluid causing a chemical reaction (drop of the ohmic resistance of the medium, selective faradaic regime).
In particular, the cycle describes the electrochemical energy exchange for pyroelectrics with surfaces that are stable within the parameter regime of operation. From an electronic point of view, the density of states of the pyroelectric is inert with respect to the accumulated threshold voltage, so that apart from physisorption effects redox reactions will take place at the surface. In that way, this model is more general than that presented by Kakekhani and Ismail-Beigi18 for catalytic surfaces.
2.2 Cycle description
We postulate the thermodynamic cycle shown in Fig. 3, in which the pyroelectrocatalytic work is displayed as an area in a DE-diagram (equivalent to a QV-diagram). The dielectric displacement D relates to the electric field E and the polarisation P (eqn (4)), whereby P is caused by bound charges (material inner dipoles), D is caused by free charges (attached external charges) and E is the resultant physical field considering both internal and external charge. ε0 represents the vacuum permittivity. Isotherms are drawn as diagonal lines, since D increases with E. The isotherm crossing through the origin corresponds to the Curie temperature TC, above which the spontaneous polarisation is lost.![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) = ε0 = ε0![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) + + ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) | (4) |
The pyroelectrocatalytic threshold cycle (PTC) can be read as follows (↑: rise/↓: decrease/=: constant):
• 1: E = 0. A pyroelectric at the low temperature Tcold has a certain polarisation P1 and is electrically compensated by free surface charges D1 = −P1.
• 1 → 1′: T↑, P↓, E↑, D=. A charge imbalance in the order of Qth,c (threshold charge at low temperature, c stands for ‘cold’) is thermally induced in the form of surface-bound charge by the polarisation decrease without charge transfer. The potential difference rises to +Vth. The field increase matches the polarisation decrease and D remains constant at D1.
• 1′ → 2: T↑, P↓, E=, D↓. The charge imbalance induces electrolysis. The electric potential is maintained constant, as the shrinking Ps is compensated by the reacting charges. The electric potential moves along a sawtooth-type path at +Vth, as shown in the zoom inset of Fig. 3. The magnitude of dV is estimated to be: dV = dQ/C = e/(ε0εra) ≈ 10−19/(10−11 × 102 × 10−6) = 10−4 V for particle sizes a in the μm-range (refer to eqn (6)). A charge equal to Qth,c is transferred with the fluid. The amount of free surface charge Qf on the pyroelectric is reduced and so is the electric displacement.
• 2 → 3: T↑, P↓, E=, D↓. The temperature increase further induces charge imbalance and electrolysis. The charge Qrx (‘rx’ stands for ‘reaction’) is exchanged with the medium, reducing the amount of free surface charge of the pyroelectric and thus the electric displacement down to D3 at the highest temperature Thot (<TC). The electric field E and potential difference +Vth remain constant.
• 3 → 4: T↓, P↑, E↓, D=, Qf=. Cooling begins. The initial increase in polarisation cancels out the charge imbalance through surface-bound charges (intersect with D-axis). Then the pyroelectric surface potential is reversed to −Vth. The charge Qth,h (threshold charge at high temperature) is required for pole reversal. No chemical reactions occur (the free surface charge Qf remains constant).
• 4 → 5: T↓, P↑, E=, D↑. Charge imbalance induces electrolysis. The charge Qrx is transferred on the way to Tcold. The crystal sides where oxidation and reduction occur are reversed in comparison to the heating process (2 → 3). The displacement increases from D3 to D2.
• 5 → 2: T↑, P↓, E↑, D=, Qf=. Heating restarts. The decrease in polarisation reverses the charge imbalance caused by surface-bound charges by Qth,c. The pyroelectric surface potential is reversed from −Vth to +Vth at constant displacement D2. No chemical reactions occur.
Note that the path 5 → 2 is not equivalent to the two-step path first along the isotherm Tcold and then at constant potential +Vth over 1′ to 2. Even if both pathways require the charge Qth,c, work is a function of the actual path. As a consequence, the PTC (path 5 → 2) loses the thermodynamic work contained in the triangle under the isotherm (whose area will be approximately equivalent to the rectangle area Qth,c × 2Vth).
2.3 Work calculation
The following derivation is based on cuboid pyroelectric particles of edge length a, which can be regarded as small parallel-plate capacitors. Eqn (5) shows the capacitance C, in which the plate area is A = a2 and the plate separation d is the particle thickness a. Eqn (6), derived from eqn (2) and the capacitor equation, is used to calculate the potential V on the pyroelectric surface. | (5) |
 | (6) |
Fig. 4 plots the time courses of relevant parameters. We assume Thot remains below TC, so that no external field is required for repoling. In this aspect, the PTC resembles the resistive cycle (ESI†). According to eqn (2), the displaced charge Q follows the same course as the temperature and the generated current is proportional to its first time derivative (dQ/dt). In vacuum, the voltage follows the same course as the temperature, reaching Vvac and 0. However, in aqueous media it will reach Vth to remain constant afterwards due to the ongoing charge transfer during electrolysis. An electrochemical reaction (charge Qrx flowing into or from the medium) occurs only after Vth has been reached with a rate dQrx/dt proportional to dQ/dt. Starting from 0 V, it takes less time to reach Vth than starting at −Vth, so that reactions set in earlier on the first run than in all consecutive cycles (note the extra W1′ produced on the first run, processes 1 → 1′ → 2 in Fig. 3, as well as the extra effective charge Qrx,1′ in Fig. 4, which is lost to the threshold in subsequent runs).
 | ||
| Fig. 4 Time courses of temperature excitation (sinusoidal profile), displaced polarisation charge Q, polarisation current dQ/dt, surface potential V, free surface charge Qf, electrolytic current into the medium dQf/dt = Qrx and moles of hydrogen H2 ∝ Wrx (cumulative) formed on a pyroelectric particle. Schematic representation. Digits 1–5 correspond to the cycle stages in Fig. 3. Starting from the potential, the time windows lost to the creation of the threshold (Qth,c/h) and those leveraged to produce chemical work (Qrx,c/h) can be seen on the x-axis (time). Areas of dQ/dt represent the work enclosed in Fig. 3. | ||
The pyroelectric material performing the PTC delivers electric work for the whole duration of the temperature change. Owing to the fact that the voltage remains pinned at Vth during charge transfer, the work can be calculated with eqn (7). The total thermodynamic work Wtot released by the displacement of bound charges with a total integrated charge of 2Qtot (= twice the charge per event) according to eqn (2) will be proportional to the total area enclosed between the isotherms and the threshold voltage [−Vth, +Vth] in Fig. 3 (eqn (8)). If p is nearly constant in the working temperature window, then the charge at the hot end Qtot,h (and thus the work Wh) will be as large as that at the cold end Qtot,c (and Wc). The pyroelectrocatalytic work Wpc (eqn (9)), chequered area, results from the actual course of the state of the pyroelectric within the DE-diagram. It has lost the ‘triangular’ areas merely used to create the threshold potential. Only a fraction of this pyroelectrocatalytic work is chemically stored in the form of reaction products Wrx (eqn (10)), represented by the blue areas. We need to estimate Qrx and Vth and analyse the factors which further reduce the extractable work when chemical energy – as opposed to total electric work – is targeted.
| W = QV | (7) |
| Wtot = Wh + Wc = Qtot,hVth + Qtot,cVth = 2QtotVth | (8) |
| Wpc = 2QrxVth | (9) |
| Wrx = 2QrxVrx | (10) |
2.4 Efficiency factors
For the estimation of the threshold loss factor, corresponding to a loss of polarisation current of the pyroelectric, we can first calculate the total charge Qtot displaced per particle during one event – a half cycle – by integrating eqn (2) and second subtract the fraction used for generating the threshold potentials Qth,h/c (eqn (11)). The displaced charge is given by eqn (12). For narrow temperature ranges, in which p is nearly constant, the result of integration can be simplified with the average pyroelectric coefficient as ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ·ΔT.
·ΔT.
| Qtot = Qth,h + Qrx,h = Qth,c + Qrx,c | (11) |
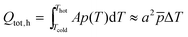 | (12) |
To determine Qth,h/c, we need to relate charge and potential (capacitance). Displacing the charge Qth,h or Qth,c generates a potential difference of 2Vth at each particle (eqn (13)). Similarly, the total charge displaced for one event generates the maximum potential difference Vvac in a non-reactive medium such as vacuum (eqn (14)). ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) r is the temperature averaged relative permittivity.
r is the temperature averaged relative permittivity.
| Qth = Qth,c/h = 2VthC = 2Vthε0εr(Tc/h)a | (13) |
Qtot = VvacC = Vvacε0![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) ra ra | (14) |
The charge loss associated with the generation of the threshold can now be expressed through the efficiency factor ηth (eqn (15)), which represents the vertical area loss between the isotherms at Tcold and Thot in Fig. 3. ηth depends on p and ε, as well as on the particle size a and ΔT. As a consequence, for a too small particle size, ΔT or p the whole cycle duration would be dead time and no reactions would occur. The same effect would be observed for a large εr.
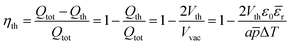 | (15) |
| Vth = Vrx + Vop | (16) |
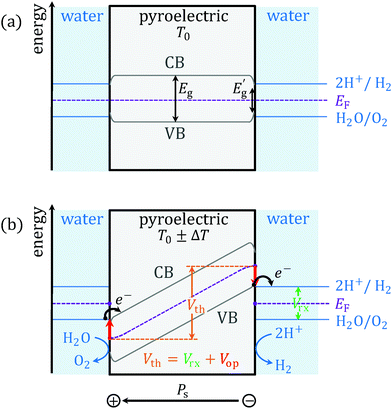
2.4.2.1 Band bending (Vrx). Because all pyroelectrics are piezoelectrics, we can adapt the band model by Starr and Wang26 to pyroelectrocatalysis (Fig. 5). At constant temperature and field, the conduction band (CB) and the valence band (VB) of the pyroelectric have the same energy throughout the bulk of the crystal. Since common pyroelectrics have a large band gap Eg, the CB will be completely empty while the VB will be full. When the temperature changes, the bands tilt due to the displaced charge and polarisation change (Fig. 5b). In order to produce electrolysis and allow for electronic charge transfer with the fluid, the electrons, which can only be provided by the VB, must be raised in energy above the lowest unoccupied molecular orbital (LUMO) of H+. At the opposite surface, the holes – only available in the CB – must be lowered in energy below the highest occupied molecular orbital (HOMO) of water. Then the VB becomes a source of reducing electrons, whilst the CB acts as electron acceptor. The difference between HOMO and LUMO corresponds to the reaction of interest, here water splitting, which requires a minimum potential difference of Vrx = 1.23 V (= E° = −ΔG°/nF, where G° is the standard Gibbs free energy, n is the number of transferred electrons and F is the Faraday constant). This potential difference needs to be provided by the heated/cooled pyroelectric. The continuous electronic charge transfer with the fluid maintains a constant imbalance of free surface charges on the pyroelectric, fixing the band tilt and pinning the potential at Vth, even though changes in polarisation proceed.
2.4.2.2 Band gap and entropy (Vop). However, water will not react at Vrx due to missing appropriate reactive sites on the surface. An overpotential is required to compensate this phenomenon. (Other causes for the overpotential such as electric resistance of the aqueous medium, concentration gradients,27 bubble formation, etc. are of lesser significance since the current density in a PTC system is orders of magnitude smaller than in a typical electrolysis setup.) Since the electrons can only be transferred into the CB and out of the VB, an additional band tilt that corresponds to the band gap is needed (red arrows in Fig. 5b). However, due to surface phenomena, adding the full Eg would result in overestimation. Lattice defects and surface stabilisation phenomena such as atomic relaxations and reconstruction commonly create near-surface electronic states at the interface to the fluid reducing the local energy gap to Eg′ (Fig. 5a).28,29 Such reduction depends on the local density of surface states and thus on the specific surface of the pyroelectric. The local density of states can even span the full range of Eg (Eg′ = 0), making the surface metallic. For the simulation, we have taken several values within the range [0, Eg]. In the specific case of a metallic surface, the reaction still requires a minimum overpotential to at least compensate for the entropy increase (eqn (3)). The thermoneutral voltage Vn = −ΔH/nF = 1.48 V, obtained by replacing H, the enthalpy, for G (see ESI†),30 accounts for this.
To sum up, Vn is taken only for the case Eg′ = 0 (eqn (17)). The overpotential efficiency term ηop – the horizontal component of area loss – is given by eqn (18).
 | (17) |
 | (18) |
2.5 Cycle efficiency
The product of the three efficiency factors ηth, ηop and ηF, named here ηchem (eqn (19)), characterises the loss in the conversion of (pyro)electric to chemical energy in the form of hydrogen WH2. | (19) |
 | (20) |
 | (21) |
The next step is to calculate the efficiency of the thermal-to-chemical conversion. For this purpose, the net extractable chemical work WH2 is multiplied by the number of particles Nparticles and divided by the energy input qin, which is the thermal energy required to heat the pyroelectric. It is assumed that cooling the pyroelectric back to Tcold requires no additional energy input. Nparticles is given by the total volume of pyroelectric divided by the particle volume. With a material density ρ and total employed mass m, Nparticles is given by eqn (22)
 | (22) |
 | (23) |
Eqn (23) approximates the specific heat capacity cP as a constant ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) P in the temperature window. The final efficiency of the heat-to-hydrogen conversion is shown in eqn (24).
P in the temperature window. The final efficiency of the heat-to-hydrogen conversion is shown in eqn (24).
 | (24) |
The study of eqn (24) reveals which parameters can improve the PTC hydrogen yield. The minuend relates to the total charge displaced pyroelectrically Qtot, whilst the subtrahend is associated to the threshold loss Qth. If the subtrahend is equal to the minuend, ηH2 becomes zero. That gives rise to a critical particle size (eqn (25)) below which no chemical reactions can take place. In that case, the small surface charges would be merely compensated by an electrochemical double-layer.
 | (25) |
Above acrit, the minuend in eqn (24) is greater than the subtrahend and the course of the efficiency goes up. By taking the partial derivative of ηH2 (eqn (26)), the optimum particle size aopt – yielding the highest efficiency – can be determined (eqn (27)). For values of a higher than aopt, the efficiency decreases due to a reduction of the active area for chemical reactions. Table 1 shows aopt for some common pyroelectrics.
 | (26) |
 | (27) |
| Material | −![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (C m−2 K−1) (C m−2 K−1) |
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) r
r
|
E g (eV) | V th (V) | a opt (m) |
|---|---|---|---|---|---|
| BaTiO332 | 1.74 × 10−4 | 186 | 3.0833 | E g/2 | 1.2 × 10−6 |
| LiTaO334 | 1.80 × 10−4 | 56 | 4.935 | E g/2 | 5.4 × 10−7 |
| LiNbO336 | 8.20 × 10−5 | 30.3 | 4.7 | E g/2 | 6.2 × 10−7 |
| Sr0.5Ba0.5Nb2O637 | 6 × 10−4 | 400 | 3.2838 | E g/2 | 7.7 × 10−7 |
| PZT G-1306 (Gulton)36 | 4.60 × 10−4 | 1900 | 3.2539 | E g/2 | 4.8 × 10−6 |
| PVDF40 | 2.20 × 10−5 | 8 | — | V n | 3.8 × 10−7 |
| PMN-0.26PT41 | 1.80 × 10−3 | 643 | — | V n | 3.7 × 10−7 |
We can also obtain an expression for the maximum efficiency (eqn (28)) by inserting aopt in eqn (24). Clearly, for maximum efficiency p must be maximised and εr minimised. Unfortunately, both p and εr are mostly not decoupled from one another, so that it is difficult to increase p while keeping εr small.42
 | (28) |
Temperature also plays a crucial role in the generation of the threshold potential. From eqn (24) it is possible to calculate the minimum temperature difference necessary for reaction by equating Qtot to Qth (eqn (29)).
 | (29) |
In addition, it would be advantageous to minimise cP, as the same chemical conversion could be achieved with a reduced heat input qin. That would allow for quicker temperature cycling, too. Fig. 6 schematically shows the roles of the aforementioned parameters on the hydrogen yield.
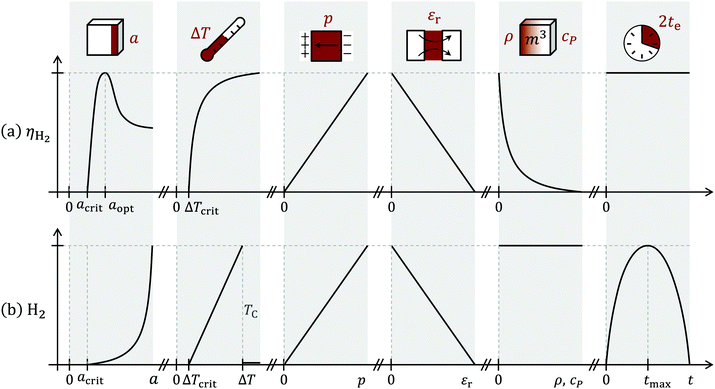 | ||
| Fig. 6 Influence of particle size a, temperature difference ΔT, pyroelectric coefficient p, relative permittivity εr, density ρ, heat capacity cP and cycle duration 2te on (a) the efficiency of the chemical conversion ηH2 and (b) hydrogen generation per time. Schematic representation based on eqn (24) (a) and eqn (21) (b). Both equations are time-independent. However, high cycling times may lead to non-selective oxidation/corona discharge while low cycling times may be screened by sheer electrostatics (capacitive regime), thus reducing the hydrogen output.25 For a high H2 generation output, ΔT and p should be maximised, while keeping εr, ρ and cP low. | ||
2.6 Figure of merit
Upon examination of eqn (28) we encounter four types of quantities: constants (such as ε0), pseudo-constants (e.g. ηF or Vrx), process-related factors (such as ΔT) and the material properties ρ, p(T), cP, εr and Vth. When it comes to comparing different pyroelectric materials, the pseudo-constants will be determined by the experimental setup used – that is the reaction of interest, reactor characteristics, etc. We propose a figure of merit (FoM) for the PTC based on eqn (28), which depends on these parameters as well as on ηop in order to account for the reaction of interest and band gap. | (30) |
3 Model calculations
The PTC brings new efficiency terms into the yield calculation. Instead of directly converting the charge Qtot found in eqn (12) to the quantity of hydrogen moles – through multiplication with the number of particles Nparticles, division by the Faraday constant and the number of stoichiometric electrons (ne−(H2) = 2, see eqn (3)) – the charge is first multiplied with ηchem. The corrected charge Qrx is the one that relates to hydrogen.We set up the model on Python43 and calculated the outputs for all three hydrogen experiments reported in literature. The temperature excitation was assumed to be sinusoidal, as that shown in Fig. 4. The results are shown in Table 2. Eqn (12) represents the output without the PTC efficiency correction ηchem. The comparison between the columns experiment – retrieving the authors measurements – and PTC – showing the model outputs – reveals very good correlations in two of three cases. For black phosphorene, a unique pyroelectric in terms of a large pyroelectric coefficient with a tiny relative permittivity, a large amount of charge is displaced with temperature, so that it reaches a thermal-to-chemical conversion efficiency of ηH2 = 0.228 (refer to the ESI†). The model predicts the hydrogen outcome very accurately.
| Material | ΔT (K) | Experiment (mol g−1) | PTC (mol g−1) | Eqn (12) (mol g−1) | η chem (—) | E g′ (eV) | FoM (—) | η H2 |
|---|---|---|---|---|---|---|---|---|
| Black phosphorene16 | 50 | 2.25 × 10−5 | 2.49 × 10−5 | 3.35 × 10−3 | 0.0074 | 0.6 | 2.09 × 101 | 2.28 × 10−1 |
| BaTiO344 | 30 | 2 × 10−12 | 29 × 10−12 | 110 × 10−12 | 0.275 | 3.08 | 4.29 × 10−5 | 1.52 × 10−6 |
| Ba0.7Sr0.3TiO331 | 25 | 1.30 × 10−6 | 0 | 3.36 × 10−7 | 0 | 0.25 | 3.04 × 10−4 | 0 |
For BaTiO3, the model predicts about one order of magnitude more than reported. The authors of this study provided neither blank measurements nor exactly quantifiable figures on reactor volume and number of cycles, so that it is not meaningful trying to improve the accuracy further. The following model parameters were employed: ηF = 1 (experiments will be likely to have a lower value), a particle size a = 200 nm (the particle size distribution reported was neglected). The predicted outcomes still represent an improvement of roughly one order of magnitude in comparison to eqn (12).
The case of Ba0.7Sr0.3TiO3 is different. Due to the very large value of ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) r, the displaced charge is far from producing the electric potential Vth, required for reactions. The PTC expresses this insufficiency in form of a ΔTcrit = 498 K (see Table S1, ESI†) for the given particle size or alternatively a critical particle size acrit = 3.98 × 10−6 m for the temperature difference applied. Both parameters are 20 times larger than their experimental counterparts. Accordingly, the model predicts an outcome of 0 mol H2. We believe the experiment might have been affected by some level of interference with sonolytically produced radicals or with simultaneous piezoelectric phenomena (all pyroelectrics are piezoelectric). The PTC model is concerned only with pyroelectrocatalysis.
r, the displaced charge is far from producing the electric potential Vth, required for reactions. The PTC expresses this insufficiency in form of a ΔTcrit = 498 K (see Table S1, ESI†) for the given particle size or alternatively a critical particle size acrit = 3.98 × 10−6 m for the temperature difference applied. Both parameters are 20 times larger than their experimental counterparts. Accordingly, the model predicts an outcome of 0 mol H2. We believe the experiment might have been affected by some level of interference with sonolytically produced radicals or with simultaneous piezoelectric phenomena (all pyroelectrics are piezoelectric). The PTC model is concerned only with pyroelectrocatalysis.
Essential parameters for the simulation are particle size and band gap. The small ηchem value for black phosphorene is a consequence of the very thin material layer used, which is just above the critical thickness for the creation of the threshold voltage. You et al.16 report a band gap narrowing for increasing number of phosphorene layers. The band gap varies between 1.8 eV in the monolayer and 0.3 eV in the bulk, being around 0.7 eV for a few layers. Tables S1 and S2 in the ESI† present all calculated values as well as the influence of the surface band gap on the outputs. To generalise, the broader Eg′, the more energy is used for reaching the threshold voltage, the less charge is available for chemistry.
4 Conclusion
Pyroelectrocatalysis is the process of converting thermal energy directly into chemical energy with a pyroelectric material. The pyroelectric must be in contact with the chemically labile medium (here water) and chemical reactions occur by transferring charges into and out of the reactive medium.This article introduces a new thermodynamic cycle, termed pyroelectrocatalytic threshold cycle, PTC, which models pyroelectrocatalysis more accurately. Its main characteristic is the need for a minimum threshold potential Vth which depends on the chemical reaction of interest on the one hand and the band structure of the pyroelectric semiconductor – and its surface – on the other hand. Before this potential is built up, no chemical conversion can take place and the thermal energy is lost. After the potential reaches Vth, it does not increase further because the emerging surface-bound charges are compensated through charge transfer with the fluid. The potential remains constant until the next event begins.
The temperature difference and the particle size determine whether enough charge can accumulate for reaction. Smaller particles invest comparatively more energy in reaching the threshold and leave less room for reactions. At the same time they possess more active area, so that a trade-off between charge efficiency and active site utilisation arises.
Reported experimental hydrogen yields could be modelled with the PTC to an accuracy of about one order of magnitude. The current yields correspond to conversion efficiencies in the range 10−1–10−6, even for small temperature differences. This waste-heat utilisation potential should encourage further studies on the physical and chemical limits of pyroelectric materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We dedicate this article to Prof. Peter Paufler (TU Dresden) as mentor of crystal physics. This work was initially performed within the junior research group PyroConvert (100109976, 100152607) financially supported by the Ministry of Science and Art of Saxony (SMWK), the Sächsische Aufbaubank (SAB) and the European Union (ESF, EFRE). Further research was performed within the collaborative research projects CryPhysConcept (03EK3029A) and R2RBattery (03SF0542A) funded by the German Federal Ministry of Education and Research (BMBF). We are grateful to Ms Kerstin Annassi from Project Management Jülich for her professional assistance in these projects, thanks to whom the results included in this publication have been achieved.Notes and references
- C. Forman, I. K. Muritala, R. Pardemann and B. Meyer, Renewable Sustainable Energy Rev., 2016, 57, 1568–1579 CrossRef.
- M. Pehnt, J. Bodeker, M. Arens, E. Jochem and F. Idrissova, Proceedings of ECEEE, 2011 Search PubMed.
- U.S. Department of Energy, Waste Heat Recovery: Technology and Opportunities in U.S. Industry, 2008.
- European Commission, 100 Radical Innovation Breakthroughs for the future, 2019.
- S. B. Lang, Sourcebook of Pyroelectricity, Gordon and Breach, Science Publishers, Inc., New York, 1974, vol. 2 Search PubMed.
- S. Jachalke, E. Mehner, H. Stöcker, J. Hanzig, M. Sonntag, T. Weigel, T. Leisegang and D. C. Meyer, Appl. Phys. Rev., 2017, 4, 021303 Search PubMed.
- P. Paufler, Physikalische Kristallographie, Akademie-Verlag Berlin, 1986, p. 325 Search PubMed.
- R. E. Newnham, Properties of Materials: Anisotropy, Symmetry, Structure, Oxford University Press, 1st edn, 2005 Search PubMed.
- W. Kleber, Einführung in die Kristallographie, De Gruyter Oldenbourg, 19th edn, 2010 Search PubMed.
- Q. Leng, L. Chen, H. Guo, J. Liu, G. Liu, C. Hu and Y. Xi, J. Mater. Chem. A, 2014, 2, 11940–11947 RSC.
- F. Y. Lee, A. Navid and L. Pilon, Appl. Therm. Eng., 2012, 37, 30–37 CrossRef CAS.
- S. K. T. Ravindran, M. Kroener and P. Woias, Procedia Eng., 2012, 47, 33–36 CrossRef CAS.
- S. Krishnan, D. Ezhilarasi, G. Uma and M. Umapathy, IEEE Trans. Sustain. Energy, 2014, 5, 73–81 Search PubMed.
- E. Gutmann, A. Benke, K. Gerth, H. Böttcher, E. Mehner, C. Klein, U. Krause-Buchholz, U. Bergmann, W. Pompe and D. C. Meyer, J. Phys. Chem. C, 2012, 116, 5383–5393 CrossRef CAS.
- J. Wu, W. Mao, Z. Wu, X. Xu, H. You, A. Xue and Y. Jia, Nanoscale, 2016, 8, 7343–7350 RSC.
- H. You, Y. Jia, Z. Wu, F. Wang, H. Huang and Y. Wang, Nat. Commun., 2018, 9, 2889 CrossRef PubMed.
- A. Benke, E. Mehner, M. Rosenkranz, E. Dmitrieva, T. Leisegang, H. Stöcker, W. Pompe and D. C. Meyer, J. Phys. Chem. C, 2015, 119, 18278–18286 CrossRef CAS.
- A. Kakekhani and S. Ismail-Beigi, J. Mater. Chem. A, 2016, 4, 5235–5246 RSC.
- M. Xie, S. Dunn, E. L. Boulbar and C. R. Bowen, Int. J. Hydrogen Energy, 2017, 42, 23437–23445 CrossRef CAS.
- Y. Zhang, S. Kumar, F. Marken, M. Krasny, E. Roake, S. Eslava, S. Dunn, E. Da Como and C. R. Bowen, Nano Energy, 2019, 58, 183–191 CrossRef CAS.
- R. B. Olsen, D. A. Bruno and J. M. Briscoe, J. Appl. Phys., 1985, 58, 4709–4716 CrossRef CAS.
- C. Bowen, J. Taylor, E. LeBoulbar, D. Zabek, A. Chauhan and R. Vaish, Energy Environ. Sci., 2014, 7, 3836–3856 RSC.
- E. Lefeuvre, A. Badel, C. Richard and D. Guyomar, J. Intell. Mater. Syst. Struct., 2005, 16, 865–876 CrossRef.
- G. Sebald, E. Lefeuvre and D. Guyomar, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2008, 55, 538–551 Search PubMed.
- J. Schlechtweg, S. Raufeisen, M. Stelter and P. Braeutigam, Phys. Chem. Chem. Phys., 2019, 21, 23009–23016 RSC.
- M. B. Starr and X. Wang, Sci. Rep., 2013, 3, 1–8 Search PubMed.
- C. Grimes, O. Varghese and S. Ranjan, in Light, Water, Hydrogen, ed. C. Grimes, O. Varghese and S. Ranjan, Springer US, 2008, pp. 35–113 Search PubMed.
- V. E. Henrich, The Surface Science of Metal Oxides, Cambridge Univ. Press, 2000 Search PubMed.
- V. E. Henrich, The Chemical Physics of Solid Surfaces, in The Chemical Physics of Solid Surfaces, ed. D. Woodruff, Elsevier, 2001, vol. 9, pp. 1–34 Search PubMed.
- R. L. LeRoy, C. T. Bowen and D. J. LeRoy, J. Electrochem. Soc., 1980, 127, 1954–1962 CrossRef CAS.
- X. Xu, L. Xiao, Y. Jia, Z. Wu, F. Wang, Y. Wang, N. O. Haugen and H. Huang, Energy Environ. Sci., 2018, 11, 2198–2207 RSC.
- T. Perls, T. Diesel and W. Dobrov, J. Appl. Phys., 1958, 29, 1297–1302 CrossRef CAS.
- S. H. Wemple, Phys. Rev. B: Solid State, 1970, 2, 2679–2689 CrossRef.
- M. Srinivasan, Bull. Mater. Sci., 1984, 6, 317–325 CrossRef CAS.
- S. Kase and K. Ohi, Ferroelectrics, 1974, 8, 419–420 CrossRef CAS.
- H. P. Beerman, Infrared Phys., 1975, 15, 225–231 CrossRef CAS.
- R. B. Maciolek and S. T. Liu, J. Electron. Mater., 1973, 2, 191–200 CrossRef CAS.
- F.-P. Koffyberg, K. Dwight and A. Wold, Solid State Commun., 1979, 30, 433–437 CrossRef CAS.
- M. Durruthy-Rodríguez, J. Costa-Marrero, M. Hernández-García, F. Calderón-Piñar and J. Yañez-Limón, Appl. Phys. A: Mater. Sci. Process., 2010, 98, 543–550 CrossRef.
- M. Olszowy, E. Nogas-Ćwikiel and K. Ćwikiel, J. Phys.: Conf. Ser., 2011, 289, 012017 CrossRef.
- Y. Tang, X. Wan, X. Zhao, X. Pan, D. Lin, H. Luo, J. Sun, X. Meng and J. Zhu, J. Appl. Phys., 2005, 98, 0841041 Search PubMed.
- S. T. Liu, J. D. Zook and D. Long, Ferroelectrics, 1975, 9, 39–43 CrossRef CAS.
- G. van Rossum, Python tutorial, Centrum voor Wiskunde en Informatica (CWI) Technical Report CS-R9526, 1995.
- R. Belitz, P. Meisner, M. Coeler, U. Wunderwald, J. Friedrich, J. Zosel, M. Schelter, S. Jachalke and E. Mehner, Energy Harvest. Syst., 2017, 4, 107–113 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Section S1: Olsen and resistive cycles; Section S2: Calculation of the overpotential; Section S3: Calculated pyroelectrochemical yields; Section S4: Pyroelectric coefficients and permittivities; Section S5: Python simulation code. See DOI: 10.1039/d0cp01288b |
| ‡ These authors contributed equally to this work. |
| § About 2600 patents are known (google patent search for ‘pyroelectr*’ and ‘harvest*’, November 2019). |
| This journal is © the Owner Societies 2020 |