Density-functional theory models of Fe(IV)O reactivity in metal–organic frameworks: self-interaction error, spin delocalisation and the role of hybrid exchange

Abstract

We study the reactivity of Fe(IV)O moieties supported by a metal–organic framework (MOF-74) in the oxidation reaction of methane to methanol using all-electron, periodic density-functional theory calculations. We compare results concerning the electronic properties and reactivity obtained using two hybrid (B3LYP and sc-BLYP) and two standard generalised gradient corrected (PBE and BLYP) semi-local density functional approximations. The semi-local functionals are unable to reproduce the expected reaction profiles and yield a qualitatively incorrect representation of the reactivity. Non-local hybrid functionals provide a substantially more reliable description and predict relatively modest (ca. 60 kJ mol⁻¹) reaction energy barriers for the H-atom abstraction reaction from CH₄ molecules. We examine the origin of these differences and we highlight potential means to overcome the limitations of standard semi-local functionals in reactivity calculations in solid-state systems.

---

1 Introduction

Methane is the predominant component of natural gas and a natural resource of major economic impact on a planetary scale, largely because of its use as a fuel for domestic and industrial applications and as a basic feedstock for the industrial production of hydrogen gas. Methane is typically transported from source sites in the form of liquefied natural gas via gas pipelines. Its conversion into a liquid species (e.g. dimethyl ether, formaldehyde, acetic acid or liquid fuels) via Fischer–Tropsch catalysis, can however offer an appealing and sustainable alternative to direct transportation.¹ Recent studies have suggested that solid-state catalysts, such zeolites^2–4 and metal–organic frameworks (MOFs)^5,6 can provide efficient systems for the direct conversion of methane into liquid methanol. This process requires the hydroxylation of an extremely unreactive hydrocarbon, and therefore it can be carried out efficiently only in the presence of catalytic species of exceptional oxidative strength.

The Fe(IV)oxo (ferryl) moiety has been proposed as a potential candidate in the context of hydrocarbon,^7,8 alcohol⁹ and water¹⁰ oxidation, in view of its peculiar electrophilic character and its occurrence in several enzymatic cycles involved in the oxidation of hydrocarbons and other substrates in vivo.^11,12 Considerable work has therefore been devoted to synthesise new Fe(IV)oxo-based species with enhanced catalytic activity^11,13 along to developing an understanding of the structural and electronic factors that determine its exceptional reactivity. Most of this work has been devoted to biological systems or bio-mimetic species for homogeneous catalysis. Comparatively less is known on the properties of Fe(IV)oxo systems in the solid state, particularly concerning their electronic and chemical properties.

In recent work based on solid-state calculations carried out at the B3LYP level of density-functional theory (DFT), we have shown that the MOFs can provide a close to ideal coordination environment for the stabilisation of highly reactive Fe(IV)O groups.¹⁴ MOFs¹⁵ are an intriguing and widely studied class of solid-state materials with a variety of applications, including heterogeneous catalysis, gas separation, carbon capture, and hydrogen storage. Extensive work, both experimental and theoretical has been devoted to characterise the structural and chemical properties of these materials and to optimise their ability to act as catalysts for a variety of synthetic processes.^16–21 Our DFT calculations indicate that Fe(IV)O supported in MOF-74 exhibits an oxidation ability comparable to gas-phase and aqueous Fe(IV)O complexes in a quintet ground state, including the “Fenton catalyst” [Fe(IV)O·(H₂O)₅]₂⁺ (aq).^22,23 Similar to what is observed in these systems, this high reactivity can be attributed to the stabilisation of a low-lying 3σ* virtual orbital localised on the Fe(IV)O group, which acts as an electron acceptor in the first stages of the H-atom transfer from methane. The oxygen-rich Fe(IV)O coordination environment in MOF-74 enhances the stability of the quintet state of Fe(IV)O, which in turn lowers the energy of the 3σ* orbital through exchange stabilisation.

From a computational perspective, modelling the Fe(IV)O species in the solid state presents a number of challenges. Even within the DFT framework, some characteristic properties of Fe(IV)O may not be captured quantitatively, or even qualitatively, depending on the choice of the exchange–correlation approximation. Furthermore, advanced exchange–correlation methods (like, e.g., hybrid or double hybrid functionals), which are employed routinely in calculations on gas-phase molecules, may be prohibitively CPU-intensive in solid-state calculations, especially in the context of ab initio molecular dynamics simulations.

Therefore, the goal of this work is to address these limitations by examining the influence of exchange–correlation functional choice specifically on the predicted reactivity of MOF-74 supported Fe(IV)O. We show that conventional generalised-gradient approximations (GGAs), like PBE²⁴ and BLYP,^25,26 which typically provide an accurate description both of the structural/vibrational properties of MOFs²⁷ and of Fe(IV)O catalysed hydroxylation reactions in the gas phase and in aqueous solution^28,29 yield a qualitatively incorrect description of the H-abstraction reaction profile from methane in the solid state. We attribute this failure to the self-interaction error (SIE) affecting these functionals, which brings about a spurious mixing between reactant (CH₄) orbitals and extended MOF-74 states. This effect is responsible for the unphysical delocalisation of the electron associated with the H atom transferred to the Fe(IV)O group, which prevents a transition state from being reached. A (partial) cancellation of the self-interaction error, e.g. through the inclusion of exact Hartree–Fock exchange in the density-functional approximation (e.g. B3LYP^25,26,30 or sc-BLYP³¹), is sufficient to recover the correct reaction profile.

The manuscript is organised as follows. In Section 2, we describe the DFT methodology that we used to model the Fe(IV)O/MOF-74 structure and to calculate several electronic properties of interest and to determine energy barriers for the oxidation of a methane molecule. In Section 3 we show how these electronic properties are influenced by the choice of the exchange–correlation functional and the ground spin state. We then study the hydrogen atom abstraction reaction from a methane molecule in the presence of Fe(IV)O supported in MOF-74. Finally, Section 4 summarises our main findings and indicates potential directions for future works.

2 Simulation methods

We build the initial structure of Fe(IV)O/MOF-74 with the data provided by the Cambridge Crystallographic Database³² concerning acetylene/MOF-74³³ using the Materials Studio suite package.³⁴ The Space group is R3̄ (148), with a unit cell of dimensions of 25.89 × 25.89 × 6.95 ų and angles α = β = 90° and γ = 120°. Fig. 1 shows that this cell contains 60 atoms and corresponds to 6 primitive cells. The primitive unit cell of Fe(IV)O/MOF-74 contains 10 atoms: one Fe atom, three framework O atoms, four C atoms, one H atoms and one O(oxo) atom bonded to Fe. We substitute the acetylene molecule present in the original structure with an oxygen atom O(oxo), at a distance of 1.68 Å from the Fe atom, which is slightly larger than typical Fe(IV)–O(oxo) distances determined for gas-phase complexes (1.60–1.62 Å).²⁸ We then relax the atomic positions with the COMPASS2³⁵ force field. After optimisation, the Fe(IV)–O(oxo) bond length decreases to 1.65 Å.

Fig. 1 Representations of the periodic Fe(IV)O/MOF-74 cavity with a methane molecule in the centre, with the top (a) and side (b) views of the unit cell and the replicated cell (c). Fe atoms are blue, O atoms red (notice the O(oxo) atoms oriented toward the cavity centre), C atoms green, and H atoms grey. The cells in panels (a) and (b) show the same system that is used in the simulations. Panel (a) shows the position of alternatives sites O1, C1, and C2 to Ooxo for the adsorption of methane molecule.

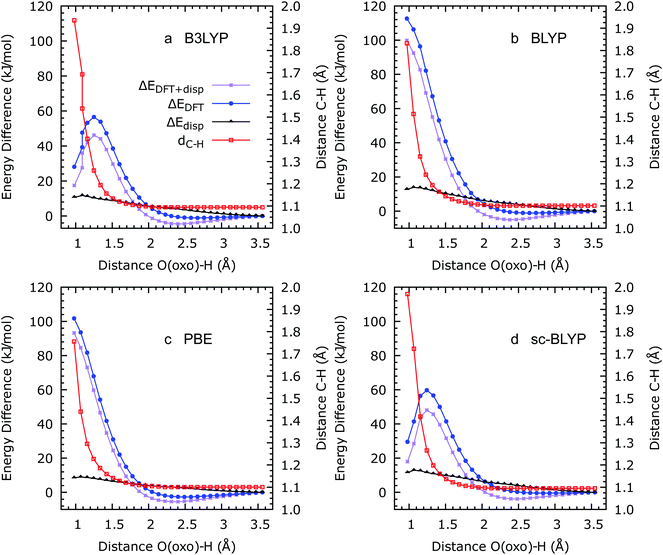
The atomic positions from the resulting configurations are then optimised with the ab initio CRYSTAL17 code.³⁶ For the geometry optimisation, we employ the default convergence criteria set in CRYSTAL17: 7.5 × 10⁻⁴ Ha Bohr⁻¹ for the largest component of the force, 5.0 × 10⁻⁴ for the largest displacement and 10⁻⁷ Ha for the energy change between optimisation steps similarly to those employed in the optimisation of graphenylene.³⁷ The DFT calculations are carried out using periodic boundary conditions with four different exchange–correction functionals. We consider two pure density functionals (PBE and BLYP) and one range-separated hybrid functional (sc-BLYP), to assess their applicability as potential alternatives to B3LYP. Pure density functionals are typically preferred in solid state applications, because of their reduced computational cost, especially in plane-wave based calculations and ab initio molecular dynamics simulations.^38–44 In previous work¹⁴ we showed that B3LYP, which provides a reasonably accurate description of high-spin Fe(IV)oxo states,^45,46 is also more adequate than most generalised-gradient approximations (e.g. PBE and BLYP) in the solid state. We do however notice that, for gas-phase or solvated systems, the OPBE functional may also provide an accurate alternative to B3LYP (ref. 46). A standard all-electron 6-31G**⁴⁷ basis set is used to represent the local atomic orbitals in terms of primitive Cartesian Gaussian functions. Polarization functions (p-functions for hydrogen and d-functions for carbon, oxygen and silicon) are used to ensure that the orbitals can distort from their original atomic symmetry, to better adapt to the molecular surroundings. Accurate truncation thresholds for the tolerances of the Coulomb and exchange bielectronic integral series are used in all calculations³⁶ to improve the convergence rate during the self-consistent solution of the Kohn–Sham equations. Brillouin zone integrations are carried out using a Monkhorst–Pack net of 2 × 2 × 2 k-points, and a ground-state energy convergence is enforced of 1 × 10⁻⁵ Hartree. Long-range forces are included by adding van der Waals dispersion correction with Grimme's DF2 scheme.⁴⁸ Note that when including this scheme, some self-interaction might exist between the images of the methane molecule, whose separation is 6.95 Å as shown in Fig. S1 (ESI†). Nonetheless, this distance is long enough to avoid self-interactions between these molecules. Note that at this separation, only van der Waals forces might be significant, however these are weak in the gas phase. This weakness is reflected in the changes of the system's total energy in Fig. 4. In addition, our current work on these systems with ab initio molecular dynamics reveals that the forces between the methane's atoms and those in the MOFs are very weak for distance ca. 3.5 Å; thus, interactions between images of methane are likely to be even weaker.

3 Results and discussion

In Table 1 we list the total energies, quintet–singlet energy differences, Fe(IV)O bond distances, and Kohn–Sham gaps obtained for the optimised Fe(IV)O/MOF-74 structure in the absence of methane. The triplet and the singlet are known to be the predominant spin states of Fe(IV)O compounds, and the quintet is by far the most reactive state, both in biological and in organometallic/biomimetic compounds.^28,49

Table 1 Total energies E of the quintet spin state (Ha), differences in energy with respect to the singlet state ΔE_s (eV), Fe–O(oxo) distances (Å) and Kohn–Sham band gaps for α bands (eV)

XC	E	ΔEs	d Fe–O(oxo)	E g	Gap
PBE	−10301.476	−6.067	1.617	1.095	Indirect
BLYP	−10305.558	−5.515	1.632	1.048	Indirect
sc-BLYP	−10305.433	−10.633	1.607	1.505	Direct
B3LYP	−10303.776	−11.059	1.601	2.078	Direct

---

The largest stabilisation of the quintet state in Fe(IV)O/MOF-74 is observed in the hybrid functional calculations, along with a shorter Fe(IV)–O(oxo) bond length and a substantially higher Kohn–Sham gap relative to the two pure density functionals. Furthermore, the Kohn–Sham gap appears to be direct at the zone centre in hybrid calculations (Fig. 2), whereas it is indirect in GGA calculations. The Kohn–Sham gap opening in solid state systems as a consequence of the inclusion of Hartree–Fock exchange in the exchange–correlation functional is well understood.⁵⁰ The shorter Fe(IV)–O(oxo) bond distance is likely to be attributable to an improved description of the exchange interactions responsible for the stabilisation of occupied Fe(IV)O molecular orbitals, which increases the Fe(IV)O bond order.⁵¹ We observe that the band gap with sc-BLYP has the best agreement with those reported in from the oxidised Fe–MOF-74/CPO-27–Fe with a value of ca. 1.3 eV.⁵²

Fig. 2 Band structures of the FeO–MOF-74 represented by the highest occupied (HOMO), and the first four lowest unoccupied molecular orbitals (LUMO, LUMO+1, LUMO+2, and LUMO+3) for B3LYP (a), BLYP (b), PBE (c), sc-BLYP (d) along the path Γ = [0 0 0] to Y = [1 0 0] to F = [1 1 0] to = Z [1 1 1] to Γ with the Fermi level set at 0.0 eV.

We have calculated the adsorption energy E_ads of methane as

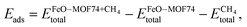where the right-hand terms of eqn (1) represent the total energies of the systems constituted by the CH₄ molecule adsorbed on one site of FeO–MOF74 , the energy of FeO–MOF74 with its cavity unoccupied , and the isolated methane molecule . These energies were calculated for the three MOF atoms that can act as adsorption sites: one oxygen (O1) and two carbons (C1 and C2). We have computed the energies using all four functionals and compared them with the stabilisation energy of the reactant complex, in which CH₄ is coordinated to O(oxo). This leads to a total of 24 configurations. Our results indicate that the methane molecule coordinates preferentially to O(oxo). This is consistent with previous work on solvated and gas-phase CH₄–Fe(IV)O complexes, for which it has been shown that the formation of a reactant complex is related to an incipient interaction between the acceptor Fe(IV)O 3σ* orbital and the highest occupied methane orbital, which acts as a donor of a single electron.⁵¹ This kind of chemical interaction is unavailable at other adsorption sites. Therefore, according to our results, the most likely adsorption site for methane in MOF-74/Fe(IV)O is at the O(oxo) atom (Table 2).

Table 2 Adsorption energies (in kJ mol⁻¹) of methane on the nearest neighbor sites to Fe(IV)Ooxo

Functional	E ads,O1	E ads,C1	E ads,C2	E ads,Ooxo
PBE	−336.80	−264.07	−249.26	−359.78
BLYP	−492.42	−255.78	−313.26	−579.55
sc-BLYP	−335.70	−222.23	−233.26	−664.79
B3LYP	−233.32	−180.90	−177.30	−561.11

---

In Fig. 3 we show the projected densities of states (PDOSs) corresponding to the band structures of Fig. 2. With the two hybrid functionals, the valence band is composed purely of framework atoms, whereas the two GGAs exhibit a non-negligible contribution from Fe(IV)O states. In the case of hybrid-DFT calculations, the valence is composed of extended π bonding bands originating from framework's phenyl groups (cf.Fig. 4 below), with negligible contributions from either CH₄ or the Fe(IV)O moiety. The change in the nature of the occupied states in the vicinity of the Fermi energy in non-hybrid calculations is associated with the change from direct to indirect character of the Kohn–Sham gap. We also observe notable differences between hybrid and non-hybrid PDOSs in the −5 eV energy region. The two hybrid functionals exhibit a well defined and isolated peak corresponding to the highest occupied molecular orbital (HOMO) of the methane molecule, whereas, in the two non-hybrid PDOSs, this peak overlaps with occupied Fe(IV)O states. This is suggestive of a more pronounced electronic coupling between occupied orbitals of Fe(IV)O and the substrate molecule in non-hybrid calculations. As we will show below, this spurious coupling is responsible for the inability of the two non-hybrid functionals to account for the bond breaking and formation processes during the H-atom transfer from methane to the Fe(IV)oxo moiety.

Fig. 3 Density of valence states for all (total) atoms and projected on Fe, O(oxo) and CH₄ at an O(oxo)–H for B3LYP (a), BLYP (b), PBE (c), sc-BLYP (d).

Fig. 4 The difference of the total (ΔE_DFT+disp), DFT (ΔE_EDFT), and long-range dispersion (Δ_disp) energies with respect to their values at 3.56 Å, and the distance between the central carbon atom with the reactive hydrogen (d_C–H) vs. the distance between the O(oxo) and methane's hydrogen with B3LYP (a) and BLYP (b), PBE (c), and sc-BLYP (d).

As shown in ref. 14, the first step in the oxidation of methane via a proton-coupled electron transfer process can be modelled using a series of geometry optimisations, in which the O(oxo)–H(methane) distance is constrained to progressively shorter distances. We remark that in all these optimisation processes, the whole structure is allowed to relax, and the methane molecule to move away from its initial position at the centre of a MOF-74 pore, to minimise the system's total energy. Total energies obtained using this procedure with the four functionals used in this work are shown in Fig. 4. Whereas B3LYP and sc-BLYP yield the expected reaction profile, with a minimum at ca. 2.5 Å (corresponding to a CH₄–OFe(IV) reactant complex) and a maximum at ca. 1.4 Å (corresponding to the CH₃–H–OFe(IV) transition state), the two non-hybrid functionals yield a qualitatively incorrect monotonic increase in energy as the O(oxo)–H(methane) distance decreases. Effectively, according to the two non-hybrid functional calculations, the H-abstraction should not take place, whereas with the two hybrid functionals the reaction occurs with modalities analogous to other Fe(IV)O molecular catalysts in gas phase and in water solution. Similar reaction barriers are obtained, in this case, of ca. 60 kJ mol⁻¹.

During the H-abstraction reaction, an H atom is transferred from CH₄ to the O(oxo) end of the Fe(IV)O moiety. Simultaneously, one electron is transferred to a virtual 3σ* orbital localised on Fe(IV)O. The ability of Fe(IV)O to act as an oxidant species is determined by the energy of this acceptor orbital, as extensively demonstrated, on the basis of DFT calculations and ab initio molecular dynamics simulations, by Baerends and co-workers:²⁸ the lower the energy of the 3σ* orbital, the higher is the electrophilic character of Fe(IV)O. The coordination environment of Fe(IV)O plays a crucial role in stabilising or destabilising this orbital, with weak donor coordinating groups reducing the 3σ* energy orbital more. As shown in ref. 14 and confirmed in this work, MOF-74 provides an oxygen-rich coordinating environment that stabilises the 3σ* sufficiently for Fe(IV)O to act as an efficient oxidant for methane. Along the lines of ref. 14, we have verified that a Fe(IV)O 3σ* orbital is the global lowest unoccupied molecular orbital (LUMO) in Fe(IV)O/MOF-74 for all functionals used in the present work. It is therefore surprising that our calculations with the two non-hybrid functionals, in which the conduction band energy is markedly reduced compared to the hybrid calculations, does not yield a satisfactorily reaction profile.

In Table 3 we list the average atomic spin moments of Fe, O (framework), C and H in the quintet state; the average values for oxygen atoms bound to Fe(IV) are indicated as O(oxo). As expected, the largest spin moment is observed on Fe atoms, which account for ca. 80% of the global spin. B3LYP and sc-BLYP exhibit the largest Fe spin moments, which are ca. 6% higher than in BLYP. By contrast, the hybrid functionals yield lower moments on the O(oxo) atoms compared to the pure density functionals, despite the lower Fe(IV)–O bond distances. This indicates that the Hartree–Fock exchange component of the functional tends to enhance the localisation of the electronic spin on the metal atom and to reduce the transfer of spin via the Fe(IV)–O covalent bond compared to the pure density functionals. In all cases, only very modest spin moments are observed on framework atoms, consistent with the predominantly ionic nature of the Fe(IV)O–MOF interaction.

Table 3 Density-functional dependence of the average atomic spin moments of Fe, O, C, H and O(oxo) (in Bohr magnetons μ_B). The last two rows represent the fraction of the initial spin retained by Fe and transferred to O(oxo)

Atom	B3LYP	PBE	BLYP	sc-BLYP
Fe	3.289	3.099	3.051	3.273
O	0.034	0.031	0.037	0.032
O	0.069	0.082	0.090	0.070
O	0.074	0.105	0.116	0.073
C	0.004	0.014	0.014	0.004
C	0.012	0.018	0.019	0.012
C	0.002	0.015	0.016	0.000
C	0.006	0.019	0.021	0.007
H × 10^3	0.620	0.558	0.390	0.582
O(oxo)	0.510	0.615	0.637	0.529
Fe/all (%)	82.23	77.49	76.27	81.82
O(oxo)/all (%)	12.75	15.37	15.91	13.23

---

In Fig. 5 we show the atomic spin moments of Fe, O(oxo), C(methane), and H(methane) as a function of the H–O(oxo) separation. Fe, O(oxo) and C(methane) exhibit very similar trends with all functionals, which are consistent with an electron being transferred to a majority spin orbital predominantly localised on Fe as the O(oxo)–H distance is reduced. However, the spin moment of the H atom that approaches the Fe(IV) group is substantially reduced in the pure density functionals compared to the hybrid functionals. In particular, the pronounced maximum (with a positive spin moment) at ca. 1 Å observed in B3LYP and sc-BLYP is absent in PBE and BLYP, and the overall spin of H remains close to zero or modestly negative. The behaviour exhibited by the H spin moment computed with the two hybrid functionals is consistent with a homolytic cleavage of the C(methane)–H bond. This process is correctly described as a proton coupled electron transfer reaction⁵³ from methane to the Fe(IV)oxo moiety. By contrast, the modest PBE/BLYP spin moment of H at all O(oxo)–H distances lower than the predicted transition state distance suggests that the C(methane)–H bond breaking occurs heterolytically, i.e. that a proton, rather than an H atom is being transferred to the O end of the Fe(IV)O group. Even in this case, at the end of the H transfer process, C(methane) acquires a net spin moment −1, which indicates that a CH˙ has been created as one of the final products. This is, however, apparently inconsistent with a heterolytic bond cleavage process.

Fig. 5 Spin populations of Fe, O(oxo), H(methane) and C(methane) as a function of the O(oxo)–H distance for B3LYP (a), BLYP (b), PBE (c), sc-BLYP (d).

In Fig. 6 we compare electron density isosurfaces for the HOMO orbital of the Fe(IV)O/MOF-74/CH₄ system obtained at the B3LYP and BLYP levels of theory at large O(oxo)–H separation (3.5 Å). A large degree of mixing is observed in BLYP between the HOMO of the methane molecule and orbitals of the framework. Such mixing, which is virtually absent in the B3LYP orbital, involves the diffuse π orbitals of phenyl rings, which constitute the MOF-74 valence band. This orbital mixing results in the appearance of non-negligible spin moments on the MOF C atoms. For instance, at an H(methane)–O(oxo) distance of 1.1 Å, the spin distributed on the C atoms is roughly four times larger in PBE and BLYP compared to the two hybrid functionals and the sums of all moments are 0.16, 0.15, 0.40, and 0.40 for B3LYP, sc-BLYP, PBE and BLYP respectively. The spin moment of the Fe atom bonded the reactive O(oxo) is also notably larger in B3LYP (4.08) and in sc-BLYP (4.08) than in PBE (3.44) and BLYP (3.32). Similarly, the spin on the H atom being transferred to O(oxo) is roughly 4 times larger in B3LYP and sc-BLYP than in PBE and BLYP. We interpret this spin distribution in the two pure density functionals as a consequence of the transfer of spin moment from the H atom to the framework, via orbital mixing of the methane HOMO with the MOF-74 π states. This mixing provides a channel for “diluting” in the framework the spin moment progressively accumulating on H during a homolytic transfer to Fe(IV)O. By contrast, the B3LYP and sc-BLYP spin moments are consistent with the standard proton coupled electron transfer mechanism observed in Fe(IV)O catalyzed hydrocarbon hydroxylations in gas phase and in water solution (Fig. 7).

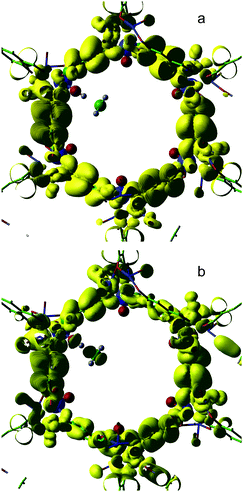Fig. 6 95% charge density isosurface of the HOMO for B3LYP (a) and BLYP (b) at an O(oxo)–H distance of 3.55 Å.

Fig. 7 Spin moment dependence of the C atoms belonging to the MOF on the exchange–correlation functional.

We believe that the higher delocalisation seen in the spins of PBE and BLYP over the carbon atoms is caused by the well-known self-interaction error (SIE) present in GGA functionals. This error has been reported to cause the delocalisation of unpaired electrons over many atoms to reduce the Coulomb repulsion.^54–56 In contrast, spin delocalisation is lower with B3LYP and sc-BLYP because these functionals contain a Hartree–Fock contribution, which is free of such error because the self-interaction part of the Coulomb energy cancels that of the exchange part. In our work, the SIE causes the energy of the methane HOMO to lay too close to that of framework O bands, which induces the mixing responsible for the spin spilling to the framework.

Spurious electron delocalisation caused by the SIE is observed in several classes of approximate exchange–correlation functionals, including, in particular, most GGAs.^54–56 It is also known to affect transition-state barriers for many organic reactions in the gas phase,⁵⁷ which results in anomalously low reaction barriers. This is related to the fact that transition states have, in general, more delocalised densities than minima, and they are therefore artificially stabilised by the SIE. The SIE is reduced in hybrid functionals, because the self-interaction component of the Coulomb energy in pure Hartree–Fock exactly cancels the exchange component. In molecules, this cancellation typically increases reaction barriers for simple organic reactions^58–60 and yields satisfactory rearrangement barriers,⁶¹ although B3LYP is known to provide an incorrect description of dissociation processes.⁶² Extensive DFT calculations on the Fe(IV)O reactivity with water, alcohol, and saturated hydrocarbons have shown, on the other hand, that hydroxylation reactions in the gas phase can be accurately modelled using standard GGA functionals, in particular OPBE.⁴⁶ Similar conclusions have been obtained for analogous reactions in water solution on the basis of ab initio molecular dynamics simulation results.⁵³ In the latter case, the water environment has been shown to influence reaction barriers, but not to promote charge or spin delocalisation in the reaction medium, likely as a consequence of the orbital localisation caused by the dynamically disordered solution environment. Such an orbital localisation mechanism is absent in the highly ordered MOF environment, which, therefore, enhances the spurious effect of the SIE on the hydrogen abstraction reaction. Preliminary results based on ab initio molecular dynamics simulations⁶³ also confirm that, at room temperature, the thermal disorder is not sufficient to prevent the unpaired electron on the H atom from delocalising in the MOF host.

4 Conclusions

In summary, based on pure and hybrid DFT calculations, we have shown that the first step of the methane hydroxylation reaction catalysed by MOF-74 supported Fe(IV)O moieties occurs with modalities similar to analogue reactions in gas-phase and in water solution, i.e. through a proton-coupled electron transfer from the substrate to the O atom of the Fe(IV)O group. In the MOF environment, however (which we model here as a truly infinite solid-state system) spurious SIE effects prevent the electron on the H atom from moving in concert with the proton, and result in the absence of a well defined reaction profile. Hybrid functionals (either global or range separated) offer a convenient means to recover the expected reaction mechanism. Alternatively, DFT+U^64–66 and self-interaction corrected DFT with standard GGAs could provide results similar to hybrid functionals, and work is in progress to verify this suitability of SIE-corrected schemes. Recent work⁶⁷ has also shown that semi-local functionals with a non-local correlation contribution, like the BEEF-vdW functional⁶⁸ may provide a convenient route to accurate energetics, structures, and reactivity of MOFs.

The results obtained in this work using the range-separated sc-BLYP functional confirm the B3LYP findings of ref. 14 concerning the extraordinary reactivity of MOF-supported Fe(IV)O species in the oxidation of methane. In particular, both functionals indicate that the H-abstraction from methane occurs with relatively low (ca. 60 kJ mol⁻¹) enthalpy barriers for B3LYP. Work is in currently in progress, based on ab initio molecular dynamics simulations, to estimate the entropic contribution to the reaction barrier, as well as to develop a complete model of the oxidation profile, including both the initial H-abstraction step and the subsequent OH rebound process during the hydroxylation of methane in MOF-74 at room temperature. We can anticipate that from these simulations we obtain a free energy of reaction that is close to the enthalpy barrier computed here. As we will explain in a future paper (in preparation) this finding can be explained by the reduced entropic effects in the solid-state MOF-74 environment, compared to e.g. gas-phase or solvated calculations. At variance with reaction barrier calculations based on transition state search approaches (see e.g. ref. 69 and 70), the ab initio molecular dynamics method can be used to include entropic effects beyond the harmonic approximation.

Finally, a related aspect that will also be the subject of future work based on the computational framework presented in this paper, is the generation of reactive Fe(IV)O centres in Fe(II)/MOF-74 by activation of O₂,^71,72 a situation in which electronic exchange effects are likely to play a major role in the binding of O₂ to Fe(II) centres and in its ensuing reduction.⁷³ Previous DFT work on the reduction of dioxygen in the presence of Fe(II) complexes in the gas phase and in solution [see e.g. the work of Baerends and coworkers^74–76] has put forward evidence for a staggeringly complex reaction profile during the cleavage of the O–O bond, involving states of different spin multiplicities. Modelling this reaction in the solid state, especially at finite temperatures, therefore presents a number of hurdles. We hope that the work described in our manuscript will be a first step toward more systematic studies of Fe(IV)O generation and reactivity in the solid state.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported in part by the University of Pittsburgh Center for Research Computing through the resources provided and the Supercomputing Center of Galicia (CESGA), Spain.

References

1. T. Mokrani and M. Scurrell, Catal. Rev., 2009, 51, 1–145.
2. N. V. Beznis, B. M. Weckhuysen and J. H. Bitter, Catal. Lett., 2010, 138, 14–22.
3. C. Hammond, M. M. Forde, M. H. Ab Rahim, A. Thetford, Q. He, R. L. Jenkins, N. Dimitratos, J. A. Lopez-Sanchez, N. F. Dummer and D. M. Murphy, et al. , Angew. Chem., Int. Ed., 2012, 51, 5129–5133.
4. M. H. Mahyuddin, A. Staykov, Y. Shiota and K. Yoshizawa, ACS Catal., 2016, 6, 8321–8331.
5. D. Y. Osadchii, A. I. Olivos-Suarez, Á. Szécsényi, G. Li, M. A. Nasalevich, I. A. Dugulan, P. S. Crespo, E. J. Hensen, S. L. Veber and M. V. Fedin, et al. , ACS Catal., 2018, 8, 5542–5548.
6. J. Baek, B. Rungtaweevoranit, X. Pei, M. Park, S. C. Fakra, Y.-S. Liu, R. Matheu, S. A. Alshmimri, S. Alshehri and C. A. Trickett, et al. , J. Am. Chem. Soc., 2018, 140, 18208–18216.
7. E. B. Bauer, Isr. J. Chem., 2017, 57, 1131–1150.
8. S. Lindsay, S. L. Mader, V. R. Kaila and C. R. Hess, ChemistrySelect, 2018, 3, 1602–1608.
9. L. Cheng, J. Wang, M. Wang and Z. Wu, Phys. Chem. Chem. Phys., 2010, 12, 4092–4103.
10. Y.-Y. Li, L.-P. Tong and R.-Z. Liao, Inorg. Chem., 2018, 57, 4590–4601.
11. M. Costas, M. P. Mehn, M. P. Jensen and L. Que, Chem. Rev., 2004, 104, 939–986.
12. L. Que and W. B. Tolman, Nature, 2008, 455, 333–340.
13. B. Meunier, S. P. De Visser and S. Shaik, Chem. Rev., 2004, 104, 3947–3980.
14. F. Saiz and L. Bernasconi, Phys. Chem. Chem. Phys., 2019, 21, 4965–4974.
15. H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444.
16. C. Bai, A. Li, X. Yao, H. Liu and Y. Li, Green Chem., 2016, 18, 1061–1069.
17. K. Shen, X. Chen, J. Chen and Y. Li, ACS Catal., 2016, 6, 5887–5903.
18. Y.-B. Huang, J. Liang, X.-S. Wang and R. Cao, Chem. Soc. Rev., 2017, 46, 126–157.
19. F. R. Fortea-Pérez, M. Mon, J. Ferrando-Soria, M. Boronat, A. Leyva-Pérez, A. Corma, J. M. Herrera, D. Osadchii, J. Gascon and D. Armentano, et al. , Nat. Mater., 2017, 16, 760.
20. S. Siwaipram, S. Impeng, P. A. Bopp and S. Bureekaew, Density Functional Theory, IntechOpen, 2018.
21. M. Barona, S. Ahn, W. Morris, W. Hoover, J. M. Notestein, O. K. Farha and R. Q. Snurr, ACS Catal., 2020, 10, 1460–1469.
22. J. T. Groves and M. Van der Puy, J. Am. Chem. Soc., 1974, 96, 5274–5275.
23. J. T. Groves and G. A. McClusky, J. Am. Chem. Soc., 1976, 98, 859–861.
24. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
25. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
26. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
27. M. R. Ryder, B. Civalleri, T. D. Bennett, S. Henke, S. Rudić, G. Cinque, F. Fernandez-Alonso and J.-C. Tan, Phys. Rev. Lett., 2014, 113, 215502.
28. L. Bernasconi, M. J. Louwerse and E. J. Baerends, Eur. J. Inorg. Chem., 2007, 3023–3033.
29. L. Bernasconi, P. Belanzoni and E. J. Baerends, Phys. Chem. Chem. Phys., 2011, 13, 15272–15282.
30. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
31. H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544.
32. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
33. E. D. Bloch, W. L. Queen, R. Krishna, J. M. Zadrozny, C. M. Brown and J. R. Long, Science, 2012, 335, 1606–1610.
34. D. S. Biovia, Materials Studio Suite, v.5.5.2, 2017.
35. H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364.
36. R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D’Arco, Y. Noël, M. Causà, M. Rérat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317.
37. Y.-X. Yu, J. Mater. Chem. A, 2013, 1, 13559–13566.
38. D. Marx and J. Hutter, Ab initio molecular dynamics: basic theory and advanced methods, Cambridge University Press, 2009.
39. A. Aguado, L. Bernasconi and P. A. Madden, Chem. Phys. Lett., 2002, 356, 437–444.
40. A. Aguado, L. Bernasconi and P. A. Madden, J. Chem. Phys., 2003, 118, 5704–5717.
41. F. Saiz, N. Quirke, L. Bernasconi and D. Cubero, Chem. Phys. Lett., 2016, 664, 143–148.
42. F. Saiz and N. Quirke, Phys. Chem. Chem. Phys., 2018, 20, 27528–27538.
43. F. Saiz, D. Cubero and N. Quirke, Phys. Chem. Chem. Phys., 2018, 20, 25186–25194.
44. F. Saiz, J. Phys. Chem. Solids, 2020, 137, 109204.
45. S. Choomwattana, T. Maihom, P. Khongpracha, M. Probst and J. Limtrakul, J. Phys. Chem. C, 2008, 112, 10855–10861.
46. M. Swart, A. R. Groenhof, A. W. Ehlers and K. Lammertsma, J. Phys. Chem. A, 2004, 108, 5479–5483.
47. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218.
48. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
49. S. Shaik, H. Hirao and D. Kumar, Acc. Chem. Res., 2007, 40, 532–542.
50. K. Doll, V. Saunders and N. Harrison, Int. J. Quantum Chem., 2001, 82, 1–13.
51. M. J. Louwerse and E. J. Baerends, Phys. Chem. Chem. Phys., 2007, 9, 156–166.
52. M. Märcz, R. E. Johnsen, P. D. Dietzel and H. Fjellvåg, Microporous Mesoporous Mater., 2012, 157, 62–74.
53. L. Bernasconi and E. J. Baerends, J. Am. Chem. Soc., 2013, 135, 8857–8867.
54. H. Jónsson, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 944–949.
55. S. Klüpfel, P. Klüpfel and H. Jónsson, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 050501.
56. S. Klüpfel, P. Klüpfel and H. Jónsson, J. Chem. Phys., 2012, 137, 124102.
57. M. Lundberg and P. E. M. Siegbahn, J. Chem. Phys., 2005, 122, 224103.
58. B. G. Johnson, C. A. Gonzales, P. M. Gill and J. A. Pople, Chem. Phys. Lett., 1994, 221, 100–108.
59. G. I. Csonka and B. G. Johnson, Theor. Chem. Acc., 1998, 99, 158–165.
60. S. Patchkovskii and T. Ziegler, J. Chem. Phys., 2002, 116, 7806–7813.
61. J. L. Durant, Chem. Phys. Lett., 1996, 256, 595–602.
62. V. Hrouda, M. Roeselová and T. Bally, J. Phys. Chem. A, 1997, 101, 3925–3935.
63. F. Saiz and L. Bernasconi, 2020, in preparation.
64. G. W. Mann, K. Lee, M. Cococcioni, B. Smit and J. B. Neaton, J. Chem. Phys., 2016, 144, 174104.
65. C. Ricca, I. Timrov, M. Cococcioni, N. Marzari and U. Aschauer, APS Meeting Abstracts, 2019.
66. A. S. Rosen, M. R. Mian, T. Islamoglu, H. Chen, O. K. Farha, J. M. Notestein and R. Q. Snurr, J. Am. Chem. Soc., 2020, 142, 4317–4328.
67. L. Li, S. Zhang, J. P. Ruffley and J. K. Johnson, ACS Sustainable Chem. Eng., 2019, 7, 2508–2515.
68. J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149.
69. R. Gholizadeh and Y.-X. Yu, Appl. Surf. Sci., 2015, 357, 1187–1195.
70. Y.-X. Yu, J. Phys. Chem. C, 2018, 123, 205–213.
71. E. D. Bloch, L. J. Murray, W. L. Queen, S. Chavan, S. N. Maximoff, J. P. Bigi, R. Krishna, V. K. Peterson, F. Grandjean, G. J. Long, B. Smit, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14814–14822.
72. P. Verma, R. Maurice and D. G. Truhlar, J. Phys. Chem. C, 2015, 119, 28499–28511.
73. T. Thonhauser, S. Zuluaga, C. A. Arter, K. Berland, E. Schroeder and P. Hyldgaard, Phys. Rev. Lett., 2015, 115, 136402.
74. L. Bernasconi and E. J. Baerends, Inorg. Chem., 2009, 48, 527–540.
75. P. Belanzoni, L. Bernasconi and E. J. Baerends, J. Phys. Chem. A, 2009, 113, 11926–11937.
76. L. Bernasconi, P. Belanzoni and E. J. Baerends, Phys. Chem. Chem. Phys., 2011, 13, 15272–15282.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01285h

---