Open Access Article
Open Access ArticleHydration interactions beyond the first solvation shell in aqueous phenolate solution
Roberto
Cota†
 ab,
Ambuj
Tiwari†
a,
Bernd
Ensing
ab,
Ambuj
Tiwari†
a,
Bernd
Ensing
 a,
Huib J.
Bakker
*b and
Sander
Woutersen
a,
Huib J.
Bakker
*b and
Sander
Woutersen
 *a
*a
aVan 't Hoff Institute for Molecular Sciences, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands. E-mail: s.woutersen@uva.nl
bAMOLF, Science Park 104, 1098 XG Amsterdam, The Netherlands. E-mail: h.bakker@amolf.nl
First published on 14th August 2020
Abstract
We investigate the orientational dynamics of water molecules solvating phenolate ions using ultrafast vibrational spectroscopy and density functional theory-based molecular dynamics simulations. To assess the roles of the hydrophobic and hydrophilic parts of the anion, we also perform experiments and simulations on solutions of phenol. The experiments show that phenolate immobilizes (τor > 10 ps) 6.2 ± 0.5 water molecules beyond the first solvation shell of its oxygen atom, whereas phenol immobilizes only ∼2 water molecules, including the water molecules in its first solvation shell. The simulations reproduce the experiments very well, and show that phenolate causes a local ordering of the hydrogen-bond structure that extends beyond the first solvation shell, thus explaining the experimental observations. The comparison with phenol solution shows that the solvation interaction of phenolate beyond its first solvation shell is due to the high charge density of its negatively charged oxygen atom.
1 Introduction
Due to the strong local electric fields that they generate, ions dissolved in water modify the hydrogen-bond structure, and give rise to local structural ordering in the form of solvation shells. These structures play an important role in many biological, chemical and physical processes, such as the ion selectivity of ionic transmembrane channels and the salting in or out of proteins as exemplified in the Hofmeister series.1–10 For this reason, numerous experimental and theoretical studies have been carried out to investigate the interactions between ions and solvation water.11–23Time-resolved vibrational spectroscopy is very well suited for investigating aqueous solvation, because the hydrogen bonds between a solute and the OH groups of solvating water molecules can be probed in a direct manner by tracking the dynamics (frequency fluctuations and orientational diffusion) of the OH-stretch (or OD-stretch) mode.24–37 Up to now, time-resolved OH-stretch (and OD-stretch) spectroscopy studies of anion solvation have focused mostly on single-atom anions, notably the halides.24,26,27,31,38 These experiments have shown that the local restructuring of the hydrogen-bond network by the anions leads to a slowing down of the dynamics of the water molecules in the first solvation shell: for some anions, the correlation time of the random orientational motion of the OH bonds involved in the water-anion hydrogen bonds is more than an order of magnitude slower than in bulk water.24 Whereas the halide anions have been extensively investigated with vibrational spectroscopy and advanced calculations,11,12,14,39 much less is known about the oxygen-containing anions.
Here, we investigate the solvation of the molecular anion phenolate. In this anion oxygen has a single negative charge, which renders its ionic radius comparatively small. In addition, phenolate is of particular interest since simulations show that the negatively charged oxygen of this anion can form multiple hydrogen bonds with surrounding water molecules, while the phenyl ring is only weakly solvated.40,41 It is not clear how these opposing effects influence the dynamics of the solvating water. Phenolate ions and phenol are also the subject of active research because they are widely observed in nature as organic pollutants,42,43 can be used as ionic liquids for CO2 chemisorption,44,45 and can function as precursors in organic syntheses.46 Previous studies suggest that phenol and the phenolate ion (and their corresponding derivatives) can have a strong impact on the chemical reactivity of aqueous solutions, in particular at the water–air interface due to their amphiphilic character.47–50
We investigate the influence of phenolate ions on the reorientation dynamics of solvating water molecules using two complementary methods: time-resolved vibrational spectroscopy and density functional theory-based molecular dynamics simulations (DFT-MD). To distinguish the effects of the hydrophobic and hydrophilic parts of the anion, we also perform experiments and simulations on solutions of phenol. The experiments show that the local water dynamics is much more affected by phenolate than by phenol. This difference finds its origin in the strong hydrogen bonding between water and the negatively charged oxygen of phenolate. The simulations confirm this observation, and show that phenolate has an effect on the hydrogen-bond structure and dynamics of water that extends beyond the first solvation shell.
2 Materials and methods
2.1 Sample preparation
Commercially purchased phenol PhOH (≥99.5%, Sigma Aldrich) and PhONa (99%, Sigma Aldrich) were used to prepare solutions in isotope-diluted water (HDO:H2O fraction 8%) prepared by mixing D2O (99.96% D, Eurisotop) and deionized H2O (conductivity 5.5 μS m−1). Phenol was investigated in a solution of 0.84 molal (close to its maximum solubility of 0.88 m), while sodium phenolate solutions were prepared with concentrations of 0.84, 1, 2 and 3 m. For pump–probe experiments, samples were kept in a CaF2 sample cell with a 50 μm path length, while the path length was set to 25 μm for linear IR spectra.2.2 Vibrational pump–probe experiments
We perform polarization-resolved infrared transient-absorption measurements using pulses resonant with the OD-stretch mode (2510 cm−1). Mid-infrared pulses are generated by parametric down conversion of a Yb:KGW amplified laser system (repetition rate 1 kHz) in a KTA crystals (Orpheus-ONE-HP, Light Conversion). At 2510 cm−1, the pulses have an energy of 12 μJ, a bandwidth of 120 cm−1 and a duration of ∼200 fs. A ZnSe window at an incidence angle of 45° is used to generate the pump (transmission), while the reflected beam is further split off in a second ZnSe window to generate probe and reference beams. A zero-order λ/2 plate is used to rotate the polarization of the pump pulse by 45° with respect to that of the probe and the reference pulse. The pump and probe beams are focused and spatially overlapped in the liquid sample (focal diameter ∼ 50 μm). The parallel and perpendicular components of the probe pulse are measured separately using a wire-grid polarizer, and detected together with the reference in a spectrally resolved manner using a spectrograph and a 3 × 32 MCT-array detector.The transient spectral response is defined as Δα = −ln[T/T0], with T and T0 the pumped and unpumped transmittance. We use the parallel and perpendicular transient absorption changes to construct the isotropic transient signal as
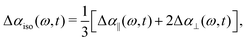 | (1) |
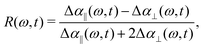 | (2) |
2.3 Simulations
All DFT-MD simulations were performed with the CP2K package53 using the combined Gaussian and plane-wave method as implemented in the Quickstep module.54 We used the BLYP55,56 functional in conjunction with Grimme's D3 correction for van der Waals interactions57 with a TZVP basis set58 and a 300 Ry plane-wave cutoff. Core electrons were represented by GTH pseudopotentials.59 A CSVR thermostat60 maintained a temperature of T = 325 K. The systems contained a single solute molecule and 63 water molecules in a cubic supercell subject to periodic boundary conditions. The number of water molecules are calculated to match the experimental density with a cubic box that has an edge length of 12.43 Å. The trajectory was saved every 50 fs. The simulations were performed at 325 K, since previous studies61,62 and our own benchmark calculations show that this yields good agreement of the structural and dynamical properties of water at the BLYP-D3 level of theory with experimental data at 298 K.The validity of our choice of level of theory (DFT XC functional, dispersion correction, pseudopotentials, and basis functions) has been demonstrated in simulations on various aqueous systems.63,64 In particular, it has been shown that this setup gives densities that match the experimental value very well over a considerable range of temperatures. This allows us to simply setup and equilibrate the system at the experimental density and perform the simulations in the canonical (NVT) ensemble. The systems contained a single solute molecule and 63 water molecules in a cubic supercell subject to periodic boundary conditions. The number of water molecules are calculated to match the experimental density with a cubic box that has an edge length of 12.43 Å. The solute concentration in the simulation was 0.86 M, which is very similar to the concentration used in the experiments. The trajectory was saved every 50 fs.
To calculate the orientational autocorrelation function, we first calculate the vector ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) along the OH bond associated with each water molecule. Next, the time evolution of this vector
along the OH bond associated with each water molecule. Next, the time evolution of this vector ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) is determined by calculating the autocorrelation function C2(t) defined as
is determined by calculating the autocorrelation function C2(t) defined as
| C2(t) = 〈P2[û(0)·û(t)]〉, | (3) |
 | (4) |
3 Results and discussion
3.1 Linear absorption spectra
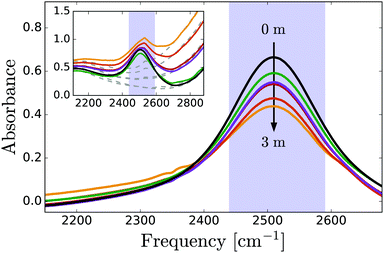
Fig. 1 shows linear absorption spectra of PhOX (X = H+, Na+) solutions in isotopically diluted HDO:H2O, with the OD-stretch band of HDO at 2510 cm−1. Phenol has negligible influence on the OD-stretch spectrum (mainly a decrease in absorption due to water dilution at high concentrations), whereas in phenolate solutions, the OD-stretch band has a low-frequency wing centered at approximately 2300 cm−1 which we assign to OD groups coordinating to the phenolate O atom. The frequency of these OD vibrations is redshifted compared to neat HDO:H2O as a result of the strong hydrogen bonding with the negatively charged oxygen atom of phenolate. A similar redshift is observed for the OH-stretch band (centered at ∼2900 cm−1) in crystalline NaPhO·3H2O due to OH groups coordinated to PhO−, and for the OH-stretch band of H2O in NaOH solutions.65 At high frequencies we observe the low-frequency wing of the OH stretch vibrations coordinated to phenolate. In view of the pKa value of phenol of 10, the fraction of phenolate that will react to phenol is negligible (∼10−2 M) compared to the phenolate fraction.3.2 Time-resolved vibrational spectroscopy
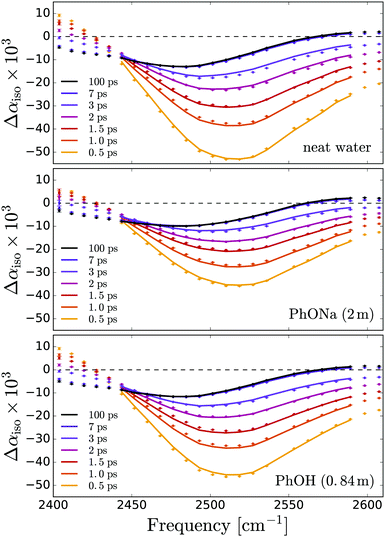
In the time-resolved experiments, the infrared pump pulse excites a small fraction (∼2%) of the OD stretch vibrations from the v = 0 to the v = 1 state, and the resulting absorption change Δα is measured with the probe pulse as a function of the infrared frequency ω and the delay t with respect to the excitation pulse. Fig. 2 shows the results for neat HDO:D2O and two of the investigated solutions. The reduced density of absorbers in the v = 0 state leads to a decrease in absorption (Δα < 0) at the v = 0 → 1 transition frequencies. The population of the v = 1 state gives rise to v = 1 → 0 stimulated emission, thus enhancing the bleaching at the v = 0 → 1 frequencies, and an induced absorption (Δα > 0) at the v = 1 → 2 frequencies, which constitute the lowest observed frequencies in Fig. 2. The relaxation of the vibrationally excited OD-groups is observed as a decay of the signal amplitude on a picosecond time scale. For long time delays (>10 ps), all the OD groups are back in the v = 0 state, but there is a residual Δα signal due to local heating in the sample: in the relaxation process, the energy is thermalized (transferred from the OD-stretch mode to low-frequency degrees of freedom), and the resulting increase in local temperature gives rise to a blueshift and an intensity decrease of the OD-stretch band.51 Complete thermalization (diffusion of the locally deposited heat out of the focal volume) takes place on a much slower time scale (hundreds of microseconds).The transient absorption spectra measured for phenolate and phenol have similar shapes and dynamics. The main difference is that the overall amplitude of the transient signal in the phenolate solution is slightly reduced. This reduction is due to the fact that the pump pulses are partially absorbed by OH groups of water that are strongly hydrogen bonded to phenolate. These OH groups are not visible in Fig. 2 since they relax on a very fast (∼300 fs)66 time scale compared to that of the excited OD stretch vibrations, 1.7 ps.51 For the transient absorption spectra of the PhOH solution (Fig. 2c), the overall amplitude is the same as that of neat HDO:H2O. In our analysis of the transient data we only use delay times larger than 0.5 ps for which the contribution of the OH groups that are strongly hydrogen bonded to phenolate is negligible.
Previous work has shown that the vibrational relaxation of the OD-stretch mode in HDO:H2O (both for the neat liquid and for solutions) occurs in two steps, see Fig. 3: after the vOD = 1 → 0 relaxation, the vibrational energy is first redistributed over local low-frequency modes, and subsequently is fully thermalized (typically on a time scale of about 1 ps), leading to a local temperature increase (on the order of a few K).67 In the thermalized state the OD-stretch spectrum is different from that at t = 0 (the OD-stretch spectrum is sensitive to temperature), so that the bimodal relaxation is mirrored in biexponential kinetics of the transient OD-stretch absorption change.51,52 In our experiments we also observe this two-step relaxation mechanism: a singular value decomposition of the data matrices Δαiso(ω,t) shows that in all cases the transient signal is well described (99%) by two spectral and temporal components. Hence, we describe our experimental data using the model of ref. 51:
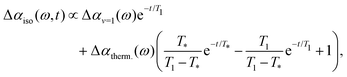 | (5) |
 | ||
| Fig. 3 Two-step mechanism of the vibrational relaxation of the OD-stretching mode of HDO:H2O (see eqn (5)). | ||
In order to determine the anisotropy of the transient absorption change associated with only the excitation of the OD-stretch vibrations, we must subtract the time-dependent spectral contribution due to the hot ground state (the second term in eqn (5)) from both the parallel and perpendicular transient Δα signals.51Fig. 4 shows the thermalization-corrected anisotropy for all the samples investigated. In all samples the anisotropy decays on a time scale of about 2 ps, but in the phenolate and phenol solutions there is a residual anisotropy at long delay times. This residual anisotropy, the amplitude of which increases with the concentration of solute, implies that a fraction of the water OD groups are rotationally immobilized (i.e. have an orientational relaxation time much longer than our accessible time window of 7 ps). We find that we can fit the anisotropy curves very well with a function
| R(t) = Ae−t/τ + B, | (6) |
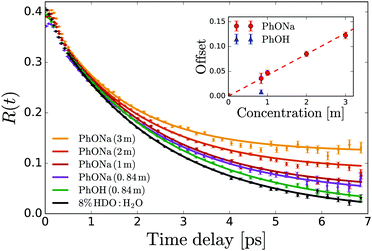 | ||
| Fig. 4 Anisotropy decay of the OD stretch vibration of HDO in NaOH:H2O and NaOH:H2O. The curves are determined from the averaged anisotropy over the frequency range of 2450–2535 cm−1. The solid lines represent fits of eqn (6) to the data. The inset shows the offset B extracted from the fits as a function of solute concentration. | ||
From the residual anisotropy B we can estimate the number of water molecules that are rotationally immobilized by the solute.68 For phenol this is straightforward; for phenolate the situation is slightly more complicated. In a 1 m PhONa:H2O solution there are 55 water molecules per phenolate, of which ∼4 are contained in the first solvation shell. These primary water molecules are not visible in the transient absorption spectra (they absorb at a much lower infrared frequency, see above), and so do not contribute to the anisotropy in Fig. 4. The experimentally observed residual anisotropy of ∼12 ± 1% thus implies that 0.12 ± 0.01 × (55 − 4) = 6.2 ± 0.5 water molecules beyond the first solvation shell of the ion are rotationally immobilized. On the other hand, only 1.5 ± 0.7 water molecules are immobilized per phenol molecule, including the first solvation shell.
The significant difference in the number of water molecules immobilized by phenolate and phenol might be due to two effects: (i) a difference in the solvation interaction of these two solutes, or (ii) phenol molecules might form clusters by π stacking (electrostatic repulsion would prohibit this for phenolate), so that the solvent exposed area per phenol molecule might be much smaller than in the case of phenolate. In order to study the latter possibility, we measure the concentration dependence of the UV absorption spectrum of aqueous phenol solution. If phenol would form clusters by π-stacking, excitonic effects should cause a significant change in the S0 → S1 absorption band (at ∼270 nm) of these clusters as compared to monomeric phenol. Since the cluster/monomer ratio should increase with the phenol concentration, any clustering should result in a concentration-dependent shape of the 270 nm absorption band. Hence, we recorded UV absorption spectra of a series of PhOH:H2O solutions with concentrations ranging from 2.5 to 400 mM. The scaled spectra overlap perfectly, so that clustering of phenol can be ruled out. We conclude that the different numbers of water molecules that are immobilized by phenolate and phenol must be due to a difference in solvation between these two solutes.
3.3 DFT-MD simulations
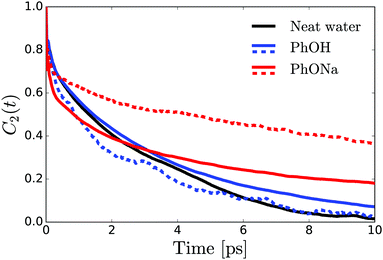
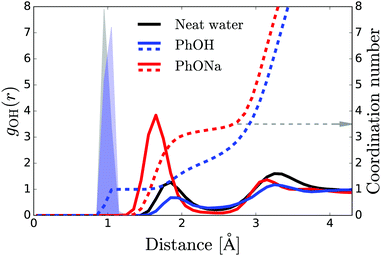
To investigate the aqueous solvation structure and dynamics of phenolate in more detail, we perform DFT-MD simulations of phenolate and phenol solutions. DFT-MD simulations have been shown to accurately model the aqueous solvation of small solutes69–71 and to predict the anisotropy decay of water in such solutions reasonably well.36Fig. 5 shows the OH-anisotropy decays of water molecules in phenol and phenolate solutions and in neat water, as obtained from our simulations. As in the experiment, we observe a significant residual anisotropy in the phenolate solution, which is absent in the phenol solution. By partitioning the water molecules, we can study the orientational dynamics of the water molecules in more detail. We distinguish between (1) hydrogen-bond donating water molecules (w) in the first solvation shell of the phenolate/phenol (s) oxygen (distance rHw–Os < 2.6), which we will refer to as solvation water, and (2) the remaining water, denoted as bulk. The solvation water of phenolate shows considerably slower rotational dynamics compared to the solvation water of phenol, which is not surprising in view of the strong hydrogen bonds between phenolate and the water molecules in its first solvation shell. In the phenolate solution the rotational dynamics of the water outside the first solvation shell is also found to be significantly slower compared to the rotational dynamics of neat water (red solid line in Fig. 5). The correlation function of the water molecules beyond the first solvation shell decays to a residual offset of ∼15%, which is similar to the experimental value of 12%. This extended effect on the water reorientation dynamics, with the ion immobilizing water molecules beyond its first solvation shell, is not present in the phenol solution.The radial distribution functions obtained from the simulations (Fig. 6) reveal that there are three to four water H atoms in the first coordination shell of the phenolate oxygen, whereas in the case of the phenol oxygen there is only one. Furthermore, the water molecules are at a much shorter distance from the phenolate oxygen than they are from the phenol oxygen. Both these effects can be attributed to the negative charge on the phenolate oxygen atom. In addition, the radial distribution curve for phenolate shows a well-defined second coordination shell. In contrast, phenol has a rather labile solvation structure, leading to a significant overlap between the first and second coordination shells, as indicated by the lack of a clear minimum in the interval 2–3 Å of the radial distribution. These results show that in the case of phenolate the effect on the hydrogen-bond structure and dynamics of water extends over a significantly longer distance than in the case of phenol, in agreement with the experimentally observed larger number of water molecules that are rotationally immobilized by phenolate in comparison to phenol.
4 Discussion
Both in the experiments and in the simulations, we observe a residual anisotropy due to water molecules that are rotationally immobilized by the solute. The number of water molecules immobilized by phenolate is surprisingly large, and corresponds to about 6 water molecules beyond its first solvation shell. Comparison with the results obtained on phenol shows that the relatively large spatial extent of the hydration interaction of phenolate is likely due to its negatively charged oxygen atom. The low-frequency OD-stretch wing observed in the absorption spectrum of the phenolate solution indicates that the negatively charged oxygen of phenolate forms very strong (i.e. short) hydrogen bonds with water, and the simulations show that these phenolate-water hydrogen bonds are sufficiently strong to increase also the hydrogen bond strength in the second solvation shell, leading to an enhancement of the hydrogen bond structure in the second solvation shell, thus explaining the experimentally observed rotational immobilization of these water molecules.At first sight the solvation of phenolate may appear similar to the solvation of halide anions, for which also a slowing down of the water reorientation was observed.72,73 However, the origins of the slowdown are distinctly different: in the case of the halide anions, the solvating water molecules are hydrogen-bonded very weakly to the solute (as reflected by their OD-stretch frequency, which is higher than that of neat water), and the slowdown of the reorientation dynamics is due to the fact that reorienting a water molecule requires breaking and formation of hydrogen bonds, and solvating water molecules in the first hydration shell have less hydrogen-bond acceptors at their disposal than water molecules in the bulk.74 For this reason the effect of the anions on the hydrogen-bond structure and dynamics is limited to the first solvation shell. In the case of phenolate, the hydrogen bonds between water and the ions are stronger than in neat water (as reflected by their low OD-stretch frequency), causing an increase in the strength and ordering of the hydrogen-bond network, and thus immobilizing water molecules beyond the first solvation shell.
5 Conclusions
We have investigated the solvation of phenolate and phenol in water using a combination of time-resolved pump–probe spectroscopy and density functional theory-based molecular dynamics simulations. In the experiments, we probe the reorientation dynamics of the hydroxyl groups of water molecules in the presence of the solute. We find that phenolate rotationally immobilizes ∼6 water molecules beyond its first solvation shell, a surprisingly large number that is confirmed by the simulations. Phenol immobilizes only 2 water molecules, including the water molecules in its first hydrations shell. The simulations reveal that the effect of phenolate on the reorientation dynamics of water beyond the first solvation shell is due to a local strengthening of the water hydrogen bond network, induced by the high charge density of the negatively charged oxygen atom of phenolate.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Hans Sanders, Michiel Hilbers and Hinco Schoenmakers for technical support. This work was financially supported by the Netherlands Organisation for Scientific Research (NWO). Grant number: 12PR2989. AT gratefully acknowledges support from the Industrial Partnership Programme (IPP) “Computational sciences for energy research” of the Netherlands Organisation for Scientific Research (NWO), co-financed by Shell Global Solutions International B.V.Notes and references
- R. Pomès, Isr. J. Chem., 1999, 39, 387–395 CrossRef.
- J. M. Swanson, C. M. Maupin, H. Chen, M. K. Petersen, J. Xu, Y. Wu and G. A. Voth, J. Phys. Chem. B, 2007, 111, 4300–4314 CrossRef CAS PubMed.
- P. Ball, Chem. Rev., 2008, 108, 74–108 CrossRef CAS PubMed.
- H. Kim, H. Lee, G. Lee, H. Kim and M. Cho, J. Chem. Phys., 2012, 136, 124501 CrossRef PubMed.
- P. Jungwirth, J. Phys. Chem. Lett., 2013, 4, 4258–4259 CrossRef CAS PubMed.
- W. Ensing, J. Hunger, N. Ottosson and H. J. Bakker, J. Phys. Chem. C, 2013, 117, 12930–12935 CrossRef CAS.
- H. Deng, S. Huo, Y. Chang, Y. Zhou and K. Jiao, Int. J. Hydrogen Energy, 2013, 38, 6509–6525 CrossRef CAS.
- P. Jungwirth and P. S. Cremer, Nat. Chem., 2014, 6, 261–263 CrossRef CAS PubMed.
- H. T. Kratochvil, J. K. Carr, K. Matulef, A. W. Annen, H. Li, M. Maj, J. Ostmeyer, A. L. Serrano, H. Raghuraman, S. D. Moran, J. L. Skinner, E. Perozo, B. Roux, F. I. Valiyaveetil and M. T. Zanni, Science, 2016, 353, 1040–1044 CrossRef CAS PubMed.
- G. Schwaab, F. Sebastiani and M. Havenith, Angew. Chem., Int. Ed., 2019, 58, 3000–3013 CrossRef CAS PubMed.
- J. D. S. R. J. Saykally and P. L. Geissler, J. Am. Chem. Soc., 2007, 129, 13847–13856 CrossRef PubMed.
- B. S. Mallik, A. Semparithi and A. Chandra, J. Chem. Phys., 2008, 129, 194512 CrossRef PubMed.
- Y. Marcus, Chem. Rev., 2009, 109, 1346–1370 CrossRef CAS PubMed.
- I. A. Heisler and S. R. Meech, Science, 2010, 327, 857–860 CrossRef CAS PubMed.
- S. Funkner, G. Niehues, D. A. Schmidt, M. Heyden, G. Schwaab, K. M. Callahan, D. J. Tobias and M. Havenith, J. Am. Chem. Soc., 2012, 134, 1030–1035 CrossRef CAS PubMed.
- J. R. Choudhuri, V. K. Yadav, A. Karmakar, B. S. Mallik and A. Chandra, Pure Appl. Chem., 2013, 85, 27–40 CAS.
- K. Morgenstern, D. Marx, M. Havenith and M. Muhler, Phys. Chem. Chem. Phys., 2015, 17, 8295–8296 RSC.
- L. Comez, M. Paolantoni, P. Sassi, S. Corezzi, A. Morresi and D. Fioretto, Soft Matter, 2016, 12, 5501–5514 RSC.
- E. Pluharova, D. Laage and P. Jungwirth, J. Phys. Chem. Lett., 2017, 8, 2031–2035 CrossRef CAS PubMed.
- P. Schienbein, G. Schwaab, H. Forbert, M. Havenith and D. Marx, J. Phys. Chem. Lett., 2017, 8, 2373–2380 CrossRef CAS PubMed.
- T. Morawietz, A. S. Urbina, P. K. Wise, X. Wu, W. Lu, D. Ben-Amotz and T. E. Markland, J. Phys. Chem. Lett., 2019, 10, 6067–6073 CrossRef CAS PubMed.
- E. Pluharova, P. Jungwirth, N. Matubayasi and O. Marsalek, J. Chem. Theory Comput., 2019, 15, 803–812 CrossRef PubMed.
- D. Ben-Amotz, J. Am. Chem. Soc., 2019, 141, 10569–10580 CrossRef CAS PubMed.
- M. F. Kropman, H.-K. Nienhuys and H. J. Bakker, Phys. Rev. Lett., 2002, 88, 77601 CrossRef CAS PubMed.
- D. Laage and J. T. Hynes, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11167–11172 CrossRef CAS PubMed.
- S. Park and M. D. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 16731–16738 CrossRef CAS PubMed.
- S. Park, D. E. Moilanen and M. D. Fayer, J. Phys. Chem. B, 2008, 112, 5279–5290 CrossRef CAS PubMed.
- S. Park, M. Odelius and K. J. Gaffney, J. Phys. Chem. B, 2009, 113, 7825–7835 CrossRef CAS PubMed.
- Y. S. Lin, B. M. Auer and J. L. Skinner, J. Chem. Phys., 2009, 131, 144511 CrossRef PubMed.
- M. Ji, M. Odelius and K. J. Gaffney, Science, 2010, 328, 1003–1005 CrossRef CAS PubMed.
- J. Boisson, G. Stirnemann, D. Laage and J. T. Hynes, Phys. Chem. Chem. Phys., 2011, 13, 19895–19901 RSC.
- K. F. Rinne, S. Gekle and R. R. Netz, J. Phys. Chem. A, 2014, 118, 11667–11677 CrossRef CAS PubMed.
- Q. Zhang, T. Wu, C. Chen, S. Mukamel and W. Zhuang, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10023–10028 CrossRef CAS PubMed.
- Q. Zhang, H. Chen, T. Wu, T. Jin, Z. Pan, J. Zheng, Y. Gao and W. Zhuang, Chem. Sci., 2017, 8, 1429–1435 RSC.
- C. H. Giammanco, D. B. Wong and M. D. Fayer, J. Phys. Chem. B, 2012, 116, 13781–13792 CrossRef CAS PubMed.
- B. Ensing, A. Tiwari, M. Tros, J. Hunger, S. R. Domingos, C. Pérez, G. Smits, M. Bonn, D. Bonn and S. Woutersen, Nat. Commun., 2019, 10, 2893 CrossRef.
- A. Kundu, P. K. Verma and M. Cho, J. Phys. Chem. B, 2019, 123, 5238–5245 CrossRef CAS.
- A. W. Omta, M. F. Kropman, S. Woutersen and H. J. Bakker, Science, 2003, 301, 347–349 CrossRef CAS.
- J. R. Choudhuri, V. K. Yadav, A. Karmakar, B. S. Mallik and A. Chandra, Pure Appl. Chem., 2013, 85, 27–40 CAS.
- G. Graziano, Biophys. Chem., 1999, 82, 69–79 CrossRef CAS.
- D. Ghosh, A. Roy, R. Seidel, B. Winter, S. Bradforth and A. I. Krylov, J. Phys. Chem. B, 2012, 116, 7269–7280 CrossRef CAS.
- M. R. Heal, M. A. Harrison and J. Neil Cape, Atmos. Environ., 2007, 41, 3515–3520 CrossRef CAS.
- S. Rayne, K. Forest and K. J. Friesen, Environ. Int., 2009, 35, 425–437 CrossRef CAS PubMed.
- T. B. Lee, S. Oh, T. R. Gohndrone, O. Morales-Collazo, S. Seo, J. F. Brennecke and W. F. Schneider, J. Phys. Chem. B, 2016, 120, 1509–1517 CrossRef CAS PubMed.
- K. R. Gorantla and B. S. Mallik, J. Phys. Chem. A, 2020, 124, 836–848 CrossRef CAS PubMed.
- J. P. Lajiness, W. M. Robertson, I. Dunwiddie, M. A. Broward, G. A. Vielhauer, S. J. Weir and D. L. Boger, J. Med. Chem., 2010, 53, 7731–7738 CrossRef CAS PubMed.
- Y. Rao, M. Subir, E. A. McArthur, N. J. Turro and K. B. Eisenthal, Chem. Phys. Lett., 2009, 477, 241–244 CrossRef CAS.
- X. Lu, J. Han, N. Shephard, S. Rhodes, A. D. Martin, D. Li, G. Xue and Z. Chen, J. Phys. Chem. B, 2009, 113, 12944–12951 CrossRef CAS.
- R. Kusaka, T. Ishiyama, S. Nihonyanagi, A. Morita and T. Tahara, Phys. Chem. Chem. Phys., 2018, 20, 3002–3009 RSC.
- B. Minofar, P. Jungwirth, M. R. Das, W. Kunz and S. Mahiuddin, J. Phys. Chem. C, 2007, 111, 8242–8247 CrossRef CAS.
- Y. L. A. Rezus and H. J. Bakker, J. Chem. Phys., 2005, 123, 114502 CrossRef CAS PubMed.
- Y. L. A. Rezus and H. J. Bakker, J. Chem. Phys., 2006, 125, 144512 CrossRef CAS PubMed.
- The CP2K developers group, http://www.cp2k.org.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- S. Yoo and S. S. Xantheas, J. Chem. Phys., 2011, 134, 121105 CrossRef PubMed.
- R. Jonchiere, A. P. Seitsonen, G. Ferlat, A. M. Saitta and R. Vuilleumier, J. Chem. Phys., 2011, 135, 154503 CrossRef PubMed.
- S. Biswas, D. Chakraborty and B. S. Mallik, ACS Omega, 2018, 3, 2010–2017 CrossRef CAS PubMed.
- J. Schmidt, J. VandeVondele, I.-F. W. Kuo, D. Sebastiani, J. I. Siepman, J. Hutter and C. J. Mundy, J. Phys. Chem. B, 2009, 113, 11959–11964 CrossRef CAS PubMed.
- A. Mandal, K. Ramasesha, L. De Marco and A. Tokmakoff, J. Chem. Phys., 2014, 140, 204508 CrossRef PubMed.
- L. Liu, J. Hunger and H. J. Bakker, J. Phys. Chem. A, 2011, 115, 14593–14598 CrossRef CAS PubMed.
- T. Steinel, J. B. Asbury, J. Zheng and M. D. Fayer, J. Phys. Chem. A, 2004, 108, 10957–10964 CrossRef CAS PubMed.
- Y. L. A. Rezus and H. J. Bakker, J. Phys. Chem. B, 2009, 113, 4038–4044 CrossRef CAS PubMed.
- A. Pérez de Alba Ortíz, A. Tiwari, R. C. Puthenkalathil and B. Ensing, J. Chem. Phys., 2018, 149, 072320 CrossRef PubMed.
- J. M. Park, A. Laio, M. Iannuzzi and M. Parrinello, J. Am. Chem. Soc., 2006, 128, 11318–11319 CrossRef CAS PubMed.
- T. De Meyer, B. Ensing, S. M. Rogge, K. De Clerck, E. J. Meijer and V. Van Speybroeck, ChemPhysChem, 2016, 17, 3447–3459 CrossRef CAS PubMed.
- M. F. Kropman and H. J. Bakker, Science, 2001, 291, 2118–2120 CrossRef CAS PubMed.
- S. T. van der Post, S. Scheidelaar and H. J. Bakker, J. Mol. Liq., 2012, 176, 22–28 CrossRef CAS.
- D. Laage and J. T. Hynes, J. Phys. Chem. B, 2008, 112, 14230–14242 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © the Owner Societies 2020 |