Effects of inter-crystalline space on the adsorption of ethane and CO2 in silicalite: implications for enhanced adsorption
Abstract
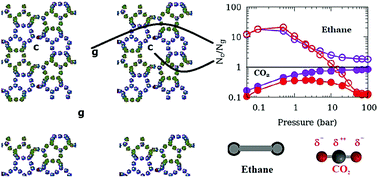
Adsorption of fluids in nanoporous materials is important for a variety of industries including catalysis and is a promising strategy for hydrogen storage and CO2 sequestration. It has therefore been studied extensively. In a typical adsorption experiment, the sorbent sample is usually in powder form which consists of several crystallites separated by an inter-crystalline space. This inter-crystalline space may compete with the nanopores in engineered as well as natural materials for fluid adsorption. While in computer simulations that are used to complement experiments, much attention is focused on the choice of force-field parameters, the effect of inter-crystalline spaces on the properties of adsorbed fluids remains largely ignored. We attempt to study the effects of inter-crystalline space on the simulated adsorption of ethane and CO2 modelled in TraPPE formalism in a silicalite model composed of crystallites separated by different inter-crystalline spaces. The effect of inter-crystalline space is found to be profound and differs for the two sorbates. Presence of quadrupole moment makes CO2 adsorption in the inter-crystalline space more favorable and suggests that increasing surface area of a catalytic substrate for enhanced adsorption might be a relatively more effective strategy for adsorption of a quadrupolar molecule as compared to an apolar molecule. Also, the results imply that in experiments investigating molecules confined in porous media using powder samples, apolar molecules are less likely to give undesired bulk-like contribution from inter-crystalline spaces to the experimental data. CO2 molecules adsorbed on the crystallite surfaces are found to exhibit a high degree of orientational ordering and exhibit a preferred orientation favorable for higher amounts of adsorption. While larger inter-crystalline spacings lead to higher adsorption, the effect of using a larger crystallite is to reduce the amount of adsorption. The mutual negation of these two effects explains the apparent agreement of the experimental data obtained on a powder sample and the simulation data obtained using a perfect crystal model. This work has implications for both simulations of adsorption isotherms in nanoporous materials and the interpretation of experimental data obtained for these systems.
- This article is part of the themed collection: 2020 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...