Functional movements of the GABA type A receptor

Abstract

We have performed a parallel tempering crankshaft motion Monte Carlo simulation on a model of the GABA type A receptor with the aim of exploring a wide variety of local conformational space. We develop a novel method to analyse the protein movements in terms of a correlation tensor and use this to explore the gating process, that is, how agonist binding could cause ion channel opening. We find that simulated binding impulses to varying clusters of GABA binding site residues produce channel opening, and that equivalent impulses to single GABA sites produce partial opening.

---

1 Introduction

The family of GABA_A receptors is responsible for the majority of fast neuronal inhibition in the mammalian central nervous system, and is a target of general anaesthetics, benzodiazepines, barbiturates and neurosteroids. These pentameric proteins belong to the cys-loop family of ligand-gated ion channels that includes the nicotinic acetylcholine, glycine and 5HT₃ receptors. The GABA_A receptors are composed of five subunits arranged pseudosymmetrically around the integral anion channel.¹ The subunits, of which nineteen have thus far been identified, are separated into classes based on their sequence similarity: there are six α-subunits, three β, three γ, three ρ and single representatives of δ, ε, θ and π.² The precise subunit isoform composition of the pentamer defines the recognition and biophysical characteristics of the particular receptor subtype.

The most ubiquitous subtype, which accounts for approximately 30% of GABA_A receptors in the mammalian brain,³ contains two α₁-, two β₂- and a single γ₂-subunit.⁴ The GABA_A receptors can be divided into three structural domains, the extracellular (EC) domain, the transmembrane (TM) domain and the intracellular (IC) domain.

Several structures of the GABA_A receptor have been published. Miller and Aricescu⁵ determined the structure of a human β3-pentamer using X-ray crystallography. Laverty et al.⁶ created a chimaeric homopentameric GABA_A receptor with the extracellular domain from the GLIC protein of the bacterium Gloeobacter violaceus and the transmembrane domain from the α1-subunit of the human GABA_A receptor, and determined its structure by X-ray crystallography. Miller et al.⁷ created a chimaeric homopentameric GABA_A receptor with the extracellular domain from the human β3-subunit and the transmembrane domain from the human α5-subunit and determined its structure crystallographically. Zhu et al.⁸ used cryo-electron microscopy to determine the structure of a truncated heteropentameric human GABA_A receptor of subtype (α1)₂(β2)₂γ2. Phulera et al.⁹ performed a similar study using a truncated heteropentameric rat GABA_A receptor of subtype (α1)₂(β1)₂γ2S. In all these unnatural receptors, the intracellular domain is absent; previous experiments show that the intracellular domain of this receptor is important in determining the conductance, the gating properties and the speed of desensitisation of the ion channel.¹⁰

Laverty et al.¹¹ determined the structure of the GABA_A receptor of subtype (α1)₂(β3)₂γ2, and Masiulis et al.¹² determined the structures of the same GABA_A receptor bound to different ligands. However, the GABA_A receptor was also bound to a megabody Mb38 in all cases. Masiulis et al.¹² reported that Mb38 activated the GABA_A receptor, but they did not report the time elapsed between receptor activation and structure determination. Thus it was not possible to determine whether these structures were of the resting, open or desensitised receptor, though most probably they are in the desensitised state. Moreover, the intracellular domain was undetermined in all these structures.

Previous experiments have shown that, in the absence of GABA, the GABA_A receptor is in the resting state. Administration of GABA will cause the receptor ion channel to open in tens of milliseconds and the receptor then spontaneously desensitises in a few hundred milliseconds.¹³ There have not been structural studies of the GABA_A receptor to study its resting, open and desensitised states and to define how GABA binding to the receptor induces the receptor to open its central ion channel.

The GABA_A receptor of subtype (α1)₂(β2)₂γ2 accounts for 30% of all GABA_A receptors in the brain and is the target of a large number of therapeutic drugs. Ernst et al.¹⁴ and Mokrab et al.¹⁵ have made models of its structure based on similar proteins as the template, and simulations have been performed to study GABA binding and how this process leads to channel opening.

Payghan et al.¹⁶ created a model of the GABA_A receptor of subtype (α1)₂(β2)₂γ2 using bacterial ligand-gated ion channel structures as templates. Closed-channel and open-channel states were generated, and GABA was docked to either one of, or both, binding sites of the closed-channel state. United-atom molecular dynamics simulations of 100 ns were carried out on these five structures. These authors observed changes in the pore radius when the channel opens, but they did not identify the gating mechanism. The gating mechanism describes the process whereby agonist binding leads to the opening of its central ion channel.

Carpenter et al.¹⁷ created a model of the GABA_A receptor of subtype (α6)₂(β3)₂δ using the nAChR as template; they chose this subtype because it has the highest affinity for GABA. They then performed 100 independent molecular dynamics simulations on this protein, with a GABA molecule placed randomly 25 Å away from the centre of its binding site. Binding occurred in 19 of the 100 simulations; a consistent pathway was found to be taken by GABA, and electrostatic steering was found to be important in guiding the ligand to its binding site. Significantly, these authors noted that the C- and F-loops on either side of the binding site need not open and close to let GABA in, as there is a pathway from the cytoplasmic side of these two loops.

Ayan and Essiz¹⁸ made a homology model of the GABA_A receptor of subtype (α1)₂(β2)₂γ2 using the Caenorhabditis elegans GluCl protein as the template. They performed a 100 ns molecular dynamics simulation on the structure embedded in a hydrated palmitoyl-oleoyl phosphatidylcholine (POPC) membrane; on removing ivermectin, the ion channel closes. Correlation analysis shows the extracellular domain β1–β2 and transmembrane domain M2–M3 loops to be important in ion channel closure.

These studies are very valuable, but none of them have systematically approached the problem of how ligand binding causes the ion channel to open. In this work, we simulate the GABA_A receptor using a semi-coarse-grained protein model and an efficient Monte Carlo method^19,20 which allows fast exploration of protein conformations. Despite some short-comings of our model, we shall show that the main findings of our work are not affected: using the correlated motions of the amino acids from the simulation, we present a linear response theory based method, which identifies possible gating mechanisms upon GABA binding.

2 Methods

2.1 Structure

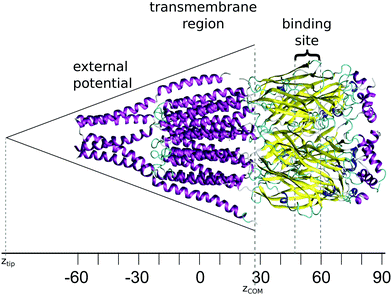
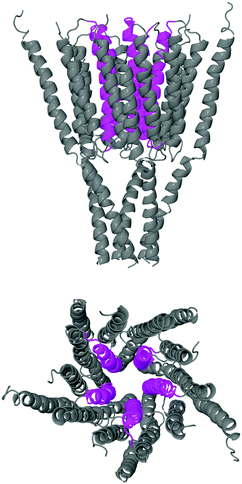
The starting structure used for the simulation is a model of the human GABA_A receptor.¹⁵Fig. 1 shows a diagram of this structure with its long axis aligned to the z-axis. The z-value at each level of the protein is labelled on the axis below. The GABA binding site is surrounded by two tyrosines, two phenylalanines, a threonine and an arginine. These amino acids are situated at a z-distance of 50 Å ≤ z ≤ 60 Å. The ion channel in the transmembrane region is lined by the M2 helix; Fig. 2 shows the transmembrane and intracellular domains, with the M2 helices highlighted in magenta. The narrow part of the ion channel is situated in the transmembrane domain, at a z-distance of −25 Å ≤ z ≤ 25 Å. There are three annuli of positively-charged amino acids lining the ion channel: a lysine annulus at about z = 20 Å, and two arginine annuli at, respectively, about z = 11.5 Å and approximately z = −15.5 Å (Fig. 3, top panel). There are four annuli of amino acids inside the transmembrane part of the ion channel which contain the –OH group; they are situated at z-distances of about z = −6 Å, z = 0 Å, z = 3 Å and z = 15.5 Å (Fig. 3, bottom panel). These annuli are probably important in controlling the passage of ions through the ion channel.

Fig. 1 Diagram showing a model of the GABA_A receptor with the z-axis aligned horizontally; the marked distances are in Å. Helices are shown in purple and β-sheets in yellow. The transmembrane domain is in the region −25 Å ≤ z ≤ 25 Å, while the binding site is in the z-region of 50 Å ≤ z ≤ 60 Å.

Fig. 2 Diagram showing the transmembrane and intracellular domains of the GABA_A receptor model viewed from the side (top panel) and from the extracellular space towards the cytoplasm (bottom panel). The M2 helices lining the central ion channel are coloured magenta.

Fig. 3 Diagram showing M2 helices of the GABA_A receptor model viewed from the side. In the top panel, the top Lys annulus is shown in cyan, the middle Arg annulus is shown in magenta, and the bottom Arg annulus is shown in yellow. In the bottom panel, the four –OH annuli are shown in different colours.

2.2 Simulations

For the molecular simulations, we used CRANKITE,¹⁹ a Monte Carlo simulation programme that employs a Gō-like coarse-grained force field. We chose CRANKITE because its Monte Carlo move set consists of local moves of crankshaft rotations of the protein backbone and changes of the side chain dihedral angles, the former of which allows a fast conformational sampling of proteins. CRANKITE uses a full atom representation of the protein backbone, together with explicit side chain β atoms and γ atoms, to include entropic contributions arising from the torsional flexibility of side chains. Each amino acid is treated as hydrophobic or amphipathic. The γ atoms represent the rest of the side chain, with an elongated distance between β and γ atoms to place them near the centre-of-mass of the side chain. In the energy function, volume exclusion of beads, hydrogen bonds between backbone amide H atoms and carbonyl O atoms, and a hydrophobic interaction between γ atoms are modelled explicitly. The secondary structure of the protein is held together by an additional energy term, which keeps the backbone of α-helices and β-strands at the correct backbone twist, and a Gō-like contact potential term which keeps β-sheets well-formed. The secondary structure of proteins is predetermined and does not change within a simulation.

We used the force field parameters optimised previously,²⁰ with the addition of a conical external potential on the transmembrane region to mimic the membrane, as the force field had been optimised using a set of non-transmembrane proteins. The energy contribution of this external potential on an amino acid in this region is:

if z/z_tip ∈ [0,1] and x² + y² > r₀², otherwise E = 0, and where x, y and z are the coordinates of the centre-of-mass of the amide N, C_α and carbonyl C of the amino acid, k = 100RT, r₀ = 45 Å, z_tip = −120 Å, z_com is the z-coordinate of the centre-of-mass of the whole protein where the pore of the protein was aligned to the z axis with the intracellular domain pointing in the positive direction. The shape of the potential was chosen such that it helps maintain the initial structure of the GABA_A receptor, but it does not squeeze the pore close (there is a minimal energy penalty in the initial state). We have performed other simulations with k = 50RT; the results are qualitatively the same. This shows that the order of magnitude chosen for k is appropriate. In this work, we concentrated our analysis on the case where k = 100RT.

To explore the possible conformations of the protein while keeping its secondary structure intact, we used parallel tempering simulations with 512 temperature levels ranging from 310 K to 1023 K, sampling conformations at the lowest temperature level, every 1000 steps. In our simulation, 10⁸ Monte Carlo steps were carried out at each temperature level, and temperature swapping took place every 1000 steps, using the Metropolis–Hastings acceptance criterion. Our simulation took 23 hours on 512 cores of the Cambridge University supercomputer CSD3.

2.3 Analysis

The parallel tempering simulation generated 10⁵ configurations in various states at 310 K. Equilibration was determined by examining the log of the absolute value of the auto-correlation function of the energy of the system against the lag between the energies sampled, and finding where it crossed a given y-value that is no higher than the background. Fig. S1 of the ESI† shows this graph. The first 25 000 configurations were treated as equilibration data and only the remaining 75 000 were used for data analysis. This loose cutoff was determined by monitoring the energy reported by the CRANKITE software (Fig. S1, ESI†), and the observation of spatial correlations between different parts of the protein over 1000 configuration windows (Fig. S2–S7, ESI†).

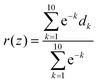2.3.1 Radial profiles. An estimate of the pore radius was taken at sampling points along the z-axis to which the protein ion channel was aligned. Samples were taken at 1 Å intervals from −40 Å < z < +60 Å which was considered to cover the main parts of interest of the protein. At each sampling point the ten nearest neighbour residues were considered and the approximate exponentially smoothed radius was reported as:where d_k is the distance to the kth nearest neighbour.

2.3.2 Linear response theory. We examine the movements of the residues, and would like to evaluate how movements of one residue affect the movements of another residue. To do this, we first note the positions of each residue in three-dimensional space by averaging over the CRANKITE coarse grained atom representations.

We assume that during a CRANKITE simulation each residue has a set of principal directions which can be defined by a roughly ellipsoidal cloud of coordinates x_at = (x_at1, x_at2, x_at3), with a center of mass μ_a = (μ_a1, μ_a2, μ_a3), for a residue a, at snapshot t of the simulation which has N_t snapshots. We construct the vector correlation matrix R⁽¹⁾_a of all vector positions of the residue a across frames in the simulation as 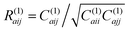for a single residue vector covariance matrix C⁽¹⁾_a defined by

the eigenvectors of R⁽¹⁾_a are these principal directions and they are ordered by their eigenvalues. From this, a residue a has a matrix U_a interpreted as a row vector filled with column vectors which are eigenvectors u_a1, u_a2, u_a3, with eigenvalues vector λ_a whose elements are λ_a1 ≥ λ_a2 ≥ λ_a3. Note that this correlation matrix refers to correlation in space as opposed to correlation in time. It relies on all valid structures, rather than all samples having to come from consecutive samples in a temporal order. Hence the parallel tempering Monte Carlo simulation technique can be used here. Fig. S2–S7 (ESI†) show the correlation matrix of this system as it evolves during the simulation.

Consider the situation where residue a receives a vector impulse f_a when it is at its equilibrium position x_a. The component of the impulse in the u_i direction is simply f_a·u_i. Hence the impulse resolved along the principal directions of a is given by g_a = f_a·U_a.

We then construct a rank three tensor of projections of each residue displacement from μ_a into each eigenvector in U_a, as T_a = U_a⁻¹(X_a − 1 ⊗ μ_a)^T, along with frame averaged terms τ_ai = 〈T_ait〉_t We then construct a 3 × 3 correlation matrix for each pair of residues a and b, denoted R⁽²⁾_ab whose elements are given by

describing the correlation between motions of the two residues in the u_ai and u_bj directions respectively. This determines the correlated response r^(a)_b at residue b due to the impulse at residue a as r^(a)_b = g_aR⁽²⁾_ab. This motion is given in terms of the principal directions of motion of residue b, so to convert this displacement back into the original axes we use the inverse of the eigenvector matrix at b, giving the response in terms of Cartesian coordinates as δx^(a)_b = r^(a)_bU_b⁻¹ or written explicitly:

δx^(a)_b = f_a·U_aR⁽²⁾_abU_b⁻¹ (5)

then the total response at residue b is obtained by summing over all residues with individual impulses to give:where is the set of residues. We note that the coefficients relating impulses at a to responses at b are given by a rank four tensor K_ab = U_aR⁽²⁾_abU_b⁻¹, and these coefficients are purely determined by the CRANKITE trajectory or analogous MC/MD simulation data. This is a relatively computationally expensive step, requiring high memory. By deriving and storing these coefficients we can measure the response of any residue or any set of residues in the system to any arbitrary set of input impulses. The equation to extract responses from inputs is then

In practice we have a large linear model whose coefficients are defined by spatial correlations across a simulation. The input to the model is a list of 3 dimensional impulse vectors in (x,y,z) coordinates. In our case, for the GABA_A receptor which consists of 1823 amino acids residues, F_ai is an (1823 × 3) matrix. In practice, when we measure the impulse response to GABA binding, F_ai is non-zero for only a handful of residues at the binding site. This is then left multiplied to the coefficient tensor of K_abij of size (1823 × 1823 × 3 × 3), to produce an output matrix ΔX_bj of size (1823 × 3). The output ΔX_bj gives the magnitude and direction of the response for amino acid b in direction j. From the response of all residues in the transmembrane region, using eqn (2), we can estimate changes in the pore size. The correlation matrix presented here informs us about correlated amino acid motions at physiological temperatures. Reconstructing the free energy path between closed and open states is beyond the scope of this study.

Implementation. To determine the impulses required to mimic GABA binding, we compare the coordinates of the binding site amino acids of two desensitised structures of the GABA_A receptor: the first structure is of the receptor complexed with a megabody (PDB code 6I53) and the other structure is of the receptor complexed with picrotoxin, GABA and the same megabody (PDB code 6HUJ). We superimposed these two structures onto one of the equilibrated configurations from our simulation. We then examined the movements of the binding site amino acids from the uncomplexed state to the state where GABA is bound. We describe the vectors corresponding to these movements as the ‘forward vectors’ (see Table 1 for the magnitudes of these vectors); they roughly denote the movements of the binding site amino acids when GABA binds.

Table 1 Table showing the binding site amino acids and the magnitude of the forward vectors. The first column shows the amino acid number from the structure simulated in this work, which is the model from (Mokrab et al.).¹⁵ The second column shows the corresponding amino acid from 6I53¹¹ and 6HUJ.¹² Note that the latter two structures contain β3-subunits but the modelled structure contains β2-subunits

Amino acid from model	Amino acid from 6I53/6HUJ	Forward vector/Å
α1-Subunit
Phe E 92	Phe A 65	0.570
Arg E 94	Arg A 67	0.453
Leu E 145	Leu A 118	0.606
Thr E 157	Thr A 130	0.735
Phe C 92	Phe D 65	0.788
Arg C 94	Arg D 67	0.454
Leu C 145	Leu D 118	0.493
Thr C 157	Thr D 130	0.729
β2-Subunit
Tyr A 121	Tyr B 97	0.904
Glu A 179	Glu B 155	0.862
Ser A 180	Ser B 156	1.047
Tyr A 181	Tyr B 157	1.116
Phe A 224	Phe B 200	0.918
Ser A 225	Ala B 201	0.974
Thr A 226	Thr B 202	0.437
Tyr A 229	Tyr B 205	0.987
Tyr D 121	Tyr E 97	0.690
Glu D 179	Glu E 155	0.799
Ser D 180	Ser E 156	0.915
Tyr D 181	Tyr E 157	0.830
Phe D 224	Phe E 200	0.844
Ser D 225	Ala E 201	0.895
Thr D 226	Thr E 202	0.736
Tyr D 229	Tyr E 205	0.856

---

In order to determine the number of binding site residues required to induce gating (that is, the process whereby agonist binding causes ion channel opening) we measured the responses of forward vectors on either GABA binding site 1, 2 or both 1 and 2, and for the following sets of residues: (a) the principal four residues, Phe 92 and Arg 94 from the α1-subunit and Tyr 181 and Tyr 229 from the β2-subunit, of each binding site (denoted minimal); (b) all residues within 4 Å of where GABA would have bound (limit distance 4 Å); (c) all residues within 5 Å of where GABA would have bound (limit distance 5 Å); (d) all residues within 6 Å of where GABA would have bound (limit distance 6 Å).

3 Results

We performed a parallel tempering simulation of the GABA_A receptor, using the CRANKITE coarse-grained protein model resulting in a trajectory comprising of 100 000 structures. The first 25 000 structures were assumed to be associated with thermalisation, as the correlation matrix between the amino acids varies greatly until after 25 000 structures. The remaining 75 000 structures were used to derive the coefficient tensor K_abij. Note that the correlation matrix describes the spatial correlation of amino acid positions, rather than temporal correlations, and so equilibration in time is not a problem.

3.1 Impulse-response suggests gating mechanism

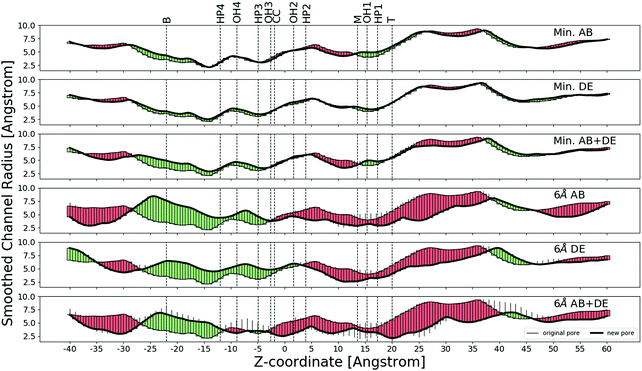
We applied ‘forward vectors’ using the correlation tensor method and noted that the movements of the binding site amino acids caused different parts of the ion channel to open.

We differentiate between two binding sites: the AB site is the binding site where the β2-subunit is adjacent to the γ2-subunit, and the DE site is the binding site where the α1-subunit is adjacent to the γ2-subunit. We find that the effect of applying forward vectors to only the principal four residues of each binding site (Fig. 4) is slightly different from that of applying forward vectors to residues within a certain distance limit. The effect of increasing the limit distance from 4 Å to 6 Å is qualitatively not very different, as can be seen in Fig. 4 and Fig. S8–S19 (ESI†). We thus show results of applying the forward vectors to the principal four residues and those of applying the forward vectors to residues within 6 Å of where GABA would have bound. Results pertaining to 4 Å and 5 Å are shown in the ESI.† In these diagrams, we also indicate the following annuli that might be important in ion passage. The lysine annulus is labelled T (top), the two arginine annuli are labelled, respectively, M (middle) and B (bottom). The four annuli of amino acids bearing the OH group are labelled OH1 to OH4. Close to these four OH annuli are four hydrophobic annuli, and they are labelled HP1 to HP4.

Fig. 4 Diagram showing the effect of GABA binding to the AB site, the DE site and both the AB and DE sites. The AB site is the binding site where the β2-subunit is adjacent to the γ2-subunit, and the DE site is the binding site where the α1-subunit is adjacent to the γ2-subunit. ‘Min’ denotes that forward vectors are applied to Phe 92 and Arg 94 from the α1-subunit and Tyr 181 and Tyr 229 from the β2-subunit. ‘6 Å’ denotes that forward vectors are applied to those amino acids within 6 Å of the bound GABA. The green bars indicate the positions where the ion channel radius increases, while the red bars indicate the positions where the ion channel radius decreases. Sometimes as the magnitude of applied impulse increased from 0 to 1, the direction of opening changed; this is shown by the stick parts that overshoot the bars. The original profile of the ion channel is denoted by the thin black line and the final profile by the bold black line.

In the following figures green corresponds to opening, and red to closing. The forward vector impulse was applied in stages with magnitude varying from 0 to 1. Some parts of the channel were seen to open or close monotonically (solid green or red bar), other parts of the channel opened at a partial application of the forward vectors and then closed again (or vice versa), this kind of motion is represented by a thin black stick above or below the solid bar.

The top profile in Fig. 4 shows the effect of applying forward vectors to the principal four amino acids of the AB site only. There is slight widening of the transmembrane domain at the cytoplasmic end and the intracellular end, and there is slight narrowing of the middle part of the transmembrane domain. The second profile from the top in Fig. 4 shows the effect of applying forward vectors to the principal four amino acids of the DE site only. There is slight widening of the transmembrane domain in most regions, but there is slight narrowing in a short section of the middle region. The third profile from the top in Fig. 4 shows the effect of applying forward vectors to the principal four amino acids of both the AB and DE sites. There is widening of the transmembrane domain in most regions, but there is narrowing in a short part of the middle region.

The fourth profile from the top in Fig. 4 shows the effect of applying forward vectors to 6 Å amino acids of the AB site only. There is slight narrowing of the extracellular half of the transmembrane part of the ion channel (0 Å < z < +30 Å), and extensive widening of the cytoplasmic half of the transmembrane part of the ion channel (−25 Å < z < 0 Å). The narrowest part of the ion channel is situated in the cytoplasmic half, so the net effect is to widen the ion channel. The fifth profile from the top in Fig. 4 shows the effect of applying forward vectors to the DE site only. The effect is similar to applying forward vectors to the AB site, except the widening of the cytoplasmic half of the transmembrane part now extends to +5 Å. The bottom profile from the top in Fig. 4 shows the effect of applying forward vectors to both binding sites. The widening effect is now restricted to −25 Å < z < −11 Å and −8 Å < z < −3 Å. There is slight constriction in the region −11 Å < z < −8 Å and also in the region −3 Å < z < +38 Å. Note that the transmembrane domain ends at about z = +25 Å, so some of the slight constriction is observed in the extracellular domain.

It can immediately be seen that the effect of moving more amino acids in the resting state is to make the ion channel movements larger. There are also changes in the movement direction as the forward vectors are applied to more amino acids. Moreover, we would expect some of the annuli to be crucial in the opening movements. The widening and narrowing effects do not seem to be related to any of the identified annuli.

In summary, we have used information from advanced Monte Carlo simulations to generate three-dimensional correlation tensor coefficients for a large linear model and subsequently analysed the response motions of the GABA_A receptor under experimentally derived binding impulses. The results show how movements in the binding site region can widen or narrow the central ion channel and that impulses at a single site induce partial opening.

4 Discussion

Simulating the gating of pentameric ligand-gated ion channels is a challenge of theoretical biochemistry, but it has only been made possible by the development of simulation methods²¹ and the emergence of fast supercomputers. One of the more recent research has been the simulation of the GluCl channel from an open-channel state to a closed-channel state.²² In this work, the authors simulated a structure of the Caenorhabditis elegans GluCl protein that has been prised open by L-glutamate and ivermectin (PDB code: 3RIF). They performed a data collection simulation of 100 ns of this structure, and also a 140 ns of this structure with ivermectin taken away. They showed that the GluCl channel ion pore area decreased and the channel closed with changes in the tilt of the M2 helices. It is not known if the channel closed fully, as the simulation times were short and the agonist L-glutamate was still bound to the protein.

Yuan et al.²³ performed molecular dynamics simulations on the 5-HT_3A receptor. They used the structure with PDB code 4PIR, repaired the structural defects and put it in a hydrated POPC membrane. They simulated the apo-structure twice for 700 ns, and the holo-structure (five 5-HT molecules inserted into every interface binding site) twice for 700 ns. They find that putting 5-HT into the binding site forced the 5-HT_3A receptor subunits to twist and tilt in such a way that the ion channel opens but with distinct asymmetry in the receptor structure. They have also performed a correlation analysis and principal component analysis. Whilst the central ion channel is blocked by hydrophoic amino acids in the apo-structure, in the holo-structure it becomes unblocked and a continuous water structure is formed. Water and ion exit at the intracellular end via the five side portals. These portals are blocked by the M4-MA helix, but these helices move on 5-HT binding so the portals become available for water and ion passage.

To enhance the sampling of rare events such as channel opening, one can apply the ‘swarms of trajectories’ method. This was carried out on the Gloeobacter violaceus GLIC protein;²⁴ the PDB code for its closed-channel structure is 4NPQ and that for its open-channel structure is 4HFI. The authors studied these two structures in detail and applied 35 collective variables in their simulations of gating. They were able to define the gating pathways, the free energy profiles of the conformation space and the gating kinetics. This impressive work is only possible if one knows the beginning and end structures of gating.

Guros et al.²⁵ performed a 20 μs molecular dynamics simulation on the apo-form of the 5-HT_3A receptor (PDB code: 4PIR) in a POPC/SDPC/cholesterol membrane. They performed two 15 μs simulations with the receptor immersed in 5 mM and 15 mM 5-HT, respectively, and also carried out a 15 μs simulation of the receptor embedded in a POPC-only membrane immersed in 5 mM 5-HT. They discovered that 5 mM 5-HT was adequate to activate the receptor, and noted that the receptor went through a number of pre-active states but did not observe the fully activated state (PDB code: 6HIN) probably because more simulation time was required.

Dämgen and Biggin²⁶ created a model of the human glycine receptor using the glycine receptor of Danio rerio as the template. They placed this modelled receptor into a hydrated POPC membrane and fill the simulation box with a NaCl solution. They also placed five glycine molecules into the binding sites, and applied restraints for 150 ns to open the ion channel. Once the channel was open, they carried out a 300 ns data production simulation. They showed that the open-channel state conducted Cl⁻ ions with a selectivity ratio over Na⁺ similar to that found in experiments (28 : 1). Their simulations also show that hydrophobic voids between the subunits were filled by Leu residues; this was not observed in the experimental cryo-EM structure of the glycine receptor.

These simulations are very important in giving us insight into the gating process. Nevertheless, they all require a very large amount of supercomputer time. Some of the methods used also require prior knowledge of the detailed structural changes. It would be useful to have a method that requires less computer time and can also allow us to trace the mechanistic pathway driving the gating process.

In this work, we have developed a novel method to define the effect of an impulse on the response of the protein. This is a general method which we have applied to a model of the GABA_A receptor to demonstrate gating. We show that the results are consistent with existing knowledge about ion channel opening of ligand-gated ion channels.^{23,25,27–30} Specifically, we observe the same widening of the ion channel pore on channel gating. Significantly, we also show that a single GABA molecule can open the GABA_A receptor, but that the effect of two GABA molecules binding to the receptor is greater; the magnitude of the movements is larger. This is consistent with previous experiments.³¹ We are currently developing a method to identify the mechanistic pathway from the binding site to the narrowest part of the ion channel. This will be the subject of another article, where we shall compare our theoretical predictions with results from previous experiments and simulations in detail.

There are, however, some issues with our study. We do not know the exact effect of GABA binding to the binding site. We have used experimental structures of receptors bound to megabodies, but the GABA-bound form is also bound to picrotoxin and both 6I53 and 6HUJ are probably in the desensitised state. To determine the forward vectors, we should ideally compare the positions of the binding site amino acids of an empty GABA_A receptor in the resting state with those of a GABA_A receptor bound to GABA in the open state, not in the desensitised state and with no other ligands bound. However, structures from 6I53 and 6HUJ are the closest we can get so far. In this work, applying the forward vectors calculated from 6I53 and 6HUJ suggest parts of the transmembrane ion channel close upon GABA binding, but we cannot be sure that this happens naturally as the forward vectors are determined from receptors in the desensitised state with extra ligands bound.

This work has established the feasibility of using Monte Carlo simulation results to predict protein movements. This research is a preliminary study and further work will be carried out to identify the mechanistic pathway linking the binding site to the gating amino acids. The template for our model of the GABA_A receptor is the neuromuscular junction nAChR, PDB code 2BG9. The nAChR structure 2BG9 is a good template because this structure contains the complete, intact protein, and has been resolved under near-physiological conditions; the protein is embedded in its native plasma membrane in a liposome-like structure that resembles its native muscle cell. However, Mnatsakanyan and Jansen³² have shown that the identity of amino acids in the M2 and M3 helices of 2BG9 could be one turn out; the α-subunit of the nAChR has been re-modelled recently,³³ and a structure of the nAChR of higher resolution confirms this problem.³⁴

A semi-coarse-grained model such as CRANKITE is an attractive choice to model such a protein; it is less sensitive to the identity of amino acids. Moreover, coarse graining reduces the degrees of freedom, which allows faster exploration of the conformational space of the protein. This allows us to model proteins with slow motions, for which all-atom simulations are prohibitively expensive. On the other hand, one has to be careful not to oversimplify the protein model, and we need to model all relevant features of the GABA_A receptor protein that are essential for the gating. In a future study, we will explore the effect of an explicit ligand, more finely tuned electrostatics and even the presence of a membrane and solvents.

Conflicts of interest

The authors declare that they have no conflicts of interest.

Acknowledgements

The authors thank Nigel Unwin, Ian Martin and Katarzyna Macieszczak for useful discussions, and Stuart Rankin and Michael Rutter for help with computing. Some of the simulations in this work were carried out on the Darwin Supercomputer of the University of Cambridge High Performance Computing Service using Strategic Research Infrastructure Funding from the Higher Education Funding Council for England, and other simulations were performed using resources provided by the Cambridge Service for Data Driven Discovery (CSD3) operated by the University of Cambridge Research Computing Service, provided by Dell EMC and Intel using Tier-2 funding from the Engineering and Physical Sciences Research Council (capital grant EP/P020259/1), and DiRAC funding from the Science and Technology Facilities Council. BWJI acknowledges financial support from the UK Engineering and Physical Sciences Research Council Centre for Doctoral Training in Computational Methods for Materials Science under Grant No. EP/L015552/1. PC was partly supported by the INCEPTION project ANR-16-CONV-0005.

References

1. N. Nayeem, T. P. Green, I. L. Martin and E. A. Barnard, Quaternary structure of the native GABA_A receptor determined by electron microscopic image analysis, J. Neurochem., 1994, 62, 815–818.
2. E. Sigel and M. E. Steinmann, Structure, function, and modulation of GABA_A receptors, J. Biol. Chem., 2012, 282, 40224–40231.
3. P. J. Whiting, GABA-A receptor subtypes in the brain: a paradigm for CNS drug discovery?, Drug Discovery Today, 2003, 8, 445–450.
4. S. J. Farrar, P. J. Whiting, T. P. Bonnert and R. M. McKernan, Stoichiometry of a ligand-gated ion channel determined by fluorescence energy transfer, J. Biol. Chem., 1999, 274, 10100–10104.
5. P. S. Miller and A. Radu Aricescu, Crystal structure of a human GABA_A receptor, Nature, 2014, 512, 27–275.
6. D. Laverty, P. Thomas, M. Field, O. J. Andersen, M. G. Gold, P. C. Biggin, M. Gielen and T. G. Smart, Crystal structures of a GABA_A-receptor chimera reveal new endogenous neurosteroid-binding sites, Nat. Struct. Mol. Biol., 2017, 24, 977–985.
7. P. S. Miller, S. Scott, S. Masiulis, L. De Colibus, E. Pardon, J. Steyaert and A. Radu Aricescu, Structural basis for GABA_A receptor potentiation by neurosteroids, Nat. Struct. Mol. Biol., 2017, 24, 986–992.
8. S. Zhu, C. M. Noviello, J. Teng, R. M. Walsh, J. J. Kim and R. E. Hibbs, Structure of a human synaptic GABA_A receptor, Nature, 2018, 559, 67–72.
9. S. Phulera, H. Zhu, J. Yu, D. P. Claxton, N. Yoder, C. Yoshioka and E. Gouaux, Cryo-EM structure of the benzodiazepine-sensitive α1β1γ2S tri-heteromeric GABA_A receptor in complex with GABA, eLife, 2018, 7, 39383.
10. K. K. O'Toole and A. Jenkins, Discrete M3-M4 intracellular loop subdomains control specific aspects of γ-aminobutyric acid type A receptor function, J. Biol. Chem., 2011, 286, 37990–37999.
11. D. Laverty, R. Desai, T. Uchanski, S. Masiulis, W. J. Stec, T. Malinauskas, J. Zivanov, E. Pardon, J. Steyaert, K. W. Miller and A. Radu Aricescu, Cryo-EM structure of the human α1β3γ2 GABA_A receptor in a lipid bilayer, Nature, 2019, 565, 516–520.
12. S. Masiulis, R. Desai, T. Uchanski, I. Serna Martin, D. Laverty, D. Karia, T. Malinauskas, J. Zivanov, E. Pardon, A. Kotecha, J. Steyaert, K. W. Miller and A. Radu Aricescu, GABA_A receptor signalling mechanisms revealed by structural pharmacology, Nature, 2019, 565, 454–459.
13. D. J. Maconochie, J. M. Zempel and J. H. Steinbach, How quickly can GABA_A receptors open?, Neuron, 1994, 12, 61–71.
14. M. Ernst, S. Bruckner, S. Boresch and W. Sieghart, Comparative models of GABA_A receptor extracellular and transmembrane domains: important insights in pharmacology and function, Mol. Pharmacol., 2005, 68, 1291–1300.
15. Y. Mokrab, V. N. Bavro, K. Mizuguchi, N. P. Todorov, I. L. Martin, S. M. J. Dunn, S. L. Chan and P.-L. Chau, Exploring ligand recognition and ion flow in comparative models of the human GABA type A receptor, J. Mol. Graphics Modell., 2007, 26, 760–774.
16. P. V. Payghan, I. Bera, D. Bhattacharyya and N. Ghoshal, Capturing state-dependent dynamic events of GABA_A receptors: a microscopic look into the structural and functional insights, J. Biomol. Struct. Dyn., 2016, 34, 1818–1837.
17. T. S. Carpenter and F. C. Lightstone, An electrostatic funnel in the GABA-binding pathway, PLoS Comput. Biol., 2016, 12, e1004831.
18. M. Ayan and S. Essiz, The neural γ2α1β2α1β2 gamma amino butyric acid ion channel receptor: structural analysis of the effects of the ivermectin molecular and disulfide bridges, J. Mol. Model., 2018, 24, 206.
19. A. A. Podtelezhnikov and D. L. Wild, CRANKITE: a fast polypeptide backbone conformation sampler, Source Code Biol. Med., 2008, 3, 12.
20. C. Várnai, N. S. Burkoff and D. L. Wild, Efficient parameter estimation of generalizable coarse-grained protein force fields using constrative divergence: a maximum likelihood approach, J. Chem. Theory Comput., 2013, 9, 5718–5733.
21. E. Flood, C. Boiteux, B. Lev, I. Vorobyov and T. W. Allen, Atomistic simulations of membrane ion channel conduction, gating and modulation, Chem. Rev., 2019, 119, 7737–7832.
22. N. Calimet, M. Simoes, J.-P. Changeux, M. Karplus, A. Taly and M. Cecchini, A gating mechanism of penatmeric ligand-gated ion channels, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E3987–E3996.
23. S. Yuan, S. Filipek and H. Vogel, A gating mechanism of the serotonin 5-HT₃ receptor, Structure, 2016, 24, 816–825.
24. B. Lev and T. W. Allen, Simulating ion channel activation mechanisms using swarms of trajectories, J. Comput. Chem., 2020, 41, 387–401.
25. N. B. Guros, A. Balijepalli and J. B. Klauda, Microsecond-timescale simulations suggest 5-HT-mediate preactivation of the 5-HT_3A serotonin receptor, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 405–414.
26. M. A. Dämgen and P. C. Biggin, A refined open state of the glycine receptor obtained via molecular dynamics simulations, Structure, 2020, 28, 130–139.
27. G. G. Wilson and A. Karlin, Acetylcholine receptor channel structure in the resting, open and desensitized states probed with the substituted-cysteine-accessibility method, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 1241–1248.
28. I. H. Yamodo, D. C. Chiara, J. B. Cohen and K. W. Miller, Conformational changes in the nicotinic acetylcholine receptor during gating and desensitization, Biochemistry, 2010, 49, 156–165.
29. N. Unwin and Y. Fujiyoshi, Gating movement of acetylcholine receptor caught by plunge-freezing, J. Mol. Biol., 2012, 422, 617–634.
30. G. Gonzalez-Gutierrez and C. Grosman, The atypical cation-conduction and gating properties of ELIC underscore the marked functional versatility of the pentameric ligand-gated ion-channel fold, J. Gen. Physiol., 2015, 146, 15–36.
31. D. A. Mathers and Y. Wang, Effect of agonist concentration on the lifetime of GABA-activated membrane channels in spinal cord neurons, Synapse, 1988, 2, 627–632.
32. N. Mnatsakanyan and M. Jansen, Experimental determination of the vertical alignment between the second and third transmembrane segments of muscle nicotinic acetylcholine receptors, J. Neurochem., 2013, 125, 843–854.
33. J. Newcombe, A. Chatzidaki, T. D. Sheppard, M. Topf and N. S. Millar, Diversity of nicotinic acetylcholine receptor positive allosteric modulators revealed by mutagenesis and a revised structural model, Mol. Pharmacol., 2018, 93, 128–140.
34. M. M. Rahman, J. Teng, B. T. Worrell, C. M. Noviello, M. Lee and A. Karlin, et al., Structure of the native muscle-type nicotinic receptor and inhibition by snake venom toxins, Neuron, 2020, 106, 1–11.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01128b

‡ These two authors contributed equally.

---