 Open Access Article
Open Access ArticleHierarchically organized materials with ordered mesopores: adsorption isotherm and adsorption-induced deformation from small-angle scattering†
Lukas
Ludescher
 a,
Roland
Morak
a,
Stephan
Braxmeier
b,
Florian
Putz
a,
Roland
Morak
a,
Stephan
Braxmeier
b,
Florian
Putz
 c,
Nicola
Hüsing
c,
Nicola
Hüsing
 c,
Gudrun
Reichenauer
b and
Oskar
Paris
c,
Gudrun
Reichenauer
b and
Oskar
Paris
 *a
*a
aInstitute of Physics, Montanuniversität Leoben, Franz-Josef Strasse 18, 8700, Leoben, Austria. E-mail: oskar.paris@unileoben.ac.at
bBavarian Center for Applied Energy Research, Magdalene-Schoch-Str. 3, 97074 Wuerzburg, Germany
cChemistry and Physics of Materials, Paris Lodron University Salzburg, Jakob-Haringer Str. 2a, 5020 Salzburg, Austria
First published on 28th May 2020
Abstract
In situ small angle scattering is used to study the pore filling mechanism and the adsorption induced deformation of a silica sample with hierarchical porosity upon water adsorption. The high structural order of the cylindrical mesopores on a 2D hexagonal lattice allows obtaining adsorption induced strains from the shift of the corresponding Bragg peaks measured by in situ small-angle X-ray scattering (SAXS). However, apparent strains due to scattering contrast induced changes of the Bragg peak shapes emerge in SAXS. In contrast, small-angle neutron scattering (SANS) allows determining the real adsorption induced strains by employing a H2O/D2O adsorbate with net coherent scattering length density of zero. This allows separating the apparent strains from the real strains experimentally and comparing them with strains obtained from model calculations of the SAXS intensity. It is shown that the apparent strains cannot be described at all by a simple mesopore model of film growth and capillary condensation. A hierarchical model taking the scattering of the micropores and the outer surface of the mesoporous struts in the hierarchically porous sample properly into account, together with a modified mesopore filling mechanism based on a corona model, leads to satisfactory description of both, the adsorption isotherm and the measured apparent strains as derived by SAXS.
1 Introduction
Nanoporous materials are used for a variety of applications including separation technologies and catalysis, gas- and energy storage, as well as sensors and actuators.1–4 Detailed information on the pore space characteristics of such materials is usually obtained from gas adsorption isotherms,5 supported by imaging methods such as scanning- or transmission electron microscopy,6 and by small-angle X-ray scattering (SAXS).7,8 Although 3D imaging techniques using X-rays and electrons are developing quickly, micropores and small mesopores below 10 nm are still hardly accessible to these methods, particularly in highly disordered nanoporous systems. In this regime, SAXS has proven a powerful method to characterize surface area and porosity9,10 as well as size and shape of nanopores in detail.11,12 Moreover, SAXS allows studying the structure of host species within the pore space in situ during, e.g., gas adsorption at the nanopore surfaces,12,13 gas–liquid- or liquid–solid phase transitions in confinement,14 or ion arrangement in electrical double layers during charging.15However, the analysis of the SAXS data is usually not straightforward since at least three phases (i.e., pores, solid host, and at least one liquid- or solid-like guest phase) are present. One of the assumptions often made is that the structure of the porous material does not change upon the uptake or phase-change of the guest phase. In other words, the structure of the “empty” porous material is determined first, and the changes observed in the SAXS signal are assumed exclusively to result from the occupation of the pore space by the guest phases and by their rearrangement. This assumption is however seldom met in reality, since the interaction of the guest phase with the solid pore walls leads to volume changes of the pore space, and potentially also to volume changes of the solid phase ranging from some fractions of percent16,17 to 50 vol%.18,19 Indeed, adsorption induced deformation has been a topic of interest for a long time,20,21 but also volume changes induced by liquid–solid phase transitions22 or by electrosorption of ions in electrical double layers23–27 have both, scientific and application related relevance. In particular, the adsorption induced deformation observed as a function of relative gas pressure along an adsorption isotherm has been investigated in numerous experimental studies,28–30 and quite detailed theoretical descriptions based on fluid thermodynamics in confinement, coupled with solid mechanics have been developed, both for highly ordered as well as for disordered porous materials.31–36 This allowed detailed modeling of adsorption induced deformation of cylindrical mesopores without34 and with microporous walls.37 This synergistic combination of experiments and theoretical modeling was possible by using hierarchical silica model materials comprising macroscopic samples with three hierarchical pore levels, i.e., macropores, mesopores and micropores, allowing the adsorption induced deformation to be measured using in situ dilatometry.18 The mesopores in these materials consist of cylinders with narrow diameter distribution, arranged on a hexagonal pore lattice, similar to the well-known SBA-15 material.38 This leads to Bragg reflections in SAXS measurements, and the adsorption induced deformation of the pore lattice was assumed to be directly accessible from the shift of the Bragg peaks.30,39 However, considerable differences between adsorption strains from SAXS and dilatometry on the same samples were detected,40 which are not consistent with the predictions of the theoretical models for radial mesopore deformation measured by SAXS, and a combination of radial and axial deformation measured by dilatometry.34
It was already recognized earlier that the filling of the mesopore space in SBA-15 or MCM-4141 can lead to so called “apparent strains” when analyzing the Bragg reflections from SAXS that are superimposing the actual deformation of the materials’ backbone. These apparent effects are due to subtle peak shifts as a consequence of intensity changes during pore filling with the adsorbate.42 For this reason, small-angle neutron scattering (SANS) using water as an adsorbate with the scattering length density tuned to zero by a proper H2O/D2O isotope mixture was recently employed.16 Hence, no intensity changes due to the scattering contrast, but only due to adsorption induced volume changes affect the scattering pattern, thus allowing the determination of the “real” adsorption induced deformation.17 Yet, the application of SANS is limited by several factors, such as limited availability of neutrons and limited resolution. Therefore, the determination of adsorption induced deformation using SAXS would be desirable, since such measurements can easily be performed using laboratory SAXS instruments with potentially considerably better strain resolution. This requires however the detailed modeling of the SAXS data, enabling the separation of “real” and “apparent” adsorption induced strains.
Here we develop a comprehensive model to simulate SAXS data from hierarchical silica with disordered micropores and ordered cylindrical mesopores during the adsorption of water. The model fully considers the three-phase nature of the system and predicts the SAXS profiles as a function of relative water pressure. Since we assume an infinitely stiff porous system in the model, the peak shifts deduced from the simulations are solely due to the apparent strains. These simulated apparent strains are then compared to apparent experimental strain data from a combined SAXS/SANS experiment.
2 Materials and methods
The investigated sample is a silica sample with hierarchical porosity (Fig. 1a). Materials synthesis was described in detail in a previous paper,17 and the sample was calcined at 500 °C to effectively remove organic residues from synthesis while limiting sintering, thus revealing micropores in the mesopore walls.43 Subsequently, the sample was aged at 74% relative humidity and 50 °C for 3 weeks to prevent reversible changes of the porous silica upon water adsorption.17 The sample was characterized by scanning electron microscopy (SEM) as well as with nitrogen adsorption as described in detail in ref. 17. | ||
| Fig. 1 (a) SEM images (taken from ref. 17) of the macroporous structure of the sample consisting of interconnected struts (left), where each strut comprises an array of ordered cylindrical mesopores (right). In situ SANS (b) and in situ SAXS (c) profiles in a Kratky plot representation for the empty sample (blue) and for the micro- and mesopores filled with neutron Z-SLD water (red). The numbers given in brackets are the Miller indices of a 2D hexagonal pore lattice. The insets show the normalized (10) peaks to visualize the peak shifts. | ||
In situ small-angle neutron scattering (SANS) measurements were conducted at the SANS 1 instrument44 at the Heinz Maier-Leibnitz Zentrum (MLZ, Garching near Munich, Germany), using a custom-built vapor dosing system16 connected to the sample cell. The adsorbate was a mixture of 91.95 wt% water and 8.05 wt% heavy water, chosen to obtain a net scattering length density of zero for neutrons (Z-SLD water). The relative pressure of the adsorbate in the sample cell was adjusted incrementally until equilibrium was reached for each measurement point and was kept constant during SANS data collection. The sample temperature was kept constant at 290.15 K. Details of the SANS experiments and data treatment are given in ref. 16.
In situ small-angle X-ray scattering (SAXS) experiments employing a similar vapor dosing setup and sample cell were conducted in-house using a laboratory instrument (NanoStar, Bruker AXS, Karlsruhe), equipped with a microfocus X-ray source with a copper anode. The beam was monochromatized to the Cu-Kα line by cross-coupled Göbel mirrors and collimated with two 300 μm diameter scatterless pinholes. SAXS patterns were collected with a Vantec 2000 detector at a sample–detector distance of 72 cm. SAXS measurement time was 45 min for each pressure point. The adsorptive was an identical H2O/D2O mixture as for the neutrons at the same sample temperature of 290.15 K.
SAXS and the SANS experiments were performed on the identical sample, and despite of the different illuminated sample areas due to different beam cross sections (neutron beam: 5 mm, X-ray beam ≈0.3 mm), they were absolute identical. While SANS data were normalized to absolute units, SAXS measurements are given in arbitrary units here.
3 Experimental results
Fig. 1a shows SEM images of the meso- and macropore structure of the hierarchically porous silica sample. On the macropore scale, the monolithic sample consists of a network of interconnected struts with a length of roughly one micron and a thickness of 200–400 nm. Each strut contains well aligned parallel cylindrical mesopores. SANS (Fig. 1b) and SAXS (Fig. 1c) profiles confirm the ordered arrangement of the mesopores on a 2D hexagonal lattice similar to SBA-15.38 The resolution of the SANS data is not as good as the one of the SAXS data because of limited SANS detector resolution and broad wavelength spread from the neutron velocity selector (10%), leading to considerable peak broadening. Scattering data for the sample are shown for the completely empty state (p/p0 = 0) and for a high relative pressure close to the bulk water saturation pressure, such that the micro- and mesopores are completely filled, while the macropores are still empty. For both datasets a constant background scattering term was subtracted. For the SANS experiment (Fig. 1b), almost no intensity changes are observed between the empty and the filled sample as expected for Z-SLD water. For the SAXS experiment (Fig. 1c) however, a large drop in the scattering intensity occurs at large values of the scattering vector q for the filled sample, while at the same time, the intensity at small q is increased. This effect is due to the changed electron density (empty versus water-filled micro and mesopores) in the sample. Interestingly, the complete micro- and mesopore filling does not simply result in an overall shift of the SAXS curves, which is a consequence of the hierarchical structure of the sample. The scattering at small q is dominated by the surface scattering of the whole strut. Since the overall electron density of the strut increases upon filling, its scattering contrast versus the empty macropores increases, leading to an increase of the intensity with filling. In the intermediate and large q-region, however, the scattering contrast is determined by the electron density difference between the meso-/micropores and the silica matrix. This scattering contrast decreases upon pore filling, thus leading to an intensity decrease. More generally speaking, with increasing relative pressure, the SAXS intensity profile is strongly affected by the adsorption of water molecules in the micropores and at the mesopore walls, and eventually by capillary condensation in the mesopores.For the SANS data, a small peak shift to lower q is clearly observed for the filled mesopores (visualized more clearly in the inset of Fig. 1b), suggesting adsorption induced expansion of the mesopore lattice. A slight peak shift is also observed in the SAXS data when normalized to the maximum of the (10) Bragg peak, although this shift is clearly smaller as compared to SANS (inset of the Fig. 1c). After quantitatively evaluating the peak position using the center of mass of the (10) peak,28 the mesopore lattice strain as a function of relative pressure is obtained from the relative peak shift, with the empty sample being the reference state. In Fig. 2a the strain isotherms using SAXS and SANS are shown for the adsorption branch of the sample. There are obviously clear differences between the SANS and the SAXS data. In particular, after an initial similar increase of the strain with relative pressure, the SAXS strain isotherm shows a pronounced strain drop at capillary condensation, while the SANS strain isotherm exhibits only a slight dip. Beyond capillary condensation, the strain values in both isotherms increase again in a similar manner, but there remains a large offset between the SANS and the SAXS strain isotherms. A similar discrepancy was already observed earlier on a hierarchical silica sample, where the strain isotherm from SAXS was compared to a strain isotherm obtained from in situ dilatometry.40 However, theoretical models for cylindrical mesopores predict that the isotherms for axial and radial strains34,37 should approach the same value at p/p0 = 1, which was also confirmed experimentally in ref. 17 by SANS using Z-SLD water.
 | ||
| Fig. 2 (a) Experimental SANS (black symbols) and SAXS (red symbols) adsorption strain isotherms obtained from the shift of the (10) Bragg reflection during adsorption of water. In (b) the apparent strain isotherm (black symbols) is determined from the data in (a) using eqn (1). The green curve is the simulated apparent strain isotherm using a model for film growth and capillary condensation in a purely mesoporous system (Model 1 and Section 4.2). | ||
From the strain isotherms in Fig. 2, we conclude that the strains extracted from the SAXS data are strongly affected by pore filling induced contrast changes, leading to apparent strain contributions. The isotherms obtained from SANS, however, can be taken as the true strains because of the use of Z-SLD water as adsorbate. Since both, the true strains (SANS) as well as the sum of apparent and true strains (SAXS) were measured on the same sample, the experimentally determined apparent strain is simply given by
| εapparent = εSAXS − εSANS | (1) |
4 Theoretical modeling
Here we develop SAXS models aiming to quantitatively predict the measured apparent strains in Fig. 2b. Prass et al.42 have determined the apparent strains in cylindrical mesopores analytically and numerically in the relative pressure region close to capillary condensation. Here, we extend this approach aiming at deriving the apparent strains quantitatively for the whole range of relative pressures by calculating the SAXS patterns of a single mesoporous model-strut containing mesopores with microporous mesopore walls. Model 1 deals with the simplified case of liquid film formation in ordered mesoporous silica with no micropores, while Model 2 takes the micropores and their filling as well as a more realistic mesopore model into account.4.1 SAXS from cylindrical mesopores on a hexagonal lattice
In the first step we set up a model to calculate the SAXS intensity for a purely mesoporous strut in its empty state. Since the length of the struts is much larger than the diameter of the mesopores (see Fig. 1a), a two-dimensional description is sufficient. The form factor of a circular mesopore cross-section is approximated by a step density model adapted from Zickler et al.12 | (2) |
| α = ρcorona/ρSiO2 | (3) |
 | (4) |
For the empty sample we have χ = 0, and the two radii R1 and R2 as well as the volume fraction of silica in the corona, α = α0, can be determined from the corresponding SAXS data of the empty sample by fitting the integrated Bragg peak intensities with eqn (2).12 From these parameters, an “equivalent mesopore radius”  can be determined.45 The results of the fitting procedure (see ESI† for details) are given in Table 1, together with the center to center distance of the mesopores,
can be determined.45 The results of the fitting procedure (see ESI† for details) are given in Table 1, together with the center to center distance of the mesopores,  , obtained from the position q10 of the (10) reflection. The total mesopore volume fraction (mesoporosity) is then calculated geometrically by
, obtained from the position q10 of the (10) reflection. The total mesopore volume fraction (mesoporosity) is then calculated geometrically by  , with the contribution of the corona
, with the contribution of the corona  and the remaining volume fraction of mesopore space outside the corona, ϕm,0.
and the remaining volume fraction of mesopore space outside the corona, ϕm,0.
| R 1 (nm) | R 2 (nm) | α 0 | R m (nm) | d (nm) | ϕ m | ϕ corona | ϕ m,0 |
|---|---|---|---|---|---|---|---|
| 3.81 | 2.39 | 0.5 | 3.19 | 10.1 | 0.36 | 0.16 | 0.20 |
To simulate the SAXS of the whole strut, we construct a single mesoporous strut of quadratic cross-section hosting an assembly of 30 × 30 hexagonally arranged cylindrical mesopores (Fig. 4a). It turns out that the specific cross-sectional shape of the strut is not critical for the results, since the spherical average of different geometrical shapes results in the same surface scattering. The arrangement chosen corresponds roughly to a strut diameter of 350 nm which is in the same order of magnitude as in the real system (see Fig. 1a). The total scattered intensity from the mesoporous strut is then calculated numerically using the two-dimensional Debye scattering equation.46
 | (5) |
4.2 Model 1: film growth and capillary condensation in cylindrical mesopores
In this model we assume perfect cylindrical mesopores with equivalent mesopore radius Rm and no micropores. The filling of the mesopores with water is modeled by assuming an increasing liquid film thickness on the mesopore walls with increasing relative pressure until the pores completely fill at capillary condensation. The form factor is described by eqn (2)–(4) with R1 = Rm, R2 = Rfilm and α = ρH2O/ρSiO2. We note that the film thickness t(p/p0) = Rm − Rfilm(p/p0) is the only pressure dependent quantity in this approach (Fig. 3a). The film thickness as a function of relative pressure was determined from the fit of the water adsorption isotherm (Fig. S1, ESI†) using the Derjaguin–Broekhoff–de Boer (DBdB) approach for cylindrical mesopores.47,48 This procedure to determine the film thickness of cylindrical mesopores was already successfully applied to nitrogen34,37 and pentane49 adsorption in silica, using corresponding reference isotherms for the silica–adsorbate interaction. Recently, we applied this approach also to water adsorption by combining the information from nitrogen and water adsorption isotherms to estimate the unknown water–silica interaction.17 The film-thickness as a function of relative pressure for the present sample is shown in Fig. S2 (ESI†) for the equivalent mesopore radius Rm = 3.19 nm taken from Table 1. It should be noted that the film thickness also depends on the mesopore radius, and therefore, it needs to be calculated for every single pore in eqn (5). This also leads to different capillary condensation pressures for the different pore classes, thus covering the apparent strains in the region of capillary condensation as described by Prass et al.42 To this end, the equivalent mesopore radii used to calculate the intensity with eqn (5) were normal distributed around the equivalent mesopore radius Rm (Table 1), with the width of the distribution estimated from the capillary condensation interval in the adsorption isotherm50 (see ESI† for details). | ||
| Fig. 3 (a) Step density model for mesopore filling by growth of a film with thickness t = R1 − R2, R1 being the equivalent mesopore radius Rm. The vertical axis represents the electron densities of water (blue) and silica (grey). (b) Simulated SAXS patterns using eqn (3) for three different relative pressures corresponding to various film thicknesses (t = 0 nm, t = 0.34 nm and t = Rm), with the inset depicting a zoom of the (10) peaks scaled to one for better visibility of the apparent strains. | ||
Fig. 3b shows the simulated SAXS patterns for the empty state (film thickness t = 0 nm), for a film with thickness t = 0.34 nm, and completely filled mesopores. A slight peak shift is observed in the inset of Fig. 3b for the state with t = 0.34 nm, confirming the presence of an apparent strain due to film formation. For the completely water filled sample, however, the peak position is exactly back to the situation at p/p0 = 0. This is also expected from eqn (2), since χ = 0 for the empty sample and χ = α for the filled sample after capillary condensation, leading to a simple reduction of the intensity by a factor (α − 1)2 but no change in the shape of the SAXS curve. SAXS curves were simulated using eqn (5) for 20 distinct, evenly spaced relative pressures between 0 and 95% using the film thickness shown in Fig. S2 (ESI†). From the simulated SAXS patterns, the apparent strains were determined from the shift of the center of mass of the (10) Bragg peak in the Kratky representation. They are shown in Fig. 2b along with the corresponding experimental apparent strains. It is obvious that the model completely fails to predict the apparent strain isotherm of the investigated sample, both, in magnitude and direction. The simulated apparent strain is progressively negative with increasing pressure and jumps back to zero after capillary condensation. In contrast, the measured apparent strain is positive and increases until capillary condensation, where it drops to a large negative value and remains approximately constant there. From this observation we conclude that Model 1 is way too simple for micro-/mesoporous materials, suggesting that the filling of the corona and the micropores needs to be taken into account. We note however that this model might be applicable to purely mesoporous materials with reasonably smooth pore walls such as MCM-41.30
4.3 Model 2: film growth and capillary condensation in cylindrical mesopores
We start with the hierarchical pore model previously introduced by Gommes et al.,10 with its three hierarchical contributions sketched in Fig. 4. The total SAXS intensity is assumed to be an incoherent superposition of scattering contributions from macro- (index M), meso- (index m) and micropores (index μ)| ISAXS(q) = IM(q) + Im(q) + Iμ(q) | (6) |
 | (7) |
 | ||
Fig. 4 Individual contributions to the hierarchical pore model (eqn (6)). (a) Sketch of a single strut of length L and side-length D; the number of mesopores used for the simulation (30 × 30) is not presented correctly here. (b) Top view of the mesopore level. The cylindrical mesopores are arranged in a 2-D hexagonal lattice with lattice parameter d. The unit cell of the pore lattice is highlighted by the opaque, red area, with a detailed zoom sketched in (c). The mean mesopore radius is ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) , and micropores (assumed to be of spherical shape with radius rμ) are embedded in the silica mesopore walls. , and micropores (assumed to be of spherical shape with radius rμ) are embedded in the silica mesopore walls. | ||
The scattering intensity from the micropores within the walls of the mesopores is given by
| Iμ(q,p/p0) = 8π3VGK(p/p0)(1 − ϕm)ϕμ(1 − ϕμ)fμ2(q,rμ,σμ). | (8) |
| K(p/p0) = (1 − ϒμ(p/p0))(ρSiO2)2 + ϒμ(p/p0)(ρSiO2 − ρH2O)2 | (9) |
The mesopore contribution to the SAXS intensity, Im(q), is essentially the one outlined in Section 4.1 (eqn (2)–(5)). In depth analysis of the SAXS data reveals that the Bragg peak intensities of the investigated sample can be well depicted by eqn (2) along the whole adsorption isotherm, with α = α(p/p0) describing the successive filling of the corona with liquid-like water until capillary condensation takes place. In other words, there seems to be no distinct film of liquid-like water growing at the mesopore surface. The attempt to employ a form factor which includes a liquid-like film on top of the corona (three-step model)12 did not result in improved fit quality compared to a model, where only the relative corona density α was varied and a liquid film covering the mesopore walls was omitted (see Fig. S5 and S6, ESI†). This suggests a different pore filling mechanism than usual for water in highly corrugated silica mesopores, a hypothesis which is also supported by the quite different shape of the water adsorption isotherm as compared to the nitrogen adsorption isotherm (Fig. S1, ESI†).
We also note here that the way the scattering of the mesoporous strut is calculated by eqn (5) already includes scattering from the strut surface. However, this contribution does not correspond to the real surface scattering, because in this case the material outside the strut is silica instead of vacuum. Since the (true) surface scattering is already covered by eqn (7), we must correct the result of Im(q) from eqn (5) by subtracting the corresponding “wrong” surface scattering contribution. Details are given in the ESI,† Section 5.
Before simulating the SAXS curves using eqn (6), we analyze two limiting cases, i.e., the intensity at large and at small scattering vector lengths. Because the in situ SAXS measurements were not collected in absolute units, only relative differences in intensity can be analyzed. Denoting x(p/p0) the water filling fraction of the micro- and mesopores, the ratio of eqn (7) for the empty sample (x = 0) and for the sample containing the water fraction x at a relative pressure p/p0 reads
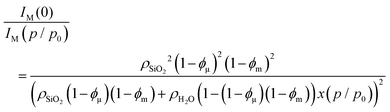 | (10) |
 determined from nitrogen adsorption and ϕSAXSμ obtained from eqn (10), variance of mesopore radii σmeso estimated from the water adsorption isotherm and micropore diameter 2rμ with variance σ2rμ obtained from the SAXS pattern of empty samples
determined from nitrogen adsorption and ϕSAXSμ obtained from eqn (10), variance of mesopore radii σmeso estimated from the water adsorption isotherm and micropore diameter 2rμ with variance σ2rμ obtained from the SAXS pattern of empty samples
In the limiting case of large scattering vectors, the intensity ratio of the reference state (empty sample) with respect to any state of pore filling can be analyzed in terms of a three-phase model (silica, water, and pore space), assuming this region to be dominated by scattering from the micropores (see ESI† for details):
 | (11) |
 | ||
| Fig. 5 Pore filling fractions x from SAXS using eqn (11) (red line) and eqn (12) (blue line). The water adsorption isotherm measured independently using a vapor adsorption instrument17 is shown by the black symbols. | ||
To model the SAXS curves over the whole pressure range, the volume fraction of water in the micro- and mesopores must be determined as a function of relative pressure. The micropore filling factor ϒμ(p/p0)(0 ≤ ϒμ ≤ 1) is obtained from the water adsorption isotherm using the theoretical Langmuir isotherm (see ESI†). The Langmuir isotherm was used in previous studies on this material to model adsorption of water and adsorption induced deformation of micropores17,37 and is therefore a reasonable choice to approximate ϒμ(p/p0) in eqn (9). The mesopore filling consists of two parts: the filling of the corona, described by the parameter α(p/p0) (eqn (3)) and capillary condensation described by the filling factor ϒm(p/p0)(0 ≤ ϒm ≤ 1), describing the fraction of completely filled mesopores during capillary condensation (eqn (S7), ESI†). Both parameters are derived from the fit of the Bragg reflections using eqn (2) and keeping the radii R1 and R2 constant at the values given in Table 1 (see Fig. S4, ESI†). The relative electron density of the corona does not reach its maximum possible value (α = 0.76 here, see Fig. S5, ESI†) for relative pressures below capillary condensation. This indicates that the corona is only partially filled and no true multilayer film growth of water occurs at pressures below capillary condensation. For relative pressures above capillary condensation, α reaches the theoretical value for the filled corona in the conducted fits (Fig. S5, ESI†). For this reason, α was set to its maximum value once capillary condensation occurred and was kept constant for larger pressures.
Given the three parameters α, ϒm and ϒμ (Fig. S5, ESI†), the volume fraction of water at a given relative pressure can easily be calculated
 | (12) |
Given the reasonable agreement of the adsorption isotherm determined from SAXS by eqn (12) with the water adsorption isotherm measured independently, the simulations of the SAXS curves were now performed to quantitatively determine the apparent strain isotherm (see ESI† for more details). The results of these simulations are shown in Fig. 6 for selected relative pressures. The apparent strains extracted from the relative peak shift of the simulated (10) Bragg reflections are depicted in Fig. 7.
 | ||
| Fig. 6 (a) Electron density profile for Model 2. This model assumes no film formation but gradual filling of the corona until capillary condensation, simulated SAXS profiles using the hierarchical pore model (eqn (6)) are shown for p/p0 = 0 (b) and p/p0 = 0.95 (c) with the individual contributions from macro-, meso-, and micropore scattering highlighted. In (d), the (10) peak scaled to one is shown for three selected relative pressures together with a zoom of the peak intensities close to the peak maximum. | ||
 | ||
| Fig. 7 (a) Measured (black symbols) and simulated (green and black lines) apparent strains using Model 2. The green line represents only the contribution of the mesopores (green profiles in Fig. 6b and c), while the black line takes the contribution of micro- and macropores into account as well. (b) Measured SAXS (red symbols) and SANS (black symbols) strains, as well as the SANS strain modified by the apparent strain shown in (a) via application of eqn (1). | ||
5 Discussion and conclusion
It is obvious from Fig. 2b, that Model 1, assuming the growth of a liquid-like film on the mesopore surface, is not able to describe the measured apparent strain isotherm. In contrast, the agreement of the simulated apparent strains using Model 2 with the measured ones (see Fig. 7a) is remarkable. In particular, the strong drop of the apparent strain at capillary condensation is well reproduced by the model. In Fig. 7b the resulting strain isotherm after addition of the apparent strain to the SANS strain isotherm by application of eqn (1) is shown. Within experimental accuracy, good agreement is achieved with the experimental SAXS strain isotherm, justifying eqn (1). Fig. 6b and c, showing simulated SAXS patterns for the empty and filled sample, give a qualitative insight for the reason of the strong apparent peak shift at capillary condensation. The micro- and macropore scattering contribute to a considerable amount to the SAXS intensity at the position of the Bragg reflection, thus strongly modifying the diffuse scattering below the peak. Of special note is the crossing point of the macro- and microporous contributions in Fig. 6b and c, which shifts strongly to the right after capillary condensation, introducing a strong change of the slope of the diffuse scattering. This behavior originates in the decrease of the electron density difference of micro- and mesopores upon filling (see eqn (9) and (2) for the respective contributions), and the increase of the difference in electron density of the strut surface scattering with respect to the empty space surrounding it (eqn (7)). Consequently, the scattering intensity of micro- and mesopores decreases and the strut surface scattering increases upon adsorption, which shifts the crossing point of IM and Im + Iμ (Fig. 6b and c) to larger values of the scattering vector magnitude q. This eventually results in an asymmetric broadening of the Bragg peak (see Fig. 6d) resulting in an effective shift of the average peak position to larger q (i.e. to negative apparent strains) due to a considerable reduction of the peak intensity on the left flank of the peak. Since the micro- and mesopores are completely filled after capillary condensation has occurred, Iμ (eqn (2)), Im (eqn (9)) and IM (eqn (7)) remain all constant, which leads to a constant negative apparent strain for p > pcap in SAXS (Fig. 7a).In contrast, for pressures below capillary condensation the peak shift to smaller q (positive apparent strain) is supposed to be due to the change of the mesopore formfactor (see inset in Fig. 6d). There is hardly an influence of the macro- and micropore scattering in this region (compare green and black lines in Fig. 7a). Most interestingly, by applying Model 2 the net apparent strain for relative pressures below capillary condensation is positive, as opposed to the application of Model 1 (see Fig. 2b). We recall that in Model 1 a liquid-like water film growing with increasing relative pressure was assumed, while in Model 2 the corona was progressively filled with water without any film growth. Since the micro- and macropore scattering do not influence the peak position markedly in this region, the effect must be due to the mesopore formfactor, which is highly sensitive to the pore filling mechanism. This is a further strong hint that when using water as an adsorbate, the mesopore filling in the present silica material is quite different from the classical picture of homogeneous film growth.
The film thickness derived from structural data derived from SAXS (Tables 1 and 2) and thermodynamic parameters using the DBdB – model (taken from Ludescher et al.17) indicates that no closed liquid water film exists for p/p0 < 0.5 (see Fig. S2, ESI†). As the corona represents roughly one third of the total mesopore space (see Table 1), and assuming that the corona is built up by strong surface corrugations and micropores, it is not surprising that no pronounced film is discernible in SAXS. Gommes51 proposed already several years ago that adsorption in corrugated cylindrical mesopores occurs by filling progressively larger corrugations, until capillary condensation in the mesopores takes place. The effect of this corrugation filling on the position and shape of the hysteresis is not trivial. However, shifts to lower relative pressures of adsorption and evaporation have been demonstrated,51 and hence, the adsorption model proposed by Gommes explains tentatively both, the adsorption behavior of water in our material, as well as the discrepancy in mesopore radii between SAXS and nitrogen adsorption (see Fig. S3, ESI†). However, here we can only give highly indirect evidence for a different adsorption mechanism, and further experiments using different adsorbates will be needed to elucidate the water adsorption mechanism in such materials.
The results from this investigation clarify several points related to adsorption induced deformation in hierarchically nanoporous silica materials using small-angle scattering. First, the difference between the measured strains at low relative pressures between SANS and SAXS show that the apparent strains induced in SAXS mask the contraction of micropores found in Ludescher et al.17 for this exact same material. Because subtle effects of the filling of micropores at low relative pressures on SAXS are difficult to model, their correction can only be achieved once the mechanism is well understood. Second, the constant apparent strains at high relative pressures in the filled pore regime show that the concepts introduced by Prass et al.30 to extract mechanical properties (the pore load modulus) remain unaffected in SAXS. Yet, higher resolution measurements covering a larger interval in q, such as synchrotron X-ray radiation, should help to elucidate more details of the filling mechanism and consequently allow to accurately correct measured strains from apparent effects.
In conclusion, we have developed quantitative models to describe apparent strains by simulation of SAXS data from a hierarchically macro-, meso- and microporous silica material. The SAXS simulations are able to predict apparent strains for a hierarchically porous silica sample quantitatively. In particular, when taking both, the scattering contributions from the ordered mesopores as well as from the micro- and macropores into account, satisfactory correction of strains measured by in situ adsorption SAXS is possible over the whole adsorption isotherm. This is not the case in the capillary condensation regime, however, if only the scattering from the ordered mesopores is considered, due to a strong influence of the diffuse scattering from macro- and micropores. Moreover, there seems to be no film growth of water on the mesopore walls, but rather a continuous filling of strong surface corrugations (corona) at the surface of the mesopore walls. Yet, no real quantitative model for the details of pore filling of these materials with water is available so far.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from the Austrian Science Foundation FWF (Project I 1605-N20) and the German Science Foundation DFG (Project GZ: RE1148/10-1). This work is based upon experiments performed at the SANS-1 instrument operated by HZG and FRM II at the Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany.Notes and references
- F. Chang, J. Zhou, P. Chen, Y. Chen, H. Jia, S. M. I. Saad, Y. Gao, X. Cao and T. Zheng, Asia-Pac. J. Chem. Eng., 2013, 8(4), 618 CrossRef CAS.
- A. Taguchi and F. Schüth, Microporous Mesoporous Mater., 2005, 77(1), 1 CrossRef CAS.
- G. Y. Gor, P. Huber and N. Bernstein, Appl. Phys. Rev., 2017, 4(1), 11303 Search PubMed.
- T. Wagner, S. Haffer, C. Weinberger, D. Klaus and M. Tiemann, Chem. Soc. Rev., 2013, 42(9), 4036 RSC.
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. W. Sing, Pure Appl. Chem., 2015, 87(9–10), 1051 CAS.
- K. J. Chao, C. N. Wu, A.-S. Chang and S. F. Hu, Microporous Mesoporous Mater., 1999, 27(2–3), 287 CrossRef CAS.
- M. Impéror-Clerc, Interface Focus, 2012, 2(5), 589 CrossRef PubMed.
- Scattering Methods and the Properties of Polymer Materials, ed. N. Stribeck and B. Smarsly, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005 Search PubMed.
- B. Smarsly, M. Groenewolt and M. Antonietti, Scattering Methods and the Properties of Polymer Materials, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, pp. 105–113 Search PubMed.
- C. J. Gommes, G. Prieto and P. E. de Jongh, J. Phys. Chem. C, 2016, 120(3), 1488 CrossRef CAS.
- M. Impéror-Clerc, P. Davidson and A. Davidson, J. Am. Chem. Soc., 2000, 122(48), 11925 CrossRef.
- G. A. Zickler, S. Jähnert, W. Wagermaier, S. S. Funari, G. H. Findenegg and O. Paris, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(18), 17 CrossRef.
- G. Reichenauer, Structural Characterization of Aerogels, in Aerogels Handbook, ed. M. A. Aegerter, N. Leventis and M. M. Koebel, Springer New York, New York, NY, 2011, pp. 449–498 Search PubMed.
- M. Erko, D. Wallacher, A. Brandt and O. Paris, J. Appl. Crystallogr., 2010, 43(1), 1 CrossRef CAS.
- C. Prehal, D. Weingarth, E. Perre, R. T. Lechner, H. Amenitsch, O. Paris and V. Presser, Energy Environ. Sci., 2015, 8(6), 1725 RSC.
- R. Morak, S. Braxmeier, L. Ludescher, F. Putz, S. Busch, N. Hüsing, G. Reichenauer and O. Paris, J. Appl. Crystallogr., 2017, 50(Pt 5), 1404 CrossRef CAS PubMed.
- L. Ludescher, R. Morak, C. Balzer, A. M. Waag, S. Braxmeier, F. Putz, S. Busch, G. Y. Gor, A. V. Neimark, N. Huesing, G. Reichenauer and O. Paris, Langmuir, 2019, 35(35), 11590 CrossRef CAS PubMed.
- G. Reichenauer and G. W. Scherer, J. Non-Cryst. Solids, 2000, 277(2–3), 162 CrossRef CAS.
- G. Reichenauer and G. W. Scherer, J. Non-Cryst. Solids, 2001, 285(1–3), 167 CrossRef CAS.
- J. W. McBain and J. Ferguson, J. Phys. Chem., 1927, 31(4), 564 CrossRef CAS.
- D. H. Bangham and N. Fakhoury, Nature, 1928, 122(3079), 681 CrossRef CAS.
- M. Erko, D. Wallacher and O. Paris, Appl. Phys. Lett., 2012, 101(18), 181905 CrossRef.
- J. M. Black, G. Feng, P. F. Fulvio, P. C. Hillesheim, S. Dai, Y. Gogotsi, P. T. Cummings, S. V. Kalinin and N. Balke, Adv. Energy Mater., 2014, 4(3), 1300683 CrossRef.
- M. M. Hantel, V. Presser, R. Kötz and Y. Gogotsi, Electrochem. Commun., 2011, 13(11), 1221 CrossRef CAS.
- M. M. Hantel, D. Weingarth and R. Kötz, Carbon, 2014, 69, 275 CrossRef CAS.
- F. Kaasik, T. Tamm, M. M. Hantel, E. Perre, A. Aabloo, E. Lust, M. Z. Bazant and V. Presser, Electrochem. Commun., 2013, 34, 196 CrossRef CAS.
- C. Koczwara, S. Rumswinkel, C. Prehal, N. Jäckel, M. S. Elsässer, H. Amenitsch, V. Presser, N. Hüsing and O. Paris, ACS Appl. Mater. Interfaces, 2017, 9(28), 23319 CrossRef CAS PubMed.
- G. A. Zickler, S. Jähnert, S. S. Funari, G. H. Findenegg and O. Paris, J. Appl. Crystallogr., 2007, 40(s1), s522–s526 CrossRef CAS.
- D. Bellet and G. Dolino, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(23), 17162 CrossRef CAS PubMed.
- J. Prass, D. Müter, P. Fratzl and O. Paris, Appl. Phys. Lett., 2009, 95(8), 83121 CrossRef.
- G. W. Scherer, J. Am. Ceram. Soc., 1986, 69(6), 473 CrossRef CAS.
- P. I. Ravikovitch and A. V. Neimark, Langmuir, 2006, 22(26), 11171 CrossRef CAS PubMed.
- G. Y. Gor and A. V. Neimark, Langmuir, 2011, 27(11), 6926 CrossRef CAS PubMed.
- C. Balzer, A. M. Waag, S. Gehret, G. Reichenauer, F. Putz, N. Hüsing, O. Paris, N. Bernstein, G. Y. Gor and A. V. Neimark, Langmuir, 2017, 33(22), 5592 CrossRef CAS PubMed.
- R. Salazar and L. D. Gelb, Mol. Phys., 2004, 102(9–10), 1015 CrossRef CAS.
- A. L. Kolesnikov, N. Georgi, Y. A. Budkov, J. Möllmer, J. Hofmann, J. Adolphs and R. Gläser, Langmuir, 2018, 34(25), 7575 CrossRef CAS PubMed.
- C. Balzer, A. M. Waag, F. Putz, N. Huesing, O. Paris, G. Y. Gor, A. V. Neimark and G. Reichenauer, Langmuir, 2019, 35(8), 2948 CrossRef CAS PubMed.
- D. Zhao, J. Feng, Q. Huo, N. Melosh, G. H. Fredrickson, B. F. Chmelka and G. D. Stucky, Science, 1998, 279(5350), 548 CrossRef CAS PubMed.
- G. Günther, J. Prass, O. Paris and M. Schoen, Phys. Rev. Lett., 2008, 101(8), 86104 CrossRef PubMed.
- C. Balzer, R. Morak, M. Erko, C. Triantafillidis, N. Hüsing, G. Reichenauer and O. Paris, Z. Phys. Chem., 2015, 229(7–8), 526 Search PubMed.
- C. T. Kresge, M. E. Leonowicz, W. J. Roth, J. C. Vartuli and J. S. Beck, Nature, 1992, 359(6397), 710 CrossRef CAS.
- J. Prass, D. Müter, M. Erko and O. Paris, J. Appl. Crystallogr., 2012, 45(4), 798 CrossRef CAS.
- F. Putz, A. Waag, C. Balzer, S. Braxmeier, M. S. Elsaesser, L. Ludescher, O. Paris, W. J. Malfait, G. Reichenauer and N. Hüsing, Microporous Mesoporous Mater., 2019, 288, 109578 CrossRef CAS.
- A. Heinemann and S. Mühlbauer, Journal of Large-Scale Research Facilities, 2015, 1(A10) DOI:10.17815/jlsrf-1-32.
- S. Jähnert, D. Müter, J. Prass, G. A. Zickler, O. Paris and G. H. Findenegg, J. Phys. Chem. C, 2009, 113(34), 15201 CrossRef.
- P. Debye, Ann. Phys., 1915, 351(6), 809 CrossRef.
- J. Broekhoff, J. Catal., 1967, 9(1), 8 CrossRef CAS.
- B. Derjaguin, Prog. Surf. Sci., 1992, 40(1–4), 46 CrossRef.
- G. Y. Gor, O. Paris, J. Prass, P. A. Russo, M. M. L. Ribeiro Carrott and A. V. Neimark, Langmuir, 2013, 29(27), 8601 CrossRef CAS PubMed.
- D. Müter, S. Jähnert, J. W. C. Dunlop, G. H. Findenegg and O. Paris, J. Phys. Chem. C, 2009, 113(34), 15211 CrossRef.
- C. J. Gommes, Langmuir, 2012, 28(11), 5101 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01026j |
| This journal is © the Owner Societies 2020 |

