First principles calculations on order and disorder in La2Ce2O7 and Nd2Ce2O7†
Abstract
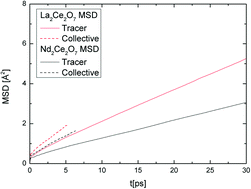
In this paper, we highlight the connection between the local structure and collective dynamics of the defective fluorites La2Ce2O7 and Nd2Ce2O7. The local and average structure is explored by investigating a large number of different structural models and snapshots from Born–Oppenheimer Molecular dynamics calculations. Both compounds show a strong preference for local oxygen vacancy order similar to that found in the C-type structure. This suggests that previous studies, where Nd2Ce2O7 and La2Ce2O7 are viewed as disordered defective fluorites, or as a pyrochlore for the latter, did not capture the nature of local order in the disordered phase. We observe more collective chains of migrating oxygen in Nd2Ce2O7 – a manifestation of a stronger preference for a dynamic local oxygen vacancy order – than in La2Ce2O7. The stronger preference for 〈210〉 vacancy–vacancy alignments can explain why long range ordering is identified by distinct C-type like superlattice peaks in neutron diffraction patterns for Nd2Ce2O7 whereas they appear to be almost invisible in La2Ce2O7.
- This article is part of the themed collection: 2020 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...