The infrared spectra of protic ionic liquids: performances of different computational models to predict hydrogen bonds and conformer evolution

Abstract

The temperature dependence of the far- and mid-infrared spectrum of two prototypical protic ionic liquids (PILs) sharing a common trialkylammonium cation, but having different anions, is investigated. The exploitation of both the FIR and MIR ranges provides complementary information about the microscopic configurations and the intermolecular interactions, which determine the structure and the properties of ILs. The analysis of the data collected for all the measured frequencies in a wide temperature range reveals several phase transitions and allows the evaluation of the conformer distribution in the different physical states. The difference in the average energy between the H-bonded configurations and the dispersion-governed ones was also determined for the two PILs. Moreover, a computational model for ionic couples based on the ωB97X-D functional and a polar solvent is here successfully exploited for the description of the hydrogen bonding between anion and cation. For the attribution of vibrational lines of the conformers of the cation, the picture based on single ion calculations at the B3LYP level is more valuable and provides better agreement with the experiments.

---

Introduction

Ionic liquids (ILs) exhibit exceptional properties, such as low volatility, nonflammability, high conductivity and chemical stability, allowing applications in the field of extractive distillation, synthesis of new materials, green solvents and electrochemical devices like batteries and fuel cells. The choice of the cation and of the anion composing the liquids allows tailoring specific properties. In particular, protic ionic liquids (PILs), obtained by the neutralization reaction of a Brønsted acid and a Brønsted base, possess exchangeable protons and strong hydrogen bonds,¹ which make them particularly attractive for proton exchange membrane fuel cells.^2–6 To completely master the properties of ILs in view of the different applicative requirements, complete knowledge of the microscopic configuration and of the intermolecular forces is essential.⁷ Indeed, besides the coulombic forces, hydrogen bonding and dispersion forces can also play a crucial role in the determination of the structure and properties of ILs,^7–14 especially for the protic ILs that show stronger hydrogen bonding networks.

Vibrational spectroscopies such as Raman and infrared (IR) spectroscopy have provided useful information about the possible ionic configurations, the intermolecular interactions and their variation as a function of temperature and pressure.^1–24 Indeed, the IR absorption spectra of ILs in the mid-infrared (MIR) range display the signatures of the different ion conformers; analysis of the evolution of the spectrum as a function of the temperature and/or pressure provides a detailed picture of the evolution of the concentration of the conformers as a function of pressure and temperature and of the changes occurring in the intramolecular structure during the phase transitions. For instance, infrared spectroscopy combined with DFT simulations^16,17 has shown that in mixtures of ammonium- or pyrrolidinium-based ionic liquids sharing the bis(trifluoromethanesulfonyl)imide (TFSI) anion and having alkyl chains of different lengths, the competition between the two conformers of TFSI hinders crystallization and gives rise to a glass transition.

Absorption spectra in the far-infrared (FIR) range instead provide information about the intermolecular dynamics of ionic liquids.¹⁵ The studies based on FIR spectroscopy of ILs are scarce due to the more demanding experimental setup required for such measurements, but interesting results have been provided, in particular on hydrogen bonding¹⁵ and the dispersion interactions governing IL properties. In this framework, the exploitation of the FIR range is particularly worthwhile for PILs due to their strong directional hydrogen bonding. While the evaluation of the different noncovalent interactions still requires significant efforts, the hydrogen bonding results are easier to analyze, because H bonds are at the same time short-ranged and highly directional.^9,10 In particular, in the FIR range, the hydrogen bond is detectable as a well-isolated and narrow peak around 150–170 cm⁻¹, similar to what is detected in ice at ∼100 K, for which the two bands located around 230 and 160 cm⁻¹ correspond to intermolecular hydrogen bond stretching modes, with motions in different directions.²⁵

For the PILs containing an ammonium cation with a single proton–donor group N–H, an isolated vibrational band has been observed between 150 and 170 cm⁻¹, which is assigned to the stretching of the hydrogen bond between the cationic NH and the anion. Indeed, this band is a signature of the H-bond-enhanced anion–cation directional interaction.^7–9 In the last few years, Fumino and coworkers^7–9,26,27 focused their studies on the dispersion interactions in ILs by means of a combined use of FIR spectroscopy and different computational approaches, trying to quantify those noncovalent interactions and provide a description of the competition between hydrogen bonding and dispersion-forces in a Coulomb-dominated fluid. They revealed that local and directional hydrogen bonding in aprotic ILs makes the liquid more fluid rather than more viscous and they suggested that H bonds may lower melting points, viscosities and enthalpies of vaporization because they act as defects.^26,27

In the present paper, we present a detailed study of the temperature dependence of the vibrational spectrum in the FIR and the MIR ranges (between 40 and 4000 cm⁻¹) of two prototypical PILs sharing a common trialkylammonium cation combined with two different anions, with different interaction forces, namely, methanesulfonate anion (MS) and trifluoromethanesulfonate (TfO) anion. PILs with the trialkylammonium cation have been largely investigated by vibrational spectroscopy, but diethylmethylammonium (DEMA) methanesulfonate is poorly studied.

Spectra in the far IR range allow the detection of the strong and directional hydrogen bonds between the NH bond of the cation and the anions; moreover, analysis of the spectra allows assessing the difference in the average energy between the H-bonded and the dispersion-governed configurations. A comparison of different DFT models for ionic couples suggests that the hydrogen bond between anion and cation can be successfully described using the ωB97X-D functional when considering a polar solvent. Moreover, the MIR spectra show a phase transition at low temperatures and allow the detection of modifications in the concentration of conformers of the cations as a function of T. The analysis of the spectra provides an evaluation of the enthalpy difference between the low energy DEMA conformers. From a computational point of view, such low energy conformers are better described when using an isolated single ion approach and the B3LYP functional, which has been previously used in the literature for the calculation of the infrared spectra of many ILs.

Experimental

The presently investigated ionic liquids, diethylmethylammonium methanesulfonate (DEMA-MS) and diethylmethylammonium trifluoromethanesulfonate (DEMA-TfO), were purchased from Iolitec; DEMA-MS has a purity higher than 98%, while the purity of DEMA-TfO is 99.0% (Fig. 1). The samples were stored in a glove box; moreover, before measurements, both ILs were dried in a vacuum better than 10⁻⁵ mbar for 48 hours to minimize the water content.

Fig. 1 Geometric structures of methanesulfonate (MS) and trifluoromethanesulfonate (TfO) anions and of the diethylmethylammonium (DEMA) cation.

Infrared spectroscopy measurements were performed using a Bruker IFS125 HR spectrometer at the AILES beamline of the SOLEIL Synchrotron. The spectra were recorded in the mid-infrared range with a resolution of 0.5 cm⁻¹, by combining a KBr beamsplitter and a wide range low noise MCT,²⁸ while in the far-infrared range, they were recorded using a Si-coated mylar beamsplitter and a bolometer. Thin layers of ILs were placed between the diamond windows of a vacuum tight cell. The transmission was calculated using the spectrum of the bare optical windows as a reference. Transmission measurements were converted into absorbance data. The samples were cooled down to 120 K using a Cryomec cryostat at a temperature rate of 5 K min⁻¹, and the data were collected both upon cooling and heating in the range between this minimum temperature and 330 K.

Computational details

Calculations of the structures and conformers of the isolated anion and cation or of a single ion pair were performed using the Spartan software.^29,30 Preliminary calculations of the possible geometries were performed at the molecular mechanics level. All structures were then optimized by means of DFT calculations using various functionals: B3LYP, B3LYP-D (including empirical dispersion corrections) or the ωB97X-D functional (also including empirical dispersion corrections); in all cases, the 6-31G** basis set was employed. In the case of ionic couples composed of one anion and one cation, the effect of a polar (dimethylformamide, ε_r = 37.22) or non-polar solvent (tetrahydrofuran, ε_r = 7.43) was also considered. Finally, infrared vibrational frequencies and intensities were calculated at the same level of theory and with the basis set used for the geometry optimization, taking also into account the possible presence of a polar or non-polar solvent. In order to compare the experimental infrared spectrum with the calculations, we constructed calculated infrared spectra by summing Gaussian curves centered at each calculated vibration frequency, with a 10 cm⁻¹ line width and intensity proportional to the calculated one.

Results and discussion

Performances of the different DFT models

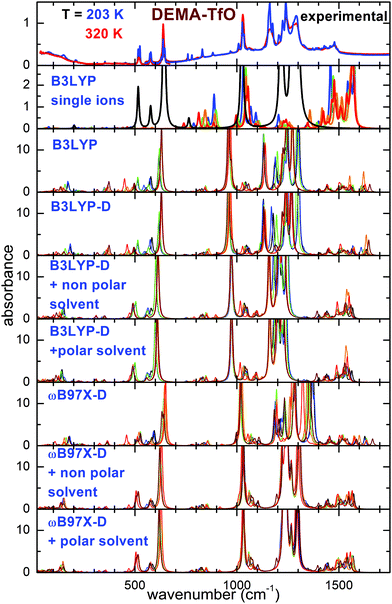
Fig. 2 and 3 report the experimental spectra of the two ionic liquids measured at the highest and the lowest investigated temperatures, compared with the results of the calculations performed using the different models. Concerning the experimental absorbance, the intense lines centered around 540, 770, 1038, 1166 and 1220 cm⁻¹ for DEMA-MS and around 200, 518, 575, 638, 1029, 1162, 1241, 1290 cm⁻¹ for DEMA-TfO are known to be due to the vibrations of the anions. Moreover, both ILs present a broad peak in the far infrared region centered around 100 cm⁻¹, superimposed with a clear isolated secondary peak centered at the lowest temperature around 165 cm⁻¹ for DEMA-MS and around 150 cm⁻¹ for DEMA-TfO, which can be attributed to the stretching modes of NH–anion hydrogen bonding, similar to the feature reported by Ludwig et al. for equivalent protic ionic liquids.^7–9,26,27 The absorption lines between 780 and 1000 cm⁻¹ can be attributed to the cation vibrations, as they were not observed in the anion spectra.

Fig. 2 Comparison of the experimental spectra of DEMA-MS measured at the highest and lowest temperature with the calculated spectra for different conformers of the ionic couples or for single ions. Single ion calculated spectra: black lines: MS, all other colors: DEMA conformers. For calculations of ion pairs: black, blue, green, orange, red and wine lines correspond to Conf. A, B, C, D, E, and F, respectively.

Fig. 3 Comparison of the experimental spectra of DEMA-TfO measured at the highest and lowest temperature with the calculations for different conformers of the ionic couples or for single ions. Single ion calculated spectra: black lines: TfO, all other colors: DEMA conformers. For calculations of ion pairs: black, blue, green, orange, red and wine lines correspond to Conf. A, B, C, D, E, and F, respectively.

As a starting point, the calculated absorption of the isolated anion and cations at the B3LYP/6-31G** level is reported. This particular model has been largely used in the recent past to investigate single ions composing ionic liquids and their vibrational properties, and it is considered as a benchmark for this type of calculations.^16–20,31 For the cation, a scaling factor of 1.03 was applied; for the anions, a scaling factor of the vibration frequencies equal to 1.03 for TfO and 1.05 for MS had to be used, to adapt the position of the calculated absorptions of the anion to the intense measured absorption lines. Concerning the cation, it was found to possess five different conformers (labeled from C1 to C5), whose geometries and relative energies are reported in Fig. S1 and Table S1 of the ESI.† For both ILs, the calculated spectrum at the B3LYP/6-31G** level of single ions presents a general good agreement with the experimental spectrum above 400 cm⁻¹; however, some drawbacks of this model can be mentioned: firstly, there is no feature in the far infrared range, around 150–160 cm⁻¹, associated with the hydrogen bonding stretching. This could be expected as this movement requires the presence of both anion and cation. Moreover, the frequency of intense lines centered around 1200 cm⁻¹ is largely overestimated compared to the experimental spectrum, and the same is true for the C–H bending vibrations centered between 1300 and 1500 cm⁻¹.

Taking into account the interaction of anion and cation, calculations at the B3LYP/6-31G** level on the ionic couple provide six possible conformers. A peak centered around 200 cm⁻¹ for DEMA-MS and 180 cm⁻¹ for DEMA-TfO, corresponding to the stretching modes of the NH–anion hydrogen bonding, is clearly visible, even though the frequency of such a mode is too high in comparison with the experiments. However, the B3LYP model applied to the ionic couples is not able to reproduce the intense absorbance lines found experimentally between 1000 and 1300 cm⁻¹. Introducing an empirical correction for dispersion forces with the B3LYP-D functional or considering the presence of a polar or non-polar solvent does not considerably improve the correspondence with the experiments (see Fig. 2 and 3). These discrepancies motivated the exploiting of the functional ωB97X-D as previous studies reported that the ωB97 functional gave better results than any other DFT functional.³² However, this functional has been limitedly used before for ionic liquids. An empirical correction for dispersion forces was included in this model. The ωB97X-D functional applied to the single ionic couple is able to give a general agreement with the measurements; in particular, it is able to reproduce the presence of the stretching modes of the NH–anion hydrogen bonding, but it still fails in the region between 900 and 1300 cm⁻¹. However, when adding a solvent (either polar or non-polar), one finally obtains a good agreement of the calculated absorbance spectra with the measured ones. It must be noted that while for the calculations with isolated ions, a scaling factor for the vibrational frequency of the anion was utilized, in the case of all calculations on ionic couples, no scaling factor was applied. The geometry of the six conformers of the two ionic couples, their relative energies and calculated infrared vibration frequencies and intensities are reported in the ESI.†

The main effect of the inclusion of a solvent in the calculation is the increase of the distance between anion and cation. Table 1 reports the distance between the O atom of the anion and the H atom of the cation directly attached to N.

Table 1 Comparison of the distances in Å between the closest O atom of the anion and H atom of the cation, obtained by the two functionals ωB97X-D and B3LYP-D and the common 6-31G** basis set

	In vacuum	Non-polar solvent	Polar solvent
ωB97X-D
DEMA-MS	1.495	1.622	1.668
DEMA-TfO	1.548	1.724	1.752
B3LYP-D
DEMA-MS	1.477	1.627	1.655
DEMA-TfO	1.525	1.689	1.752

---

The main advantages of the calculations performed in the present paper on ion couples are their simplicity and efficiency as lower calculation times are required compared to the computations based on multiple ion pairs (from 2 up to 8 couples) previously proposed for the analysis of the far infrared spectra of protic liquids.^7–9 Calculations based on the interaction of many ionic couples are relatively common for the prediction or interpretation of macroscopic properties, such as viscosity, melting point of heat of fusion and vaporization,^33–35 but only in a few cases were they used to calculate the vibrational spectra. We will show in the following that, despite their relative simplicity, the presently proposed calculations using the ωB97X-D functional and a polar or non-polar medium are able to provide quantitative information about the hydrogen bonding network.

In the following, we will focus on two relevant ranges of the infrared spectra and we will interpret them in more detail by means of DFT calculations: (1) the region between 700 and 1000 cm⁻¹, where the spectral signatures of the conformers of the ionic couples can be found; (2) the far infrared part of the spectrum, below 300 cm⁻¹, where the hydrogen bonding between anion and cation can be identified.

A study of conformers

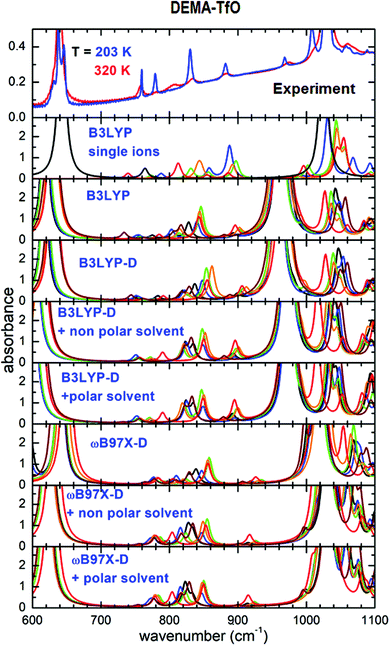
The mid-infrared range of the absorption spectra of ILs can provide information about the occurrence of different conformers of the ions. This fact has been largely utilized in the case of TFSI anions and for a number of cations, such as imidazolium, pyrrolidinium and quaternary ammonium. In many ILs, the abrupt change in the relative concentration of conformers or the disappearance of the lines attributable to one or more conformers has been interpreted as a sign of the occurrence of phase transitions, in most cases from a liquid to a solid state.

Fig. 4 reports the absorption spectra in the interval between 600 and 1100 cm⁻¹ for DEMA-TfO, at room temperature and at the lowest measured T, compared with the absorption spectra calculated for all conformers using the different theoretical models, as previously described. In the experimental spectra, one can observe two intense absorption bands at 640 and 1030 cm⁻¹; the comparison with the computational results obtained for the isolated anion and cation and the previous literature indicate that they are due to anion vibrations. Additional lines are visible around 758, 780, 806, 833 and 883 cm⁻¹ for T = 320 K. Upon cooling (Fig. S4, ESI†) to around 250 K, the intensity of lines at 883, 833, 780 and 758 cm⁻¹ noticeably increases and they become significantly narrower, while the intensity of the line at 806 cm⁻¹ decreases. This abrupt modification of the spectrum is in agreement with the formation of a solid phase, i.e., with the occurrence of crystallization around 250 K. Moreover, on heating (Fig. S4, ESI†) to around 270 K, this trend reverses; the intensity of the line at 806 cm⁻¹ increases, while that of the line at 780 cm⁻¹ decreases. These features can clearly be assigned to the occurrence of a melting transition. At the same temperatures, one observes a clear splitting of the anion lines on cooling and a progressive broadening on heating, thus reinforcing the evidence of a solid–liquid phase transition. The strong reduction of the intensity of the line at 806 cm⁻¹ below 250 K is interpreted as evidence of the disappearance of one or more conformers below the solid phase transition.

Fig. 4 Comparison of the experimental spectra of DEMA-TfO measured at the highest and lowest temperature in the mid-infrared range with the calculations of different conformers of the ionic couples or single ions (for spectra calculated with single ions: black lines: TfO with a scaling factor of 1.03; blue, green, orange and red lines: DEMA conformers C1, C2, C3 and C4, respectively, with a scaling factor of 1.03).

Concerning the computational results, it appears from Fig. 4 that all models based on the B3LYP functional applied to the anion–cation couple fail to predict the correct frequency position of the intense absorption line experimentally found around 1040 cm⁻¹. The ωB97X-D-based models, in contrast, nicely reproduce the intense absorption lines found around 640 and 1040 cm⁻¹ in the experiments. However, all calculations based on ion pairs, both with the B3LYP and the ωB97X-D models, seem not adequate to reproduce the evolution of the lines between 700 and 900 cm⁻¹, which would need some conformer with the absorption line at 780 cm⁻¹ and another with a vibration frequency around 806 cm⁻¹, whose relative intensities can vary as a function of temperature. Indeed, the absorption spectra calculated for all conformers can almost be superimposed. In contrast, such details of the experimental spectra can be nicely explained considering the results of the calculations on single ions by means of the B3LYP functional, as largely reported in the literature. In this context, with reference to Fig. 4, in the frequency range between 600 and 1100 cm⁻¹, only three absorbance peaks are expected for the anion, and they likely correspond in the measured spectrum to the high intensity lines at 640 and 1020 cm⁻¹ and to the less intense line at 760 cm⁻¹. All the other observed absorptions are due to the cation conformers, and in particular between 770 and 900 cm⁻¹, where there is no signature from the anion, one can distinguish two lines, at 780 and 806 cm⁻¹, which can be respectively assigned to the C1 and C4 cation conformers.

The abrupt modification of the spectrum observed on cooling indicates the formation of a solid phase, inducing a drastic change in the concentration of the cation conformers (a strong increase of C1 conformer). On heating to around 270 K, this trend reverses; the intensity of the line attributed to C4 at 806 cm⁻¹ increases, while that of the line of the C1 conformer at 780 cm⁻¹ decreases. These features can clearly be assigned to the occurrence of the melting transition. Indeed, with this phase transition, a variation of the relative concentration of the different conformers is expected, in particular an increase of the lowest energy configuration in the solid state, as already observed in other ILs.^{16–20,36,37} More indications can be obtained by a quantitative analysis of the IR spectrum, which provides a detailed picture of the temperature evolution of the conformers in the sample.^{16,17,31,36–39}

In particular, the ratio of the intensities, r, of the lines attributable to the different conformers is proportional to their relative concentration:

where I_x indicates the integrated IR intensity of the band centered at wavenumber x^{16,17,30,35–37} after subtraction of a background. In the present case, it was calculated as:
It can be observed that in the liquid state, the relative concentration of the two conformers is expected to follow the Boltzmann law, which leads to the following van't Hoff relation:where ΔH and ΔS are the enthalpy and entropy difference between the two conformers and R is the universal gas constant. Upon entering the glass state, however, the distribution of the conformer population completely freezes and the quantity ln(r) does not depend on the temperature.^16–19,31 The intensity of the bands is obtained by fitting the absorbance spectrum in the frequency range between 740 and 900 cm⁻¹ with five Lorentzian peaks (see the inset in Fig. 5), and the plots of ln(r) vs. 1/T for the spectra measured in the liquid state both on cooling and on heating are reported in Fig. 5.

Fig. 5 Logarithm of the intensity ratio of the two DEMA conformer bands C1 and C4 as a function of temperature upon cooling (black points) and heating (red points) and best fit lines for both. In the inset, an example of the fit of the measured absorbance spectrum (black points) and its deconvolution (red line) into Gaussians (other colors) is reported.

The slope of the linear regression of ln(r) vs. 1/T provides the value of ΔH (Fig. 5). The ΔH values obtained for the liquid phase of DEMA-TfO are 3.1 ± 0.2 kJ mol⁻¹ for the cooling run and 3.4 ± 0.1 kJ mol⁻¹ on heating. These values are equivalent (within the errors) and are also comparable with the one obtained by DFT calculations (3.52 kJ mol⁻¹) (see Table S1, ESI†), further corroborating the hypothesized attribution of the lines. Moreover, both values are positive, in agreement with the increase of the C4 concentration with increasing temperature in the liquid phase.

The infrared spectrum measured between 600 and 4000 cm⁻¹ of the sample DEMA-MS presents several absorption peaks that, in agreement with what was previously observed for the TfO-based sample, can be compared with the calculated absorbance spectra of the anion and of the cation (C1 to C4) conformers. In particular, the spectral interval between 700 and 1100 cm⁻¹ contains the markers of the cation conformers, as presented in Fig. 6. Considering the B3LYP model on isolated ions, the anion presents two absorbance peaks that can be identified as the two intense absorptions at 770 and 1040 cm⁻¹. It is worth noting that the absorbance lines of these MS anion vibrations are red-shifted in frequency compared to the TfO anion. Indeed, all the other observed lines are due to the cation conformers, but, for DEMA-MS, because of their superposition with anion contributions, they cannot be univocally attributed to distinct conformers. On cooling, the absorbance peaks monotonously narrow and increase in intensity, without showing any abrupt modification, i.e., any sudden narrowing of lines and/or appearance of new lines, a behavior that would indicate the occurrence of crystallization. This smooth evolution resembles the one observed in other ILs,^16,17 which, for certain temperature rates, do not crystallize but undergo a glass transition behaving like an undercooled system. However, on heating (panel b in Fig. 6), one can notice that around 200 K, some lines (in particular the two at 840 and 880 cm⁻¹) expected to broaden and decrease in intensity upon increasing temperature, instead narrow and increase in intensity, suggesting the occurrence of cold crystallization. Moreover, upon further heating, the measured spectra between 280 and 300 K become drastically less structured with all lines abruptly broadening and lowering in intensity. This evolution points toward the occurrence of sample melting. Unfortunately, the lack of specific assignment for the lines to the various conformers prevents a quantitative analysis for DEMA-MS. It is worth noting that the occurrence of the so-called ‘‘cold crystallization’’ has been reported for many ionic liquids^17–20,36 and that this kind of transition corresponds to the transformation of a metastable phase, reached at low temperatures, towards the stable crystalline state.

Fig. 6 Experimental spectra of DEMA-MS between 700 and 1100 cm⁻¹ measured on cooling (panel a) and subsequent heating (panel b). In the lower part of each panel, the absorbance of the isolated anion and of the four lowest energy cation configurations calculated at the B3LYP/6-31G** level is reported. For the cation conformers, a frequency scaling factor of 1.03 was used, while a frequency scaling factor of 1.05 was applied for the MS anion.

Hydrogen bonding probed in the far-infrared region

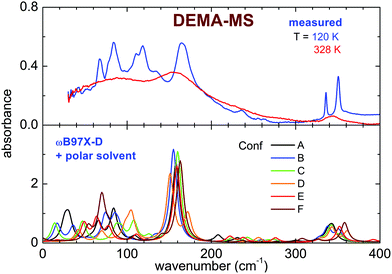
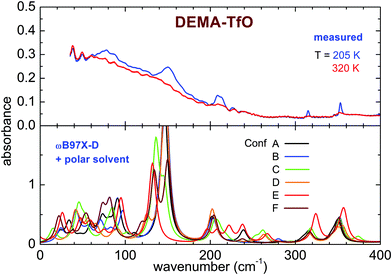
The far infrared spectra of both ILs measured around room temperature present broad peaks centered below 100 cm⁻¹ (80 cm⁻¹ for DEMA-MS and 60 cm⁻¹ for DEMA TfO) and broad shoulders, more visible for DEMA-MS, whose maxima are located above 100 cm⁻¹ (158 cm⁻¹ for DEMA-MS and ∼150 cm⁻¹ for DEMA-TFO). For DEMA-MS (see Fig. 7 for selected temperatures and Fig. S5, ESI† for additional temperatures), at lower temperatures, one can note several narrower additional contributions between 150 and 50 cm⁻¹, superimposed on the broader feature at 80 cm⁻¹. On heating from low temperature, one observes a change in line positions and shapes around 216 K, likely due to the cold crystallization discussed in the previous section, and, on further heating, the spectrum changes again around 274 K, i.e., the lines broaden and the narrow contributions below 100 cm⁻¹ disappear, in agreement with the occurrence of melting.

Fig. 7 Far infrared experimental spectra of DEMA-MS measured at the highest and lowest temperature (top) and calculated spectra for different conformers of the ionic couples obtained at the ωB97X-D/6-31G** level of theory with the inclusion of a polar solvent (bottom).

The spectrum of the DEMA-TfO sample at room temperature (Fig. 8) presents a large feature peaking around 60 cm⁻¹ with a shoulder at ∼150 cm⁻¹, which resembles that displayed by the MS-based sample at a slightly higher frequency. Moreover, the spectrum also displays another peak around 210 cm⁻¹, growing at low temperatures, which was assigned to an anion vibration by the previous literature. In contrast to what is observed for the MS sample, for the TfO-based sample, in this frequency range, one cannot observe additional vibrational modes below 100 cm⁻¹ at low temperature. However, the feature around 150 cm⁻¹ becomes much more defined and well evident at low temperature, especially below the crystallization temperature (see Fig. S5, ESI†).

Fig. 8 Far infrared experimental spectra of DEMA-TfO measured at the highest and lowest temperature (top) and calculated spectra for different conformers of the ionic couples obtained at the ωB97X-D/6-31G** level of theory with the inclusion of a polar solvent (bottom).

As previously discussed in the introduction, the far infrared modes probe mostly the intermolecular interactions. In particular, the two main features observed in the DEMA-MS and DEMA-TfO sample, i.e., the broad band around 80 (60) cm⁻¹ and the narrower peak around 158 (150) cm⁻¹, resemble the other previously observed PIL features and can be attributed to the dispersion forces and to the NH–anion interaction,^7–10 which is the typical hydrogen bond of this family of protic liquids. Indeed, this assignment has been suggested by previous combined FIR and computational studies on methylammonium-based protic ionic liquids having either MS or TfO as anion.^7–15,26,27 In particular, in the present work, the vibrational band assigned to the directional hydrogen bonding of NH–anion at room temperature (see Fig. 7 and 8) is detected for DEMA-MS at 158 cm⁻¹ and for DEMA-TfO at 150 cm⁻¹. This frequency shift, closely linked to the anion substitution, is in agreement with that previously observed also for triethylammonium methylsulfonate [(C₂H₅)₃NH][CH₃SO₃] (TEA-MS) and triethylammonium triflate [(C₂H₅)₃NH][CF₃SO₃] (TEA-TfO), where the same band is detected respectively at 149 and 129 cm⁻¹, and for trihexylammonium methylsulfonate [(C₆H₁₃)₃NH][CH₃SO₃] (THA-MS) and trihexylammonium triflate [(C₆H₁₃)₃NH][CF₃SO₃] (THA-TfO),^7–9 where the band is detected at 160 and 145 cm⁻¹, respectively. The replacement of the strong interacting MS anion with the weaker TfO is expected to weaken the hydrogen bonding interaction due to the fluorination of the methyl groups, thus inducing a shift to lower frequency and a superposition with the broad feature attributed to other intermolecular interactions. Moreover, the substitution of the TEA cation with the DEMA cation in PILs sharing the same anion (either MS or TfO) is expected to shift the hydrogen bonding peak to higher frequencies, similar to what has been observed when the TEA cation is replaced by the long chain THA cation, where the increase of the alkyl-chain length results in a potentially enhanced dispersion interaction with the “alkane-side” of the ammonium cation. Moreover, it has been suggested that the frequency shift of the intermolecular interaction peaks detected in the FIR range can be due to a strengthening of the interaction between ions as well as to the variation of the reduced mass.^7–10 In the presently measured samples, the modification induced by the anion substitution in the intermolecular interactions (between anion and cation) also gives rise to different phase transitions displayed by the two samples when measured at the same temperature rate.

The computational study of the conformers (see Fig. 7 and 8) of both DEMA-MS and DEMA-TfO by means of DFT theory at the ωB97X-D/6-31G** level with the inclusion of a polar solvent (dimethylformammide, ε_r = 37.22) suggests the presence of many low frequency contributions whose frequencies change with the particular considered conformer, and in particular an intense absorption peak centered around 160 (140) cm⁻¹ is predicted for all conformers of DEMA-MS (DEMA-TfO). It must be noted that all the models considered in the previous section provide evidence for the appearance of this latter peak, whenever the ionic couple is taken into account, i.e., the interaction between anion and cation. For these simulations, a visual inspection of the movements of the ions confirms that the low energy mode corresponds to the stretching modes of the NH–anion hydrogen bonding. Moreover, all calculations predict the red-shift of the hydrogen bonding peak in the IL containing the weaker interacting TfO anion, with respect to the stronger interaction with the MS anion.

A quantitative analysis of the temperature dependence of the FIR spectra can provide indications about the changes occurring in the intermolecular interactions and, in particular, in the hydrogen bonding involved in the different phases. To the best of our knowledge, only a few studies have investigated⁹ the competition between hydrogen bonding and dispersion forces as a function of the temperature. Here, similar to the analysis performed to evaluate the enthalpy difference between the two cation conformers, we estimate the difference in the average energy between the H-bonded and the dispersion-governed configurations.⁹ To perform such analysis, one has to properly deconvolute the observed absorbance; based on the model proposed by Fumino et al.,⁹ on the basis of the DFT calculated vibrations, we assign these vibrational bands to the bending and stretching modes of the NH–anion hydrogen bond superimposed on a vibrational band that describes the dispersion interactions between the SO₃ group and the alkyl chain of the anion and cation. In particular, according to their model, the broad absorption around 80 cm⁻¹ and the narrower peak at 160 cm⁻¹ can be deconvoluted in three contributions: one at higher frequency (around 140 cm⁻¹) corresponding to the stretching modes of the NH–anion hydrogen bonding, one around 70 cm⁻¹ corresponding to the bending modes of the NH–anion hydrogen bonding and a third contribution, with frequency ranging between these two, which corresponds to the dispersion-interaction contribution. This analysis was carried out for temperatures corresponding to the liquid phase of both samples.

The absorbance spectrum measured on heating in the frequency range between 40 and 250 cm⁻¹ was fitted with three Lorentzian curves for the DEMA-MS sample, while for the DEMA-TfO sample, a fourth Lorentzian peak was introduced to account for the anion feature detectable around 210 cm⁻¹, as already discussed from the comparison with the DFT results reported in Fig. 7 and 8.

The ratio between the intensities of the vibrational bands corresponding to the two configurations provides the equilibrium constants, whose temperature variation can be described by the van't Hoff relation (see eqn (2)). The slope of the linear regression of ln(r) vs. 1/T provides the value of the difference in energy between the H-bonded and the dispersion-governed configurations.

In particular, in agreement with the model used by Fumino et al.,⁹ we define:

For the DEMA-MS sample, we identified the band at 130 cm⁻¹ as due to the dispersion governed configuration, while the two peaks at 80 and 160 cm⁻¹ were attributed to the hydrogen bond configuration. Similarly, for the DEMA-TfO sample, we used the band at 120 cm⁻¹ for the dispersion governed configuration and the absorptions at 60 and 150 cm⁻¹ for the hydrogen bond configuration. The plots of ln(r) vs. 1/T, with 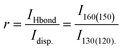, for the spectra measured in the liquid state of both samples are reported in Fig. 9.

Fig. 9 Logarithm of the intensity ratio of the bands due to the dispersion or hydrogen bonding governed configurations and best fit lines, as a function of temperature. The deconvolution of the absorbance spectrum is reported in the ESI† (Fig. S6 and S7).

The results obtained in these two cases appear very close. In particular, for both samples, the resulting van’t Hoff slope indicates that the H-bonded ion pairs are favored in energy over the dispersion-interaction, by about 8 kJ mol⁻¹ for the DEMA-TfO sample and 10 kJ mol⁻¹ for the MS-based sample. This result confirms that the NH–anion bond dominates at low temperatures, in agreement with previous analysis carried out on THA-TfO,⁹ even though the values obtained for the energy difference are lower in the presently investigated samples. It is worth noting that the MS-based sample displays a higher value for the difference in the average energy between the H-bonded and the dispersion-governed configurations, in agreement with the reinforcing of the hydrogen bonding interaction by the substitution of the TfO anion with the stronger MS, as previously displayed also by the comparison of the frequency of the vibrational band assigned to the directional hydrogen bonding of NH–anion.

Conclusions

The temperature dependence of the IR spectra of two prototypical PILs, diethylmethylammonium methanesulfonate and diethylmethylammonium trifluoromethanesulfonate, has been measured in the far- and mid-infrared range. The measurements indicate that DEMA-TfO undergoes a crystallization around 250 K, while DEMA-MS displays a cold crystallization on heating between 200 and 240 K. Both these transitions are detected by strong changes in the cation conformer distribution. For the attribution of vibrational lines of these conformers, single ion calculations at the B3LYP level are able to provide a good agreement with the experiments. In the far IR region, the bending and stretching modes of the strong hydrogen bond between NH of the cation and O of the anion are detected and their thermal analysis allows us to calculate the difference in energy between the hydrogen bonded configurations and the geometries governed by the dispersion forces. Calculations based on ionic couples, the ωB97X-D functional (including empirical dispersion corrections) and the presence of a polar or non-polar solvent could provide quantitative information about this hydrogen bond and the vibration frequencies observed in the far IR range. For all these simulations, the harmonic potential allows good agreement of the predicted vibrational modes with the measured spectra even in the lowest energy range, although in future simulations, one can expect higher accuracy when anharmonic effects are taken into account.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research leading to this result has been supported by the project CALIPSOplus under the Grant Agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON 2020 (Beamtime 20170928).

References

1. T. L. Greaves and J. Drummond, Chem. Rev., 2015, 115, 11379–11448.
2. N. Yaghini, J. Pitawala, A. Matic and A. Martinelli, J. Phys. Chem. B, 2015, 119, 1611–1622.
3. A. B. H. Susan, A. Noda, S. Mitsushima and M. Watanabe, Chem. Commun., 2003, 938–939.
4. R. D. Rogers and K. R. Seddon, Science, 2003, 302, 792–793.
5. M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629.
6. S.-Y. Lee, A. Ogawa, M. Kanno, H. Nakamoto, T. Yasuda and M. Watanabe, J. Am. Chem. Soc., 2010, 132, 9764–9773.
7. K. Fumino, V. Fossog, K. Wittler, R. Hempelmann and R. Ludwig, Angew. Chem., Int. Ed., 2013, 52, 2368–2372.
8. K. Fumino, E. Reichert, K. Wittler, R. Hempelmann and R. Ludwig, Angew. Chem., Int. Ed., 2012, 51, 6236–6240.
9. K. Fumino, V. Fossog, P. Stange, D. Paschek, R. Hempelmann and R. Ludwig, Angew. Chem., Int. Ed., 2015, 54, 2792–2795.
10. R. Ludwig, Phys. Chem. Chem. Phys., 2015, 17, 13790–13793.
11. S. B. C. Lehmann, M. Roatsch, M. Schöppke and B. Kirchner, Phys. Chem. Chem. Phys., 2010, 12, 7473–7486.
12. H. Watanabe, H. Doi, S. Saito, M. Matsugami, K. Fujii, R. Kanzaki, Y. Kameda and Y. Umebayashi, J. Mol. Liq., 2016, 217, 35–42.
13. K. Dong, S. Zhang, D. Wang and X. Yao, J. Phys. Chem. A, 2006, 110, 9775–9782.
14. K. Dong, S. Zhang and J. Wang, Chem. Commun., 2016, 52, 6744–6764.
15. V. H. Paschoal, L. F. O. Faria and M. C. C. Ribeiro, Chem. Rev., 2017, 117, 7053–7112.
16. O. Palumbo, F. Trequattrini, G. B. Appetecchi and A. Paolone, J. Phys. Chem. C, 2017, 121, 11129–11135.
17. O. Palumbo, F. Trequattrini, M. A. Navarra, J.-B. Brubach, P. Roy and A. Paolone, Phys. Chem. Chem. Phys., 2017, 19, 8322–8329.
18. F. Capitani, F. Trequattrini, O. Palumbo, A. Paolone and P. Postorino, J. Phys. Chem. B, 2016, 120, 2921–2928.
19. F. Capitani, S. Gatto, P. Postorino, O. Palumbo, F. Trequattrini, M. Deutsch, J.-B. Brubach, P. Roy and A. Paolone, J. Phys. Chem. B, 2019, 120, 1312–1318.
20. F. M. Vitucci, D. Manzo, M. A. Navarra, O. Palumbo, F. Trequattrini, S. Panero, P. Bruni, F. Croce and A. Paolone, J. Phys. Chem. C, 2014, 118, 5749–5755.
21. J. C. Lassègues, J. Grondin, R. Holomb and P. Johansson, J. Raman Spectrosc., 2007, 38, 551–558.
22. M. Thomas, M. Brehm, O. Hollóczki, Z. Kelemen, L. Nyulászi, T. Pasinszki and B. Kirchner, J. Chem. Phys., 2014, 141, 024510.
23. R. Cooper, A. M. Zolot, J. A. Boatz, D. P. Sporleder and J. A. Stearns, J. Phys. Chem. A, 2013, 117, 12419–12428.
24. F. Shi and Y. Deng, Spectrochim. Acta, Part A, 2005, 62, 239–244.
25. S. Le Caer, G. Klein, D. Ortiz, M. Lima, S. Devineau, S. Pin, J.-B. Brubach, P. Roy, S. Pommeret, W. Leibl, R. Righini and J. P. Renault, Phys. Chem. Chem. Phys., 2014, 16, 22841–22852.
26. K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2008, 47, 8731–8734.
27. K. Fumino, T. Peppel, M. Geppert-Rybczynska, D. H. Zaitsau, J. K. Lehmann, S. P. Verevkin, M. Köckerling and R. Ludwig, Phys. Chem. Chem. Phys., 2011, 13, 14064–14075.
28. M. Faye, M. Bordessoule, B. Kanouté, J. B. Brubach, P. Roy and L. Manceron, Rev. Sci. Instrum., 2016, 87, 063119.
29. Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. Gilbert, L. V. Slipchenko, S. V. Levchenko, D. P. O’Neill, R. A. DiStasio Jr., R. C. Lochan, T. Wang, G. J. Beran, N. A. Besley, J. M. Herbert, C. Y. Lin, T. Van Voorhis, S. H. Chien, A. Sodt, R. P. Steele, V. A. Rassolov, P. E. Maslen, P. P. Korambath, R. D. Adamson, B. Austin, J. Baker, E. F. Byrd, H. Dachsel, R. J. Doerksen, A. Dreuw, B. D. Dunietz, A. D. Dutoi, T. R. Furlani, S. R. Gwaltney, A. Heyden, S. Hirata, C. P. Hsu, G. Kedziora, R. Z. Khalliulin, P. Klunzinger, A. M. Lee, M. S. Lee, W. Liang, I. Lotan, N. Nair, B. Peters, E. I. Proynov, P. A. Pieniazek, Y. M. Rhee, J. Ritchie, E. Rosta, C. D. Sherrill, A. C. Simmonett, J. E. Subotnik, H. L. Woodcock 3rd, W. Zhang, A. T. Bell, A. K. Chakraborty, D. M. Chipman, F. J. Keil, A. Warshel, W. J. Hehre, H. F. Schaefer III, J. Kong, A. I. Krylov, P. M. Gill and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 3172–3191.
30. W. J. Hehre, A Guide to Molecular Mechanics and Quantum Chemical Calculations, Wavefunction, Inc., Irvine, CA, 2003.
31. O. Palumbo, F. M. Vitucci, F. Trequattrini and A. Paolone, Vib. Spectrosc., 2015, 80, 11–16.
32. N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372.
33. E. I. Izgorodina, Z. L. Seeger, D. L. A. Scarborough and S. Y. S. Tan, Chem. Rev., 2017, 117, 6696–6754.
34. G. Saielli, Adv. Theory Simul., 2018, 1, 1800084.
35. K. Karu, A. Ruzanov, H. Ers, V. Ivaništšev, I. Lage-Estebanez and J. M. García de la Vega, Computation, 2016, 4, 25.
36. O. Palumbo, F. Trequattrini, F. M. Vitucci, M. A. Navarra, S. Panero and A. Paolone, Adv. Condens. Matter Phys., 2015, 2015, 11.
37. M. Vitucci, F. Trequattrini, O. Palumbo, J.-B. Brubach, P. Roy and A. Paolone, J. Phys. Chem. A, 2014, 118, 8758–8764.
38. F. M. Vitucci, O. Palumbo, F. Trequattrini, J.-B. Brubach, P. Roy, I. Meschini, F. Croce and A. Paolone, J. Chem. Phys., 2015, 143, 094707.
39. A. Martinelli, A. Matic, P. Johansson, P. Jacobsson, L. Borjesson, A. Fernicola, S. Panero, B. Scrosati and H. Ohno, J. Raman Spectrosc., 2011, 42, 522–528.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp00907e

---