Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Order–disorder phase transition of the subsurface cation vacancy reconstruction on Fe3O4(001)†
Björn
Arndt
 ab,
Barbara A. J.
Lechner
ab,
Barbara A. J.
Lechner
 *c,
Alexander
Bourgund
c,
Elin
Grånäs
*c,
Alexander
Bourgund
c,
Elin
Grånäs
 a,
Marcus
Creutzburg
ab,
Konstantin
Krausert
ab,
Jan
Hulva
d,
Gareth S.
Parkinson
a,
Marcus
Creutzburg
ab,
Konstantin
Krausert
ab,
Jan
Hulva
d,
Gareth S.
Parkinson
 d,
Michael
Schmid
d,
Michael
Schmid
 d,
Vedran
Vonk
d,
Vedran
Vonk
 a,
Friedrich
Esch
a,
Friedrich
Esch
 c and
Andreas
Stierle
c and
Andreas
Stierle
 *a
*a
aDeutsches Elektronen-Synchrotron (DESY), D-22607 Hamburg, Germany. E-mail: andreas.stierle@desy.de
bUniversity of Hamburg, Physics Department, D-20355 Hamburg, Germany
cDepartment of Chemistry & Catalysis Research Center, Technical University of Munich, D-85748 Garching, Germany. E-mail: bajlechner@tum.de
dInstitute of Applied Physics, TU Wien, A-1040 Vienna, Austria
First published on 30th March 2020
Abstract
We present surface X-ray diffraction and fast scanning tunneling microscopy results to elucidate the nature of the surface phase transition on magnetite (001) from a 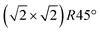 reconstructed to a non-reconstructed surface around 720 K. In situ surface X-ray diffraction at a temperature above the phase transition, at which long-range order is lost, gives evidence that the subsurface cation vacancy reconstruction still exists as a local structural motif, in line with the characteristics of a 2D second-order phase transition. Fast scanning tunneling microscopy results across the phase transition underpin the hypothesis that the reconstruction lifting is initiated by surplus Fe ions occupying subsurface octahedral vacancies. The reversible near-surface iron enrichment and reduction of the surface to stoichiometric composition is further confirmed by in situ low-energy ion scattering, as well as ultraviolet and X-ray photoemission results.
reconstructed to a non-reconstructed surface around 720 K. In situ surface X-ray diffraction at a temperature above the phase transition, at which long-range order is lost, gives evidence that the subsurface cation vacancy reconstruction still exists as a local structural motif, in line with the characteristics of a 2D second-order phase transition. Fast scanning tunneling microscopy results across the phase transition underpin the hypothesis that the reconstruction lifting is initiated by surplus Fe ions occupying subsurface octahedral vacancies. The reversible near-surface iron enrichment and reduction of the surface to stoichiometric composition is further confirmed by in situ low-energy ion scattering, as well as ultraviolet and X-ray photoemission results.
1 Introduction
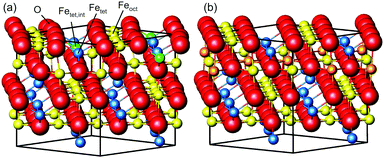
Magnetite is a material used in many different areas. Its electronic and magnetic properties make it a promising material for spintronics. Its magnetism and biocompatibility triggered development of magnetite nanoparticles for use in waste-water cleaning1 and application in cancer treatment.2,3 In addition, it is used as a catalyst for several different reactions, such as the high-temperature water–gas shift reaction.4,5 For hierarchical materials, magnetite in form of nanoparticles linked together by organic molecules as a first building block shows remarkable mechanical properties.6,7 Since these applications depend on surface properties such as adsorption sites, binding strength and geometries, which are closely related to the surface structure, determining and understanding the surface structure is vital to get an understanding of the surface properties and therefore of the parameters that determine the performance of the material.The surface structure of the (001) surface of magnetite, one of the predominant facets on nanoparticles,6 was studied extensively at room temperature. When prepared in ultra-high vacuum, it exhibits a 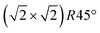 reconstruction based on a reordering of cations in the near-surface layers.8,9 Compared to a bulk-truncated surface, it contains one additional iron cation in a tetrahedral site of the second layer, and two octahedral vacancies in the third layer directly underneath.8,9 A perspective view of both the reconstructed surface and the bulk terminated surface is shown in Fig. 1. This surface was found to be stable over a large range of oxygen chemical potentials.8 Many of the aforementioned applications, however, require temperatures above room temperature. One obvious example is the high-temperature water–gas shift reaction, which is performed at temperatures between 620 and 720 K. But also the synthesis and pre-processing of the material is often done at elevated temperatures – such as the interlinking of organic molecules for the formation of hierarchical materials, which requires heating to temperatures up to 620 K.6 Iron cations are relatively mobile in magnetite, which can lead to incorporation of metal adatoms into the lattice at elevated temperatures10 or even the growth of new layers or etching into the surface in the vicinity of nanoparticles.11 On the clean surface, it is known that the
reconstruction based on a reordering of cations in the near-surface layers.8,9 Compared to a bulk-truncated surface, it contains one additional iron cation in a tetrahedral site of the second layer, and two octahedral vacancies in the third layer directly underneath.8,9 A perspective view of both the reconstructed surface and the bulk terminated surface is shown in Fig. 1. This surface was found to be stable over a large range of oxygen chemical potentials.8 Many of the aforementioned applications, however, require temperatures above room temperature. One obvious example is the high-temperature water–gas shift reaction, which is performed at temperatures between 620 and 720 K. But also the synthesis and pre-processing of the material is often done at elevated temperatures – such as the interlinking of organic molecules for the formation of hierarchical materials, which requires heating to temperatures up to 620 K.6 Iron cations are relatively mobile in magnetite, which can lead to incorporation of metal adatoms into the lattice at elevated temperatures10 or even the growth of new layers or etching into the surface in the vicinity of nanoparticles.11 On the clean surface, it is known that the 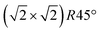 reconstruction present at room temperature is reversibly lifted at temperatures around 720 K.12 An earlier study based on low-energy electron diffraction experiments12 identified the origin of the lifting process as an order–disorder phase transition. The continuous transition was observed to be second-order Ising-like with a gradual loss of long-range order but persisting short-range order above the transition temperature. The structural interpretation of this transition, however, was based on a previously proposed model of a bulk-truncated magnetite surface,13 and no quantitative structural analysis was performed.
reconstruction present at room temperature is reversibly lifted at temperatures around 720 K.12 An earlier study based on low-energy electron diffraction experiments12 identified the origin of the lifting process as an order–disorder phase transition. The continuous transition was observed to be second-order Ising-like with a gradual loss of long-range order but persisting short-range order above the transition temperature. The structural interpretation of this transition, however, was based on a previously proposed model of a bulk-truncated magnetite surface,13 and no quantitative structural analysis was performed.
In this study, we investigate the crystallographic and electronic structure of the magnetite (001) surface at elevated temperatures by a combination of surface X-ray diffraction (SXRD), fast in situ scanning tunneling microscopy (STM), X-ray and ultraviolet photoemission spectroscopy (XPS, UPS) and low-energy ion scattering (LEIS). We followed the transition from a long-range ordered 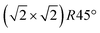 reconstructed surface at room temperature to a (1 × 1) surface at elevated temperatures. We interpret our results in view of the subsurface cation vacancy reconstruction (SCV) structural model for this surface,8 and provide a quantitative analysis of the surface structure at elevated temperatures above the phase transition temperature.
reconstructed surface at room temperature to a (1 × 1) surface at elevated temperatures. We interpret our results in view of the subsurface cation vacancy reconstruction (SCV) structural model for this surface,8 and provide a quantitative analysis of the surface structure at elevated temperatures above the phase transition temperature.
2 Experimental details
The surface of magnetite single crystals was cut and mechanically polished to exhibit the (001) surface with a miscut below 0.2°. Three different crystals were used for the SXRD, STM and XPS, LEIS and UPS experiments, respectively. Note that the exact phase transition temperature varies slightly between crystals, as reported previously.12 In each experiment, the crystal was cleaned in ultra-high vacuum with a base pressure of 10−10 mbar by multiple cycles of sputtering with 1 keV Ar-ions for 15 minutes and subsequent annealing. For the SXRD experiments, the annealing temperature of 920 K was held for 15 minutes, with the last annealing step performed in 5 × 10−6 mbar of oxygen; for the scanning tunneling microscopy (STM) experiments, 20 minutes annealing at 983 K was chosen, with the last annealing step in 1 × 10−6 mbar oxygen. This resulted in a contamination-free,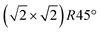 reconstructed surface.
reconstructed surface.
We carried out surface X-ray diffraction (SXRD) experiments at the ID03 beamline of the ESRF14 at a photon energy of 14 keV using a 2D detector in stationary mode15 at grazing incidence. The momentum transfer is given in relative reciprocal lattice coordinates (H, K, L) in units of 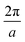 with a magnetite lattice constant of a = 8.394 Å. A set of crystal truncation rod data was taken from the clean surface. The sample was subsequently heated in several steps, and the surface structure was probed in each step by scanning through the (2,1) superstructure rod at L = 1.6 after waiting ∼15 minutes for the temperature to stabilize. This was done until no further changes were observed which was the case at 770 K. This point in reciprocal space [(1/2, 3/2) with respect to the unreconstructed 5.93 Å surface unit cell] was chosen because it lies on a surface rod only arising from the
with a magnetite lattice constant of a = 8.394 Å. A set of crystal truncation rod data was taken from the clean surface. The sample was subsequently heated in several steps, and the surface structure was probed in each step by scanning through the (2,1) superstructure rod at L = 1.6 after waiting ∼15 minutes for the temperature to stabilize. This was done until no further changes were observed which was the case at 770 K. This point in reciprocal space [(1/2, 3/2) with respect to the unreconstructed 5.93 Å surface unit cell] was chosen because it lies on a surface rod only arising from the 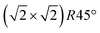 reconstruction, and is therefore only sensitive to this superstructure and not to the bulk-like structure of the subsurface region underneath. At 770 K, another set of crystal truncation rods was measured, and the surface was cooled down using the same steps, again probing the (2,1,1.6) peak at each temperature step. The SXRD data was analyzed using the ANAROD program package.16 The intensities of the Bragg peaks from the 3D bulk lattice do not contain surface structural information and are therefore not included in the surface structural analysis.
reconstruction, and is therefore only sensitive to this superstructure and not to the bulk-like structure of the subsurface region underneath. At 770 K, another set of crystal truncation rods was measured, and the surface was cooled down using the same steps, again probing the (2,1,1.6) peak at each temperature step. The SXRD data was analyzed using the ANAROD program package.16 The intensities of the Bragg peaks from the 3D bulk lattice do not contain surface structural information and are therefore not included in the surface structural analysis.
The STM experiments were performed using an Omicron variable-temperature (VT) instrument complemented with a FAST electronics module17,18 which enables the recording of movies at up to 20 frames per second (fps). A low defect density and large, atomically flat terraces were confirmed by STM and long-range order by low-energy electron diffraction (LEED) before commencing experiments. A boron nitride heater in the sample holder was used to heat the sample and a K-type thermocouple directly attached to the crystal and internally referenced to the chamber temperature was used to record the temperature. Temperature-dependent LEED measurements confirmed that our temperature reading is calibrated well and the phase transition temperature of this magnetite crystal is around 725 K, in agreement with previous reports12 (see ESI†). In so-called FastSTM measurements, the feedback gain was lowered to only correct for thermal drift but not follow the surface topography. A sinusoidal tip movement in the fast scan direction was employed, resulting in images and movies which exhibit a higher pixel density at the left and right edges. FastSTM data were recorded as a one-dimensional data stream which was subsequently Fourier filtered to remove known interference frequencies (e.g. from turbomolecular pumps), background leveled by FFT filtering of the fast and slow scan directions and their overtones, and reconstructed into movies using a specially built Python script. The resulting movies were then further processed and analyzed in ImageJ.19 The images were corrected for linear and nonlinear distortions based on (1 × 1) spots in the Fourier transform, similar to the process described in ref. 20. Thermal drift was corrected for by laterally shifting frames with respect to each other in time. The frames of drift-corrected movies could then be averaged to a noise level that is vastly superior compared to standard (slow) STM images: subtle structural details with little corrugation which are typically drowned by highly diffusive transient species can thus be recovered as long as the time window for averaging is appropriate. The averaged frames could further be Fourier transformed to provide a comparison with reciprocal-space measurements and give a clear indication whether the 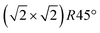 reconstruction was still observable in the images. When reconstruction spots were absent in this FFT, we also examined the average of the Fourier transforms of the individual frames, to ensure that the reconstruction spots are not missing due to rapidly moving domains, which could cause the reconstruction to disappear in the average of the real-space images. Finally, we extracted image lines and rows from the drift-corrected movies and plotted them versus time to investigate contrast changes along and across the Fe rows.
reconstruction was still observable in the images. When reconstruction spots were absent in this FFT, we also examined the average of the Fourier transforms of the individual frames, to ensure that the reconstruction spots are not missing due to rapidly moving domains, which could cause the reconstruction to disappear in the average of the real-space images. Finally, we extracted image lines and rows from the drift-corrected movies and plotted them versus time to investigate contrast changes along and across the Fe rows.
Ultraviolet and X-ray photoelectron spectroscopy (UPS, XPS), low-energy ion scattering (LEIS), and LEED experiments were performed in a UHV system described in detail in ref. 21. A SPECS FOCUS 500 monochromatized X-ray source (Al Kα anode) was used for XPS. UPS was performed using a SPECS UVS 10/35 source emitting either He I or He II radiation, and LEIS utilized 1 keV He+ ions generated by a SPECS IQE 12/38 ion source with a scattering angle of 90°. The same SPECS PHOIBOS 150 energy analyzer was used for all these measurements. The XPS measurements were performed at a grazing emission angle (80° with respect to the surface normal) for maximum surface sensitivity. The LEED measurements were performed using a commercial rear-view LEED optics. The sample used in these experiments was prepared by Ne+ sputtering (1 keV) for 10 minutes followed by annealing at 950 K. Every other annealing step and the last before an experiment was performed in 5 × 10−7 mbar O2.
3 Results and discussion
3.1 SXRD results
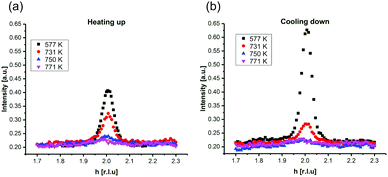
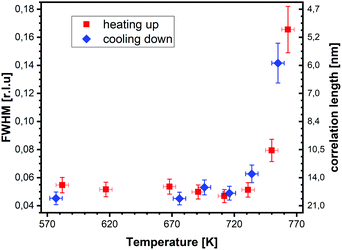
In Fig. 2, SXRD scans through the (2,1) surface rod only sensitive to the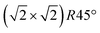 superstructure at different temperatures are shown both during heating up (a) and cooling back down (b) to room temperature. Below 570 K, no changes were visible. Above this temperature, a decrease of the peak intensity of the reconstruction signal is observed. At a temperature of 750 K, the reconstruction peak vanished almost completely, and no further changes could be observed when increasing the temperature to 770 K. When cooling back down, the superstructure signal reappeared. Due to the realignment that was necessary during the heating, the intensities had to be scaled. For this, the background level was used as a reference. Since this level is not absolute and expected to increase due to an increase in thermal diffuse scattering during heating and can also change with the alignment, the absolute intensities cannot be compared directly. The differences stemming from this, however, are rather small and do not fully explain the observed increase in intensity on the superstructure signal during cooling down compared to that during heating up at the same temperature. This is most likely related to desorption of adsorbates during the time the sample was kept at elevated temperatures and slight re-annealing after cooling back down. Next we will discuss the full width at half maximum (FWHM) values extracted from these scans, which can be converted into the lateral correlation length Lc of the surface via
superstructure at different temperatures are shown both during heating up (a) and cooling back down (b) to room temperature. Below 570 K, no changes were visible. Above this temperature, a decrease of the peak intensity of the reconstruction signal is observed. At a temperature of 750 K, the reconstruction peak vanished almost completely, and no further changes could be observed when increasing the temperature to 770 K. When cooling back down, the superstructure signal reappeared. Due to the realignment that was necessary during the heating, the intensities had to be scaled. For this, the background level was used as a reference. Since this level is not absolute and expected to increase due to an increase in thermal diffuse scattering during heating and can also change with the alignment, the absolute intensities cannot be compared directly. The differences stemming from this, however, are rather small and do not fully explain the observed increase in intensity on the superstructure signal during cooling down compared to that during heating up at the same temperature. This is most likely related to desorption of adsorbates during the time the sample was kept at elevated temperatures and slight re-annealing after cooling back down. Next we will discuss the full width at half maximum (FWHM) values extracted from these scans, which can be converted into the lateral correlation length Lc of the surface via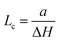 ,22 with magnetite bulk lattice constant a and ΔH the full width at half maximum of the H scans (Fig. 3). In both the crystals used for the present SXRD experiments and in the previous experiments mentioned above,12 the onset temperature of the lifting process is around 720 K, and the lateral correlation length Lc is gradually decreasing up to a temperature of 770 K, where the intensity becomes too low to determine the FWHM. Overall, these measurements agree very well with the order–disorder phase transition that was found for this surface in an earlier study,12 as does the temperature range in which the transition occurs.
,22 with magnetite bulk lattice constant a and ΔH the full width at half maximum of the H scans (Fig. 3). In both the crystals used for the present SXRD experiments and in the previous experiments mentioned above,12 the onset temperature of the lifting process is around 720 K, and the lateral correlation length Lc is gradually decreasing up to a temperature of 770 K, where the intensity becomes too low to determine the FWHM. Overall, these measurements agree very well with the order–disorder phase transition that was found for this surface in an earlier study,12 as does the temperature range in which the transition occurs.
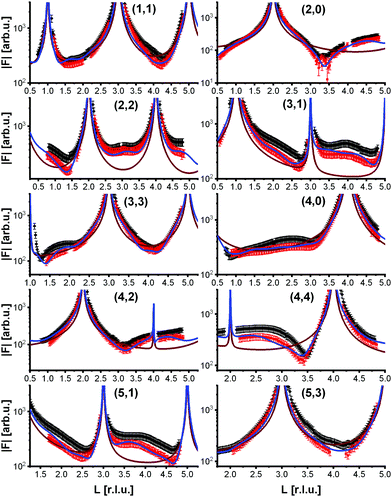
To analyze the surface structure in more detail, crystal truncation rods were measured at room temperature and at 770 K, shown in Fig. 4. They demonstrate that the phase transition is not simply a lifting of the reconstruction. The crystal truncation rods at room temperature fit very well to those of the reconstructed surface.9 But although the superstructure signal from the reconstruction vanishes at 770 K, the crystal truncation rods at this temperature are fairly similar to those of the reconstructed surface, and show a huge difference to those expected from a bulk-truncated surface23 (also shown in Fig. 4). This allows us to hypothesize that locally the structure of the reconstruction is still partially intact, i.e., the layer occupations (additional Fe in the first tetrahedral layer, missing Fe in the subsurface octahedral layer) do not substantially change, although the long-range  order is lost. The absence of the superstructure order does not influence the signal on the crystal truncation rods since they are only sensitive to the smaller periodicity of the bulk crystal lattice and not to the larger one of the superstructure.
order is lost. The absence of the superstructure order does not influence the signal on the crystal truncation rods since they are only sensitive to the smaller periodicity of the bulk crystal lattice and not to the larger one of the superstructure.
To get more insights into the structural arrangement of the Fe cations, different models were fitted to the SXRD data, and the reduced χ2, also called goodness of fit, was used to check and compare the level of agreement between fit and data. As expected, a bulk-truncated surface shows a bad agreement with the data (χred2 = 5.66). A reconstructed surface shows a better, but still suboptimal agreement (χred2 = 3.88). To improve the agreement, the possibility that not all lattice sites were fully occupied or unoccupied had to be taken into account. This possibility was included in the models by introducing occupation parameters for several iron lattice positions. In the first double layer, occupation parameters were introduced for the tetrahedral iron positions that are normally fully occupied in both the bulk truncated and the reconstructed surface (Fetet), for the additional tetrahedral site that is occupied in the reconstructed surface but unoccupied in the bulk-truncated structure (Fetet,int) and for the tetrahedral site that is equivalent to this one under bulk symmetry, but usually not occupied in either structure (Fetet,add). In the second double layer, occupation parameters were introduced for the octahedral lattice sites that are vacant in the reconstructed surface but occupied in the bulk-truncated structure (Feoct,vac; orange in Fig. 1(b)), and the octahedral lattice sites that are occupied in both structures (Feoct). Occupation parameters for octahedral and tetrahedral interstitial cation sites adjacent to regular lattice sites were tested, but not found to have any significant impact on the fits and therefore omitted in the final fitting. In addition, the positions of all iron atoms in the uppermost unit cell were fitted, only allowing distortions according to the symmetry of the 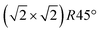 reconstruction. Fitting of the oxygen atom positions did not further improve the fit, which is related to their lower X-ray diffraction atomic form factor, as compared to Fe. An overview of the fit result is shown in Table 1.
reconstruction. Fitting of the oxygen atom positions did not further improve the fit, which is related to their lower X-ray diffraction atomic form factor, as compared to Fe. An overview of the fit result is shown in Table 1.
| Model | χ red 2 | Positions | Occupancies | |||||
|---|---|---|---|---|---|---|---|---|
| Fe | O | Fetet | Fetet,int | Fetet,add | Feoct | Feoct,vac | ||
| 1 | 2.78 | — | — | 0.90 | 0.45 | 0.34 | 0.70 | 0.85 |
| 2 | 0.73 | + | — | 0.86 | 0.62 | 0.05 | 0.80 | 0.58 |
These fits show that, at elevated temperatures, the additional tetrahedral iron position becomes partially depleted, and the octahedral vacant sites underneath are partially filled, in good agreement with the STM data which we will discuss below. This is accompanied by a partial depletion of the regular tetrahedral lattice sites in the first double layer and the octahedral sites in the second one that are occupied in both the bulk-truncated and the reconstructed surface, and slight distortions of the lattice of up to 0.1 Å in the first layer and 0.06 Å in the second layer. This change in site occupations rules out a loss of long-range order diffraction signal simply due to an increase in thermal vibrations, especially since the Debye–Waller-factor values of the surface atoms did not increase significantly when included in the fitting. Together with the fact that the local structure seems rather unchanged, this observation points towards a statistical reorganization by diffusion at the surface mainly of the additional tetrahedral iron atoms through the octahedral vacant sites underneath as the source for the lifting of the reconstruction. The reorganization leads to a fluctuating occupation of lattice sites, lattice distortions and an increase in the concentration of defects at the surface like anti-phase domain boundaries and interstitial subsurface cations.24,25
At high temperature, the occupation of the sites deviates too much from that of the ideal SCV reconstruction, thus the long-range order is lost. Nevertheless, the site occupations are not too far from that of the SCV model, in line with the reported surface diagram from theoretical calculations8 which shows that the reconstruction should indeed be stable at 770 K under all O2 partial pressures that can be attained in a UHV system. In addition, regular cation lattice sites are also found to be involved in the near surface diffusion process, as can be concluded from the reduced Feoct and Fetet occupancies at the surface, providing vacancies available for hopping events.
3.2 FastSTM results
Having determined from SXRD the average atomic surface structure, the question arises how the structure evolves locally in real space and whether the change in occupations is static or dynamic. Looking at FastSTM movies at and around the phase transition, several structural features can still be resolved. While standard STM images (in particular in constant-current mode) are dominated by streaks from fast moving species, averaging many consecutive FastSTM frames preserves atomic resolution. Fig. 5 shows the average of several hundred frames each at the onset of the phase transition at 701 K (a), right in the middle at 745 K (b), and beyond at 784 K (c) (cf. ESI† for a temperature calibration by LEED). At the onset, the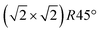 reconstruction can still be clearly observed with atomic resolution.8 An FFT of the average frame at this temperature confirms that the reconstruction spots are fairly sharp and clearly visible (circled in red). Furthermore, by marking the same location in each unit cell with a yellow dot, we can unambiguously assign domains on the surface. The domain boundaries between them are increasingly mobile at elevated temperatures. FastSTM Movie S1 (ESI†) shows that at this temperature, the domain boundaries move rapidly back and forth around an average location but do not move extended distances across the surface. As a result, they appear as smeared-out bright regions that zigzag across the surface in the average frame. One example is marked in the average frame by yellow dashed lines, as a guide to the eye. Comparing the average domain size in Fig. 5(a) with the correlation length from SXRD (Fig. 3), we find good agreement: the FastSTM movie reveals typical domain sizes in the range from 5 to 25 nm. In the middle of the phase transition (745 K), such structures were more difficult to distinguish, as can be seen in Fig. 5(b). A smaller surface area was scanned here which is entirely covered in a single domain, as indicated by the overlaid yellow dots. Perhaps surprisingly, even though the reconstruction spots lost more than half of their intensity in LEED at this temperature (see Fig. S1, ESI†), they are still clearly visible in the FFT of the averaged frame (red circles). Finally, at a temperature just beyond the phase transition, the FFT of drift-corrected and averaged frames does not show any
reconstruction can still be clearly observed with atomic resolution.8 An FFT of the average frame at this temperature confirms that the reconstruction spots are fairly sharp and clearly visible (circled in red). Furthermore, by marking the same location in each unit cell with a yellow dot, we can unambiguously assign domains on the surface. The domain boundaries between them are increasingly mobile at elevated temperatures. FastSTM Movie S1 (ESI†) shows that at this temperature, the domain boundaries move rapidly back and forth around an average location but do not move extended distances across the surface. As a result, they appear as smeared-out bright regions that zigzag across the surface in the average frame. One example is marked in the average frame by yellow dashed lines, as a guide to the eye. Comparing the average domain size in Fig. 5(a) with the correlation length from SXRD (Fig. 3), we find good agreement: the FastSTM movie reveals typical domain sizes in the range from 5 to 25 nm. In the middle of the phase transition (745 K), such structures were more difficult to distinguish, as can be seen in Fig. 5(b). A smaller surface area was scanned here which is entirely covered in a single domain, as indicated by the overlaid yellow dots. Perhaps surprisingly, even though the reconstruction spots lost more than half of their intensity in LEED at this temperature (see Fig. S1, ESI†), they are still clearly visible in the FFT of the averaged frame (red circles). Finally, at a temperature just beyond the phase transition, the FFT of drift-corrected and averaged frames does not show any 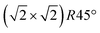 reconstruction spots anymore and there is also no sign of the reconstruction in the real-space images (see Fig. 5(c)). The STM data are thus consistent with the picture that a long-range SCV reconstruction is no longer present at this temperature.
reconstruction spots anymore and there is also no sign of the reconstruction in the real-space images (see Fig. 5(c)). The STM data are thus consistent with the picture that a long-range SCV reconstruction is no longer present at this temperature.
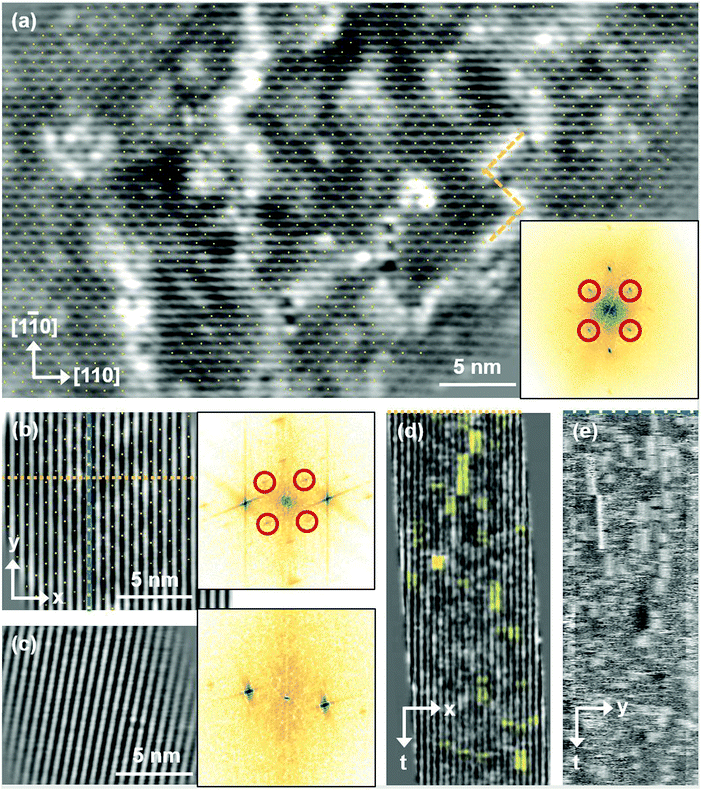 | ||
Fig. 5 FastSTM data of Fe3O4(001). Average of movie frames (a) at the onset of the phase transition (701 K, Vb = 1.5 V, It = 0.9 nA, 4 fps, 520 frames), (b) in the middle of the phase transition (745 K, Vb = 1.3 V, It = 1.0 nA, 11.7 fps, 706 frames), and (c) beyond the phase transition (784 K, Vb = 1.5 V, It = 1.0 nA, 11.7 fps, 818 frames). Full movies see Movies S1–S3 (ESI†). In (a), the periodicity of the  reconstruction is indicated by yellow dots. Dashed yellow lines indicate an example of a domain boundary, i.e. where the dots do not align. In (b), a single domain is visible (yellow dots), while in (c) the reconstruction is no longer apparent. The insets show the FFT of the respective averaged frames, clearly indicating reconstruction spots in (a) and (b) (circled in red), while they are no longer present in (c). Frames (d) and (e) show a line in the x- and y-directions of the movie at 745 K vs. time, cut at the locations marked by the yellow dotted and blue dashed lines in (b), respectively. The time axis spans 60 s. Some example features which extend across two Fe rows are highlighted in yellow in (d). reconstruction is indicated by yellow dots. Dashed yellow lines indicate an example of a domain boundary, i.e. where the dots do not align. In (b), a single domain is visible (yellow dots), while in (c) the reconstruction is no longer apparent. The insets show the FFT of the respective averaged frames, clearly indicating reconstruction spots in (a) and (b) (circled in red), while they are no longer present in (c). Frames (d) and (e) show a line in the x- and y-directions of the movie at 745 K vs. time, cut at the locations marked by the yellow dotted and blue dashed lines in (b), respectively. The time axis spans 60 s. Some example features which extend across two Fe rows are highlighted in yellow in (d). | ||
Looking at the FastSTM movies, it is clear that the surface is anything but static at such elevated temperatures. At the onset of the phase transition, in Movie S1 (ESI†), defects and domain boundaries are mobile but their dynamics can still be resolved reasonably well. One obvious type of defect appears as bright squares spanning two adjacent Feoct rows. Just 44 K higher, in Movie S2 (ESI†), the dynamics resemble more closely fluctuations in apparent brightness than discrete hops. However, a more detailed analysis of the movie reveals that mobile species are similar as at 701 K. To better understand which features might be the mobile ones, it is useful to look at temporal changes in a single row or column of a FastSTM movie. Although not immediately obvious in the movie, we thus find that the same type of bright squares spanning two adjacent Fe rows is still present at 745 K, as shown by the x–t scan (“kymograph”) in Fig. 5(d), in which it often appears that two adjacent rows appear bright at the same time (marked in yellow to guide the eye). In addition, we observe many fluctuation-like local changes of the apparent height without a correlation between neighboring rows, which we attribute to a change in local electron density. An increase in brightness on an Fe row typically results from a local surplus of Fe in the surface or subsurface: one example thereof are antiphase domain boundaries, which are Fe rich, and which appear bright in STM. In an antiphase domain boundary, four Fe atoms can align in the subsurface where domain boundaries occur, resulting in elongated bright features which are arranged diagonally with respect to the surface octahedral Fe rows [see Fig. 5(a)].25 Unreconstructed unit cells are a different type of local defects, where an additional Fe atom in an octahedral site in the third layer causes the Fe atom in the tetrahedral site in the second layer to move into another octahedral site,23 thus resulting in six adjacent Fe atoms in a subsurface Feoct row. Then, at the surface, two elongated bright features appear on neighboring Fe rows.25 Additionally, cation interstitials in octahedral sites in the subsurface appear as bright spots on an Fe row which has been shown recently for Ni interstitials.26 By comparing these known defects with the signatures obtained in the time evolution of a horizontal slice across the Fe rows (Fig. 5(d)), the bright features extending across two Fe rows most likely indicate that unreconstructed unit cells are present on the surface, in line with the statistically increased occupancy of the Feoct,vac sites of 0.58, as found by SXRD. In addition, many bright species that do not extend across two rows are also visible which could be due to the presence of impurity cations.
Looking instead at the time evolution of the brightness along a surface Feoct row, shown in Fig. 5(e), it becomes clear that the residence times of bright features (both those in a single row and those spanning two rows) vary between one and many frames. Since the entire movie spans a time of 60 s, this corresponds to residence times between 0.08 and 8 s. In addition to the bright features, we occasionally observe dark (vacancy-like) features usually spanning two adjacent Feoct rows, one of them appearing as a dark line in Fig. 5(e); the rows adjacent to them appear brighter (see ESI,† Fig. S2). For the STM movie taken above the phase transition (784 K), a kymograph similar to Fig. 5(d) shows only horizontal streaks (not shown), indicating that most of the bright features remain stationary for a very short time (less than the interval between the frames, 0.1 seconds). Nevertheless, when viewing the movie (see Movie S3, ESI†), one can see several isolated bright species diffusing at the surface. The bright features spanning two adjacent Feoct rows are very rare, possibly only a random arrangement of isolated species. The only features remaining stationary for a somewhat longer times (up to 3 s) are the vacancy-like dark spots spanning two adjacent rows, mentioned earlier.
3.3 XPS and LEIS results
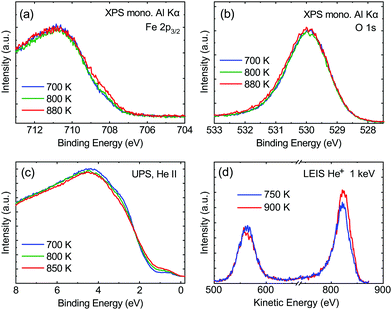
From the SXRD data analysis at 773 K, we obtain an Fe enrichment of ∼10% in the topmost layers. This would by necessity lead to an appearance of more reduced Fe cations. Fig. 6(a and b) show grazing-emission XPS data for the Fe 2p and O 1s regions, respectively. The shoulder at 708.5 eV due to Fe2+ increases over the transition, consistent with the reduction of Fe at the surface. The O 1s peak does not change visibly over the same temperature range. A similar conclusion can be drawn from UPS experiments shown in Fig. 6(c), where the increase in the Fe2+-related states at approximately 1 eV occurs at the same time as a decrease in the intensity of the Fe3+-related states at 3 eV. The LEIS data shown in Fig. 6(d) reveal that the peaks from Fe and O change in relative intensity over the transition. The increase in the Fe signal is consistent with the interpretation that the (1 × 1) surface is enriched in Fe. In reference LEED experiments, shown in Fig. S3 (ESI†), we confirmed that the lifting of the reconstruction occurs in the same temperature range on this sample as for the crystals used in the SXRD and STM experiments.4 Conclusions
In conclusion, we demonstrated that the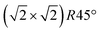 reconstruction of the magnetite (001) surface undergoes a continuous order–disorder phase transition, during which its long-range order gets lost when reaching the transition temperature. The analysis of the crystal truncation rod data gives evidence that the main structural motif of the
reconstruction of the magnetite (001) surface undergoes a continuous order–disorder phase transition, during which its long-range order gets lost when reaching the transition temperature. The analysis of the crystal truncation rod data gives evidence that the main structural motif of the 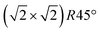 reconstruction, namely the existence of subsurface octahedral vacancy pairs and surface tetrahedral interstitials, is also present on a local scale above the phase transition temperature under ultra-high vacuum conditions. This demonstrates that the local structural motif of the subsurface cation vacancy reconstruction is an intrinsic defect of the magnetite (001) surface even at elevated temperatures. The continuous nature of the phase transition is also reflected by the FastSTM results, giving evidence that the long-range order of the
reconstruction, namely the existence of subsurface octahedral vacancy pairs and surface tetrahedral interstitials, is also present on a local scale above the phase transition temperature under ultra-high vacuum conditions. This demonstrates that the local structural motif of the subsurface cation vacancy reconstruction is an intrinsic defect of the magnetite (001) surface even at elevated temperatures. The continuous nature of the phase transition is also reflected by the FastSTM results, giving evidence that the long-range order of the 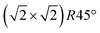 reconstruction on magnetite (001) is lifted by the more and more frequent occurrence of local defect structures across the phase transition with increasing temperature. The observed cation defect dynamics can have an important impact on the reactivity of magnetite surfaces at elevated temperatures, since they lead to a dynamically evolving surface with heterogeneous adsorption sites. This can be of special importance for the high-temperature water gas shift reaction, involving continuous reduction and oxidation. Similar surface phenomena are expected to occur on the whole class of spinel-based materials with a comparable cation sublattice.
reconstruction on magnetite (001) is lifted by the more and more frequent occurrence of local defect structures across the phase transition with increasing temperature. The observed cation defect dynamics can have an important impact on the reactivity of magnetite surfaces at elevated temperatures, since they lead to a dynamically evolving surface with heterogeneous adsorption sites. This can be of special importance for the high-temperature water gas shift reaction, involving continuous reduction and oxidation. Similar surface phenomena are expected to occur on the whole class of spinel-based materials with a comparable cation sublattice.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Projektnummer 192346071 SFB 986 for the SXRD work and ES 349/1-2 and HE 3454/18-2 for the STM work. FastSTM was developed with funds from the EU-H2020 Research and Innovation Programme under grant agreement no. 654360 NFFA-Europe. B. A. J. L. gratefully acknowledges a Marie Skłodowska-Curie Individual Fellowship under grant ClusterDynamics (no. 703972) from the European Union Horizon 2020 research and innovation program and financial support from the Young Academy of the Bavarian Academy of Sciences and Humanities. The authors at TUM acknowledge Sebastian Kaiser and Ke Zhang for help with the LEED measurements. J. H. and G. S. P. acknowledge funding from the Austrian Science Fund (FWF) START prize Y847-N20. We acknowledge excellent support by the ID03 beamline staff during our SXRD experiment at the ESRF.References
- M. Hua, S. Zhang, B. Pan, W. Zhang, L. Lv and Q. Zhang, J. Hazard. Mater., 2012, 211–212, 317–331 CrossRef CAS PubMed.
- T. K. Jain, M. A. Morales, S. K. Sahoo, D. L. Leslie-Pelecky and V. Labhasetwar, Mol. Pharmaceutics, 2005, 2, 194–205 CrossRef CAS PubMed.
- F. Dilnawaz, A. Singh, C. Mohanty and S. K. Sahoo, Biomaterials, 2010, 31, 3694–3706 CrossRef CAS PubMed.
- Z. Fu, J. Wang, N. Zhang, Y. An and Z. Yang, Int. J. Hydrogen Energy, 2015, 40, 2193–2198 CrossRef CAS.
- M. Zhu and I. E. Wachs, ACS Catal., 2016, 6, 722–732 CrossRef CAS.
- A. Dreyer, A. Feld, A. Kornowski, E. D. Yilmaz, H. Noei, A. Meyer, T. Krekeler, C. Jiao, A. Stierle, V. Abetz, H. Weller and G. A. Schneider, Nat. Mater., 2016, 15, 522 CrossRef CAS PubMed.
- B. Domenèch, A. Plunkett, M. Kampferbeck, M. Blankenburg, B. Bor, D. Giuntini, T. Krekeler, M. Wagstaffe, H. Noei, A. Stierle, M. Ritter, M. Mueller, T. Vossmeyer, H. Weller and G. A. Schneider, Langmuir, 2019, 35, 13893–13903 CrossRef PubMed.
- R. Bliem, E. McDermott, P. Ferstl, M. Setvin, O. Gamba, J. Pavelec, M. A. Schneider, M. Schmid, U. Diebold, P. Blaha, L. Hammer and G. S. Parkinson, Science, 2014, 346, 1215–1218 CrossRef CAS PubMed.
- B. Arndt, R. Bliem, O. Gamba, J. E. S. Van Der Hoeven, H. Noei, U. Diebold, G. S. Parkinson and A. Stierle, Surf. Sci., 2016, 653, 76–81 CrossRef CAS.
- R. Bliem, J. Pavelec, O. Gamba, E. McDermott, Z. Wang, S. Gerhold, M. Wagner, J. Osiecki, K. Schulte, M. Schmid, P. Blaha, U. Diebold and G. S. Parkinson, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075440 CrossRef.
- R. Bliem, J. van der Hoeven, A. Zavodny, O. Gamba, J. Pavelec, P. E. de Jongh, M. Schmid, U. Diebold and G. S. Parkinson, Angew. Chem., Int. Ed., 2015, 54, 13999–14002 CrossRef CAS PubMed.
- N. C. Bartelt, S. Nie, E. Starodub, I. Bernal-Villamil, S. Gallego, L. Vergara, K. F. McCarty and J. de la Figuera, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 235436 CrossRef.
- R. Pentcheva, F. Wendler, H. L. Meyerheim, W. Moritz, N. Jedrecy and M. Scheffler, Phys. Rev. Lett., 2005, 94, 126101 CrossRef CAS PubMed.
- O. Balmes, R. van Rijn, D. Wermeille, A. Resta, L. Petit, H. Isern, T. Dufrane and R. Felici, Catal. Today, 2009, 145, 220–226 CrossRef CAS.
- C. M. Schlepütz, R. Herger, P. R. Willmott, B. D. Patterson, O. Bunk, C. Brönnimann, B. Henrich, G. Hülsen and E. F. Eikenberry, Acta Crystallogr., Sect. A: Found. Crystallogr., 2005, 61, 418–425 CrossRef PubMed.
- E. Vlieg, J. Appl. Crystallogr., 2000, 33, 401–405 CrossRef CAS.
- F. Esch, C. Dri, A. Spessot, C. Africh, G. Cautero, D. Giuressi, R. Sergo, R. Tommasini and G. Comelli, Rev. Sci. Instrum., 2011, 82, 053702 CrossRef PubMed.
- C. Dri, M. Panighel, D. Tiemann, L. L. Patera, G. Troiano, Y. Fukamori, F. Knoller, B. A. J. Lechner, G. Cautero, D. Giuressi, G. Comelli, J. Fraxedas, C. Africh and F. Esch, Ultramicroscopy, 2019, 205, 49–56 CrossRef CAS PubMed.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671 CrossRef CAS PubMed.
- J. I. J. Choi, W. Mayr-Schmälzer, F. Mittendorfer, J. Redinger, U. Diebold and M. Schmid, J. Phys.: Condens. Matter, 2014, 26, 225003 CrossRef CAS PubMed.
- J. Pavelec, J. Hulva, D. Halwidl, R. Bliem, O. Gamba, Z. Jakub, F. Brunbauer, M. Schmid, U. Diebold and G. S. Parkinson, J. Chem. Phys., 2017, 146, 014701 CrossRef PubMed.
- B. Warren, X-Ray Diffraction, Dover Publications, 2012 Search PubMed.
- B. Arndt, K. Sellschopp, M. Creutzburg, E. Grånäs, K. Krausert, V. Vonk, S. Müller, H. Noei, G. Feldbauer and A. Stierle, Commun. Chem., 2019, 2, 92 CrossRef.
- G. S. Parkinson, T. a. Manz, Z. Novotný, P. T. Sprunger, R. L. Kurtz, M. Schmid, D. S. Sholl and U. Diebold, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195450 CrossRef.
- O. Gamba, J. Hulva, J. Pavelec, R. Bliem, M. Schmid, U. Diebold and G. S. Parkinson, Top. Catal., 2017, 60, 420–430 CrossRef CAS PubMed.
- Z. Jakub, J. Hulva, F. Mirabella, F. Kraushofer, M. Meier, R. Bliem, U. Diebold and G. S. Parkinson, J. Phys. Chem. C, 2019, 123, 15038 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp00690d |
| This journal is © the Owner Societies 2020 |