Temperature-cycle electron paramagnetic resonance

Abstract

We report on a novel approach to the study of rates and short-lived intermediates of (bio)chemical reactions that involve paramagnetic species. Temperature-cycle Electron Paramagnetic Resonance (EPR) concerns the repeated heating of a reaction mixture in the cavity of an EPR spectrometer by pulsed irradiation with a near-infrared diode laser combined with intermittent characterization of the sample by 275 GHz EPR at a lower temperature at which the reaction does not proceed. The new technique is demonstrated for the reduction of TEMPOL with sodium dithionite in aqueous solution down to the sub-second time scale. We show that a single sample suffices to obtain a complete kinetic trace. Variation of the length and power of the laser pulse offers great flexibility as regards the time scale of the experiment and the temperature at which the reaction can be studied. For water/glycerol mixtures we introduce a simple way to obtain and load an unreacted sample into the spectrometer at low temperature.

---

Introduction

The determination of reaction rates and the detection of short-lived intermediates of fast chemical reactions are important research goals in fields that involve molecular chemistry, as the rates and intermediates shed light on the reaction mechanism. With this aim in mind, many methods have been developed and several make use of the response of a molecular system to a temperature jump (T-jump). The idea of using a T-jump was put forward by Eigen and De Maeyer in 1963,¹ who devised a method to induce a T-jump via an electrical discharge of a high-voltage capacitor through a conductive solution. Typically, heating times on the order of microseconds for a T-jump of a few degrees were achieved. The idea became more widely applicable upon the introduction of lasers as means to induce a T-jump, which also enabled studies at even shorter time scales.^2–4 To follow the development of a reacting system, the laser-induced T-jump has been combined with various optical detection techniques.⁵ Many (bio)chemical reactions involve paramagnetic species, either as reactant, intermediate or product, which argues for the combination of a laser-induced T-jump with Electron Paramagnetic Resonance (EPR) detection. Here we report on the development of such a technique for reactions in aqueous solution, where we couple T-jumps induced by near-infrared pulses with EPR at 275 GHz.

For fast processes that are not light-induced, rapid freeze-quench (RFQ) methods are as yet the standard for kinetic EPR studies.^6,7 In such experiments, a reaction is triggered by rapidly mixing the reacting components, then the reaction proceeds for a controlled time interval before being quenched in cold isopentane. Subsequently, the reaction mixture trapped at low temperature is transferred into an EPR-tube. The RFQ approach is complicated. A new sample has to be prepared for each point in time, and sample availability, reproducibility and handling limit its application. The quenched sample concerns frozen particles, which are dispersed in the cryo medium isopentane and are difficult to handle.^8–10 This is all the more true when the RFQ technique has to follow the developments in EPR spectroscopy towards microwave frequencies higher than 9 GHz.^11–15 At high microwave frequencies the resonant cavities become smaller in size and so do the corresponding sample volumes and sample holders. For example, the sample in the 275 GHz spectrometer used in the present study has a volume of only 20 nL and is contained in a capillary with an inner diameter of 150 μm, which obviously makes the transfer of the RFQ particles into this capillary much more difficult than for the 4 mm EPR tube used for 9 GHz. Moreover, for all RFQ experiments holds that a series of samples has to be prepared to obtain a kinetic trace, which can introduce errors and requires a substantial amount of material that is largely wasted and may not always be available. All in all, an alternative method that allows mechanistic studies of molecular reactions with high-frequency EPR, including the detection of paramagnetic intermediates and the study of reaction kinetics, can be advantageous.

We describe the development of T-cycle EPR at 275 GHz, which concerns the repeated heating of the sample in the EPR cavity by pulsed irradiation with a near-infrared laser combined with intermittent EPR investigation of the sample at lower temperature where the reaction does not proceed during the measurement. For reactions in water/glycerol mixtures we introduce a simple way to obtain and load an unreacted sample into the EPR spectrometer at low temperature. We show that a single sample suffices to obtain a complete kinetic trace by T-cycle EPR. We demonstrate sub-second time resolution and argue that millisecond time resolution is feasible.

Results

The T-cycle EPR experiment

A T-cycle EPR experiment starts with the preparation of a sample of reactants at a temperature low enough that no reaction takes place. After loading the sample in the probe head of the EPR spectrometer, this “t = 0” sample is stabilized at the measurement temperature T_m (at which no reaction occurs), and characterized by EPR, either by a continuous wave or any pulsed experiment. Subsequently, a number of T-cycle steps follow, each consisting of (i) warming the sample to the preparation temperature T_p, low enough for the sample not yet to react, but high enough to reach by a T-jump a temperature at which the reaction does take place, (ii) applying an IR-induced T-jump of arbitrary length by which the sample reaches the reaction temperature T_r at which the reaction evolves, (iii) cooling down from T_p to T_m followed by EPR characterization of the reacted sample. Both T_m and T_p are regulated by the temperature control of the flow cryostat, which carries the probe head. The T-cycle experiment is schematically represented in Fig. 1. The series of T-cycle steps allows to follow the evolution in time of paramagnetic species involved in the reaction from one single sample, as the laser-induced T-jumps are applied in situ to the sample located in the cavity of the spectrometer.

Fig. 1 Scheme of a T-cycle EPR experiment. The insert schematically represents the temperature course of the sample during one cycle: from the measurement temperature T_m (A) to the preparation temperature T_p (B) owing to a change in the temperature of the cryostat, to the reaction temperature T_r by a laser pulse (C), back to the T_p by switching off the laser (D) and to T_m by the cryostat (E).

The T-cycle experiment has been implemented on a home-built 275 GHz spectrometer.¹⁶ The insert in the flow cryostat is wired with a multimode optical fiber that couples the cavity with an infrared diode laser operating at 1550 nm. The nominal laser power referred to in the text corresponds to the total optical output power. Part of the IR light reaches the sample through a tangential slit in the bottom of the cylindrical cavity, and is absorbed by the solvent molecules. They release heat upon relaxation, which causes the aqueous solution in the cavity to warm up.

Calibration of the T-jump

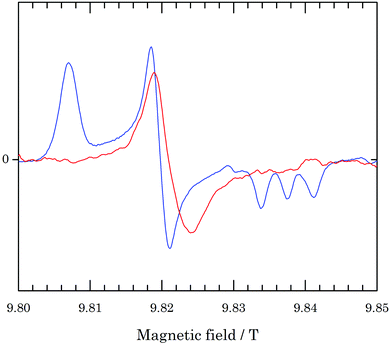
The temperature of the sample under infrared irradiation can be determined from the comparison of the EPR spectra of the nitroxide radical TEMPOL at various temperatures with the spectrum under irradiation.¹⁷ For the T-cycle EPR experiments to be described below, the cryostat temperature amounted to −47 °C during the EPR measurements, while laser powers of 2 and 3.5 W were applied. As an example, Fig. 2 shows 275 GHz cw EPR spectra at a cryostat temperature of −47 °C of a TEMPOL solution in a mixture of water and glycerol 1 : 1 in volume in the absence and in the presence of irradiation at 3.5 W. Comparison of the spectrum under irradiation with spectra obtained in a range of temperatures, reveals that the power of 3.5 W results in a temperature jump of 52 °C. Similarly, irradiation at 2 W was found to correspond to a temperature jump of 19 °C. For the underlying analysis we refer to the ESI,† where the variation with temperature of the EPR spectra is described in terms of the rotation correlation time of TEMPOL and the viscosity of the mixture of water and glycerol. Such analysis enables to quantify the variation of the T-jump with laser power, and shows that our setup allows T-jumps up to about 100 degrees. T-Jumps beyond this value may well be possible. The magnitude of the T-jump is determined by the power of the laser, the wavelength of the laser in combination with the optical density of the solvent at that wavelength, and the efficiency of the coupling of the infrared radiation into the cavity.

Fig. 2 275 GHz cw EPR spectra of TEMPOL (1 mM) in water and glycerol 1 : 1 in volume at a cryostat temperature of −47 °C. The spectrum in red is taken under continuous laser irradiation at a nominal power of 3.5 W, which increases the temperature of the sample to 5 °C.

T-Cycle EPR for a model reaction

To investigate whether it is possible to study the rate of a chemical reaction by T-cycle EPR, we considered the reduction of the nitroxide radical TEMPOL by sodium dithionite in a buffered mixture of water and glycerol 1 : 1 in volume, which represents a model reaction for kinetic EPR studies on the millisecond time scale.^13,18–20 In the presence of a large excess of dithionite (S₂O₄²⁻) over TEMPOL (TL), the reaction exhibits a pseudo first-order kinetics, as expressed in eqn (1) and (2):

k′ = k [S₂O₄²⁻] (2)

with k′ being the apparent rate constant.

A small amount of MnCl₂ is added to the sample as internal standard. In order to quantitatively analyse the reaction kinetics, we define the quantity Y(t), the ratio of the g_x-component of the EPR-signal of TEMPOL around 9.807 T at time t and the Mn²⁺-signal around 9.83 T in the same spectrum. As the Mn²⁺-signal does not vary in time, the change of the ratio Y with time represents the decay of the TEMPOL concentration.

The reduction of TEMPOL by sodium dithionite is too fast to prepare the t = 0 sample by simply mixing the two components at room temperature. A convenient feature of mixtures of water and glycerol is their low freezing point, which makes them highly viscous fluids at temperatures well below 0 °C.²¹ Based on this property, a mixing method was devised, henceforth referred to as “sub-zero mixing”, that allows an effective and simple mixing of solutions of TEMPOL and sodium dithionite down to about −50 °C (ESI,† Fig. S7). While kept at low temperature, the mixture is pushed in a pre-cooled capillary, which is then transferred into the pre-cooled probe head of the EPR spectrometer.¹⁵ The sub-zero mixing ensures that the two reagents have not reacted prior to exposure to the laser-induced T-jumps, so that the reaction is effectively observed from t = 0.

For the study of the TEMPOL/dithionite reaction, the temperatures T_p and T_m have been taken equal at a value of −47 °C. This was possible because at this temperature the 275 GHz EPR spectrum of TEMPOL is easy to detect, while the reaction is slow enough to largely prevent the reduction of TEMPOL during the time between the laser pulses in which the EPR spectrum is measured. At this temperature the apparent rate constant was found to be 4 × 10⁻⁵ s⁻¹, which corresponds to a decrease of the TEMPOL concentration by about 25% in two hours, i.e., the total time of a complete T-cycle experiment. The kinetic data that we present for the experiments reported below have been corrected for the decay of the TEMPOL signal during the time between the laser pulses at −47 °C.

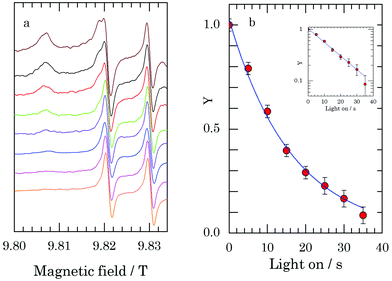
Fig. 3a shows the progressive decrease of the intensity of the EPR spectrum upon a series of laser pulses with a duration of 5 s at a nominal power of 2 W, until no signal is detected anymore except for the lines of Mn²⁺. Fig. 3b represents the decay of Y as a function of time the light is on. The observed decrease refers to the reduction of TEMPOL by sodium dithionite. Under the same experimental conditions, we considered a solution of identical composition but without sodium dithionite, and measured the EPR spectrum of TEMPOL with the laser off and with the laser continuously on (similar to the experiment in Fig. 2). As outlined above, these spectra revealed that the sample temperature during laser irradiation was −28 °C, corresponding to a temperature jump of 19 °C. The decay in Fig. 3b then corresponds to the apparent reaction rate k′(−28 °C) = (63 ± 3) × 10⁻³ s⁻¹, which according to eqn (2), with a concentration of sodium dithionite of 50 mM, yields k (−28 °C) = 1.25 ± 0.05 M⁻¹ s⁻¹.

Fig. 3 (a) 275 GHz cw EPR spectra at −47 °C of the mixture of TEMPOL (1 mM) and sodium dithionite (50 mM) in water and glycerol 1 : 1 in volume upon successive application of laser-induced T-jumps of 5 s at a nominal power of 2 W. The spectra are scaled to the intensity of the Mn²⁺ line at about 9.83 T. The spectrum at the top corresponds to t = 0, while the spectrum at the bottom is taken after 7 T-jumps. (b) Corresponding decay of Y (inset log Y) as a function of the laser-irradiation time.

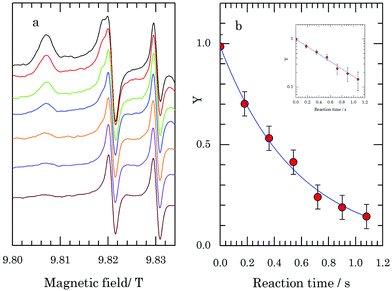
A similar experiment was performed on a solution of identical composition with shorter laser pulses of higher power, i.e., at a higher reaction temperature. Laser pulses of a duration of 250 ms were applied at a nominal power of 3.5 W. The result is the decrease of the 275 GHz EPR signal of TEMPOL as a function of the laser time shown in Fig. 4a.

Fig. 4 (a) 275 GHz cw EPR spectra at −47 °C of the mixture of TEMPOL (1 mM) and sodium dithionite (50 mM) in water and glycerol 1 : 1 in volume upon successive application of laser-induced T-jumps of 250 ms at a nominal power of 3.5 W. The spectra are scaled to the intensity of the Mn²⁺ line at about 9.83 T. The spectrum at the top corresponds to t = 0, while the spectrum at the bottom is taken after 6 T-jumps. (b) Decay of Y (inset log Y) as a function of the effective reaction time (180 ms per pulse).

Since the time it takes the sample in the present setup to reach thermal equilibrium under laser irradiation is about 300 ms, such equilibrium is not reached during the laser pulses of 250 ms. The sample does not attain the temperature of 5 °C, which corresponds to the temperature of the sample under continuous irradiation at 3.5 W. In order to interpret the observed decay, we have determined the temperature profile of the sample during and immediately after a laser pulse of 250 ms at 3.5 W. The approach makes use of the change of the 275 GHz spectrum of a solution of TEMPOL (i.e., no dithionite present) as a function of temperature. A detailed description is given in the ESI.† In particular, the EPR intensity of the peak at 9.8182 T is sensitive to temperature changes (Fig. S8, ESI†). The variation of the EPR intensity at this field during the 250 ms laser pulse reflects the temperature change of the solution. Fig. 5 (red line) shows the EPR intensity at 9.8182 T of the TEMPOL solution before, during and after the laser pulse. The EPR intensity before the laser pulse corresponds to the temperature of about −47 °C set by the cryostat. Translation of the change of the EPR intensity with time during the 250 ms laser pulse and directly after into the change of the temperature of the sample with time, results in the temperature profile of the sample as a function of time represented in Fig. 5 (blue dots). Upon application of the laser pulse, the temperature of the sample increases and a temperature of about 2 °C is reached at the end of the 250 ms laser pulse, when cooling back to −47 °C sets in. From Fig. 5 we see that the sample spends a time of about 180 ms at a temperature between −8 and 2 °C. Within this time, the temperature of the sample first increases, with correspondingly higher reaction rates, and then decreases. We neglect the reaction for temperatures below −8 °C and interpret the decay of the TEMPOL signal during the laser pulse to correspond to the reaction with dithionite during 180 ms at the (average) temperature of −3 °C. By taking 180 ms as the effective duration of the T-jump produced by a laser pulse of 250 ms, the time axis of the reaction is generated. In Fig. 4b the Y function, derived from the spectra in Fig. 4a, is plotted versus this reaction time. This decay corresponds to an apparent rate constant k′(−3 °C) = 1.8 ± 0.2 s⁻¹, which according to eqn (2), with a concentration of sodium dithionite of 50 mM, yields k (−3 °C) = 37 ± 4 M⁻¹ s⁻¹. A more detailed analysis of the decay, in which the variation of the reaction rate with temperature is explicitly taken into account, is described in the ESI.†

Fig. 5 Time profile (red line) of the 275 GHz EPR spectral intensity at the magnetic field of 9.8182 T of a solution of TEMPOL (3 mM) in a mixture of glycerol and phosphate buffer (120 mM, pH 7.0), 1 : 1 in volume, before, during and after a laser pulse of 250 ms at 3.5 W. The intensity change is translated into a temperature change of the sample, as indicated by the blue dots (scale on the right). The dashed line serves as a guide to the eye.

Discussion

The kinetic studies on the reduction of TEMPOL by sodium dithionite present a proof-of-principle of T-cycle EPR. The two pilot experiments are essentially different as regards the temperature profile of the sample during the laser pulse. In the first one, laser pulses of 5 s have been applied. The configuration in the present setup is such that it takes about 300 ms for the sample in the cavity to reach the equilibrium temperature under laser irradiation, and a slightly longer time to return to the bath temperature after switching off the laser. The length of the laser pulse thus virtually equals the reaction time, and the observed decay effectively reflects the characteristic time of the reaction, 16 s at −28 °C. In the second experiment, the same reaction was studied at higher temperatures where it is significantly faster. Shorter laser pulses of 250 ms were applied and the temperature of the sample did not reach equilibrium during the pulse. Consequently, a more detailed analysis of the course of the temperature of the sample during the laser pulse was necessary to derive the reaction rate. This yields a characteristic time of the reaction of 0.56 s at −3 °C.

The rate constants obtained here can be compared with those found in the literature for the reaction of TEMPOL and dithionite at room temperature. Based on a more detailed analysis of the observed decays (ESI†) an estimate of the rate constant at room temperature can be obtained assuming Arrhenius behaviour. This yields a rate constant k (19 °C) = 360 ± 50 M⁻¹ s⁻¹. Kaufmann et al.¹³ report a rate constant k (RT) = 800 ± 100 M⁻¹ s⁻¹. The relevant difference between the present conditions and those of ref. 13 is the amount of glycerol in the solution, being 30% in volume, while 50% was used in this study. Further, in ref. 13 comparison is made with the k (RT) = 4000 M⁻¹ s⁻¹ obtained in earlier work on the same system,^19,20 except for the absence of glycerol in the solution. From this literature data, a 5-fold decrease of the rate constant is observed when the glycerol content is increased from 0 to 30% (from 4000 to 800 M⁻¹ s⁻¹). Here, another twofold decrease is found (from 800 to 360 M⁻¹ s⁻¹) in the presence of 50% glycerol, which is plausible in view of the change of the solvent properties upon changing the water/glycerol ratio.

For the present demonstration experiments of the novel T-cycle EPR method, we have chosen a reaction for which the measurement time T_m could be taken equal to the preparation time T_p. This clearly adds to the efficiency of the kinetic study, but will not always be possible. In case T_m ≠ T_p, each cycle includes warming up from T_m to T_p before the laser pulse can be applied and cooling back to T_m after the laser pulse (cf.Fig. 1). This in no way limits the applicability of T-cycle EPR because the reaction does not proceed during these times, only lengthens the total time the full kinetic study takes. For example, for a study of a reaction at room temperature that requires EPR detection at T_m = 77 K, and making use of laser-induced T-jumps of 100 degrees, i.e., T_p = 193 K, cycling from T_m to T_p and back to T_m takes less than an hour in our set-up. A kinetic study can then still be completed in one day. This may no longer be true for detection at liquid helium temperatures, and an overnight experiment may be required.

The question arises as to the time resolution that can be achieved with T-cycle EPR. With the present setup we have realized T-jumps of the sample in the cavity by 100 degrees (see ESI†) and minimum reaction times of about in 50 ms. Laser pulses can be arbitrarily short and the time resolution is fully determined by the rise and decay times of the temperature jump of the sample. The shorter these are, the higher the time resolution that can be achieved. The temperature rise takes a little less time than the temperature decay. This asymmetry is understandable considering that during the temperature rise, the process of infrared absorption adds on the active cooling constantly acting on the sample by the surrounding cryogenic atmosphere. The rate of sample cooling is determined by the thermal conductivity of the sample itself, of the capillary that holds the sample and of the helium gas. Cooling becomes faster the smaller the volume of the sample, the larger the temperature difference between sample and surrounding and the better the thermal conductivity. The quartz capillary can be replaced by a sapphire one (unless signals of paramagnetic centers of the sapphire interfere with signals of the sample).

To be more precise, what is decisive for the time resolution of the T-cycle EPR experiment is not the time it takes to reach thermal equilibrium, but the initial rise and decay times: for the rise time because the laser pulse can be switched off at any time during temperature increase, for the decay time because a decrease of the temperature of the sample by some tens of degrees will in general be sufficient to effectively stop the reaction. Model calculations (ESI†) predict that for the configuration in the present setup, for a starting temperature of the sample of 303 K and a bath temperature of 243 K, it takes about 45 ms to cool the sample to 270 K, consistent with our experimental observations. By reducing the inner diameter of the quartz capillary from 150 to 75 μm and decreasing the bath temperature to 223 K, the time to cool to 270 K becomes 5 ms, i.e., a reduction by about an order of magnitude. Both the reduction of the sample volume and the increase of the temperature difference between the sample and the bath contribute significantly to the reduction of the cooling time of the sample, which thus in principle enables a better time resolution. Of course the reduction of the volume of the sample might mean fewer spins, and sensitivity will ultimately become an issue. Moreover, less sample implies less absorption of the infrared radiation. These considerations suggest that the combination of efficient laser absorption with efficient cooling will allow kinetic investigations by T-cycle EPR in time regimes of a few tens of milliseconds, if not less.

Conclusions

For T-cycle EPR only a single sample is required to obtain the complete reaction kinetics, in the examples above 20 nL of 1 mM concentration. Reproducibility of sample preparation, which is an issue when separate samples have to be prepared for each reaction time as in rapid freeze-quench, does not limit the accuracy of the kinetic investigation. Moreover, only a small amount of material is needed, which is beneficial for precious samples as often applies to biochemical studies. For water/glycerol mixtures we have introduced “sub-zero mixing” as a simple tool to prepare the t = 0 sample, i.e., mixing the reactants at a temperature where the reaction is quenched. In this way we totally circumvent rapid freeze-quench. In case “sub-zero mixing” is impossible, rapid freeze-quench is only necessary to prepare a single sample. The use of caged compounds presents another way to start a reaction, and is fully compatible with T-cycle EPR.

The temperature jump is induced by a pulse of infrared radiation absorbed by the matrix, which introduces great flexibility. Duration and optical power of the laser pulse can be arbitrarily varied. The duration can be adapted to the rate of the reaction, while the laser power in combination with the cryogenic bath determines the temperature at which the reaction is studied. The laser also introduces flexibility as regards the matrix, because its frequency can be adapted to the infrared absorption of the matrix.

The coupling of RFQ to EPR at microwave frequencies higher than 9 GHz remains difficult, although a number of approaches have been proposed. The present development particularly concerns 275 GHz, but the application of T-cycle EPR does not seem to be limited to that high microwave frequency. The requirement is that the sample is homogeneously irradiated and that temperature jumps are fast enough compared to the reaction rate. This obviously limits the size of the sample.

In summary, we present the proof-of-principle of T-cycle EPR through the quantitative study of the kinetics of the model reaction of TEMPOL with sodium dithionite, following the decrease of the reactant on the time scale of hundreds of milliseconds. Another straightforward application of course concerns the detection of paramagnetic intermediates involved in a reaction. We argue that time scales of milliseconds are within reach and conclude that T-cycle. EPR promises to offer an easy, effective and flexible way to follow the fate of paramagnetic species during chemical reactions.

Experimental

Samples

Oxygen-free mixtures of TEMPOL (4-hydroxy-TEMPO, Sigma-Aldrich) and sodium dithionite (Na₂S₂O₄, sodium hydrosulphite 85%, Sigma-Aldrich) were prepared from batch solutions at concentrations of 2 and 100 mM, respectively, in a mixture of phosphate buffer and glycerol 1 : 1 in volume. In view of the high reactivity of sodium dithionite with oxygen,²² both the TEMPOL and buffer batch solutions, together with the sodium dithionite powder prior to dissolution, were bubbled with argon while kept in air-tight vials sealed with rubber septa caps, to ensure removal of oxygen. In order to transfer the buffer:glycerol solution into the vial containing the sodium dithionite powder, and to transfer the de-oxygenated solutions to the beaker for the mixing, a Hamilton air-tight syringe was employed. The phosphate buffer solution had a concentration of 120 mM and a pH of 7.0, and was prepared from stock solutions of sodium phosphate monobasic (G-Biosciences) and sodium phosphate dibasic (Sigma-Aldrich) dissolved in Milli-Q water; glycerol was purchased from Sigma-Aldrich (puriss.).

The samples for the EPR experiments were obtained through “sub-zero mixing” of the TEMPOL and sodium dithionite solutions, which results in concentrations of 1 and 50 mM, respectively. MnCl₂ at a concentration of 10 μM was added to both solutions prior to mixing, to be used as an internal standard.

The samples are introduced in the single-mode cavity of a pre-cooled (200 K) home-built probe head,¹⁵ which is then inserted in the pre-cooled He-flow cryostat of the home-built 275 GHz spectrometer.

T-Cycle setup

The probe head of the 275 GHz spectrometer¹⁶ is wired with a multi-mode optical fiber that couples the cavity to a diode laser operating at 1550 nm. The diode laser concerned a model 15P-110 (SemiNex Corp.) coupled to an optical fiber of core size 200 μm, 0.22 NA (Thorlabs, FG200LC, HPSMA connector to the laser). The diode laser is mounted on a home-built power supply and fan-cooling unit, which can be regulated in order to control the output power of the laser. The duration of the laser pulses was controlled by an electronic clock that triggered the current fed to the diode laser.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr M. Azarkh for his contribution in the early stages of the development of the T-cycle EPR experiment, and H. van der Meer and B. Crama for their essential technical support.

References

1. M. Eigen and L. De Maeyer, Technique of Organic Chemistry, Part II, Wiley Interscience, New York, 2nd edn, 1963, vol. 8, pp. 895–1054.
2. H. Staerk and G. Czerlinski, Nanosecond heating of aqueous systems by giant laser pulses, Nature, 1965, 205, 63–64.
3. H. Hoffmann, E. Yeager and J. Stuehr, Laser temperature-jump apparatus for relaxation studies in electrolytic solutions, Rev. Sci. Instrum., 1968, 39, 649–653.
4. R. Rigler, A. Jost and L. De Maeyer, Chemical kinetics at the micro level: A laser micro temperature jump apparatus for relaxation studies in micro samples, Exp. Cell Res., 1970, 62, 197–203.
5. J. Kubelka, Time-resolved methods in biophysics. 9. Laser temperature-jump methods for investigating biomolecular dynamics, Photochem. Photobiol. Sci., 2009, 8, 499–512.
6. R. C. Bray, Sudden freezing as a technique for the study of rapid reactions, Biochem. J., 1961, 81, 189–195.
7. D. P. Ballou and G. A. Palmer, Practical rapid quenching instrument for the study of reaction mechanisms by electron paramagnetic resonance spectroscopy, Anal. Chem., 1974, 46, 1248–1253.
8. A. L. Tsai, V. Berka, R. J. Kulmacz, G. Wu and G. Palmer, An improved sample packing device for rapid freeze-trap electron paramagnetic resonance spectroscopy kinetic measurements, Anal. Biochem., 1998, 264, 165–171.
9. S. Oellerich, E. Bill and P. Hildebrandt, Freeze-quench resonance Raman and electron paramagnetic resonance spectroscopy for studying enzyme kinetics: application to azide binding to myoglobin, Appl. Spectrosc., 2000, 54, 1480–1484.
10. F. Nami, P. Gast and E. J. J. Groenen, Rapid freeze-quench EPR spectroscopy: improved collection of frozen particles, Appl. Magn. Reson., 2016, 47, 643–653.
11. V. Schuenemann, F. Lendzian, C. Jung, J. Contzen, A. L. Barra, S. G. Sligar and A. X. Trautwein, Tyrosine radical formation in the reaction of wild type and mutant cytochrome P450cam with peroxy acids, J. Biol. Chem., 2004, 279, 10919–10930.
12. J. Manzerova, V. Krymov and G. J. Gerfen, Investigating the intermediates in the reaction of ribonucleoside triphosphate reductase from Lactobacillus leichmannii: an application of HF EPR-RFQ technology, J. Magn. Reson., 2011, 213, 32–45.
13. R. Kaufmann, I. Yadid and D. Goldfarb, A novel microfluidic rapid freeze-quench device for trapping reactions intermediates for high field EPR analysis, J. Magn. Reson., 2013, 230, 220–226.
14. R. Pievo, B. Angerstein, A. J. Fielding, C. Koch, I. Feussner and M. Bennati, A rapid freeze-quench setup for multi-frequency EPR spectroscopy of enzymatic reactions, ChemPhysChem, 2013, 14, 4094–4101.
15. E. G. Panarelli, H. van der Meer, P. Gast and E. J. J. Groenen, Effective coupling of rapid freeze-quench to high-frequency electron paramagnetic resonance, PLoS One, under review.
16. H. Blok, J. A. J. M. Disselhorst, S. B. Orlinskii and J. Schmidt, A continuous-wave and pulsed electron spin resonance spectrometer operating at 275 GHz, J. Magn. Reson., 2004, 166, 92–99.
17. M. Azarkh and E. J. J. Groenen, Temperature determination by EPR at 275 GHz and the detection of temperature jumps in aqueous samples, J. Phys. Chem. B, 2015, 119, 13416–13421.
18. A. Potapov and D. Goldfarb, A calibration reaction for rapid freeze-quench W-band EPR, Appl. Magn. Reson., 2010, 37, 845–850.
19. G. Lassmann, P. P. Schmidt and W. Lubitz, An advanced EPR stopped-flow apparatus based on a dielectric ring resonator, J. Magn. Reson., 2005, 172, 312–323.
20. V. M. Grigoryants, A. V. Veselov and C. P. Scholes, Variable velocity liquid flow EPR applied to submillisecond protein folding, Biophys. J., 2000, 78, 2702–2708.
21. Glycerine Producers' Association, Physical Properties of Glycerine and its Solutions, New York, 1963.
22. S. G. Mayhew, The redox potential of dithionite and SO₂⁻ from equilibrium reactions with flavodoxins, methyl viologen and hydrogen plus hydrogenase, Eur. J. Biochem., 1978, 85, 535–547.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp00664e

---