Monolayer Ti2C MXene: manipulating magnetic properties and electronic structures by an electric field†
Abstract
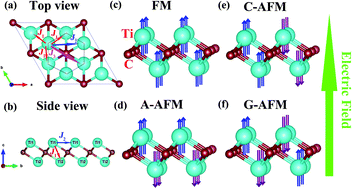
Two-dimensional (2D) layered Ti2C MXene has been synthesized experimentally, and the magnetism of monolayer Ti2C MXene has been predicted theoretically. In this study, based on first-principles calculations, five magnetic configurations of monolayer Ti2C were constructed to predict the magnetic ground state. We have found that the antiferromagnetic (AFM) state has the lowest energy. By applying an external electric field, monolayer Ti2C changes from an AFM semiconductor to a ferrimagnetic (FIM) semiconductor, half-metal, magnetic metal, non-magnetic (NM) metal, and NM semiconductor. When the electric field increases beyond a certain value, the magnetic moments of Ti atoms sharply decrease. With the increase in the electric field, the effective masses decrease significantly, carrier mobility increases and conductivity increases. The magnetic anisotropy energies were calculated and the results showed that the out-of-plane direction was the magnetic easy axis. Using the mean-field approximation method, the Néel temperature of monolayer Ti2C is estimated to be 50 K. By applying an electric field, the Néel temperature significantly decreases, which shows that the electric field can effectively reduce the high Néel temperature. Therefore, our research suggests that the magnetic and electronic properties of 2D materials can be manipulated by an external electric field, which provides a feasible direction for the tuning of nanomagnetic devices.


 Please wait while we load your content...
Please wait while we load your content...