Open Access Article
Open Access ArticleTunable relativistic quasiparticle electronic and excitonic behavior of the FAPb(I1−xBrx)3 alloy
Zeeshan
Muhammad†
ab,
Peitao
Liu†
 c,
Rashid
Ahmad
ad,
Saeid
Jalali Asadabadi
c,
Rashid
Ahmad
ad,
Saeid
Jalali Asadabadi
 e,
Cesare
Franchini
e,
Cesare
Franchini
 *c and
Iftikhar
Ahmad
af
*c and
Iftikhar
Ahmad
af
aCenter for Computational Material Science, University of Malakand, Chakdara, Pakistan
bDepartment of Physics, University of Malakand, Chakdara, Pakistan
cUniversity of Vienna, Faculty of Physics and Center for Computational Materials Science, Sensengasse 8, A-1090 Vienna, Austria. E-mail: cesare.franchini@univie.ac.at
dDepartment of Chemistry, University of Malakand, Chakdara, Pakistan
eDepartment of Physics, Faculty of Sciences, University of Isfahan, HezarGerib Avenue, Isfahan 81744-73441, Iran
fVice Chancellor, Gomal University, Dera Ismail Khan, Pakistan
First published on 1st May 2020
Abstract
We study the structural, electronic, and excitonic properties of mixed FAPb(I1−xBrx)3 0 ≤ x ≤ 1 alloys by first-principles density functional theory as well as quasiparticle GW and Bethe Salpeter equation (BSE) approaches with the inclusion of relativistic effects through spin orbit coupling. Our results show that the system volume decreases with increasing Br content. The quasiparticle band gaps vary from 1.47 eV for pure α-FAPbI3 to 2.20 eV for Br-rich α-FAPbBr3 and show stronger correlation with the structural changes. The optical property analysis reveals that the overall excitonic peaks are blue shifted with the Br fraction. Our results further reveal strong Br concentration dependence of the variation in the exciton binding energy (from 74 to 112 meV) and the carrier effective masses as well as the high frequency dielectric constants. These findings provide a way to tune the carrier transport properties of the material by doping, which could be utilized to improve the short circuit currents and power conversion efficiencies in multijunction solar cell devices.
Introduction
The growth in the human population and improvement of living standards across the globe have placed the search for efficient, economical and clean sources of renewable energy at the forefront of scientific research in the 21st century. An alternative to expensively processed silicon-based photovoltaics, hybrid organic–inorganic perovskites (HOIPs) having general formula ABX3 are a new class of low-cost, clean and efficient promising materials for affordable solar cell technologies.1–17 The rapid rise in power-conversion efficiencies within less than a decade increased the importance of such novel materials among the research community and hence these materials are progressively leading towards commercialization. The development of the revolutionary mixed type hybrid organic–inorganic perovskites has sparked much interest in the field of photovoltaics5,16–37 because of their low-cost compositional chemical management of constituents, allowing tailoring of the electrical and optical parameters. Some of the key characteristics of these materials that make them exceptional are their tunable optimal band gap for appropriate sunlight absorption,5,19–25,27–34,36 longer carrier lifetimes,5,38,39 high charge carrier mobility,40–43 long charge carrier diffusion length39,40,44 and weak exciton binding energy.45–52 The first reported material of this family was synthesized by Miyasaka et al.1 with a demonstrated solar cell efficiency of 3.8%. Recently, Gharibzadeh et al.17 have attained an efficiency of 25.7% using a mixed-cation lead mixed-halide perovskite/Si heterojunction in a tandem solar cell. The prominent feature of a tandem solar cell is that it uses two or more semiconducting layers, which absorb different parts of sunlight, yielding low thermalization losses and high-power conversion efficiencies (PCEs) as compared to single junction solar cells.53According to recent studies, progress in the efficiency and chemical stability of perovskite based solar cells can be accomplished by the compositional chemical management of the A site having larger cations like cesium (Cs+), methylammonium MA (CH3NH3+) and formamidinium FA (CH(NH2)2)+,25–27,30,54 of the B site having smaller divalent inorganic cations e.g., Pb2+ and Sn2+,32,33,55 and of the X site containing monovalent metal halides including I−, Br− and Cl−.18,19,22,28,29,36,37,56,57 For example, gradual substitution of the FA cation in MAPbI3 will reduce the band gap from 1.57 eV to 1.48 eV,30,58 thus yielding improved transport properties,59 long photoluminescence (PL) lifetimes,60 and lower recombination and device hysteresis with high PCEs.19,61,62 Similarly, slowly replacing the Pb2+ cation with less toxic Sn2+ at the B site will vary the band gap between 1.51 eV and 1.28 eV.55 The rapid oxidation of Sn2+ to Sn4+ especially in SnI2 and precursor solutions leads to high defect densities and short carrier diffusion lengths, which restricts its widespread use because of low PCEs.63,64 In order to have a wide range of variations in the electronic as well as in the optical properties, the mixing of metal halides at the X site provides an effective way to give such a fine-tuning property suitable for designing and improving the performance of multijunction solar cell devices. In addition to MAPb(I1−xClx)318,56 and MAPb(I1−xBrx)3,28,36,37,57 FAPb(I1−xBrx)319,22,29 has also been successfully synthesized and demonstrated in solar cells. To date mixed hybrid perovskites containing the FAPb(I1−xBrx)3 system have achieved the highest efficiency so far in perovskite based solar cells.17
Although the FAPb(I1−xBrx)3 alloy has been experimentally studied, a thorough in-depth theoretical description and understanding of the structural parameters, electronic density of states (DOS), band gaps, carrier excitations and exciton binding energies has not been fully addressed. In the present work, the FAPb(I1−xBrx)3 system is studied with density functional theory (DFT), which proves to be a powerful tool for modeling and simulations of materials.65,66 The commonly used generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE)67,68 provides structural lattice parameters close to the experimental values, but it is well known that DFT fails to describe the excited state properties such as quasiparticle (QP) band gaps and excitonic properties.69,70 An additional complication in relativistic HOIPs is the need to include spin–orbit coupling (SOC) effects, which causes further reduction of the bandgaps.46,71–77 Moreover, the use of hybrid functionals like HSE06 including SOC does not satisfactorily improve the issue of band gap underestimation.76 The state-of-the-art approach to improve the band gap is the GW method,78,79 which provides a good approximation in evaluating the self-energy operator as contraction of the one-body Green's function (G) with the screened Coulomb interaction (W). The GW method has been widely used for many systems ranging from elemental semiconductors69,70,80 to HOIPs,46,71,72,74–77,81 yielding band gaps in better agreement with experiments.
Since during the optical excitation the interactions of the electron–hole pairs create excitons which strongly couple to the incoming photons, this leads to substantial modification of the optical spectrum both below and above the quasiparticle band gaps. To explore the excitonic peaks in the optical spectra, it is necessary to account for electron–hole pair interactions, which is normally done by solving the Bethe–Salpeter equation (BSE) on top of GW calculations.46,82–85
By means of density functional theory and many-body methods with the inclusion of spin–orbit coupling, we have performed a systematic first-principles study of the structural, electronic, and optical properties of the FAPb(I1−xBrx)3 alloy with 0 ≤ x ≤ 1. Our results show that as the Br concentration increases, the volume of the FAPb(I1−xBrx)3 alloy decreases, the band gap increases from 1.47 eV for pure α-FAPbI3 to 2.20 eV for Br-rich α-FAPbBr3, and the excitonic peaks are blue shifted. Our results further reveal strong Br concentration dependence of the exciton binding energy (varies from 74 to 112 meV) and the carrier effective masses as well as the high frequency dielectric constants. Our findings open the way to fine-tune the carrier transport properties of the material by chemical substitution and provide important insights to improve short circuit currents and power conversion efficiencies in solar cell devices.
Computational details
The FAPb(I1−xBrx)3 alloy was modelled based on the experimental geometry of α-FAPbI3 at 298 K86 and α-FAPbBr3 at 275 K.87 The position of the FA molecule for the present system was taken from the molecular dynamics simulations of Taylor et al.88 The modeling of the FAPb(I1−xBrx)3 alloy was carried out by compositional assembly of seven independent configurations i.e., for x = 0, 0.17, 0.33, 0.50, 0.67, 0.83 and 1. The unit cell of FAPbI3 is expanded to a 1 × 1 × 2 tetragonal supercell, where an appropriately random substitution of I atoms with Br atoms is performed to obtain the corresponding compositions.89–91 Our DFT calculations were performed using the Vienna ab initio simulation package (VASP)92,93 with projector augmented (PAW) pseudopotentials.94 For the exchange correlation functional, PBE was used.67,68 An energy cutoff of 600 eV and Γ-centered 6 × 6 × 3 k-point sampling of the Brillouin zone were adopted for all structures. The valence electron configurations that were included in the calculations are 5d106s26p2 for Pb, 5s25p5 for I, 4s24p5 for Br, 2s22p3 for N, 1s1 for H and 2s22p2 for C. All the structural parameters were relaxed with a convergence threshold of 10−6 eV in the total energy and the stopping convergence criterion for the forces on each atom was set to be 0.01 eV Å−1. To account for the van der Waals dispersion interactions, we used the rev-vdW-DF2 functional of Hamada.95 Due to the presence of heavy elements, the relativistic SOC effect was included in calculating the electronic and optical properties.For the accurate electronic structure, in particular the band gap, we carried out delicate one-shot G0W0 calculations using Γ-centered 4 × 4 × 2 k-point sampling with 2200 empty bands, a dielectric cutoff energy of 150 eV and 128 points on the frequency grid. The electron–hole interactions were accounted for by solving the BSE for the polarizability. 16 occupied and unoccupied QP energies were employed in constructing the BSE Hamiltonian and the screened interactions W were from the preceding G0W0 calculations. The broadening parameter used in evaluation of the polarizability was chosen to be 0.1 eV. For the detailed GW + BSE methodology that the VASP code follows, we refer the readers to ref. 96.
It is known that to obtain converged optical spectra and exciton binding energies, many k points are normally needed.46,82 However, for the relatively large systems studied here, this is already prohibitive for the G0W0 calculations. To address this issue, we followed the strategy proposed in ref. 46, where the optical spectra and exciton binding energies were calculated by a simplified approximation of BSE [termed as model BSE (mBSE)]. In mBSE calculations, the QP energies from G0W0 calculations are approximated by the PBE one-electron energies with a scissor operator on the unoccupied orbitals such that the PBE one-electron gap matches the G0W0 calculated band gap. This turns out to be a good approximation for the systems studied here (see good agreement between G0W0 + SOC and PBE + SCISSOR + SOC band structures in Fig. 4). In addition, the expensive calculations of the dielectric function matrix from G0W0 are approximated by a simple analytical model dielectric function within the diagonal element approximation:46,82,96,97
| ε−1(|G|) = 1 − (1 − ε−1∞)e−|G|2/4μ2, | (1) |
By performing PBE + SCISSOR + mBSE calculations, we are able to check the k-point convergence by adopting a dense k-point mesh up to 18 × 18 × 9. Our test calculations indicate that the spectra and exciton binding energies are well converged on a 16 × 16 × 8 k-point mesh with an accuracy of about 3 meV in the exciton binding energies [see Fig. 9(b) and (c)]. Therefore, the 16 × 16 × 8 k-point mesh was used for all mBSE calculations. The exciton binding energies were calculated by the energy difference between the G0W0 band gap and the first bright mBSE eigenvalue. Furthermore, for comparison purposes, the exciton binding energies were also estimated by using the Wannier Mott model:98Eb ≈ 13.6mr*/ε∞2, where mr* is the reduced mass 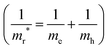 .
.
Results and discussion
A. Structural properties
The possible synthesis of a halide mixed perovskite is confirmed through the effective Goldsmith tolerance factor teff.99–102 The atomic-ratio weighted average of the two different anions is used as the estimated effective anion size reff. For the FAPb(I1−xBrx)3 composition:| reff = xrBr + (1 − x)rI, | (2) |
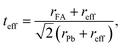 | (3) |
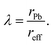 | (4) |
Generally, for ABX3 perovskite-like structures, the tolerance factor is in the range 0.80 ≤ t ≤ 1.06 and the octahedral factor lies between 0.442 and 0.895.99,102 The calculated effective tolerance factor for the FAPb(I1−xBrx)3 system ranges from 0.987 to 1.008, thus confirming the perovskite structure as summarized in Table 1. The octahedral factor values also affirm the stable perovskite structure as they lie between 0.541 and 0.607 for the FAPb(I1−xBrx)3 composition.
| Br fraction x | 0 | 0.17 | 0.33 | 0.50 | 0.67 | 0.83 | 1 |
|---|---|---|---|---|---|---|---|
| Goldsmith tolerance factor t | 0.987 | 0.990 | 0.993 | 0.997 | 1.000 | 1.004 | 1.008 |
| Octahedral factor λ | 0.540 | 0.550 | 0.561 | 0.572 | 0.583 | 0.594 | 0.607 |
Table 2 summarizes the calculated lattice parameters of the FAPb(I1−xBrx)3 system for x = 0, 0.17, 0.33, 0.50, 0.67, 0.83, and 1. The calculated averaged ground state lattice parameters for FAPbI3 (a = 6.38 Å) and FAPbBr3 (a = 6.01 Å) using the PBE functional are in good agreement with experimental data, i.e., 6.36 Å and 5.99 Å for FAPbI3 and FAPbBr3, respectively,29,39,103,104 and the relaxed structure of α-FAPbI3 is shown in Fig. 1. In the full relaxation of the structures, the deviation from tetragonal symmetry is caused by the steric effect of the FA+ cation.
| Composition x | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) |
|---|---|---|---|---|---|---|
| 0 | 6.33 | 6.51 | 12.66 | 90.00 | 92.80 | 90.00 |
| 0.17 | 6.31 | 6.50 | 12.32 | 90.00 | 93.05 | 90.00 |
| 0.33 | 6.29 | 6.52 | 11.99 | 90.00 | 93.28 | 90.00 |
| 0.50 | 6.30 | 6.37 | 12.00 | 90.00 | 93.34 | 90.00 |
| 0.67 | 6.30 | 6.17 | 12.09 | 90.00 | 93.49 | 90.00 |
| 0.83 | 6.01 | 6.17 | 12.27 | 90.00 | 94.51 | 90.00 |
| 1 | 5.96 | 6.16 | 11.92 | 90.00 | 94.90 | 90.00 |
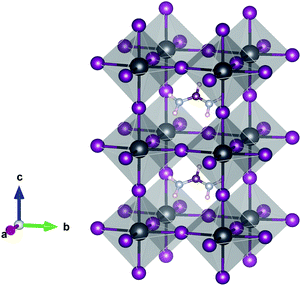 | ||
| Fig. 1 Crystal structure of the 1 × 1 × 2 supercell of α-FAPbI3. Pb (grey), I (purple), C (brown), N (light blue) and H (pink). The FAPb(I1−xBrx)3 alloy is obtained by substituting I with Br. | ||
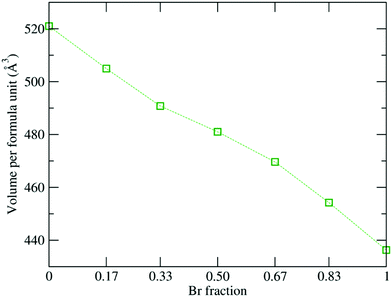
Fig. 2 shows the overall decrease in volume of the 1 × 1 × 2 supercell from 520.9 Å3 to 454.2 Å3 as the Br content increases, which is consistent with the decreasing experimental lattice constants.19,29 Also, the Pb–X (where X = I and Br) bond length reduces from 3.26 Å to 2.96 Å, which can be attributed to the smaller ionic radius of the Br atom, which influences the interplanar geometry. Moreover, the electronic charge distribution is much stronger around the Br atom due to its higher electronegativity value (2.96) as compared to I (2.66). Thus, the heavy Pb atom will interact strongly with the Br atom due to the high electronegativity difference, which leads to the reduction in the bond length.105
B. Electronic structures and band gaps
In order to give an insight on the electronic structure, different approaches have been carried out. Table 3 summarizes the calculated band gaps for the FAPb(11−xBrx)3 system with increasing Br percentage obtained at various levels of theory. The comparison of the band gaps clearly shows the underestimation in the calculated band gaps of FAPbI3 and FAPbBr3 by PBE, as expected. Inclusion of the relativistic SOC effect reduces the band gaps of FAPbI3 and FAPbBr3 to 0.41 eV and 0.87 eV respectively, underestimating the experimental band gap further and consistent with previous SOC-DFT results for MA(Pb, Sn)X3.46,71–77,81 To improve the underestimation in the PBE derived gaps, we carried out G0W0 calculations including SOC effects. The G0W0 + SOC calculated band gaps of 1.47 eV and 2.20 eV for FAPbI3 and FAPbBr3, respectively, are in excellent agreement with the experimental band gaps.19,29 Similarly, we have calculated the electronic band gaps using the G0W0 + SOC approach for all other configurations of FAPb(11−xBrx)3 having different Br compositions and the results are compiled in Table 3.The G0W0 + SOC calculated band gaps for various Br fractions are plotted in Fig. 3. Such a linear trend in the band gaps with the x composition in the alloy can be expressed by the quadratic equation known as Vegard's law:107,108
| Eg[FAPb(BrxI1−x)3] = Eg[FAPbI3] + (Eg[FAPbBr3] − Eg[FAPbI3] − b)x + bx2, | (5) |
| Eg(x) = 1.47 + 0.71x + 0.02x2, | (6) |
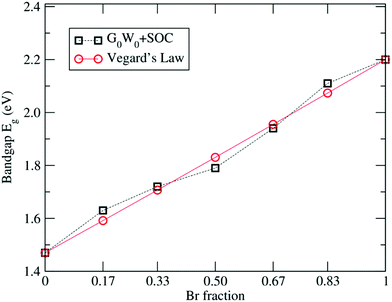 | ||
| Fig. 3 Linear variation in the G0W0 + SOC calculated band gaps with respect to the Br concentration. | ||
The G0W0 + SOC derived QP band structures along the high-symmetry points Γ(0, 0, 0), M(0.5, 0.5, 0) and X(0.5, 0, 0) for each FAPb(11−xBrx)3 configuration are shown in Fig. 4. The band structures are plotted by using the Wannier interpolation scheme,109,110 in which the Wannier orbitals are constructed on a Γ-centered 4 × 4 × 2 k-point mesh and all the relevant orbitals are included for the initial representation of the Kohn Sham states. With the 1 × 1 × 2 supercell, both the valence band maximum (VBM) and conduction band minimum (CBM) fold to the M-point and the band gaps are found to be direct in nature. Fractional deviations from the M-point are observed for the VBM and CBM due to the presence of Rashba–Dresselhaus splitting.111–113 The dispersion of both the conduction band and valence band slightly increases with the Br content, leading to different effective masses for electrons and holes near the CBM and VBM. Such dispersions can be understood by the enhanced orbital interaction with decreasing structural volume.
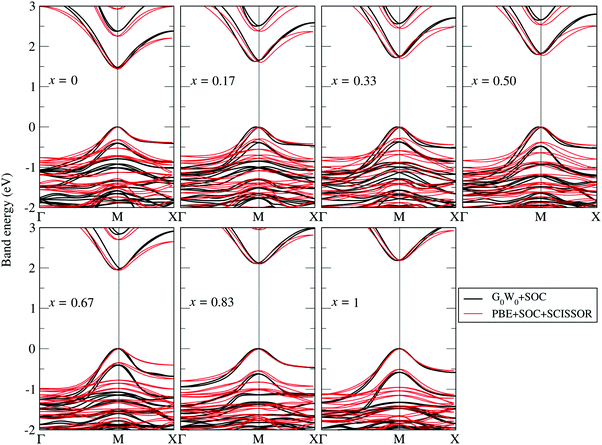 | ||
| Fig. 4 G0W0 + SOC calculated QP band structures obtained by Wannier interpolation109,110 (black lines) superposed by the PBE + SOC band structures with a scissor operator to match the G0W0 band gap (red lines). The Fermi level is set to zero. | ||
To study the carrier transport properties for the FAPb(11−xBrx)3 alloy, we calculated the effective masses m* for electrons and holes around the CBM and VBM, respectively, by fitting the dispersion relation on the basis of the parabolic approximation
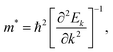 | (7) |
| Br fraction x | Effective mass (M–Γ) | Effective mass (M–X) | Average | m r* | |||
|---|---|---|---|---|---|---|---|
| m e*/m0 | m h*/m0 | m e*/m0 | m h*/m0 | m e*/m0 | m h*/m0 | ||
| 0 | 0.212 | 0.267 | 0.225 | 0.279 | 0.218 | 0.273 | 0.121 |
| 0.17 | 0.227 | 0.288 | 0.234 | 0.298 | 0.231 | 0.293 | 0.129 |
| 0.33 | 0.232 | 0.279 | 0.228 | 0.287 | 0.230 | 0.283 | 0.127 |
| 0.50 | 0.253 | 0.296 | 0.255 | 0.304 | 0.254 | 0.300 | 0.138 |
| 0.67 | 0.275 | 0.336 | 0.277 | 0.372 | 0.276 | 0.354 | 0.155 |
| 0.83 | 0.369 | 0.467 | 0.364 | 0.431 | 0.367 | 0.449 | 0.202 |
| 1 | 0.351 | 0.412 | 0.353 | 0.404 | 0.352 | 0.408 | 0.189 |
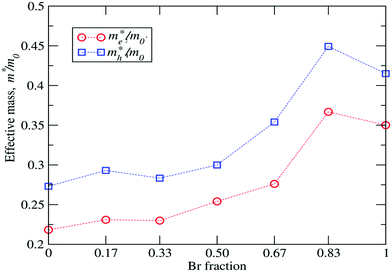 | ||
| Fig. 5 Calculated me*/m0 and mh*/m0 ratios as a function of the Br content, where me*(mh*) is the effective electron (hole) mass and m0 is the mass of a free electron. | ||
Fig. 6 depicts the G0W0 + SOC calculated partial density of states (PDOS) to reveal the possible origin of the band gap variations. One can see that the electronic states near the band gap are mostly governed by the orbital overlap of the BX6 octahedron. The organic part does not contribute to the Fermi energy but acts as a charge compensating center, because the organic molecule weakly interacts with the inorganic part via possible hydrogen bonding through the organic cation groups. Thus, for the sake of clarity, around the band gap only the contributions from the orbitals (s and p) of Pb, I and Br atoms are presented and analyzed. From the PDOS, the valence band is mainly composed of X-p orbitals, mixed in minor fractions with B-s orbitals, while the conduction band is mainly contributed by B-p orbitals, partly hybridized with X-s states. The gradual replacement of I with Br causes the Br-4p orbital to dominate at the VBM, which tends to strongly hybridize with Pb-s states as compared to I-p states. This pushes the CBM towards the high energy region and thus increases the band gap. Such orbital behavior has also been observed in a DFT study of the MAPb(11−xBrx)3 system.57
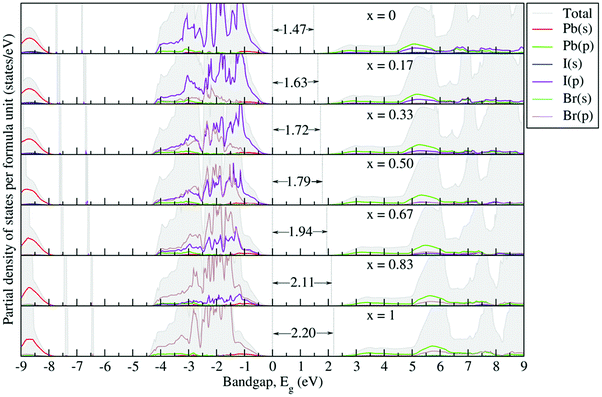 | ||
| Fig. 6 G0W0 + SOC calculated partial density of states for the FAPb(I1−xBrx)3 system. The Fermi level is set to zero. | ||
C. Optical properties and exciton binding energies
To explore the excitonic behavior for each FAPb(11−xBrx)3 configuration, we carried out PBE + SCISSOR + mBSE calculations including the SOC effect. An exciton is a neutral bound electron–hole pair, which plays a crucial role in the optical excitation process and is highly influential for both fundamental science and applications in solar cells.45–52 Therefore, it is essential to consider the electron–hole Coulomb interactions for an accurate excitonic description of the optical spectra.Previously, it has been revealed that the polaronic effects in HOIPs contribute to excitonic features due to the interacting longitudinal optical phonons with electronic states of the carriers, thereby forming polarons, which influences the dielectric behavior and exciton binding energies.38,46,48,114 However, polaronic effects are not considered here, since they are beyond the scope of this work. Fig. 7 shows the imaginary part of the dielectric function Im[ε(ω)] with increasing Br composition along with the corresponding optical transition oscillator strengths. One can see that Im[ε(ω)] for all compositions shows a typical three peak feature in the considered energy range: two peaks are above the G0W0 band gap and one peak is below the G0W0 band gap, which is an exciton peak resulting from the electron–hole interactions upon photoexcitation. Our PBE + SCISSOR + mBSE calculated spectra for x = 0, x = 0.67, and x = 1 are in good agreement with available experimentally measured data,115–118 in particular the first two peaks. The spectrum of x = 0 from M. Kato et al.116 is largely blue-shifted for the first two peaks as compared to that of T. J. Whitcher et al.115 and P. F. Ndion et al.117 as well as our simulated one. As the Br fraction increases from x = 0 to x = 1, the optical spectra are systematically blue-shifted along with the gradual reduction in the overall amplitude of oscillator strengths. This trend is consistent with the increasing band gaps and can be attributed to variation in the electronic charge distribution of X-p states with changing halide component as evident from the PDOS of Fig. 6.
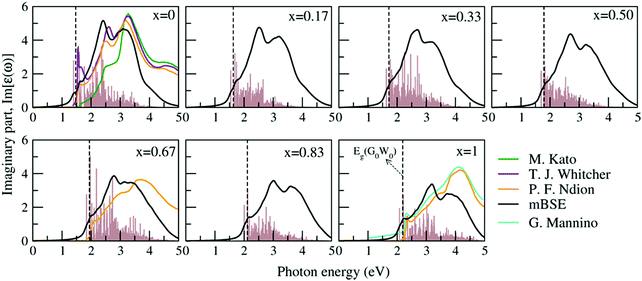 | ||
| Fig. 7 PBE + SCISSOR + mBSE calculated imaginary part Im[ε(ω)] of the dielectric function of the FAPb(I1−xBrx)3 alloy. The corresponding G0W0 derived fundamental gap Eg(G0W0) and optical transition oscillator strengths are represented by dashed lines and brown histograms, respectively. The available experimental data on FAPbI3,115–117 FAPbIBr2117 and FAPbBr3118 are shown for comparison. Note that the Im[ε(ω)] data shown here from ref. 117 are indirectly calculated from the experimentally measured refractive index and extinction coefficient. | ||
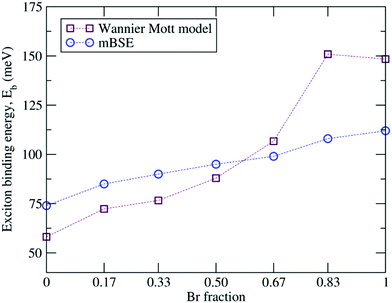
Since changes in the halide components affect the bound state of an electron–hole pair, we evaluated the exciton binding energies Eb within Wannier–Mott theory by using the effective mass approximation as well as via mBSE. The resulting exciton binding energies are summarized in Table 5 and depicted in Fig. 8. One can observe that the mBSE calculated exciton binding energies almost show linear behavior as the Br concentration increases and this trend is in general captured by Wannier–Mott theory, though the values deviate. The mBSE calculated Eb for α-FAPbI3 (74 meV) is significantly large as compared to the experimental value of 2.4 meV,119 whereas for the pure α-FAPbBr3 the calculated Eb (112 meV) is in reasonable agreement with the experimental value of 170 meV.103 For the latter, Wannier–Mott theory yields a better value of Eb towards the experimental value. From Wannier–Mott theory, we can infer that the overall increase in Eb with increasing Br concentration in FAPb(I1−xBrx)3 is both affected by increasing mr* and decreasing ε∞. The smaller value of Eb in the I-rich configuration requires smaller energy to dissociate the electron–hole pair, which in turn leads to high optical absorption and high PCE as compared to the Br-rich material.
| Br fraction x | 0 | 0.17 | 0.33 | 0.50 | 0.67 | 0.83 | 1 |
|---|---|---|---|---|---|---|---|
| High frequency dielectric constant ε∞ | 5.320 | 4.929 | 4.746 | 4.613 | 4.447 | 4.266 | 4.173 |
| E b (Wannier Mott model) | 58 | 72 | 77 | 88 | 107 | 151 | 149 |
| E b (mBSE) | 74 | 85 | 90 | 95 | 99 | 108 | 112 |
Conclusions
We have performed a first-principles study of the structural, electronic, and optical properties of the FAPb(I1−xBrx)3 alloy 0 ≤ x ≤ 1 by means of density functional theory and many-body methods with the inclusion of spin–orbit coupling. The calculated geometrical parameters show that the overall Pb–X bond length decreases with the Br content and thus reduces the volume, which is in agreement with experiments. The G0W0 derived band gap increases from 1.47 eV to 2.20 eV with increasing Br fraction, which has been clearly demonstrated from the evolution of the electronic density of states. The G0W0 + BSE calculated optical spectra show that the overall excitonic peaks are blue shifted with increasing Br concentration, which shows a strong correlation with the increase in the band gap and is consistent with the decreasing dielectric constants. The variation in the exciton binding energy from 74 meV to 112 meV reveals that excitons are more bound for Br rich compounds due to the reduced carrier mobility and thus require a higher energy for exciton dissociation. Our findings provide an efficient and controllable way to tune the electronic as well as the optical properties for mixed HOIPs that will be beneficial for material design of high performance tandem solar cells.Conflicts of interest
There are no conflicts to declare.Appendix A
In this appendix, we show in Table 6 the required parameters used for PBE + SCISSOR + mBSE calculations and in Fig. 9 we take FAPbI3 as an example to illustrate how mBSE performs as compared to the full BSE and how the calculated optical spectra as well as exciton binding energies converge with respect to the number of k points.| Br fraction x | 0 | 0.17 | 0.33 | 0.50 | 0.67 | 0.83 | 1 |
|---|---|---|---|---|---|---|---|
| ε ∞ | 5.320 | 4.929 | 4.746 | 4.613 | 4.447 | 4.266 | 4.173 |
| μ (Å−1) | 1.055 | 1.060 | 1.070 | 1.073 | 1.081 | 1.095 | 1.109 |
| SCISSOR (eV) | 1.062 | 1.095 | 1.133 | 1.171 | 1.233 | 1.283 | 1.319 |
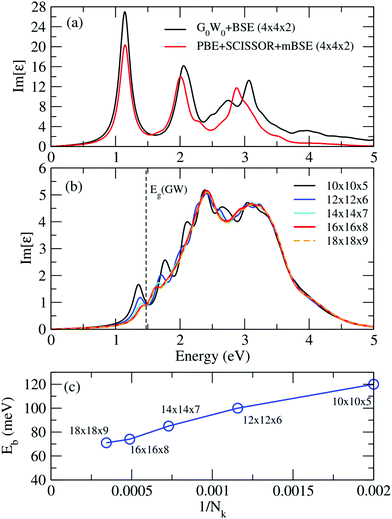
Fig. 9(a) shows a comparison of the imaginary part of the dielectric function calculated from G0W0 + BSE and PBE + SCISSOR + mBSE on a 4 × 4 × 2 k-point mesh. One can see that PBE + SCISSOR + mBSE in general reproduces very well the spectra obtained from G0W0 + BSE, in particular the first bright peak, suggesting that PBE + SCISSOR + mBSE is a suitable method to describe the optical spectra for FAPbI3 with an accuracy that is comparable with the more demanding G0W0 + BSE.
Fig. 9(b) and (c) display the convergence of the optical spectra and exciton biding energies calculated from PBE + SCISSOR + mBSE with respect to the number of k points. Clearly and expectedly, the convergence is very slow. Our calculations indicate that the spectra and exciton binding energies are converged with a 16 × 16 × 8 k-point mesh, with an accuracy of about 3 meV in the exciton binding energies.
Acknowledgements
Z. Muhammad is thankful to M. Reticcioli for helpful discussions. This work was supported by the Higher Education Commission of Pakistan (HEC) under the Research Project No. 20-3959/NRPU/R&D/HEC2014/234. P. Liu and C. Franchini acknowledge support from the Austrian Science Fund (FWF). The Vienna Scientific cluster (VSC) is gratefully acknowledged for computing facilities.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- J.-H. Im, C.-R. Lee, J.-W. Lee, S.-W. Park and N.-G. Park, 6.5% efficient perovskite quantum-dot-sensitized solar cell, Nanoscale, 2011, 3, 4088 RSC.
- H.-S. Kim, C.-R. Lee, J.-H. Im, K.-B. Lee, T. Moehl, A. Marchioro, S.-J. Moon, R. Humphry-Baker, J.-H. Yum, J. E. Moser, M. Grätzel and N.-G. Park, Lead Iodide Perovskite Sensitized All-Solid-State Submicron Thin Film Mesoscopic Solar Cell with Efficiency Exceeding 9%, Sci. Rep., 2012, 2, 591 CrossRef PubMed.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Efficient hybrid solar cells based on meso-superstructured organometal halide perovskites, Science, 2012, 338, 643–647 CrossRef CAS PubMed.
- J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. Il Seok, Chemical management for colorful, efficient, and stable inorganic-organic hybrid nanostructured solar cells, Nano Lett., 2013, 13, 1764–1769 CrossRef CAS PubMed.
- M. Liu, M. B. Johnston and H. J. Snaith, Efficient planar heterojunction perovskite solar cells by vapour deposition, Nature, 2013, 501, 395–398 CrossRef CAS PubMed.
- J. M. Ball, M. M. Lee, A. Hey and H. J. Snaith, Low-temperature processed meso-superstructured to thin-film perovskite solar cells, Energy Environ. Sci., 2013, 6, 1739 RSC.
- J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Sequential deposition as a route to high-performance perovskite-sensitized solar cells, Nature, 2013, 499, 316–319 CrossRef CAS PubMed.
- Q. Chen, H. Zhou, Z. Hong, S. Luo, H.-S. Duan, H.-H. Wang, Y. Liu, G. Li and Y. Yang, Planar Heterojunction Perovskite Solar Cells via Vapor-Assisted Solution Process, J. Am. Chem. Soc., 2014, 136, 622–625 CrossRef CAS PubMed.
- D. Liu and T. L. Kelly, Perovskite solar cells with a planar heterojunction structure prepared using room-temperature solution processing techniques, Nat. Photonics, 2014, 8, 133–138 CrossRef CAS.
- H. Zhou, Q. Chen, G. Li, S. Luo, T. Song, H.-S. Duan, Z. Hong, J. You, Y. Liu and Y. Yang, Photovoltaics. Interface engineering of highly efficient perovskite solar cells, Science, 2014, 345, 542–546 CrossRef CAS PubMed.
- W. S. Yang, J. H. Noh, N. J. Jeon, Y. C. Kim, S. Ryu, J. Seo and S. Il Seok, SOLAR CELLS. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange, Science, 2015, 348, 1234–1237 CrossRef CAS PubMed.
- M. Saliba, T. Matsui, J.-Y. Seo, K. Domanski, J.-P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate, A. Hagfeldt and M. Grätzel, Cesium-containing triple cation perovskite solar cells: improved stability, reproducibility and high efficiency, Energy Environ. Sci., 2016, 9, 1989–1997 RSC.
- W. S. Yang, B.-W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. Il Seok, Iodide management in formamidinium-lead-halide–based perovskite layers for efficient solar cells, Science, 2017, 356, 1376–1379 CrossRef CAS PubMed.
- K. A. Bush, A. F. Palmstrom, Z. J. Yu, M. Boccard, R. Cheacharoen, J. P. Mailoa, D. P. McMeekin, R. L. Z. Hoye, C. D. Bailie, T. Leijtens, I. M. Peters, M. C. Minichetti, N. Rolston, R. Prasanna, S. Sofia, D. Harwood, W. Ma, F. Moghadam, H. J. Snaith, T. Buonassisi, Z. C. Holman, S. F. Bent and M. D. McGehee, 23.6%-efficient monolithic perovskite/silicon tandem solar cells with improved stability, Nat. Energy, 2017, 2, 17009 CrossRef CAS.
- F. Sahli, J. Werner, B. A. Kamino, M. Bräuninger, R. Monnard, B. Paviet-Salomon, L. Barraud, L. Ding, J. J. Diaz Leon, D. Sacchetto, G. Cattaneo, M. Despeisse, M. Boccard, S. Nicolay, Q. Jeangros, B. Niesen and C. Ballif, Fully textured monolithic perovskite/silicon tandem solar cells with 25.2% power conversion efficiency, Nat. Mater., 2018, 17, 820–826 CrossRef CAS PubMed.
- S. Gharibzadeh, I. M. Hossain, P. Fassl, B. A. Nejand, T. Abzieher, M. Schultes, E. Ahlswede, P. Jackson, M. Powalla, S. Schäfer, M. Rienäcker, T. Wietler, R. Peibst, U. Lemmer, B. S. Richards and U. W. Paetzold, 2D/3D Heterostructure for Semitransparent Perovskite Solar Cells with Engineered Bandgap Enables Efficiencies Exceeding 25% in Four-Terminal Tandems with Silicon and CIGS, Adv. Funct. Mater., 2020, 1909919 CrossRef CAS.
- S. Colella, E. Mosconi, P. Fedeli, A. Listorti, F. Gazza, F. Orlandi, P. Ferro, T. Besagni, A. Rizzo, G. Calestani, G. Gigli, F. De Angelis and R. Mosca, MAPbI3−xClx mixed halide perovskite for hybrid solar cells: The role of chloride as dopant on the transport and structural properties, Chem. Mater., 2013, 25, 4613–4618 CrossRef CAS.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Formamidinium lead trihalide: A broadly tunable perovskite for efficient planar heterojunction solar cells, Energy Environ. Sci., 2014, 7, 982–988 RSC.
- F. Hao, C. C. Stoumpos, R. P. H. Chang and M. G. Kanatzidis, Anomalous Band Gap Behavior in Mixed Sn and Pb Perovskites Enables Broadening of Absorption Spectrum in Solar Cells, J. Am. Chem. Soc., 2014, 136, 8094–8099 CrossRef CAS PubMed.
- Y. Ogomi, A. Morita, S. Tsukamoto, T. Saitho, N. Fujikawa, Q. Shen, T. Toyoda, K. Yoshino, S. S. Pandey, T. Ma and S. Hayase, CH3NH3SnxPb(1−x)I3 perovskite solar cells covering up to 1060 nm, J. Phys. Chem. Lett., 2014, 5, 1004–1011 CrossRef CAS PubMed.
- W. Rehman, R. L. Milot, G. E. Eperon, C. Wehrenfennig, J. L. Boland, H. J. Snaith, M. B. Johnston and L. M. Herz, Charge-Carrier Dynamics and Mobilities in Formamidinium Lead Mixed-Halide Perovskites, Adv. Mater., 2015, 27, 7938–7944 CrossRef CAS PubMed.
- B. Slimi, M. Mollar, I. Ben Assaker, I. Kriaa, R. Chtourou and B. Marí, Perovskite FA1−xMAxPbI3 for Solar Cells: Films Formation and Properties, Energy Procedia, 2016, 102, 87–95 CrossRef CAS.
- D. Bi, W. Tress, M. I. Dar, P. Gao, J. Luo, C. Renevier, K. Schenk, A. Abate, F. Giordano, J. P. Correa Baena, J. D. Decoppet, S. M. Zakeeruddin, M. K. Nazeeruddin, M. Grätzel and A. Hagfeldt, Efficient luminescent solar cells based on tailored mixed-cation perovskites, Sci. Adv., 2016, 2, e1501170 CrossRef.
- F. Xu, T. Zhang, G. Li and Y. Zhao, Mixed cation hybrid lead halide perovskites with enhanced performance and stability, J. Mater. Chem. A, 2017, 5, 11450–11461 RSC.
- D. J. Kubicki, D. Prochowicz, A. Hofstetter, P. Péchy, S. M. Zakeeruddin, M. Grätzel and L. Emsley, Cation Dynamics in Mixed-Cation (MA)x(FA)1−xPbI3 Hybrid Perovskites from Solid-State NMR, J. Am. Chem. Soc., 2017, 139, 10055–10061 CrossRef CAS PubMed.
- L. Li, N. Liu, Z. Xu, Q. Chen, X. Wang and H. Zhou, Precise Composition Tailoring of Mixed-Cation Hybrid Perovskites for Efficient Solar Cells by Mixture Design Methods, ACS Nano, 2017, 11, 8804–8813 CrossRef CAS.
- B. Zhang, F. Guo, J. Xue, L. Yang, Y. Zhao, M. Ge, Q. Cai, B. Liu, Z. Xie, D. Chen, H. Lu, R. Zhang and Y. Zheng, Photoluminescence Study of the Photoinduced Phase Separation in Mixed-Halide Hybrid Perovskite CH3NH3Pb(BrxI1−x)3 Crystals Synthesized via a Solvothermal Method, Sci. Rep., 2017, 7, 17695 CrossRef PubMed.
- B. Slimi, M. Mollar, I. Ben Assaker, A. Kriaa, R. Chtourou and B. Marí, Synthesis and characterization of perovskite FAPbBr3−xIx thin films for solar cells, Monatsh. Chem., 2017, 148, 835–844 CrossRef CAS.
- A. Pisanu, C. Ferrara, P. Quadrelli, G. Guizzetti, M. Patrini, C. Milanese, C. Tealdi and L. Malavasi, The FA1−xMAxPbI3 System: Correlations among Stoichiometry Control, Crystal Structure, Optical Properties, and Phase Stability, J. Phys. Chem. C, 2017, 121, 8746–8751 CrossRef CAS.
- K. A. Bush, K. Frohna, R. Prasanna, R. E. Beal, T. Leijtens, S. A. Swifter and M. D. McGehee, Compositional Engineering for Efficient Wide Band Gap Perovskites with Improved Stability to Photoinduced Phase Segregation, ACS Energy Lett., 2018, 3, 428–435 CrossRef CAS.
- E. S. Parrott, T. Green, R. L. Milot, M. B. Johnston, H. J. Snaith and L. M. Herz, Interplay of Structural and Optoelectronic Properties in Formamidinium Mixed Tin-Lead Triiodide Perovskites, Adv. Funct. Mater., 2018, 28, 1802803 CrossRef.
- A. Pisanu, A. Mahata, E. Mosconi, M. Patrini, P. Quadrelli, C. Milanese, F. De Angelis and L. Malavasi, Exploring the Limits of Three-Dimensional Perovskites: The Case of FAPb1−xSnxBr3, ACS Energy Lett., 2018, 3, 1353–1359 CrossRef CAS.
- A. Leblanc, N. Mercier, M. Allain, J. Dittmer, T. Pauporté, V. Fernandez, F. Boucher, M. Kepenekian and C. Katan, Enhanced Stability and Band Gap Tuning of α-[HC(NH2)2]PbI3 Hybrid Perovskite by Large Cation Integration, ACS Appl. Mater. Interfaces, 2019, 11, 20743–20751 CrossRef CAS PubMed.
- T. Jiang, Z. Chen, X. Chen, X. Chen, X. Xu, T. Liu, L. Bai, D. Yang, D. Di, W. E. I. Sha, H. Zhu and Y. M. Yang, Power Conversion Efficiency Enhancement of Low-Bandgap Mixed Pb–Sn Perovskite Solar Cells by Improved Interfacial Charge Transfer, ACS Energy Lett., 2019, 4, 1784–1790 CrossRef CAS.
- F. Lehmann, A. Franz, D. M. Többens, S. Levcenco, T. Unold, A. Taubert and S. Schorr, The phase diagram of a mixed halide (Br, I) hybrid perovskite obtained by synchrotron X-ray diffraction, RSC Adv., 2019, 9, 11151–11159 RSC.
- W. Fan, Y. Shi, T. Shi, S. Chu, W. Chen, K. O. Ighodalo, J. Zhao, X. Li and Z. Xiao, Suppression and Reversion of Light-Induced Phase Separation in Mixed-Halide Perovskites by Oxygen Passivation, ACS Energy Lett., 2019, 4, 2052–2058 CrossRef CAS.
- Y. Chen, H. T. Yi, X. Wu, R. Haroldson, Y. N. Gartstein, Y. I. Rodionov, K. S. Tikhonov, A. Zakhidov, X. Y. Zhu and V. Podzorov, Extended carrier lifetimes and diffusion in hybrid perovskites revealed by Hall effect and photoconductivity measurements, Nat. Commun., 2016, 7, 12253 CrossRef CAS PubMed.
- A. A. Zhumekenov, M. I. Saidaminov, M. A. Haque, E. Alarousu, S. P. Sarmah, B. Murali, I. Dursun, X.-H. Miao, A. L. Abdelhady, T. Wu, O. F. Mohammed and O. M. Bakr, Formamidinium Lead Halide Perovskite Crystals with Unprecedented Long Carrier Dynamics and Diffusion Length, ACS Energy Lett., 2016, 1, 32–37 CrossRef CAS.
- G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Grätzel, S. Mhaisalkar and T. C. Sum, Long-range balanced electron- and hole-transport lengths in organic–inorganic CH3NH3PbI3, Science, 2013, 342, 344–347 CrossRef CAS PubMed.
- C. Wehrenfennig, G. E. Eperon, M. B. Johnston, H. J. Snaith and L. M. Herz, High charge carrier mobilities and lifetimes in organolead trihalide perovskites, Adv. Mater., 2014, 26, 1584–1589 CrossRef CAS PubMed.
- J. Lim, M. T. Hörantner, N. Sakai, J. M. Ball, S. Mahesh, N. K. Noel, Y. H. Lin, J. B. Patel, D. P. McMeekin, M. B. Johnston, B. Wenger and H. J. Snaith, Elucidating the long-range charge carrier mobility in metal halide perovskite thin films, Energy Environ. Sci., 2019, 12, 169–176 RSC.
- N. T. P. Hartono, S. Sun, M. C. Gélvez-Rueda, P. J. Pierone, M. P. Erodici, J. Yoo, F. Wei, M. Bawendi, F. C. Grozema, M. Sher, T. Buonassisi and J.-P. Correa-Baena, The effect of structural dimensionality on carrier mobility in lead-halide perovskites, J. Mater. Chem. A, 2019, 7, 23949–23957 RSC.
- G. W. P. Adhyaksa, L. W. Veldhuizen, Y. Kuang, S. Brittman, R. E. I. Schropp and E. C. Garnett, Carrier Diffusion Lengths in Hybrid Perovskites: Processing, Composition, Aging, and Surface Passivation Effects, Chem. Mater., 2016, 28, 5259–5263 CrossRef CAS.
- K. Galkowski, A. Mitioglu, A. Miyata, P. Plochocka, O. Portugall, G. E. Eperon, J. T.-W. Wang, T. Stergiopoulos, S. D. Stranks, H. J. Snaith and R. J. Nicholas, Determination of the exciton binding energy and effective masses for the methylammonium and formamidinium lead tri-halide perovskite family, Energy Environ. Sci., 2015, 9, 962–970 RSC.
- M. Bokdam, T. Sander, A. Stroppa, S. Picozzi, D. D. Sarma, C. Franchini and G. Kresse, Role of Polar Phonons in the Photo Excited State of Metal Halide Perovskites, Sci. Rep., 2016, 6, 28618 CrossRef CAS PubMed.
- A. Miyata, A. Mitioglu, P. Plochocka, O. Portugall, J. T.-W. Wang, S. D. Stranks, H. J. Snaith and R. J. Nicholas, Direct measurement of the exciton binding energy and effective masses for charge carriers in organic–inorganic tri-halide perovskites, Nat. Phys., 2015, 11, 582–587 Search PubMed.
- A. M. Soufiani, F. Huang, P. Reece, R. Sheng, A. Ho-Baillie and M. A. Green, Polaronic exciton binding energy in iodide and bromide organic–inorganic lead halide perovskites, Appl. Phys. Lett., 2015, 107, 231902 CrossRef.
- Y. Yamada, T. Nakamura, M. Endo, A. Wakamiya and Y. Kanemitsu, Photoelectronic responses in solution-processed perovskite CH3NH3PbI3 solar cells studied by photoluminescence and photoabsorption spectroscopy, IEEE J. Photovoltaics, 2015, 5, 401–405 Search PubMed.
- N. Sestu, M. Cadelano, V. Sarritzu, F. Chen, D. Marongiu, R. Piras, M. Mainas, F. Quochi, M. Saba, A. Mura and G. Bongiovanni, Absorption F-Sum Rule for the Exciton Binding Energy in Methylammonium Lead Halide Perovskites, J. Phys. Chem. Lett., 2015, 6, 4566–4572 CrossRef CAS PubMed.
- M. Saba, M. Cadelano, D. Marongiu, F. Chen, V. Sarritzu, N. Sestu, C. Figus, M. Aresti, R. Piras, A. Geddo Lehmann, C. Cannas, A. Musinu, F. Quochi, A. Mura and G. Bongiovanni, Correlated electron–hole plasma in organometal perovskites, Nat. Commun., 2014, 5, 5049 CrossRef CAS PubMed.
- V. D’Innocenzo, G. Grancini, M. J. P. Alcocer, A. R. S. Kandada, S. D. Stranks, M. M. Lee, G. Lanzani, H. J. Snaith and A. Petrozza, Excitons versus free charges in organo-lead tri-halide perovskites, Nat. Commun., 2014, 5, 3586 CrossRef PubMed.
- A. De Vos, Detailed balance limit of the efficiency of tandem solar cells, J. Phys. D: Appl. Phys., 1980, 13, 839–846 CrossRef.
- H. X. Dang, K. Wang, M. Ghasemi, M.-C. Tang, M. De Bastiani, E. Aydin, E. Dauzon, D. Barrit, J. Peng, D.-M. Smilgies, S. De Wolf and A. Amassian, Multi-cation Synergy Suppresses Phase Segregation in Mixed-Halide Perovskites, Joule, 2019, 3, 1746–1764 CrossRef CAS.
- J. Liu, G. Wang, Z. Song, X. He, K. Luo, Q. Ye, C. Liao and J. Mei, FAPb1−xSnxI3 mixed metal halide perovskites with improved light harvesting and stability for efficient planar heterojunction solar cells, J. Mater. Chem. A, 2017, 5, 9097–9106 RSC.
- C. Wehrenfennig, M. Liu, H. J. Snaith, M. B. Johnston and L. M. Herz, Homogeneous emission line broadening in the organo lead halide perovskite CH3NH3PbI3−xClx, J. Phys. Chem. Lett., 2014, 5, 1300–1306 CrossRef CAS PubMed.
- U. G. Jong, C. J. Yu, J. S. Ri, N. H. Kim and G. C. Ri, Influence of halide composition on the structural, electronic, and optical properties of mixed CH3NH3Pb(I1−xBrx)3 perovskites calculated using the virtual crystal approximation method, Phys. Rev. B, 2016, 94, 125139 CrossRef.
- G. E. Eperon, C. E. Beck and H. J. Snaith, Cation exchange for thin film lead iodide perovskite interconversion, Mater. Horiz., 2016, 3, 63–71 RSC.
- Y. Liu, J. Qian, H. Zhang, B. Xu, Y. Zhang, L. Liu, G. Chen and W. Tian, Influence of organic cations on intrinsic properties of lead iodide perovskite solar cells, Org. Electron., 2018, 62, 269–276 CrossRef CAS.
- J. Dai, Y. Fu, L. H. Manger, M. T. Rea, L. Hwang, R. H. Goldsmith and S. Jin, Carrier Decay Properties of Mixed Cation Formamidinium–Methylammonium Lead Iodide Perovskite [HC(NH2)2]1−x[CH3NH3]xPbI3 Nanorods, J. Phys. Chem. Lett., 2016, 7, 5036–5043 CrossRef CAS PubMed.
- R. S. Sanchez, V. Gonzalez-Pedro, J.-W. Lee, N.-G. Park, Y. S. Kang, I. Mora-Sero and J. Bisquert, Slow Dynamic Processes in Lead Halide Perovskite Solar Cells. Characteristic Times and Hysteresis, J. Phys. Chem. Lett., 2014, 5, 2357–2363 CrossRef CAS PubMed.
- M. Salado, L. Calio, R. Berger, S. Kazim and S. Ahmad, Influence of the mixed organic cation ratio in lead iodide based perovskite on the performance of solar cells, Phys. Chem. Chem. Phys., 2016, 18, 27148–27157 RSC.
- S. J. Lee, S. S. Shin, J. Im, T. K. Ahn, J. H. Noh, N. J. Jeon, S. Il Seok and J. Seo, Reducing Carrier Density in Formamidinium Tin Perovskites and Its Beneficial Effects on Stability and Efficiency of Perovskite Solar Cells, ACS Energy Lett., 2018, 3, 46–53 CrossRef CAS.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and Near-Infrared Photoluminescent Properties, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS.
- E. Engel and R. M. Dreizler, Density Functional Theory: An Advanced Course, Theor. Math. Phys., 2011, 2011, 499–515 Search PubMed.
- R. G. Parr, Density Functional Theory, Annu. Rev. Phys. Chem., 1983, 34, 631–656 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. M. Ceperley and B. J. Alder, Ground State of the Electron Gas by a Stochastic Method, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- M. Shishkin and G. Kresse, Self-consistent GW calculations for semiconductors and insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 235102 CrossRef.
- M. Van Schilfgaarde, T. Kotani and S. Faleev, Quasiparticle self-consistent GW theory, Phys. Rev. Lett., 2006, 96, 226402 CrossRef CAS PubMed.
- E. Mosconi, P. Umari and F. De Angelis, Electronic and optical properties of MAPbX3 perovskites (X = I, Br, Cl): A unified DFT and GW theoretical analysis, Phys. Chem. Chem. Phys., 2016, 18, 27158–27164 RSC.
- P. Umari, E. Mosconi and F. De Angelis, Relativistic GW calculations on CH3NH3PbI3 and CH3NH3SnI3 Perovskites for Solar Cell Applications, Sci. Rep., 2015, 4, 4467 CrossRef PubMed.
- C. Motta, F. El-Mellouhi, S. Kais, N. Tabet, F. Alharbi and S. Sanvito, Revealing the role of organic cations in hybrid halide perovskite CH3NH3PbI3, Nat. Commun., 2015, 6, 7026 CrossRef CAS PubMed.
- E. Menéndez-Proupin, P. Palacios, P. Wahnón and J. C. Conesa, Self-consistent relativistic band structure of the CH3NH3PbI3 perovskite, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 045207 CrossRef.
- M. R. Filip and F. Giustino, GW quasiparticle band gap of the hybrid organic–inorganic perovskite CH3NH3PbI3: Effect of spin–orbit interaction, semicore electrons, and self-consistency, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 245145 CrossRef.
- G. Giorgi, J. I. Fujisawa, H. Segawa and K. Yamashita, Cation role in structural and electronic properties of 3D organic–inorganic halide perovskites: A DFT analysis, J. Phys. Chem. C, 2014, 118, 12176–12183 CrossRef CAS.
- F. Brivio, K. T. Butler, A. Walsh and M. van Schilfgaarde, Relativistic quasiparticle self-consistent electronic structure of hybrid halide perovskite photovoltaic absorbers, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 155204 CrossRef.
- G. Strinati, H. J. Mattausch and W. Hanke, Dynamical aspects of correlation corrections in a covalent crystal, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 25, 2867–2888 CrossRef CAS.
- M. S. Hybertsen and S. G. Louie, First-principles theory of quasiparticles: Calculation of band gaps in semiconductors and insulators, Phys. Rev. Lett., 1985, 55, 1418–1421 CrossRef CAS.
- P. Liu, M. Kaltak, J. Klimeš and G. Kresse, Cubic scaling GW: Towards fast quasiparticle calculations, Phys. Rev. B, 2016, 94, 165109 CrossRef.
- I. E. Castelli, J. M. García-Lastra, K. S. Thygesen and K. W. Jacobsen, Bandgap calculations and trends of organometal halide perovskites, APL Mater., 2014, 2, 081514 CrossRef.
- X. Wang, W. Meng and Y. Yan, Electronic band structures and excitonic properties of delafossites: A GW -BSE study, J. Appl. Phys., 2017, 122, 085104 CrossRef.
- M. L. Tiago and J. R. Chelikowsky, Optical excitations in organic molecules, clusters, and defects studied by first-principles Green's function methods, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205334 CrossRef.
- G. Onida, L. Reining and A. Rubio, Electronic excitations: density-functional versus many-body Green's-function approaches, Rev. Mod. Phys., 2002, 74, 601–659 CrossRef CAS.
- M. Rohlfing and S. G. Louie, Electron–hole excitations and optical spectra from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 4927–4944 CrossRef CAS.
- M. T. Weller, O. J. Weber, J. M. Frost and A. Walsh, Cubic Perovskite Structure of Black Formamidinium Lead Iodide, α-[HC(NH2)2]PbI3, at 298 K, J. Phys. Chem. Lett., 2015, 6, 3209–3212 CrossRef CAS.
- E. C. Schueller, G. Laurita, D. H. Fabini, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, Crystal Structure Evolution and Notable Thermal Expansion in Hybrid Perovskites Formamidinium Tin Iodide and Formamidinium Lead Bromide, Inorg. Chem., 2018, 57, 695–701 CrossRef CAS PubMed.
- V. C. A. Taylor, D. Tiwari, M. Duchi, P. M. Donaldson, I. P. Clark, D. J. Fermin and T. A. A. Oliver, Investigating the Role of the Organic Cation in Formamidinium Lead Iodide Perovskite Using Ultrafast Spectroscopy, J. Phys. Chem. Lett., 2018, 9, 895–901 CrossRef CAS PubMed.
- F. Brivio, C. Caetano and A. Walsh, Thermodynamic Origin of Photoinstability in the CH3NH3Pb(I1−xBrx)3 Hybrid Halide Perovskite Alloy, J. Phys. Chem. Lett., 2016, 7, 1083–1087 CrossRef CAS PubMed.
- F. Brivio, J. M. Frost, J. M. Skelton, A. J. Jackson, O. J. Weber, M. T. Weller, A. R. Goñi, A. M. A. Leguy, P. R. F. Barnes and A. Walsh, Lattice dynamics and vibrational spectra of the orthorhombic, tetragonal, and cubic phases of methylammonium lead iodide, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 144308 CrossRef.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Atomistic Origins of High-Performance in Hybrid Halide Perovskite Solar Cells, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- I. Hamada, van der Waals density functional made accurate, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121103 CrossRef.
- P. Liu, B. Kim, X. Q. Chen, D. D. Sarma, G. Kresse and C. Franchini, Relativistic GW +BSE study of the optical properties of Ruddlesden-Popper iridates, Phys. Rev. Mater., 2018, 2, 75003 CrossRef CAS.
- P. Liu, C. Franchini, M. Marsman and G. Kresse, Assessing model-dielectric-dependent hybrid functionals on the antiferromagnetic transition-metal monoxides MnO, FeO, CoO, and NiO, J. Phys.: Condens. Matter, 2020, 32, 015502 CrossRef CAS PubMed.
- G. H. Wannier, The structure of electronic excitation levels in insulating crystals, Phys. Rev., 1937, 52, 191–197 CrossRef CAS.
- W. Travis, E. N. K. Glover, H. Bronstein, D. O. Scanlon and R. G. Palgrave, On the application of the tolerance factor to inorganic and hybrid halide perovskites: a revised system, Chem. Sci., 2016, 7, 4548–4556 RSC.
- G. Kieslich, S. Sun and A. K. Cheetham, An extended Tolerance Factor approach for organic–inorganic perovskites, Chem. Sci., 2015, 6, 3430–3433 RSC.
- G. Kieslich, S. Sun and A. K. Cheetham, Solid-state principles applied to organic–inorganic perovskites: new tricks for an old dog, Chem. Sci., 2014, 5, 4712–4715 RSC.
- C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guo, Formability of ABX3 (X = F, Cl, Br, I) halide perovskites, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 702–707 CrossRef CAS PubMed.
- A. Perumal, S. Shendre, M. Li, Y. K. E. Tay, V. K. Sharma, S. Chen, Z. Wei, Q. Liu, Y. Gao, P. J. S. Buenconsejo, S. T. Tan, C. L. Gan, Q. Xiong, T. C. Sum and H. V. Demir, High brightness formamidinium lead bromide perovskite nanocrystal light emitting devices, Sci. Rep., 2016, 6, 36733 CrossRef CAS PubMed.
- F. C. Hanusch, E. Wiesenmayer, E. Mankel, A. Binek, P. Angloher, C. Fraunhofer, N. Giesbrecht, J. M. Feckl, W. Jaegermann, D. Johrendt, T. Bein and P. Docampo, Efficient planar heterojunction perovskite solar cells based on formamidinium lead bromide, J. Phys. Chem. Lett., 2014, 5, 2791–2795 CrossRef CAS PubMed.
- M. Pazoki and T. Edvinsson, Metal replacement in perovskite solar cell materials: chemical bonding effects and optoelectronic properties, Sustain, Energy Fuels, 2018, 2, 1430–1445 CAS.
- T. M. Koh, K. Fu, Y. Fang, S. Chen, T. C. Sum, N. Mathews, S. G. Mhaisalkar, P. P. Boix and T. Baikie, Formamidinium-Containing Metal-Halide: An Alternative Material for Near-IR Absorption Perovskite Solar Cells, J. Phys. Chem. C, 2014, 118, 16458–16462 CrossRef CAS.
- R. Venugopal, P. I. Lin and Y. T. Chen, Photoluminescence and Raman scattering from catalytically grown ZnxCd1−xSe alloy nanowires, J. Phys. Chem. B, 2006, 110, 11691–11696 CrossRef CAS.
- R. Hill, Energy-gap variations in semiconductor alloys, J. Phys. C: Solid State Phys., 1974, 7, 521–526 CrossRef CAS.
- A. A. Mostofi, J. R. Yates, G. Pizzi, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, An updated version of wannier90: A tool for obtaining maximally-localised Wannier functions, Comput. Phys. Commun., 2014, 185, 2309–2310 CrossRef CAS.
- I. Souza, N. Marzari and D. Vanderbilt, Maximally localized Wannier functions for entangled energy bands, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035109 CrossRef.
- T. Etienne, E. Mosconi and F. De Angelis, Dynamical Origin of the Rashba Effect in Organohalide Lead Perovskites: A Key to Suppressed Carrier Recombination in Perovskite Solar Cells?, J. Phys. Chem. Lett., 2016, 7, 1638–1645 CrossRef CAS PubMed.
- E. M. Hutter, M. C. Gélvez-Rueda, A. Osherov, V. Bulović, F. C. Grozema, S. D. Stranks and T. J. Savenije, Direct-indirect character of the bandgap in methylammonium lead iodide perovskite, Nat. Mater., 2017, 16, 115–120 CrossRef CAS PubMed.
- A. Stroppa, D. Di Sante, P. Barone, M. Bokdam, G. Kresse, C. Franchini, M.-H. Whangbo and S. Picozzi, Tunable ferroelectric polarization and its interplay with spin–orbit coupling in tin iodide perovskites, Nat. Commun., 2014, 5, 5900 CrossRef CAS PubMed.
- M. Baranowski and P. Plochocka, Excitons in Metal-Halide Perovskites, Adv. Energy Mater., 2020, 1903659 CrossRef.
- T. J. Whitcher, J. X. Zhu, X. Chi, H. Hu, D. Zhao, T. C. Asmara, X. Yu, M. B. H. Breese, A. H. Castro Neto, Y. M. Lam, A. T. S. Wee, E. E. M. Chia and A. Rusydi, Importance of Electronic Correlations and Unusual Excitonic Effects in Formamidinium Lead Halide Perovskites, Phys. Rev. X, 2018, 8, 1–10 Search PubMed.
- M. Kato, T. Fujiseki, T. Miyadera, T. Sugita, S. Fujimoto, M. Tamakoshi, M. Chikamatsu and H. Fujiwara, Universal rules for visible-light absorption in hybrid perovskite materials, J. Appl. Phys., 2017, 121, 115501 CrossRef.
- P. F. Ndione, Z. Li and K. Zhu, Effects of alloying on the optical properties of organic-inorganic lead halide perovskite thin films, J. Mater. Chem. C, 2016, 4, 7775–7782 RSC.
- G. Mannino, I. Deretzis, E. Smecca, A. La Magna, A. Alberti, D. Ceratti and D. Cahen, Temperature-Dependent Optical Band Gap in CsPbBr3, MAPbBr3, and FAPbBr3 Single Crystals, J. Phys. Chem. Lett., 2020, 11, 2490–2496 CrossRef CAS PubMed.
- C. L. Davies, J. Borchert, C. Q. Xia, R. L. Milot, H. Kraus, M. B. Johnston and L. M. Herz, Impact of the Organic Cation on the Optoelectronic Properties of Formamidinium Lead Triiodide, J. Phys. Chem. Lett., 2018, 9, 4502–4511 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © the Owner Societies 2020 |