Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High-resolution resonance-enhanced multiphoton photoelectron circular dichroism†
Alexander
Kastner
 a,
Greta
Koumarianou
a,
Greta
Koumarianou
 b,
Pavle
Glodic
b,
Pavle
Glodic
 b,
Peter C.
Samartzis
b,
Peter C.
Samartzis
 b,
Nicolas
Ladda
a,
Simon T.
Ranecky
a,
Tom
Ring
a,
Sudheendran
Vasudevan
a,
Constantin
Witte
a,
Hendrike
Braun
b,
Nicolas
Ladda
a,
Simon T.
Ranecky
a,
Tom
Ring
a,
Sudheendran
Vasudevan
a,
Constantin
Witte
a,
Hendrike
Braun
 a,
Han-Gyeol
Lee
a,
Arne
Senftleben
a,
Han-Gyeol
Lee
a,
Arne
Senftleben
 a,
Robert
Berger
c,
G. Barratt
Park
a,
Robert
Berger
c,
G. Barratt
Park
 de,
Tim
Schäfer
de,
Tim
Schäfer
 *de and
Thomas
Baumert
*de and
Thomas
Baumert
 a
a
aUniversität Kassel, Heinrich-Plett-Str. 40, 34132 Kassel, Germany
bInstitute of Electronic Structure and Lasers, Foundation for Research and Technology – Hellas (FORTH), P. O. Box 1527, 71110 Heraklion, Greece
cFachbereich Chemie, Philipps-Universität Marburg, Hans-Meerwein-Straße 4, 35032 Marburg, Germany
dGeorg-August-Universität Göttingen, Tammannstr. 6, 37077 Göttingen, Germany. E-mail: tschaef4@gwdg.de
eMax Planck Institut für Biophysikalische Chemie, Am Fassberg 11, 37077 Göttingen, Germany
First published on 16th March 2020
Abstract
Photoelectron circular dichroism (PECD) is a highly sensitive enantiospecific spectroscopy for studying chiral molecules in the gas phase using either single-photon ionization or multiphoton ionization. In the short pulse limit investigated with femtosecond lasers, resonance-enhanced multiphoton ionization (REMPI) is rather instantaneous and typically occurs simultaneously via more than one vibrational or electronic intermediate state due to limited frequency resolution. In contrast, vibrational resolution in the REMPI spectrum can be achieved using nanosecond lasers. In this work, we follow the high-resolution approach using a tunable narrow-band nanosecond laser to measure REMPI-PECD through distinct vibrational levels in the intermediate 3s and 3p Rydberg states of fenchone. We observe the PECD to be essentially independent of the vibrational level. This behaviour of the chiral sensitivity may pave the way for enantiomer specific molecular identification in multi-component mixtures: one can specifically excite a sharp, vibrationally resolved transition of a distinct molecule to distinguish different chiral species in mixtures.
1 Introduction
Enantiomer-specific spectroscopy of chiral molecules in the gas phase1 is a dynamically evolving research field, where techniques like e.g. microwave three-wave mixing,2–5 chiral-sensitive high harmonic generation,6–8 controlled enantioselective orientation with an optical centrifuge,9 or Coulomb explosion imaging for absolute configuration determination10–14 have been developed in recent years. Chiral signatures are also present in both the photoion and photoelectron signal when chiral molecules are ionized with circularly polarized light. Circular dichroism (CD) in the ion yield has been investigated using resonance enhanced multi-photon ionization (REMPI) in combination with mass spectrometry.15–20 Coulomb explosion imaging techniques have recently allowed transient chirality to be investigated in the molecular frame.21 In contrast to REMPI-based CD of the photoion yield, which arises from weak interference effects between electric and magnetic dipole transition moments, the chiral signature of the photoelectron angular distribution after laser ionization originates from an electric dipole interaction alone. In 1976, it was theoretically predicted that the photoionization of optically active molecules by circularly polarized light would give rise to a substantial forward–backward asymmetry in the angular distribution of the photoelectrons.22 This effect, known as photoelectron circular dichroism (PECD), was first demonstrated by single-photon ionization of bromocamphor using a synchrotron source in 2001.23 Subsequently, PECD was also demonstrated on other bicyclic ketones using pulsed femtosecond table-top laser systems to drive 2 + 1 REMPI.24,25 The angular distribution of photoelectrons was measured using velocity map imaging.26–28 Multiphoton PECD has also been observed for methyloxirane29 and limonene.30,31 Because PECD has been observed when using single-photon ionization out of an achiral core–shell initial orbital,32,33 it has been interpreted as being largely a final state effect, strongly influenced by the long-range scattering potential.34 In contrast, PECD has also been observed for photoelectrons with high kinetic energy above 500 eV resulting from a Fano interference.35 PECD is sensitive to the final vibrational level of the cation,34,36,37 conformation of the molecule,37,38 and to subcycle interactions with tailored bichromatic light fields.39,40The underlying electric dipole interaction makes PECD very sensitive to small changes in the amount of enantiomeric excess (e.e.) and consequently the technique shows promise as a highly sensitive analytical tool24,25,41–44 exhibiting sub one percent sensitivity.45 It is possible to measure enantiomeric excesses in multi-component mixtures by recording mass-selected PECD spectra with electron image-ion mass coincidence methods.46 This approach requires significant experimental effort so that alternative methods are desirable. For instance, PECD in high-resolution REMPI in molecular beams using nanosecond laser systems could be a promising spectroscopic approach as speculated previously by Janssen et al.47 The technique permits vibrational resolution, so that different chiral molecules in mixtures can be distinguished by their vibrational features in the REMPI spectra. This has already been demonstrated in REMPI-CD experiments that have taken advantage of high laser resolution to observe sign changes when investigating REMPI-CD via different vibrational levels of the intermediate electronic state48 or to distinguish different conformers.49 PECD spectra belonging to a certain molecular species can also be recorded by ionizing via narrow, unambiguously assigned REMPI transitions. Of course, for these kinds of experiments rotational and vibrational degrees of freedom should be cooled, which can be efficiently achieved using supersonic molecular beams.
Recently, a femtosecond pump–probe setup was used to observe picosecond dynamics in the 3s Rydberg intermediate state of fenchone, one of the typical benchmark molecules for PECD measurements.50 The PECD value was found to vary on a picosecond timescale. However, due to the large frequency bandwidth of the femtosecond laser pulse (30 meV), no vibrational resolution could be achieved. In other studies on fenchone, the dependence on intermediate electronic state and photoelectron kinetic energy has been investigated.31,51 This information provides valuable benchmarks for emerging theoretical descriptions of multiphoton PECD,25,52–56 and coherent control approaches.57
In this contribution we demonstrate partially vibrationally resolved multiphoton PECD of fenchone, obtained by high-resolution 2 + 1 REMPI via intermediate Rydberg states with a nanosecond pulsed dye laser system. Earlier we observed nanosecond-pulse PECD without vibrational resolution with the help of a frequency tripled Nd:YAG laser.58 Experiments are supported by theoretical modeling of the electronically excited states' vibrational level structure. In the low-energy region of the 3s state, the features observed in a previous 2 + 1 REMPI spectrum51 can be assigned to single vibrational eigenstates. As the photon energy is increased, the density of vibrational states increases rapidly and intramolecular vibrational redistribution (IVR) dynamics of the vibrational wavepacket that is excited on the 3s Rydberg state become important. We do not observe significantly different PECD values when ionizing fenchone either via a resolved eigenstate or via a wavepacket made up of many strongly interacting vibrational levels. Hence, the vibrational character of the intermediate 3s Rydberg state does not substantially influence the PECD of fenchone after 2 + 1 REMPI. This work is the first demonstration of PECD employing tunable dye laser systems providing vibrational resolution. The approach presented here based on high-resolution REMPI spectroscopy has the potential to facilitate enantiomer-specific analytical measurements of multi-component mixtures.
2 Methods
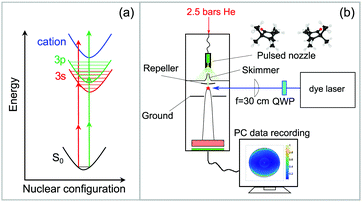
2.1 Experimental setup and data evaluation
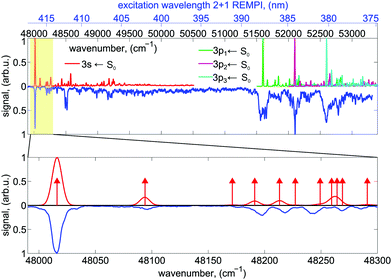
The experimental setup is shown in Fig. 1. A commercial dye laser (Lambda Physik LPD 3000) was pumped by a Lambda Physik LPX 315i XeCl excimer laser (10 Hz, 308 nm, 25 ns). The output of the dye laser was tuned over the wavelength region 375–420 nm using the laser dyes QUI, PBBO, and Exalite 416. The pulse energy was typically 3–6 mJ and the bandwidth was 0.1 cm−1. The approximate laser wavelength was measured using an Avantes AvaSpec 3648 spectrometer (324–482 nm range, about 0.04 nm resolution). A more precise calibration was obtained by comparing the peak positions in the REMPI spectrum to those that were measured previously,51 which were calibrated to an accuracy of ±0.03 cm−1 using a high-precision wavemeter (HighFinesse, WS7).The high-resolution spectrum of fenchone51 recorded with linearly polarized light shows the partially resolved vibrational structure of 3s and 3p electronic states (shown in blue in Fig. 2). It agrees in the lower wavenumber range nicely with the spectrum reported by Driscoll et al.,59 who recorded the 3s region. Different electronic intermediate states can be populated by the two-photon transition. The two lowest-lying electric dipole-allowed Rydberg transitions lead to electronic intermediates having 3s and 3p Rydberg character.60 The transition from these intermediates to the continuum was observed to be governed by a Δv = 0 propensity rule in a previous femtosecond experiment.51
The laser beam polarization was initially linear and oriented in the plane of the detector. An achromatic quarter-wave plate (B.Halle, 300–470 nm achromatic with air gap) was used to convert linearly polarized (LIN) to left circularly polarized (LCP) or right circularly polarized (RCP) light. The wavelength scan was split into three parts corresponding to the dyes used. The quality of polarization was determined using a Glan-Laser polarizer (ThorLabs GL10) and a power meter (Ophir Nova II). The circularity of polarization is expressed via the Stokes |S3| parameter and has been measured for each dye at different wavelength settings. Except for one measurement point at 396 nm, where the laser power was unstable, |S3| was well above 96%. No correction of the experimental data with respect to the |S3| value was performed.
The enantiopure (S)-(+)- and (R)-(−)-fenchone samples were purchased from Sigma-Aldrich with a specified purity of 99.2% (fenchone) and used without further purification. The enantiomeric excess (e.e.) as measured by gas chromatography was 99.9% for (S)-(+)-fenchone and 84% for (R)-(−)-fenchone.45 Liquid fenchone, soaked into an inert cotton wad, was evaporated in a heatable sample compartment near the tip of a home-built pulsed solenoid valve nozzle, which is based on the Even–Lavie design61 and has been described in detail previously.62 The fenchone sample was heated to about 100 °C, and 2.5 bars of He was used as a backing gas. The supersonic beam was singly skimmed before entering the detection chamber, where it is intersected by the laser beam at a 90° angle.
An f = 300 mm plano-convex quartz lens was used to focus the laser beam into the interaction region of an imaging photoelectron spectrometer. The focal distance was chosen to avoid power broadening of the absorption lines. The photoelectron spectrometer, which has been explained in detail in previous work,63 uses velocity map-imaging (VMI) as demonstrated by Eppink and Parker27,28 with the ion focusing lens included in the geometry of the repeller and ground plates (see Fig. 1b). The VMI provides an energy resolution of about ΔE/E ≈ 5%. Energy calibration of the VMI was performed using ionization of Xe to the 2P1/2 and 2P3/2 continuum states via a four-photon transition driven by the third harmonic of a Nd:YAG laser. The VMI can be used to project either the photoelectrons or the photoions onto a home-built imaging detector composed of multi-channel plates (BASPIK) with a 50 mm diameter and a P47 phosphor screen (Proxivision). Three dimensional photoelectron angular distributions (PADs) are projected onto the detector and measured as PAD images using a 1.4 million pixel CCD camera (Unibrain Fire-i 702b). The VMI voltage was set such that photoelectrons with kinetic energy up to about 4.1 eV could be measured. Alternatively, ion TOF mass spectra can be recorded on an oscilloscope (Hameg model 1507-3; 150 MHz, 200 MS/s) via a capacitively coupled output. At each wavelength, photoelectron images for LIN, LCP, and RCP laser light polarization were averaged for 1800 laser pulses (∼3 minutes). The PECD image was calculated by subtracting the averaged RCP PAD image from the averaged LCP PAD image.
The original three-dimensional photoelectron distribution is reconstructed using an Abel inversion routine, where two different algorithms have been used. The LIN PADs were evaluated by a polar onion peeling64 algorithm written in MATLAB. The polar onion peeling algorithm runs on the pixel grid provided by the camera. The LCP and RCP PADs were evaluated using a C++ based pBasex algorithm,65 which was kindly provided by G. A. Garcia from SOLEIL. Details on the evaluation can be found in the Supporting Information. We used a Legendre polynomial basis function set that includes both odd and even order polynomials up to the 6th order following Yang's theorem.66 Using the pBasex algorithm, different peaks in the photoelectron spectrum can be evaluated separately. The chiral signature is contained in the odd-order Legendre polynomial coefficients. The magnitude of PECD can be derived by computing a sum over the odd-order coefficients ci normalized to the total signal c0, denoted as linear PECD:41
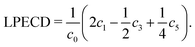 | (1) |
The LPECD value for a measurement is derived using a weighted average over the range of radii contained within the full width at half maximum (FWHM) of the peak signal.
2.2 Computational methods
Equilibrium structures and harmonic vibrational frequencies of fenchone in the electronic ground state and various Rydberg states were calculated on the approximate second order coupled cluster level (CC2) using the so-called resolution of the identity (RI) as implemented in the quantum chemistry program Turbomole.67 As in some of the calculations reported in previous work,52 we have chosen the cc-pVTZ basis set on all atoms except oxygen. For the latter we chose the t-aug-cc-pVTZ basis set. For C and H we chose the corresponding recommended RI basis sets (cbas, jkbas), for O we used the basis set recommended for d-aug-cc-pVTZ for fitting of the Coulomb and exchange terms (jkbas) and the original t-aug-cc-pVTZ basis also as RI basis set within the electron correlation treatment (cbas). The latter choice is not ideal, but resulted, in contrast to test calculations with the RI basis recommended for d-aug-cc-pVTZ, only in vertical excitation wavenumbers into the relevant Rydberg states that are systematically lower by about 46 cm−1 to 50 cm−1. Resulting structural changes in the electronic ground state were found to be negligible. Electrons in the 11 energetically lowest molecular orbitals, which are composed mostly of atomic 1s orbitals of oxygen and carbon, were kept frozen in the electron correlation treatment (frozen core approximation). Convergence criteria for the self-consistent field (SCF) energies were chosen to be 10−9Eh. Convergence criteria for the root mean square of the density matrix used in energy minimization and vibrational frequency calculations was on the order of 10−8. Ground state coupled cluster equations were iterated until the energy change between two cycles remained below 10−8Eh. The convergence threshold for the norm of residual vectors in subsequent linear response calculations of excitation energies was chosen on the 10−6 level. Convergence criteria for equilibrium structures were imposed such that the norm of analytic gradients of the energy with respect to displacements of the nuclei remained below 10−5Eha0−1 and the estimated energy change between two optimization steps was below 10−8Eh. Franck–Condon profiles for excitations from the electronic ground state into the various Rydberg states were calculated with a development version of the hotFCHT program68–70 using both time-dependent and time-independent methodologies in the harmonic approximation. In the time-dependent approach, a Gaussian lineshape function with a full width at half maximum of 10 cm−1 was chosen to mimic the approximate width of the 000 transition region of the 3s state. The time-independent approach was utilized with pre-screening criteria such that at least 97% of the total integrated FC profile could be obtained. A maximum of five simultaneously excited normal modes was included for this purpose. The graining in the time-independent calculations was chosen to be 1 cm−1. The calculated spectra are compared with experiment in Fig. 2.3 Results and discussion
3.1 Resonance enhanced multiphoton ionization
The 2 + 1 REMPI spectrum recorded with linearly polarized light shown in blue in Fig. 2 probes the excitation via the 3s state at energies >48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and the excitation via the 3p states at energies >51
000 cm−1 and the excitation via the 3p states at energies >51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1. Vibronic transitions are on average well separated below excitation energies of 48
500 cm−1. Vibronic transitions are on average well separated below excitation energies of 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1. In this region, the nanosecond laser (0.1 cm−1 bandwidth) populates mostly single vibrational eigenstates during the REMPI process.
300 cm−1. In this region, the nanosecond laser (0.1 cm−1 bandwidth) populates mostly single vibrational eigenstates during the REMPI process.
With increasing wavenumber, however, the vibrational density of states grows rapidly, so that zero-order bright states are excited that can couple to a manifold of dark vibrational states located within the 0.1 cm−1 laser bandwidth leading at higher wavenumbers to IVR probably on a sub-picosecond timescale.71 Spectral lines at energies above 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 are significantly broadened indicating a fast dissipation channel out of the 3p Rydberg states. In the plots, the origins of the computed Franck–Condon profiles were shifted by about 4500 cm−1 (namely 4348 cm−1, 4257 cm−1, 4466 cm−1, 4746 cm−1 for 3s, 3p1, 3p2, 3p3, respectively) to higher wavenumbers compared to the computed 000 transitions to match the experimentally observed spectrum. This corresponds only to one of several tentative assignments that appear possible for the three components of the 3p Rydberg state. The lowest fundamental vibration at 48
500 cm−1 are significantly broadened indicating a fast dissipation channel out of the 3p Rydberg states. In the plots, the origins of the computed Franck–Condon profiles were shifted by about 4500 cm−1 (namely 4348 cm−1, 4257 cm−1, 4466 cm−1, 4746 cm−1 for 3s, 3p1, 3p2, 3p3, respectively) to higher wavenumbers compared to the computed 000 transitions to match the experimentally observed spectrum. This corresponds only to one of several tentative assignments that appear possible for the three components of the 3p Rydberg state. The lowest fundamental vibration at 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 090 cm−1 is a delocalized butterfly motion of the ring systems. Vibrations between 48
090 cm−1 is a delocalized butterfly motion of the ring systems. Vibrations between 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 cm−1 and 48
170 cm−1 and 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 are methyl torsional and skeletal modes. More details about the vibrations can be found in the Supporting Information.
300 cm−1 are methyl torsional and skeletal modes. More details about the vibrations can be found in the Supporting Information.
We recorded photoelectron images at 27 ((R)-(−)-fenchone) and 34 ((S)-(+)-fenchone) selected excitation wavelengths between 375 nm and 420 nm for LIN, LCP, and RCP laser light. At wavelengths longer than 412 nm, the wavelength was tuned to the center of each resolved spectral feature in the REMPI spectrum. At the employed laser pulse energy no signal was observed off resonance. At wavelengths shorter than 412 nm, where the onset of a continuous unresolved background is observed, PAD images were recorded at 1 nm intervals. The photoelectron spectrum (PES) obtained for different excitation wavelengths of linearly polarized light are shown in Fig. 3(a). Each PES contains a sharp, intense peak corresponding to ionization from the 3s intermediate state. At wavelengths shorter than about 389 nm a weak second contribution originating from excitation of the 3p intermediate states is observed in the PES. As the wavelength is scanned, the photoelectron peak position shifts by an amount equal to the change in the one-photon energy in agreement with findings in a previous femtosecond experiment.51 The scaling of photoelectron energy with excitation wavelength agrees well with hc/λ − (IP − E3s,3p) (shown as white lines in Fig. 3(a)). IP = 8.5 eV is the adiabatic ionization energy of fenchone,51,72 and E3s = 5.95 eV and E3p ≈ 6.37 eV are the electronic energies of the 3s and 3p intermediate states.51 The photoelectron energy scaling indicates essentially vibrational-energy conserving one-photon ionization out of the intermediate states to the cation, which points to a negligible shift of potentials with respect to structural parameters.
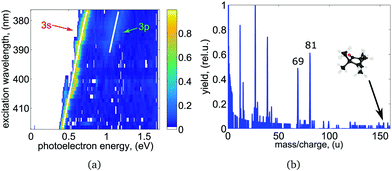 | ||
| Fig. 3 (a) Wavelength-dependent PES derived from the LIN PADs for (S)-(+)-fenchone after Abel-inversion using polar onion peeling.64 Every row represents a single measurement, where up to two distinct electronic intermediates were observed. The expected energy scaling with ħω is indicated by the white lines. (b) Mass spectrum for (S)-(+)-fenchone obtained at the 3s band origin at 416.57 nm. A detailed discussion can be found in the text. | ||
The intensity of the 3p peak relative to the 3s peak is significantly weaker than it is in the PES recorded in the same spectral range with femtosecond laser pulse ionization, where the contribution of the 3p state is larger than the contribution of the 3s state (see Fig. 5 of ref. 51). However, we observe a sharp increase in the total ion signal of about one order of magnitude when the 3p excitation threshold is reached. See excitation energies higher than 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 in Fig. 2 and compare to the signal below 51
500 cm−1 in Fig. 2 and compare to the signal below 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, which corresponds to transitions via the 3s state and is non-zero. This observation is consistent with internal conversion (IC) from the 3p state to the 3s state, leading to a shortened lifetime of the 3p state and hence to less ionization out of this state. Instead, molecules are ionized from the 3s state and emit photoelectrons carrying the energy signature of the 3s state (i.e. without the energy that has been converted to vibrational excitation in the 3s state). In general IC to the electronic ground state S0 or to the energetically low-lying S1 (n → π*) excited state is also energetically possible. These states would be highly vibrationally excited after IC and are not observed in our experiment probably due to negligible Franck–Condon factors for ionization at the energy that is probed. However, keeping in mind that the total ion signal grows when exciting via the 3p state, and that the photoelectrons carry the energy signature from the 3s state, our observations suggest that 3p → 3s IC may be much more rapid than 3p → S0/S1 IC due to the unfavorable Franck–Condon overlap for the latter processes. In contrast, when 2 + 1 REMPI via the 3p state is performed using a femtosecond laser pulse, the timescale of the experiment is too short for 3p → 3s IC to occur, and direct ionization out of the 3p state is observed more frequently.51 The intensity of the 3p Rydberg state peak in the photoelectron spectrum is therefore significantly higher than observed in the nanosecond laser experiment.
500 cm−1, which corresponds to transitions via the 3s state and is non-zero. This observation is consistent with internal conversion (IC) from the 3p state to the 3s state, leading to a shortened lifetime of the 3p state and hence to less ionization out of this state. Instead, molecules are ionized from the 3s state and emit photoelectrons carrying the energy signature of the 3s state (i.e. without the energy that has been converted to vibrational excitation in the 3s state). In general IC to the electronic ground state S0 or to the energetically low-lying S1 (n → π*) excited state is also energetically possible. These states would be highly vibrationally excited after IC and are not observed in our experiment probably due to negligible Franck–Condon factors for ionization at the energy that is probed. However, keeping in mind that the total ion signal grows when exciting via the 3p state, and that the photoelectrons carry the energy signature from the 3s state, our observations suggest that 3p → 3s IC may be much more rapid than 3p → S0/S1 IC due to the unfavorable Franck–Condon overlap for the latter processes. In contrast, when 2 + 1 REMPI via the 3p state is performed using a femtosecond laser pulse, the timescale of the experiment is too short for 3p → 3s IC to occur, and direct ionization out of the 3p state is observed more frequently.51 The intensity of the 3p Rydberg state peak in the photoelectron spectrum is therefore significantly higher than observed in the nanosecond laser experiment.
Pump–probe experiments conducted at 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ± 200 cm−1 have shown that the 3s state undergoes internal conversion to the electronic ground state on a timescale of approximately 3.3 ps.50 The width of the vibrationally resolved lines in the 48
800 ± 200 cm−1 have shown that the 3s state undergoes internal conversion to the electronic ground state on a timescale of approximately 3.3 ps.50 The width of the vibrationally resolved lines in the 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–48
000–48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 region of our spectrum provides only a lower limit to the lifetime since the rotational structure is not resolved. Assuming a 10 K rotational temperature, and using the rotational constants reported in ref. 73, we obtain a simulated rotational contour with a FWHM of approximately 5 cm−1, which depends by only a small amount on which component of the rank-two transition moment tensor is chosen. This value is only slightly narrower than the observed 9.1 cm−1 FWHM of the 000 transition. The observed width corresponds to a lower limit of about 0.6 ps for the lifetime. However, the reader should keep in mind that this value is only a lower limit as other phenomena can also lead to spectral line broadening.
500 cm−1 region of our spectrum provides only a lower limit to the lifetime since the rotational structure is not resolved. Assuming a 10 K rotational temperature, and using the rotational constants reported in ref. 73, we obtain a simulated rotational contour with a FWHM of approximately 5 cm−1, which depends by only a small amount on which component of the rank-two transition moment tensor is chosen. This value is only slightly narrower than the observed 9.1 cm−1 FWHM of the 000 transition. The observed width corresponds to a lower limit of about 0.6 ps for the lifetime. However, the reader should keep in mind that this value is only a lower limit as other phenomena can also lead to spectral line broadening.
The photoionization mass spectrum obtained at the band origin of the 3s state at 416.57 nm is shown in Fig. 3(b). No parent ion is observed and the mass spectrum shows strong fragmentation of the molecules. Prominent fragments with largest mass-to-charge ratio have masses 69 and 81 amu. The observations made here are in agreement with previous nanosecond findings.58 It should be noted that the REMPI spectrum presented in Fig. 2 and 5 has been measured in a previous study at significantly reduced laser pulse power and was recorded on the parent ion mass.51 An increase in laser intensity leads to increased fragmentation but no change in the PECD as has been observed in a previous fs experiment.41 In neither study was the PES or PECD strongly influenced by the fragmentation of the molecules. We thereby conclude that fragmentation of the molecules happens after the ionization in agreement with previous findings.41,58 In a recent coincidence experiment on methyloxirane, a link between PECD and the fragmentation channels in strong field ionization has been reported.74
3.2 PECD evaluation
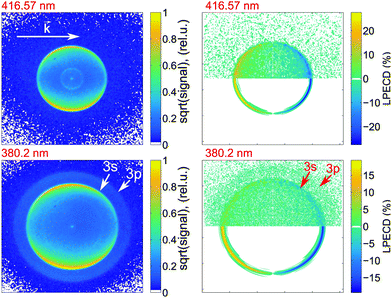
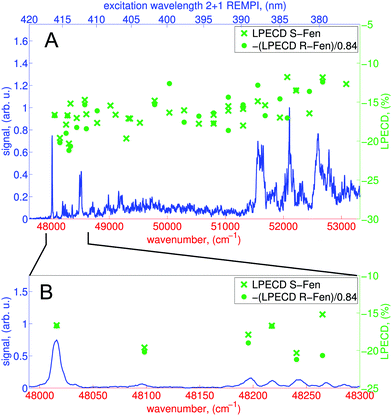
We calculate the raw PECD image at each wavelength by subtracting the RCP PAD image from the LCP PAD image.41 In Fig. 4 we show the antisymmetric part of the raw and Abel-inverted PECD image for the 000 transition at 416.57 nm and for excitation at 380.2 nm, where ionization via either the 3s or 3p states is possible. We observe a distinct forward/backward asymmetry of emitted photoelectrons with respect to the propagation axis of light.From the raw PECD images, we calculate LPECD values for ionization via the 3s Rydberg state at each selected wavelength as described in Section 2.1. The results for both enantiomers are shown in Fig. 5 alongside the high-resolution REMPI spectrum of fenchone. Within the error of our experiment we observe the same magnitude (but opposite sign) for the two enantiomers taking into account the previously determined45 enantiomeric purity of 84% of (R)-(−)-fenchone. The LPECD decreases slightly in magnitude at shorter wavelengths. We could not extract reliable LPECD values for ionization from the 3p Rydberg state due to poor signal-to-noise ratio (see Fig. 4). Therefore, we were unable to conclude whether the sign change of the LPECD value when ionizing from 3p Rydberg states observed in the femtosecond laser experiments51 also happens in the nanosecond laser experiments. In the ESI† we also show the contributions of c1, c3, and c5 to the LPECD value normalized to c0 following eqn (1). The main contribution originates from c1.
The LPECD values recorded after nanosecond laser ionization are larger in magnitude than the LPECD values recorded after femtosecond laser ionization51 over the measured energy range. The wavelength-dependent LPECD curves of the two measurements exhibit the same shape but are shifted to one another by an LPECD value of 2.5%. However, it should be noted that the femtosecond laser LPECD values were recorded using an effusive beam source, whereas the nanosecond laser LPECD values were recorded using a pulsed molecular beam. Hence, vibrational excitation in the electronic ground state was greater in the femtosecond laser experiment and caution should be taken in making a direct comparison of the results. To make such a comparison, future experiments should use the same molecular beam source to identify differences caused only by the excitation laser pulse duration.
As described in the previous section, we distinguish different regions of the spectrum in which the molecular dynamics are different. First, at wavelengths between 416.57 nm and 412 nm the density of vibrational levels in the 3s state is low so that we ionize fenchone essentially out of a true vibrational eigenstate. Second, at wavelengths between 412 nm and 388 nm, the density of states (DOS) is high, so that we ionize molecules whose vibrational energy is redistributed over a large number of coupled vibrational levels of the 3s state after IVR. Mode selective IC to the electronic ground state could also influence the vibrational state distribution.50 Third, at wavelengths shorter than 388 nm we excite both the 3s and the 3p states. However, internal conversion via 3p dominates the mechanism for ionization via 3s. With increasing wavenumber, however, the vibrational density of states grows rapidly. Hence, the character of the high-lying 3s vibrational states that are accessed in this region is no longer governed by Franck–Condon overlap with the S0 ground state, but rather by vibronic overlap with low-lying bright vibrational states of 3p.
When comparing the LPECD values in the distinct spectral regions described above, we do not observe any abrupt changes of LPECD values. Furthermore, we do not observe any pronounced features in the LPECD values that correspond with resolved vibrational bands in the REMPI spectrum at the 3s origin between 416.57 nm and 412 nm. The LPECD value varies by ca. ±3% (absolute) when ionizing via different vibrational states, which is at the level of the experimental error of this measurement.
We therefore conclude that the vibrational energy of the intermediate 3s Rydberg state does not significantly influence the PECD of fenchone after 2 + 1 REMPI. This perhaps reflects the Rydberg character of the intermediate electronic state. The electron's probability density is located relatively far from the molecular frame prior to ionization. The movement of the nuclei might therefore have only minor influence on the outgoing electron. This could be advantageous for future experiments as vibrational levels of the intermediate Rydberg state can be treated as spectator states, which do not influence the photoelectron angular distribution or energy in experiments on a nanosecond timescale. However, further experiments on different chiral molecules need to be done to clarify whether these observations can be generalized.
4 Summary and conclusion
We used nanosecond laser pulses to obtain the photoelectron circular dichroism (PECD) of the chiral molecule fenchone after 2 + 1 resonance enhanced multi-photon ionization (REMPI) via the 3s and 3p Rydberg states for selected ionization energies in the spectral range between 375 nm and 420 nm. In contrast to previous studies using femtosecond laser ionization, we resolve vibrational structure in the REMPI spectrum, and assign LPECD values to distinct intermediate vibrational levels of the 3s Rydberg state. We do not observe any strong dependence of the LPECD value on the vibrational level of the intermediate state, which might be a consequence of its Rydberg electronic character. An accompanying computational study identifies the different vibrational modes that give rise to the peaks observed in the 2 + 1 REMPI spectrum. We demonstrate the feasibility of PECD measurements with tabletop nanosecond dye laser systems, which can be used to investigate chiral mixtures via high resolution REMPI assisted PECD measurements.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Theofanis Kitsopoulos for support and feedback, and thank G. A. Garcia for sharing the algorithm. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Projektnummer 328961117 – SFB 1319 and ELCH. A. K., G. B. P. and T. S. acknowledge financial support within the LaserLab Europe network (Grant Agreement No. 654148). T. S. acknowledges support by the DFG under grant INST186/1302-1. P. S. gratefully acknowledges support by HELLAS-CH (MIS 5002735) implemented under “Action for Strengthening Research and Innovation Infrastructures”, funded by the Operational Programme “Competitiveness, Entrepreneurship and Innovation” (NSRF 2014–2020) and co-financed by Greece and the European Union (European Regional Development Fund). Open Access funding provided by the Max Planck Society. R. B. acknowledges the Center for Scientific Computing (CSC) Frankfurt for providing computer time.Notes and references
- Chiral Recognition in the Gas Phase, ed. A. Zehnacker, CRC Press, Boca Raton, 2010 Search PubMed.
- E. Hirota, Proc. Jpn. Acad., Ser. B, 2012, 88, 120–128 CrossRef CAS PubMed.
- D. Patterson and J. M. Doyle, Phys. Rev. Lett., 2013, 111, 23008 CrossRef PubMed.
- D. Patterson, M. Schnell and J. Doyle, Nature, 2013, 497, 475–477 CrossRef CAS PubMed.
- S. Eibenberger, J. Doyle and D. Patterson, Phys. Rev. Lett., 2017, 118, 123002 CrossRef PubMed.
- A. E. Cireasa, R. Boguslavskiy, B. Pons, M. C. H. Wong, D. Descamps, S. Petit, H. Ruf, N. Thiré, A. Ferré, J. Suarez, J. Higuet, B. E. Schmidt, A. F. Alharbi, F. Légaré, V. Blanchet, B. Fabre, S. Patchkovskii, O. Smirnova, Y. Mairesse and V. R. Bhardwaj, Nat. Phys., 2015, 11, 654 Search PubMed.
- D. Baykusheva and H. J. Wörner, Phys. Rev. X, 2018, 8, 031060 Search PubMed.
- O. Neufeld, D. Ayuso, P. Decleva, M. Y. Ivanov, O. Smirnova and O. Cohen, Phys. Rev. X, 2019, 9, 031002 Search PubMed.
- A. A. Milner, J. A. M. Fordyce, I. MacPhail-Bartley, W. Wasserman, V. Milner, I. Tutunnikov and I. S. Averbukh, Phys. Rev. Lett., 2019, 122, 223201 CrossRef CAS PubMed.
- M. Pitzer, M. Kunitski, A. S. Johnson, T. Jahnke, H. Sann, F. Sturm, L. P. H. Schmidt, H. Schmidt-Böcking, R. Dörner, J. Stohner, J. Kiedrowski, M. Reggelin, S. Marquardt, A. Schießer, R. Berger and M. S. Schöffler, Science, 2013, 341, 1096–1100 CrossRef CAS PubMed.
- P. Herwig, K. Zawatzky, M. Grieser, O. Heber, B. Jordon-Thaden, C. Krantz, O. Novotny, R. Repnow, V. Schurig, D. Schwalm, Z. Vager, A. Wolf, O. Trapp and H. Kreckel, Science, 2013, 342, 1084–1086 CrossRef CAS PubMed.
- M. Pitzer, G. Kastirke, P. Burzynski, M. Weller, D. Metz, J. Neff, M. Waitz, F. Trinter, L. P. H. Schmidt, J. B. Williams, T. Jahnke, H. Schmidt-Böcking, R. Berger, R. Dörner and M. Schöffler, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 234001 CrossRef.
- M. Pitzer, G. Kastirke, M. Kunitski, T. Jahnke, T. Bauer, C. Goihl, F. Trinter, C. Schober, K. Henrichs, J. Becht, S. Zeller, H. Gassert, M. Waitz, A. Kuhlins, H. Sann, F. Sturm, F. Wiegandt, R. Wallauer, L. P. H. Schmidt, A. S. Johnson, M. Mazenauer, B. Spenger, S. Marquardt, S. Marquardt, H. Schmidt-Bocking, J. Stohner, R. Dorner, M. Schoffler and R. Berger, ChemPhysChem, 2016, 17, 2465–2472 CrossRef CAS PubMed.
- M. Pitzer, R. Berger, J. Stohner, R. Dörner and M. Schöffler, Chimia, 2018, 72, 384–388 CrossRef CAS PubMed.
- U. Boesl von Grafenstein and A. Bornschlegl, ChemPhysChem, 2006, 7, 2085–2087 CrossRef PubMed.
- R. Li, R. Sullivan, W. Al-Basheer, R. M. Pagni and R. N. Compton, J. Chem. Phys., 2006, 125, 144304 CrossRef CAS PubMed.
- H. G. Breunig, G. Urbasch, P. Horsch, J. Cordes, U. Koert and K.-M. Weitzel, ChemPhysChem, 2009, 10, 1199–1202 CrossRef CAS PubMed.
- J. Lepelmeier, K. Titze, A. Kartouzian, U. Boesl and U. Heiz, ChemPhysChem, 2016, 17, 4052 CrossRef CAS PubMed.
- U. Boesl, A. Bornschlegl, C. Logé and K. Titze, Anal. Bioanal. Chem., 2013, 405, 6913–6924 CrossRef CAS.
- P. Horsch, G. Urbasch and K.-M. Weitzel, Chirality, 2012, 24, 684–690 CrossRef CAS PubMed.
- K. Fehre, S. Eckart, M. Kunitski, M. Pitzer, S. Zeller, C. Janke, D. Trabert, J. Rist, M. Weller, A. Hartung, L. P. H. Schmidt, T. Jahnke, R. Berger, R. Dörner and M. S. Schöffler, Sci. Adv., 2018, 5, 7923 CrossRef PubMed.
- B. Ritchie, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 1411–1415 CrossRef.
- N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Phys. Rev. Lett., 2001, 86, 1187–1190 CrossRef PubMed.
- C. Lux, M. Wollenhaupt, T. Bolze, Q. Liang, J. Köhler, C. Sarpe and T. Baumert, Angew. Chem., Int. Ed., 2012, 51, 5001–5005 CrossRef CAS PubMed.
- C. S. Lehmann, N. Bhargava Ram, I. Powis and M. H. M. Janssen, J. Chem. Phys., 2013, 139, 234307 CrossRef.
- D. W. Chandler and P. L. Houston, J. Chem. Phys., 1987, 87, 1445–1447 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- D. W. Chandler, P. L. Houston and D. H. Parker, J. Chem. Phys., 2017, 147, 013601 CrossRef PubMed.
- M. M. R. Fanood, I. Powis and M. M. H. Janssen, J. Phys. Chem. A, 2014, 118, 11541–11546 CrossRef PubMed.
- M. M. Rafiee Fanood, M. H. M. Janssen and I. Powis, Phys. Chem. Chem. Phys., 2015, 17, 8614–8617 RSC.
- S. Beaulieu, A. Ferré, R. Géneaux, R. Canonge, D. Descamps, B. Fabre, N. Fedorov, F. Légaré, S. Petit, T. Ruchon, V. Blanchet, Y. Mairesse and B. Pons, New J. Phys., 2016, 18, 102002 CrossRef.
- U. Hergenhahn, E. E. Rennie, O. Kugeler, S. Marburger, T. Lischke, I. Powis and G. Garcia, J. Chem. Phys., 2004, 120, 4553–4556 CrossRef CAS PubMed.
- V. Ulrich, S. Barth, S. Joshi, U. Hergenhahn, E. Mikajlo, C. J. Harding and I. Powis, J. Phys. Chem. A, 2008, 112, 3544–3549 CrossRef CAS PubMed.
- G. A. Garcia, L. Nahon, S. Daly and I. Powis, Nat. Commun., 2013, 4, 2132 CrossRef PubMed.
- G. Hartmann, M. Ilchen, P. Schmidt, C. Küstner-Wetekam, C. Ozga, F. Scholz, J. Buck, F. Trinter, J. Viefhaus, A. Ehresmann, M. S. Schöffler, A. Knie and P. V. Demekhin, Phys. Rev. Lett., 2019, 123, 043202 CrossRef CAS PubMed.
- G. A. Garcia, H. Dossmann, L. Nahon, S. Daly and I. Powis, ChemPhysChem, 2017, 18, 500–512 CrossRef CAS PubMed.
- M. M. Rafiee Fanood, H. Ganjitabar, G. A. Garcia, L. Nahon, S. Turchini and I. Powis, ChemPhysChem, 2018, 19, 921–933 CrossRef CAS PubMed.
- S. Turchini, J. Phys.: Condens. Matter, 2017, 29, 503001 CrossRef CAS PubMed.
- P. V. Demekhin, A. N. Artemyev, A. Kastner and T. Baumert, Phys. Rev. Lett., 2018, 121, 253201 CrossRef CAS PubMed.
- S. Rozen, A. Comby, E. Bloch, S. Beauvarlet, D. Descamps, B. Fabre, S. Petit, V. Blanchet, B. Pons, N. Dudovich and Y. Mairesse, Phys. Rev. X, 2019, 9, 031004 CAS.
- C. Lux, M. Wollenhaupt, C. Sarpe and T. Baumert, ChemPhysChem, 2015, 16, 115–137 CrossRef CAS PubMed.
- M. H. M. Janssen and I. Powis, Spectroscopy Online, 2017, 15, 16–23 Search PubMed.
- L. Nahon, L. Nag, G. A. Garcia, I. Myrgorodska, U. Meierhenrich, S. Beaulieu, V. Wanie, V. Blanchet, R. Géneaux and I. Powis, Phys. Chem. Chem. Phys., 2016, 18, 12696–12706 RSC.
- A. Comby, E. Bloch, C. M. M. Bond, D. Descamps, J. Miles, S. Petit, S. Rozen, J. B. Greenwood, V. Blanchet and Y. Mairesse, Nat. Commun., 2018, 9, 5212 CrossRef CAS PubMed.
- A. Kastner, C. Lux, T. Ring, S. Züllighoven, C. Sarpe, A. Senftleben and T. Baumert, ChemPhysChem, 2016, 17, 1119–1122 CrossRef CAS.
- M. M. Rafiee Fanood, N. Bhargava Ram, C. S. Lehmann, I. Powis and M. H. M. Janssen, Nat. Commun., 2015, 6, 7511 CrossRef.
- M. H. M. Janssen and I. Powis, Phys. Chem. Chem. Phys., 2014, 16, 856–871 RSC.
- J. Lepelmeier, J. L. Alonso-Gómez, F. Mortaheb, U. Boesl, U. Heiz and A. Kartouzian, Phys. Chem. Chem. Phys., 2017, 19, 21297–21303 RSC.
- A. Hong, C. M. Choi, H. J. Eun, C. Jeong, J. Heo and N. J. Kim, Angew. Chem., Int. Ed., 2014, 53, 7805–7808 CrossRef CAS PubMed.
- A. Comby, S. Beaulieu, M. Boggio-Pasqua, D. Descamps, F. Legare, L. Nahon, S. Petit, B. Pons, B. Fabre, Y. Mairesse and V. Blanchet, J. Phys. Chem. Lett., 2016, 7, 4514–4519 CrossRef CAS PubMed.
- A. Kastner, T. Ring, B. C. Krüger, G. B. Park, T. Schäfer, A. Senftleben and T. Baumert, J. Chem. Phys., 2017, 147, 013926 CrossRef PubMed.
- R. E. Goetz, T. A. Isaev, B. Nikoobakht, R. Berger and C. P. Koch, J. Chem. Phys., 2017, 146, 24306 CrossRef CAS PubMed.
- I. Dreissigacker and M. Lein, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 053406 CrossRef.
- A. N. Artemyev, A. D. Müller, D. Hochstuhl and P. V. Demekhin, J. Chem. Phys., 2015, 142, 244105 CrossRef PubMed.
- A. D. Müller, A. N. Artemyev and P. V. Demekhin, J. Chem. Phys., 2018, 148, 214307 CrossRef.
- A. D. Müller, E. Kutscher, A. N. Artemyev and P. V. Demekhin, J. Chem. Phys., 2020, 152, 044302 CrossRef PubMed.
- R. E. Goetz, C. P. Koch and L. Greenman, Phys. Rev. Lett., 2018, 122, 013204 CrossRef PubMed.
- A. Kastner, T. Ring, H. Braun, A. Senftleben and T. Baumert, ChemPhysChem, 2019, 20, 1416–1419 CAS.
- J. Driscoll, T. Baer and T. J. Cornish, J. Mol. Struct., 1991, 249, 95–107 CrossRef CAS.
- F. Pulm, J. Schram, S. Grimme and S. Peyerimhoff, Chem. Phys., 1997, 224, 143–155 CrossRef CAS.
- U. Even, J. Jortner, D. Noy, N. Lavie and C. Cossart-Magos, J. Chem. Phys., 2000, 112, 8068–8071 CrossRef CAS.
- G. B. Park, B. C. Krüger, S. Meyer, D. Schwarzer and T. Schäfer, J. Chem. Phys., 2016, 144, 194308 CrossRef PubMed.
- V. Papadakis and T. N. Kitsopoulos, Rev. Sci. Instrum., 2006, 77, 083101 CrossRef.
- G. M. Roberts, J. L. Nixon, J. Lecointre, E. Wrede and J. R. R. Verlet, Rev. Sci. Instrum., 2009, 80, 053104 CrossRef CAS.
- G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989–4996 CrossRef CAS.
- C. N. Yang, Phys. Rev., 1948, 74, 764–772 CrossRef CAS.
- TURBOMOLE V7.3 2018, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
- R. Berger, C. Fischer and M. Klessinger, J. Phys. Chem. A, 1998, 102, 7157–7167 CrossRef CAS.
- H.-C. Jankowiak, J. L. Stuber and R. Berger, J. Chem. Phys., 2007, 127, 234101 CrossRef PubMed.
- J. Huh and R. Berger, J. Phys.: Conf. Ser., 2012, 380, 012019 CrossRef.
- D. J. Nesbitt and R. W. Field, J. Phys. Chem., 1996, 100, 12735–12756 CrossRef CAS.
- D. C. Frost, N. P. C. Westwood and N. H. Werstiuk, Can. J. Chem., 1980, 58, 1659–1665 CrossRef CAS.
- D. Loru, M. A. Bermúdez and M. E. Sanz, J. Chem. Phys., 2016, 145, 074311 CrossRef PubMed.
- K. Fehre, S. Eckart, M. Kunitski, C. Janke, D. Trabert, J. Rist, M. Weller, A. Hartung, L. P. H. Schmidt, T. Jahnke, R. Dörner and M. Schöffler, J. Phys. Chem. A, 2019, 123, 6491–6495 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp00470g |
| This journal is © the Owner Societies 2020 |