Time-resolved, broadband UV-absorption spectrometry measurements of Criegee intermediate kinetics using a new photolytic precursor: unimolecular decomposition of CH₂OO and its reaction with formic acid

Abstract

We present a time-resolved broadband cavity-enhanced UV-absorption spectrometer apparatus that we have constructed and utilized for temperature- and pressure-dependent kinetic measurements of formaldehyde oxide (CH₂OO) reactions. We also introduce and utilize a new photolytic precursor, bromoiodomethane (CH₂IBr), which photolysis at 213 nm in presence of O₂ produces CH₂OO. Importantly, this precursor appears to be free from secondary reactions that may regenerate CH₂OO in kinetic experiments. The unimolecular decomposition rate coefficient of CH₂OO has been measured over wide pressure (5–400 Torr) and temperature (296–600 K) ranges and master equation simulations of the decomposition kinetics have been performed using MESMER program. The MESMER simulations of the experimental data with the calculated zero-point energy corrected transition state energy 85.9 kJ mol⁻¹ for decomposition required no adjustment and returned 〈ΔE〉_down = 123.2 × (T/298 K)^0.74 cm⁻¹ for temperature-dependent exponential-down model of the collisional energy transfer in He. A very good agreement between results of simulations and experiments is obtained. The results are compared with the previously reported unimolecular decomposition study by Stone et al. (Phys. Chem. Chem. Phys., 2018, 20, 24940–24954). Current master equation simulations suggest about 61% decomposition yield for the predominant H₂ + CO₂ channel, whereas the yields of two other channels, H₂O + CO, and HCO + OH, are sensitive on the parameters involved in the simulations. The kinetics of CH₂OO reaction with formic acid has also been investigated as function of pressure (5–150 Torr) and temperature (296–458 K). The bimolecular rate coefficient for CH₂OO + HCOOH reaction shows a negative temperature dependency, decreasing from (1.0 ± 0.03) × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹ at 296 K to (0.47 ± 0.05) × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹ at 458 K with an Arrhenius activation energy of −4.9 ± 1.6 kJ mol⁻¹, where statistical uncertainties shown are 2σ. Estimated overall uncertainty in the measured rate coefficients is about ±20%. Current bimolecular rate coefficient at room temperature agrees with the previously reported rate coefficients from the direct kinetic experiments. The reaction is found to be pressure independent over the range between 5 and 150 Torr at 296 K in He.

---

Introduction

Alkenes are important non-methane hydrocarbon species in the Earth's atmosphere. Alkenes with natural origin (e.g. isoprene, monoterpenes, and sesquiterpenes) are released into the troposphere from vegetation whereas anthropogenic alkene emissions are often byproducts of combustion and are composed of smaller hydrocarbons (ethene, propenes, butenes, etc.).¹ A major loss pathway of alkenes in the troposphere is reaction with ozone, i.e. ozonolysis. In ozonolysis a highly excited primary ozonide is formed in a very exothermic O₃ + alkene reaction.² In gas phase and at atmospheric pressure, any excited primary ozonide decomposes to a Criegee intermediate, also known as carbonyl oxide, and a carbonyl compound. In case of acyclic (e.g. trans-2-butene, isoprene) and exocyclic (e.g. β-pinene) alkenes, roughly 50% of Criegee intermediates decompose or isomerize further before stabilization, while other ∼50% are stabilized at atmospheric pressure and are consequently called stabilized Criegee intermediates, sCIs. sCIs can further react with atmospheric constituents (H₂O, (H₂O)₂, SO₂, acids, NO₂, etc.) in bimolecular reactions or decompose and/or isomerize in unimolecular reactions.^1,3

Formaldehyde oxide, CH₂OO, is the smallest and probably the most studied sCI.^4–9 It is formed in the ozonolysis of ethene and any larger terminal alkene (e.g. isoprene).¹⁰ In breakthrough experiments using multiplex photoionization mass-spectrometer (MPIMS) utilizing synchrotron radiation for ionization, Welz et al.⁵ discovered 2012 that CH₂I radical (an α-iodoalkyl radical) reaction with molecular oxygen produces the smallest sCI, CH₂OO.

CH₂I + O₂ → CH₂OO + I (R1)

→ other products

Since high [O₂] conditions are easy to prepare, sCIs do not react with O₂ at any known extent, reaction (R1) is fast¹¹ and formaldehyde oxide yield is close to unity at low pressures,^12,13reaction (R1) is the excellent source of CH₂OO for direct kinetic measurements. Impetus to study reaction (R1) with MPIMS originated from this laboratory.^11,14

Direct kinetics measurements of formaldehyde oxide have shown that CH₂OO reacts fast with SO₂,⁵ organic acids,¹⁵ and water dimer ((H₂O)₂).⁸ Bimolecular rate coefficients of the smallest sCI with the above and many other reactants, obtained from direct kinetic measurements in different laboratories, are consistent with each other.¹⁶ For example, results of direct kinetic experiments of CH₂OO reaction with SO₂¹⁷ agree with each other and show significantly faster kinetics than now outdated estimates based on results of indirect measurements suggested.¹⁰ Especially CH₂OO reactions with acids are very fast with bimolecular rate coefficients in excess of 1 × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹. Welz et al.¹⁵ measured a bimolecular rate of (1.1 ± 0.1) × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹ for the reaction of CH₂OO with HCOOH at room temperature (∼298 K) and pressure of 4 Torr.

CH₂OO + HCOOH → products (R2)

Theoretical studies have predicted that the initial reaction step is barrierless (or proceeds through a deep pre-reactive complex),^18,19 in agreement with the high bimolecular rate coefficient for the reaction at room temperature. However, direct kinetic studies of temperature or pressure dependency of reaction (R2) are not available.

In this work, we measure kinetics of CH₂OO + HCOOH reaction over extended temperature (296–458 K) and pressure (5–150 Torr) ranges, report bimolecular rate coefficients, and discuss on the observed kinetics.

Stone et al.⁹ have recently measured unimolecular decomposition kinetics of CH₂OO in the temperature 450–650 K and helium pressure 2–350 Torr ranges using a time-resolved broadband cavity enhanced absorption spectrometer (TR-BB-CEAS) and probing formaldehyde oxide at UV.

CH₂OO → products (R3)

The reported rate coefficient for unimolecular decomposition of stabilized CH₂OO was 1.1^+1.5_−1.1 × 10⁻³ s⁻¹ at atmospheric conditions (298 K and 760 Torr). Even though unimolecular decomposition of stabilized CH₂OO is not important reaction under atmospheric conditions, it may play a role under low-temperature-combustion conditions. It has been proposed that CH₂OO is an intermediate in combustion of dimethyl ether (DME, CH₃OCH₃), an important biofuel.^20,21 In addition, reaction of triplet methylene (³CH₂) radical with O₂ can produce formaldehyde oxide.²² Triplet methylene radical is formed, for example, in the combustion of acetylene.²³

Since the first study by Welz et al.,⁵ alkyl-substituted α-iodoalkyl radicals have also been shown to produce corresponding sCIs in presence of oxygen.^24–27 Hitherto CH₂I radical in the reaction (R1) has been prepared by photodissociation of CH₂I₂ at 248,⁵ 266,⁷ or 355²⁸ nm. Important for the current work, a reaction between CH₂OO and CH₂I₂ precursor has been observed in many previous studies.^9,29 This may be a significant problem in kinetic experiments, because only a few percent of the precursor is typically consumed in the photodissociation process and, most importantly, CH₂OO + CH₂I₂ reaction may generate CH₂I and thus CH₂OO, resulting in chain-propagation and distorting information from kinetic measurements. For example, Liu et al.²⁹ reported a bimolecular rate coefficient (5.2 ± 2.6) × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹ for the reaction at 298 K. The reaction becomes faster at higher temperatures. Stone et al.⁹ observed a bimolecular rate coefficient (8.2 ± 1.7) × 10⁻¹² cm³ molecule⁻¹ s⁻¹ at 450 K in their unimolecular decomposition study of CH₂OO. They also stated that the reaction might have caused a contribution to the measured decay data at the temperatures above 450 K. Buras et al.³⁰ observed a baseline offset in the 375 nm absorption of CH₂OO at high temperatures. They stated that it indicated an extra absorption by an unknown product formed in their system at high temperatures. In addition, CH₂I₂ has a relatively strong absorption at the 340 nm region, where the typical probing of CH₂OO is conducted in UV-absorption-based experiments, leading to a negative (and often non-constant) measurement baseline in most cases.

In this work, we introduce and utilize a new photolytic precursor, bromoiodomethane (CH₂IBr), which photolysis at 213 nm and in presence of O₂ produces CH₂OO. This precursor is more stable against secondary reaction chemistry, which may regenerate CH₂OO in kinetic experiments. We report a detailed study of thermal unimolecular decomposition kinetics of CH₂OO over wide pressure (5–400 Torr) and temperature (296–600 K) ranges using new CH₂IBr precursor. We also introduce and utilize our new time-resolved broadband cavity enhanced absorption spectrometer (TR-BB-CEAS) apparatus that locates in the University of Helsinki and probes in the ultraviolet (UV) region. We perform master equation simulations and compare obtained outcome with the current experimental results as well as with the results of unimolecular study by Stone et al.⁹

Experimental

A schematic figure of the new TR-BB-CEAS apparatus utilizing UV absorption to probe CH₂OO is shown in Fig. 1. The design of our TR-BB-CEAS apparatus is a modified version of the experimental setup developed by L. Sheps et al.³¹ The gas mixture flowing through a quartz tube reactor contained the radical precursor (CH₂IBr or CH₂I₂), O₂, and HCOOH (for the bimolecular reaction) diluted in helium or nitrogen carrier gas. Calibrated mass flow controllers (Omega Engineering) were used to deliver gases to a mixing manifold before flowing into the reactor. The CH₂I radicals were homogeneously generated along the flow reactor by the 5^th harmonic (213 nm) or the 4^th harmonic (266 nm) of a pulsed Nd:YAG laser (Quantel Q-smart 850). The photolysis laser beam is expanded by a 2 : 1 telescope giving an 18 mm diameter spot inside the reactor. Typical pulse fluences at 213 nm and 266 nm were about 4 mJ cm⁻² and 18 mJ cm⁻² inside the reactor, which were sufficient to dissociate approximately 2.5% and 3% of the CH₂IBr and CH₂I₂ precursors, respectively. The inner diameter of the reactor tube is 36 mm and linear gas flow speed about 1 m s⁻¹, which ensured that the gas mixture was completely replaced between laser pulses with the repetition rate of 1 Hz. The reactor tube is combined with a 2 m long confocal cavity formed by two highly reflecting concave mirrors (Layertec). The radius of curvature and the diameter of the mirrors are 2 m and half an inch (12.7 mm), respectively. The mirror holders are coupled to the reactor construction using flexible stainless-steel bellows. A beam from a continuous-wave laser-driven plasma light-source (Energetiq, EQ-99X) is used to probe the transient absorption of CH₂OO. The output of the light-source covers wavelengths from 180 to 2100 nm. UV portion of the light is coupled into the cavity using a high-pass filter (with a cut-off wavelength of ∼300 nm). The reflectivity of the mirrors as stated by the manufacturer is 99.6 ± 0.3% across the λ = 300–450 nm wavelength range, giving together with the cavity length the total effective optical path length (OPL) 30–160 m. Details of the calibration procedure of the effective OPL are given in the ESI.†

Fig. 1 Schematic figure of the time-resolved broadband cavity-enhanced absorption spectrometer. The sCI is produced along a heated quartz flow tube reactor by a single-pass photolysis laser pulse at 213 or 266 nm. The sCI is probed by overlapping incoherent laser-driven broadband light source. The sensitivity of the detection is enhanced using an optical cavity formed by two highly reflecting concave mirrors between 300 and 450 nm. The time-dependent broadband absorption spectrum of sCI is measured by a grating spectrometer combined with a fast CMOS line array camera.

The probe beam leaking out of the cavity is guided to a grating spectrometer and dispersed in wavelength horizontally by a ruled grating. The transient spectrum of CH₂OO is recorded by focusing the dispersed light onto an image sensor of a fast CMOS line array camera (JAI SW-2000M-CL-80) in vertical and horizontal directions with 100 mm and 30 mm cylindrical UV fused silica lenses, respectively. The camera (1 × 2048 pixels, 12-bit) has a maximum line rate of 80 kHz, however, to gain good enough signal-to-noise ratio (SNR), the line rate was reduced to 20 kHz leading to time resolution of about 50 μs. The use of the fast line array camera enables the transient spectrum measurements without moving parts (e.g., a spinning mirror^31,32) inside the grating spectrometer. All the transient absorption traces of CH₂OO measured in the current work were probed at 340 nm region, where the strong absorption band of CH₂OO has its maximum and the effective path length about 80 m. This region is also free from unwanted interferences of byproducts, e.g. from absorption of IO radical.

The signal from the CMOS line array camera is processed and digitized by a fast 12-bit image acquisition card (National Instruments, PCIe-1427). Single-exponential function A_t = A₀ × exp(−k′t) is subsequently fitted to a background-subtracted CH₂OO time-trace by the least squares method using the Levenberg–Marquardt algorithm in a custom-made LabVIEW program. Here k′ is the pseudo-first-order decay rate coefficient, and A_t is the absorbance at time t, and A₀ is the initial absorbance (at time t = 0). The wavelength scale of the spectrometer is calibrated with atomic (Hg and Ar) emission lamps. For the experiments described here, we averaged signal between 600 and 3000 shots for each decaying experimental time-trace. Fig. S4 in the ESI† presents a temporal absorption profile of CH₂OO measured at 340 nm with the presence of HCOOH. The estimated initial concentration of CH₂OO was ∼8.5 × 10¹⁰ molecule cm⁻³ and the observed SNR of the time-trace was ∼35 for an averaging time of 1800 s (1800 shots). This yielded a minimum detectable [CH₂OO] of ∼2.4 × 10⁹ molecule cm⁻³.

The temperature control of the flow tube reactor is achieved by two temperature-controlled custom-made aluminum blocks, which are placed around the quartz-glass reactor tube. Each aluminum block has four 300 W cartridge heaters, which are regulated using a PID-controller program from LabVIEW. The temperature of the system can be heated anywhere between 296 K and 600 K. Temperature of the gas flow was measured continuously in the middle of the reactor just outside of the photolysis beam by a K-type thermocouple. Complete axial temperature profile within the overlap volume of the probe and the photolysis beams were measured separately for all experimental conditions (temperature, pressure and flow rate) used in this work. The observed temperature uncertainty was ±3 K. The gases were pre-heated close to the setpoint temperature before entering to the reactor.

The CH₂I radicals were principally generated from CH₂IBr at 213 nm.

CH₂IBr + hν(213 nm) → CH₂I + Br (R4a)

→ other products (R4b)

The UV absorption cross-section of gaseous CH₂IBr³³ as a function of wavelength is presented in Fig. 2. In the photodissociation studies of CH₂IBr by Butler et al.,^34,35 the excitation at 210 nm resulted in selective breaking of the C–Br bond with ∼60% yield (Y) as well as concerted IBr elimination (Y < 6%) and simultaneous three-body dissociation to CH₂ + I + Br (∼35%) fragments. No fission of the C–I bond was observed at 210 nm, whereas excitation at 248.5 nm resulted in both C–I and C–Br bond fission. Based on the CH₂OO absorption signal observed in our measurements, the photodissociation quantum yield of the C–Br bond at 213 nm is estimated to ∼0.4 (see ESI†).

Fig. 2 The UV absorption cross-section of gaseous CH₂IBr as a function of wavelength.³³

A few measurements in this work were done with CH₂I₂ precursor for comparison.

CH₂I₂ + hν(266 nm) → CH₂I + I (R5a)

→ other products (R5b)

The absorption cross-section of CH₂IBr at 340 nm region (the absorption maximum of CH₂OO) is more than 20 times smaller than the cross-section of CH₂I₂ (see Fig. S2 in the ESI†).³³ In kinetic measurement, the stronger absorption of CH₂I₂ leads typically to a negative (and non-constant) baseline for the measured absorption signal (especially at long delay times). For shorter time scales (<10 ms), the depletion of CH₂I₂ can be considered as a step function (constant) in time due to photolysis depletion of CH₂I₂, and it would not affect severely on the kinetic measurement of CH₂OO (see Fig. S3 in the ESI†). However, since CH₂IBr absorbs much less than CH₂I₂, our measurements with CH₂IBr has a zero or small positive and constant baseline, even with longer measurement time scales (see Fig. S4 in the ESI†).

Theoretical methods

In this work we accompanied the same potential energy surface (PES) for the thermal unimolecular decomposition of the smallest Criegee intermediate, CH₂OO, as Stone et al.⁹ utilized in their study. Their PES was to significant extent based on Nguyen et al. calculations.³⁶ The geometry optimization along with the vibrational frequency calculations of the stationary points on the PES, viz., CH₂OO, transition states, and intermediates were performed using complete active space self-consistent field (CASSCF) method taking into account 8 electron and 8 orbital combination in the active space, i.e., CASSCF(8,8). The products and one transition state leading to the formation of H₂O + CO, were optimized with MN15³⁷ density functional. In all these cases, def2-TZVP basis set was used.

The thermal unimolecular decomposition of CH₂OO is believed to proceed via the formation of a cyclic dioxirane and the transition state leading to its formation determines the rate of reaction from CH₂OO to different products. Therefore, accurate estimation of the barrier height and the energy of the cyclic dioxirane is crucial. We performed the T1 diagnostics for the CH₂OO reactant, the transition state leading to the formation of the cyclic dioxirane, and the dioxirane intermediate. For the reactant and the TS, the T1 diagnostic has a value of 0.043 and 0.051, respectively, which is an indication of the possibility of multireference character in those systems. Hence, we chose CASSCF method to carry out the electronic structure calculations. All above methods have been implemented in Gaussian 16 suite of programs.³⁸

In order to get reliable energies, we performed single-point energy calculations with domain based local pair natural orbital coupled cluster methods or the DLPNO-CCSD(T) approach as employed in ORCA code.³⁹ The DLPNO calculations were then extrapolated to the complete basis set limit using correlation consistent Dunning's augmented basis sets, i.e., aug-cc-pVXZ (X = 5 and 6)^40,41 following the extrapolation scheme as given below⁴²

ΔE_CBS = ΔE_aug-cc-pV6Z − 0.694(ΔE_aug-cc-pV5Z − ΔE_aug-cc-pV6Z) (1)

where ΔEs are the energies relative to the reactant.

To account for the effect of helium bath-gas pressure on unimolecular decomposition rate coefficient of CH₂OO, we performed master equation simulations using MESMER 5.1 (Master Equation Solver for Multi-Energy well Reactions) program.⁴³ For well-defined transition states Rice–Ramsperger–Kassel–Marcus (RRKM) theory was used along with Eckart tunneling corrections to calculate microcanonical rate coefficients. For collisional energy transfer a temperature-dependent single-exponential-down model was used.

〈ΔE〉_down = 〈ΔE〉_down,ref(T/298 K)ⁿ (2)

Here, 〈ΔE〉_down,ref is collision energy transfer parameter at 298 K and its temperature dependency is governed by n. The terms 〈ΔE〉_down,298K and n were used as fitting parameters in the master equation simulations to best agree with experimental data by minimizing χ², i.e. principally minimizing difference of calculated and experimental unimolecular decomposition rate coefficients. MESMER uses Lennard-Jones model for calculating the collisional frequency and requires the depth of the potential well, ε_LJ and the finite length where the potential is zero, σ_LJ.

Results and discussion

CH₂OO spectrum

The absorption spectrum of CH₂OO measured in this work, produced using the CH₂IBr precursor and 213 nm photolysis followed by reaction (R1), is shown with blue line in Fig. 3. The spectrum is averaged over 0–3 ms (with ∼67 μs time resolution) after the photolysis. The corresponding transient spectrum is presented in Fig. S5 in the ESI.† The absorption cross-section is estimated using the measured absorption coefficient at t = 0 ms, and the resulting initial CH₂I concentration using the estimated yield of the channel (R4a) = 0.4. The estimated initial CH₂OO concentration in the measurement is ∼2.0 × 10¹¹ molecule cm⁻³. For comparison, the CH₂OO absorption spectrum of Ting et al.⁴⁴ is presented in Fig. 3 as black line, which was measured using the CH₂I₂ precursor and 248 photolysis, and much higher initial CH₂OO concentration, about 5 × 10¹³ molecule cm⁻³.

Fig. 3 Absorption spectrum of CH₂OO using CH₂IBr as photolytic precursor and measured at 296 K and 10 Torr (N₂). The spectrum is averaged over t = 0–3 ms. The initial CH₂OO concentration was ∼2.0 × 10¹¹ molecule cm⁻³. The O₂ concentration was ∼3.8 × 10¹⁶ molecule cm⁻³.

Bimolecular CH₂OO + HCOOH reaction

The kinetics of CH₂OO reaction with formic acid was measured as a function of temperature between 296 and 458 K at low pressure (5–15.5 Torr). Fig. 4 shows typical transient traces of CH₂OO at varying concentrations of HCOOH at 458 K. All the CH₂OO traces were fitted using a single-exponential decay function. In the absence of added acid reactant, the CH₂OO signal follows a first-order decay loss, k_loss (s⁻¹), which originates from diffusion out of the measurement volume, from slow reaction of CH₂OO with the precursor, and to some small extend from radical–radical reactions. Heterogeneous loss is negligible in our measurement system, since the radicals are generated and probed inside the same volume element in the middle of the flow reactor tube away from wall. In addition, the measurements were done in a temperature region where the unimolecular decomposition is negligible (below 475 K). The k_loss was measured by reducing the precursor concentration until its value no longer depended on the precursor concentration. Once this condition was obtained, it was concluded that radical–radical reactions, especially CH₂OO–CH₂OO reactions, were suppressed. The initial CH₂OO concentration in the measurements was typically below 1.0 × 10¹¹ molecule cm⁻³, which was estimated from the laser fluence, the precursor absorption cross-section,³³ and the effective OPL at the used wavelength (see ESI† for more details).

Fig. 4 The decay rates of CH₂OO as function of [HCOOH] at 458 K and total density of 3.3 × 10¹⁷ molecule cm⁻³ (15.5 Torr). The CH₂OO traces were probed at 338 nm.

By adding acid, the decay of CH₂OO became faster. All the measurements were performed under pseudo-first-order conditions, i.e. [CH₂OO] ≪ [HCOOH]. The photolysis of formic acid, HCOOH + hν(213 nm) → HCO + OH, was negligible (∼0.06%) in our measurements, because of low laser fluence (∼4 mJ cm⁻²) and small absorption cross-section of HCOOH at 213 nm (1.4 × 10⁻¹⁹ cm² molecule⁻¹).⁴⁶ Even at the highest [HCOOH] used, 2.06 × 10¹³ molecule cm³, the resulting [OH] was only about 1.0 × 10¹⁰ molecule cm³, which could not have any important effect on the current measurements. Concomitant product of photolysis, HCO radical, would rapidly react with O₂ and form HO₂ radical that, due to its low reactivity, would have even smaller effect than the OH radical. In Fig. 5, the obtained pseudo-first-order decay rate coefficients (k_obs) of CH₂OO are shown as function of temperature and [HCOOH]. The bimolecular rate coefficient k(CH₂OO + HCOOH) is obtained from the slope of the equation k_obs = k_loss + k(CH₂OO + HCOOH) × [HCOOH] fitted to the data, while the intercept reflects the k_loss. Obtained bimolecular rate coefficients were measured with the both precursor-photolysis wavelength combinations and the results are shown in Table 1 along with experimental conditions and statistical 2σ experimental uncertainties. Estimated overall uncertainties in the measured rate coefficients are about ±20%. The current bimolecular rate coefficient (1.0 ± 0.03) × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹ for CH₂OO + HCOOH reaction measured at room temperature agrees with the previously reported rate coefficients (1.1 ± 0.1) × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹ measured by Welz et al.¹⁵

Fig. 5 Determination of the bimolecular rate coefficients from pseudo-first-order decay rate coefficients at 296 K at total density of 1.6 × 10¹⁷ molecule cm⁻³, and 340 K, 388 K and 458 K at total density of 3.3 × 10¹⁷ molecule cm⁻³.

Table 1 Results and conditions of the experiments used to measure the bimolecular reaction CH₂OO + HCOOH

T (K)	[He] (×10^17 molecule cm^−3)	p (Torr)	[HCOOH]^c (×10^13 molecule cm^−3)	k loss (s^−1)	k (×10^−10 cm^3 molecule^−1 s^−1)
a Precursor concentrations used: 7.2 × 10^12 molecule cm^−3 for CH2IBr and 2.5 × 10^12 molecule cm^−3 for CH2I2. Estimated initial CH2OO concentration <1.0 × 10^11 molecule cm^−3. b O2 concentrations used: ∼3.8 × 10^16 molecule cm^−3 for CH2IBr and ∼2.8 × 10^16 molecule cm^−3 for CH2I2. c HCOOH reactant concentration in the reactor is calculated with accounting for the dimerization of the dilute HCOOH in helium mixture prepared in a bulb.^45 The experiments in He and N2 were conducted with different HCOOH samples. d The statistical uncertainties shown are 2σ. Estimated overall uncertainty in the measured rate coefficients is about ±20%. e The linear gas flow velocity was ∼1.5 ms^−1.
Precursor: CH2IBr^a
296	1.6	5	0.55–2.06	95	1.0 ± 0.03
340	3.3	11.5	0.55–1.70	74	0.89 ± 0.01
388	3.3	13.1	0.54–1.70	77	0.74 ± 0.03
458	3.3	15.5	0.55–1.70	123	0.51 ± 0.05

---

T (K)	[N2] (×10^17 molecule cm^−3)	p (Torr)	[HCOOH]^c (×10^13 molecule cm^−3)	k loss (s^−1)	k (×10^−10 cm^3 molecule^−1 s^−1)
Precursor: CH2I2^a
296	1.6	5	0.52–1.64	39	1.0 ± 0.03
340	1.6	5.75	0.52–1.66	38	0.81 ± 0.03
388	1.6	6.55	0.53–1.64	52	0.58 ± 0.03
458	1.6	7.75	0.53–1.66	59	0.45 ± 0.01

---

Theoretical studies suggest that CH₂OO + HCOOH reaction proceeds through a barrierless addition of the reactants leading to hydroperoxymethylformate (HPMF).^18,19 In study by Vereecken,¹⁹ the rate coefficient (1.0 ± 0.1) × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹ is predicted at room temperature with very minor negative temperature dependency (∼8%) between 250 and 350 K. Current bimolecular rate coefficient at 458 K is about factor of two slower than the rate coefficient at room temperature, giving negative temperature dependency ∼50%. Fig. 6 shows an Arrhenius plot of the measured bimolecular rate coefficients of CH₂OO + HCOOH reaction. The least squares fit to the data gives an Arrhenius expression, k = (1.5 ± 0.8) × 10⁻¹¹ exp[(−4.9 ± 1.6) kJ mol⁻¹/RT] cm³ molecule⁻¹ s⁻¹, with 2σ standard fitting uncertainties.

Fig. 6 Arrhenius plot of the measured bimolecular rate coefficients utilizing CH₂IBr photolytic precursor. The statistical uncertainties shown are 2σ.

The bimolecular rate coefficient of the reaction was measured also as a function of helium density at 296 K. Fig. 7 presents the obtained pseudo-first-order decay rate coefficients (k_obs) of CH₂OO as function of pressure and [HCOOH]. A complete set of the results and experimental conditions is shown in Table S1 (in the ESI†). The reaction appears to be pressure independent over the range between 5 and 150 Torr, especially once considering the uncertainty of the measurements. An increase in the baseline of the measured absorption signal was observed at high pressures (with added HCOOH), which is possibly due to an enhanced stabilization of ICH₂OO at higher pressure (see more details in the ESI†).

Fig. 7 Bimolecular plots of the pseudo-first-order decay rate coefficients measured at 5, 50, 100, and 150 Torr total pressures versus [HCOOH] at constant temperature of 296 K. The obtained bimolecular rate coefficients are presented in the parentheses. The statistical uncertainties shown are 2σ.

For comparison, the temperature dependency of the reaction was also measured using diiodomethane (CH₂I₂) precursor with 266 nm photolysis. The results are given in Table 1, which show that outcome of both precursor-photolysis wavelength combinations are in agreement with each other. The obtained Arrhenius expression for the CH₂I₂ study was k = (1.1 ± 0.4) × 10⁻¹¹ exp[(−5.9 ± 0.8) kJ mol⁻¹/RT] cm³ molecule⁻¹ s⁻¹, with 2σ standard fitting uncertainties. The inert buffer-gas in the measurements was nitrogen (N₂).

Unimolecular decomposition of CH₂OO

Experiments. All the transient absorption traces of CH₂OO were measured at 338 nm and fitted to first-order, single-exponential decay function shown above. The obtained thermal unimolecular decomposition rate coefficients of CH₂OO are shown in Fig. 8 as function of temperature and helium buffer-gas pressure, whereas the complete kinetic results with conditions are shown in Table 2. The initial CH₂OO concentration used in the measurements was below 2.0 × 10¹¹ molecule cm⁻³, which efficiently suppressed radical–radical, especially CH₂OO–CH₂OO, reactions. Experiments were also performed with higher precursor concentration, but with lower laser fluence, to test a possible importance of Criegee-precursor, CH₂OO + CH₂IBr reaction. The measured unimolecular decay rate coefficients are shown in Fig. 9 as function of [CH₂IBr] at various temperature and pressure conditions. Even at 575 K, the measured unimolecular decay rate coefficients do not depend on the [CH₂IBr] to any significant extent. One potentially very important advantage of the new photolytic precursor is that it is more stable against secondary/surface chemistry since it does not produce CH₂I radical (and consequently CH₂OO) in X + CH₂IBr → XI + CH₂Br reaction, where X is any species.

Fig. 8 Measured thermal unimolecular decomposition rate coefficient of CH₂OO as function of total helium density at different temperatures (coloured points). The statistical uncertainties shown are 2σ. Results of MESMER simulations (solid lines) and Troe equation fits (dashed lines) are also shown.

Table 2 Unimolecular decomposition kinetics (rate coefficients) of CH₂OO determined from the UV experiments. k_obs are the fitted single-exponential decay rate coefficients of CH₂OO, with 2σ statistical fitting uncertainties. k_uni are derived as k_uni = k_obs − k_loss. Troe fits to k_uni, k_uni,Troe, are derived using eqn (3). K_uni,MESMER are the results of MESMER simulations. Unimolecular data shown in italics (at 425 K) were not included in the MESMER fits. The stated MESMER values at 425 K were calculated using the resulted MESMER fit parameters. The unimolecular data shown in italics (at 575 and 600 K) were also not included in the Troe fits. The stated Troe values were calculated using the resulted Troe fit parameters. High pressure limiting rate coefficients (p = ∞) are taken from MESMER simulations at p = 10 atm

T (K)	[He] (×10^18 molecule cm^−3)	p (Torr)	k obs (s^−1)	k loss (s^−1)	k uni (s^−1)	k uni,Troe (s^−1)	k uni,MESMER (s^−1)
a The fixed O2 concentration was ∼3.9 × 10^16 molecule cm^−3.
296	0.16	5	99 ± 3.3	100	−1	0	0
	0.33	10	55 ± 1.3	62	−7	0	0
	1.6	50	31 ± 0.7	29	−2	0	0
	3.3	100	26 ± 0.7	24	−2	0	0
	4.9	150	26 ± 0.8	26	0	0	0
	6.5	200	22 ± 0.5	19	−3	0	0
	8.2	250	20 ± 0.6	19	−1	0	0
	9.8	300	21 ± 0.7	18	−3	0	0
		∞					0
325	0.16	5.5	104 ± 2.60	100	−4	0	0
	0.33	11	61 ± 1.2	62	−1	0	0
	1.6	55	25 ± 0.4	29	−4	0	0
	3.3	110	23 ± 0.4	24	−1	0	0
	4.9	164.6	27 ± 0.6	26	−1	0	0
	6.5	219.5	18 ± 0.3	19	−1	0	0
	8.2	274.7	19 ± 0.4	19	0	0	0
	9.8	329.5	14 ± 0.3	18	−4	0	0
		∞					0
375	0.16	6.35	96 ± 2.5	100	−4	0	0
	0.33	12.7	70 ± 1.6	62	−8	0	0
	1.6	63.5	32 ± 0.5	29	−3	0	0
	3.3	126.6	23 ± 0.4	24	−1	0	0
	4.9	190	25 ± 0.4	26	−1	0	0
	6.5	253.5	16 ± 0.3	19	−3	0	0
	8.2	317	17 ± 0.3	19	−2	0	0
	9.8	380.5	19 ± 0.4	18	−1	0	0
		∞					0
425	0.16	7.2	115 ± 4.10	100	15	8	8
	1.6	72	57 ± 1.2	29	28	32	33
	3.3	143.5	71 ± 1.7	24	47	43	49
	4.9	215.5	71 ± 2.0	26	45	51	62
	6.5	287	90 ± 3.0	19	71	55	73
	8.2	359.5	79 ± 3.0	19	60	59	83
	9.8	431	91 ± 4.7	18	73	62	92
		∞					347
475	0.16	8.05	194 ± 7.6	100	94	65	61
	0.33	16.05	200 ± 9.5	62	138	110	97
	1.6	80.5	303 ± 13	29	274	287	281
	3.3	160.5	444 ± 30	24	420	402	438
	4.9	240.5	554 ± 48	26	528	480	566
	6.5	320.5	629 ± 65	19	610	537	677
	8.2	401.5	693 ± 56	19	674	580	778
		∞					3601
500	0.16	8.45	272 ± 13	100	172	156	143
	0.33	16.9	355 ± 20	62	293	270	230
	1.6	84.5	725 ± 52	29	696	730	691
	3.3	169	1029 ± 111	24	1005	1031	1097
	4.9	253.5	1407 ± 188	26	1381	1240	1431
	6.5	338	1732 ± 172	19	1713	1397	1724
		∞					9589
525	0.16	8.9	475 ± 29	100	375	344	306
	0.33	17.75	608 ± 40	62	546	605	500
	1.6	89	1587 ± 149	29	1558	1696	1553
	3.3	177.5	2231 ± 269	24	2207	2411	2497
	4.9	266	3271 ± 407	26	3245	2917	3282
	6.5	355	3518 ± 536	19	3499	3306	3977
		∞					23 029
550	0.16	9.3	767 ± 58	100	667	706	606
	0.33	18.6	1133 ± 910	62	1071	1255	1004
	1.6	93	3083 ± 451	29	3054	3641	3205
	3.3	186	4296 ± 800	24	4272	5212	5228
	4.9	279	6199 ± 1683	26	6173	6336	6928
		∞					50 570
575	0.16	9.75	1319 ± 119	100	1219	1359	1123
	0.33	19.45	1878 ± 233	62	1816	2438	1881
	1.6	97.5	6635 ± 1791	29	6606	7303	6181
		∞					102 705
600	0.16	10.15	2170 ± 351	100	2070	2473	1956
	0.33	20.3	3093 ± 610	62	3031	4473	3318
		∞					194 777

---

Fig. 9 Measured unimolecular decomposition rate coefficients of CH₂OO as function of CH₂IBr concentration in different temperature and total density conditions. The statistical uncertainties shown are 2σ.

The unimolecular reaction rate coefficient k_uni at given temperature and total density is obtained by k_uni = k_obs − k_loss, where both k_obs and k_loss are measured decay rate coefficients from single-exponential function fits to the experimental traces. The k_loss is measured at a few temperatures below which any significant unimolecular decomposition reaction occurs, whereas the k_obs is measured at a temperature where significant unimolecular reaction occurs, i.e., k_obs > 3k_loss. At low pressures (p < 20 Torr), the k_loss depends strongly on total density, decreasing from ∼100 s⁻¹ at low total density to ∼20 s⁻¹ at high total density. However, values of k_loss at each total density stay almost constant between the temperatures 296 K and 375 K, which is reasonable, since diffusion has a weak temperature dependency. The unimolecular decomposition reaction starts to become significant at temperatures only at and above 425 K (see Fig. S9 in the ESI†). Thus, mean of the measurements performed between 296 and 375 K was used as the k_loss.

A positive baseline offset of the measured absorption signal was also present at high pressures in the thermal unimolecular decomposition measurements. The offset value increased as pressure increased indicating the possible enhanced stabilization of ICH₂OO as observed in the bimolecular CH₂OO + HCOOH reaction. However, in constant (high) density, the baseline offset decreased as the temperature increased indicating a possible decomposition of ICH₂OO. Interestingly, at high temperatures, a small offset was present already at low pressures, which might indicate possible absorption by another formed product than ICH₂OO. The baseline offset has been taken into account in the fitting of the first-order, single-exponential decays (see more details in ESI†).

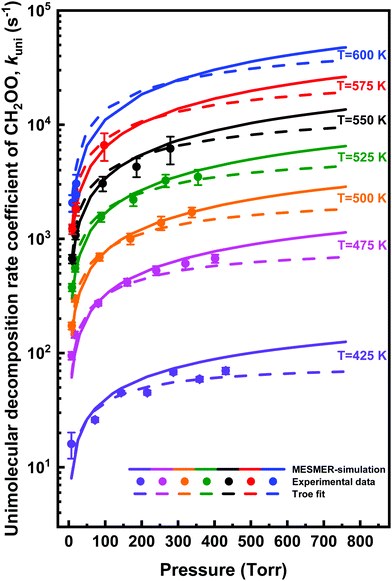
The unimolecular decomposition rate coefficient data shown in Fig. 8 were fitted simultaneously (a global fit) using the following Troe expression⁴⁷ employing the nonlinear least squares fitting method

where k₀(T) is the limiting low-pressure rate coefficient for CH₂OO decomposition, k_∞(T) is the limiting high-pressure rate coefficient for CH₂OO decomposition, M is the total number density, F_c is the broadening factor, and the exponent p is given bywhere N = 0.5 − 1.27 log₁₀ F_c is the width parameter. The global fits using eqn (3) were performed with F_c and N fixed to values of 0.6⁴⁸ and 1.0,⁴⁷ respectively, or F_c allowed to float independently at each temperature. The fits with fixed F_c and N values gave lower χ²-value, although the parameterisations from each fit were in agreement within the fitting uncertainties. The fit with fixed F_c and N values gives k₀(T) = (1.3 ± 3.0) × 10⁻⁸ exp[(−8065 ± 1170)/T] cm³ mol⁻¹ s⁻¹ and k_∞(T) = (7.8 ± 17.8) × 10¹¹ exp[(−9716 ± 1088)/T] s⁻¹, where statistical uncertainties stated are 2σ.

Master equation analysis. The PES for the unimolecular decomposition reaction of CH₂OO used in master equation simulations is plotted in Fig. 10. The energies are given in kJ mol⁻¹ and the naming of the species involved in the decomposition path were kept the same as that reported by Stone et al.⁹ for comparison. The energetics in the present work are quite similar to those obtained by Nguyen et al.³⁶ and Stone et al.,⁹ the differences originating from the use of different electronic structure theories. There are few notable exceptions that were observed in this work. The first one is the energy values obtained for TS6 and TS6a. While the present work suggests almost negligible difference between energies of these two species, previous works indicates a difference of about 16 kJ mol⁻¹. This difference, however, does not affect the product yields for different channels. The second one is related to the TS2 in Fig. 10, which has a non-superimposable mirror image and hence we set the transition state optical isomer value to 2 in MESMER. Since no LJ parameters are available for the CH₂OO, we approximated them using the corresponding values of HCOOH, for which σ = 3.79 Å and ε = 520 K.^49,50 Fitting of the 〈ΔE〉_down,298K and n parameters to the experimental rate coefficient data was done using Levenberg–Marquardt algorithm as implemented in MESMER, resulting the following relation for the collisional energy transfer expression

〈ΔE〉_down = 123.2 × (T/298 K)^0.74, (5)

where, 〈ΔE〉_down,298K = 123.2 cm⁻¹ and the temperature dependency parameter n = 0.74. As the use of single-exponential-down model in master equation simulations has been extensive in literature, a set of 〈ΔE〉_down values has emerged. In the present work, both collisional energy transfer parameters obtained from fitting are within the expected range of values at room temperature.⁴³ Interestingly, combination of DLPNO-CCSD(T)/CBS(aug-cc-pV5Z,aug-cc-pV6Z)//CASSCF(8,8)/def2-TZVP energies calculated in this work with the fitted parameters provide such an excellent agreement with the experimental rate coefficient data of CH₂OO unimolecular decomposition that we do not need to tune the energies of neither the barrier nor the intermediate dioxirane. This further exemplifies the accuracy of our theoretical calculations as well as coherence between theory and experiments. The master equation results are in very good agreement with the experimental rate coefficients and justifies the high-pressure limiting values (p = 10 atm) presented in Table 2.

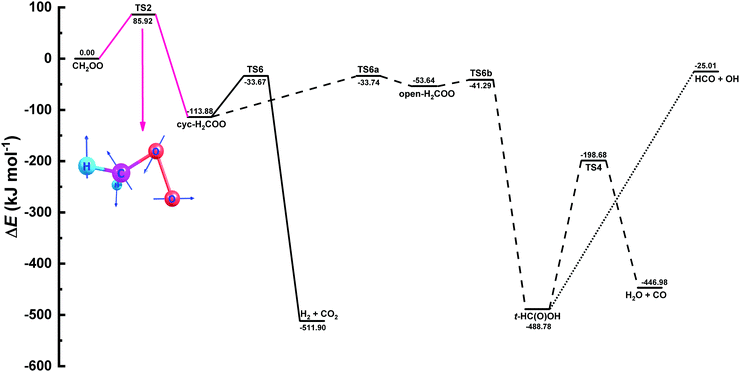Fig. 10 Zero-point inclusive potential energy surface (PES) for the unimolecular decomposition of CH₂OO in kJ mol⁻¹. The names of the species involved in the PES were taken from the works of Stone et al.⁹ and Nguyen et al.³⁶ The portion of the PES used in MESMER calculations to fit the experimental rate coefficient data is shown in pink along with the structure of the crucial transition state.

In literature several values are reported for the decomposition barrier of CH₂OO to cyc-H₂COO, ranging from 76 to 100 kJ mol⁻¹.⁴⁹ Our calculated barrier 85.92 kJ mol⁻¹ lies well within this range. To further test compatibility between the current computational and experimental results, we performed MESMER simulations by fitting simultaneously not only the collisional energy transfer parameters but also the barrier height so as to observe any change in the barrier height. We noticed that using Eckart tunneling, the decomposition barrier increases slightly by 1.6 kJ mol⁻¹, when fitting all three parameters simultaneously. On the other hand, when no tunneling is used, the barrier goes down by 1.8 kJ mol⁻¹. A comparison between the current MESMER simulation and the simulations with floating all three parameters is provided in Fig. S10 of the ESI† along with the experimental rate coefficients.

Product yields for the three different channels, viz., H₂ + CO₂, H₂O + CO, and HCO + OH presented in Fig. 10 were also estimated. According to MESMER simulations, H₂ + CO₂ is the predominant channel with 60.8% yield, whereas yields of the other two channels, H₂O + CO, and HCO + OH, can differ depending on the parameters involved in the simulations. The formation of HCO + OH is believed to proceed via irreversible decomposition of t-HC(O)OH without a clear transition state. Hence, in the present work, we have used a measured value k(HCO + OH) = 1.83 × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹, as reported by Temps et al.,⁵¹ for the pre-exponential factor in the modified Arrhenius expression, without any temperature dependency, to obtain the yield of the OH-radical formation channel. Our results indicate the formation of H₂O + CO channel with an overall yield of 30.9%, while the least dominant OH + HCO channel was having a percentage yield of 8.3.

In order to facilitate the utilization of current MESMER results in combustion or atmospheric chemistry models, we provide modified Arrhenius representations in ChemKin PLOG format (see ESI†) for the PES illustrated in Fig. 10. Also a MESMER input file is given in ESI.†

Comparison with the previous measurements. In Fig. 11, we compare the current results (filled circles and solid lines) with those of Stone et al.⁹ previous work (hollow triangles). The hollow triangles with the corresponding error bars are part of the experimental rate coefficient data that Stone et al. included in their MESMER fits at temperatures from 500 to 600 K (the fits included also data from 650 K). Due to the substantial background losses in their measurements, some of the low-pressure data at 500, 525, and 550 K, and all the data from the lowest two temperatures (450 and 475 K) were left out of their MESMER fittings. Since in the current measurements the background losses, k_loss, were generally much smaller than the observed decay rates (see Table 2), k_obs, we could fit all our unimolecular data in the master equation simulations (excluding the data from 425 K). The reported unimolecular decomposition rate coefficients of Stone et al.⁹ are more than two times smaller than our values at all temperatures shown in Fig. 11. Overall, their values are about 20–40% of our values with an average of 25%. This appreciable difference could be due to the reaction CH₂OO + CH₂I₂, which might have caused, as they also state, a contribution to their measured decay rate coefficient data at the temperatures above 450 K. Differences are also observed in the fitted energy-transfer parameters of the MESMER simulations. While simulations of the current work produce 123.2 cm⁻¹ and 0.74 values for the collisional energy transfer parameters 〈ΔE〉_down,298K and n, respectively, Stone et al.⁹ report corresponding values of 32.6 cm⁻¹ and 1.7 for the thermal unimolecular decomposition of CH₂OO.

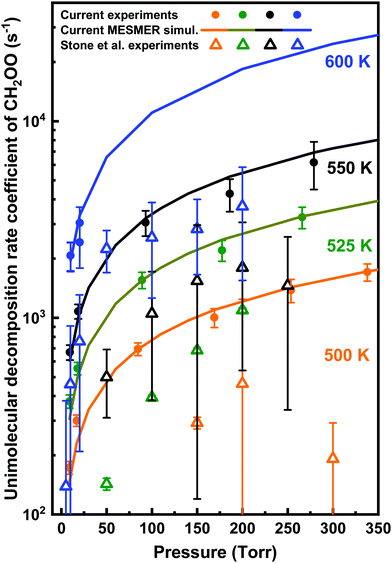Fig. 11 Comparison of the current measurements (filled circles) and MESMER simulation results (solid lines) with the results of previous experiments (hollow triangles) of Stone et al.⁹ for the unimolecular decomposition rate coefficients of CH₂OO as function of pressure at different temperatures.

Conclusions

In this work we have presented a new TR-BB-CEAS apparatus for kinetic studies of reactive intermediates, which are probed utilizing their UV-absorption. We show the capability of and use the new set-up for temperature- and pressure-dependent measurements of formaldehyde oxide (CH₂OO) reactions. The spectrometer is able to simultaneously measure transient absorption spectra over the wavelength range 300–450 nm with the time resolution of 50 μs using a fast CMOS line array camera-based grating spectrometer. The line array camera enables the transient spectra to be measured without any moving parts inside the grating spectrometer. For CH₂OO, we could reach a detection limit ∼2.4 × 10⁹ molecule cm⁻³ at 340 nm region with an averaging time of 30 min. This work also reveals a new photolytic precursor for formaldehyde oxide, bromoiodomethane (CH₂IBr), which photolysis at 213 nm in presence of O₂ produces CH₂OO. This new precursor was found to be free from secondary reactions that may regenerate CH₂OO in kinetic experiments. In addition, depletion of CH₂IBr in a photolysis does not produce a negative baseline shift for the CH₂OO absorption trace signal because of much smaller absorption cross-section of bromoiodomethane at 340 nm region.

The bimolecular rate coefficient for CH₂OO + HCOOH reaction was found to have a negative temperature dependency, decreasing from (1.0 ± 0.03) × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹ at 296 K to (0.47 ± 0.05) × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹ at 458 K with an Arrhenius activation energy −4.9 ± 1.6 kJ mol⁻¹. The obtained bimolecular rate coefficient at room temperature agrees with the previously reported rate coefficients from the direct kinetic experiments by Welz et al.¹⁵ Photodissociation of HCOOH reactant was found to be negligible and, consequently, did not have any important effect on the bimolecular kinetics of the CH₂OO + HCOOH reaction. However, if a reactant absorbs strongly at 213 nm, its photolysis could be a problem in bimolecular reaction kinetic measurements. This may well be the case with SO₂ reactant, which absorbs radiation strongly at 213 nm.⁵² In the current study, the CH₂OO + HCOOH reaction was also found to be pressure independent over the range between 5 and 150 Torr of helium at 296 K.

Our kinetic measurements of thermal unimolecular decomposition of CH₂OO over wide pressure (5–400 Torr) and temperature (296–600 K) ranges confirm the previously results that the thermal unimolecular decomposition is not an important atmospheric sink of CH₂OO^9,53 and the decomposition only becomes significant at temperatures above 425 K. Due to this reason, thermal unimolecular decomposition of CH₂OO might play an important role under low-temperature combustion conditions.

A very good agreement between the experimental results and master equation simulations performed using MESMER code was obtained by fitting collision energy transfer parameters to the experimental data without tuning any transition state energy. This evidences high coherence between experiments and theory. The MESMER simulations suggest 60.8% decomposition yield for the predominant H₂ + CO₂ channel. Yields of two other channels, H₂O + CO, and HCO + OH, are sensitive on the parameters involved in the simulations. Constraining simulations with an experimental value for (reverse) HCO + OH reaction, simulations return 30.9% and 8.3% yields for H₂O + CO and HCO + OH reaction channels, respectively.

Appreciable differences observed between the current experimental thermal unimolecular decomposition kinetics of CH₂OO and the results of Stone et al.⁹ measurements are suggested to originate from the use of different photolytic precursors.

Conflicts of interest

Authors declare no conflicts of interest.

Acknowledgements

J. P., P. S., and A. I. acknowledge support from the Academy of Finland, Grants 298910 and 311967. A. E. acknowledges support from the Academy of Finland, Grant 288377. The financial support from the University of Helsinki and the Academy of Finland (Grant 298910) to construct the apparatus is gratefully acknowledged. The authors wish to acknowledge CSC – IT Center for Science, Finland, for computational resources. We also thank Dr Leonid Sheps, Combustion Research Facility, Sandia National Laboratories, California, US, for help in design of our TR-BB-CEAS apparatus.

References

1. L. Vereecken, A. Novelli and D. Taraborrelli, Phys. Chem. Chem. Phys., 2017, 19, 31599–31612.
2. R. Criegee, Angew. Chem., Int. Ed. Engl., 1975, 14, 745–752.
3. M. A. H. Khan, C. J. Percival, R. L. Caravan, C. A. Taatjes and D. E. Shallcross, Environ. Sci.: Processes Impacts, 2018, 20, 437–453.
4. C. A. Taatjes, G. Meloni, T. M. Selby, A. J. Trevitt, D. L. Osborn, C. J. Percival and D. E. Shallcross, J. Am. Chem. Soc., 2008, 130, 11883–11885.
5. O. Welz, J. D. Savee, D. L. Osborn, S. S. Vasu, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Science, 2012, 335, 204–207.
6. Y. Su, Y. Huang, H. A. Witek and Y. Lee, Science, 2013, 340, 174–176.
7. L. Sheps, J. Phys. Chem. Lett., 2013, 4, 4201–4205.
8. W. Chao, J. Hsieh, C. Chang and J. J. M. Lin, Science, 2015, 347, 751–754.
9. D. Stone, K. Au, S. Sime, D. J. Medeiros, M. Blitz, P. W. Seakins, Z. Decker and L. Sheps, Phys. Chem. Chem. Phys., 2018, 20, 24940–24954.
10. D. Johnson and G. Marston, Chem. Soc. Rev., 2008, 37, 699–716.
11. A. J. Eskola, D. Wojcik-Pastuszka, E. Ratajczak and R. S. Timonen, Phys. Chem. Chem. Phys., 2006, 8, 1416–1424.
12. H. Huang, A. J. Eskola and C. A. Taatjes, J. Phys. Chem. Lett., 2012, 3, 3399–3403.
13. H. Huang, B. Rotavera, A. J. Eskola and C. A. Taatjes, J. Phys. Chem. Lett., 2013, 4, 3824.
14. J. L. Miller, Phys. Today, 2012, 65, 17–19.
15. O. Welz, A. J. Eskola, L. Sheps, B. Rotavera, J. D. Savee, A. M. Scheer, D. L. Osborn, D. Lowe, A. Murray Booth, P. Xiao, M. A. H. Khan, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Angew. Chem., Int. Ed., 2014, 53, 4547–4550.
16. J. J. M. Lin and W. Chao, Chem. Soc. Rev., 2017, 46, 7483–7497.
17. R. Chhantyal-Pun, A. Davey, D. E. Shallcross, C. J. Percival and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2015, 17, 3617–3626.
18. B. Long, J. Cheng, X. Tan and W. Zhang, THEOCHEM, 2009, 916, 159–167.
19. L. Vereecken, Phys. Chem. Chem. Phys., 2017, 19, 28630–28640.
20. A. Andersen and E. A. Carter, J. Phys. Chem. A, 2003, 107, 9463–9478.
21. A. Andersen and E. A. Carter, Mol. Phys., 2008, 106, 367–396.
22. B. Z. Chen, J. M. Anglada, M.-B. Huang and F. Kong, J. Phys. Chem. A, 2002, 106, 1877–1884.
23. R. A. Alvarez and C. B. Moore, J. Phys. Chem., 1994, 98, 174–183.
24. J. M. Beames, F. Liu, L. Lu and M. I. Lester, J. Chem. Phys., 2013, 138, 20045.
25. C. A. Taatjes, O. Welz, A. J. Eskola, J. D. Savee, A. M. Scheer, D. E. Shallcross, B. Rotavera, E. P. Lee, J. M. Dyke, D. K. Mok, D. L. Osborn and C. J. Percival, Science, 2013, 340, 177–180.
26. Y. Chang, C. Chang and K. Takahashi, Chem. Phys. Lett., 2016, 653, 155–160.
27. F. Liu, J. M. Beames, A. M. Green and M. I. Lester, J. Phys. Chem. A, 2014, 118, 2298–2306.
28. D. Stone, M. Blitz, L. Daubney, N. U. M. Howes and P. Seakins, Phys. Chem. Chem. Phys., 2014, 16, 1139–1149.
29. Y. Liu, F. Liu, S. Liu, D. Dai, W. Dong and X. Yang, Phys. Chem. Chem. Phys., 2017, 19, 20786–20794.
30. Z. J. Buras, R. M. Elsamra, A. Jalan, J. E. Middaugh and W. H. Green, J. Phys. Chem. A, 2014, 118, 1997–2006.
31. L. Sheps and D. W. Chandler, Time-Resolved Broadband Cavity-Enhanced Absorption Spectroscopy for Chemical Kinetics, Sandia National Laboratories, Livermore, CA, 2013, SAND2013-2664.
32. J. J. Scherer, J. B. Paul, H. Jiao and A. O’Keefe, Appl. Opt., 2001, 40, 6725–6732.
33. J. C. Mössinger, D. E. Shallcross and R. A. Cox, J. Chem. Soc., Faraday Trans., 1998, 94, 1391–1396.
34. L. Butler, E. Hintsa and Y. Lee, J. Chem. Phys., 1986, 84, 4104–4106.
35. L. Butler, E. Hintsa, S. F. Shane and Y. Lee, J. Chem. Phys., 1987, 86, 2051–2074.
36. T. Nguyen, R. Putikam and M. C. Lin, J. Chem. Phys., 2015, 142, 124312.
37. H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Inc., Wallingford, CT, 2016.
39. F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2018, 8, e1327.
40. A. K. Wilson, T. van Mourik and T. H. Dunning, THEOCHEM, 1996, 388, 339–349.
41. K. A. Peterson, D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 7410–7415.
42. T. T. Pekkanen, R. S. Timonen, G. Lendvay, M. P. Rissanen and A. J. Eskola, Proc. Combust. Inst., 2019, 37, 299–306.
43. D. R. Glowacki, C. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560.
44. W. Ting, Y. Chen, W. Chao and M. C. Smith, Phys. Chem. Chem. Phys., 2014, 16, 10438–10443.
45. A. Winkler and P. Hess, J. Am. Chem. Soc., 1994, 116, 9233–9240.
46. D. Singleton, G. Paraskevopoulos and R. Irwin, J. Photochem., 1987, 37, 209–216.
47. J. Troe, J. Phys. Chem., 1979, 83, 114–126.
48. V. P. Barber, S. Pandit, A. M. Green, N. Trongsiriwat, P. J. Walsh, S. J. Klippenstein and M. I. Lester, J. Am. Chem. Soc., 2018, 140, 10866–10880.
49. T. Berndt, R. Kaethner, J. Voigtländer, F. Stratmann, M. Pfeifle, P. Reichle, M. Sipilä, M. Kulmala and M. Olzmann, Phys. Chem. Chem. Phys., 2015, 17, 19862–19873.
50. L. I. Stiel and G. Thodos, AIChE J., 1964, 10, 266–269.
51. F. Temps and H. G. Wagner, Ber. Bunsenges. Phys. Chem., 1984, 88, 415–418.
52. G. Stark, P. L. Smith, J. Rufus, A. Thorne, J. Pickering and G. Cox, J. Geophys. Res., 1999, 104, 16585–16590.
53. T. A. Stephenson and M. I. Lester, Int. Rev. Phys. Chem., 2020, 39, 1–33.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp00302f

---