Influence of alkaline-earth metal substitution on structure, electrical conductivity and oxygen transport properties of perovskite-type oxides La0.6A0.4FeO3−δ (A = Ca, Sr and Ba)†
Received
15th January 2020
, Accepted 6th May 2020
First published on 7th May 2020
Abstract
Structural evolution, electrical conductivity, oxygen nonstoichiometry and oxygen transport properties of perovskite-type oxides La0.6A0.4FeO3−δ (A = Ca, Sr, and Ba) were investigated. La0.6Ca0.4FeO3−δ (LCF64) and La0.6Sr0.4FeO3−δ (LSF64) show a phase transformation in air at elevated temperature, i.e., from orthorhombic (Pnma) to rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) and from rhombohedral to cubic (Pm
c) and from rhombohedral to cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), respectively, while La0.6Ba0.4FeO3−δ (LBF64) remains cubic over the entire temperature range from room temperature to 1000 °C. The different phase behaviour of the solids is interpreted to reflect the decreased tendency for octahedral tilting with increasing alkaline-earth-metal dopant ion radius. The electrical conductivity of LSF64 is 191 S cm−1 in air at 800 °C, decreasing to a value of 114 S cm−1 at a pO2 of 0.01 atm, and found over this pO2 range roughly twice as high as those of LCF64 and LBF64. Failure to describe the data of electrical conductivity using Holstein's small polaron theory is briefly discussed. Chemical diffusion coefficients and surface exchange coefficients of the materials in the range 650–900 °C were extracted from data of electrical conductivity relaxation. Data of oxygen nonstoichiometry was used to calculate the vacancy diffusion coefficients from the measured chemical diffusion coefficients. The calculated migration enthalpies are found to decrease in the order LCF64 (1.08 ± 0.04 eV) > LSF64 (0.95 ± 0.01 eV) > LBF64 (0.81 ± 0.01 eV). The estimated ionic conductivities of the materials, at 900 °C, are within a factor of 1.4.
m), respectively, while La0.6Ba0.4FeO3−δ (LBF64) remains cubic over the entire temperature range from room temperature to 1000 °C. The different phase behaviour of the solids is interpreted to reflect the decreased tendency for octahedral tilting with increasing alkaline-earth-metal dopant ion radius. The electrical conductivity of LSF64 is 191 S cm−1 in air at 800 °C, decreasing to a value of 114 S cm−1 at a pO2 of 0.01 atm, and found over this pO2 range roughly twice as high as those of LCF64 and LBF64. Failure to describe the data of electrical conductivity using Holstein's small polaron theory is briefly discussed. Chemical diffusion coefficients and surface exchange coefficients of the materials in the range 650–900 °C were extracted from data of electrical conductivity relaxation. Data of oxygen nonstoichiometry was used to calculate the vacancy diffusion coefficients from the measured chemical diffusion coefficients. The calculated migration enthalpies are found to decrease in the order LCF64 (1.08 ± 0.04 eV) > LSF64 (0.95 ± 0.01 eV) > LBF64 (0.81 ± 0.01 eV). The estimated ionic conductivities of the materials, at 900 °C, are within a factor of 1.4.
Introduction
In the global effort to develop efficient alternatives to fossil fuel combustion for energy generation, solid oxide fuel cells (SOFCs) have attracted extensive attention due to their high energy conversion efficiency, wide fuel options, and low pollutant emission.1 To overcome performance degradation, researchers endeavour to lower the operating temperature. A key challenge thereby is to improve the performance of the cathode.
Mixed ionic–electronic conductivity is claimed essential to the cathode to achieve high performance.2 To date, mixed conducting acceptor-doped ABO3-type perovskite-structured oxides like La0.6Sr0.4Co0.2Fe0.8O3−δ (LSCF6428),3,4 La1−xSrxFeO3−δ5–7 and La0.6Sr0.4CoO3−δ (LSC64)8 are being investigated intensively for use as cathode in intermediate-temperature SOFCs (IT-SOFCs).9–11 Oxygen migration in these materials occurs by the vacancy mechanism. A-site substitution by divalent alkaline-earth metal ions thereby serves to create oxygen vacancies and, thus, to enhance ionic conductivity.4,12,13
A few studies have attempted to address the influence of alkaline-earth metal substitution on oxygen transport of (Co,Fe)-based perovskite-type oxides. Teraoka et al.14 first reported the oxygen permeation rate of La0.6A0.4Co0.8Fe0.2O3−δ to decrease in the order of the dopant Ba > Ca > Sr at 900 °C. A similar sequence was confirmed in a subsequent study on La0.4A0.6Co0.2Fe0.8O3−δ by Tsai et al.15 Stevenson et al.,16 on the other hand, found the oxygen flux for this series to decrease in the order Sr > Ba > Ca, similar to that observed for La0.2A0.8Co0.2Fe0.8O3−δ.17 Oxygen fluxes and ionic conductivities of several mixed-conducting perovskite oxides reported by different research groups are compiled in Table 1.
Table 1 Oxygen fluxes and ionic conductivities of La1−xAxCo1−yFeyO3−δ (A = Ca, Sr, Ba; x = 0.2, 0.4, 0.6, 0.8; y = 0, 0.2, 0.8) reported in the open literature
| Materials |
Thickness (cm) |
j
O2 (T (°C)) (cm3 cm−2 min−1) |
σ
ion (S cm−1) |
Ref. |
| La0.6Ca0.4Co0.8Fe0.2O3−δ |
0.2 |
1.80 (900 °C) |
— |
14
|
| La0.6Sr0.4Co0.8Fe0.2O3−δ |
0.2 |
0.62 (900 °C) |
— |
| La0.6Ba0.4Co0.8Fe0.2O3−δ |
0.2 |
2.11 (900 °C) |
— |
| La0.4Ca0.6Co0.2Fe0.8O3−δ |
0.055 |
0.19 (900 °C) |
— |
15
|
| La0.4Sr0.6Co0.2Fe0.8O3−δ |
0.055 |
0.11 (900 °C) |
— |
| La0.4Ba0.6Co0.2Fe0.8O3−δ |
0.055 |
0.72 (900 °C) |
— |
| La0.4Ca0.6Co0.2Fe0.8O3−δ |
0.2 |
0.07 (900 °C) |
0.03 (900 °C) |
16
|
| La0.4Sr0.6Co0.2Fe0.8O3−δ |
0.2 |
0.55 (900 °C) |
0.40 (900 °C) |
| La0.4Ba0.6Co0.2Fe0.8O3−δ |
0.2 |
0.45 (900 °C) |
0.33 (900 °C) |
| La0.2Ca0.8Co0.2Fe0.8O3−δ |
0.1 |
0.12 (950 °C) |
— |
17
|
| La0.2Sr0.8Co0.2Fe0.8O3−δ |
0.2 |
0.81 (950 °C) |
— |
| La0.2Ba0.8Co0.2Fe0.8O3−δ |
0.2 |
0.40 (950 °C) |
— |
| La0.8Ca0.2FeO3−δ |
0.3 |
— |
0.0008 (800 °C) |
19
|
| La0.8Sr0.2FeO3−δ |
0.3 |
— |
0.0045 (800 °C) |
| La0.8Ba0.2FeO3−δ |
0.3 |
— |
0.0019 (800 °C) |
As far as thermal and reduction stability is concerned, cobalt-free materials offer better opportunities to develop stable electrodes, irrespective of the relatively high costs of cobalt. Among the alkaline-earth metals, ab initio calculations predict that strontium and calcium would have the lowest solution energies in LaFeO3.18 Bidrawn et al.19 reported the oxygen permeation rate of La0.8A0.2FeO3−δ between 650 °C and 800 °C to decrease in the order Sr > Ba > Ca. To the best of our knowledge, no other studies have been conducted on the role of the dopant on oxygen transport of La1−xAxFeO3−δ. In this study, the influence of the nature of the alkaline-earth metal dopant (Ca, Sr, and Ba) on electrical conductivity and oxygen transport of La0.6A0.4FeO3−δ was investigated by means of electrical conductivity relaxation (ECR). To enable comparison materials with the same alkaline-earth metal dopant concentration were prepared. A dopant concentration of 40 mol% was chosen as Price et al.20 reported formation of secondary phases in samples La1−xCaxFeO3−δ with higher calcium substitution levels. Crystal structure and oxygen non-stoichiometry of the materials were investigated by high-temperature X-ray diffraction (HT-XRD) and thermogravimetric analysis (TGA).
Experimental
Sample preparation
Powders of La0.60A0.40FeO3−δ (A = Ca, Sr, and Ba) were prepared via a modified Pechini method as described elsewhere.21 Stoichiometric amounts of La(NO3)3·6H2O (Alfa Aesar, 99.9%), Ca(NO3)2·4H2O (Sigma-Aldrich, 99%), Sr(NO3)2 (Sigma-Aldrich, ≥99%), Ba(NO3)2 (Sigma-Aldrich, ≥99%), and Fe(NO3)3·9H2O (Sigma-Aldrich, ≥98%) were dissolved in water followed by the addition of C10H16N2O8 (EDTA, Sigma-Aldrich, >99%) and C6H8O7 (citric acid, Alfa Aesar, >99.5%) as chelating agents. The pH of the solution was adjusted to 7 using concentrated NH4OH (Sigma-Aldrich, 30% w/v). After evaporation of the water, the foam-like gel reached self-ignition at around 350 °C. The obtained raw ashes were calcined at 900 °C for 5 h, using heating/cooling rates of 5 °C min−1. Powders were pelletized by uniaxial pressing at 25 MPa followed by isostatic pressing at 400 MPa for 2 min. Subsequently, the pellets were sintered at 1100–1150 °C for 5 h in air with a heating/cooling rate of 2 °C min−1. The relative density of the pellets was above 94% of their theoretical value as measured by Archimedes’ method.
X-ray diffraction
Calcined powders were studied by room-temperature X-ray diffraction (XRD, D2 PHASER, Bruker) with Cu-Kα1 radiation (λ = 1.54060 Å). Data were collected in the step-scan mode over the 2θ range 20–90° with a step size of 0.01° and a counting time of 8 s. The thermal evolution of the structure was investigated using high-temperature X-ray diffraction (HT-XRD, D8 Advance, Bruker) in air in the range 600–1000 °C with 25 °C intervals. The sample was heated to the desired temperature with a heating rate of 25 °C min−1, followed by a dwell of 5 min to ensure equilibration. XRD patterns were recorded in the 2θ range of 20–90° with a step size of 0.015° and a counting time of 1.3 s. The FullProf software package was used for Rietveld refinements of the patterns.22
Oxygen nonstoichiometry
The oxygen nonstoichiometry of La0.60A0.40FeO3−δ (A = Ca, Sr, and Ba) was determined by thermogravimetric analysis (TGA, Netsch STA F3 Jupiter). Data were collected upon cooling from 900 °C to 650 °C, with intervals of 25 °C and a dwell time of 60 min at each temperature before the start of the measurements. The measurements were conducted in oxygen–nitrogen mixtures containing 4.5%, 10%, 21%, 42% or 90% of O2, which values correspond to those of the gas streams used in the electrical conductivity relaxation experiments (see below). Prior to data collection, the powder was heated under 4.5% O2 to 900 °C, with a heating rate of 20 °C min−1 and a dwell time of at least 2.5 h, to remove impurities like adsorbed water and CO2. The dwell time after a pO2 step at each measurement temperature was 10 min. Following prior studies on La1−xSrxFeO3−δ (0 ≤ x ≤ 0.6),23 all compositions were considered to be stochiometric (δ = 0) at a pO2 of 0.21 atm below 150 °C.
Electrical conductivity relaxation
Samples for ECR measurements were prepared by grinding and cutting the obtained dense pellets to planar sheet-shaped samples with approximate dimensions 12 × 5 × 0.5 mm3. The sample surface was polished using diamond polishing discs (JZ Primo, Xinhui China) down to 0.5 μm. A four-probe DC method was used to collect data of electrical conductivity. Two gold wires (Alfa Aesar, 99.999%, ∅ = 0.25 mm) were wrapped around both ends of the sample for current supply. Two additional gold wires were wrapped 1 mm remote from the current electrodes to act as voltage probes. To ensure good contact between the gold wires and the sample, sulphur-free gold paste (home-made) was applied on the sample surface directly underneath the gold wires. Finally, the sample was annealed at 950 °C in air for 1 h to sinter the gold paste and thermally cure the polished sample surface.
The sample was mounted on a holder and placed in an alumina sample containment chamber (or reactor). Two gas streams, each of which with a flow rate of 280 ml min−1 and with a different pO2, were created by mixing dried oxygen and nitrogen in the desired ratios using Brooks GF040 mass flow controllers. A pneumatically operated four-way valve was used to instantaneously switch between both gas streams so that one of them was fed through the reactor. Data of the transient electrical conductivity was collected following oxidation and reduction step changes in pO2 between 0.10 and 0.21 atm. Measurements were conducted following stepwise cooling from 900 °C to 650 °C with intervals of 25 °C, heating and cooling rates of 10 °C min−1 and a dwell time of 60 min at each temperature before data acquisition.
The transient conductivity after each pO2 step change was normalized according to eqn (1) and fitted to eqn (2)–(4) to obtain the chemical diffusion coefficient Dchem and the surface exchange coefficient kchem.
| | 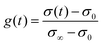 | (1) |
| | 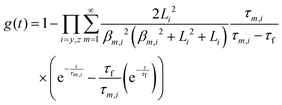 | (2) |
| | 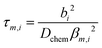 | (3) |
| | 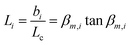 | (4) |
In these equations,
g(
t) is the normalized conductivity,
σ0 and
σ∞ are the conductivities
σ(
t) at time
t = 0 and
t = ∞, respectively,
τf is the flush time, 2
bi is the sample dimension along coordinate
i, whilst
βm,i are the non-zero roots of
eqn (4).
Lc =
Dchem/
kchem is the critical thickness below which oxygen surface exchange prevails over bulk oxygen diffusion in determining the rate of re-equilibration after a
pO
2 step change. The flush time
τf was calculated from
| | 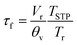 | (5) |
which equation assumes perfect mixing of the gas in the sample containment chamber. In
eqn (5),
Vr is the corresponding volume,
θv the gas flow rate through the chamber,
Tr the temperature inside the chamber, and
TSTP the temperature at standard conditions. The small chamber volume (2.58 cm
3) and the high gas flow rate (280 ml min
−1) used ensured a flush time between 0.13 s at 900 °C and 0.16 s at 650 °C. Curve fitting of the normalized transient conductivity was performed using a non-linear least-squares program based on the Levenberg–Marquardt algorithm. More detailed descriptions of the ECR technique and the model used for data fitting are given elsewhere.
24,25
Results and discussion
Crystal structure and phase transitions
Fig. 1 shows the room temperature XRD patterns of LCF64, LSF64 and LBF64 recorded in air. The corresponding structural parameters and reliability factors from Rietveld refinements are listed in Table 2. No impurity peaks are found in the patterns, suggesting that all three compositions are single phase. The pattern obtained for LCF64 could be fitted with an orthorhombic structure (space group Pnma) with cell parameters a = 5.4962(2) Å, b = 7.7658(2) Å and c = 5.5018(2) Å, which is in excellent agreement with a = 5.4941 Å, b = 7.7736 Å and c = 5.5083 Å reported by Hung et al.26 LSF64 adopts a rhombohedral structure (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) with cell parameters a = 5.5228(1) Å and c = 13.4471(3) Å (hexagonal representation), in good agreement with a = 5.5272(2) Å and c = 13.4408(4) Å reported by Yang et al.27 LBF64 appears to be cubic (space group Pm
c) with cell parameters a = 5.5228(1) Å and c = 13.4471(3) Å (hexagonal representation), in good agreement with a = 5.5272(2) Å and c = 13.4408(4) Å reported by Yang et al.27 LBF64 appears to be cubic (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with a = 3.93652(2) Å, matching precisely the value a = 3.93652(9) Å found for La0.5Ba0.5FeO3−δ reported by Ecija et al.28
m) with a = 3.93652(2) Å, matching precisely the value a = 3.93652(9) Å found for La0.5Ba0.5FeO3−δ reported by Ecija et al.28
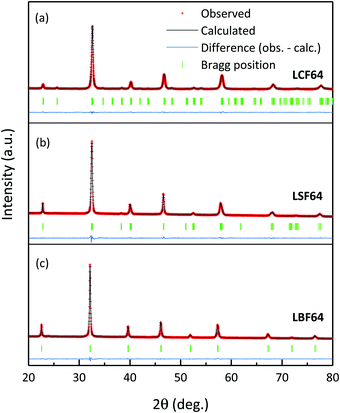 |
| | Fig. 1 Measured (red symbols) and calculated (black line) of room temperature XRD powder patterns of LCF64, LSF64 and LBF64. Bragg peaks and the residual plots are given under the patterns. | |
Table 2 Space group, lattice parameters and reliability factors obtained from the Rietveld refinements of room temperature XRD diffractograms of LCF64, LSF64 and LBF64. The lattice parameters for the rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) structure of LSF64 are listed in hexagonal settings. The numbers in parentheses denote standard deviations in units of the least significant digits
c) structure of LSF64 are listed in hexagonal settings. The numbers in parentheses denote standard deviations in units of the least significant digits
|
|
LCF64 |
LSF64 |
LBF64 |
| Space group |
Pnma
|
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
|
a/Å |
5.5138(1) |
5.5226(1) |
3.93652(2) |
|
b/Å |
7.7574(1) |
5.5226(1) |
3.93652(2) |
|
c/Å |
5.4896(1) |
13.4462(3) |
3.93652(2) |
|
V/Å3 |
234.8064(2) |
355.1558(2) |
61.0014(1) |
|
R
wp/% |
5.49 |
7.55 |
6.03 |
|
R
Bragg/% |
1.79 |
1.01 |
1.042 |
|
χ
2
|
4.78 |
2.55 |
3.545 |
HT-XRD patterns of LCF64, LSF64 and LBF64 are shown in Fig. S1 (ESI†). Pseudo-cubic lattice parameters obtained from Rietveld refinements of these are shown in Fig. 2. Price et al.20 verified the occurrence of a phase transition sequence in LCF64, i.e., from orthorhombic (space group Pnma) to rhombohedral (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) at 602 °C to cubic (space group Pm
c) at 602 °C to cubic (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) at about 1100 °C, on the basis of data of differential scanning calorimetry (DSC) and HT-XRD. Our study confirms that LCF64 remains orthorhombic until ∼600 °C, consistent with the results obtained by Price et al.20 However, our refinements yield a mixture of orthorhombic and rhombohedral phases above ∼625 °C, i.e., from 3.89% rhombohedral at 625 °C to 15.79% at 700 °C, transforming into a pure rhombohedral phase above 725 °C. The rhombohedral angle decreases from 60.29° at 625 °C to 60.09° at 1000 °C, suggesting that at a slightly higher temperature the cubic phase is formed. Fig. 2b shows the occurrence of a rhombohedral-to-cubic phase transition in LSF64 at around 850 °C, which is in agreement with previous results obtained by Fossdal et al.29 LBF64 adopts a cubic structure (space group Pm
m) at about 1100 °C, on the basis of data of differential scanning calorimetry (DSC) and HT-XRD. Our study confirms that LCF64 remains orthorhombic until ∼600 °C, consistent with the results obtained by Price et al.20 However, our refinements yield a mixture of orthorhombic and rhombohedral phases above ∼625 °C, i.e., from 3.89% rhombohedral at 625 °C to 15.79% at 700 °C, transforming into a pure rhombohedral phase above 725 °C. The rhombohedral angle decreases from 60.29° at 625 °C to 60.09° at 1000 °C, suggesting that at a slightly higher temperature the cubic phase is formed. Fig. 2b shows the occurrence of a rhombohedral-to-cubic phase transition in LSF64 at around 850 °C, which is in agreement with previous results obtained by Fossdal et al.29 LBF64 adopts a cubic structure (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) throughout the measured temperature range, as shown in Fig. 2c. The temperature dependences of the Fe–O–Fe angles and Fe–O bond lengths obtained from the Rietveld refinements are plotted in Fig. S2 (ESI†).
m) throughout the measured temperature range, as shown in Fig. 2c. The temperature dependences of the Fe–O–Fe angles and Fe–O bond lengths obtained from the Rietveld refinements are plotted in Fig. S2 (ESI†).
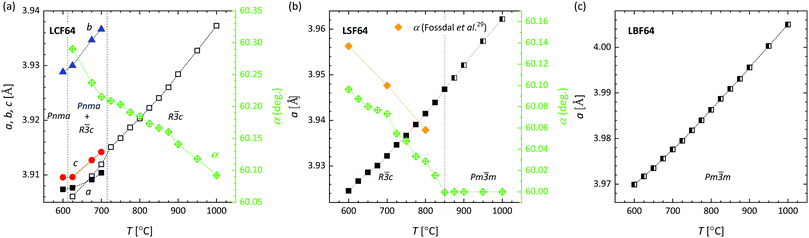 |
| | Fig. 2 Lattice parameters for (a) LCF64, (b) LSF64, (c) LBF64 as a function of temperature from Rietveld refinements of HT-XRD patterns recorded in air. Pseudo-cubic cell parameters are given for the orthorhombic (Pnma) structures, calculated using  , b = bortho/2 and , b = bortho/2 and  . For the cubic (Pm . For the cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and rhombohedral (R m) and rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) structures a = b = c. c) structures a = b = c. | |
The crystal symmetry of the room-temperature structure is found to decrease in the order LBF64, LSF64 and LCF64, i.e., from cubic to rhombohedral to orthorhombic, respectively, following the decrease in the magnitude of the radii of the alkaline-earth-metal dopant ions: Ba2+ (XII) = 1.61 Å > Sr2+ (XII) = 1.44 Å > Ca2+ (XII) = 1.34 Å, where the number between brackets designates the coordination number. Ionic radii were taken from Shannon.30 The observed lowering in symmetry is believed to result from cooperative tilting of BO6 octahedra, which is the most commonly observed distortion in perovskite structures. The tendency for distortion of the ABO3 perovskite structure is generally rationalized by the Goldschmidt tolerance factor 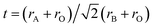 ,31 where rA, rB and rO are the ionic radii of the involved ions. The ideal cubic structure is formed for t = 1, when the A and O2− ions are matching in size to form cubic close-packed layers, while the B cations fit into the interstices formed by the O2− ions to give an array of corner-shared BO6 octahedra. For t < 1, the BO6 octahedra cooperatively tilt to accommodate the mismatch, thereby forming less symmetric rhombohedral or orthorhombic structures.32,33 The orthorhombic Pnma structure, in Glazer's notation34 denoted by a−a−c+, as adopted by LCF64 is one of the most common perovskite structures with a three-tilt system.35,36 Upon decreasing the size of the earth-alkaline cation, the out-of-phase rotation (−) along the [001] direction of the pseudo-cubic cell changes to an in-phase rotation (−) for LSF64, expressed in Glazer's notation by a−a−c− (space group R
,31 where rA, rB and rO are the ionic radii of the involved ions. The ideal cubic structure is formed for t = 1, when the A and O2− ions are matching in size to form cubic close-packed layers, while the B cations fit into the interstices formed by the O2− ions to give an array of corner-shared BO6 octahedra. For t < 1, the BO6 octahedra cooperatively tilt to accommodate the mismatch, thereby forming less symmetric rhombohedral or orthorhombic structures.32,33 The orthorhombic Pnma structure, in Glazer's notation34 denoted by a−a−c+, as adopted by LCF64 is one of the most common perovskite structures with a three-tilt system.35,36 Upon decreasing the size of the earth-alkaline cation, the out-of-phase rotation (−) along the [001] direction of the pseudo-cubic cell changes to an in-phase rotation (−) for LSF64, expressed in Glazer's notation by a−a−c− (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c), and to the no-tilt system a0a0a0 (space group Pm
c), and to the no-tilt system a0a0a0 (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) for LBF64. Note from Fig. 2a and b that similar structural changes are induced in LCF64 and LSF64 upon increasing temperature.
m) for LBF64. Note from Fig. 2a and b that similar structural changes are induced in LCF64 and LSF64 upon increasing temperature.
Oxygen stoichiometry
The oxygen stoichiometry (3 − δ) in LCF64, LSF64 and LBF64 as a function of oxygen partial pressure and temperature was investigated by thermogravimetry. A typical measurement scheme is shown in Fig. S3 (ESI†). Corresponding data obtained at different temperatures is shown in Fig. 3. For completeness, plots of log(δ) vs. log(pO2) at different temperatures for each of the compositions are given in Fig. S4 (ESI†). As can be inferred from the data of Fig. 3, the oxygen content in the experimental range of temperature and oxygen partial pressure tends to increase in the order LBF64 < LSF64 < LCF64. Good agreement was obtained between the results of this study for LSF64 and corresponding data measured at 800 °C and 900 °C by Kuhn et al.37 as demonstrated in Fig. S5 (ESI†). To the best of our knowledge, no data of oxygen stoichiometry has been reported for LCF64 and LBF64. Kharton et al.38 measured the pO2 dependence of the oxygen contents of La0.5Sr0.5FeO3−δ and La0.5Ba0.5FeO3−δ, at 950 °C, yielding trends similar to those found in Fig. 3.
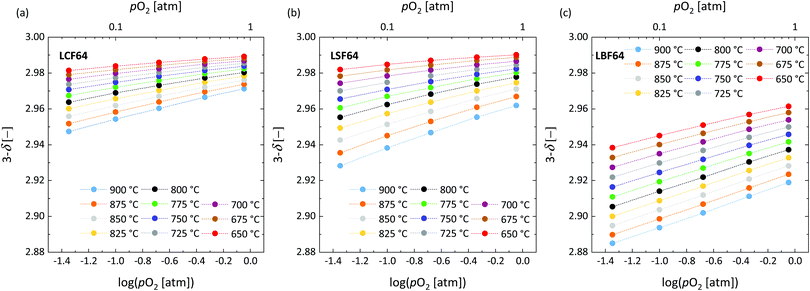 |
| | Fig. 3 Oxygen stoichiometry of (a) LCF64, (b) LSF64 and (c) LBF64 as a function of log(pO2) at different temperatures. Dashed lines are drawn to guide the eye. | |
Electrical conductivity
Fig. 4a and Fig. S6a (ESI†) show that over the entire experimental range of temperature and oxygen partial pressure, the electrical conductivity of LSF64 is roughly twice as high as those of LBF64 and LCF64. At 800 °C, the conductivity of LSF64 in air is 191 S cm−1, to be compared with values of 91 S cm−1 and 93 S cm−1 measured under these conditions for LCF64 and LBF64, respectively. Excellent agreement is found between the results for LSF64 from this study and data reported by Søgaard et al.,39 as demonstrated in Fig. 4a.
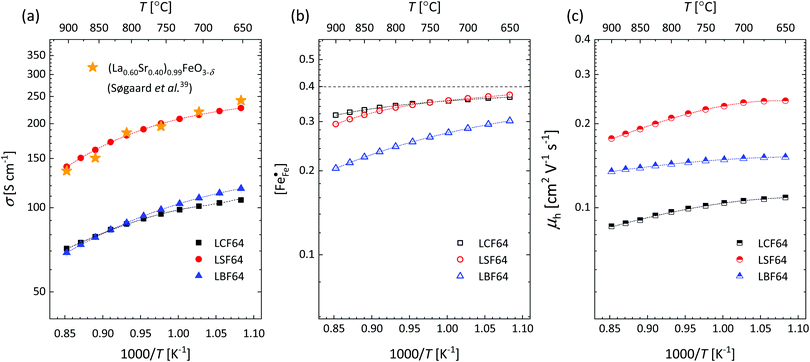 |
| | Fig. 4 Arrhenius plots of the (a) electrical conductivity, (b) defect concentration 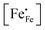 and (c) mobility of electron–holes, at pO2 = 0.21 atm, for LCF64, LSF64 and LBF64. The dashed lines through the data points are drawn to guide the eye. The horizontal line in Fig. 4b represents the and (c) mobility of electron–holes, at pO2 = 0.21 atm, for LCF64, LSF64 and LBF64. The dashed lines through the data points are drawn to guide the eye. The horizontal line in Fig. 4b represents the 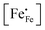 concentration when electronic compensation is predominant, noting that all three materials have the same concentration of the alkaline-earth dopant (cf.eqn (7)). concentration when electronic compensation is predominant, noting that all three materials have the same concentration of the alkaline-earth dopant (cf.eqn (7)). | |
The electrical conductivity in La1−xAxFeO3−δ (A = Ca, Sr, Ba) and related perovskite oxides is commonly interpreted on the basis of hopping of small polarons.26,40–42 Under oxidizing atmospheres, the conductivity can be expressed as,26,43
| | 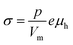 | (6) |
where
p and
μh are the concentration (mole fraction) and mobility of electron holes, respectively,
Vm is the unit cell volume, and
e is the electronic charge. Both parameters
p and
μp are considered to be thermally activated. The partial substitution of lanthanum in La
1−xA
xFeO
3−δ (A = Ca, Sr, Ba) by divalent alkaline-earth ions is charge compensated by the formation of electron holes and/or oxygen vacancies, the limiting cases being referred to as electronic and ionic compensation, respectively. Assuming oxygen vacancies to be doubly ionized, the reduced charge neutrality condition can be written as, in Kröger–Vink notation,
44| | 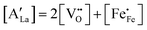 | (7) |
where
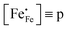
represents the concentration of p-type charge carriers.
Eqn (7) lacks n-type charge carriers,
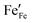
, arising as a result of the charge disproportionation reaction,
| | 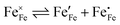 | (8) |
and which become dominant under reducing atmospheres. In the case of structural A- and B-site deficiency, also vacancies
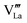
and
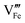
need to be taken into account. Using
eqn (7) and data of oxygen stoichiometry (
Fig. 3), the concentration of
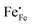
in phases LCF64, LSF64 and LBF64 may be calculated. Corresponding data are shown in
Fig. 4b and Fig. S6b (ESI
†), from which figures it can be inferred that under the conditions covered by the experiments electronic compensation dominates over ionic compensation. The lowest electron–hole concentration is found in LBF64, indicating that in this material the relative contribution of the ionic compensation mechanism is higher than those in LCF64 and LSF64. In all three phases, the concentration
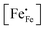
is found to decrease and, hence, ionic compensation appears to become more dominant, with increasing temperature and decreasing oxygen partial pressure.
Electrical mobilities of the electron holes calculated using eqn (6) plotted as a function of inverse temperature and log(pO2) are presented in Fig. 4c and Fig. S6c (ESI†), respectively. Below, we have analysed the inverse temperature dependence of the electron–hole mobility in terms of Holstein's generalized small polaron model (in which the initial and final states are treated on equal footing), considering both adiabatic and non-adiabatic hopping.46–48 In the adiabatic case,46 the charge carrier is able to hop to an adjacent vacant site, once an energy coincidence occurs. The corresponding mobility of electron holes is given by
| | 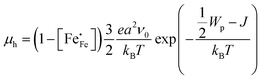 | (9) |
where
a is the hopping distance,
ν0 is the frequency of optical phonons,
Wp is the polaron binding energy,
J is the kinetic energy of the polaron, and
kB is the Boltzmann constant. The factor of 3/2 takes into account the fact that the polaron moves in a three-dimensional lattice.
46 The factor of
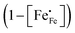
takes into account the site-blocking effect, the probability that the adjacent site to which the polaron hops may already be occupied.
48 In the non-adiabatic case,
45 the polaron misses coincidence events as it moves too slowly, lowering the net hopping rate. In this case, the mobility of electron holes is given by
| | 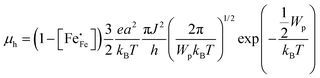 | (10) |
where
h is the Planck constant. In the adiabatic regime, the plot of
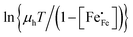 vs.
vs. 1000/
T should give a straight line with activation energy
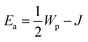
; in the non-adiabatic regime, the plot of
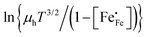 vs.
vs. 1000/
T should give a straight line with activation energy
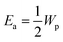
.
Corresponding plots are shown in Fig. 5. The plots obtained for LCF64 and LSF64 exhibit a double slope behaviour. At lower temperatures the curves for both materials can be interpreted in a way as characteristic for small polaron conduction (i.e., small polarons have a thermally activated mobility), but at higher temperatures the curves show a negative slope. For LBF64, the apparent activation energy of the mobility is estimated at a value of 0.039 ± 0.002 eV in the non-adiabatic case, while it tends to nearly zero in the adiabatic case. Our results are consistent with those obtained in a study by Patrakeev et al.49 who found an activation energy for the carrier mobility in La1−xSrxFeO3−δ of about 0.4 eV and 0.2 eV for x = 1.0 and x = 0.7, respectively, while tending to values near to zero in the oxides with x ≤ 0.5. The low activation energies that may be inferred from the data in Fig. 6a and b may be compared with the approximate values 0.04–0.14 eV derived from ln{σT} versus 1000/T plots for La0.8Sr0.2Co1−yFeyO3−δ (0 ≤ y ≤ 1).50 It is obvious from the above analysis that other factors need to be considered to account for the observations.
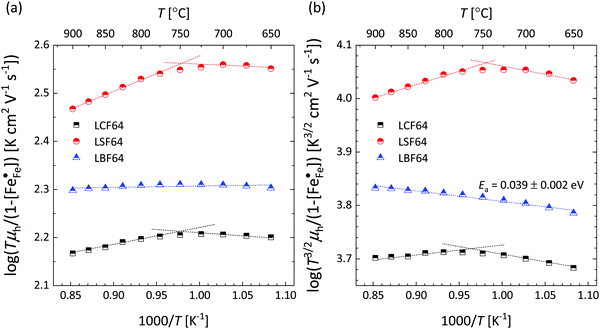 |
| | Fig. 5 Plots of (a) 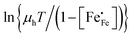 vs. 1000/T (adiabatic case) and (b) vs. 1000/T (adiabatic case) and (b) 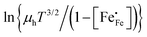 vs. 1000/T (non-adiabatic case), at pO2 = 0.21 atm. The dotted lines are drawn to guide the eye. vs. 1000/T (non-adiabatic case), at pO2 = 0.21 atm. The dotted lines are drawn to guide the eye. | |
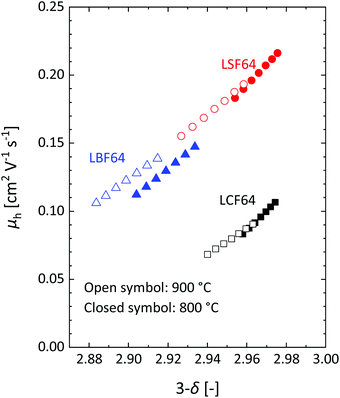 |
| | Fig. 6 Mobility of electron–holes, at 800 °C and 900 °C, as a function of oxygen content for LCF64, LSF64 and LBF64. | |
Inspection of the data in Fig. 4 and 5 suggests that the electrical mobility is correlated with the electron hole concentration in phases LCF64, LSF64 and LBF64. The observed trend deduced is that the electrical mobility is suppressed with decreasing the electron hole concentration, 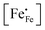 , which is contrary to what is expected from the site-blocking term,
, which is contrary to what is expected from the site-blocking term, 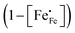 , in eqn (9) and (10). In view of eqn (7), the electron hole concentration on its turn is correlated with the concentration of oxygen vacancies. Fig. 6 shows that the hopping mobility decreases with increasing the oxygen nonstoichiometry of phases LCF64, LSF64 and LBF64. Similar observations have been reported for La1−xSrxFeO3−δ (0.1 ≤ x ≤ 1).49 Noting that the direct overlap between neighbouring Fe 3d orbitals in the La0.6A0.4FeO3−δ (A = Ca, Sr, and Ba) perovskite structure is negligible, the polaron hopping between two adjacent Fe cations is brought about by the overlapping O 2p orbitals of the bridging oxygen ion, which is known as the Zener double-exchange mechanism.51 Disruption of the Fe4+–O–Fe3+ migration pathways due to the presence of oxygen vacancies thus may affect the hopping mobility. The probability that an oxygen vacancy blocks the migration pathway scales with (1 − δ/3). The corresponding values for this parameter for each of the materials under the given experimental conditions are, however, too close to unity to have a significant impact on the effective hopping mobility. Electrostatic interactions between the electron holes and oxygen vacancies or formation of delocalized states may further affect the hopping mobility. X-ray absorption spectroscopy and density functional theory studies indicate that the electron holes in La1−xSrxFeO3−δ and La1−xCaxFeO3−δ have mixed Fe 3d and O 2p band character and, hence, are delocalized at least to some extent.51–58 This would comply with the observed low-to-zero activation energies of the carrier mobility in phases LCF64, LSF64 and LBF64 (cf.Fig. 5). This argument is, however, in contrast with results from angle-resolved photo emission spectroscopy, suggesting a strong localisation of the electron holes in La0.6Sr0.4FeO3−δ.59 Clearly, more research is warranted to clarify the nature of the charge carriers in La1−xAxFeO3−δ (A = Ca, Sr, Ba).
, in eqn (9) and (10). In view of eqn (7), the electron hole concentration on its turn is correlated with the concentration of oxygen vacancies. Fig. 6 shows that the hopping mobility decreases with increasing the oxygen nonstoichiometry of phases LCF64, LSF64 and LBF64. Similar observations have been reported for La1−xSrxFeO3−δ (0.1 ≤ x ≤ 1).49 Noting that the direct overlap between neighbouring Fe 3d orbitals in the La0.6A0.4FeO3−δ (A = Ca, Sr, and Ba) perovskite structure is negligible, the polaron hopping between two adjacent Fe cations is brought about by the overlapping O 2p orbitals of the bridging oxygen ion, which is known as the Zener double-exchange mechanism.51 Disruption of the Fe4+–O–Fe3+ migration pathways due to the presence of oxygen vacancies thus may affect the hopping mobility. The probability that an oxygen vacancy blocks the migration pathway scales with (1 − δ/3). The corresponding values for this parameter for each of the materials under the given experimental conditions are, however, too close to unity to have a significant impact on the effective hopping mobility. Electrostatic interactions between the electron holes and oxygen vacancies or formation of delocalized states may further affect the hopping mobility. X-ray absorption spectroscopy and density functional theory studies indicate that the electron holes in La1−xSrxFeO3−δ and La1−xCaxFeO3−δ have mixed Fe 3d and O 2p band character and, hence, are delocalized at least to some extent.51–58 This would comply with the observed low-to-zero activation energies of the carrier mobility in phases LCF64, LSF64 and LBF64 (cf.Fig. 5). This argument is, however, in contrast with results from angle-resolved photo emission spectroscopy, suggesting a strong localisation of the electron holes in La0.6Sr0.4FeO3−δ.59 Clearly, more research is warranted to clarify the nature of the charge carriers in La1−xAxFeO3−δ (A = Ca, Sr, Ba).
Electrical conductivity relaxation
Chemical diffusion and surface exchange coefficients.
In this study, the ECR method was used for evaluation of the oxygen transport properties of LCF64, LSF64 and LBF64. Typical fits to the normalized conductivity relaxation curves following oxidation and reduction step changes in pO2 are shown in Fig. 7. In general, the curves from oxidation and reduction runs may slightly differ due to the pO2 dependence of oxygen transport. This asymmetry will be influenced by the mean pO2 and the magnitude of the pO2 step size. Curve fitting allows simultaneous determination of the chemical diffusion coefficient Dchem and the surface exchange coefficient kchem provided that fitting is sensitive to both parameters. If the smallest dimension of the sample is much lower than the ratio Dchem/kchem, the fitting will be insensitive to Dchem. Conversely, if the sample dimensions are much lower than Dchem/kchem, curve fitting will be insensitive to kchem. Accordingly, one may define a Biot number (Bi),| | 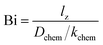 | (11) |
where lz is the half thickness of the sample. The Biot number compares the relative rates of oxygen diffusion and surface exchange to the relaxation process. If Bi ≥ 30, then the relaxation is said to predominantly controlled by diffusion; if Bi ≤ 0.03, then the relaxation is said to predominantly controlled by surface exchange.25 In the intermediate region, 0.03 ≤ Bi ≤ 30, both diffusion and surface exchange determine the relaxation. The bounds are linked to the accuracy of curve fitting, i.e., only in the mixed controlled region both Dchem and kchem can be most reliably assessed. A plot of the Biot number against temperature obtained from fitting data of ECR measurements of LCF64, LSF64 and LBF64 is shown in Fig. 8. Note from eqn (11) that the Biot number can only be calculated if both Dchem and kchem are obtained from curve fitting. Dchem and kchem may exhibit different pO2 dependencies. Therefore, in addition to varying the sample dimension lz, the measurements can be performed at different oxygen partial pressure to improve the sensitivity of fitting to either Dchem or kchem.
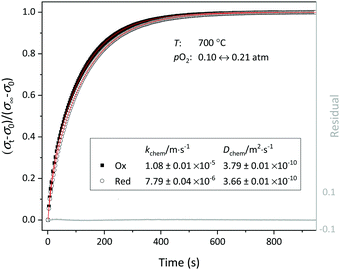 |
| | Fig. 7 Normalized conductivity curves obtained for LCF64 following step changes in pO2 between 0.1 and 0.21 atm at 700 °C. The solid lines show the least-square fits to eqn (2)–(4). | |
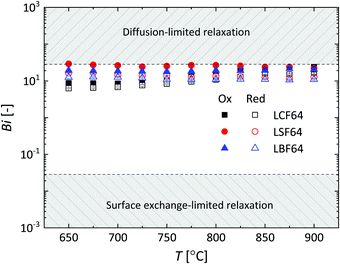 |
| | Fig. 8 Temperature dependence of the Biot number (Bi) for LCF64, LSF64 and LBF64. Errors bars are within the symbols. | |
Arrhenius plots of Dchem and kchem of LCF64, LSF64 and LBF64 derived from the data of ECR measurements are shown in Fig. 9. The corresponding apparent activation energies are listed in Table S2 (ESI†). The Dchem values of the different materials show remarkable agreement with an average activation energy close to 93 kJ mol−1. It is further noted from Fig. 9d that the values obtained for LSF64 are in good agreement with previously reported results.24,39 The values of kchem of the different materials are found to be within similar range above 850 °C. Below this temperature, however, a different activation energy for kchem is apparent for LCF64 when compared with those found for LSF64 and LBF64 for which behaviour we lack a definite explanation (cf. Table S2, ESI†). In general, the surface exchange rate on oxide surfaces may be highly influenced by, e.g., surface enrichment due to segregation, surface impurities and grain size. No attempt was made in this study to relate the elemental surface composition and morphology to the observed surface exchange rates exhibited by the samples.
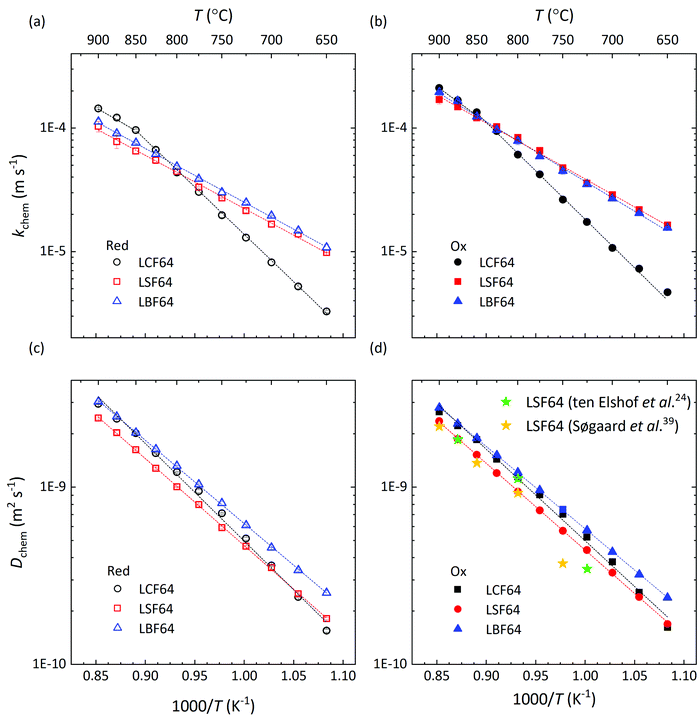 |
| | Fig. 9 Arrhenius plots of the (a and b) surface exchange coefficient, kchem, and (c and d) chemical diffusion coefficient, Dchem, for LCF64, LSF64 and LBF64. For clarity, data from oxidation (Ox) and reduction (red) runs are given in separate plots. Error bars are within the symbols. The dashed lines are from linear fitting of the data. | |
Oxygen self-diffusion and vacancy-diffusion coefficients.
The oxygen self-diffusion coefficients, Ds, and oxygen vacancy-diffusion coefficients, Dv, for phases LCF64, LSF64 and LBF64 were evaluated from the measured values of Dchem, using the relationships Dchem = γODs = γvDv,24 where γO and γv are the thermodynamic factors, defined as| | 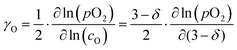 | (12) |
| | 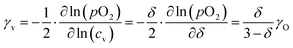 | (13) |
Herein, cO and cv are the concentrations of oxygen ions and vacancies in the lattice. The thermodynamic factors can be derived from corresponding data of the oxygen non-stoichiometry (Fig. 3) and are given for the different phases in Fig. S7 (ESI†). Arrhenius plots of the calculated values of Ds and Dv for the different materials are shown in Fig. 10, while the activation energies extracted from these are listed in Table S3 (ESI†) and Table 3, respectively.
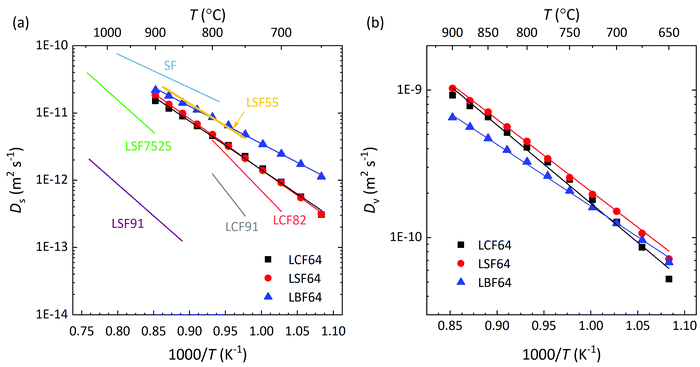 |
| | Fig. 10 Arrhenius plots of the (a) self-diffusion coefficient, Ds, and (b) vacancy-diffusion coefficient, Dv, at pO2 = 0.142 atm, for LCF64, LSF64 and LBF64. The specified pO2 corresponds to the logarithmic average of the initial and final values of the pO2 step change during ECR experiments. For clarity, only data of oxidations runs are shown in both figures. Error bars are within the symbols. The drawn lines are from linear fitting of the data. Also shown in (a) are values of Ds for La0.9Sr0.1FeO3−δ (LSF91) and La0.75Sr0.25FeO3−δ (LSF7525), at pO2 = 0.65 atm,60 calculated from data of isotopic exchange depth profiling (IEDP), and for La0.5Sr0.5FeO3−δ (LSF55) and SrFeO3−δ (SF), at pO2 = 0.05 atm, from data of ECR.61 | |
Table 3 Migration enthalpies (ΔHm) of LCF64, LSF64 and LBF64 extracted from data of ECR experiments, following pO2 step changes 0.21 → 0.1 atm (Red) and 0.1 → 0.21 atm (Ox)
| Materials |
Red |
Ox |
| ΔHm (eV) |
ΔHm (eV) |
| LCF64 |
1.11 ± 0.03 |
1.05 ± 0.03 |
| LSF64 |
0.94 ± 0.01 |
0.96 ± 0.01 |
| LBF64 |
0.80 ± 0.01 |
0.82 ± 0.01 |
Fig. 10a shows that over the temperature range 650–900 °C almost similar values of Ds are observed for LCF64 and LSF64. Slightly higher values are found for LBF64; the difference is a factor of about 3 at 650 °C, which has reduced to a factor 1.2 at 900 °C due to a slightly lower activation energy of 106 ± 1 kJ mol−1 compared with values of 138 ± 2 kJ mol−1 and 146 ± 1 kJ mol−1 observed for LCF64 and LSF64, respectively. Also shown in in this figure are values of Ds for other compositions in the series for La1−xSrxFeO3−δ from literature,60,61 demonstrating the expected increase of Ds with increasing the alkaline-earth metal dopant concentration and the consistency with the results from this study. Calculated ionic conductivities of phases LCF64, LSF64, and LBF64, using the Nernst–Einstein equation are given in Fig. 11. As the total concentration of oxygen ions remains virtually constant, the trend in ionic conductivity among the different materials is the same as that observed for Ds (cf.Fig. 9a). Fig. 10b shows that the values of Dv of phases LCF64, LSF64 and LBF64 in the experimental temperature range are very similar, which further indicates that the higher ionic conductivities and self-diffusion coefficients observed for LBF64 relative to corresponding values for LCF64 and LSF64 at similar conditions are mainly due to the higher concentration oxygen vacancies in the former material. The observed trend among the ionic conductivities of LCF64, LSF64 and LBF64 differs from that previously reported for La0.8A0.2FeO3−δ (A = Ca, Sr, Ba) by Bidrawn et al.19 (see Fig. 11). Estimating the ionic conductivity from data of oxygen permeation measurements performed in the range 650–800 °C, these authors showed that La0.8Sr0.2FeO3−δ (LSF82) exhibits the highest ionic conductivities, followed by La0.8Ba0.2FeO3−δ (LBF82) and La0.8Ca0.2FeO3−δ (LCF82). The different trend may – at least at first glance – be due to a different alkaline-earth metal dopant concentration used in the study by Bidrawn et al.19 However, estimates of the ionic conductivity from data of oxygen permeation may be erroneous in case of – and ignoring – partial rate limitations by the surface exchange reactions.62 There is some evidence for the latter when the comparison of ionic conductivities in Fig. 11 is extended to include data for La0.9Ca0.1FeO3−δ (LCF91) and La0.8Ca0.2FeO3−δ (LCF82) as derived from data of ECR experiments by Berger et al.63,64 Clearly, more work is required to resolve the apparent discrepancies between the results of different studies.
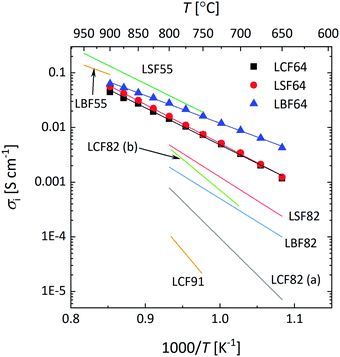 |
| | Fig. 11 Arrhenius plots of the ionic conductivity of LCF64, LSF64 and LBF64, at pO2 = 0.142 atm. The specified pO2 corresponds to the logarithmic average of the initial and final values of the pO2 step change during ECR experiments. Lines are drawn to guide the eye. Data taken from literature are shown for comparison: La0.5Sr0.5FeO3−δ (LSF55),38 La0.5Ba0.5FeO3−δ (LBF55),38 La0.8Ca0.2FeO3−δ (LCF82 (a)),19 La0.8Sr0.2FeO3−δ (LSF82),19 La0.8Ba0.2FeO3−δ (LBF82),19 La0.8Ca0.2FeO3−δ (LCF82 (b)),63 La0.9Ca0.1FeO3−δ (LCF91).64 | |
The type of alkaline-earth metal ion within the experimental temperature range appears to have little impact on the oxygen vacancy mobility. The calculated average migration enthalpies, however, show a clear trend, decreasing in the order LCF (1.08 ± 0.04 eV) > LSF64 (0.95 ± 0.01 eV) > LBF64 (0.81 ± 0.01 eV) (cf.Table 3). Oxygen migration in the perovskite structure is known to occur via an energetic saddle point defined as the triangle formed by one B site cation and two A site cations between two adjacent OA4B2 octahedra.65 From a purely ionic point of view, the observed lowering in migration enthalpy in the series is expected from the trend in polarizability, αBa2+ > αSr2+ > αCa2+,66 and on the basis of the size of the involved alkaline-earth metal ions, rBa2+(1.61 Å) > rSr2+(1.44 Å) > rCa2+(1.34 Å), which will be of influence to the open space in the critical triangle. The quoted radii are taken from Shannon's compilation.30 It is, however, likely that also other factors govern the migration barrier. Recent calculations on the formation and migration of oxygen vacancies in the series of (La,Sr)(Co,Fe)O3−δ and (Ba,Sr)(Co,Fe)O3−δ perovskites based on density functional theory suggest that it is the charge transfer from the migrating ion to the transition metal ion in the transition state and the local cation configuration in the critical triangle (containing, e.g., 0, 1 or 2 Sr2+ ions) that would determine the energetic barrier.67,68
Conclusions
It is demonstrated in this study that LCF64 and LSF64 adopt slightly-distorted perovskite structures at room temperature to become ideal cubic (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) at elevated temperatures. LBF64 adopts a cubic perovskite structure from room temperature up to 1000 °C. The different phase behaviour observed for the three compositions is suggested to be linked to the decreased tendency for tilting of the FeO6 octahedra with increasing radius of the alkaline-earth-metal dopant ion.
m) at elevated temperatures. LBF64 adopts a cubic perovskite structure from room temperature up to 1000 °C. The different phase behaviour observed for the three compositions is suggested to be linked to the decreased tendency for tilting of the FeO6 octahedra with increasing radius of the alkaline-earth-metal dopant ion.
Among the series LCF64, LSF64 and LBF64, the highest electrical conductivities in the temperature range 650–900 °C are found for LSF64. In air at 800 °C, the electrical conductivity of LSF64 is 191 S cm−1, decreasing to a value of 114 S cm−1 at a pO2 of 0.01 atm, and found over the entire pO2 range roughly twice as high as those of LCF64 and LBF64. Unlike commonly suggested in literature, the temperature dependences of the electrical conductivities of the doped ferrite perovskite compositions could not be described by Holstein's small polaron theory. It is suggested that partial delocalization due to Fe 3d–O 2p hybridisation may change the nature of electronic conduction in these materials. Further research is required to elucidate this hypothesis.
A most important finding of our work is that the ionic conductivities of LCF64 and LSF64 as derived from data of electrical conductivity relaxation experiments in the temperature range 650–900 °C are high and fairly close to each other. The ionic conductivity of LCF64 at 650 °C is 1.2 × 10−3 S cm−1 while at 900 °C it is 44.6 × 10−3 S cm−1, being a factor 3.6 and 1.44, respectively, lower than that for LBF64 showing the highest conductivity in this study. Noting that in general Ca-substituted materials are less vulnerable towards carbonation upon exposure to CO2 as compared to substitution by Sr or Ba, this observation renders LCF64 a very promising cathode for use in IT-SOFCs.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Financial support from the Dutch Technology Foundation (STW, now part of NWO; Project Nr. 15325) and the Chinese Scholarship Council (CSC 201406340102) are gratefully acknowledged.
References
- A. Choudhury, H. Chandra and A. Arora, Renewable Sustainable Energy Rev., 2013, 20, 430–442 CrossRef CAS.
- S. B. Adler, Chem. Rev., 2004, 104, 4791–4843 CrossRef CAS PubMed.
- J. A. Lane, S. J. Benson, D. Waller and J. A. Kilner, Solid State Ionics, 1999, 121, 201–208 CrossRef CAS.
- H. J. M. Bouwmeester, M. W. Den Otter and B. A. Boukamp, J. Solid State Electrochem., 2004, 8, 599–605 CrossRef CAS.
- H. Fan, Y. Zhang and M. Han, J. Alloys Compd., 2017, 723, 620–626 CrossRef CAS.
- Y. Niu, J. Sunarso, F. Liang, W. Zhou, Z. Zhu and Z. Shao, J. Electrochem. Soc., 2011, 158, 132–138 CrossRef.
- T. Yu, X. Mao and G. Ma, J. Alloys Compd., 2014, 608, 30–34 CrossRef CAS.
- J. Hayd, L. Dieterle, U. Guntow, D. Gerthsen and E. Ivers-Tiffée, J. Power Sources, 2011, 196, 7263–7270 CrossRef CAS.
- A. Jun, J. Kim, J. Shin and G. Kim, ChemElectroChem, 2016, 3, 511–530 CrossRef CAS.
- C. Sun, R. Hui and J. Roller, J. Solid State Electrochem., 2010, 14, 1125–1144 CrossRef CAS.
- N. Mahato, A. Banerjee, A. Gupta, S. Omar and K. Balani, Prog. Mater. Sci., 2015, 72, 141–337 CrossRef CAS.
-
R. J. D. Tilly, Perovskites: Structure–Property Relationships, John Wiley & Sons, Ltd, 2016 Search PubMed.
- J. Hayd, L. Dieterle, U. Guntow, D. Gerthsen and E. Ivers-Tiffée, J. Power Sources, 2011, 196, 7263–7270 CrossRef CAS.
- Y. Teraoka, T. Nobunaga and N. Yamazoe, Chem. Lett., 1988, 503–506 CrossRef CAS.
- C.-Y. Tsai, A. G. Dixon, Y. H. Ma, W. R. Moser and M. R. Pascucci, J. Am. Ceram. Soc., 1998, 81, 1437–1444 CrossRef CAS.
- J. W. Stevenson, J. Electrochem. Soc., 2006, 143, 2722–2729 CrossRef.
- S. Li, W. Jin, P. Huang, N. Xu, J. Shi, Y. S. Lin, M. Z.-C. Hu and E. A. Payzant, Ind. Eng. Chem. Res., 2002, 38, 2963–2972 CrossRef.
- F. H. Taylor, J. Buckeridge and C. R. A. Catlow, Chem. Mater., 2017, 29, 8147–8157 CrossRef CAS.
- F. Bidrawn, S. Lee, J. M. Vohs and R. J. Gorte, J. Electrochem. Soc., 2008, 155, B660–B665 CrossRef CAS.
- P. M. Price, E. Rabenberg, D. Thomsen, S. T. Misture and D. P. Butt, J. Am. Ceram. Soc., 2014, 97, 2241–2248 CrossRef CAS.
- L. Winnubst, S. A. Veldhuis, R. Ruhl, S. F. P. ten Donkelaar, H. J. M. Bouwmeester and A. Nijmeijer, Ceram. Int., 2015, 41, 13709–13715 CrossRef.
- J. Rodríguez-carvajal, Phys. B, 1993, 15, 49–55 Search PubMed.
- J. Mizusaki, M. Yoshihiro, S. Yamauchi and K. Fueki, J. Solid State Chem., 1985, 58, 257–266 CrossRef CAS.
- J. E. ten Elshof, M. H. R. Lankhorst and H. J. M. Bouwmeester, J. Electrochem. Soc., 1997, 144, 1060–1067 CrossRef.
- M. W. den Otter, H. J. M. Bouwmeester, B. A. Boukamp and H. Verweij, J. Electrochem. Soc., 2001, 148, J1–J6 CrossRef CAS.
- M. H. Hung, M. V. M. Rao and D. S. Tsai, Mater. Chem. Phys., 2007, 101, 297–302 CrossRef CAS.
- J. B. Yang, W. B. Yelon, W. J. James, Z. Chu, M. Kornecki, Y. X. Xie, X. D. Zhou, H. U. Anderson, A. G. Joshi and S. K. Malik, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 184415 CrossRef.
- A. Ecija, K. Vidal, A. Larrañaga, A. Martínez-Amesti, L. Ortega-San-Martín and M. I. Arriortua, Solid State Ionics, 2011, 201, 35–41 CrossRef CAS.
- A. Fossdal, M. Menon, I. Waernhus, K. Wiik, M.-A. Einarsrud and T. Grande, J. Am. Ceram. Soc., 2010, 87, 1952–1958 CrossRef.
- R. D. Shannon, Acta Crystallogr., 1976, 32, 751–767 CrossRef.
- V. M. Goldschmidt, Naturwissenschaften, 2005, 14, 477–485 CrossRef.
- J. B. Goodenough, Rep. Prog. Phys., 2004, 67, 1915–1993 CrossRef CAS.
- J. P. Attfield, Int. J. Inorg. Mater., 2001, 3, 1147–1152 CrossRef CAS.
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392 CrossRef CAS.
- C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 782–789 CrossRef.
- C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. A: Found. Crystallogr., 2005, 61, 93–111 CrossRef PubMed.
- M. Kuhn, S. Hashimoto, K. Sato, K. Yashiro and J. Mizusaki, Solid State Ionics, 2011, 195, 7–15 CrossRef CAS.
- V. V. Kharton, A. V. Kovalevsky, M. V. Patrakeev, E. V. Tsipis, A. P. Viskup, V. A. Kolotygin, A. A. Yaremchenko, A. L. Shaula, E. V. Kiselev and J. C. Waerenborgh, Chem. Mater., 2008, 20, 6457–6467 CrossRef CAS.
- M. Søgaard, P. Vang Hendriksen and M. Mogensen, J. Solid State Chem., 2007, 180, 1489–1503 CrossRef.
- W. H. Jung and E. Iguchi, J. Phys.: Condens. Matter, 1995, 7, 1215–1227 CrossRef CAS.
- A. Benali, A. Souissi, M. Bejar, E. Dhahri, M. F. P. Graça and M. A. Valente, Chem. Phys. Lett., 2015, 637, 7–12 CrossRef CAS.
- H. C. Wang, C. L. Wang, J. L. Zhang, W. B. Su, J. Liu, M. L. Zhao, N. Yin, Y. G. Lv and L. M. Mei, Curr. Appl. Phys., 2010, 10, 866–870 CrossRef.
- J. Mizusaki, T. Sasamoto, W. R. Cannon and H. K. Bowen, J. Am. Ceram. Soc., 1983, 66, 247–252 CrossRef CAS.
- F. A. Kröger and H. J. Vink, Solid State Phys., 1956, 3, 307–435 Search PubMed.
- T. Holstein, Ann. Phys., 1959, 8, 343–389 CAS.
- D. Emin and T. Holstein, Ann. Phys., 1969, 53, 439–520 Search PubMed.
- L. Friedman and T. Holstein, Ann. Phys., 1963, 21, 494–549 CAS.
- K. J. Yoon, P. a. Zink, S. Gopalan, U. B. Pal and L. R. Pederson, J. Electrochem. Soc., 2009, 156, B795–B800 CrossRef CAS.
- M. V. Patrakeev, I. A. Leonidov, V. L. Kozhevnikov and K. R. Poeppelmeier, J. Solid State Chem., 2005, 178, 921–927 CrossRef CAS.
- L. Tai, M. Nasrallah, H. Anderson, D. Sparlin and S. Sehlin, Solid State Ionics, 1995, 76, 259–271 CrossRef CAS.
- C. Zener, Phys. Rev., 1951, 82, 403–405 CrossRef CAS.
- M. Abbate, F. M. F. de Groot, J. C. Fuggle, A. Fujimori, O. Strebel, F. Lopez, M. Domke, G. Kaindl, G. A. Sawatzky, M. Takano, Y. Takeda, H. Eisaki and S. Uchida, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 4511–4519 CrossRef CAS PubMed.
- A. M. Ritzmann, A. B. Muñoz-García, M. Pavone, J. A. Keith and E. A. Carter, Chem. Mater., 2013, 25, 3011–3019 CrossRef CAS.
- J. Suntivich, W. T. Hong, Y. L. Lee, J. M. Rondinelli, W. Yang, J. B. Goodenough, B. Dabrowski, J. W. Freeland and Y. Shao-Horn, J. Phys. Chem. C, 2014, 118, 1856–1863 CrossRef CAS.
- R. Pushpa, D. Daniel and D. P. Butt, Solid State Ionics, 2013, 249–250, 184–190 CrossRef CAS.
-
D. G. Daniel, The Electronic and Thermodynamic Properties of Ca Doped LaFeO3 – A First Principles Study Using Density Functional Theory, 2014 Search PubMed.
- L. Wang, Y. Du, P. V. Sushko, M. E. Bowden, K. A. Stoerzinger, S. M. Heald, M. D. Scafetta, T. C. Kaspar and S. A. Chambers, Phys. Rev. Mater., 2019, 3, 025401 CrossRef CAS.
- C. L. Chang, G. Chern, M. F. Tai, Y. W. Su, C. L. Dong, S. Y. Liu, C. S. Hwang and P. K. Tseng, Jpn. J. Appl. Phys., 1999, 38, 108–110 CrossRef CAS.
- H. Wadati, A. Chikamatsu, M. Takizawa, R. Hashimoto, H. Kumigashira, T. Yoshida, T. Mizokawa, A. Fujimori, M. Oshima, M. Lippmaa, M. Kawasaki and H. Koinuma, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 115114 CrossRef.
- T. Ishigaki, S. Yamauchi, K. Kishio, J. Mizusaki and K. Fueki, J. Solid State Chem., 1988, 73, 179–187 CrossRef CAS.
- J. Yoo, A. Verma, S. Wang and A. J. Jacobson, J. Electrochem. Soc., 2005, 152, A497–A505 CrossRef CAS.
-
H. J. M. Bouwmeester and A. J. Burggraaf, in The CRC Handbook of Solid State Electrochemistry, ed. P. J. Gellings and H. J. M. Bouwmeester, CRC, New York, 1997, p. 481 Search PubMed.
- C. Berger, E. Bucher, A. Windischbacher, A. D. Boese and W. Sitte, J. Solid State Chem., 2018, 259, 57–66 CrossRef CAS.
- C. Berger, E. Bucher and W. Sitte, Solid State Ionics, 2017, 299, 46–54 CrossRef CAS.
- J. A. Kilner and R. J. Brook, Solid State Ionics, 1982, 6, 237–252 CrossRef CAS.
- J. Mitroy, M. S. Safronova and C. W. Clark, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 1–44 CrossRef.
- Y. A. Mastrikov, R. Merkle, E. A. Kotomin, M. M. Kuklja and J. Maier, Phys. Chem. Chem. Phys., 2013, 15, 911–918 RSC.
- C. Wessel, M. W. Lumey and R. Dronskowski, J. Membr. Sci., 2011, 366, 92–96 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp00247j |
|
| This journal is © the Owner Societies 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
De
Ning
b and
Henny J. M.
Bouwmeester
a,
De
Ning
b and
Henny J. M.
Bouwmeester
 *a
*a
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) and from rhombohedral to cubic (Pm
c) and from rhombohedral to cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), respectively, while La0.6Ba0.4FeO3−δ (LBF64) remains cubic over the entire temperature range from room temperature to 1000 °C. The different phase behaviour of the solids is interpreted to reflect the decreased tendency for octahedral tilting with increasing alkaline-earth-metal dopant ion radius. The electrical conductivity of LSF64 is 191 S cm−1 in air at 800 °C, decreasing to a value of 114 S cm−1 at a pO2 of 0.01 atm, and found over this pO2 range roughly twice as high as those of LCF64 and LBF64. Failure to describe the data of electrical conductivity using Holstein's small polaron theory is briefly discussed. Chemical diffusion coefficients and surface exchange coefficients of the materials in the range 650–900 °C were extracted from data of electrical conductivity relaxation. Data of oxygen nonstoichiometry was used to calculate the vacancy diffusion coefficients from the measured chemical diffusion coefficients. The calculated migration enthalpies are found to decrease in the order LCF64 (1.08 ± 0.04 eV) > LSF64 (0.95 ± 0.01 eV) > LBF64 (0.81 ± 0.01 eV). The estimated ionic conductivities of the materials, at 900 °C, are within a factor of 1.4.
m), respectively, while La0.6Ba0.4FeO3−δ (LBF64) remains cubic over the entire temperature range from room temperature to 1000 °C. The different phase behaviour of the solids is interpreted to reflect the decreased tendency for octahedral tilting with increasing alkaline-earth-metal dopant ion radius. The electrical conductivity of LSF64 is 191 S cm−1 in air at 800 °C, decreasing to a value of 114 S cm−1 at a pO2 of 0.01 atm, and found over this pO2 range roughly twice as high as those of LCF64 and LBF64. Failure to describe the data of electrical conductivity using Holstein's small polaron theory is briefly discussed. Chemical diffusion coefficients and surface exchange coefficients of the materials in the range 650–900 °C were extracted from data of electrical conductivity relaxation. Data of oxygen nonstoichiometry was used to calculate the vacancy diffusion coefficients from the measured chemical diffusion coefficients. The calculated migration enthalpies are found to decrease in the order LCF64 (1.08 ± 0.04 eV) > LSF64 (0.95 ± 0.01 eV) > LBF64 (0.81 ± 0.01 eV). The estimated ionic conductivities of the materials, at 900 °C, are within a factor of 1.4.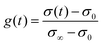
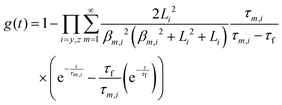
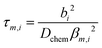
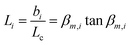
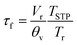
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) with cell parameters a = 5.5228(1) Å and c = 13.4471(3) Å (hexagonal representation), in good agreement with a = 5.5272(2) Å and c = 13.4408(4) Å reported by Yang et al.27 LBF64 appears to be cubic (space group Pm
c) with cell parameters a = 5.5228(1) Å and c = 13.4471(3) Å (hexagonal representation), in good agreement with a = 5.5272(2) Å and c = 13.4408(4) Å reported by Yang et al.27 LBF64 appears to be cubic (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with a = 3.93652(2) Å, matching precisely the value a = 3.93652(9) Å found for La0.5Ba0.5FeO3−δ reported by Ecija et al.28
m) with a = 3.93652(2) Å, matching precisely the value a = 3.93652(9) Å found for La0.5Ba0.5FeO3−δ reported by Ecija et al.28

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) structure of LSF64 are listed in hexagonal settings. The numbers in parentheses denote standard deviations in units of the least significant digits
c) structure of LSF64 are listed in hexagonal settings. The numbers in parentheses denote standard deviations in units of the least significant digits
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c
c![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) at 602 °C to cubic (space group Pm
c) at 602 °C to cubic (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) at about 1100 °C, on the basis of data of differential scanning calorimetry (DSC) and HT-XRD. Our study confirms that LCF64 remains orthorhombic until ∼600 °C, consistent with the results obtained by Price et al.20 However, our refinements yield a mixture of orthorhombic and rhombohedral phases above ∼625 °C, i.e., from 3.89% rhombohedral at 625 °C to 15.79% at 700 °C, transforming into a pure rhombohedral phase above 725 °C. The rhombohedral angle decreases from 60.29° at 625 °C to 60.09° at 1000 °C, suggesting that at a slightly higher temperature the cubic phase is formed. Fig. 2b shows the occurrence of a rhombohedral-to-cubic phase transition in LSF64 at around 850 °C, which is in agreement with previous results obtained by Fossdal et al.29 LBF64 adopts a cubic structure (space group Pm
m) at about 1100 °C, on the basis of data of differential scanning calorimetry (DSC) and HT-XRD. Our study confirms that LCF64 remains orthorhombic until ∼600 °C, consistent with the results obtained by Price et al.20 However, our refinements yield a mixture of orthorhombic and rhombohedral phases above ∼625 °C, i.e., from 3.89% rhombohedral at 625 °C to 15.79% at 700 °C, transforming into a pure rhombohedral phase above 725 °C. The rhombohedral angle decreases from 60.29° at 625 °C to 60.09° at 1000 °C, suggesting that at a slightly higher temperature the cubic phase is formed. Fig. 2b shows the occurrence of a rhombohedral-to-cubic phase transition in LSF64 at around 850 °C, which is in agreement with previous results obtained by Fossdal et al.29 LBF64 adopts a cubic structure (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) throughout the measured temperature range, as shown in Fig. 2c. The temperature dependences of the Fe–O–Fe angles and Fe–O bond lengths obtained from the Rietveld refinements are plotted in Fig. S2 (ESI†).
m) throughout the measured temperature range, as shown in Fig. 2c. The temperature dependences of the Fe–O–Fe angles and Fe–O bond lengths obtained from the Rietveld refinements are plotted in Fig. S2 (ESI†).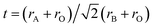 ,31 where rA, rB and rO are the ionic radii of the involved ions. The ideal cubic structure is formed for t = 1, when the A and O2− ions are matching in size to form cubic close-packed layers, while the B cations fit into the interstices formed by the O2− ions to give an array of corner-shared BO6 octahedra. For t < 1, the BO6 octahedra cooperatively tilt to accommodate the mismatch, thereby forming less symmetric rhombohedral or orthorhombic structures.32,33 The orthorhombic Pnma structure, in Glazer's notation34 denoted by a−a−c+, as adopted by LCF64 is one of the most common perovskite structures with a three-tilt system.35,36 Upon decreasing the size of the earth-alkaline cation, the out-of-phase rotation (−) along the [001] direction of the pseudo-cubic cell changes to an in-phase rotation (−) for LSF64, expressed in Glazer's notation by a−a−c− (space group R
,31 where rA, rB and rO are the ionic radii of the involved ions. The ideal cubic structure is formed for t = 1, when the A and O2− ions are matching in size to form cubic close-packed layers, while the B cations fit into the interstices formed by the O2− ions to give an array of corner-shared BO6 octahedra. For t < 1, the BO6 octahedra cooperatively tilt to accommodate the mismatch, thereby forming less symmetric rhombohedral or orthorhombic structures.32,33 The orthorhombic Pnma structure, in Glazer's notation34 denoted by a−a−c+, as adopted by LCF64 is one of the most common perovskite structures with a three-tilt system.35,36 Upon decreasing the size of the earth-alkaline cation, the out-of-phase rotation (−) along the [001] direction of the pseudo-cubic cell changes to an in-phase rotation (−) for LSF64, expressed in Glazer's notation by a−a−c− (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c), and to the no-tilt system a0a0a0 (space group Pm
c), and to the no-tilt system a0a0a0 (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) for LBF64. Note from Fig. 2a and b that similar structural changes are induced in LCF64 and LSF64 upon increasing temperature.
m) for LBF64. Note from Fig. 2a and b that similar structural changes are induced in LCF64 and LSF64 upon increasing temperature.

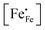 and (c) mobility of electron–holes, at pO2 = 0.21 atm, for LCF64, LSF64 and LBF64. The dashed lines through the data points are drawn to guide the eye. The horizontal line in Fig. 4b represents the
and (c) mobility of electron–holes, at pO2 = 0.21 atm, for LCF64, LSF64 and LBF64. The dashed lines through the data points are drawn to guide the eye. The horizontal line in Fig. 4b represents the 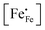 concentration when electronic compensation is predominant, noting that all three materials have the same concentration of the alkaline-earth dopant (cf.eqn (7)).
concentration when electronic compensation is predominant, noting that all three materials have the same concentration of the alkaline-earth dopant (cf.eqn (7)).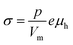
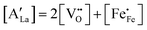
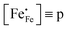 represents the concentration of p-type charge carriers. Eqn (7) lacks n-type charge carriers,
represents the concentration of p-type charge carriers. Eqn (7) lacks n-type charge carriers, 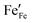 , arising as a result of the charge disproportionation reaction,
, arising as a result of the charge disproportionation reaction,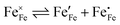
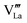 and
and 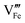 need to be taken into account. Using eqn (7) and data of oxygen stoichiometry (Fig. 3), the concentration of
need to be taken into account. Using eqn (7) and data of oxygen stoichiometry (Fig. 3), the concentration of 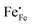 in phases LCF64, LSF64 and LBF64 may be calculated. Corresponding data are shown in Fig. 4b and Fig. S6b (ESI†), from which figures it can be inferred that under the conditions covered by the experiments electronic compensation dominates over ionic compensation. The lowest electron–hole concentration is found in LBF64, indicating that in this material the relative contribution of the ionic compensation mechanism is higher than those in LCF64 and LSF64. In all three phases, the concentration
in phases LCF64, LSF64 and LBF64 may be calculated. Corresponding data are shown in Fig. 4b and Fig. S6b (ESI†), from which figures it can be inferred that under the conditions covered by the experiments electronic compensation dominates over ionic compensation. The lowest electron–hole concentration is found in LBF64, indicating that in this material the relative contribution of the ionic compensation mechanism is higher than those in LCF64 and LSF64. In all three phases, the concentration 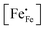 is found to decrease and, hence, ionic compensation appears to become more dominant, with increasing temperature and decreasing oxygen partial pressure.
is found to decrease and, hence, ionic compensation appears to become more dominant, with increasing temperature and decreasing oxygen partial pressure.
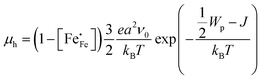
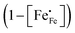 takes into account the site-blocking effect, the probability that the adjacent site to which the polaron hops may already be occupied.48 In the non-adiabatic case,45 the polaron misses coincidence events as it moves too slowly, lowering the net hopping rate. In this case, the mobility of electron holes is given by
takes into account the site-blocking effect, the probability that the adjacent site to which the polaron hops may already be occupied.48 In the non-adiabatic case,45 the polaron misses coincidence events as it moves too slowly, lowering the net hopping rate. In this case, the mobility of electron holes is given by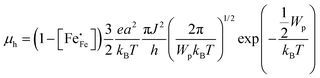
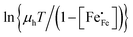 vs. 1000/T should give a straight line with activation energy
vs. 1000/T should give a straight line with activation energy 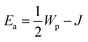 ; in the non-adiabatic regime, the plot of
; in the non-adiabatic regime, the plot of 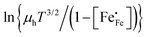 vs. 1000/T should give a straight line with activation energy
vs. 1000/T should give a straight line with activation energy 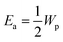 .
.

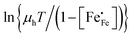 vs. 1000/T (adiabatic case) and (b)
vs. 1000/T (adiabatic case) and (b) 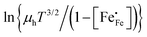 vs. 1000/T (non-adiabatic case), at pO2 = 0.21 atm. The dotted lines are drawn to guide the eye.
vs. 1000/T (non-adiabatic case), at pO2 = 0.21 atm. The dotted lines are drawn to guide the eye.
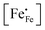 , which is contrary to what is expected from the site-blocking term,
, which is contrary to what is expected from the site-blocking term, 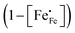 , in eqn (9) and (10). In view of eqn (7), the electron hole concentration on its turn is correlated with the concentration of oxygen vacancies. Fig. 6 shows that the hopping mobility decreases with increasing the oxygen nonstoichiometry of phases LCF64, LSF64 and LBF64. Similar observations have been reported for La1−xSrxFeO3−δ (0.1 ≤ x ≤ 1).49 Noting that the direct overlap between neighbouring Fe 3d orbitals in the La0.6A0.4FeO3−δ (A = Ca, Sr, and Ba) perovskite structure is negligible, the polaron hopping between two adjacent Fe cations is brought about by the overlapping O 2p orbitals of the bridging oxygen ion, which is known as the Zener double-exchange mechanism.51 Disruption of the Fe4+–O–Fe3+ migration pathways due to the presence of oxygen vacancies thus may affect the hopping mobility. The probability that an oxygen vacancy blocks the migration pathway scales with (1 − δ/3). The corresponding values for this parameter for each of the materials under the given experimental conditions are, however, too close to unity to have a significant impact on the effective hopping mobility. Electrostatic interactions between the electron holes and oxygen vacancies or formation of delocalized states may further affect the hopping mobility. X-ray absorption spectroscopy and density functional theory studies indicate that the electron holes in La1−xSrxFeO3−δ and La1−xCaxFeO3−δ have mixed Fe 3d and O 2p band character and, hence, are delocalized at least to some extent.51–58 This would comply with the observed low-to-zero activation energies of the carrier mobility in phases LCF64, LSF64 and LBF64 (cf.Fig. 5). This argument is, however, in contrast with results from angle-resolved photo emission spectroscopy, suggesting a strong localisation of the electron holes in La0.6Sr0.4FeO3−δ.59 Clearly, more research is warranted to clarify the nature of the charge carriers in La1−xAxFeO3−δ (A = Ca, Sr, Ba).
, in eqn (9) and (10). In view of eqn (7), the electron hole concentration on its turn is correlated with the concentration of oxygen vacancies. Fig. 6 shows that the hopping mobility decreases with increasing the oxygen nonstoichiometry of phases LCF64, LSF64 and LBF64. Similar observations have been reported for La1−xSrxFeO3−δ (0.1 ≤ x ≤ 1).49 Noting that the direct overlap between neighbouring Fe 3d orbitals in the La0.6A0.4FeO3−δ (A = Ca, Sr, and Ba) perovskite structure is negligible, the polaron hopping between two adjacent Fe cations is brought about by the overlapping O 2p orbitals of the bridging oxygen ion, which is known as the Zener double-exchange mechanism.51 Disruption of the Fe4+–O–Fe3+ migration pathways due to the presence of oxygen vacancies thus may affect the hopping mobility. The probability that an oxygen vacancy blocks the migration pathway scales with (1 − δ/3). The corresponding values for this parameter for each of the materials under the given experimental conditions are, however, too close to unity to have a significant impact on the effective hopping mobility. Electrostatic interactions between the electron holes and oxygen vacancies or formation of delocalized states may further affect the hopping mobility. X-ray absorption spectroscopy and density functional theory studies indicate that the electron holes in La1−xSrxFeO3−δ and La1−xCaxFeO3−δ have mixed Fe 3d and O 2p band character and, hence, are delocalized at least to some extent.51–58 This would comply with the observed low-to-zero activation energies of the carrier mobility in phases LCF64, LSF64 and LBF64 (cf.Fig. 5). This argument is, however, in contrast with results from angle-resolved photo emission spectroscopy, suggesting a strong localisation of the electron holes in La0.6Sr0.4FeO3−δ.59 Clearly, more research is warranted to clarify the nature of the charge carriers in La1−xAxFeO3−δ (A = Ca, Sr, Ba).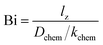


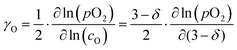
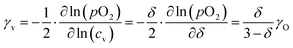


![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) at elevated temperatures. LBF64 adopts a cubic perovskite structure from room temperature up to 1000 °C. The different phase behaviour observed for the three compositions is suggested to be linked to the decreased tendency for tilting of the FeO6 octahedra with increasing radius of the alkaline-earth-metal dopant ion.
m) at elevated temperatures. LBF64 adopts a cubic perovskite structure from room temperature up to 1000 °C. The different phase behaviour observed for the three compositions is suggested to be linked to the decreased tendency for tilting of the FeO6 octahedra with increasing radius of the alkaline-earth-metal dopant ion.




