Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hygroscopic properties of NaCl nanoparticles on the surface: a scanning force microscopy study†
Xiaoxiang
Wang‡
a,
Haozhi
Lei‡
b,
Rüdiger
Berger
 *c,
Yi
Zhang
*c,
Yi
Zhang
 b,
Hang
Su
a and
Yafang
Cheng
b,
Hang
Su
a and
Yafang
Cheng
 *a
*a
aMax Planck Institute for Chemistry, Multiphase Chemistry Department, Hahn Meitner Weg 1, 55128 Mainz, Germany. E-mail: yafang.cheng@mpic.de
bKey Laboratory of Interfacial Physics and Technology, Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Shanghai 201800, China
cMax Planck Institute for Polymer Research, Ackermannweg 10, Mainz 55128, Germany. E-mail: berger@mpip-mainz.mpg.de
First published on 9th April 2020
Abstract
We investigated the hygroscopic growth of sodium chloride (NaCl) nanoparticles with curvature related diameters ranging from 10 nm to 200 nm, at different relative humidities using scanning force microscopy. Hygroscopic aerosol nanoparticles play a vital role in the Earth's climate and human health. We report that 10 nm NaCl nanoparticles adsorbed on silicon surfaces have a higher deliquescence relative humidity than larger NaCl nanoparticles (size > 30 nm). This finding is consistent with the observations for airborne nanoparticles by hygroscopicity tandem differential mobility analyzer. Therefore, the presence of silicon surfaces plays no significant role in the deliquescence relative humidity. Moreover, the study of individual airborne particles by means of scanning force microscopy revealed that the ability of water uptake, i.e. growth factor, of NaCl particles differs by as large as 40% at the same relative humidity. This finding indicates that the individual nature of NaCl particles influences the growth factor.
Introduction
Nanoparticles are a significant component of atmospheric aerosols. Aerosols are proposed to influence the Earth's climate and human health.1–4 Often, atmospheric aerosols are hygroscopic, and they can grow significantly in humid environments.5,6 Therefore, studying the hygroscopic properties of the suspended atmospheric nanoparticles at different relative humidities (RH) has received significant attention.7–10 In particular, the phase state of the atmospheric nanoparticles determines their optical properties, cloud-droplet nucleation efficiency and heterogeneous chemistry.11–16 Details of the phase transition at different humidities can be inferred from the analysis of hygroscopic growth curve of individual aerosol particles or aerosol populations.Atmospheric aerosols can adsorb water on surfaces,17,18 and the hygroscopic property of the adsorbed nanoparticles may influence chemical and physical processes on the surface. Substantial water sorption by nanoparticles may lead to surface corrosion, which is a serious problem for electronic devices.19 Therefore, the behaviors of nanoparticles on surfaces at different humidities have been studied intensively. Ghorai and Tivanski used X-ray microscopy (STXM) and near-edge X-ray absorption fine structure (NEXAFS) spectroscopy to investigate atmospherically relevant NaCl, NaBr, NaI and NaNO3 nanoparticles on Si3N4 windows.20 Freney et al. checked the phase state of mixed aerosol particles consisting of one or more hygroscopic compounds at different RHs by using a transmission electron microscope operated with an environmental cell (ETEM).21 Recently, Morris et al. used a scanning force microscope (SFM) to measure the surface area and volume equivalent diameter of NaCl nanoparticles, and malonic acid (MA) nanoparticles with binary mixtures at different RHs.22 Bondy et al. analyzed infrared spectra recorded using an SFM on nanometer-sized atmospheric model systems.23
However, the role of the surface on the response of aerosol nanoparticles to humidity is still not clear. Eom et al.24 examined the hygroscopic properties of micrometer-sized inorganic particles on different types of substrates using optical microscopy. They found that the substrate has no influence on the deliquescence relative humidity (DRH) of these micrometer-sized particles.24 The DRH is the relative humidity (RH) value corresponding to the phase transition from a solid to a liquid.25 In contrast, Morris et al. reported that NaCl particles with slightly smaller diameters of 0.5–1 μm on the surface exhibit a different growth behavior compared to airborne particles upon exposure to humidity.22 In addition, the shape and size of particles varies at different RHs.26 The latter was measured by using a humidified tandem differential mobility analyzer (HTDMA). These measurements indicate that the diameter of the particles is not the only parameter that controls the growth factor. It seems likely that the morphology and shape of particles play a role in the growth behavior, too. Consequently, methods allowing one to measure the size and shape dependence of the hygroscopicity of nanoparticles are required. In particular, aerosol nanoparticles <100 nm on surfaces have not been studied, although these particles may be more important for climate change and human health than larger ones.3,27,28
In this study, NaCl particles, which are one of the most important components of atmospheric aerosol particles,29,30 were chosen. Particles with different sizes were generated and collected onto a silicon substrate. In particular, we focused on small particles with mobility diameters Dmobility of 200 ± 15 nm, 30 ± 2 nm and 10 ± 0.5 nm, which may be prone to surface effects more than particles >200 nm.8,31 The error in sizes is given by the DMA transfer function. The morphology and hygroscopic growth at different RHs were analyzed by using SFM. Based on SFM parameters, we calculated the volume of NaCl particles and we introduce a model to calculate the curvature related diameter (Dcurvature). Changes in Dcurvature upon humidity exposure allowed us to determine the DRH of different particle sizes. The data from this study was compared to the values for suspended particles from HTDMA. This comparison confirms results of the previous theory about the nano-size effect on particle phase transition9 and indicates that the method developed for airborne nanoparticles applies to the deliquescence of nanoparticles on surfaces as well.
Methods and materials
Generation and collection of NaCl aerosol nanoparticles
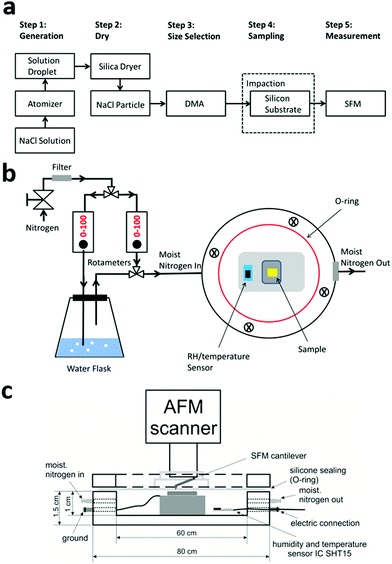
Sodium chloride (NaCl) was purchased from Sigma-Aldrich (reagent grade, 99.99% purity) and prepared in deionized water (18 MΩ cm). The aqueous solution containing NaCl was atomized using a TSI 3076 constant output atomizer (TSI, Inc.), and dried (∼5% RH) by passing through a diffusion silica dryer. The aim of our study is to measure size dependent hygroscopic properties of particles attached to a surface. Thus, the dehydrated aerosol particles with different values of Dmobility were selected using a differential mobility analyzer (DMA; TSI, Inc. Model 3081A) and then deposited on silicon substrates (Ted Pella Inc., Part No. 16008) via impaction using a pump running with a flow of 1.5 L min−1. Prior to the sampling, the silicon substrates were cleaned in Argon plasma for 2 min. The mobility diameters of the NaCl particles that we collected for later SFM measurements are monodispersed particles with a peak diameter at 200 nm, 30 nm and 10 nm. A flow diagram of all preparation steps is shown in Fig. 1a.Scanning force microscopy analysis
All SFM data were obtained in a tapping mode by adjusting the minimum force between the tip and the sample while imaging (Dimension Icon, Bruker). Silicon substrates with deposited nanoparticles were placed in a custom made SFM Teflon cell (Fig. 1b and c). This cell has a volume of 25 cm3 and allowed us to adjust the RH during the SFM measurements with a precision of <5%.26 Silicon cantilevers (OMCL-AC240TN-R3, OLYMPUS) with a nominal spring constant of 2 N m−1 and a nominal tip radius of 7 nm were used. The half angle of probe's conical angle is about 17.5°.32 The SFM analysis started at an initial RH of ∼5%, followed by gradual increases until the RH reached 90%. After adjusting one RH value by flow controllers (rotameters), an equilibrium RH was reached within 10–15 minutes in the Teflon cell. The SFM images of the particles were then recorded at each RH, respectively. After increasing the RH, we decreased the RH again in order to check the reversibility and stability of the particles. The raw SFM data were analyzed using the NanoScope Analysis 1.5 package.Quantifying the size of nanoparticles and DRH
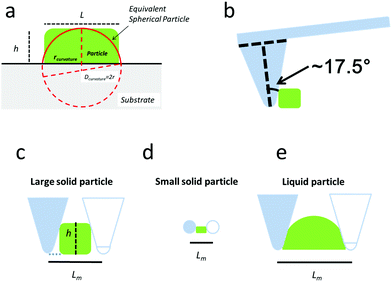
Different parameters have been used to quantify the sizes of airborne particles (aerosol) and deposited particles. The parameter Dmobility is given by the diameter of a particle with the same electrical mobility.33,34 Alternatively, the Stokes diameter (DStokes), which is the diameter of a sphere with the same terminal settling velocity and density as the particle, was also used.34 In addition, the volume equivalent diameter (Dvolume) of non-spherical particles was used to quantify the size of deposited particles at different RHs in previous SFM studies.22,35 The Dvolume is equal to the diameter of a spherical particle which exhibits an identical volume. Principally, all the above parameters are reasonable for quantifying the hygroscopic growth of particles. Therefore, we have analyzed the volume of particles at different RHs based on SFM measurements. However, this parameter does not reflect changes in the shape. Many physical properties of nanoparticles are caused by changes of its surface properties, such as curvature, but are not solely dependant on the change in its volume.36,37 For example, the equilibrium between water vapor and solution droplet is strongly affected by the curvature of the nanoparticle surface.38 Additionally, in order to address changes in shape with a single parameter, we used a curvature related diameter Dcurvature to quantify the size of particles (Fig. 2a). In order to calculate Dcurvature of particles, we measured the height of particles, h. The lateral elongation of particles, L, is calculated by considering SFM-tip convolution effects. In particular, the size and phase of particles determine the degrees of overestimations of L (Fig. 2b–e). In our analysis, we approximated the tip apex shape with a semi-sphere having a radius of 10 nm followed by a cone with an opening angle of 35°32 (Fig. 2b). When the height of a solid particle is higher than the radius of the tip, the edge of the cone touches the particle (Fig. 2c). In this case, we useL = Lm − 2h·tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17.5° 17.5° | (1) |
| L = Lm − 20 nm | (2) |
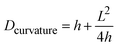 | (3) |
| V = L2·h | (4) |
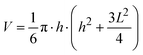 | (5) |
Results and discussion
Distribution and morphology
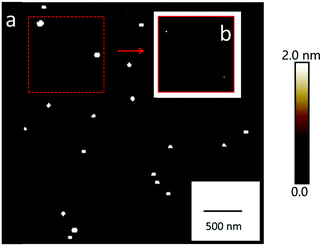
Aerosol particles (Dmobility 10 nm, 30 nm or 200 nm) deposited on silicon substrates were imaged by SFM at a RH of 5% firstly. At this condition, the heights of particles range between ∼10 nm and ∼200 nm (Fig. 3a). These height values correspond to the Dmobility size range of particles that we adjusted with the differential mobility analyzer. Up to a RH of 60%, no changes of position or shape of the particles were detected after repeated SFM scans (Fig. 3b–d).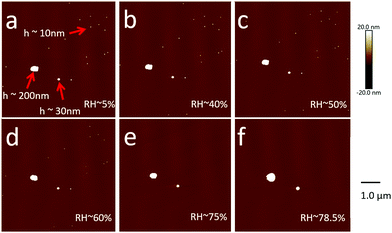 | ||
| Fig. 3 SFM images of NaCl particles with different sizes on the same substrate at different RH conditions. The corresponding phase contrast images are provided in the ESI† (Fig. S1). | ||
To summarize, we can image and analyze NaCl nanoparticles with a Dcurvature from 10 nm up to 772 nm and at a RH from 5% up to 90%. Next, we analyzed the Dcurvature changes in dependence of RH in more detail with the aim to calculate the growth factors (GFs) and the deliquescence relative humidity (DRH).
Growth factor and deliquescence relative humidity
The growth factor (GFC) of particles can be defined by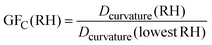 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RH) is the curvature related diameter at the lowest RH (5–20%) studied for the corresponding particle. Here we plotted the GFC of two populations of particles, i.e., Dcurvature ∼ 200 nm and ∼10 nm (Fig. 7a). In addition, GFs from HTDMA measurements for particles with a Dmobility of 100 nm and 10 nm at different RH conditions were plotted for comparison, as well as curves based on the Köhler theory.7,9,42 For comparison, we also calculated the GF based on the change of volume of particles (GFV) by using eqn (7),22,43 and the results are presented (Fig. 7b) and discussed below.
RH) is the curvature related diameter at the lowest RH (5–20%) studied for the corresponding particle. Here we plotted the GFC of two populations of particles, i.e., Dcurvature ∼ 200 nm and ∼10 nm (Fig. 7a). In addition, GFs from HTDMA measurements for particles with a Dmobility of 100 nm and 10 nm at different RH conditions were plotted for comparison, as well as curves based on the Köhler theory.7,9,42 For comparison, we also calculated the GF based on the change of volume of particles (GFV) by using eqn (7),22,43 and the results are presented (Fig. 7b) and discussed below.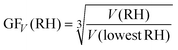 | (7) |
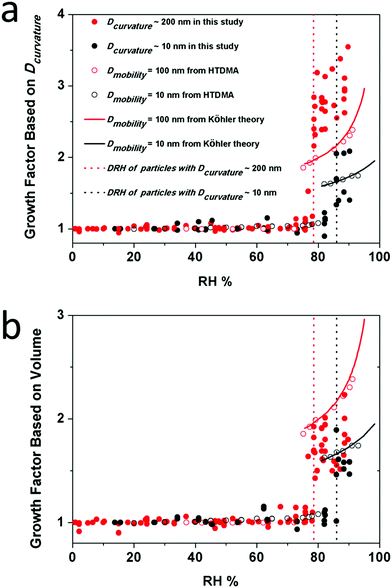 | ||
| Fig. 7 Hygroscopic growth curves of NaCl based on the Dcurvature (a) and the volume (b). Red solid circles, red open circles, black solid circles and black open circles represent the growth factor of particles with a Dcurvature of ∼200 nm, Dmobility = 100 nm, Dcurvature of ∼10 nm and Dmobility= 10 nm at different RHs. Solid lines represent hygroscopic growth factors calculated based on the Köhler theory. Dashed lines indicate the DRH of particles with a Dcurvature of ∼200 nm and ∼10 nm. For larger particles, i.e., Dcurvature of ∼200 nm, we measured 7 individual ones. For smaller particles, i.e., Dcurvature of ∼10 nm, we measured 5 individual ones (Tables S2–S5 in the ESI†). | ||
Notably, the magnitude of the GF calculated by volume changes is in good agreement with the HTDMA data (Fig. 7b). However, the GF magnitude calculated by the curvature related diameter is significantly higher for 200 nm-sized NaCl nanoparticles. The latter probably indicate that the calculation of Dcurvature accentuates changes from a crystalline state into a liquid state, where the solid to liquid phase transition could be resolved more clearly. The calculation Dcurvature of the latter is enabled by using an imaging technique where the height and the width of nano-scale particles can be measured.
The SFM method allowed us to analyze different particles of almost the same Dcurvature. Interestingly, the GF of particles with the same Dcurvature can be different at the same RH. For example, at a RH of 77%, GFs of different particles with a Dcurvature of ∼200 nm vary from 1.5 to 3.2 (Fig. 7a). For comparison at a RH of 77%, the GFV varies only from 1.4 to 1.9. Therefore, different NaCl nanoparticles exhibit different abilities for water uptake. In other words, the parameter of Dcurvature, as well as the volume, does not solely define the growth factor of the particles, and the population of particles with the same Dcurvature may behave differently. This difference has been rarely reported so far because the HTDMA method yields an ensemble with an average of thousands of particle measurements. SFM allows us to study individual particles, though at a significantly reduced statistic.
The HTDMA method revealed a DRH of ∼87% and ∼75% for airborne particles with a Dmobility of 10 nm and 100 nm, respectively.7,42 Both DRH values are not much different from those measured for smaller and larger particles on surfaces, i.e., 86 ± 1%, and 78 ± 1%. Therefore, we conclude that the substrate has a negligible influence on the DRH of NaCl nanoparticles down to a size of 10 nm. This conclusion is in agreement with the findings of Eom et al. who reported that the substrate has no influence on the DRH of micrometer-sized particles.24 In addition, the size dependence of the DRH of nanoparticles, i.e., DRH increases as the size decreases, was explained in our previous study,9 and the same size dependence was confirmed here in this study. Therefore, we conclude that the theory developed there to explain the size dependent phase transition for airborne nanoparticles and the Differential Köhler Analysis (DKA) can be applied to the NaCl nanoparticles on the surface as well.
Summary
Previously, experimental and theoretical studies have reported a change of DRH for airborne particles of different sizes.7,9,25,44,45 For airborne NaCl particles, the DRH increases by ∼5% when the diameter decreases from 100 nm to 10 nm. Our measurements confirm this dependence for particles deposited on silicon surfaces. Thus, we conclude that the theory developed in our previous study9 to explain the size-dependent phase transition for airborne nanoparticles can describe the deliquescence of airborne nanoparticles on surfaces as well.Particles on hydrophobic surfaces at a high humidity might behave differently. Small particles on hydrophobic surfaces could be more stable. SFM is a suitable tool for comparing similar-sized airborne nanoparticle surfaces with different surface energies at a high humidity. Our study of individual nanoparticles revealed that the corresponding GFs can vary. The latter indicates that different airborne particles have different abilities for water uptake. Here, possibly, the exact shape, composition or orientation of the particle plays a role.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study is supported by the Max Planck Society (MPG). Xiaoxiang Wang acknowledges the support from the China Scholarship Council (CSC, 201406190170) and from the Program for Guangdong Introducing Innovative and Entrepreneurial Teams (2017ZT07Z479). Haozhi Lei acknowledges the Project-related exchange of Persons Program (201600110073) from CSC and German Academic Exchange Service. Yafang Cheng acknowledges the Minerva Program from MPG. We thank Ulrich Pöschl (MPIC) and Hans-Jürgen Butt (MPI-P) for the constructive discussions and support. We thank Michael Kappl for discussions and the design of the SFM-Teflon cell. In addition, we thank Helma Burg and Uwe Rietzler for continuous support in the SFM lab. Open Access funding provided by the Max Planck Society.References
- M. Kulmala and V.-M. Kerminen, Atmos. Res., 2008, 90, 132–150 CrossRef CAS.
- P. R. Buseck and K. Adachi, Elements, 2008, 4, 389–394 CrossRef CAS.
- J. N. Smith, K. C. Barsanti, H. R. Friedli, M. Ehn, M. Kulmala, D. R. Collins, J. H. Scheckman, B. J. Williams and P. H. McMurry, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6634–6639 CrossRef CAS PubMed.
- B. Nowack and T. D. Bucheli, Environ. Pollut., 2007, 150, 5–22 CrossRef CAS PubMed.
- T. Lei, A. Zuend, Y. Cheng, H. Su, W. Wang and M. Ge, Atmos. Chem. Phys., 2018, 18, 1045–1064 CrossRef CAS.
- O. H. Berg, E. Swietlicki, G. Frank, B. G. Martinsson, S. I. Cederfelt, P. Laj, L. Ricci, A. Berner, U. Dusek and Z. Galambos, Contrib. Atmos. Phys., 1998, 71, 47–64 Search PubMed.
- G. Biskos, A. Malinowski, L. Russell, P. Buseck and S. Martin, Aerosol Sci. Technol., 2006, 40, 97–106 CrossRef CAS.
- G. Biskos, L. Russell, P. Buseck and S. T. Martin, Geophys. Res. Lett., 2006, 33, L07801 CrossRef.
- Y. Cheng, H. Su, T. Koop, E. Mikhailov and U. Pöschl, Nat. Commun., 2015, 6, 5923 CrossRef CAS PubMed.
- E. Mikhailov, S. Vlasenko, R. Niessner and U. Pöschl, Atmos. Chem. Phys., 2004, 4, 323–350 CrossRef CAS.
- S. T. Martin, Chem. Rev., 2000, 100, 3403–3454 CrossRef CAS.
- R. M. Harvey, A. P. Bateman, S. Jain, Y. J. Li, S. Martin and G. A. Petrucci, Environ. Sci. Technol., 2016, 50, 4997–5006 CrossRef CAS PubMed.
- M. Tang, D. J. Cziczo and V. H. Grassian, Chem. Rev., 2016, 116, 4205–4259 CrossRef CAS PubMed.
- M. M. Chim, C. Y. Chow, J. F. Davies and M. N. Chan, J. Phys. Chem. A, 2017, 121, 1666–1674 CrossRef CAS PubMed.
- E. Mikhailov, S. Vlasenko, S. Martin, T. Koop and U. Pöschl, Atmos. Chem. Phys., 2009, 9, 9491–9522 CrossRef CAS.
- Y. Cheng, G. Zheng, C. Wei, Q. Mu, B. Zheng, Z. Wang, M. Gao, Q. Zhang, K. He and G. Carmichael, Sci. Adv., 2016, 2, e1601530 CrossRef PubMed.
- B. Dahneke, J. Colloid Interface Sci., 1971, 37, 342–353 CrossRef CAS.
- J. K. Jokiniemi, T. Lind, J. Hokkinen, J. Kurkela and E. I. Kauppinen, presented in part at the Aerosols from Biomass Combustion, Zurich, Switzerland, 2001.
- A. J. Gadgil and W. J. Fisk, Indoor Air, 2000, 10, 47–56 CrossRef PubMed.
- S. Ghorai and A. V. Tivanski, Anal. Chem., 2010, 82, 9289–9298 CrossRef CAS PubMed.
- E. J. Freney, K. Adachi and P. R. Buseck, J. Geophys. Res.: Atmos., 2010, 115, D19210 CrossRef.
- H. S. Morris, A. D. Estillore, O. Laskina, V. H. Grassian and A. V. Tivanski, Anal. Chem., 2016, 88, 3647–3654 CrossRef CAS PubMed.
- A. L. Bondy, R. M. Kirpes, R. L. Merzel, K. A. Pratt, M. M. Banaszak Holl and A. P. Ault, Anal. Chem., 2017, 89, 8594–8598 CrossRef CAS PubMed.
- H.-J. Eom, D. Gupta, X. Li, H.-J. Jung, H. Kim and C.-U. Ro, Anal. Chem., 2014, 86, 2648–2656 CrossRef CAS PubMed.
- G. Biskos, D. Paulsen, L. Russell, P. Buseck and S. Martin, Atmos. Chem. Phys., 2006, 6, 4633–4642 CrossRef CAS.
- J. Baltrusaitis and V. H. Grassian, J. Phys. Chem. A, 2012, 116, 9001–9009 CrossRef CAS PubMed.
- M. Hussain, P. Madl and A. Khan, Health, 2011, 2, 51–59 Search PubMed.
- H.-E. Wichmann and A. Peters, Ultrafine Particles in the Atmosphere, World Scientific, 2000, pp. 243–267 Search PubMed.
- E. R. Lewis, R. Lewis and S. E. Schwartz, Sea salt aerosol production: mechanisms, methods, measurements, and models, American Geophysical Union, 2004 Search PubMed.
- B. Finlayson-Pitts, Chem. Rev., 2003, 103, 4801–4822 CrossRef CAS PubMed.
- R. McGraw and E. R. Lewis, J. Chem. Phys., 2009, 131, 194705 CrossRef PubMed.
- Olympus, Micro cantilever, http://topview-photonics.com/mw/cufiles/files/EN/Olympus_AFM_Probes/datasheet/omcl-ac240tn-r3_spec_v1_2.pdf.
- B. Y. Liu, D. Pui and A. Kapadia, Electrical aerosol analyzer: history, principle, and data reduction, Minnesota Univ., Dept. of Mechanical Engineering, Minneapolis, USA, 1976 Search PubMed.
- J. H. Seinfeld and S. N. Pandis, Atmospheric chemistry and physics: from air pollution to climate change, John Wiley & Sons, 2016 Search PubMed.
- P. Gwaze, H. J. Annegarn, J. Huth and G. Helas, Atmos. Res., 2007, 86, 93–104 CrossRef CAS.
- R. C. Tolman, J. Chem. Phys., 1949, 17, 333–337 CrossRef CAS.
- R. Kofman, P. Cheyssac, A. Aouaj, Y. Lereah, G. Deutscher, T. Ben-David, J. Penisson and A. Bourret, Surf. Sci., 1994, 303, 231–246 CrossRef CAS.
- W. Thomson, Proc. R. Soc. Edinburgh, 1872, 7, 63–68 CrossRef.
- B. L. Weeks, M. W. Vaughn and J. J. DeYoreo, Langmuir, 2005, 21, 8096–8098 CrossRef CAS PubMed.
- O. Laskina, H. S. Morris, J. R. Grandquist, Z. Qin, E. A. Stone, A. V. Tivanski and V. H. Grassian, J. Phys. Chem. A, 2015, 119, 4489–4497 CrossRef CAS PubMed.
- D. A. Bruzewicz, A. Checco, B. M. Ocko, E. R. Lewis, R. L. McGraw and S. E. Schwartz, J. Chem. Phys., 2011, 134, 044702 CrossRef PubMed.
- C. N. Cruz and S. N. Pandis, Environ. Sci. Technol., 2000, 34, 4313–4319 CrossRef CAS.
- H. Yu, W. Li, Y. Zhang, P. Tunved, M. Dall'Osto, X. Shen, J. Sun, X. Zhang, J. Zhang and Z. Shi, Atmos. Chem. Phys., 2019, 19, 10433–10446 CrossRef CAS.
- K. Hämeri, A. Laaksonen, M. Väkevä and T. Suni, J. Geophys. Res.: Atmos., 2001, 106, 20749–20757 CrossRef.
- R. Bahadur and L. M. Russell, Aerosol Sci. Technol., 2008, 42, 369–376 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp00155d |
| ‡ Xiaoxiang Wang and Haozhi Lei contributed equally to this work. |
| This journal is © the Owner Societies 2020 |