Enhanced conductivity of water at the electrified air–water interface: a DFT-MD characterization
Abstract
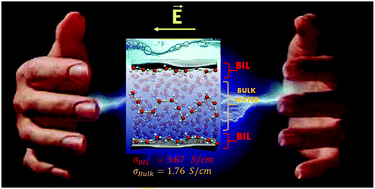
DFT-based molecular dynamics simulations of the electrified air–liquid water interface are presented, where a homogeneous field is applied parallel to the surface plane. We unveil the field intensity for the onset of proton transfer and molecular dissociation; the protonic current/proton conductivity is measured as a function of the field intensity/voltage. The air–water interface is shown to exhibit a proton conductivity twice the one in the liquid water for field intensities below 0.40 V Å−1. We show that this difference arises from the very specific organization of water in the binding interfacial layer (BIL, i.e. the air–water interface region) into a 2D-HBond-network that is maintained and enforced at the electrified interface. Beyond fields of 0.40 V Å−1, water in the BIL and in the bulk liquid are aligned in the same way by the rather intense fields, hence leading to the same proton conductivity in both BIL and bulk water.
- This article is part of the themed collections: 2020 PCCP HOT Articles and Frontiers in Molecular Simulation of Solvated Ions, Molecules and Interfaces


 Please wait while we load your content...
Please wait while we load your content...