Model building analysis – a novel method for statistical evaluation of Pt L3-edge EXAFS data to unravel the structure of Pt-alloy nanoparticles for the oxygen reduction reaction on highly oriented pyrolytic graphite†
Abstract
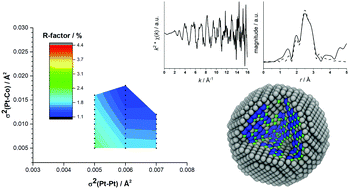
Extended X-ray absorption fine structure (EXAFS) is a powerful tool to determine the local structure in Pt nanoparticles (NP) on carbon supports, active catalysts for fuel cells. Highly oriented pyrolytic graphite (HOPG) covered with Pt NP gives samples with flat surfaces that allow application of surface science techniques. However, the low concentration of Pt makes it difficult to obtain good quality EXAFS data. We have performed in situ highly sensitive BCLA-empowered Back Illuminated EXAFS (BCLA + BI-EXAFS) measurements on Pt alloy nanoparticles. We obtained high quality Pt L3-edge data. We have devised a novel analytical method (model building analysis) to determine the structure of multi-component nanoparticles from just a single absorption edge. The generation of large numbers of structural models and their comparison with EXAFS fits allows us to determine the structures of Pt-containing nanoparticles, catalysts for the oxygen reduction reaction. Our results show that PtCo, PtCoN and AuPtCoN form a Pt-shell during electrochemical dealloying and that the ORR activity is directly proportional to the Pt–Pt bond length.
- This article is part of the themed collections: 2020 PCCP HOT Articles and Synchrotron Radiation Techniques in Catalytic Science


 Please wait while we load your content...
Please wait while we load your content...