Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electric-field control of single-molecule tautomerization†
Shai
Mangel
a,
Maxim
Skripnik
bc,
Katharina
Polyudov
a,
Christian
Dette
a,
Tobias
Wollandt
a,
Paul
Punke
a,
Dongzhe
Li
 c,
Roberto
Urcuyo‡
a,
Fabian
Pauly
c,
Roberto
Urcuyo‡
a,
Fabian
Pauly
 bc,
Soon Jung
Jung
bc,
Soon Jung
Jung
 *a and
Klaus
Kern
ad
*a and
Klaus
Kern
ad
aMax Planck Institute for Solid State Research, Heisenbergstrasse 1, 70569 Stuttgart, Germany. E-mail: s.jung@fkf.mpg.de; Tel: +49-711-689-5249
bOkinawa Institute of Science and Technology Graduate University, Onna-son, Okinawa 904-0495, Japan
cDepartment of Physics, University of Konstanz, 78457 Konstanz, Germany
dInstitute de Physique, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland
First published on 25th February 2020
Abstract
The electric field is an important parameter to vary in a single-molecule experiment, because it can directly affect the charge distribution around the molecule. Yet, performing such an experiment with a well-defined electric field for a model chemical reaction at an interface has proven to be extremely difficult. Here, by combining a graphene field-effect transistor and a gate-tunable scanning tunneling microscope (STM), we reveal how this strategy enables the intramolecular H atom transfer of a metal-free macrocycle to be controlled with an external field. Experiments and theory both elucidate how the energetic barrier to tautomerization decreases with increasing electric field. The consistency between the two results demonstrates the potential in using electric fields to engineer molecular switching mechanisms that are ubiquitous in nanoscale electronic devices.
Introduction
Over the last 50 years there has been great interest in the influence of external electric fields on both molecular structure and chemical reactivity.1–9 Several enduring examples have firmly established that adsorption structures, vibrational frequencies and oxidation states are all affected by electric fields.10–14 Since electric fields alter the energies of molecular orbitals, they can also change activation barriers and the associated kinetic parameters for specific chemical reactions. This impact makes electric fields highly relevant to surface chemistry.3,6,7,9Recent advances in the synthesis, characterization and computational modeling of catalytic materials have inspired detailed predictions and verifications of electric field effects therein,5,8,9,15–17 but extant technical challenges still remain to be overcome.4 Unlike theoretical modelling, in an experiment it is not possible to set the surface electric field to any arbitrary value, nor always have a well-defined field. For instance, since the orientation and magnitude of the local electric field can vary significantly from one adsorption site to another on a surface, its overall effect on catalytic activity can be challenging to predict. Furthermore, due to the complex morphology of catalytic surfaces and the lack of surface-sensitive experimental techniques specifically adapted to them, it is extremely difficult to characterize surface electric fields and their effect on chemical reactions.4 Fortunately, in both these aspects, STM contributes enormously due to its ability to apply oriented electric fields to adsorbed molecules and to detect the resulting effects at the atomic level. In particular, the sharp apex of an STM tip can sustain very high electric fields (|E| ≈ 1 V nm−1) with low applied tip-substrate bias voltages (|Vb| ≈ 1 V). The ability to produce a high electric field in combination with precisely adjustable parameters makes STM-based methods ideal for testing the effects of electric fields on single-molecule reactions in a spatially resolved way.
Argonès et al. reported an STM characterization of an electric-field-induced Diels–Alder reaction, where a diene, covalently bonded to a gold tip, was brought into contact with a dienophile-covered substrate.17 The electric-field-induced chemical-bonding events were detectable by measuring the electric current. Alemani et al. noted similar effects that involved the isomerization of azobenzene under varying electric field conditions.18 Recently, STM tip induced electric field is shown to catalyze the cis-to -trans isomerization of cumulenes in solution.19
A drawback of STM for studying electric-field effects is the inseparability of its control parameters. Since only two of the three factors (tip-sample distance, bias voltage and tunneling current) can be varied independently, it is not easy to identify system responses that are directly attributable to electric-field effects alone. Here, we overcome this challenge by combining a graphene field-effect transistor with a gate-tunable STM. This combination enables an applied back-gate voltage to change the charge-carrier density on the graphene surface, which in turn varies the tip height in constant-current mode. In other words, the back-gating enables changing the tip-induced electric field without varying the set-point current and set-point voltage. Using this method, we observe the impact of the electric field on the tautomerization reaction of metal-free phthalocyanine (H2Pc) deposited onto these back-gated graphene devices at a temperature of 5 K. We show that an increase of the absolute magnitude of the applied electric field leads to an increase in the reaction rate, which we attribute to a decrease in the activation barrier. The activation barrier is found to scale linearly with the applied electric field, which offers the possibility to control tautomerization reactions at the molecular level.
Methods
A. Experimental details
We used the back-gated graphene/SiO2/Si device, shown schematically in Fig. 1. The graphene sample was grown via chemical-vapor deposition20 and transferred on top of a heavily doped Si wafer coated with a 300 nm thick SiO2 layer. The graphene was characterized with an optical microscope and Raman spectroscopy.21 Electrical contacts were made by depositing Cr (10 nm thick)/Au (30 nm thick) electrodes with a stencil mask. Free-base phthalocyanine molecules (Alfa Aesar) were evaporated onto the graphene in ultra-high vacuum at room temperature (298 K) using a Knudsen cell prior to cooling the sample to a temperature of 5 K. STM/STS measurements were performed with a home-built 5 K STM. It was equipped with electrochemically etched Pt–Ir tips bought from Agilent Technologies (N9801A), USA. The lock-in modulation for dI/dV measurements was 700 mV at a frequency of 425 Hz. We determined the reaction rate k by counting the number of switching events Nswitch in every current–time trace and dividing it by the total measurement time ttot, i.e., k = Nswitch/ttot.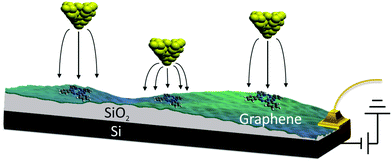 | ||
| Fig. 1 Schematic of the method used to control the tip-induced electric field without varying the set-point current and voltage. | ||
B. Computational details
We investigated the influence of the electric field and charging on the activation barrier with the help of density functional theory (DFT). By using the nudged-elastic-band method22 implemented in Quantum Espresso,23 we were able to find the minimum-energy path between two trans states. We used the PBE functional24 and ultrasoft pseudopotentials25 with a 40 Ry cutoff for the wavefunctions and a 400 Ry cutoff for the charge density. The total energy was converged to a precision better than 5 × 10−5 Ha. For each calculation we used 15 nudged-elastic-band images and allowed for the geometrical optimization of each, including initial and final ones. To calculated the influence of the accumulated charge on the tautomerization reaction, we placed the H2Pc on graphene. There, the simulated supercell was built from 8 by 8 graphene unit cells (128 carbon atoms in the graphene sheet). The lattice constant of the hexagonal supercell was 19.7 Å. The distance between the periodic images perpendicular to the graphene layer was 30 Å. In a second type of calculations we considered only the molecule in a cubic unit cell with a side length of 20 Å.Results and discussion
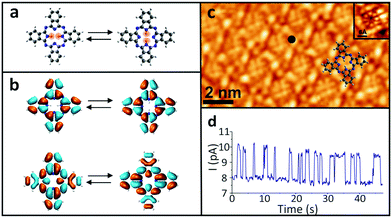
In order to examine the influence of the electric field on the tautomerization reaction, an external voltage source was connected to the Si substrate so that back-gate voltages can be applied (Fig. 1) in an STM setting. This potential difference causes some charge accumulation at the Si/SiO2 interface, accompanied by an image charge on the graphene. This enables the back-gating to fill or deplete electronic states in the graphene, which shifts the Fermi energy with respect to the Dirac point. When measuring data with the STM in constant-current mode, the change in the density of states (DOS) of the graphene causes an adjustment in the tip-sample distance, which consequently modifies the tip-applied electric field (Fig. 1). The ability to disentangle the tip-sample distance, bias voltage and tunneling current is especially important for the study of many chemical reactions, because the activation of a particular reaction mechanism is strongly correlated with the number and the potential energy of the injected electrons used to trigger said mechanism.The ability to control the external electric field without varying the set-point current and voltage was applied to investigate the electric-field effect on the hydrogen-transfer reaction of H2Pc. H2Pc is a planar π-conjugated molecule with D2h symmetry. As shown in Fig. 2a, H2Pc undergoes a tautomerization reaction in which two hydrogen atoms hop between four nitrogen atoms in the cavity, switching between two different trans conformations. The tautomerization in H2Pc can be triggered by an STM-induced electronic excitation process at 5 K.26–29 According to DFT calculations (Fig. 2b), the highest occupied molecular orbitals (HOMOs) of both tautomers exhibit almost identical spatial shapes, and thus cannot be used to detect the position of the hydrogen atoms in the cavity or, in other words, to infer the state of the tautomerization of the molecule. The inset of Fig. 2c shows an STM image of H2Pc taken at the molecule's HOMO resonance. Despite of a continuous change of the tautomerization state of the molecule during recording, the HOMO can be clearly recognized due to the theoretically predicted indistinguishability of the computed HOMOs. On the other hand, the lowest unoccupied molecular orbital (LUMO) has twofold symmetry (Fig. 2b). Thus, when we rotate the LUMO of one tautomer by 90°, it becomes equivalent to the LUMO of the other tautomer. The LUMO can hence be used to detect the position of hydrogen atoms inside the molecular cavity.
All the measurements were taken at a bias voltage of Vb = 1.6 V, which is high enough to induce the tautomerization but also low enough to ensure the stability of the tip during the measurements.29 The tunnelling current was kept at 10 pA in all experiments. Since the tautomerization is faster than the STM scanning rate, when the H2Pc molecules were imaged, the superposition of the LUMOs of the different tautomers appears as an octothorpe in the molecular cavity (Fig. 2c). Thus, the tautomeric state is still obscured even though the LUMOs of the two tautomers are in principle, distinguishable. Nevertheless, the change in the local density of states (LDOS) due to the tautomerization reaction can be easily detected in a current–time trace as a two-level telegraphic noise recorded at a fixed lateral position in constant-height mode. These fluctuations originate from the tautomerization itself, whose high- and low-conductance states can be assigned to the two tautomeric forms of H2Pc.
Since the rate of the tautomerization reaction strongly depends on the position of the electron injection into the molecule,26 we measured the switching rates at various positions over the H2Pc molecule. To achieve a sufficiently low dispersion in the measured switching rate, we chose to perform them at an empirically determined location that maximizes the number of switching events (black dot in Fig. 2c). After the tip location was set in constant-current mode, the feedback loop was disabled to measure the reaction rate of the tautomerization by recording a current–time trace in constant-height mode (Fig. 2d and SI 1, ESI†).
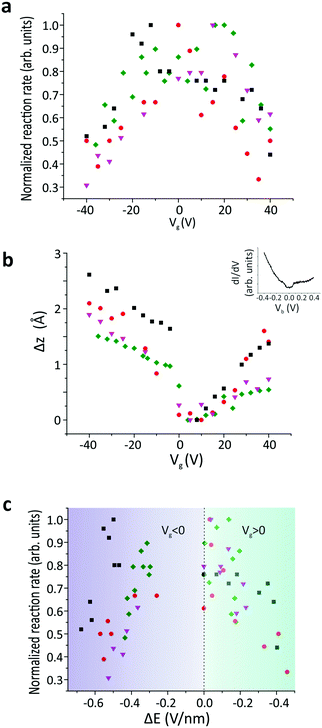
Due to the spatial dependence of the switching rate, the molecules were rescanned following each measurement to verify that the tip remained at the predetermined position above the molecule. The reaction rate was then measured as a function of the applied gate voltage (Vg) (SI 2, ESI†), as shown in Fig. 3a. The experiment was then repeated for several different molecules. All these reaction rates were normalized with respect to their maximum value to reduce the influence of any local surface corrugation or impurities that create “charge-puddles” below the molecules30 and perturb the measured reaction rate (see SI 3, ESI†). The maximum reaction rate is attained when no gate voltage is applied (Vg = 0 V). We expect that the electric field applied between the tip and sample is around E = 2.2 V nm−1 at Vg = 0 V, based on the simple plate–capacitor model (see the discussion in SI 5, ESI†). The reaction rate decreases symmetrically with increasing |Vg| (Fig. 3a). The reaction rate exhibits an inverse correlation with the tip-molecule distance (Fig. 3b and SI 4, ESI†). Since sweeping the gate voltage is equivalent to shifting the Fermi energy with respect to the Dirac point, the changes in the tip height Δz as a function of the applied gate voltage are correlated with the DOS of the underlying graphene (inset in Fig. 3b). The modification of the electric field (ΔE) was derived from the change in the tip height (see the discussion in SI 5, ESI†). The correlation between the reaction rate and the changes in the electric field induced by the tip is clearly visible in Fig. 3c, where the reaction rate decreases when the tip-induced electric field is reduced. The gap in the electric-field spectrum at −0.2 V nm−1 < ΔE < 0 V nm−1 for Vg < 0 originates from a jump in the tip position around Vg = 0 V when sweeping towards negative gating values (see Fig. 3b).
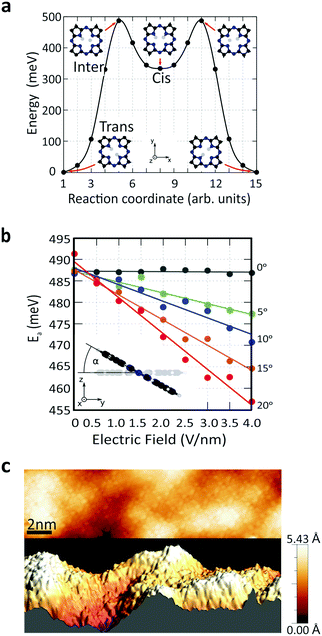
To understand the role of the applied electric field on the reaction rate, we employed DFT calculations. The minimum-energy path (MEP) for hydrogen transfer in the molecule is shown in Fig. 4a. The DFT calculations predict that this transfer occurs through one of the cis states, regardless of whether the molecule is in the gas phase or on graphene. A direct transition that bypasses the cis state contributes negligibly due to its prohibitively high energy barrier (SI 6, ESI†). A transition complex between the trans and cis states exists with an intermediate-state energy Einter that defines the activation energy Ea for the tautomerization reaction with respect to the initial energy Etrans, i.e., Ea = Einter − Etrans. Using this definition, the calculated activation barrier is 487 meV (11.23 kcal mol−1). The activation barrier is lower than the value of previous report, 622 meV (14.34 kcal mol−1). The difference can be attributed to the differences in the ab initio approaches (SI 6, ESI†).
We studied the activation energy as a function of the magnitude of the electric field. The direction of the applied electric field is defined by the tilting angle α between the electric field and the normal vector of the molecule's plane (Fig. 4b). When the electric field is applied perpendicular to the molecule's plane (α = 0), the energy variation due to electric field is negligible. However, considering the corrugation of the graphene surface, molecules generally experience an electric field from different tilting angles (Fig. 4c and SI 7, ESI†). As we increase α, the electric field effect on the activation barrier becomes increasingly pronounced (Fig. 4b and SI 8, ESI†). This calculated strong dependence on α explains the variation in the absolute value of the reaction rates across different molecules (Fig. S 3, ESI†). In addition, theory predicts that an applied electric field reduces the activation barrier. This is consistent with the experimental observations in Fig. 3c that the reaction rate drops as the electric field is reduced due to an increased tip height. In other words, an applied electric field of increasing magnitude reduces the activation barrier and increases the reaction rate.
To verify our conclusions, we also calculated the direct influence of accumulated charges on the hydrogen transfer. Our simulations predict that the activation barrier typically decreases as the absolute value of the accumulated charge increases at a constant electric field (SI 10, ESI†), which would correspond to an increase of the reaction rate with |Vg|. This is in contradiction to the experimental trends, and from this analysis we therefore conclude that the effect of accumulated charge alone cannot account for the observed change of reaction rate. Additionally, we examined molecular energy level shifts in relation to the applied gate voltage (SI 11, ESI†). This was done because the alignment of molecular levels with respect to the graphene substrate can be tuned through Vg, which in turn affects the number of injected electrons that activate the tautomerization reaction. The calculations show that the molecular energy levels shift monotonically when the applied back-gate voltage is increased from −40 V to +40 V. Since the reaction rate decreases symmetrically around Vg = 0 V (see Fig. 3c), the energy level shift also cannot account for the changes of reaction rate observed in the experiment. To summarize, experimentally we observe the change of the tautomerization reaction rate as a function of gate voltage. By examining theoretically the roles of electric field, accumulated charge and molecular energy shifts that occur in the system, we find that the independent variable that best explains the functional dependence is the electric field. We note that our theoretical modelling does not account for inhomogeneous distributions of the electric field or charge. We expect that such inhomogeneities due to the tip geometry or surface defects will lead to non-vanishing tilt angles α on the H2Pc molecules and thus enhance the tilting effects of surface corrugation.
Conclusions
Tautomerization is an attractive mechanism to be used for controlling molecular switches because it is well-defined, reversible, intrinsic to the molecule, and does not involve any changes to the molecular frame. In particular, each of the different tautomeric states can be distinguished in conductance measurements.31 Finding a method of controlling the tautomerization reaction is central to enabling efficient molecular switching. Here, we have shown that the external electric field can be used to tune the tautomerization reaction in metal-free phthalocyanine molecules using a combination of a graphene field-effect transistor and a gate-tunable STM. By modulating the back-gate voltage, the electric field can be adjusted while keeping tunnelling current and applied bias voltage constant. Our results show that the tip-induced electric field reduces the activation barrier of the tautomerization reaction. Calculations demonstrate that the activation barrier is affected by the external electric field, especially when the tilting angle of the molecule is increased. Our work shows the value of using the electric field as a complementary control parameter in its own right, and represents a tangible step forward in the pursuit of integrated molecular electronics.Author contributions
S. M., S. J. J. and K. K. designed the research. The gate-tunable graphene FETs were prepared by S. M. and K. P. with help of R. U. and P. P. Measurements were performed and analysed by S. M., K. P. and S. J. J. with help of C. D. The theoretical modelling and simulation was done by M. S., D. L. and F. P. The manuscript was drafted by S. M. and S. J. J. All authors participated in the writing and review of the final draft. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. S. and F. P. acknowledge financial support from the University of Konstanz through a stipend provided by the “Landesgraduiertenförderungsgesetz (LGFG)” and through the Collaborative Research Center (SFB) 767 of the German Research Foundation (DFG). Part of the numerical modeling was performed using the computational resources of the bwHPC program, namely the bwUniCluster and the JUSTUS HPC facility. Open Access funding provided by the Max Planck Society.References
- R. Vanselow and R. Howe, Chemistry and Physics of Solid Surfaces VIII, Springer, Berlin Heidelberg, 1990 Search PubMed.
- R. F. Copeland, Effect of Coulombic fields in the vicinity of metal surfaces upon the entropy and absolute rate of reaction of absorbed molecules, J. Phys. Chem., 1971, 75(19), 2967–2969 CrossRef CAS.
- S. Shaik, D. Mandal and R. Ramanan, Oriented electric fields as future smart reagents in chemistry, Nat. Chem., 2016, 8, 1091 CrossRef CAS PubMed.
- F. Che, J. T. Gray, S. Ha, N. Kruse, S. L. Scott and J.-S. McEwen, Elucidating the Roles of Electric Fields in Catalysis: A Perspective, ACS Catal., 2018, 8(6), 5153–5174 CrossRef CAS.
- V.-J. Lee, Heterogeneous Catalysis: Effect of an Alternating Electric Field, Science, 1966, 152(3721), 514 CrossRef CAS PubMed.
- T. Stuyver, D. Danovich, J. Joy and S. Shaik, External electric field effects on chemical structure and reactivity, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, e1438 Search PubMed.
- S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Structure and reactivity/selectivity control by oriented-external electric fields, Chem. Soc. Rev., 2018, 47(14), 5125–5145 RSC.
- S. Ciampi, N. Darwish, H. M. Aitken, I. Díez-Pérez and M. L. Coote, Harnessing electrostatic catalysis in single molecule, electrochemical and chemical systems: a rapidly growing experimental tool box, Chem. Soc. Rev., 2018, 47(14), 5146–5164 RSC.
- X. Huang, C. Tang, J. Li, L.-C. Chen, J. Zheng, P. Zhang, J. Le, R. Li, X. Li and J. Liu, et al., Electric field–induced selective catalysis of single-molecule reaction, Sci. Adv., 2019, 5(6), eaaw3072 CrossRef PubMed.
- R. P. Madenach, G. Abend, M. S. Mousa, H. J. Kreuzer and J. H. Block, Influence of electrostatic fields on binding energy (NO on Rh), Surf. Sci., 1992, 266(1), 56–61 CrossRef CAS.
- P. Br
![[a with combining cedilla]](https://www.rsc.org/images/entities/char_0061_0327.gif) giel, Surface reactions in an external electrostatic field, Surf. Sci., 1992, 266(1), 35–39 CrossRef.
giel, Surface reactions in an external electrostatic field, Surf. Sci., 1992, 266(1), 35–39 CrossRef. - J. Pancíř and R. Zahradník, Automatic Geometry Optimization and Vibrational Analysis in External Electric Field: Ethylene, Helv. Chim. Acta, 1978, 61(1), 59–66 CrossRef.
- J. A. Rabo and P. H. Kasai, Caging and electrolytic phenomena in zeolites, Prog. Solid State Chem., 1975, 9, 1–19 CrossRef CAS.
- P. S. Bagus and G. Pacchioni, Electric field effects on the surface—adsorbate interaction: cluster model studies, Electrochim. Acta, 1991, 36(11), 1669–1675 CrossRef CAS.
- F. Che, J. T. Gray, S. Ha and J.-S. McEwen, Catalytic water dehydrogenation and formation on nickel: Dual path mechanism in high electric fields, J. Catal., 2015, 332, 187–200 CrossRef CAS.
- Y. Sekine, M. Tomioka, M. Matsukata and E. Kikuchi, Catalytic degradation of ethanol in an electric field, Catal. Today, 2009, 146(1), 183–187 CrossRef CAS.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Electrostatic catalysis of a Diels–Alder reaction, Nature, 2016, 531, 88 CrossRef PubMed.
- M. Alemani, M. V. Peters, S. Hecht, K.-H. Rieder, F. Moresco and L. Grill, Electric Field-Induced Isomerization of Azobenzene by STM, J. Am. Chem. Soc., 2006, 128(45), 14446–14447 CrossRef CAS PubMed.
- Y. Zang, Q. Zou, T. Fu, F. Ng, B. Fowler, J. Yang, H. Li, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Directing isomerization reactions of cumulenes with electric fields, Nat. Commun., 2019, 10(1), 4482 CrossRef PubMed.
- X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung and E. Tutuc, et al., Large-Area Synthesis of High-Quality and Uniform Graphene Films on Copper Foils, Science, 2009, 324(5932), 1312–1314 CrossRef CAS PubMed.
- A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov and S. Roth, et al., Raman Spectrum of Graphene and Graphene Layers, Phys. Rev. Lett., 2006, 97(18), 187401 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113(22), 9901–9904 CrossRef CAS.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al., Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29(46), 465901 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(11), 7892–7895 CrossRef PubMed.
- P. Liljeroth, J. Repp and G. Meyer, Current-induced hydrogen tautomerization and conductance switching of naphthalocyanine molecules, Science, 2007, 317(5842), 1203–1206 CrossRef CAS PubMed.
- W. Auwärter, K. Seufert, F. Bischoff, D. Ecija, S. Vijayaraghavan, S. Joshi, F. Klappenberger, N. Samudrala and J. V. Barth, A surface-anchored molecular four-level conductance switch based on single proton transfer, Nat. Nanotechnol., 2012, 7(1), 41 CrossRef PubMed.
- T. Kumagai, F. Hanke, S. Gawinkowski, J. Sharp, K. Kotsis, J. Waluk, M. Persson and L. Grill, Controlling intramolecular hydrogen transfer in a porphycene molecule with single atoms or molecules located nearby, Nat. Chem., 2014, 6(1), 41 CrossRef CAS PubMed.
- J. Kügel, L. Klein, M. Leisegang and M. Bode, Analyzing and Tuning the Energetic Landscape of H2Pc Tautomerization, J. Phys. Chem. C, 2017, 121(50), 28204–28210 CrossRef.
- Y. Zhang, V. W. Brar, C. Girit, A. Zettl and M. F. Crommie, Origin of spatial charge inhomogeneity in graphene, Nat. Phys., 2009, 5(10), 722 Search PubMed.
- J. Prasongkit, A. Grigoriev, R. Ahuja and G. Wendin, Interference effects in phthalocyanine controlled by H-H tautomerization: potential two-terminal unimolecular electronic switch, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(16), 165437 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp06868f |
| ‡ Present address: Centro de Electroquímica y Energía Química (CELEQ) and Escuela de Química, Universidad de Costa Rica, 11501-2060, San José, Costa Rica. |
| This journal is © the Owner Societies 2020 |