Mechanical properties of tantalum carbide from high-pressure/high-temperature synthesis and first-principles calculations

Abstract

As a member of the refractory metal carbide family of materials, TaC is a promising candidate for ultra-high temperature ceramics (UHTC) with desirable mechanical strength. TaC sample quality and therefore mechanical properties are strongly dependent on synthesis method, and atomistic origins of mechanical failure are difficult to assign. Here, we have successfully synthesized high quality densified TaC samples at 5.5 GPa and 1400 °C using the high pressure and high temperature (HPHT) sintering method, with Vickers hardness determined to be 20.9 GPa. First-principles calculations based on the recently developed strain–stress method show that the ideal indentation strength of TaC is about 23.3 GPa in the (11̄0)[001] direction, in excellent agreement with experimental results. The detailed indentation shear deformation analysis and structural snapshots from the calculations indicate that the slip dislocations of TaC layers are the main structural deformation mode during the Vickers indentation process, and that the strong directional Ta–C bonds are responsible for the high mechanical strength of TaC. HPHT synthesis is shown to produce TaC samples with superior strength, and together with accurate first-principles calculations offers crucial insights for rational design and synthesis of novel and advanced UHTC materials.

---

1 Introduction

Transition-metal carbides (TMC) are candidate materials for ultra-high temperature ceramics (UHTC), due to their high melting points (2000–4000 °C), huge modulus and resistance to chemical attack.^1–3 Amongst UHTC materials, tantalum carbide, TaC, is a desirable candidate for next generation thermal heat protection, scramjet components, and rocket propulsion-exposed components.^4,5 Its melting point reaches an extremely high 3983 °C and TaC has therefore attracted great research interest.^6–8 Up to now, mostly fully dense TaC has been synthesized, with Vickers hardness about 11.1–15.7 GPa,^9–11 thus limiting extended engineering applications. To fully exploit TaC's potential and to extend the application range of TaC-based ceramic materials it is of crucial importance to understand the origin of TaC's mechanical properties and the underlying deformation mechanisms in the structural failure process at an atomic level.

TaC has been synthesized by a range of techniques, microstructure and mechanical properties can vary widely. Kumashiro et al.¹² reported TaC single crystal growth by the floating-zone method. The hardness of these TaC samples could reach about 3000 kg mm⁻² under different cleavage planes, and were subsequently characterized using X-ray analysis to be significantly carbon-deficient (TaC_0.83). Unfortunately, the highly covalent bonding nature and low self-diffusion coefficient in TaC restrict attempts at further densification.¹ Balani et al.¹³ synthesized Ta–C samples in different C/Ta ratios using vacuum plasma-spray technique (VPS), resulting in TaC_x with 0.83 ≤ x ≤ 0.94. Experimental micro-Vickers indentation values about 21.3 GPa (axial) and 26.9 GPa (transverse) indicate the anisotropy inherent in TaC.¹³ However, many researchers have reported higher nano-hardnesses of about 25 GPa in TaC samples, which are overestimated by different loading force, variation of carbon contents and Ta/C ratios.^8,14,15 The dominant mechanism responsible for the material strength was identified as a slip along the (111) planes due to inherent stacking faults in TaC.^16,17 Recent reports studied the effects of Al and Si₃N₄ as sintering aids on the formation of TaC ceramics,¹⁸ which effectively increase the density and strength of sintered materials. With the advancement of experimental technology, higher quality stoichiometric TaC samples have been obtained under high temperature and pressure. High-densification monolithic TaC ceramics were prepared by the hot pressing method, leading to a Vickers hardness between 11.1 and 15.7 GPa.^9–11,19 TaC synthesized using spark plasma sintering (SPS)^20,21 is reported to have a hardness of 13.9 GPa,²² while high-pressure high-temperature (HPHT) synthesis of TaC yielded a hardness of 19.2 GPa.²³ This leads to the question, what is the underlying mechanism behind those different hardnesses in the same TaC system? How to improve TaC's mechanical strength to extend its engineering applications? To answer these questions requires careful Vickers hardness measurements and detailed analysis of the structure and deformation mechanism of TaC under different loading conditions.

First-principles calculations of materials strengths have, since their inception two decades ago,^24,25 provided invaluable atomistic insights into the deformation mechanisms of crystalline materials. The ideal shear strength is determined from a series of finite shear strain calculations, and defined as the maximum stress reached before structural failure. In some materials, this strength can deviate substantially from that determined in indentation experiments.²⁶ One potential reason is the neglect of the compressive strain present in the indentation process. Accounting for the actual shape of the indenter can then drastically improve the comparison with experiment^27,28 and lead to new insights into materials responses to complex strain patterns. For instance, materials can benefit from “strain stiffening”, where the Vickers strength is larger than the pure shear strength,^29–33 but also suffer from the opposite effect.^34,35 Either way, the analysis of different types of stress–strain calculations allows one to develop a better understanding of the atomistic origins of materials strengths.

In our work, high quality densified TaC has been synthesized by the HPHT method, which can limit grain sizes and greatly reduces the synthesis temperature.^36,37 The elastic properties and microstructure of the TaC sample have been characterized, and the Vickers hardness tests indicate a hardness about 20.9 GPa, which is higher than existing measurements (usually below 15.7 GPa). We have also performed extensive first principles calculations of the strain–stress curves of TaC under different loading conditions to uncover the underlying atomistic mechanisms. The ideal indentation strength of TaC, 23.3 GPa, agrees very well with our experiments. The atomistic deformations of TaC reveal that the slip dislocation in the medium TaC layer is the main resistance to the Vickers shear deformations, and strong directional Ta–C bonds are responsible for the high strength of TaC.

The densified TaC samples are synthesized at 5.5 GPa and 1400 °C using the HPHT sintering method. A precompressed TaC powder is initially compressed to 5.5 GPa, followed by heating to 1400 °C with a heating rate of 150 °C min⁻¹. After 20 minutes, the samples are quenched to room temperature at a cooling rate of 150 °C min⁻¹, and then decompressed to ambient pressure. Vickers hardness (H_v) tests are conducted on the ends-polished samples by means of a Vickers single crystalline diamond indenter. H_v is determined as: H_v = 1854.4 × F/L², where F is the applied load, and L is the arithmetic mean of the two diagonals of the Vickers indentation. More details on the HPHT synthesis and characterization of TaC can be found elsewhere.³⁸

2 Computational method

We have used the CALYPSO package^39–41 in conjunction with the Vienna Ab Initio Simulation Package (VASP)⁴² to search various candidates of TaC and to determinate the true global structural minimum of TaC. The structure searches have successfully identified the cubic structure ground state of TaC, with Fm3̄m symmetry, as its ground state, which agrees with our experiment. We have performed calculations of the ideal indentation strength using the newly developed Vickers indenter method.^27,28,43 These calculations consider biaxial stresses, where the total stress is projected onto a shear stress (σ_zx) and a normal compressive stress (σ_zz) component that satisfy the relation σ_zz = σ_zx tan ϕ, where ϕ stands for the centerline-to-face angle of the Vickers indenter. An angle ϕ = 68° describes the indenter from our experimental apparatus. During the structural relaxations under different loading conditions, the residual stresses are less than 0.5 GPa for both pure shear and biaxial Vickers shear deformations. Thus, the calculated ideal indentation strengths can realistically reflect experimental measurements which has been shown successfully in many transition metal borides and nitrides.^{33–35,44–46} This microscopic simulation of the failure process is arguably superior to the application of various empirical models for hardness that are based purely on electronic ground state information,^47–49 but is naturally restricted to capture failure modes that are commensurate with the atomic supercell used (here we used the eight-atom conventional cell of TaC). We further analysed the electron localization function (ELF)⁵⁰ and quantified electron transfer from Ta atoms to C atoms through the Bader charge analysis.⁵¹ The integrated Crystal Overlap Hamiltonian Populations (ICOHP)^52,53 were obtained with the LOBSTER code.^54,55

3 Results and discussion

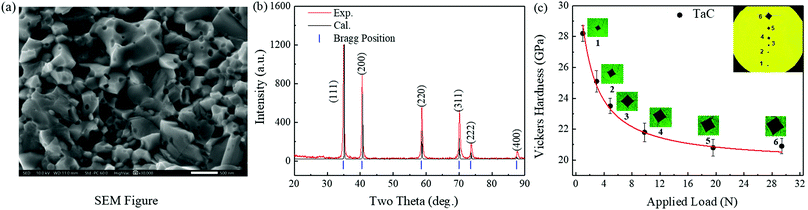
Fig. 1(a) shows a representative scanning electron microscope (SEM) micrograph of high quality densified TaC samples synthesized under HPHT conditions of 5.5 GPa and 1400 °C. SEM micrograph images of samples synthesized at different temperatures are shown in Fig. S1(a)–(f) in the ESI.† The grains are very small, on the order of 0.5–1 μm, and are well connected by interfacial bonding, which is how a higher density could be achieved compared to other synthesis methods.^13,20,21 The samples have excellent crystallinity and contain only two elements of Ta and C, with the corresponding molar ratio of 1 : 1, as confirmed by energy dispersive X-ray spectroscopy (EDS, see Fig. S2 in the ESI†). The XRD pattern in Fig. 1(b) confirms the rock-salt structure for TaC, with no other peaks present and excellent agreement with our calculated XRD pattern. Fig. 1(c) shows the experimentally measured Vickers hardness H_v as a function of the applied loading force. The Vickers hardness of TaC is 28.2 GPa under an applied load of 0.98 N, and it decreases to 20.9 GPa as the loading force is increased to 29.4 N. The asymptotic Vickers hardness is about 20.9 ± 0.5 GPa, reached when the loading force approaches 19.6 N, as seen in Fig. 1(c). The samples' hardness is significantly higher than those reported in the literature, around 11.1–15.7 GPa in previous studies.^9–11,19 This surprising result may be due to the different synthesis methods and conditions.

Fig. 1 (a) SEM micrograph of TaC sample synthesised at 5.5 GPa and 1400 °C. (b) X-ray diffraction pattern (λ = 1.5404 Å) of recovered TaC sample. Calculated XRD pattern for lattice constant a = 4.455 Å. (c) Vickers hardness (H_v) test results of TaC for applied loads from 0.98 N to 29.4 N. The inset displays the Vickers indentation impression at different loading force. The red line is an asymptotic fit to the data with the following relation: H_v = 19.8 × exp 1.2/(F + 2.1), where F is the load (N). The asymptotic measured hardness value is 20.9 GPa for TaC.

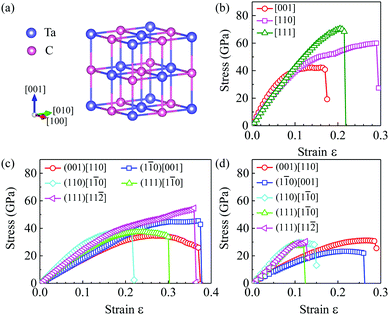
To confirm these experimental results, we have performed comprehensive structure searches combined with first principles calculations to obtain the theoretical Vickers hardness and directly compare with our experiments. As shown in Fig. 2(a), we have identified that the ground state structure of TaC is the B1 type structure (space group Fm3̄m) with a lattice constant a = 4.475 Å, which is consistent with prior theoretical and experiment values of 4.453–4.488 Å,^22,47 and agrees very well with our XRD measurement of a = 4.455 Å for the recovered sample. The elastic constants of TaC have been calculated and are collected in Table 1: C₁₁ = 623 GPa, C₁₂ = 166 GPa, C₄₄ = 167 GPa and Poisson's ratio μ = 0.25 satisfy the mechanical stability criteria of cubic crystals and are in good agreement with experimental and other theoretical values.^57–63 The phonon dispersion curves in Fig. S4(b) (ESI†) show that no imaginary phonon frequencies can be seen over the entire Brillouin zones, implying the dynamical stability of this rock-salt type structure of TaC.

Fig. 2 (a) The crystal structure of TaC. (b–d) Calculated stress–strain curves of TaC along various crystallographic directions under (b) tensile, (c) pure shear and (d) indentation shear deformation.

Table 1 Calculated and experimental equilibrium lattice parameters (in Å), elastic constants, Voigt bulk modulus (B), Voigt shear modulus (G), Young's modulus (E) (all in GPa) and Poisson's ratio (μ) for TaC in the B1–NaCl structure

Properties	TaC
	This work	Literature
Experiment: ref. 56, 57, 58, 59 and 60. Theory: ref. 58 and 61–63.
a	4.475	4.453^56
C 11	623	595^57
C 12	166	150^58
C 44	167	153^57
B	335	329^59
G	253	234^60
E	495	477^61
G/B	0.76	0.67^62
μ	0.25	0.22,^57 0.24^63

---

To determine the easy cleavage planes of TaC, we calculated the tensile strain–stress relation along the high symmetry [001], [110] and [111] directions as shown in Fig. 2(b). The results are also listed in Table S1 (ESI†). It is found that TaC has the lowest tensile strength of 42.3 GPa at strain ε = 0.140 along the [001] direction. This indicates that the (001) plane is the easiest cleavage plane of TaC. As shown in Fig. 2(b), along the [110] and [111] directions, the peak tensile strength can reach 60.0 GPa (at ε = 0.290) and 70.5 GPa (at ε = 0.205), respectively. Next, five different inequivalent directions, (001)[110], (110)[11̄0], (11̄0)[001], (111)[11̄0] and (111)[112̄], are selected to calculate strain–stress curves under pure shear and Vickers indentation shear deformations. The calculated pure shear results indicate that the weakest shear plane is the (001) plane as shown in Fig. 2(c), with the lowest peak stress of 34.7 GPa along the (001)[110] slip direction. The peak stresses along various slip directions under pure shear deformations are displayed in Table 2. The pure shear strengths of TaC exhibit large anisotropy along different directions. The maximum shear strengths obtained for TaC are 54.7 GPa (at ε = 0.360) along the (111)[112̄] direction, 45.4 GPa (at ε = 0.370) along the (11̄0)[001] direction, and 37.5 GPa (at ε = 0.195) along the (110)[11̄0] direction. The shear strength in the (111)[11̄0] direction is very close to the (110)[11̄0] direction with a peak stress of 37.4 GPa at ε = 0.235.

Table 2 The calculated peak strains ε_max and stresses σ_max (in GPa) for TaC in various directions under pure shear and Vickers shear deformation, as well their relative difference [Δσ_max = (σ^V_max − σ^P_max)/σ^P_max]

Direction	Pure shear		Vickers shear		Δσmax
	ε max	σ max	ε max	σ max
(001)[110]	0.265	34.7	0.265	31.2	−10.1%
(110)[11̄0]	0.195	37.5	0.110	29.7	−20.8%
(11̄0)[001]	0.370	45.4	0.215	23.3	−48.7%
(111)[11̄0]	0.235	37.4	0.120	28.7	−23.2%
(111)[112̄]	0.360	54.7	0.125	30.4	−44.4%

---

We now discuss the Vickers indentation strength of TaC. The calculated strain–stress curves are shown in Fig. 2(d) and details on the calculated peak stresses and the corresponding strains along various crystallographic directions are listed in Table 2. The lowest peak stress of 23.3 GPa appears for the (11̄0)[001] direction, and is in very good agreement with our experimental result of 20.9 ± 0.5 GPa. Note that there is no strain-stiffening effect in TaC under Vickers shear deformation. The ideal indentation strength of TaC in the (11̄0)[001] direction is a significant reduction (about 49%) from the pure shear strength along the same direction and also (by about 33%) from the lowest pure shear stress. Such a significant reduction of Vickers against pure shear strength is unusual. In TaC, this is because the Vickers indenter produces a high compressive pressure normal to the loading surface, which further weakens the bonds of Ta–C in addition to the effect of the shear deformation in the Vickers hardness tests.

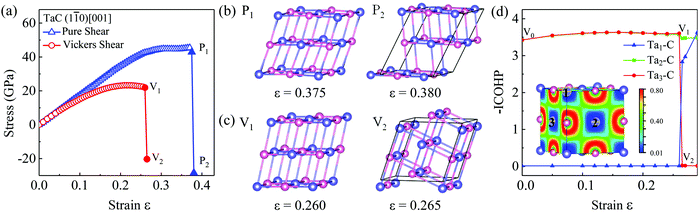
To get a deeper insight into the underlying atomistic mechanisms, it is instructive to study the structural deformations of the TaC crystal under pure shear and (Vickers) indentation shear tests. We plot the pure and Vickers strain–stress curves and structural snapshots at critical strains along the (11̄0)[001] direction in Fig. 3. As the pure shear strain reaches 0.370 corresponding to the maximum shear stress 45.4 GPa, the Ta–C bonds stretch slightly and anisotropically without breaking. In the strained crystal, each Ta (and C, vice versa) is 2+4-coordinated, with Ta–C bond lengths of 2.25–2.26 Å along the [001] axis and 2.31–2.33 Å in the [001] plane. In the relaxed structure, all Ta–C bonds are 2.237 Å (2.227 Å in experiment⁵⁶). After passing the peak stress, the stress reduces to 42.8 GPa, marked as P₁ in Fig. 3(b). With shear strain increased to 0.380, the structure becomes unstable and Ta–C bonds along [001] are broken, leading to the dislocation compared with the equilibrium structure, shown as P₂ in Fig. 3(b). There, every second layer along the [001] direction slips from their original position along the [110] direction, which results in a sharp drop of the strength from 42.8 GPa to −28.4 GPa (shown in Fig. 3(a)). Finally, the topology of the Ta–C network recovers to the cubic connectivity of the B1 structure type, but now in 4+2-coordination, with Ta–C bonds of 2.195 Å in the [001] plane and 2.37 Å along the [001] axis.

Fig. 3 (a) Calculated stress response curves of TaC under pure shear and Vickers indentation shear strains along the (11̄0)[001] direction. (b and c) Structural snapshots show TaC at key points before and after the strain-induced structural change in (11̄0)[001] direction under (b) pure shear and (c) Vickers indentation shear deformations. (d) Integrated crystal orbital Hamilton population (ICOHP) curves for Vickers shear strains along the (11̄0)[001] direction. The inset displays the electron localization function (ELF) and marks the three different Ta–C bonds in the equilibrium TaC structure.

Using the more realistic indentation shear deformation along (11̄0)[001], the Vickers shear curve of TaC shown in Fig. 3(a) implies that the Vickers shear deformations along the (11̄0)[001] direction are more sensitive to the strains than if the pure shear is considered. The peak strength of 23.3 GPa under the Vickers shear occurs at a strain of ε = 0.215, which is much lower than ε = 0.370 under pure shear. The Vickers indenter causes asymmetric changes to the Ta–C bond: in a 4+2-coordination, bonds in the [001] plane are shortened to 2.21 Å, while bonds along the [001] axis are stretched to 2.30–2.31 Å at ε = 0.260 (shown as V₁ in Fig. 3(c)). As the strain increases to 0.265, the three-dimensional network breaks and reconstructs, through sliding [010] planes of atoms along the [1̄01] direction. This suddenly releases the indentation strength from 23.3 GPa to −20.3 GPa, see the Vickers shear curve shown in Fig. 3(a). It also results in low-symmetry 2+2+2 coordination of Ta, with three distinct Ta–C bond lengths 2.211, 2.242, and 2.39–40 Å at V₂. The easier breakup of covalent bonds under Vickers shear deformation as compared to pure shear deformation is a ubiquitous trend that has been found in transition metal borides, for instance in the ReB₂,⁴⁴ CrB₄,⁴⁵ MoB₃,⁴⁶ and WB₃⁴⁶ compounds.

An analysis of the electron localization function (ELF) in TaC reveals a large ionic component to the bonding in this metallic material: quasi-spherical ELF shells around the C atoms (see Fig. 3(d)) are consistent with charge transfer from Ta to C – about 1.7 electrons per atom in equilibrium, according to a Bader analysis. Covalent bonding can not be ruled out a priori (the Pauling electronegativities of Ta and C differ only by about 1), but usual ELF signatures, a maximum between the bonded atoms, are not present here. The dominant ionic character of TaC remains largely unchanged under strain, see Fig. S5 (ESI†). Better insight into the structural reconstruction and bond evolution is provided by the Crystal Orbital Hamilton Populations (COHP) analysis. In Fig. 3(d) we show the integrated COHP (–ICOHP) of different Ta–C bonds along the Vickers strain (see Fig. S6 in the ESI† for the full COHP data). This clearly corroborates the mechanism of bond breaking and re-forming described in the previous paragraph: the strong Ta–C bonds along the cubic axes remain almost unchanged up to the critical strain V₁, beyond which bonds strongly re-organise. Beyond V₂ the new Ta–C bonds recover the same pairwise strength as in the equilibrium structure.

The mechanical strength of conventionally synthesized TaC is due to (111) slip planes along stacking faults in the crystallites.^16,17 The formation energy of stacking faults in face-centered cubic lattices can increase dramatically with pressure⁶⁴ and this, together with the small grain size, suggests that TaC synthesized through the HPHT route has a much lower defect density. In fact, if the defect density decreases sufficiently that their average separation becomes comparable to the grain size, it is possible that other failure mechanisms become more relevant, at higher strength compared to conventionally synthesised TaC. This is consistent with our observations and calculations.

4 Conclusion

In summary, using the HPHT synthesis method, high quality densified TaC has been successfully synthesized at 5.5 GPa and 1400 °C. The Vickers indentation test of the present TaC sample shows a superior mechanical strength of 20.9 ± 0.5 GPa, which is about 35% higher than previous reports. We have also performed systematic first principles calculations to examine the indentation shear strength of TaC by the newly developed strain–stress method. Our calculations predict the ideal indentation strength of TaC to be about 23.3 GPa along the (11̄0)[001] direction, a value in very good agreement with experiments. Taking into account the realistic shape of the indenter is crucial to obtain the correct strength, the associated slip direction, and the atomistic mechanism of bond breaking and re-formation. More importantly, our calculated results show that there is no strain-stiffening effect in TaC under Vickers shear deformation, instead the strength is substantially reduced (∼33%) compared to pure shear deformation, and that the strong directional Ta–C bonds are responsible for the high mechanical strength of the TaC. These findings offer insights to further understanding the microscopic mechanism of TaC with superior mechanical strength and suggest experimental avenues for synthesis and application of emerging UHTC materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 11574220, 11874043, 11304167, and U1804121). Computational resources provided in part by the UK's National Supercomputer Service through the UK Car–Parrinello consortium (EPSRC Grant No. EP/P022561/1) and by the UK Materials and Molecular Modelling Hub (No. EP/P020194) are gratefully acknowledged. W. Sun also acknowledges support of the State Scholarship Fund from the China Scholarship Council.

References

1. L. E. Toth, Transition Metal Carbides and Nitrides, Elsevier, 2014.
2. R. Riedel, A. Kienzle, W. Dressler, L. Ruwisch, J. Bill and F. Aldinger, Nature, 1996, 382, 196.
3. N. P. Padture, M. Gell and E. H. Jordan, Science, 2002, 296, 280–284.
4. A. Krajewski, L. D'Alessio and G. D. Maria, Cryst. Res. Technol., 1998, 33, 341.
5. Q. J. Hong and A. Van De Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 020104.
6. C. Peng, X. Gao, M. Wang, L. Wu, H. Tang, X. Li, Q. Zhang, Y. Ren, F. Zhang, Y. Wang, B. Zhang, B. Gao, Q. Zou, Y. Zhao, Q. Yang, D. Tian, H. Xiao, H. Gou, W. Yang, X. Bai, W. L. Mao and H. K. Mao, Appl. Phys. Lett., 2019, 114, 011905.
7. X. Zhang, G. E. Hilmas, W. G. Fahrenholtz and D. M. Deason, J. Am. Ceram. Soc., 2007, 99, 393.
8. J. X. Liu, Y. M. Kan and G. J. Zhang, J. Am. Ceram. Soc., 2010, 93, 370.
9. F. Rezaei, M. G. Kakroudi, V. Shahedifar, N. P. Vafa and M. Golrokhsari, Ceram. Int., 2017, 43, 3489.
10. A. Nino, T. Hirabara, S. Sugiyama and H. Taimatsu, Int. J. Refract. Met. Hard Mater., 2015, 52, 203.
11. S. A. Shvab and F. F. Egorov, Sov. Powder Metall. Met. Ceram., 1982, 21, 894.
12. Y. Kumashiro, Y. Nagai, H. Kato, E. Sakuma, K. Watanabe and S. Misawa, J. Mater. Sci., 1981, 16, 2930.
13. K. Balani, G. Gonzalez, A. Agarwal, R. Hickman, J. S. O'Dell and S. Seal, J. Am. Ceram. Soc., 2006, 89, 1419.
14. B. R. Kim, K. D. Woo, J. M. Doh, J. K. Yoon and I. J. Shon, Ceram. Int., 2009, 35, 3395.
15. S. R. Bakshi, V. Musaramthota, D. Lahiri, V. Singh, S. Seal and A. Agarwal, Mater. Sci. Eng., A, 2011, 528, 1287.
16. D. J. Rowcliffe and G. E. Hollox, J. Mater. Sci., 1971, 6, 1261.
17. N. D. Leon, X. Yu, H. Yu, C. R. Weinberger and G. B. Thompson, Phys. Rev. Lett., 2015, 114, 165502.
18. L. Liu, G. Geng, Y. Jiang, Y. Wang, W. Hai, W. Sun, Y. Chen and L. Wu, Ceram. Int., 2017, 43, 5136.
19. L. Silvestroni, A. Bellosi, C. Melandri, D. Sciti, J. Liu and G. Zhang, J. Eur. Ceram. Soc., 2011, 31, 619.
20. J. P. Kelly and O. A. Graeve, Acta Mater., 2015, 84, 472.
21. E. Khaleghi, Y.-S. Lin, M. A. Meyers and E. A. Olevsky, Scr. Mater., 2010, 63, 577.
22. O. Cedillos-Barraza, S. Grasso, N. A. Nasiri, D. D. Jayaseelan, M. J. Reece and W. E. Lee, J. Eur. Ceram. Soc., 2016, 36, 1539.
23. H. Chen, H. Liang, L. Liu, H. Li, K. Liu and F. Peng, Results Phys., 2017, 7, 3859.
24. D. Roundy, C. R. Krenn, M. L. Cohen and J. W. Morris, Phys. Rev. Lett., 1999, 82, 2713.
25. R. H. Telling, C. J. Pickard, M. C. Payne and J. E. Field, Phys. Rev. Lett., 2000, 84, 5160.
26. Y. Zhang, H. Sun and C. Chen, Phys. Rev. Lett., 2004, 93, 195504.
27. Z. Pan, H. Sun and C. Chen, Phys. Rev. Lett., 2007, 98, 135505.
28. Z. Pan, H. Sun, Y. Zhang and C. Chen, Phys. Rev. Lett., 2009, 102, 055503.
29. Y. Tian, B. Xu, D. Yu, Y. Ma, Y. Wang, Y. Jiang, W. Hu, C. Tang, Y. Gao, K. Luo, Z. Zhao, L. M. Wang, B. Wen, J. He and Z. Liu, Nature, 2013, 493, 385.
30. Q. Huang, D. Yu, B. Xu, W. Hu, Y. Ma, Y. Wang, Z. Zhao, B. Wen, J. He, Z. Liu and Y. Tian, Nature, 2014, 510, 250.
31. B. Li, H. Sun and C. Chen, Nat. Commun., 2014, 5, 4965.
32. B. Li, H. Sun and C. Chen, Phys. Rev. Lett., 2016, 117, 116103.
33. C. Lu, Q. Li, Y. Ma and C. Chen, Phys. Rev. Lett., 2017, 119, 115503.
34. B. Li, H. Sun and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 014106.
35. C. Zang, H. Sun and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 180101.
36. V. L. Solozhenko, O. O. Kurakevych and Y. L. Godec, Adv. Mater., 2012, 24, 1540.
37. T. Irifune, K. Kawakami, T. Arimoto, H. Ohfuji, T. Kunimoto and T. Shinmei, Nat. Commun., 2016, 7, 13753.
38. Z. Zhang, H. Liang, H. Chen, J. Wang, F. Peng and C. Lu, Inorg. Chem., 2020, 59, 1848.
39. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063.
40. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
41. B. Gao, P. Gao, S. Lu, J. Lv, Y. Wang and Y. Ma, Sci. Bull., 2019, 64, 301.
42. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
43. J. Yang, H. Sun and C. Chen, J. Am. Chem. Soc., 2008, 130, 7200.
44. C. Zang, H. Sun, J. S. Tse and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 014108.
45. Q. Li, D. Zhou, W. Zheng, Y. Ma and C. Chen, Phys. Rev. Lett., 2015, 115, 185502.
46. B. Li, H. Sun, C. Zang and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 174106.
47. F. Gao, J. He, E. Wu, S. Liu, D. Yu, D. Li, S. Zhang and Y. Tian, Phys. Rev. Lett., 2003, 91, 015502.
48. A. Šimunek and J. Vacká, Phys. Rev. Lett., 2006, 96, 085501.
49. A. Šimunek, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 172108.
50. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397.
51. R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9.
52. T. Hughbanks and R. Hoffmann, J. Am. Chem. Soc., 1983, 105, 3528.
53. R. Dronskowski and P. E. Blochl, J. Phys. Chem., 1993, 97, 8617.
54. V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461.
55. S. Maintz, V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030.
56. K. Nakamura and M. Yashima, Mater. Sci. Eng., B, 2008, 148, 69.
57. L. López-de-la Torre, B. Winkler, J. Schreuer, K. Knorr and M. Avalos-Borja, Solid State Commun., 2005, 13, 245.
58. W. Weber, Phys. Rev. B: Solid State, 1973, 8, 5082.
59. C. K. Jun and P. T. B. Shaffer, J. Less-Common Met., 1971, 23, 367.
60. S. P. Dodd, M. Cankurtaran and B. James, J. Mater. Sci., 2003, 38, 1107.
61. R. W. Bartlett and C. W. Smith, J. Appl. Phys., 1967, 38, 5428.
62. X. Jiang, J. Zhao and X. Jiang, Comput. Mater. Sci., 2011, 50, 2287.
63. J. E. Sundgren and H. T. G. Hentzell, J. Vac. Sci. Technol., A, 1986, 4, 2259.
64. E. Kim, M. Nicol, H. Cynn and C. S. Yoo, Phys. Rev. Lett., 2006, 96, 035504.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional computational details and calculated electronic density of states, electron localization function and phonon dispersion curve for TaC at equilibrium structure, COHP analysis of the structural reconstruction and bond evolution under different Vickers shear strain along the (11̄0)[001] direction. See DOI: 10.1039/c9cp06819h

‡ Weiguo Sun and Xiaoyu Kuang contributed equally to this work.

---