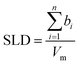Revealing the interfacial nanostructure of a deep eutectic solvent at a solid electrode

Abstract

Deep eutectic solvents (DESs) are both green and sustainable, making them an increasingly attractive alternative to conventional solvents. One of their applications is the electrochemical deposition of metals that cannot be deposited from aqueous solution because of the limited electrochemical window of water. The electrodeposition process is influenced by the structure and dynamics of the solvent at the solid–liquid interface. Therefore,the nanoscale structure of the interface between a silicon substrate and deep eutectic solvent (choline chloride–ethylene glycol) was studied by neutron reflectometry (NR) and molecular dynamics (MD) simulations. It is not possible to model NR measurements of this system without simulating a dense DES layer at the solid–liquid interface. This study used an MD simulation trajectory to extract the density, thickness, and roughness of this DES layer. With this input, the model reproduces the reflectometry data at all measured H/D contrasts very well. The thickness of the layer does not change appreciably when applying charge or at higher temperatures. Further analysis revealed a reorganization of ions and reorientation of the choline cations in the interface layer when the electrodes are charged. These changes in ion orientation are not observed with the NR technique since they do not influence the neutron scattering length density profile due to the high number of ethylene glycol molecules at the interface. However, the agreement between measured neutron reflectometry data and model parameters obtained from MD simulations justified subnanoscale analysis of the MD trajectory and confirmed that these two complementary techniques can be successfully combined to reveal the solid/DES interface structure.

---

Introduction

Finding the ideal solvent for a specific industrial application is a constant quest for the optimal trade-off between performance, price, and environmental impact. The electrochemical deposition of metals and alloys is only one among many technologies where performance is directly influenced by solvent properties. The narrow electrochemical window of aqueous solutions (1.23 V) and safety issues related to volatile and flammable organic solvents directed research towards finding new classes of solvents that can overcome present limitations.¹ Low melting point salts composed entirely of ions that, as a result, were generically named ionic liquids (ILs) emerged as a new class of solvents with desirable properties. In particular, the electrochemical and thermal stability as well as the low vapor pressure² of these salts make them very attractive for practical applications.^3–7 However, ILs are often toxic and their synthesis is generally expensive. An alternative to ILs can be found in deep eutectic solvents (DESs), which are obtained by mixing a hydrogen bond donor with a hydrogen bond acceptor. These can form an eutectic mixture, i.e., a system undergoing a single solid–liquid transition like a pure compound when heated. In these systems, the eutectic melting point is depressed by up to 200 °C with respect to the individual components; this enables practical use of DESs as solvents at – or even below – room temperature.⁸ During the last decade, numerous review articles covered the field of DESs,^2,8–13 including the recent review by Clarke et al.¹⁴ that placed ILs and DESs within a wider perspective of green and sustainable solvents.

The focus of this work is to better understand the interfacial properties in DES-based systems used for the electrodeposition of metals. In particular, we are focusing on systems used for the electrodeposition of zinc (Zn). In a previous work by Starykevich et al.¹⁵ it was observed that the potentiostatic (DC) deposition of Zn on an alumina layer from an ethaline/ZnCl₂ solution is kinetically hindered. It was hypothesized that the constituents of ethaline, choline cations, and ethylene glycol molecules adsorb on the alumina surface because of the interactions of the hydroxyl groups of these species with the oxygen-rich alumina surface. The hypothesized existence of this effectively passivating layer was supported by the observation that raising the deposition temperature or superimposing a rapidly alternating potential to the potentiostatic voltage made Zn deposition possible. Both increased temperature and oscillating potential were thought to be able to disrupt the interfacial solvent layer and provide the Zn ions with access to the surface. Indeed, adsorption of the ethaline components on different electrode materials has been proposed and investigated by several research groups. A compact layer on a glassy carbon (GC) electrode surface was proposed by Vieira et al.,¹⁶ investigating a ZnCl₂ containing DES using polarization modulation reflection–absorption spectroscopy. Blocking of the active sites on the GC electrode by adsorbed species was also proposed by Whitehead et al.,¹⁷ based on electrochemical measurements as well as by Pereira et al.¹⁸ for a steel electrode.

In this work, we will address the very question of the liquid structure at the interface in order to understand the processes taking place during electrodeposition. Our approach is based on the complementary use of neutron reflectometry (NR) as a structural measurement technique with molecular dynamics (MD) simulations. In this two-fold approach, the simulations of the interface help to remove the ambiguity of the NR data while the simulations themselves are validated by checking the consistency of the structural profile with observed NR data.

NR is a powerful technique for probing structures along the direction perpendicular to a planar interface, i.e., for investigating composition and scattering length density profiles across interfaces. In contrast to local probes such as surface microscopy, the use of a beam to illuminate a macroscopic surface ensures that the neutron scattering method provides a statistically relevant signal that is immune to local defects. Reflectometry measurements revealing atomic ordering at surfaces can also be performed using X-rays as a probe, but using neutrons offers significant advantages. In contrast to X-rays, neutrons interact in a non-destructive fashion with the material under examination. This makes it easy to follow processes in situ over a longer period. Moreover, due to their weak interaction with matter, neutrons have a large penetration depth for most materials. Finally, the large neutron scattering length difference between hydrogen and deuterium makes the NR technique perfectly suited for the study of hydrogen-rich systems.

This is particularly exploited in soft condensed matter studies involving organic and biological samples. Using selective deuteration of a given component makes it possible to specifically adjust the scattering contrast with respect to the non-deuterated environment. It is thus possible to accurately locate each interfacial component while keeping the chemical structure at the interface essentially intact. In the work of Cooper et al.¹⁹ neutron reflectometry gave insight into the structure and composition of an IL layer formed at the oil–silica interface. They observed an 8–11 Å thick layer that remains in place even at temperatures up to 80 °C. Using the same technique, the structure of a pyrrolidinium-based ionic liquid was also investigated at a charged gold interface.²⁰ These results indicate non-electrostatic adsorption of the cation onto the gold electrode. X-ray reflectometry (XRR) studies of different ionic liquid–solid interfaces were performed by several research groups²¹ confirming the layering of ions on sapphire,^22,23 gold,²⁴ and silicon²⁵ surfaces. However, as stated in Hammond et al.,²⁶ based on their investigation, it appears that conclusions obtained for ionic liquid systems will not necessarily be valid for DESs. Their atomic force microscopy study of a DES/platinum interface reveals that adding water to a DES has an unexpected effect on the interface, actually increasing the interfacial nanostructure by up to 40%. Therefore, more experimental, computational, and theoretical work is still needed in order to understand the interfacial properties of DESs on different solid materials.

Molecular dynamics (MD) simulations are a widely used computational technique that can give valuable information about the composition, structure, and dynamics of the layers formed at liquid–solid interfaces. Even though bulk DESs are often studied by MD simulations, literature on the DES–electrode interface is scarce. Atilhan et al.²⁷ studied interfacial properties for different DES nanodroplets on graphene, utilizing density functional theory and classical MD. A combined X-ray reflectometry and MD simulations approach was used by Steinrück et al.²⁸ to investigate electrolyte ordering near solid surfaces relevant to Li-ion batteries.

The main aim of this work is to reveal the structure of the layer formed at the interface between a DES and an electrode with and without applied constant electric potential using neutron reflectometry and MD simulations. As such, we have chosen to concentrate on a system where the electrode surface is well characterized and does not introduce additional complexity. Due to the availability of large single crystals whose surface can be polished, silicon was chosen as an electrode. Further development of this work will focus on other electrode materials with a more direct link to industrial applications.

Materials and methods

Sample cell

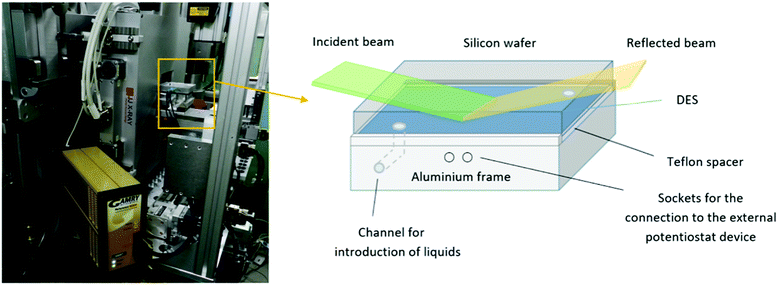
A two-electrode electrochemical cell, shown schematically in Fig. 1, was used to carry out NR measurements. One electrode was a polished single-crystal Si block n-doped (Phosphorous, specific resistivity 20 Ω cm, r.m.s. roughness ≤5 Å, dimensions: 8.0 × 5.0 × 1.5 cm³, [100] oriented) obtained from Andrea Holm GmbH (Tann, Germany). As a counter and reference electrode, a custom made Al block was used and separated from the Si block by a Teflon spacer. The liquid phase was introduced through channels in the Al block. This two-electrode system was then sandwiched between two aluminium plates able to seal the whole system from the outside. Teflon slabs were used to separate the electrodes from the external plates. The Al electrode was connected directly to the external potentiostat (Gamry Reference 600+ Potentiostat/Galvanostat with a Gamry framework system), while the Si electrode was contacted by interfacing it with a copper sheet.

Fig. 1 Sample cell mounted at the REFSANS instrument (Heinz Maier-Leibnitz Zentrum, Germany) sample holder and connected to the GAMRY potentiostat (left); scheme of the electrochemical cell constructed for the electrochemical measurements (right).

Neutron reflectometry

In an NR experiment, the specular reflectivity R is measured as a function of the momentum transfer Q_z along the z-direction perpendicular to the interface. In the Born approximation, the reflectivity is the Fourier transform of the scattering length density (SLD) profile ρ(z) which directly reveals the local composition. Such experiments thus deliver highly resolved structural information about the interfaces.

Neutron reflectometry measurements were carried out at REFSANS, the horizontal time-of-flight reflectometer operated by the Helmholtz-Zentrum Geesthacht at the Heinz Maier-Leibnitz Zentrum in Garching, Germany.²⁹ A polychromatic pulsed beam with wavelengths ranging between 3 Å and 21 Å and a wavelength resolution Δλ/λ ≈ 3% was used. A 10 m collimation system was used to define the vertical divergence of the beam. The neutron beam hit the sample from the silicon side as shown in Fig. 1. The neutron incident angles were adjusted by tilting the goniometer head on which the sample was mounted. A two-dimensional 256 × 256 pixel-based array ³He detector registered the neutrons scattered from the samples at a sample-to-detector distance of 10.38 m. Two different incident angles, namely θ₁ = 0.50° and θ₂ = 2.50°, allowed collecting data in the interval 0.005 Å⁻¹ ≤ Q_z ≤ 0.14 Å⁻¹.

Beam size and measurement times were set according to the incident angle, to maximize the incident flux and increase the data statistics. Measurements of the direct beam were also performed: using the settings of the small angle, a direct beam was measured directly on the detector, whereas for the high incident angle a calibrated neutron monitor was used. Raw data were reduced and the experimental reflectivity R was obtained as a ratio of the reflected to the incident beam. The thickness of the SiO₂ layer covering the wafer was determined by NR measurements of this waver vs. H₂O and D₂O and a simultaneous fit of both datasets to 1.0 nm. In all sample measurements, three different contrast mixtures of ethylene glycol (anhydrous, 99.8%) and choline chloride (≥99%) were used: deuterated ethylene glycol (98% atom D):hydrogenated choline chloride (D-EG:H-Cho, SLD = 3.58 × 10⁻⁶ Å⁻²), hydrogenated ethylene glycol:deuterated choline chloride (98% atom D) (H-EG:D-CHO SLD = 2.68 × 10⁻⁶ Å⁻²) and both hydrogenated compounds (H-EG:H-CHO, SLD = 0.28 × 10⁻⁶ Å⁻²). All chemicals were purchased from Sigma-Aldrich. For the application of the electric voltage, the two electrodes were connected to the Gamry Potentiostat: all potentials reported in this paper are measured vs. the aluminum electrode. All electrochemical experiments were performed at room temperature.

Molecular dynamics simulations

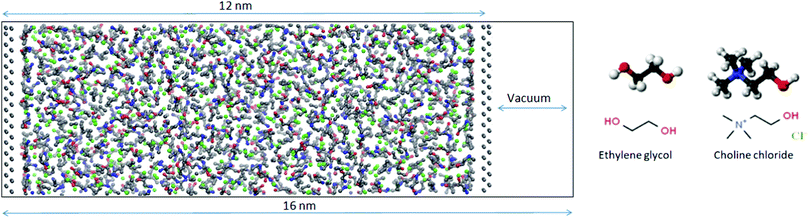
MD simulations were carried out on a bulk DES system as well as on a mixture enclosed between two flat silicon walls using GROMACS 2018.1.³⁰ Initial configurations were generated using Packmol.³¹ In order to establish the density of the liquid, NPT simulations were run with 512 choline chloride ion pairs and 1024 ethylene glycol molecules. The pressure was set to 1 atm using a Parrinello–Rahman barostat with a coupling constant of 0.5 ps while the temperature was kept at 300 K using the Nosé–Hoover method with a coupling constant of 0.1 ps. The bulk simulations were run for 10 ns with a time step of 1 fs. The density averaged over the last 5 ns of the simulation was found to be within 1% of the experimentally measured value of 1.11584 g cm⁻³ (Rudolph Research Analytical DDM 2911 densimeter). The equations of motion were integrated using the Verlet leap-frog algorithm with a time-step of 1 fs. The long-range electrostatic interactions after a cut-off distance at 1.4 nm were accounted for by the Particle-Mesh-Ewald (PME) algorithm.³² The 12-6 Lennard-Jones interactions were treated by the conventional shifted force technique with a switch region between 1.2 and 1.3 nm. Cross interactions between different atom types were derived using the standard Lorentz–Berthelot combination rules.³³

All-atom force field parameters (refined and improved OPLS parameters) for DES were taken from the work of Ferreira et al.³⁴ while Lennard-Jones parameters for Si (σ = 0.3385 nm, ε = 2.4471 kJ mol⁻¹) were taken from the standard OPLS force field.^35,36 Knowing the bulk densities obtained from the NPT simulations, a new simulation box with fixed dimensions was constructed and confined by two silicon electrode sheets prepared with the help of VMD.³⁷ Periodic boundary conditions (PBC) were applied in all dimensions and in order to neutralize any image charge effects, the box was expanded to 16 nm in one direction by introducing a region of vacuum beyond the silicon sheets (Fig. 2). In order to improve statistics twelve replicas of this system were simulated. Each of the replicas had the same initial configuration obtained using Packmol but the atoms were assigned different random velocities at the start of the equilibration. The first step of the simulation was an annealing process from 800–300 K for 5 ns in a stepwise fashion. After that 20 ns of NVT simulation were performed with 1 fs time steps. In the first set of simulations, the silicon electrodes were uncharged. In the second set to each silicon atom a constant charge was assigned to give wall charge of 1 e nm⁻². Even though the fixed-charge method has some shortcomings including deviations in relaxation dynamics, it has been used successfully for structural studies of IL/electrode interfaces.^38,39 The trajectories were analyzed using TRAVIS-1.14.0 and results averaged for all 12 replicas.⁴⁰

Fig. 2 Snapshot of the DES mixture enclosed between two flat silicon walls with a vacuum layer added to neutralize any image charge effects. The chemical structures of DES components are shown on the right.

Results and discussion

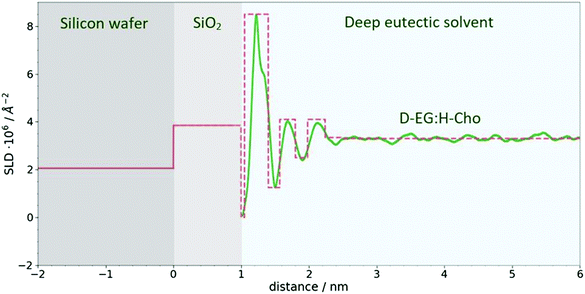
Neutron reflectometry data for the investigated system were analyzed by means of the Parratt algorithm⁴¹ describing the SLD distribution, along the z-direction, in terms of a stack of distinct layers. A set of parameters, namely the thickness (d), scattering length density (ρ) and interfacial roughness (σ) of the different layers is usually sought by minimizing the sum of the squares of the differences between the experimental and the calculated reflectivity. Because of the loss of the neutron phase information during their detection, totally different sets of parameters can lead to the same reflectivity pattern. To partially solve this ambiguity, measurements with different contrasts are usually performed. For the present research, three different contrasts were used in the experimental investigations of the system: in one experiment both the components were fully hydrogenated H-EG:H-Cho, whereas in two other experiments one of the two substances was, in turn, used in a fully deuterated form D-EG:H-Cho and H-EG:D-Cho.

In the application of the algorithm, the Si substrate (SLD = 2.07 × 10⁻⁶ Å⁻²) was modeled as an infinitely thick planar surface. This surface is always covered with a thin layer of silicon oxide (SiO₂) whose actual morphology depends on the preparation method.⁴² The thickness and roughness of this layer were determined through separated NR measurements performed against water/heavy water mixtures. The SiO₂ layer (SLD = 3.85 × 10⁻⁶ Å⁻²) was found to be 10 ± 2 Å thick, with a roughness of 4 ± 1 Å. The thickness and roughness of the SiO₂ layer obtained from H₂O/D₂O measurements were fixed for the models of the sample reflectivity measurements.

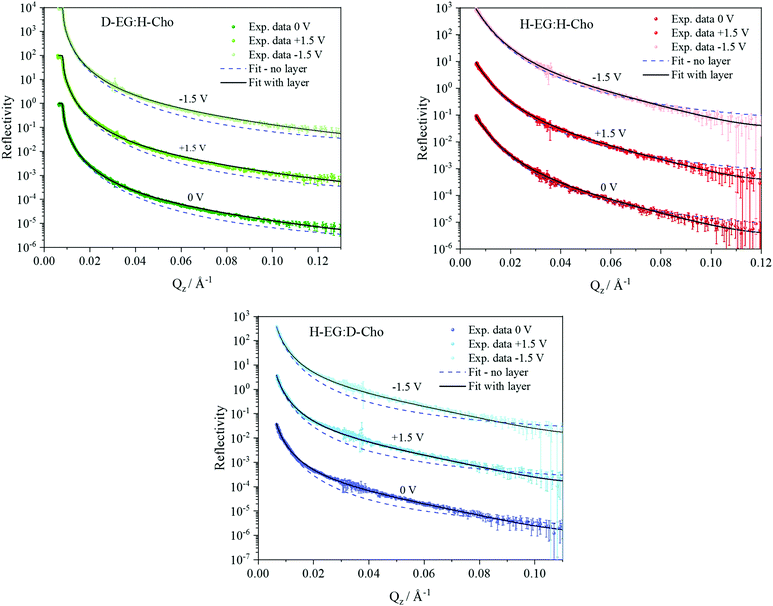
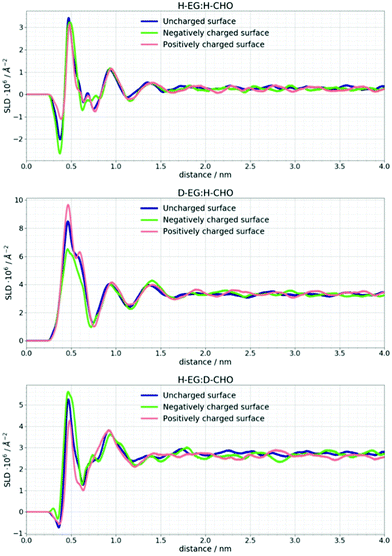
NR data versus Q_z for the 1 : 2 ChoCl/EG mixtures for different contrasts at the Si wafer are presented in Fig. 3. It can be seen that all curves are smooth, without fringes. The critical edge can only be seen for the D-EG:H-Cho contrast. Applied voltage has no influence on the reflectivity. As a first step, the Si/SiO₂/DES model was used for modeling the measured reflectivity, assuming that there is no structured DES layer at the interface. Dashed lines in Fig. 3 clearly show that the values of the reflectivity as simulated for a uniform DES density lie well below the experimental values. In order to introduce a DES layer in the model, one requires its SLD, thickness, and roughness. These values can be obtained through analysis of the MD simulation trajectory. The number distribution of each atom in the mixture is extracted from the MD trajectory as function of its distance from the electrode. After binning this distribution in small distance steps, the number density was converted into the scattering length density SLD by

where b_i is the coherent scattering length of the i-th atom of n atoms in a molecule with molecular volume V_m. This discretized SLD profile can then be used in a conventional reflectivity calculation algorithm to obtain the reflectivity curves corresponding to the simulations. Fig. 4 shows the SLD profiles of different DES contrasts at neutral, positively charged and negatively charged Si surfaces. One can observe three distinctive peaks in these SLD profiles which are not appreciably influenced by increasing temperature or charging the surface. These oscillations in SLD near the interface are progressively damped out until the bulk values are recovered after approximately 1.5–2 nm. The experimental NR data can be modeled very well using a crude model involving such dense interfacial layers as illustrated in Fig. 5. This model, obtained from MD simulations, reproduces all the data at all contrasts simultaneously very well. Slight differences in SLD profiles between uncharged and charged surfaces do not affect the calculated reflectivity curves. This explains why no change in reflectivity is observed in experiments with applied potential. Trying to reproduce additional details of the SLD profile, such as the oscillations observed in the MD simulations, does affect the reflectivity oscillations at high Q, however well beyond values accessible to a neutron reflectometry experiment.

Fig. 3 Neutron reflectivity R for different H/D contrasts as a function of momentum transfer Q_z for the Si/SiO₂/DES interface with and without applied potential. Reflectivity curves for +1.5 V and −1.5 V are scaled for clarity by factors 10² and 10⁴ respectively. Dashed lines represent reflectivity calculated for a Si/DES model without a DES layer at the interface.

Fig. 4 Neutron scattering length density profiles for different H/D contrasts of DES compounds at uncharged and charged Si surfaces calculated from the MD simulation trajectory. These values are an average of 12 MD simulation replicas.

Fig. 5 SLD profile for Si/SiO₂/DES. The green line represents SLD calculated from MD simulations for D-EG:H-Cho contrast, while the dashed red line represents crude model used to model reflectivity data. The same procedure was used for other contrasts.

The difference in SLD values between DES layers and the bulk could originate from changes in composition and/or density. In Fig. 3 it can be seen that an applied voltage does not induce any change in the reflectivity patterns, i.e. there is no apparent change in SLDs. Based on the previous discussion, this means that DES layers are present at the interface even without applied voltage. Further analysis of the MD trajectory can give more information about the structure of this layer and how the applied charge and increased temperature influence this layer.

In Fig. 6 the number density distribution is shown for each component of the DES calculated for its center of mass. It can be seen that the Stern layer⁴³ at a neutral silicon surface primarily consists of ethylene glycol molecules and Cho⁺ cations with alcohol groups located closer to the electrode. Excess positive charge in the Stern layer favors an anionic chloride enriched layer followed by an EG–Cho rich layer and another EG rich layer before the bulk structure is recovered. As mentioned in the experimental section the charges on Si atoms are set to obtain a charge density of 1 e nm⁻² which would correspond to the order of magnitude of the experimental voltage. As expected at charged surfaces, a reorganization of choline and chloride ions occurs. However, this cation–anion reorganization will not noticeably change the SLD profile of the DES since a high number of EG molecules is still present at the interface.

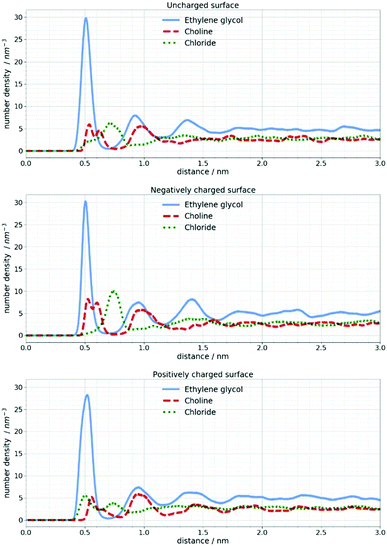Fig. 6 Number density distribution of DES components at uncharged and charged silicon surfaces calculated for their center of mass.

In the work of Cooper et al.¹⁹ a NR study of ionic liquids confirmed the existence of the interfacial IL layer even at 80 °C. In the present work, MD simulations were performed at 25 °C and 100 °C in order to see if this would be the case with the investigated Si/DES system. No noticeable changes could be observed when the simulations were performed at 100 °C. Since the negative potential is of particular interest for the electrochemical deposition of metals, Fig. 7 shows how the orientation of choline and EG molecules is changed by introducing a negative charge of the silicon surface.

Fig. 7 MD simulation snapshot of the first 5 nm from the uncharged and negatively charged silicon surface. (a) N–C–C–O atoms of choline, (b) C–C of ethylene glycol. Other atoms are excluded from the figure for clarity.

It is apparent that two peaks in the number density profile of choline center of mass correspond to two spatial orientations of choline cations. A part of choline cations lays on the electrode while the other fraction orients perpendicular to the electrode. When the Si surface is uncharged choline cations are layered with the alcohol groups closer to the surface.

A negative charge of the electrode will induce reorientation of the choline cation perpendicular to the surface so that the positively charged part of the cation stays closer to the surface. This is in agreement with the work of Hammond et al.²⁶ where the authors proposed that application of −0.25 V promotes the orientation of Cho charged groups towards the Pt electrode and alcohol groups towards the bulk liquid. It can also be observed that neither positive nor negative potential have a noteworthy influence on EG molecules. In all cases, three distinctive peaks in the number density profiles appear around 0.5, 0.9 and 1.4 nm. It should be emphasized that these changes in molecule orientations cannot be confirmed with the NR technique since the change in the SLD is not large enough to influence the reflectivity curves.

According to the work of Starykevich et al.¹⁵ elevated temperature (up to 100 °C) allows electrodeposition of Zn from ethaline DES on an alumina surface, through disruption of the DES layer at the interface. Since the results of this work indicate the existence of the DES layer at the interface with and without applied potential even at 100 °C and no considerable change in its structure, other effects should also be taken into account. For example, higher temperature leads to a viscosity reduction and increased conductivity as well as increased void volume of the DES.^44,45 Therefore further experimental and computational investigations are needed to fully understand the phenomena observed in these electrochemical experiments.¹⁵ This work shows that NR measurements and MD simulations can be used as complementary techniques to reveal the nanostructure of solid/liquid interface.

Conclusions

The study of the structure and dynamics of deep eutectic solvents on solid materials is of great importance for understanding electrochemical processes occurring at the interface and further development of DES-based solutions for electrochemical deposition of metals. This work shows that neutron reflectometry measurements and molecular dynamics simulations are two complementary methods allowing for nanoscale understanding of solid–liquid interface phenomena. The MD simulations hint at a localized increase of the DES density in the vicinity of the substrate surface. The experimental reflectivity data can be very well modeled using a crude model involving such a dense interfacial layer. In contrast, the values of the reflectivity as simulated for a uniform DES density lie well below the experimental values. Additional details of the SLD profile, observed in the MD simulations, affect the reflectivity oscillations at high Q values, which are not accessible to a neutron reflectometry experiment. This work brings two main conclusions, the first one is relative to the methodology used in our work: it has been demonstrated that joined use of NR and MD is an approach, which provides new insights in the structure of solid/DES interfaces. The cross-validation of the partial results makes it possible to draw conclusions which would have otherwise been weakly founded since NR data are sometimes ambiguous. In the same way, MD simulation results should be considered with caution since they might be showing a transient configuration actually bound to disappear at large timescales. Once these observations are brought together though, one can confidently draw our second conclusion, which is relative to the investigated system itself: DES do indeed present a layered structure at the interface to a silicon oxide covered substrate. SLD peaks observed in the surface vicinity are linked to local density variations of the otherwise chemically homogeneous liquid. In other words, the layering observed here does not correspond to a phase separation. Future work will focus on solid materials with higher relevance for industrial applications, like copper and aluminium as well as new, designed solvents based on ionic liquids and deep eutectics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is based upon experiments performed at the REFSANS instrument operated by Helmholtz-Zentrum Geesthacht at the Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany. We thank S. Gadžurić and M. Vraneš for providing the densimeter and L. C. Pardo for discussions.

Notes and references

1. Y. Wang and W.-H. Zhong, ChemElectroChem, 2015, 2, 22–36,  DOI:10.1002/celc.201402277.
2. E. L. Smith, A. P. Abbott and K. S. Ryder, Chem. Rev., 2014, 114, 11060–11082,  DOI:10.1021/cr300162p.
3. M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190–7239,  DOI:10.1021/acs.chemrev.6b00504.
4. K. S. Egorova, E. G. Gordeev and V. P. Ananikov, Chem. Rev., 2017, 117, 7132–7189,  DOI:10.1021/acs.chemrev.6b00562.
5. D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis Jr., M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7, 232–250,  10.1039/c3ee42099j.
6. N. V. Plechkova and K. R. Seddon, Applications of ionic liquids in the chemical industry, Chem. Soc. Rev., 2008, 37, 123–150,  10.1039/b006677j.
7. M. Galinski, A. Lewandowski and I. Stepniak, Electrochim. Acta, 2006, 51, 5567–5580,  DOI:10.1016/j.electacta.2006.03.016.
8. Q. Zhang, K. De Oliveira Vigier, S. Royer and F. Jérôme, Chem. Soc. Rev., 2012, 41, 7108–7146,  10.1039/c2cs35178a.
9. B. Tang and K. H. Row, Monatsh. Chem., 2013, 144, 1427–1454,  DOI:10.1007/s00706-013-1050-3.
10. D. V. Wagle, H. Zhao and G. A. Baker, Acc. Chem. Res., 2014, 47, 2299–2308,  DOI:10.1021/ar5000488.
11. A. Paiva, R. Craveiro, I. Aroso, M. Martins, R. L. Reis and A. R. C. Duarte, ACS Sustainable Chem. Eng., 2014, 2, 1063–1071,  DOI:10.1021/sc500096j.
12. A. Shishov, A. Bulatov, M. Locatelli, S. Carradori and V. Andruch, Microchem. J., 2017, 135, 33–38,  DOI:10.1016/j.microc.2017.07.015.
13. B. Kudłal, K. Owczarek and J. Namieśnik, Environ. Sci. Pollut. Res., 2015, 22, 11975–11992,  DOI:10.1007/s11356-015-4794-y.
14. C. J. Clarke, W.-C. Tu, O. Levers, A. Bröhl and J. P. Hallett, Chem. Rev., 2018, 118, 747–800,  DOI:10.1021/acs.chemrev.7b00571.
15. M. Starykevich, A. N. Salak, D. K. Ivanou, A. D. Lisenkov, M. L. Zheludkevich and M. G. S. Ferreira, Electrochim. Acta, 2015, 170, 284–291,  DOI:10.1016/j.electacta.2015.04.150.
16. L. Vieira, R. Schennach and B. Gollas, Electrochim. Acta, 2016, 197, 344–352,  DOI:10.1016/j.electacta.2015.11.030.
17. A. H. Whitehead, M. Pölzler and B. Gollas, J. Electrochem. Soc., 2010, 157, D328–D334,  DOI:10.1149/1.3364930.
18. N. M. Pereira, P. M. V. Fernandes, C. M. Pereira and A. Fernando-Silva, J. Electrochem. Soc., 2012, 159, D501–D506,  DOI:10.1149/2.004209jes.
19. P. K. Cooper, H. Li, N. R. Yepuri, A. Nelson, G. B. Webber, A. P. Le Brun, T. A. Darwish, G. G. Warr and R. Atkin, J. Phys. Chem. C, 2018, 122, 24077–24084,  DOI:10.1021/acs.jpcc.8b05952.
20. Y. Lauw, M. D. Horne, T. Rodopoulos, V. Lockett, B. Akgun, W. A. Hamilton and A. R. J. Nelson, Langmuir, 2012, 28, 7374–7381,  DOI:10.1021/la3005757.
21. P. Fenter and S. S. Lee, MRS Bull., 2014, 39, 1056–1061,  DOI:10.1557/mrs.2014.252.
22. M. Mezger, H. Schröder, H. Reichert, S. Schramm, J. S. Okasinski, S. Schöder, V. Honkimäki, M. Deutsch, B. Ocko, J. Ralston, M. Rohwerder, M. Stratmann and H. Dosch, Science, 2008, 332, 424–428,  DOI:10.1126/science.1164502.
23. M. Mezger, S. Schramm, H. Schröder, H. Reichert, M. Deutsch, E. J. De Souza, J. Okasinski, B. M. Ocko, V. Honkimäki and H. Dosch, J. Chem. Phys., 2009, 131, 094701,  DOI:10.1063/1.3212613.
24. R. Yamamoto, H. Morisaki, O. Sakata, H. Shimotani, H. Yuan, Y. Iwasa, T. Kimura and Y. Wakabayashi, Appl. Phys. Lett., 2012, 101, 053122,  DOI:10.1021/la3005757.
25. A. J. Carmichael., C. Hardacre, J. Holbrey, M. Nieuwenhuyzen and K. R. Seddon, Mol. Phys., 2001, 99, 795–800,  DOI:10.1080/00268970010012301.
26. O. S. Hammond, H. Li, C. Westermann, A. Y. M. Al-Murshedi, F. Endres, A. P. Abbott, G. G. Warr, K. J. Edler and R. Atkin, Nanoscale Horiz., 2019, 4, 158–168,  10.1039/c8nh00272j.
27. M. Atilhan, L. T. Costa and S. Aparicio, Langmuir, 2017, 33, 5154–5156,  DOI:10.1021/acs.langmuir.7b00767.
28. H.-G. Steinrück, C. Cao, Y. Tsao, C. J. Takacs, O. Konovalov, J. Vatamanu, O. Borodin and M. F. Toney, Energy Environ. Sci., 2018, 11, 594–602,  10.1039/C7EE02724A.
29. J.-F. Moulin and M. Haese, Journal of Large-scale Research Facilities, 2015, 1, A9,  DOI:10.17815/jlsrf-1-31.
30. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447,  DOI:10.1021/ct700301q.
31. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164,  DOI:10.1002/jcc.21224.
32. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092,  DOI:10.1063/1.464397.
33. H. A. Lorentz, Ann. Phys., 1881, 248, 127–136,  DOI:10.1002/andp.18812480110.
34. E. S. C. Ferreira, I. V. Voroshylova, C. M. Pereira and M. N. D. S. Cordeiro, J. Phys. Chem. B, 2016, 120, 10124–10137,  DOI:10.1021/acs.jpcb.6b07233.
35. W. L. Jorgensen, J. Phys. Chem., 1986, 90, 1276–1284,  DOI:10.1021/j100398a015.
36. W. L. Jorgensen, D. S. Maxwell and J. T. Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236,  DOI:10.1021/ja9621760.
37. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38,  DOI:10.1016/0263-7855(96)00018-5.
38. S. Begić, E. Jonsson, F. Chen and M. Forsyth, Phys. Chem. Chem. Phys., 2017, 19, 30010–30020,  10.1039/c7cp03389c.
39. T. Mendez-Morales, J. Carrete, M. Perez-Rodriguez, O. Cabeza, L. J. Gallego, R. M. Lynden-Bell and L. M. Varela, Phys. Chem. Chem. Phys., 2014, 16, 13271–13278,  10.1039/c4cp00918e.
40. M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023,  DOI:10.1021/ci200217w.
41. L. G. Parratt, Phys. Rev., 1954, 95, 359–369,  DOI:10.1103/PhysRev.95.359.
42. G. Fragneto-Cusani, J. Phys.: Condens. Matter, 2001, 13, 4973–4989,  DOI:10.1088/0953-8984/13/21/322.
43. O. Stern, Z. Elektrochem. Angew. Phys. Chem., 1924, 30, 508–516,  DOI:10.1002/bbpc.192400182.
44. A. P. Abbott, Chem. Phys. Chem., 2005, 6, 2502–2505,  DOI:10.1002/cphc.200500283.
45. A. P. Abbott, R. C. Harris and K. S. Ryder, J. Phys. Chem. B, 2007, 111, 4910–4913,  DOI:10.1021/jp0671998.

---