Open Access Article
Open Access ArticleOil-in-water emulsions based on hydrophobic eutectic systems†
Dannie J. G. P.
van Osch
 ab,
Jaap
van Spronsen
a,
A. Catarina C.
Esteves
ab,
Jaap
van Spronsen
a,
A. Catarina C.
Esteves
 ab,
Remco
Tuinier
ab,
Remco
Tuinier
 abc and
Mark
Vis
abc and
Mark
Vis
 *abd
*abd
aLaboratory of Physical Chemistry, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands. E-mail: m.vis@tue.nl
bInstitute for Complex Molecular Systems, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
cVan 't Hoff Laboratory for Physical and Colloid Chemistry, Debye Institute for Nanomaterials Science, Faculty of Science, Utrecht University, Hugo R. Kruyt Building, Padualaan 8, 3584 CH Utrecht, The Netherlands
dLaboratoire de Chimie, Ecole Normale Supérieure de Lyon, 46 Allée d'Italie, 69364 Lyon CEDEX 07, France
First published on 8th January 2020
Abstract
We demonstrate that oil-in-water emulsions can be prepared from hydrophobic eutectic systems (ES). Light microscopy and dynamic light scattering show that droplets are formed and zeta potential measurements indicate sufficient stability against coalescence. We investigate whether Ostwald ripening occurs in these ES-in-water emulsions by following the droplet growth over time and comparing it with an emulsion comprising decane in water. At first sight, the Ostwald ripening rate of the ES-in-water emulsion is expected to be orders of magnitude larger than the ripening of the decane-in-water emulsion due to a much higher solubility of the dispersed phase. However, experimentally we find that the ES-in-water emulsion actually grows a factor of two slower than the decane-in-water emulsion. We attribute this to the two-component nature of the ES, since the growth rate is mainly set by the least-soluble component of the ES. Thus, ESs offer the advantage of creating liquid emulsions of solid components, while setting the emulsion stability through their composition.
1 Introduction
Eutectic mixtures have come increasingly into focus as alternative solvents since 2003,1 when mixtures of amides and choline chloride were shown to feature a pronounced melting point depression yielding a liquid near room temperature2 starting from two solids. These mixtures are sometimes denoted deep eutectic solvents (DES), although the term deep (which implies a larger melting point depression than for an ideal eutectic mixture) is not always supported by evidence.3,4 Regardless of their ‘deepness’, these eutectic systems (ESs) feature properties that could make them interesting solvents. For instance, ESs may be engineered to reduce toxicity.5 Further, the composition of ESs may be tailored to a certain solute or application. For instance, a subclass of ESs are hydrophobic,6–8 which makes them suitable for performing extractions of hydrophobic species.9–14 It must be stressed here that, while ESs are often investigated with a view of sustainability, this aspect is dictated by the selection of the components and not a general property of all ESs. In the present manuscript, the focus therefore will be on the physical chemical properties of such mixtures, rather than their sustainability.An important physical chemical aspect for the application of alternative solvents, like ionic liquids and ESs, is how to prepare stable emulsions using them. An emulsion is a liquid–liquid two-phase system of droplets of a dispersed phase in a continuous phase that are stabilized by an emulsifier.15 Examples of emulsifiers include surfactants,16 polymers,17 and colloids.18 We focus here on macroemulsions, which generally have droplet sizes of 1 to 100 μm which are, at best, kinetically stable.
The emulsification of novel solvents may have been sparked in 2003 by Binks et al.,19 who investigated emulsions based on ionic liquids (ILs), both IL-in-H2O and H2O-in-IL, stabilized by silica nanoparticles. More recently, an oil-in-ES emulsion was prepared with a hydrophilic ES. Cyclohexane droplets were stabilized with sodium dodecyl sulfate (SDS) to form an emulsion with a hydrophilic ES composed of urea and choline chloride as the continuous phase.20 The major advantage of using ESs in an emulsion is the fact that it allows to use a larger range of (otherwise solid) components as a liquid, leading to potentially higher tunability than conventional solvents. The preparation of aqueous ES-based emulsions, i.e., based on hydrophobic eutectic mixtures, is as of yet an unexplored field.
Since ESs are composed of (at least) two components, it is crucial to understand if and how the multi-component nature of ESs affects the stability of these emulsions. For conventional emulsions it is known that droplets may grow over time via Ostwald ripening, i.e., by mass transport through the continuous phase. The two constituents of ESs may have different solubilities and may dissolve independently of each other in the continuous phase, in stark contrast to ionic liquid-based emulsions where electroneutrality poses additional restrictions. Therefore, the prime focus of the present work is to understand Ostwald ripening in ES-based emulsions.
The system we investigate is based on a dispersed hydrophobic eutectic mixture in water. These ES-in-H2O emulsions comprise a hydrophobic ES of 1-tetradecanol (1-tdc) and menthol (Men),21 which has a liquid window at room temperature, with sodium dodecyl sulphate (SDS) as surfactant. The effects of surfactant concentration, mass fraction of oil (ES) droplets, the addition of salt and sonication time on the droplet size evolution are studied. The results are compared to prototype conventional emulsions with decane as a dispersed oil phase.
2 Theory
2.1 Adsorbed amount of surfactant
The minimum surfactant concentration csurf needed to cover the interface of oil droplets in an emulsion can be estimated, assuming all surfactant is adsorbed, from: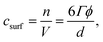 | (1) |
2.2 Lifshitz–Slyozov–Wagner theory
The growth of droplets in case of Ostwald ripening can be described using Lifshitz–Slyozov–Wagner (LSW) theory.24 By assuming steady state kinetics, the change of the droplet volume in time follows as:15,24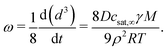 | (2) |
Integration of eqn (2) gives:
| d3 = d03 + 8ωt. | (3) |
3 Results and discussion
3.1 Microscopy
Fluorescence microscopy was used to validate visually that spherical droplets were formed after dispersing the ES into water in presence of SDS (see Fig. 1).3.2 Influence of SDS concentration on the droplet growth
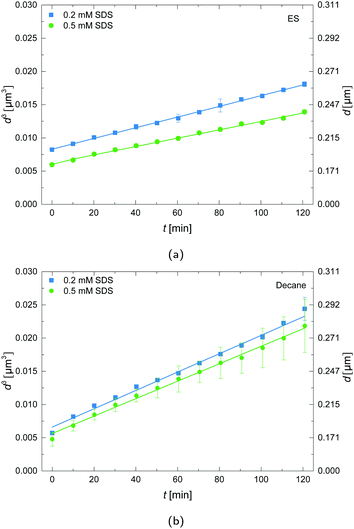
Dynamic light scattering (DLS) measurements were performed during the first two hours after preparation of the ES-in-H2O emulsions to investigate the growth of droplets over time. The measured diffusion coefficients of the droplets were converted to z-averaged hydrodynamic diameters using the Stokes–Einstein equation. The resulting hydrodynamic diameters for emulsions prepared with decane and ES are plotted in Fig. 2, where the effect of SDS concentration is illustrated.The LSW theory predicts that the droplets grow as d3 ∝ t, so all experimental data were plotted as d3versus t and fitted to eqn (3). It follows that the ES-in-water emulsions have a lower droplet growth rate than the decane-in-water emulsions. For decane as oil the linear slope is similar for 0.2 and 0.5 mM SDS, while for ES as oil the slope is slightly larger for the lowest SDS concentration. As follows from LSW theory, the major factors that influence the growth rate are: (1) the oil–water interfacial tension, (2) solubility of the disperse phase in the continuous phase, and (3) the diffusion coefficient of the disperse phase in the continuous phase. The SDS concentration directly affects the interfacial tension, which may therefore be the main reason behind the slight change in growth rate.
3.3 Influence of sonication on droplet growth
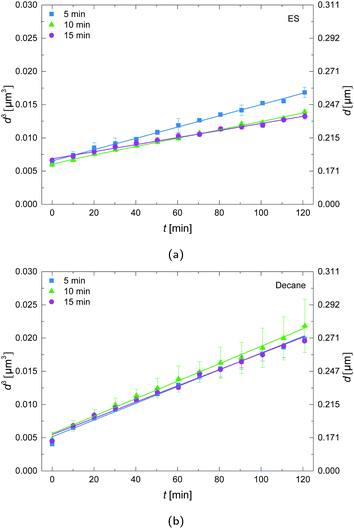
The influence of the sonication time on the droplet growth for both decane-in-water and the ES-in-water emulsions was investigated as shown in Fig. 3. The conventional solvent decane as oil shows no clear differences in growth rate upon variation of the sonication time. For 10 minutes sonication a steeper slope was detected, but the standard deviation of this measurement is also bigger in comparison with 5 and 15 minutes of sonication. For the ES as oil, 5 minutes sonication time shows a larger slope in comparison with 10 and 15 minutes sonication time. This may indicate that with 5 minutes of sonication the mixture is not yet fully emulsified due to the higher viscosity of the ES in comparison to decane (see ESI†). A shorter sonication time may cause an initially broader size distribution, which may enhance ripening.3.4 Influence of ES mass fractions
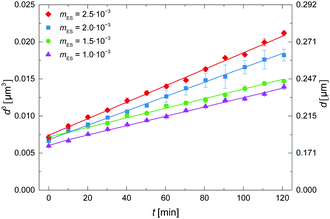
In Fig. 4 the effect of the ES mass fraction is plotted, where upon dilution 0.5 mM SDS was present in the aqueous phase. The droplet size evolution is quite similar for moil = 1 × 10−3 and 1.5 × 10−3. This suggests that these low mass fractions of ES are sufficiently dilute for which LSW theory to hold. Similar mass fractions were also used in literature for decane-in-water emulsions in the regime where LSW theory holds.23 The growth rate increases with mass fraction of ES above moil = 1.5 × 10−3, which may indicate that interactions between droplets become important, or that the composition of the droplets changes due to a different solubility of the two ES components.3.5 Influence of salt addition on the droplet growth
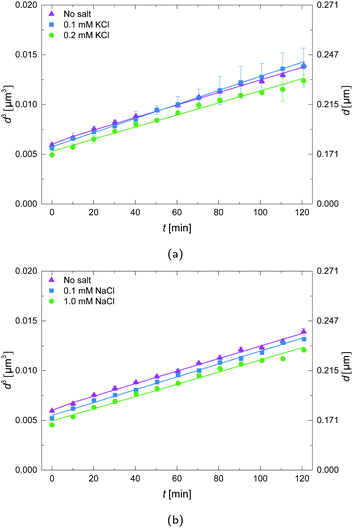
The effect of different salt concentrations was investigated, illustrated in Fig. 5. It is clear that for these salt concentrations, there is virtually no influence; the differences fall within the experimental error.3.6 Zeta-potentials
The zeta-potentials of the droplets were measured to characterize the stability against coalescence of the droplets (Table 1). The results show that all the prepared emulsions are negatively charged, which is expected since SDS is an anionic surfactant. All studied emulsions have a zeta-potential in the range of −50 to −60 mV, indicating sufficient stability against coalescence.| Oil phase (after dilution) | c SDS [mM] | Salt addition | Zeta-potential [mV] |
|---|---|---|---|
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.04 | No | −54.6 ± 0.7 |
| Decane | 0.1 | No | −58.4 ± 2.0 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.1 | No | −59.0 ± 0.6 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.1 | 0.02 mM KCl | −53.6 ± 1.0 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.1 | 0.04 mM KCl | −60.2 ± 1.3 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.1 | 0.02 mM NaCl | −59.6 ± 2.9 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.1 | 0.2 mM NaCl | −60.7 ± 0.8 |
3.7 Comparison with LSW theory
We estimated the ripening rates of emulsion droplets prepared with decane and ES based on Fig. 2–5. The growth rate is obtained by fitting the measured z-average diameters as a function of time to eqn (3). Note that we carry out multiple measurements per sample. We fit each time-resolved measurement individually and present the average and standard deviation of the obtained growth rate ω. These (z-averaged) growth rates are presented in Table 2.| Oil phase | c SDS [mM] | m oil | Salt addition | ω [nm3 s−1] |
|---|---|---|---|---|
| Decane | 0.2 | 1 × 10−3 | No | 287.7 ± 2.1 |
| Decane | 0.5 | 1 × 10−3 | No | 273.7 ± 47.9 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.2 | 1 × 10−3 | No | 167.7 ± 2.2 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.5 | 1 × 10−3 | No | 131.2 ± 3.5 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.5 | 1.5 × 10−3 | No | 134.9 ± 0.4 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.5 | 2.0 × 10−3 | No | 201.5 ± 29.7 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.5 | 2.5 × 10−3 | No | 231.6 ± 2.0 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.5 | 1 × 10−3 | 0.1 mM KCl | 147.3 ± 24.2 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.5 | 1 × 10−3 | 0.2 mM KCl | 126.4 ± 11.4 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.5 | 1 × 10−3 | 0.1 mM NaCl | 134.8 ± 1.9 |
1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
0.5 | 1 × 10−3 | 1.0 mM NaCl | 127.9 ± 2.1 |
The growth rates of the emulsions with decane as oil phase are comparable to the experimental results of Soma et al.23 Although they used a slightly higher oil concentration, we estimate that this will only have a minor impact on the results. Comparing these growth rates with the growth rates of our emulsions based on a hydrophobic ES, it is evident that the growth of the ES-in-water emulsions is generally slower by a factor of two than the decane-in-water emulsions.
To put this difference in perspective, we estimated the theoretical ripening rates using eqn (2). The parameters for decane are known from the literature, and are presented in Table 3 together with the parameters known for the ES. Unknown parameters for the ES-in-water emulsion are the diffusion coefficient and the interfacial tension, which we estimated from literature values of hexane to hexadecane,25 yielding for the diffusion coefficient 5 × 10−3 m2 s−1 and for the interfacial tension 8 mN m−1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1
Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2).21 The interfacial tension is of the oil–water interface, where the water phase contains SDS at bulk concentrations above the CMC
2).21 The interfacial tension is of the oil–water interface, where the water phase contains SDS at bulk concentrations above the CMC
| Parameters | Decane | 1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1 Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
|---|---|---|
| D [m2 s−1] | 7.15 × 10−10 | ≈5 × 10−10 |
| c sat,∞ [kg m−3] | 5.20 × 10−5 | 0.273 |
| γ [N m−1] | 8.41 × 10−3 | ≈8 × 10−3 |
| M [kg mol−1] | 142.28 × 10−3 | 175.64 × 10−3 |
| ρ [kg m−3] | 727 | 872 |
This gives a predicted LSW growth rate for decane of 31 nm3 s−1 and for 1-tdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1
Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) of 92 × 103 nm3 s−1. This striking difference is mainly due to the comparatively large solubility of the ES in the aqueous phase. For the decane-based emulsion, the difference in theoretical and experimentally observed growth rate is in the same order as observed in the literature: in the experiments the growth rate is approximately one order of magnitude larger than predicted.26 However, for the ES we observe that the growth rate is three orders of magnitude slower than predicted, resulting even in the fact that the ES emulsions show growth twice as slow as the decane-based emulsions, seemingly contradicting the theoretical expectation.
2) of 92 × 103 nm3 s−1. This striking difference is mainly due to the comparatively large solubility of the ES in the aqueous phase. For the decane-based emulsion, the difference in theoretical and experimentally observed growth rate is in the same order as observed in the literature: in the experiments the growth rate is approximately one order of magnitude larger than predicted.26 However, for the ES we observe that the growth rate is three orders of magnitude slower than predicted, resulting even in the fact that the ES emulsions show growth twice as slow as the decane-based emulsions, seemingly contradicting the theoretical expectation.
However, our initial estimation assumed that the ES could be treated as a single-component liquid. In fact, ESs should not be considered as new compounds, but simply as mixtures.3,4 For emulsions comprising, for instance, two-component oils as the dispersed phase, it is well-known that the growth rate can be described as:17
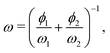 | (4) |
Arguably the most important consequence of eqn (4) is that it predicts that if component 1 has a much smaller growth rate ωi than component 2 (e.g., component 1 is much more insoluble than component 2), ω is dominated by component 1 for sufficient ϕ1. For our ES, the solubility of 1-tetradecanol is about three orders of magnitude lower than that of menthol (see Table 4), thus the decreasing the growth rate by approximately the same factor. Using the assumed parameters listed in Table 4, we now estimate ω ≈ 204 nm3 s−1 for the ES. This is much closer to (but still larger than) the experimental results. The remaining difference might be attributed to uncertainties in the actual composition of the droplets and/or interactions between the ES constituents. It should also be noted that the calculated rate is not very sensitive to the precise value of ϕi, since it is dominated by the least-soluble compound as long as its volume fraction is sufficiently large. We estimate that this may make it challenging to verify experimentally eqn (4) for the present system, due to limitations in the extent of the liquid window of the ES and the accuracy in determining the growth rate. We therefore leave this aspect to future work.
In any case, it can be concluded that the total solubility of the ES is not a good indicator for the actual Ostwald ripening rate, but one should instead take the individual solubilities into account through eqn (4). This highlights two important advantages of using eutectic mixtures in emulsions. First, by making an ES, otherwise solid components can be liquefied and therefore emulsified using standard approaches. Second, the addition of a relatively insoluble ES constituent to a more soluble constituent effectively suppresses the Ostwald ripening of the relatively soluble compound.
4 Conclusions
Oil-in-water emulsions based on a hydrophobic eutectic system (ES) were presented. The liquid oil phase was a binary eutectic mixture composed of 1-tetradecanol and menthol in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio, while the surfactant used to stabilize the emulsion against coalescence was sodium dodecylsulphate. We tested whether the ES-based emulsion followed classic Ostwald ripening to verify whether the nature of a two-component solvent such as an ES affects the properties of the emulsion. Qualitatively, it can be concluded that Ostwald ripening indeed occurs in oil-in-water emulsions prepared from a hydrophobic eutectic system. Under dilute conditions, we see a small to negligible variation of the growth rate with surfactant concentration, oil concentration, and salt concentration, in line with predictions from LSW-theory. Quantitatively, we see however distinct differences between conventional and ES-based emulsions: ripening of ES-based emulsions occurs about three orders of magnitude slower than expected based on the total solubility of the ES. We relate this to the two-component nature of the ES, since the component with the lowest solubility essentially limits the rate of Ostwald ripening. Additionally, the interactions between the two ES constituents may play a role. This highlights that ES-based emulsions offer the advantage of allowing solid components to be liquefied and subsequently emulsified, and that through selection of the ES constituents the Ostwald ripening can be effectively controlled. Future research should be directed to elucidating the possible role of interactions between the ES constituents in the stability of ES-based emulsions. Additionally, attention should be paid to the possible effect of surfactant and dispersion medium on the extent of the liquid window of the eutectic mixture, since the addition of these components effectively turns the binary eutectic system into a quaternary mixture.
2 molar ratio, while the surfactant used to stabilize the emulsion against coalescence was sodium dodecylsulphate. We tested whether the ES-based emulsion followed classic Ostwald ripening to verify whether the nature of a two-component solvent such as an ES affects the properties of the emulsion. Qualitatively, it can be concluded that Ostwald ripening indeed occurs in oil-in-water emulsions prepared from a hydrophobic eutectic system. Under dilute conditions, we see a small to negligible variation of the growth rate with surfactant concentration, oil concentration, and salt concentration, in line with predictions from LSW-theory. Quantitatively, we see however distinct differences between conventional and ES-based emulsions: ripening of ES-based emulsions occurs about three orders of magnitude slower than expected based on the total solubility of the ES. We relate this to the two-component nature of the ES, since the component with the lowest solubility essentially limits the rate of Ostwald ripening. Additionally, the interactions between the two ES constituents may play a role. This highlights that ES-based emulsions offer the advantage of allowing solid components to be liquefied and subsequently emulsified, and that through selection of the ES constituents the Ostwald ripening can be effectively controlled. Future research should be directed to elucidating the possible role of interactions between the ES constituents in the stability of ES-based emulsions. Additionally, attention should be paid to the possible effect of surfactant and dispersion medium on the extent of the liquid window of the eutectic mixture, since the addition of these components effectively turns the binary eutectic system into a quaternary mixture.
5 Materials and methods
This section details the experimental procedures. First, the materials and preparation of the systems are detailed. Next, the analytical methodologies are discussed. For results of physicochemical characterizations of the ES (density, viscosity, ES–air surface tension) the reader is referred to the ESI.†5.1 Materials and preparation
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio was prepared on a 5 g and a 100 g scale. A Mettler Ax205 balance was used for weighing the chemicals. 1-Tetradecanol was directly added to the glass vial or jar, while menthol was first proportioned in a weighing boat. The menthol was transferred to the vial, after which the solids were mixed with a VWR Analog Vortex Mixer. Finally, the ES was stirred until all the solids were liquefied. An IKA RCT basic was used for monitoring the stirring speed and temperature (300 rpm and room temperature). An IKA ETS-D5 temperature controller with an uncertainty of ±0.1 K was used for temperature control.
2 molar ratio was prepared on a 5 g and a 100 g scale. A Mettler Ax205 balance was used for weighing the chemicals. 1-Tetradecanol was directly added to the glass vial or jar, while menthol was first proportioned in a weighing boat. The menthol was transferred to the vial, after which the solids were mixed with a VWR Analog Vortex Mixer. Finally, the ES was stirred until all the solids were liquefied. An IKA RCT basic was used for monitoring the stirring speed and temperature (300 rpm and room temperature). An IKA ETS-D5 temperature controller with an uncertainty of ±0.1 K was used for temperature control.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1
Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) was mixed with water to investigate the amount of water it would take up. Centrifuge tubes (CELLSTAR) of 50 mL were used, in which 15 g of water and 15 g of ES were added. The mixture was vigorously stirred with a vortex mixer for 120 min on a IKA KS 4000 I incubating shaker (500 rpm, room temperature) and afterwards placed in the centrifuge (Sigma 2–16 KL) for 10 min at 6000 rpm. The phases were separated and the ES phase was further analyzed for its water content, density and viscosity.
2) was mixed with water to investigate the amount of water it would take up. Centrifuge tubes (CELLSTAR) of 50 mL were used, in which 15 g of water and 15 g of ES were added. The mixture was vigorously stirred with a vortex mixer for 120 min on a IKA KS 4000 I incubating shaker (500 rpm, room temperature) and afterwards placed in the centrifuge (Sigma 2–16 KL) for 10 min at 6000 rpm. The phases were separated and the ES phase was further analyzed for its water content, density and viscosity.
5.2 Analytical methodologies
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Men (1
Men (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) was measured with an Anton Paar DMA 4500 M over the temperature range of 293.15 to 333.15 K. The density meter has a temperature variation of ±0.05 K and an accuracy in the density of ±0.05 kg m−3. Reference oils were used to measure the discrepancy of the density, which was not more than ±0.01 kg m−3.
2) was measured with an Anton Paar DMA 4500 M over the temperature range of 293.15 to 333.15 K. The density meter has a temperature variation of ±0.05 K and an accuracy in the density of ±0.05 kg m−3. Reference oils were used to measure the discrepancy of the density, which was not more than ±0.01 kg m−3.
An Anton Paar Lovis 2000 ME rolling ball viscometer was used for measuring the viscosity. A glass capillary with an inner diameter of 1.8 mm was used. This capillary was equipped with a golden ball. The maximum coefficient of variation was below 0.2%, while the forward/backforward deviation was less than 1.0%. An N26 calibration oil, supplied by Anton Paar, was used for calibration.
For the surface tensions three consecutive measurements were performed. After each measurement the Wilhelmy plate was burned with a Bunsen burner to remove the ES. Before a new measurement, the system is equilibrated for at least 15 minutes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Nicole M. W. van der Heijden for performing experiments. The van 't Hoff Laboratory for Physical and Colloid Chemistry (Utrecht University) is acknowledged for assistance with fluorescence microscopy. The members of the ISPT “Deep Eutectic Solvents in the pulp and paper industry” consortium are acknowledged for their financial and in kind contribution. This cluster consists of the following organisations: Altri-Celbi, Buckman, Crown Van Gelder, CTP, DS Smith Paper, ESKA, Essity, Holmen, ISPT, Mayr-Melnhof Eerbeek, Metsä Fibre, Mid Sweden University, Mondi, Omya, Parenco BV, The Navigator Company, Sappi, Essity, Smurfit Kappa, Stora Enso, Eindhoven University of Technology, University of Aveiro, University of Twente, UPM, Valmet Technologies Oy, Voith Paper, VTT Technical Research Centre of Finland Ltd, WEPA and Zellstoff Pöls. Furthermore, this project received funding from the Bio-Based Industries Joint Undertaking under the European Union's Horizon 2020 research and innovation programme under grant agreement Provides No. 668970. Mark Vis acknowledges the Netherlands Organisation for Scientific Research (NWO) for a Veni grant (No. 722.017.005). The authors acknowledge Prof. I. M. Marrucho for valuable discussions.References
- A. P. Abbott, G. Capper, D. L. Davies, R. Rasheed and V. Tambyrajah, Chem. Commun., 2003, 70–71 RSC
.
- X. Meng, K. Ballerat-Busserolles, P. Husson and J.-M. Andanson, New J. Chem., 2016, 40, 4492–4499 RSC
.
- L. J. B. M. Kollau, M. Vis, A. van den Bruinhorst, A. C. C. Esteves and R. Tuinier, Chem. Commun., 2018, 54, 13351–13354 RSC
.
- M. A. R. Martins, S. P. Pinho and J. A. P. Coutinho, J. Solut. Chem., 2019, 48, 962–982 CrossRef CAS
.
- I. P. E. Macário, S. P. M. Ventura, J. L. Pereira, A. M. M. Gonçalves, J. A. P. Coutinho and F. J. M. Gonçalves, Ecotoxicol. Environ. Saf., 2018, 165, 597–602 CrossRef PubMed
.
- H. H. Lee and J. C. Warner, J. Am. Chem. Soc., 1935, 57, 318–321 CrossRef CAS
.
- D. J. G. P. van Osch, L. F. Zubeir, A. van den Bruinhorst, M. A. Rocha and M. C. Kroon, Green Chem., 2015, 17, 4518–4521 RSC
.
- B. D. Ribeiro, C. Florindo, L. C. Iff, M. A. Z. Coelho and I. M. Marrucho, ACS Sustainable Chem. Eng., 2015, 3, 2469–2477 CrossRef CAS
.
- S. Zhu, J. Zhou, H. Jia and H. Zhang, Food Chem., 2018, 243, 351–356 CrossRef CAS PubMed
.
- J. Cao, M. Yang, F. Cao, J. Wang and E. Su, ACS Sustainable Chem. Eng., 2017, 5, 3270–3278 CrossRef CAS
.
- L. F. Zubeir, D. J. G. P. Van Osch, M. A. A. Rocha, F. Banat and M. C. Kroon, J. Chem. Eng. Data, 2018, 63, 913–919 CrossRef CAS PubMed
.
- D. J. G. P. van Osch, D. Parmentier, C. H. J. T. Dietz, A. van den Bruinhorst, R. Tuinier and M. C. Kroon, Chem. Commun., 2016, 52, 11987–11990 RSC
.
- E. E. Tereshatov, M. Y. Boltoeva and C. M. Folden, Green Chem., 2016, 18, 4616–4622 RSC
.
- M. A. R. Martins, E. A. Crespo, P. V. A. Pontes, L. P. Silva, M. Bülow, G. J. Maximo, E. A. C. Batista, C. Held, S. P. Pinho and J. A. P. Coutinho, ACS Sustainable Chem. Eng., 2018, 54, 8104–8107 Search PubMed
.
-
J. Lyklema, Fundamentals of Interface and Colloid Science: Soft Colloids, Elsevier, 2005, vol. 5 Search PubMed
.
-
T. F. Tadros, Emulsion Formation and Stability, John Wiley & Sons, 2013 Search PubMed
.
-
B. P. Binks, Modern Aspects of Emulsion Science, RSC Publishing, 1998, pp. P007–P012 Search PubMed
.
- B. P. Binks and C. P. Whitby, Langmuir, 2004, 20, 1130–1137 CrossRef CAS PubMed
.
- B. P. Binks, A. K. Dyab and P. D. Fletcher, Chem. Commun., 2003, 2540–2541 RSC
.
- M. Pal, R. Rai, A. Yadav, R. Khanna, G. A. Baker and S. Pandey, Langmuir, 2014, 30, 13191–13198 CrossRef CAS PubMed
.
- D. J. G. P. van Osch, C. H. J. T. Dietz, J. van Spronsen, M. C. Kroon, F. Gallucci, M. van Sint Annaland and R. Tuinier, ACS Sustainable Chem. Eng., 2019, 7, 2933–2942 CrossRef CAS
.
- S. J. Rehfeld, J. Phys. Chem., 1967, 71, 738–745 CrossRef CAS
.
- J. Soma and K. D. Papadopoulos, J. Colloid Interface Sci., 1996, 181, 225–231 CrossRef CAS
.
- P. Taylor, Adv. Colloid Interface Sci., 1998, 75, 107–163 CrossRef CAS
.
- E. Nazarzadeh, T. Anthonypillai and S. Sajjadi, J. Colloid Interface Sci., 2013, 397, 154–162 CrossRef CAS PubMed
.
- J. Weiss, N. Herrmann and D. J. McClements, Langmuir, 1999, 15, 6652–6657 CrossRef CAS
.
-
CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press/Taylor and Francis, Boca Raton, FL, 90th edn, 2009 Search PubMed
.
-
H. Samuel, H. Yalkowsky and P. Jain, Handbook of aqueous solubility data, 2010 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Physicochemical characterizations of the eutectic mixture. See DOI: 10.1039/c9cp06762k |
| This journal is © the Owner Societies 2020 |