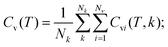First-principles comparative study of perfect and defective CsPbX₃ (X = Br, I) crystals

Abstract

First principles Density Functional Theory (DFT) hybrid functional PBESOL0 calculations of the atomic and electronic structure of perfect CsPbI₃, CsPbBr₃ and CsPbCl₃ crystals, as well as defective CsPbI₃ and CsPbBr₃ crystals are performed and discussed. For the perfect structure, decomposition energy into binary compounds (CsX and PbX₂) is calculated, and a stability trend of the form CsPbBr₃ > CsPbI₃ > CsPbCl₃ is found. In addition, calculations of the temperature-dependent heat capacity are performed and shown to be in good agreement with experimental data. As far as the defect structure is considered, it is shown that interstitial halide atoms in CsPbBr₃ do not tend to form di-halide dumbbells Br₂⁻ while such dimers are energetically favoured in CsPbI₃, analogous to the well-known H-centers in alkali halides. In the case of CsPbBr₃, a loose trimer configuration (Br₃²⁻) seems to be energetically preferred. The effects of crystalline symmetry and covalency are discussed, alongside the role of defects in recombination processes.

---

Introduction

Halide perovskites have attracted great interest as light absorbers for photovoltaic applications.¹ Among these materials, hybrid organic–inorganic systems based on methylammonium (MA) and/or formamidinium (FA) lead iodide have shown the highest performances in solar cell devices. Such hybrid compositions, however, suffer from high instability under operation. One currently explored alternative is to move to the fully inorganic CsPbX₃ (with X = I, Br), as these compounds could potentially fulfill both performance and stability criteria. However, many aspects regarding the phase stability of these inorganic materials, as well as the influence of ionic defects on their properties have yet to be thoroughly investigated experimentally and theoretically. Indeed, so far most of the theoretical studies on the atomic and electronic structure of halide perovskites (inorganic as well as hybrid organic–inorganic compositions) were focused on defect-free materials.^2–7 However, due to the low temperature fabrication, and also due to the fact that these materials are mixed ionic–electronic conductors,^8–11 one could expect a considerable concentration of ionic defects in these systems. However, despite their potential role in influencing electronic transport and device performance, there are only a few investigations of point defects in Cs compounds,^12,13 while there was recently a systematic study on hybrid perovskites.^11,14,15 Note that this aspect concerns not only mobile defects (coupling of ionic and electronic transport, interfacial redistribution processes), but also static ones (electronic carrier trapping and recombination). Even more, their importance lies in the fact that there is evidence showing that such ionic defects can be photo-generated.¹⁶

A few studies published so far include first principles calculations of native defects in MAPbI₃,¹⁷ self-trapped holes therein,¹⁸ as well as native defects in CsPbI₃.^12,13,19 Recently, we investigated point defect formation and basic properties in CsPbI₃ crystals from first principles calculations.²⁰ It was shown that interstitial iodine atoms tend to form I₂⁻ dimers (‘dumbbells’) within the crystal structure, in agreement with previous studies for MAPbI₃,^17,18,21 and with the well-known situation in alkali halides.^22–26 In alkali halides, the X₂⁻ dumbbells (called H centers) can be created under UV light irradiation. A similar situation, but under visible light irradiation, has been hypothesized to be the cause for the light-enhanced ion conduction reported in MAPbI₃.¹⁶ Thus, studying interstitial halide ions is important to understand charge transport properties in halide perovskites, both in the dark and under illumination.

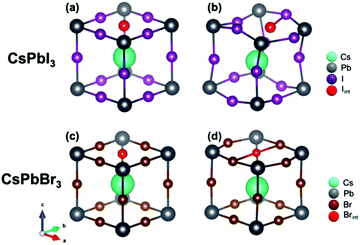
In this paper, we continue our first principles calculations²⁰ by calculating the formations energies of CsPbI₃, CsPbBr₃ and CsPbCl₃ from their parent binary compounds, and include also vibrational effects by performing heat capacity calculations. We compare these with experimental heat capacities, showing an excellent agreement. We also expand our study of the defective structure of Cs-based halide perovskites by considering interstitial bromide ions in cubic CsPbBr₃. We show that the formation of Br₂⁻ dumbbells is energetically unfavorable, in contrast with the situation in CsPbI₃. Instead, the energetically more favorable configuration for an interstitial bromide is a loose trimer (Br₃²⁻) (Fig. 1). Calculations of the one electron energies show that one electron levels of the interstitial defects in both CsPbI₃ and CsPbBr₃ lie in the middle of the bandgap, thus may act as traps for photo-generated carriers.

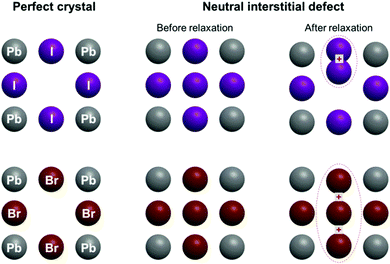Fig. 1 Schematic view of the perfect CsPbI₃ and CsPbBr₃ crystals, and of the structures including interstitial halide atoms, before and after structural relaxation.

Theoretical methods

Our first-principles periodic calculations were performed in the frame of the hybrid DFT PBESOL0 implemented in the CRYSTAL17 code.^27,28 This is a hybrid version of PBE exchange–correlation (XC) functional with 25% of Hartree–Fock exchange and revised for solids PBESOL²⁹ XC functional instead of the PBE XC functional. The hybrid exchange correlation functionals allow us to obtain a much better agreement with experiments concerning the band gap of perovskite materials.

Spin–orbital (SO) interactions were neglected in our calculations, since we expect these to have negligible influence on defect formation energies as well as phase stability. On the other hand, SO interactions significantly affect the band gap results. It has been shown for CsPbI₃¹⁷ that including SO interactions leads to the increase of the valence band top by 0.2 eV and to the decrease of the Pb-based conduction band bottom by 0.8 eV. For CsPbBr₃ and CsPbCl₃, SO corrections were extracted from LMTO calculations.³⁰ Taking these into account, our calculations are found in good agreement with experimental band gaps.

Gaussian atomic orbitals³¹ were used to expand the crystalline Bloch functions. The interaction between the core electrons and the valence and sub-valent electrons in iodine, lead and cesium atoms and the valence electrons was described by means of effective core pseudopotentials.

The Brillouin zone (BZ) sampling was performed with 8 × 8 × 8 k-point meshes generated according to the Monkhorst Pack scheme.³² Kohn–Sham equations were solved iteratively to self-consistency within 10⁻⁸ eV. Full geometry optimization was carried out both in perfect and defective crystals calculations. The Mulliken analysis was used for effective atomic charges.

In the point defects calculations, the supercell model^33,34 was used and a supercell composed by 8 primitive cells (2 × 2 × 2) was chosen (the main conclusions were confirmed by also using a 16 primitive cells supercell). In the perfect cubic CsPbX₃ crystal, three Wyckoff positions of the space group Pm3̄m with the simple cubic lattice are occupied: Cs 1b (0.5,0.5,0.5), Pb 1a (0,0,0), X (= I, Br) 3d (0.5,0,0). The neutral iodine and bromine atoms X_i were initially placed into the interstitial c-position with the coordinates (0.25, 0.25, 0) in the supercell and allowed to move, in order to find the configuration with the minimum total energy. All symmetry restrictions were lifted in the calculations of the defective crystals, in order not to constrain the optimization of lattice parameters and atomic coordinates.

The X_i formation energies E_f were calculated using the following relation:

E_f = E_def − (E_perf + U_i) (1)

where E_perf is the energy of a perfect supercell, E_def that of the supercell with a defect, and U_i is the chemical potential of a X atom (1/2 of the total energy of X₂ molecule in a gas phase).

The CsPbX₃ decomposition energies into binary compounds were taken from total energies of binary parent compounds (Table 1)

E_dec = E(CsPbX₃) − [E(CsX) + E(PbX₂)], (2)

Note that CsX has a cubic structure for all three halides, whereas PbI₂ has trigonal symmetry (space group P3̄m1) with one formula unit per primitive unit cell, in contrast to PbBr₂ and PbCl₂ which are orthorhombic (Pnam) and contain four formula units per unit cell.

Table 1 Calculated basic properties of bulk parent binary crystals: a₀ cubic lattice constant, q effective atomic charges (e), U_Cs, U_Pb are extracted Cs, Pb chemical potentials (a.u.). Chemical potentials of Cl, Br, I were calculated in ref. 20

	Space group	Z	a 0, b0, c0 expt^36 (Å)	a 0, b0, c0 calc (Å)	|q| (e)	U Cs, UPb (a.u.)
CsI	Pm3̄m	1	4.57	4.66	0.99	−20.011333
CsBr	Pm3̄m	1	4.29	4.39	0.99	−20.023117
CsCl	Pm3̄m	1	4.12	4.19	0.99	−20.052488
PbI2	P3̄m1	1	4.56, 6.78	4.69, 6.57	0.84, −0.42	−3.659705
PbBr2	Pnam	4	8.06, 4.73, 9.54	8.01, 4.75, 9.56	1.12, −0.54, −0.58	−3.684755
PbCl2	Pbnm	4	7.61, 4.53, 9.03	7.54, 4.51, 9.03	1.32, −0.63, −0.69	−3.745345

---

The heat capacity at constant volume (C_v) was calculated in a harmonic approximation according to ref. 34 and 35

where k_B is the Boltzmann constant, h the Planck constant and i the number of phonon modes with frequency ν_i over N_ν branches. As one can see from eqn (3), C_v calculations require summation over k set in the Brillouin zone. Our phonon calculations are made by the so-called direct method which requires the supercell-zone folding transformation to include in (3) non-zero k-points. We used three sets: only Γ-point, 8 and 16 k-points. These sets are discussed in ref. 29 and generated by supercell-zone folding transformation for the simple cubic lattice. More methodological details have been given in our previous study.²⁰ It has been shown therein that the chosen hybrid functional reproduces well both the atomic structure and band gap of three related materials CsPbI₃, CsPbBr₃ and CsPbCl₃. The calculated lattice constants deviate by less than 1% from the experimental values. The effective ionic charges for Cs ions are always close to +1e. Pb shows some covalency due to chemical bonding with halides, the charges of which are −0.62e for I and −0.65e for Br ions. 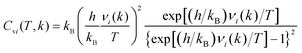This indicates, as expected, that CsPbBr₃ shows a more pronounced ionic character with respect to CsPbI₃.

Experimental methods

The heat capacities at constant pressure (C_p) of polycrystalline samples of CsPbBr₃ and CsPbI₃ were measured in the temperature range 0.4 K ≤ T ≤ 100 K employing the relaxation method using a Physical Property Measurement System (PPMS, Quantum Design). The samples were thermally coupled with Apiezon N grease to the sapphire platform. The heat capacities of the platform and the vacuum grease were measured before in separate runs and subsequently subtracted from the total heat capacities. The comparison between theory and experiments is based on the assumption that the calculated heat capacities at constant volume (C_v) do not differ significantly from the experimental heat capacities measured at constant pressure (C_p). These two values are linked by the relation:³⁷

C_p(T) = C_v(T) + E(T)·T (4)

E(T) = α_v²(T)·B·V_mol (5)

where α_v(T) is the volume coefficient of thermal expansion, B the bulk modulus and V_mol the molar volume at 0 K. Based on eqn (5), we therefore expect negligible differences between C_p and C_v, especially at low temperatures.

To fit the experimental heat capacities, a standard Debye behavior (with its characteristic Debye temperature Θ_D) has been initially considered. However, the experimental curves deviate quite strongly from this standard behavior, therefore this simple approximation has been complemented with the Einstein modes (corresponding to maxima in the phonon density of states due to acoustic phonon modes with low dispersion at zone boundaries, typically originating from vibrations of heavy atoms within compounds^38,39). These Einstein modes are generated with 2 parameters, a characteristic temperature (Θ_E) indicating the position of the maximum in the phonon density of states, and a weight (W_E) representing the fraction of atoms participating in this behavior.

Results and discussion

The calculations presented here consider primarily the cubic structure of CsPbI₃ and CsPbBr₃ crystals. It is known experimentally that these cubic structures are found above 400 K and 580 K, respectively, whereas below these temperatures the crystals are orthorhombic.⁴⁰ (Note that, in the case of CsPbI₃, significant distortions from the ideal cubic perovskite structure remain even above the transition temperature).⁴⁰ This structural instability is confirmed by our calculations of the phonons in cubic CsPbBr₃, which show imaginary frequencies at the R point of the Brillouin zone. The reason for the choice of the cubic cell relies on the fact that, especially for CsPbI₃, the orthorhombic phase has a large bandgap, and thus is not of interest for photovoltaic applications. Owing to this, many efforts have been devoted to the stabilization of the perovskite (distorted cubic) structure at room temperature.⁴¹ Nevertheless, as presented later, comparison with the orthorhombic crystal structure will also be given, in particular concerning structural parameters and formation energies.

Let us start by discussing the perfect structure. Our calculations, as already shown previously,²⁰ are able to satisfactorily capture both the crystal phase and the electronic structure of CsPbI₃, CsPbBr₃ and CsPbCl₃. From this basis, we move to calculate the decomposition energies of all these compounds (in the cubic phase) into the binary parent materials CsX and PbX₂ (eqn (2)). Unsurprisingly, these energies are rather small (see Table 2): 0.23 eV, 0.26 eV and only 0.02 eV per formula unit for I, Br and Cl respectively. According to our calculations, the chloride perovskite is expected to be the least stable of all three compounds, while bromide and iodide show comparable stabilities. The strong deviation of the formation energy of CsPbCl₃ from the trend may be connected with the more ionic nature of this compound (compared with the other two ones) and will require a more detailed study. The lack of experimental observations on the stability of these compounds makes any further conclusion at the moment unreliable.

Table 2 Phase energetics of cubic CsPbX₃ crystals into binary compounds calculated through total energies. Subscript pro represents the products and pre the precursors. E_dec indicate the decomposition energies from eqn (2)

Product (Pm3̄m)	E pro (a.u.)	Precursors	E pre (a.u.)	Σ pre (a.u.)	E dec (a.u.)	E dec (eV)
CsPbI3	−57.847	CsI + PbI2	−31.402 −26.436	−57.838	0.0086	0.23
CsPbBr3	−63.725	CsBr + PbBr2	−33.359 −30.357	−63.715	0.0094	0.26
CsPbCl3	−68.417	CsCl + PbCl2	−34.925 −33.491	−68.417	0.0007	0.02

---

We have also performed the calculations for the orthorhombic CsPbI₃, CsPbBr₃ and CsPbCl₃, which now have four formula units per unit cell. Table 3 shows the obtained decomposition energies, which are larger than for the cubic crystal, consistently with the orthorhombic phase being more stable at the temperature represented by the calculations. The value for the decomposition energy of orthorhombic CsPbI₃ also agrees well with recent experimental work,⁴² where the formation enthalpy of the phase from its solid halide precursors was estimated to be −0.18 eV.

Table 3 The same as Table 2 for orthorhombic (Z = 4) CsPbX₃ crystals (energies are given per formula unit)

Product (Pnma)	E pro (a.u.)	Precursors	E pre (a.u.)	Σ pre (a.u.)	E dec (a.u.)	E dec (eV)
CsPbI3	−57.849	CsI + PbI2	−31.402 −26.436	−57.838	0.011	0.30
CsPbBr3	−63.726	CsBr + PbBr2	−33.359 −30.356	−63.715	0.011	0.30
CsPbCl3	−68.419	CsCl + PbCl2	−34.925 −33.491	−68.417	0.002	0.08

---

In further agreement is the fact that the experiments show the orthorhombic phase being more stable than the cubic one, albeit the experimental difference between the formation energy of cubic and orthorhombic CsPbI₃ (0.15 eV)⁴² is found to be higher than our calculated one (0.08 eV).

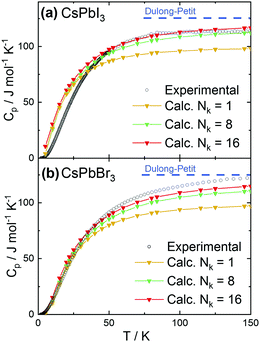
In addition, we have calculated and measured the heat capacity of CsPbI₃ and CsPbBr₃ in the cubic crystal structure. Fig. 2a and b shows the experimental and theoretical dependence of the heat capacity on the temperature. The experimental curves tend to reach the classical limit given by the Dulong–Petit law (C_p = 3N_A·R, with R being the molar gas constant and N_A is the number of atom in the formula unit). This approximation yields limit values of ∼125 J (mol K)⁻¹ for CsPbX₃. The calculation results depend on the number of k-points (N_k) used for the phonon calculations. Using only the gamma point (the simplest approximation) leads to a considerable underestimate (∼20%) of the heat capacity at high temperatures.

Fig. 2 Theoretical and experimental temperature dependence of the heat capacity for (a) CsPbI₃ and (b) CsPbBr₃. Calculations have been performed on the cubic structure for different numbers of k-points (N_k, indicated in the figure).

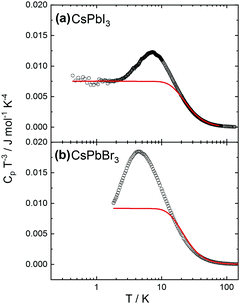
An increase of the number of k-points reduces the discrepancy, with 16 k-points providing sufficiently good agreement with experiments. Preliminary calculations also show that moving away from the cubic structure to consider an orthorhombic distortion yields no substantial difference in the calculated heat capacity values. This finding indicates that the crystal phase does not strongly affect the thermal behavior. More detailed calculations are on the way. The experimental heat capacities were also plotted in the coordinates useful to check for deviations from the Debye approximation (ω ∝ k), with C_pvs. T³ at low temperatures. As shown in Fig. 3, the peak at low temperatures in the quantity C_P/T³ indicates deviations from Debye behavior, as demonstrated by the comparison with the heat capacities (red solid lines) calculated assuming constant Debye temperatures as indicated. Such peaks typically result from maxima in the phonon density of states originating from acoustic phonon modes with low dispersion at the zone boundaries, originating from vibrations of heavy atoms in the compounds (see e.g.ref. 38 and 39).

Fig. 3 Experimental heat capacity of (a) CsPbI₃ and (b) CsPbBr₃ divided by T³. The red solid lines represent the Debye heat capacity assuming Debye temperatures of 109 K for CsPbI₃ and 102 K for CsPbBr₃, respectively.

We also noticed that the very low temperature behavior can be sample-dependent, likely due to structural defects and/or impurity which are difficult to control during the liquid-base synthesis. This aspect is discussed in more detail in the ESI.†

Let us now turn to important points concerning the modelling of the defective structure, namely the effect of the insertion of an interstitial halide in CsPbI₃ and CsPbBr₃. Fig. 4 shows the initial and final crystalline structure for the interstitial halide atoms inserted into the cubic crystals. In the case of CsPbI₃, introduction of an interstitial I leads to the formation of an I₂⁻ dumbbell through interaction with one of the neighboring I ions. This process is accompanied by a considerable distortion of the lattice surrounding the defect (Fig. 4b), not only locally but also at long range (Table 4).

Fig. 4 Comparison between the structure of CsPbI₃ and CsPbBr₃ with the addition of an interstitial halide atom. Structure (a) and (c) before and (b) and (d) after optimizing geometry. For simplicity, only a schematic representation of a single unit cell containing the defect is given, but the calculations have been performed on a 2 × 2 × 2 supercell. Note that the additional neutral iodide in CsPbI₃ interacts during geometry optimization with regular lattice iodide ions, forming a dumbbell. A different process (trimer formation) takes instead place for CsPbBr₃.

Table 4 Structural properties and energies involved in the insertion of an interstitial halide defect in CsPbI₃ and CsPbBr₃ (calculated in a 40 atom supercell with full geometry optimization and without fixing symmetry). a₀, b₀, c₀, and the angles are the structural parameters after geometry optimization (values in brackets correspond to the perfect crystal); q are the atomic charges on the various atoms in the perfect crystals; E_f is the defect formation energy for a halide interstitial insertion (eqn (1)); R, q are the distance and charge of a halide dimer (X₂⁻); ΔR is the distance change after structural optimization between the introduced interstitial X_i atom and 3 nearest neighbors X₁, X₂, X₃; q are the atomic charges of such halide ions

	CsPbI3	CsPbBr3
a 0, b0, c0 (Å)	12.630, 12.703, 12.595 (12.660)	11.911, 11.799, 11.988 (11.880)
Angles (°)	90.09, 89.76, 89.01 (90)	89.95, 89.85, 90.02 (90)
q Cs, qPb, qX (e)	0.99, 0.85, −0.62	0.99, 0.95, −0.65
E f (eV)	−0.37 eV	+0.22 eV
R, q (Å, e)	3.35, −0.50	2.96, −0.50
ΔR (Xi, X1, X2, X3) (Å)	−0.03, +0.48, +0.52	+0.11, +0.18, +0.95
q (Xi, X1, X2, X3) (e)	−0.35, −0.42, −0.61, −0.63	−0.39, −0.54, −0.56, −0.63

---

We found in our previous study²⁰ that the dumbbell (H center) formation is energetically favorable (E_f = −0.37 eV), notwithstanding the inclusion of the interstitial I atom at low temperatures. The I₂⁻ bond distance within the dumbbell (3.32 Å) is slightly shorter that in a free I₂⁻ ion (3.35 Å), as also observed for the H centers in alkali halides.²² In addition, the dumbbell formation causes a charge redistribution that leaves an almost identical charge on the two constituting I atoms (0.35e and 0.42e, with a small difference due to lattice distortions). Our previous calculations²⁰ predicted also that the formation of larger aggregates e.g. trimers I₃²⁻, is possible, but energetically less favorable (by 0.62 eV). A comparison with CsPbBr₃ reveals a very different situation (Fig. 4d): the lowest in energy configuration after incorporating a neutral interstitial Br is a loose trimer, where distances between a central Br atom and two nearest halides are considerably larger (by 0.11 A and 0.18 A) than in a typical Br₂⁻ dimer as found in alkali bromides (the comparison with the dimer is carried out due to the lack of literature data on bromide trimers).^22,26,43

The formation energy of this complex defect is substantially larger (by 0.59 eV) than for the I₂⁻ dimer. In the trimer, a charge of 1.5e is spread over all three participating Br atoms. Considering that, due to some covalent character, the charge of the regular host Br ions (not participating in the trimer) is −0.65e, this indicates that the trimer is best denoted as Br₃²⁻. To check the influence of the supercell size on the results obtained, we also performed time-consuming calculations doubling the supercell size (16 primitive unit cells instead of 8). The main conclusions are maintained, i.e. the H center formation energy is lower for CsPbI₃ than CsPbBr₃ (Br₂⁻ and I₂⁻ formation energy difference is 0.51 eV for a supercell of 16 unit cells). The X–X distance and Mulliken atomic charges are practically the same for supercells composed of 8 and 16 primitive cells. This substantial difference in behavior between the H center formation in CsPbI₃ and CsPbBr₃ could be related to the difference in the crystalline structure of the parent PbX₂, as PbI₂ has a rhombohedral P3̄m1 symmetry (one formula unit per unit cell), while PbBr₂ takes an orthorhombic Pnam space group (4 formula units per unit cell). As a consequence, the bromide ion sublattice has 4 atoms in the unit cell and their interatomic interactions become stronger in the perfect crystal, making the formation of a Br₂⁻ dumbbell more difficult when the interstitial bromide atom is inserted.

Considering the potential importance that this material has for photovoltaic and optoelectronic applications, we calculated positions of the energy levels of the interstitial defects in both crystals and found that in both cases these lie in the middle of the band gap (0.7 eV and 1 eV above the valence band maximum in CsPbI₃ and CsPbBr₃ respectively, with calculated bandgaps of 1.7 and 2.1 eV²⁰).

Due to their energy levels in the middle of the band gap, these defects could trap both electrons and holes. However, as such states are unstable (e.g. dimer or trimer dissociates after trapping an electron), these defects may not strongly affect the efficiency of the recombination processes in photovoltaic devices. The same is true for halide vacancies and V_k centers, but because they form shallow energy states.

Conclusions

In conclusion, we have confirmed the high quality of our hybrid DFT PBESOL0 calculations, not only by finding excellent agreement with experimental lattice parameters and properties, but also by obtaining reasonable values for formation energies and heat capacities in CsPbX₃ (X = Cl, Br, I).

The decomposition energies of CsPbX₃ crystals in both cubic and orthorhombic phases were estimated using the results of PBESOL0 calculations of binary parent CsX and PbX₂ crystals. The perovskite stability sequence was found as CsPbBr₃ > CsPbI₃ > CsPbCl₃ for both crystalline phases.

The frozen phonon method was applied to obtain the temperature dependence of the heat capacity in the cubic phase. The good agreement obtained with the experimental data confirms the high accuracy of our calculations.

Concerning the defective structure, our first principles supercell calculations on CsPbBr₃ show that the interstitial Br atoms (unlike the interstitial I atoms in CsPbI₃) do not form a Br₂⁻ dimer (commonly known as H center in alkali bromides),⁴⁴ but rather a loosely bound trimer (Br₃²⁻). Simple chemical arguments indicate that, due to the much higher polarizability, iodine atoms and ions are expected to form higher aggregates (e.g. polyiodides). The same situation is not expected (at least to a similar extent) in bromides.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank R. Merkle for numerous fruitful discussions and G. Siegle for experimental assistance. This study was partly supported by the M-ERA-NET project SunToChem (EK). Calculations were performed using computational facilities of St. Petersburg State University and Max Planck Institute for Solid State Research. Open Access funding provided by the Max Planck Society.

References

1. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051.
2. J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, J. Phys. Chem. Lett., 2013, 4, 2999–3005.
3. E. Mosconi, A. Amat, M. K. Nazeeruddin, M. Grätzel and F. De Angelis, J. Phys. Chem. C, 2013, 117, 13902–13913.
4. L. Lang, J.-H. Yang, H.-R. Liu, H. J. Xiang and X. G. Gong, Phys. Lett. A, 2014, 378, 290–293.
5. R. J. Sutton, M. R. Filip, A. A. Haghighirad, N. Sakai, B. Wenger, F. Giustino and H. J. Snaith, ACS Energy Lett., 2018, 3, 1787–1794.
6. M. G. Goesten and R. Hoffmann, J. Am. Chem. Soc., 2018, 140, 12996–13010.
7. J. Even and C. Katan, Halide Perovskites: Photovoltaics, Light Emitting Devices, and Beyond, 2019, p. 312.
8. J. Mizusaki, K. Arai and K. Fueki, Solid State Ionics, 1983, 11, 203–211.
9. K. Yamada, Y. Kuranaga, K. Ueda, S. Goto, T. Okuda and Y. Furukawa, Bull. Chem. Soc. Jpn., 1998, 71, 127–134.
10. K. Yamada, K. Isobe, T. Okuda and Y. Furukawa, Z. Naturforsch., A: Phys. Sci., 1994, 49, 258–266.
11. T.-Y. Yang, G. Gregori, N. Pellet, M. Grätzel and J. Maier, Angew. Chem., Int. Ed., 2015, 54, 7905–7910.
12. Y. Huang, W.-J. Yin and Y. He, J. Phys. Chem. C, 2018, 122, 1345–1350.
13. Y. Li, C. Zhang, X. Zhang, D. Huang, Q. Shen, Y. Cheng and W. Huang, Appl. Phys. Lett., 2017, 111, 162106.
14. A. Senocrate, I. Moudrakovski, G. Y. Kim, T.-Y. Yang, G. Gregori, M. Grätzel and J. Maier, Angew. Chem., Int. Ed., 2017, 56, 7755–7759.
15. A. Senocrate and J. Maier, J. Am. Chem. Soc., 2019, 141, 8382–8396.
16. G. Y. Kim, A. Senocrate, T.-Y. Yang, G. Gregori, M. Grätzel and J. Maier, Nat. Mater., 2018, 17, 445–449.
17. M. H. Du, J. Mater. Chem. A, 2014, 2, 9091–9098.
18. L. D. Whalley, R. Crespo-Otero and A. Walsh, ACS Energy Lett., 2017, 2713–2714.
19. Y.-H. Kye, C.-J. Yu, U.-G. Jong, K.-C. Ri, J.-S. Kim, S.-H. Choe, S.-N. Hong, S. Li, J. N. Wilson and A. Walsh, J. Phys. Chem. C, 2019, 123, 9735–9744.
20. R. A. Evarestov, A. Senocrate, E. A. Kotomin and J. Maier, Phys. Chem. Chem. Phys., 2019, 21, 7841–7846.
21. J. L. Minns, P. Zajdel, D. Chernyshov, W. van Beek and M. A. Green, Nat. Commun., 2017, 8, 15152.
22. ed. J. H. Crawford and L. M. Slifkin, Point Defects in Solids, Springer US, Boston, MA, 1972.
23. E. A. Kotomin and A. I. Popov, Nucl. Instrum. Methods Phys. Res., Sect. B, 1998, 141, 1–15.
24. A. Lushchik, M. Kirm, C. Lushchik and E. Vasil’chenko, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 166–167, 529–537.
25. R. T. Williams and K. S. Song, J. Phys. Chem. Solids, 1990, 51, 679–716.
26. A. M. Stoneham, Theory of Defects in Solids, Oxford University Press, 2001.
27. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D’Arco, M. Llunell, M. Causà, Y. Noël, L. Maschio, A. Erba, M. Rerat and S. Casassa, CRYSTAL17 User's Manual, http://www.crystal.unito.it/Manuals/crystal17.pdf.
28. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360.
29. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
30. A. Yaresco, Private communication, 2019.
31. G. Sofia, P. Baranek, C. Sarrazin, M. Rerat and R. Dovesi, CRYSTAL17 Basis Set, http://crystal.unito.it.
32. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
33. R. A. Evarestov, A. V. Bandura and I. I. Tupitsyn, Theor. Chem. Acc., 2018, 137, 14.
34. A. V. Bandura, V. V. Porsev and R. A. Evarestov, J. Comput. Chem., 2016, 37, 641–652.
35. D. C. Wallace, Thermodynamics of Crystals, John Wiley & Sons, Inc., Dover, 1998.
36. Crystallography Open Database, http://www.crystallography.net/cod/.
37. N. W. Ashcroft and N. D. Mermin, Solid state physics, Saunders College, 1976.
38. R. K. Kremer, M. Cardona, E. Schmitt, J. Blumm, S. K. Estreicher, M. Sanati, M. Bockowski, I. Grzegory, T. Suski and A. Jezowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075209.
39. M. Cardona, R. K. Kremer, R. Lauck, G. Siegle, A. Muñoz, A. H. Romero and A. Schindler, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075207.
40. C. K. Møller, Nature, 1958, 182, 1436.
41. G. E. Eperon, G. M. Paterno, R. J. Sutton, A. Zampetti, A. A. Haghighirad, F. Cacialli and H. J. Snaith, J. Mater. Chem. A, 2015, 3, 19688–19695.
42. B. Wang, N. Novendra and A. Navrotsky, J. Am. Chem. Soc., 2019, 141, 14501–14504.
43. K. S. Song and R. T. Williams, Self-Trapped Excitons, Springer Berlin Heidelberg, Berlin, Heidelberg, 1993, vol. 105.
44. T. Suzuki, K. Tanimura and N. Itoh, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 9298–9305.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp06322f

---