Lattice and thermodynamic characteristics of N-stearoyl-allo-threonine monolayers

Abstract

The effect of the second chiral center of diastereomeric N-alkanoyl-allo-threonine on the main monolayer characteristics has been investigated. The characteristic features of the enantiomeric and racemic forms of N-stearoyl-allo-threonine monolayers are studied on a thermodynamic basis and molecular scale. The π–A curves of the enantiomeric and racemic allo-forms show similar features to those of N-stearoyl-threonine. The compression curves are always located above the corresponding decompression curves and the decompression curves can be used as equilibrium isotherms for both the enantiomeric and racemic N-stearoyl-allo-threonine. The absolute T₀-values (disappearance of the LE/LC-transition) are 4–5 K larger compared with the corresponding N-stearoyl-threonines, but the ΔT₀ between the enantiomeric (D) and the racemic (DL) forms is only slightly larger than that of N-stearoyl-threonine. The difference in the critical temperatures T_c, above which the monolayer cannot be compressed into the condensed state, between the enantiomeric and the racemic forms, is quite small (ΔT_c = 0.8 K) and is smaller compared to that of the corresponding threonines (ΔT_c = 1.8 K). This is consistent with the dominance of the van der Waals interactions between the alkyl chains reducing the influence of chirality on the thermodynamic parameters. GIXD studies of N-stearoyl-allo-threonine monolayers provide information about the lattice structure of condensed monolayer phases on the Angstrom scale and stipulate the homochiral or heterochiral preference in the condensed phases. Comparable to N-stearoyl-threonine, the enantiomers exhibit an oblique lattice structure, whereas the racemates form a NNN tilted orthorhombic structure demonstrating the dominance of heterochiral interactions in the racemates independent of the diasteomeric structure change of the polar head group. The A₀ values are characteristic for rotator phases. The smaller A₀ value obtained for the racemic monolayers indicates their tighter packing caused by heterochiral interactions. The program Hardpack was used to predict the geometric parameters of possible 2-dimensional packings. For comparison with the experimental GIXD data, the two-dimensional lattice parameters and characteristic features of the enantiomeric and racemic diastereomeric stearoyl-threonine monolayers were calculated and are in reasonable agreement with the experimental GIXD data.

---

Introduction

The complex composition of biological membranes containing amino acids at the primary structural hierarchy initiated studies using model monolayers. They are frequently used to facilitate understanding of the complicated physicochemical mechanisms effective in the membrane structure.

In particular, monolayers of N-alkanoyl-substituted amino acid amphiphiles have been frequently studied as informative model systems.¹ Improvements in the experimental preparation of the enantiomeric forms of N-alkanoyl-substituted amino acid amphiphiles have been crucial for their use as amino acid-type model substances for chiral discrimination studies.^1–5

The main monolayer characteristics of N-alkanoyl substituted threonine amphiphiles, similar to those of other N-alkanoyl-substituted amino acid amphiphiles, revealed substantial differences from the usual amphiphilic monolayers. Generally, it was found that independent of the alkyl chain length and chirality in the surface pressure–molecular area (π–A) measurements of the enantiomeric and racemic forms, all compression curves are located above the corresponding decompression curves. Additionally, under the same conditions, the π–A isotherms of the racemic forms are situated under those of the enantiomeric forms.

The use of highly-sensitive imaging techniques, such as Brewster angle microscopy (BAM), provided valuable information on the mesoscopic morphology of the condensed phase domains formed in the two-phase coexistence region of the monolayers. Large topological differences in the condensed phase domains of several amino acid amphiphiles were observed and homo- and heterochiral preferences for chiral interaction were discussed.^6–17

Grazing incidence X-ray diffraction (GIXD) results of N-alkanoyl substituted α-amino acid amphiphiles, defining the lattice structure at the Angstrom level, are rather scarce.

However, recent GIXD studies of N-alkanoyl-threonine monolayers have shown that at all pressures, the enantiomers form an oblique lattice structure whereas the racemates develop a NNN tilted orthorhombic structure.¹⁸

It is interesting to note that threonine is one of the two proteinogenic amino acids with two chiral centers and can exist in four possible stereoisomers with the following configurations: (2S,3R), (2R,3S), (2S,3S) and (2R,3R). The designation L-threonine is used for one single diastereomer, (2S,3R)-2-amino-3-hydroxybutanoic acid. The second stereoisomer (2S,3S), which is rarely present in nature, is called L-allo-threonine.¹⁹ The other two stereoisomers (2R,3S)- and (2R,3R)-2-amino-3-hydroxybutanoic acid are only of minor biological importance. So far, as we know, the effect of the second chiral center within the head group of the other diastereomeric form of N-alkanoyl-allo-threonine has not yet been studied, and therefore is unknown.

The objective of the present study is to study the monolayer characteristics of N-stearoyl-allo-threonine in its enantimeric and racemic state and to compare them with those of the corresponding N-stearoyl-threonine. In order to stipulate the specific features of N-stearoyl-L-allo-threonine monolayer characteristics, they have been investigated on a thermodynamic basis and molecular scale. The thermodynamic results were obtained from π–A experiments, whereas GIXD was employed for defining the monolayer structure at the Angstrom level. Theoretical calculations of the molecular structure were performed to predict the 2-dimensional packing. The theoretical results are compared with the experimental data.

Experimental section

The enantiomeric allo-threonine methylester and stearoyl chloride were used in a condensation reaction in chloroform and aqueous potassium carbonate to synthesize the enaniomeric N-alkanoyl-substituted allo-threonine amphiphiles N-stearoyl-D-allo-threonine and N-stearoyl-L-allo-threonine (Fig. 1, left) according to ref. 20. For comparison diastereomeric N-stearoyl-D-threonine and N-stearoyl-L-threonine (Fig. 1, right) are presented. The reaction products were purified by repeated crystallization in methanol. The chemical and enantiomeric purity (99%) of the final products were verified by elemental analysis and HPLC.

Fig. 1 Chemical structures of N-stearoyl-D-allo-threonine and N-stearoyl-L-allo-threonine (left). N-Stearoyl-D-threonine and N-stearoyl-L-threonine are shown for comparison (right).

The surface pressure–molecular area (π–A) isotherms were recorded with a self-made, computer-interfaced film balance using the Wilhelmy method with a roughened glass plate.²¹ The N-stearoyl-allo-threonine amphiphiles dissolved in a heptane/ethanol (9 : 1) (Merck p.a. grade) mixture were spread on water with a specific resistance of 18.2 MΩ cm, purified by a Millipore desktop system. Compression and decompression curves were measured at a compression rate of ≤10 Ų (molecule min)⁻¹ with an accuracy of the surface tension of ±0.1 mN m⁻¹ and the molecular area of ±0.5 Ų.

The grazing incidence X-ray diffraction patterns were obtained using the liquid-surface diffractometer at the undulator beamline BW1 at HASYLAB (DESY, Hamburg, Germany).²² For the experiments, a thermostated Langmuir film balance is positioned in an air-tight container with a Kapton (polyimide film) window under a helium atmosphere. A monochromatic X-ray beam (λ = 1.304 Å) comes into contact with the water surface at a grazing incidence angle α_i = 0.85α_c illuminating approximately 2 × 50 mm² monolayer surface on the film balance. α_c = 0.13° is the critical angle for total reflection of the X-ray beam at the water surface. Slow lateral movement of the trough avoids sample damage by the strong X-ray beam. For the measurement of the diffracted signal, a linear position-sensitive MYTHEN detector system (PSI, Villigen, Switzerland) was used. The in-plane Q_xy component of the scattering vector was scanned by rotation of the detector, and the out-of-plane Q_z component of the scattering vector between 0.0 and 0.75 Å⁻¹ was obtained by the vertical strips of the MYTHEN. The analysis of the diffraction patterns yields the lattice structures. The Bragg peaks (integrated scattering intensity (corrected for polarization, effective area, and Lorentz factor) over a certain Q_z window) and the Bragg rods (integrated scattering intensity over a certain Q_xy window) specify the unit cell dimensions (lattice parameters a, b, c, in-plane area A_xy, cross-sectional area A₀, tilt angle t). The ellipse passing through 6 nearest neighbors of one chain is used to determine the distortion of the hexagonal lattice by d = (a_e² − b_e²)/(a_e² + b_e²) with a_e and b_e defined by the long and short axes of the ellipse, respectively.^23,24 For determination of the extent of the crystalline order in the monolayer, the in-plane coherence length L_xy was estimated from the full-width at half maximum (FWHM) of the Bragg peak using L_xy ∼ 0.9(2π)/FWHM(Q_xy). The thickness of the monolayer was assessed from the FWHM of the Bragg rod using 0.9(2π)/FWHM(Q_z). More details can be found in the literature.^25–28

To predict the 2-dimensional packing of the molecules, quantum chemical calculations of the molecular structure were performed at which the structures of the single molecules were optimized by the program Gaussian 09²⁹ using the B3LYP method and the 6-31G basis set.²⁹

The molecular packing was calculated by the program Hardpack. This program uses a Monte Carlo algorithm to find the global minimum of the energy of the 2-dimensional packings. The molecules are assumed to be semi-rigid with fixed bond length and bond angles and selected rotatable groups in the molecule. The 2-dimensional space group can be chosen by the user. The energy is calculated by a classical physics model and consists of van der Waals and electrostatic interactions between different molecules and rotatable groups. The charges are given in the form of point charges at the atom positions. Polarization and thermal motion are ignored. The parameters for the van der Waals interactions were taken from the DREIDING force field³⁰ and the point charges from the Gaussian 09 calculations. For the packing of the enantiomers, the 2-dimensional space group p1 was used, for the racemates it was the space group pg (which leads to an orthorhombic lattice). For each packing type, a few hundred molecular packings with varying cell constants, molecular positions and orientations, and seven internal rotations, were produced, and those with the lowest energies were compared with the experimental results.

Results and discussion

In a recent paper,¹⁸ we investigated C18-L-threonine and the corresponding racemate C18-DL-threonine (equimolar mixture of the (2S,3R)- and (2R,3S)-stereoisomers). For the present paper, we studied the corresponding enantiomeric C18-L-allo-threonine and racemate C18-DL-allo-threonine (equimolar mixture of the (2S,3S)- and (2R,3R)-stereoisomers). The comparison of the thermodynamic and structural results should provide information about the effect of the second chiral center within the head group of the other diastereomeric forms of N-alkanoyl-allo-threonine.

The π–A measurements of the enantiomeric N-stearoyl-D-allo-threonine monolayers spread on pH 3 water and measured at different temperatures in the range between 21 and 31 °C are shown at compression (left) and decompression (right) in Fig. 2. The corresponding π–A isotherms of racemic N-stearoyl-DL-allo-threonine monolayers measured at different temperatures in the range between 19 and 26 °C are presented at compression (left) and decompression (right) in Fig. 3.

Fig. 2 π–A isotherms of the enantiomeric N-stearoyl-D-allo-threonine monolayers spread on pH 3 water and measured in the temperature range between 21 and 31 °C at compression (left) and at decompression (right).

Fig. 3 π–A isotherms of the racemic N-stearoyl-DL-allo-threonine monolayers spread on pH 3 water and measured in the temperature range between 19 and 26 °C at compression (left) and at decompression (right).

The π–A curves of the enantiomeric and racemic allo-forms show the usual shift to higher transition pressures with increasing temperature. In both cases, characteristic differences exist between compression (left) and decompression (right) of the monolayers assigned as hysteresis by Stine et al. for other N-alkanoyl-substituted amino acid amphiphiles.⁶ For any fixed temperature, the compression curves are always located above the corresponding decompression curves, as already observed for the N-alkanoyl-threonines.¹⁸ This hysteresis increases with increasing compression rate.³¹ Similar studies, realized with monolayers N-palmitoyl-D-allo-threonine methylester and N-palmitoyl/stearoyl-threonines at different compression rates, have confirmed this behavior. According to the results accomplished with N-palmitoyl-D-allo-threonine methylester monolayers at different compression rates, the slowest compression curve approaches the decompression curve. Thus, the decompression curves can be used as the best representation of the equilibrium isotherms for both enantiomeric and racemic N-alkanoyl-substituted threonine amphiphiles.³¹ Consequently, the decompression curves can be used as equilibrium isotherms for both the enantiomeric and racemic N-stearoyl-allo-threonine. The observed extended horizontal plateau region, characteristic for the coexistence of fluid and condensed parts of the monolayer during the first-order phase transition, is gradually more inclined and less extended with increasing temperatures. A theoretical model developed to understand the dynamic π–A experiments using different compression rates of the N-palmitoyl-D-allo-threonine methylester monolayers provided a reasonable explanation for the compression curves and the corresponding hysteresis.³¹

The temperature dependence of the phase transition pressure (π_t), determined as the kink point in the π–A isotherms, offers interesting information about the thermodynamic characteristics of the transition between the fluid and condensed phases. Fig. 4 presents the π_t–T relationship of the N-stearoyl-allo-threonine monolayers on pH 3 water. The slope dπ_t/dT of the linear fit to the experimental data amounts to 1.481 mN (m K)⁻¹ for the enantiomeric N-stearoyl-D-allo-threonine and 1.13 mN (m K)⁻¹ for the racemic N-stearoyl-DL-allo-threonine. The corresponding values obtained for N-stearoyl-D-threonine (1.768 mN (m K)⁻¹) and for N-stearoyl-DL-threonine (1.245 mN (m K)⁻¹) have been added.¹⁸ The linearly fitted curves reach zero pressure (π_t = 0 mN m⁻¹) at the following T₀-values: 297.2 K (24.0 °C) for N-stearoyl-D-allo-threonine and 293.7 K (20.5 °C) for N-stearoyl-DL-allo-threonine, respectively, which are clearly larger (4–5 K) compared to the corresponding N-stearoyl-threonines. The slopes are quite similar, but the temperature of the LE/LC-transition pressure is clearly higher for the N-stearoyl-threonines compared to the corresponding N-stearoyl-allo-threonines, ∼8 K for the D-enantiomers and ∼6 K for the corresponding racemates.

Fig. 4 Temperature dependence of the main phase-transition pressure π_t of enantiomeric N-stearoyl-D-allo-threonine monolayers (left) and racemic N-stearoyl-DL-allo-threonine monolayers (right) spread on pH 3 water. The experimental points are red circles (). For comparison, the corresponding values (black circles, ●) of N-stearoyl-D-threonine and racemic N-stearoyl-DL-threonine have been added.

The LE/LC-transition disappears at the T₀-values. The ΔT₀ of 3.5 K between the enantiomeric (D) and the racemic (DL) forms of N-stearoyl-allo-threonine is only slightly larger compared with the corresponding difference (ΔT₀ = 2.9 K) between the enantiomeric (D) and the racemic (DL) forms of N-stearoyl-threonine.

The transition entropy (ΔS), presented in Fig. 5, is calculated using the two-dimensional Clapeyron equation, ΔS = ΔA × dπ_t/dT, based on the experimental data of the temperature dependence of the phase transition pressure (dπ_t/dT) and the area change (ΔA). The absolute ΔS values increase as the temperature decreases, indicating the increase of the condensed phase ordering at lower temperatures. The linear fit and extrapolation to zero ΔS stipulate the critical temperature T_c, above which the monolayer cannot be compressed into the condensed state. The ΔT_c difference between the enantiomeric and the racemic forms is quite small (ΔT_c = 0.8 K) and only slightly smaller compared with that observed for the corresponding threonines (ΔT_c = 1.8 K). The strong van der Waals interactions between the long alkyl chains reduce, in both diastereomeric forms, the impact of chirality on the thermodynamic parameters, which is even smaller in N-stearoyl-allo-threonine monolayers.

Fig. 5 Temperature dependence of the entropy change ΔS at the LE/LC phase transition of enantiomeric N-stearoyl-D-allo-threonine monolayers (left) and racemic N-stearoyl-DL-allo-threonine monolayers (right) spread on pH 3 water. The experimental points are red circles (). For comparison, the corresponding values (black circles, ●) of N-stearoyl-D-threonine and racemic N-stearoyl-DL-threonine have been added.

GIXD studies of N-stearoyl-allo-threonine monolayers were performed to obtain information about the characteristic features of the lattice structure of condensed monolayer phases in the Angstrom scale. The measurements have been carried out at 20 °C on the pH 3 subphase at different lateral pressures.

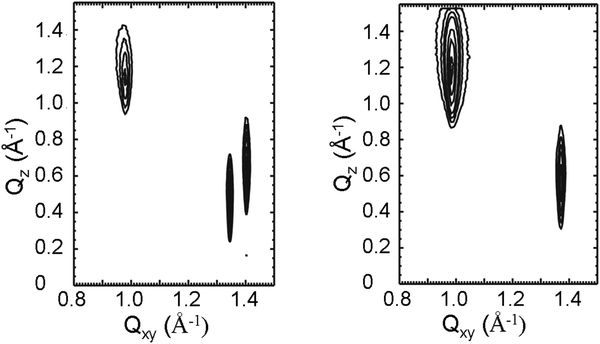
Fig. 6 presents representative contour plots of equal intensity versus the in-plane component Q_xy and the out-of-plane component Q_z of the scattering vector for N-stearoyl-allo-threonine monolayers at 14 mN m⁻¹ and 20 °C. The enantiomer shows three Bragg peaks at all pressures investigated. The Bragg peak positions, their full-widths at half-maximum, and all lattice parameters obtained at different surface pressures are listed in Tables 1 and 2.

Fig. 6 Contour plots of equal intensity vs. the in-plane component Q_xy and the out-of-plane component Q_z of the scattering vector of N-stearoyl-D-allo-threonin (left) and N-stearoyl-DL-allo-threonin (right) monolayers on the pH 3 subphase at 14 mN m⁻¹ and 20 °C. The racemate forms a NNN tilted orthorhombic structure (2 out-of-plane diffraction peaks) whereas the enantiomer exhibits an oblique unit cell (3 diffraction peaks).

Table 1 Bragg peak and rod positions and the corresponding full-widths at half-maximum of the enantiomeric N-stearoyl-D-allo-threonine monolayers as well as the lattice parameters of the monolayers at different lateral pressures and at 20 °C

π, mN m^−1	Q xy , Å^−1	Q z , Å^−1	Q xy , Å^−1	Q z , Å^−1	Q xy , Å^−1	Q z , Å^−1
Bragg parameters
4.9	0.974	1.14	1.345	0.49	1.399	0.65
	0.031	0.32	0.009	0.30	0.012	0.30
14.0	0.978	1.13	1.346	0.48	1.404	0.65
	0.045	0.32	0.010	0.28	0.015	0.29
23.0	0.979	1.11	1.348	0.47	1.404	0.64
	0.056	0.31	0.013	0.29	0.015	0.30

---

π, mN m^−1	a/b/c, Å	α/β/γ, °	D	t, °	A xy , Å^2	A 0, Å^2
Lattice parameters
4.9	4.906	138.5	0.4001	49.5	31.6	20.6
	6.775	113.7
	7.047	107.8
14.0	4.898	138.4	0.3988	49.1	31.5	20.6
	6.741	114.0
	7.031	107.6
23.0	4.894	138.4	0.3982	48.6	31.4	20.8
	6.738	113.9
	7.018	107.7

---

Table 2 Bragg peak and rod positions and the corresponding full-widths at half-maximum of the racemic N-stearoyl-DL-allo-threonine monolayers as well as the lattice parameters of the monolayers at different lateral pressures and 20 °C

π, mN m^−1	Q xy , Å^−1	Q z , Å^−1	Q xy , Å^−1	Q z , Å^−1
Bragg parameters
4.8	0.982	1.20	1.370	0.60
	0.032	0.32	0.014	0.32
14.0	0.986	1.18	1.371	0.59
	0.031	0.32	0.013	0.32
23.3	0.987	1.18	1.373	0.59
	0.034	0.32	0.020	0.32

---

π, mN m^−1	a/b = c, Å	α/β = γ, °	D	t, °	A xy , Å^2	A 0, Å^2
Lattice parameters
4.8	4.913	138.0	0.386838	50.7	31.4	19.9
	6.854	111.0
14.0	4.911	137.8	0.383578	50.1	31.3	20.1
	6.829	111.1
23.0	4.904	137.9	0.384013	50.1	31.2	20.0
	6.822	111.1

---

The structure of the condensed monolayer phase of the enantiomer is oblique with strongly tilted chains (Fig. 6, left). The two Bragg peaks at larger Q_xy and smaller Q_z values are close to each other so that the structure is near to an orthorhombic one with NNN (next-nearest neighbor) tilted alkyl chains, as observed for the racemate (Fig. 6, right). The transition from the oblique lattice structure, as detected for enantiomeric monolayers, to orthorhombic structure, as can be found in racemic monolayers, demonstrates clearly the formation of a compound with congruent transition point by the dominant heterochiral interactions in the racemic mixture.

These results show a considerably smaller alkyl chain cross-sectional area with ∼20.0 Ų for the racemate compared to that of the enantiomer with ∼20.7 Ų. Both values are characteristic for rotator phases implying free rotation of the alkyl chains. However, the smaller A₀ value of the racemic monolayers in comparison to the enantiomeric monolayers indicates the tighter packing of racemic structures suggesting a heterochiral interaction. It is interesting to note that the tilt angle t with respect to the surface normal is 50° which is extremely large, nearly independent of the lateral pressure and quite similar to the one of the corresponding diastereomers D-threonine and DL-threonine.

Therefore, the transition pressure into a non-tilted phase, calculated by extrapolation towards 1/cos(t) = 1 assuming a linear relationship between pressure and molecular area and a constant cross-sectional area in the condensed phase,³² cannot be determined (see Fig. 7).

Fig. 7 Alkyl chain tilt angle (as 1/cos(t)) of N-stearoyl-allo-threonine vs. lateral pressure. Left: Enantiomeric C18 and right: racemic C18. The experimental points are red circles (). For comparison, the corresponding values (black circles, ●) of N-stearoyl-D-threonine and racemic N-stearoyl-DL-threonine have been added.

As already discussed for the diastereomers stearoyl-D-threonine and stearoyl-DL-threonine, a strong hydrogen bonding network between the head groups is formed, which prevents on one hand the change of the alkyl chain lattice and leads on the other hand, to a large in-plane area requirement of the head groups. Due to the smaller chain cross-sectional area, the chains have to tilt strongly to optimize their van der Waals interactions by filling the space above the head groups. Correspondingly, such strong head group interactions have been discussed as the reason for the observed high and almost constant distortion d values. As can be seen in Fig. 8, the d values of the diastereomeric N-stearoyl-allo-threonine (both the enantiomeric and racemic forms) are even higher than those of the corresponding N-stearoyl-threonine. Therefore, a strong hydrogen bonding head group network can be assumed also as a reason for the special feature of the diastereomeric N-stearoyl-allo-threonine monolayers showing high and nearly constant distortion d values despite large cross-sectional areas typical for rotator phases.

Fig. 8 Distortion of the chain lattice versus sin²(t) of N-stearoyl-allo-threonine. Left: Enantiomeric C18, right: racemic C18. The experimental points are red circles (). For comparison, the corresponding values (black circles, ●) of N-stearoyl-D-threonine and racemic N-stearoyl-DL-threonine have been added.

Calculations on the basis of the program Hardpack were performed to predict the 2-dimensional packing of the N-stearoyl-allo-threonine and the corresponding N-stearoyl-threonine molecules. For each packing type, a few hundred molecular packings with varying cell constants, molecular positions and orientations, and seven internal rotations, were produced, and those with the lowest energies were used. For comparison of the diastereomeric monolayers the two-dimensional lattice parameters of the enantiomeric and racemic stearoyl-threonine were calculated. The lattice parameters of the unit cell, the tilt angles t, the in-plane areas, A_xy, and the cross-sectional area of alkyl chains, A₀, are listed in Table 3.

Table 3 Optimized two-dimensional lattice parameters of stearoyl-allo-threonine and stearoyl-threonine

C18-compound	a, Å	b, Å	c, Å	α, °	β, °	γ, °	A xy , Å^2	A 0, Å^2	t, °
D-Allo-threonine	5.05	6.94	7.75	140.3	118.5	101.2	34.4	18.3	57.9
DL-Allo-threonine	4.69	6.39	6.39	136.9	111.5	111.5	27.4	18.8	56.6
D-Threonine	4.58	6.74	7.12	141.5	113.7	104.7	29.9	18.0	53.1
DL-Threonine	4.94	6.67	6.67	136.5	111.7	111.7	30.6	17.9	54.3

---

In particular, it should be highlighted that the used quantum chemical procedure allows the determination of the fundamental monolayer characteristics. All calculated values of the characteristic features are in reasonable agreement with the experimental data, obtained by GIXD (see Tables 1 and 2 for stearoyl-allo-threonines and Table 2 in ref. 18). The calculated lattice parameters of the unit cell agree well with the experimental GIXD data and verify the difference between the oblique structure obtained for the enantiomeric forms and the orthorhombic structure obtained for the racemic form. The calculated data corroborate the results of the GIXD measurements, indicating that the diastereomeric difference between the polar headgroups is only marginal. Also, the calculated A₀ values and the calculated tilt angles t with respect to the surface normal agree reasonably well with the experimental GIXD results. This is interesting to note because the chosen assumptions correspond only roughly with the experimental conditions.

Fig. 9 shows the package of two molecules, quantum chemically calculated for stearoyl-D-allo-threonine (1), stearoyl-rac-allo-threonine (2), stearoyl-D-threonine (3) and stearoyl-rac-threonine (4). The conformations of the headgroups were obtained by the same packing calculations.

Fig. 9 Visualization of 4 selected theoretical packings: (1) stearoyl-D-allo-threonine, (2) stearoyl-DL-allo-threonine, (3) stearoyl-D-threonine and (4) stearoyl-DL-threonine.

Each theoretical packing is shown as a pair of 2 neighboring molecules, viewed along the horizontal surface plane. In the case of enantiomeric packings (1 and 3), both molecules are related by a simple translation parallel to the plane of the figure. In case of the racemates (2 and 4), the molecules are additionally related by a mirror plane parallel to the plane of the figure, i.e., they have D- and L-forms. The mirror plane exchanges the front with the back parts of the molecule.

Conclusions

Substantial differences exist between the main monolayer characteristics of N-alkanoyl substituted threonine amphiphiles and the usual amphiphiles. In a recent study,¹⁸ the special features of N-alkanoyl substituted threonine amphiphile monolayers have been presented. However, the other diastereomeric form, N-alkanoyl-allo-threonine, has not yet been studied. To fill this gap, N-stearoyl-allo-threonine monolayers have been used to investigate their special thermodynamic and structural features in order to obtain information on the effect of the second chiral center within the head group in the present paper.

The π–A curves of the enantiomeric and racemic allo-forms show similar features as those of N-stearoyl-threonine. The compression curves are always located above the corresponding decompression curves, and the decompression curves can be used as equilibrium isotherms for both the enantiomeric and racemic N-stearoyl-allo-threonine.

The temperature dependence of the phase transition pressure (π_t) provides information on the thermodynamic characteristics of the transition between the fluid and condensed phases. It indicates a lower LE/LC-transition pressure for the N-stearoyl-allo-threonines in comparison to the corresponding N-stearoyl-threonines with ∼8 K for the D-enantiomers and ∼6 K for the corresponding racemates.

The T₀-values for the disappearance of the LE/LC-transition of the N-stearoyl-allo-threonines are 4–5 K larger compared with the corresponding N-stearoyl-threonines. However, the ΔT₀ = 3.5 K between the enantiomeric (D) and the racemic (DL) forms is only slightly larger than that of N-stearoyl-threonine (ΔT₀ = 2.9 K).

The difference of the critical temperatures T_c, above which the monolayer cannot be compressed into the condensed state, between the enantiomeric and the racemic forms is rather small (ΔT_c = 0.8 K) and even smaller compared to that of the corresponding threonines (ΔT_c = 1.8 K). This is consistent with the dominance of the van der Waals interactions between the alkyl chains reducing the influence of chirality on the thermodynamic parameters.

GIXD studies of N-stearoyl-allo-threonine monolayers provide information about the lattice structure of condensed monolayer phases in the Angstrom scale and stipulate the homochiral or heterochiral preference in the condensed phases. Analogous to N-stearoyl-threonine, the enantiomers reveal an oblique lattice structure, whereas the racemates form a NNN tilted orthorhombic structure demonstrating that the dominance of the heterochiral interactions in the racemates is independent of the diastereomeric structure change of the polar head group. The transition to the orthorhombic structure clearly indicates dominant heterochiral interactions in the condensed phase of racemic mixtures resulting in the formation of a compound with a congruent transition point. The A₀ values are characteristic for rotator phases. The smaller A₀ value obtained for the racemic monolayers corroborate the tighter packing caused by the heterochiral interaction.

Quantum chemical calculations of the molecular structure were performed to predict theoretically the 2-dimensional packing. The obtained results show that the used quantum chemical procedure allows the determination of fundamental monolayer characteristics. The two-dimensional lattice parameters and characteristic features of the enantiomeric and racemic N-stearoyl-allo-threonine as well as N-stearoyl-threonine monolayers were calculated and are in reasonable agreement with the experimental GIXD data.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank HASYLAB at DESY, Hamburg, Germany, for beamtime and excellent support, Dr K. Schinkowski for the preparation of threonine amphiphiles, and Irina Berndt for careful Langmuir isotherm experiments. Open Access funding provided by the Max Planck Society.

References

1. E. M. Arnett, N. G. Harvey and P. L. Rose, Acc. Chem. Res., 1989, 22, 131–138.
2. N. G. Harvey, P. L. Rose, D. Mirajovsky and E. M. Arnett, J. Am. Chem. Soc., 1990, 112, 3547–3554.
3. J. G. Heath and E. M. Arnett, J. Am. Chem. Soc., 1992, 114, 4500–4514.
4. P. L. Rose, N. G. Harvey and E. M. Arnett, Adv. Phys. Org. Chem., 1993, 28, 45–138.
5. E. M. Arnett, K. Amarnath, N. G. Harvey and J. Cheng, J. Am. Chem. Soc., 1990, 112, 344–355.
6. K. J. Stine, J. Y.-J. Uang and S. D. Dingman, Langmuir, 1993, 9, 2112–2118.
7. K. J. Stine, S. A. Whitt and J. Y.-J. Uang, Chem. Phys. Lipids, 1994, 69, 41–50.
8. S. Akamatsu, O. Bouloussa, K. To and F. Rondelez, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 4504–4507.
9. J. Parazak, Y.-J. Uang, B. Turner and K. J. Stine, Langmuir, 1994, 10, 3787–3793.
10. F. Hoffmann, K. J. Stine and H. Hühnerfuss, J. Phys. Chem. B, 2005, 109, 240–252.
11. A. Gericke and H. Hühnerfuss, Langmuir, 1994, 10, 3782–3786.
12. F. Hoffmann, H. Hühnerfuss and K. J. Stine, Langmuir, 1998, 14, 4525–4534.
13. H. Hühnerfuss, V. Neumann and K. J. Stine, Langmuir, 1996, 12, 2561–2569.
14. H. Hühnerfuss, A. Gericke, V. Neumann and K. J. Stine, Thin Solid Films, 1996, 284, 694–697.
15. N. Nandi and D. Vollhardt, Colloids Surf., A, 2001, 183–185, 67–83; N. Nandi and D. Vollhardt, Colloids Surf., A, 2002, 198–200, 207–221.
16. N. Nandi and D. Vollhardt, J. Phys. Chem. B, 2003, 107, 3464–3475.
17. N. Nandi and D. Vollhardt, Chem. Rev., 2003, 103, 4033–4075.
18. D. Vollhardt, C. Stefaniu and G. Brezesinski, Phys. Chem. Chem. Phys., 2019, 21, 96–103.
19. H. B. F. Dixon, A. Cornish-Bowden, C. Liebecq, K. L. Loening, G. P. Moss, J. Reedijk, S. F. Velick and J. F. G. Vliegenthart, Pure Appl. Chem., 1984, 56(5), 595–624.
20. F. J. Zeelen and E. Havinga, Recl. Trav. Chim. Pays-Bas, 1958, 77, 267–272.
21. D. Vollhardt, Curr. Opin. Colloid Interface Sci., 2014, 19, 183–197.
22. R. Frahm, J. Weigelt, G. Meyer and G. Materlik, Rev. Sci. Instrum., 1995, 66, 1677–1680.
23. M.-H. Ropers and G. Brezesinski, Soft Matter, 2013, 9, 9440–9448.
24. V. M. Kaganer and E. B. Loginov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1995, 51, 2237–2249.
25. J. Als Nielsen, F. Christensen and P. S. Pershan, Phys. Rev. Lett., 1982, 48, 1107–1111.
26. J. Als-Nielsen, D. Jacquemain, K. Kjaer, F. Leveiller, M. Lahav and L. Leiserowitz, Phys. Rep., 1994, 246, 251–313.
27. K. Kjaer, Phys. B, 1994, 198, 100–109.
28. D. Vollhardt and G. Brezesinski, in Recent Progress in Colloid and Surface Chemistry with Biological Applications, ed. C. Wang, et al., ACS Symposium Series, American Chemical Society, Washington, DC, 2015, pp. 377–419.
29. M. J. Frisch et al. , Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009.
30. S. L. Mayo, B. D. Olafson and W. G. Goddard, J. Phys. Chem., 1990, 94, 8897–8909.
31. D. Vollhardt and V. B. Fainerman, J. Phys. Chem. B, 2002, 106, 345–351.
32. F. Bringezu, B. Dobner and G. Brezesinski, Chem. – Eur. J., 2002, 8, 3203–3210.

---