Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
i-Rheo: determining the linear viscoelastic moduli of colloidal dispersions from step-stress measurements
Rodrigo
Rivas-Barbosa
a,
Manuel A.
Escobedo-Sánchez
 b,
Manlio
Tassieri
b,
Manlio
Tassieri
 c and
Marco
Laurati
c and
Marco
Laurati
 *ad
*ad
aDivisión de Ciencias e Ingenierías, Universidad de Guanajuato, Lomas del Bosque 103, 37150 León, Mexico. E-mail: mlaurati@fisica.ugto.mx
bSoft Matter Laboratory, Heinrich-Heine University, Universitätsstrasse 1, 42150 Düsseldorf, Germany
cDivision of Biomedical Engineering, James Watt School of Engineering, University of Glasgow, Glasgow G12 8LT, UK. E-mail: Manlio.Tassieri@glasgow.ac.uk
dDepartment of Chemistry “Ugo Schiff” and CSGI, University of Florence, Sesto Fiorentino, Florence I-50019, Italy
First published on 24th January 2020
Abstract
We report on the application of a Fourier transform-based method, ‘i-Rheo’, to evaluate the linear viscoelastic moduli of hard-sphere colloidal dispersions, both in the fluid and glass states, from a direct analysis of raw step-stress (creep) experimental data. We corroborate the efficacy of i-Rheo by comparing the outputs of creep tests performed on homogenous complex fluids to conventional dynamic frequency sweeps. A similar approach is adopted for a number of colloidal suspensions over a broad range of volume fractions. For these systems, we test the limits of the method by varying the applied stress across the materials' linear and non-linear viscoelastic regimes, and we show that the best results are achieved for stress values close to the upper limit of the materials' linear viscoelastic regime, where the signal-to-noise ratio is at its highest and the non-linear phenomena have not appeared yet. We record that, the range of accessible frequencies is controlled at the higher end by the relative weight between the inertia of the instrument and the elasticity of the complex material under investigation; whereas, the lowest accessible frequency is dictated by the extent of the materials' linear viscoelastic regime. Nonetheless, despite these constrains, we confirm the effectiveness of i-Rheo for gaining valuable information on the materials' linear viscoelastic properties even from ‘creep ringing’ data, confirming its potency and general validity as an accurate method for determining the material's rheological behaviour for a variety of complex systems.
1 Introduction
In rheology, the determination of the linear viscoelastic (LVE) properties of materials is of great importance for the determination of their states; i.e., whether a material could be classified as a viscoelastic solid or fluid. This is because, over the years, the LVE properties of materials have been successfully correlated both theoretically and experimentally to their microscopic structure and dynamics occurring at different time and length scales.1 These are fully described by the frequency-dependent viscoelastic moduli, G′(ω) (storage modulus) and G′′(ω) (loss modulus), which are classically measured over a finite set of frequencies via oscillatory measurements called dynamic frequency sweeps (DFSs).2 However, due to the mechanical inertia carried by the electric motor of rheometers, the frequency of oscillation cannot exceed typically 100 Hz, whereas the lowest accessible frequency is limited by the measurement duration and the stability of the sample. Typically, frequencies lower than 0.1 Hz require exceedingly extensive measuring times. In a recent work3 Tassieri et al. proposed a novel rheological ‘tool’ to derive the frequency-dependent viscoelastic moduli via a discrete Fourier transform4 of step-strain and relaxation experiments. This tool has been made available to the scientific community in the form of an open access executable called ‘i-Rheo’ and it has been recently adapted to analyse atomic force microscopy measurements5,6 and molecular dynamic simulations.7 An advantage of using i-Rheo is that there is no need of assuming any rheological model for data interpretation nor idealisation of the real measurements. Moreover, thanks to the fast sampling of modern rheometers, this tool is particularly useful for accessing the materials' high frequency responses, especially for strain-controlled rheometers, for which the motor inertia is less disruptive than in the case of stress-controlled rheometers; but, would still limit anyway the range of accessible frequencies to 100 Hz for oscillatory measurements. In this work, we exploit the efficacy of i-Rheo for the analysis of step-stress (creep) measurements that suit better the stress-controlled rheometers. In particular, we first validate the use of i-Rheo for the analysis of creep measurements performed on homogeneous complex fluids and then we exploit it for the investigation of the LVE properties of hard-sphere colloidal suspensions, over a broad range of colloidal volume fractions ϕ including non-equilibrium glass states. Despite their complex rheological behaviour, colloidal suspensions are a class of soft-materials widely used in daily applications including paints, food products, cosmetics and cleaning products.1,8 Moreover, due to their inherent complexity, model suspensions, such as one-component hard-sphere colloids (for which the volume fraction ϕ is the only control parameter), have been extensively studied for a better understanding of the rheological behaviour of more complex suspensions.9,10 It is known that for such systems the equilibrium state diagram shows fluid states for ϕ < 0.494, fluid-crystal coexistence for 0.494 < ϕ < 0.545 and a crystalline solid for ϕ > 0.545.9,10 Moreover, when the width of the size distribution of the colloidal particles exceeds 7% circa, the increase of ϕ above ϕg ≈ 0.58 leads to the formation of a non-equilibrium amorphous solid (glass)11,12 instead of a crystal.13 Glass formation is attributed to the trapping of a particle by the nearest neighbors (the so-called cage formation)9 and is detected due to the appearance of a solid-like response of the suspension.14,15 The LVE moduli of dense fluids and glasses are well described by the mode coupling theory (MCT) of the glass transition.14–16 The experimental determination of these moduli by means of conventional DFS measurements is time consuming especially at low frequencies, where the relaxation processes of these samples eventually occur. In addition to the linear viscoelastic moduli,15,17 also the shear viscosity rapidly increases at the glass transition.18–20 When a constant shear rate or a stress (creep) is suddenly applied to a dense suspension, the system yields and flows due to the rupture of the cages.21–28 The transition to flow can be affected by shear banding,29–32 ageing and history effects.33 Here, we demonstrate that the evaluation of the materials' LVE moduli by means of i-Rheo applied to creep measurements is a reliable and faster alternative to conventional DFS measurements, also in the case of colloidal suspensions. The linear viscoelastic moduli obtained via i-Rheo are in good agreement with conventional DFS measurements of hard-sphere dispersions in both fluid and glass states. We discuss the results obtained for a range of different applied stresses across the materials' linear and non-linear response regimes, identifying the best choice of the applied stress. We also discuss the limits of the accessible range of frequencies for such systems, in particular in the non-equilibrium glass state, where non-homogeneous flows are observed for the majority of the experimental conditions.2 Theoretical background
2.1 Linear rheology in the frequency-domain: oscillatory measurements
The LVE properties of a material are fully described by its frequency-dependent complex shear modulus G*(ω), which is a complex number whose real and imaginary parts provide information on the elastic and the viscous nature of the material, respectively. The complex shear modulus is defined as the ratio between the Fourier transforms of the stress σ(t) and the strain γ(t), whatever their temporal forms and regardless of whichever has been imposed or measured:34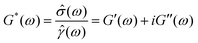 | (1) |
The standard method of measuring G*(ω) over a finite set of frequencies is based on the imposition of an oscillatory stress σ(ω,t) = σ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) (where σ0 is the amplitude of the stress function) and the measurement of the resulting oscillatory strain, which would have a form of γ(ω,t) = γ0(ω)sin(ωt + φ(ω)), where γ0(ω) is the strain amplitude and φ(ω) is the phase-shift between the stress and the strain. From eqn (1) it follows that:
sin(ωt) (where σ0 is the amplitude of the stress function) and the measurement of the resulting oscillatory strain, which would have a form of γ(ω,t) = γ0(ω)sin(ωt + φ(ω)), where γ0(ω) is the strain amplitude and φ(ω) is the phase-shift between the stress and the strain. From eqn (1) it follows that:
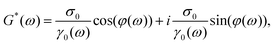 | (2) |
2.2 Fourier series of a square wave
In this section, we wish to remind the reader of an important mathematical equivalence that underpins the effectiveness of creep-measurements for the evaluation of the materials' LVE properties over a wide frequency spectrum. This is related to the equipollence of a square wave to an infinite sum of sinusoidal functions having different frequencies and weighted amplitudes; i.e., a Fourier series. In particular, in the case of real experiments, where a step-measurement cannot last for infinite time (for obvious reasons), the temporal behaviour of the step-function assumes the form of a half square wave u(t) with a relatively long period T (as drawn in Fig. 1). It follows that u(t) could be expressed as: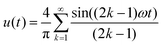 | (3) |
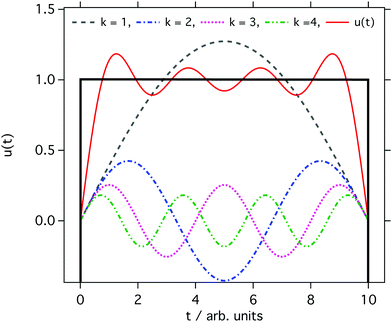 | ||
| Fig. 1 A schematic representation of half square wave u(t) and its approximation obtained by considering only the first four terms of the Fourier series shown in eqn (3). | ||
2.3 Linear rheology in the time-domain; step-stress measurements
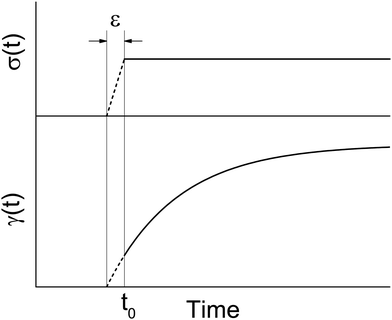
In the case of creep measurements in simple shear, where a constant shear stress of magnitude σ0 (i) is applied to the sample within a brief period of time ε (Fig. 2), (ii) is achieved with a constant rate of stress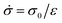 and (iii) holds for an unlimited period of time, the following constitutive equation simplifies:
and (iii) holds for an unlimited period of time, the following constitutive equation simplifies: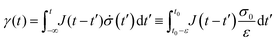 | (4) |
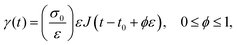 | (5) |
| γ(t) = σ0J(t) | (6) |
Eqn (6) has been accepted by the rheology community because the data acquisition rates of rheometers were (until few years ago) slower than ε. However, nowadays, thanks to the development of sensitive and fast transducers, it is possible to acquire a significant number of experimental data within the time window defined by ε. Nevertheless, these data are commonly discarded because of the condition on which eqn (6) relies on, i.e. t ≫ ε.
2.4 Evaluating the Fourier transform of raw data
An analytical procedure for the evaluation of the Fourier transform of any generic function sampled over a finite time window was proposed by Evans et al.,36,37 to convert creep compliance J(t) into G*(ω) directly, without the use of Laplace transforms nor fitting functions. This method is based on the interpolation of the finite data set by means of a piecewise-linear function. In particular, the general validity of the proposed procedure makes it equally applicable to find the Fourier transform ĝ(ω) of any time-dependent function g(t) that vanishes for negative t, sampled at a finite set of data points (tk,gk), where k = 1…N, which extend over a finite range, and need not be equally spaced:37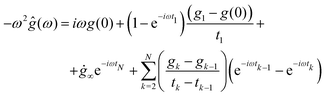 | (7) |
This method has been improved by Tassieri et al.,38 while analysing microrheology measurements performed with optical tweezers. The authors found that a substantial reduction in the size of the high-frequency artefacts, from which some high-frequency noise tends to spill over into the top of the experimental frequency range, can be achieved by an over-sampling technique. The technique involves first numerically interpolating between data points using a standard non-overshooting cubic spline, and then generating a new, over-sampled data set, by sampling the interpolating function not only at the exact data points but also at a number of equally-spaced points in between. Notice that, over-sampling is a common procedure in signal processing and it consists of sampling a signal with a sampling frequency fs much higher than the Nyquist rate 2B, where B is the highest frequency contained in the original signal. A signal is said to be oversampled by a factor of β ≡ fs/(2B).39
The advantages of an analytical tool, such as i-Rheo, which allows the evaluation of the Fourier transform of raw experimental data, become apparent when both eqn (4) and the relationship between the material's complex shear modulus and the creep compliance are considered together in the frequency domain:
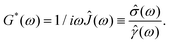 | (8) |
3 Materials and methods
3.1 Samples
3.2 Rheology
Rheological measurements on homogeneous complex fluids were performed with a stress-controlled rotational rheometer MCR 302 (Anton Paar) having the lowest torque value of ∼0.1 μN m. The instrument was equipped with a cone and plate geometry of D = 50 mm in diameter and 1° angle. For the PDMS sample, a stress of σ0 = 500 Pa was applied to the sample for a duration of 103 s. For the 1% weight polyacrilamide solution a stress of σ0 = 0.5 Pa was applied to the sample for a duration of 104 s. Conventional dynamic frequency sweep measurements were performed with strain amplitudes of γ = 5% and γ = 20%, respectively, in the frequency range of 10−2 < ω < 102 rad s−1. All the tests performed on these two samples were carried out at a temperature of T = 5 °C. This temperature was chosen to shift the crossing point of the viscoelastic moduli well within the explored range of frequencies.Measurements on the colloidal suspensions were performed with a DHR3 stress-controlled rotational rheometer (TA instruments), using a plate-plate geometry of diameter D = 30 mm and a gap d = 0.5 mm. We used a solvent trap to minimize solvent evaporation. The temperature was set to T = 20 °C and controlled within 0.1 °C via a Peltier system. For all samples, a dynamic strain sweep (DSS) at frequency ω = 1 rad s−1 was performed directly after loading to determine the linear response regime and, for glassy samples, the strain amplitude at which fluidization occurs. For these last samples, corresponding to dispersions with ϕ = 0.58 and 0.60, the effects of sample loading and ageing were reduced by performing the following rejuvenation procedure before each test. First, a dynamic time sweep with a large strain amplitude, typically γ = 500%, well above the yield strain, with a duration of 200 s and a frequency ω = 1 rad s−1 was performed in order to fluidize the sample. After that, another dynamic time sweep with the same frequency but strain amplitude within the linear viscoelastic regime, typically γ = 1% was applied until a steady-state response, i.e. a time-independent storage G′(ω) and loss modulus G′′(ω), was observed, which typically took about 150 s. This indicated that no further structural changes occurred and hence a reproducible state of the sample was obtained. The linear viscoelastic moduli where measured using a conventional DFS with a strain amplitude of γ = 0.1–1%, depending on the sample, in the frequency range 10−1 < ω < 102 rad s−1. Creep experiments for different applied stress σ values were measured for all the samples for a duration of 103 s using the fast sampling option, which provides a sampling time tsam ≈ 1.5 × 10−3 s.
4 Results and discussion
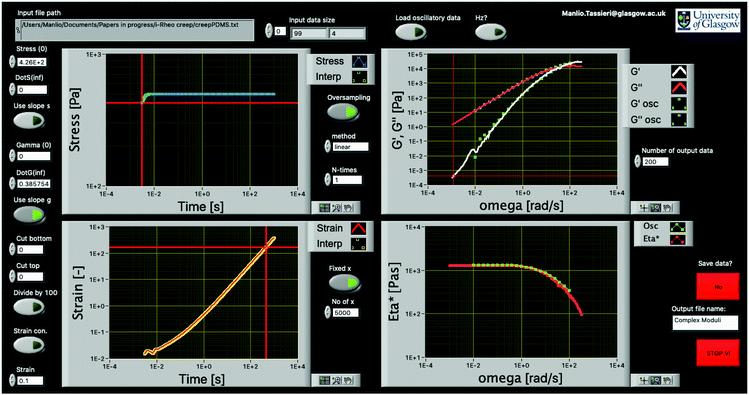
Fig. 3 shows the front panel of the executable i-Rheo, which reads the experimental raw data (i.e., [tk,σk,γk]) in the form of a tab-separated .txt file and generates a new oversampled set of data (with a sufficiently high value of β ≡ fstsam/2 ≫ ωtsam, usually fs ≅ 10 MHz); then it applies eqn (7) to this new data set and returns the viscoelastic moduli of the material under investigation.It is important to highlight that the values of the two parameters g(0) and ġ∞ required by eqn (7) have been set equal to zero for γ(0) = 0, and 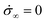 ; whereas, σ(0) and
; whereas, σ(0) and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∞ are obtained from the experimental data as follows: (i) σ(0) is the first experimental value of the stress (e.g., in Fig. 3σ(0) = 426 Pa); (ii)
∞ are obtained from the experimental data as follows: (i) σ(0) is the first experimental value of the stress (e.g., in Fig. 3σ(0) = 426 Pa); (ii) ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∞ is obtained from a linear regression of the long-time behaviour of γ(t). Notably, the assumptions made for γ(0) and
∞ is obtained from a linear regression of the long-time behaviour of γ(t). Notably, the assumptions made for γ(0) and  are actually exact, because the sample is initially undeformed and when the stress is constant its time derivative is null. In the cases of σ(0) and
are actually exact, because the sample is initially undeformed and when the stress is constant its time derivative is null. In the cases of σ(0) and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∞, they are sensible approximations. Indeed, for viscoelastic fluids, whose linear response is characterised by the existence of the terminal region at low frequencies (where G′(ω) ∝ ω2 and G′′(ω) ∝ ω for ω → 0), the long-time behaviour of the strain is expected to be: γ(t) ∝ t/η for t → ∞ and therefore
∞, they are sensible approximations. Indeed, for viscoelastic fluids, whose linear response is characterised by the existence of the terminal region at low frequencies (where G′(ω) ∝ ω2 and G′′(ω) ∝ ω for ω → 0), the long-time behaviour of the strain is expected to be: γ(t) ∝ t/η for t → ∞ and therefore ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∞ ∝ 1/η for t → ∞, where η is the fluid's steady state shear viscosity. A similar conclusion is achieved in the case of viscoelastic solids (e.g., gels and rubbers), for which J(t) tends to a finite value J0 at long times and for which
∞ ∝ 1/η for t → ∞, where η is the fluid's steady state shear viscosity. A similar conclusion is achieved in the case of viscoelastic solids (e.g., gels and rubbers), for which J(t) tends to a finite value J0 at long times and for which ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∞ ≅ 0. The effectiveness of i-Rheo to evaluate the LVE properties of complex materials from conventional bulk rheology step-stress measurements has been initially corroborated by investigating the rheological properties of two homogeneous complex fluids (Section 4.1), then applied to the rheological study of concentrated suspensions of colloidal particles, including glasses (Section 4.2).
∞ ≅ 0. The effectiveness of i-Rheo to evaluate the LVE properties of complex materials from conventional bulk rheology step-stress measurements has been initially corroborated by investigating the rheological properties of two homogeneous complex fluids (Section 4.1), then applied to the rheological study of concentrated suspensions of colloidal particles, including glasses (Section 4.2).
4.1 Creep experiments of homogeneous complex fluids
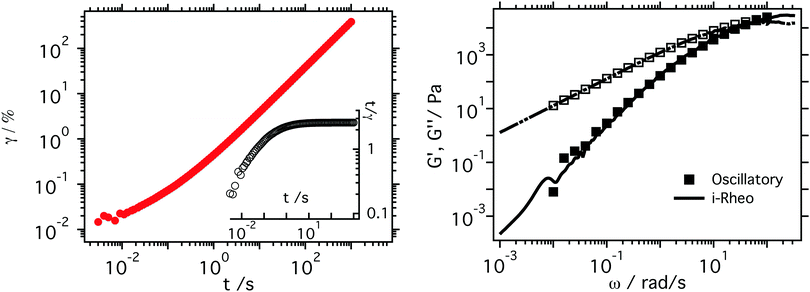
In order to corroborate the applicability of i-Rheo to creep measurements, preliminary tests were performed on two homogeneous complex fluids; i.e., a polydimethylsiloxane (PDMS) sample and a solution of polyacrylamide at a concentration of 1 wt%. The results are reported in Fig. 4 and 5, respectively. In particular, in the main plot of both the figures, the material strain γ is reported as a function of time t. The inset shows the temporal behaviour of the ratio t/γ(t), which in the case of viscoelastic fluids should approach a plateau value over long time frames. This is because at sufficiently longer time the fluids' compliance should assume the temporal form of: J(t) ≅ t/η; as the elastic character of the complex fluid should vanish towards zero (i.e., G′(1/t) ∝ (1/t)2 → 0 for t → ∞). Therefore, it is a valid approximation to extract the value of![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∞ from the terminal (plateau) region of the measurements. Once all the parameters required for the application of eqn (7) have been assigned, then the raw experimental data of both stress and strain functions can be fed to i-Rheo for their conversion into the materials' LVE properties viaeqn (8). The efficacy of i-Rheo is validated by the results reported in both Fig. 4 and 5 (right), where the transformed data are directly compared with conventional oscillatory measurements performed on the same samples prior to performing the creep test. In particular, in the case of PDMS (Fig. 4, right), the two experimental methods agree over a range of frequencies spanning four decades, with a net gain of half decade at frequencies higher than 100 rad s−1 in favour of i-Rheo. In the case of the polyacrylamide solution (Fig. 5, right), it is interesting to highlight the effects of instrument inertia at relatively short time scales (i.e., for t < 1 s in this case), where one could identify a characteristic time tI (dotted lines in Fig. 5, left) before which the instrument is not able to account for the inertia of the electric motor and the strain rapidly increases from zero up to a region where the ‘creep ringing’45,46 phenomenon is observed (which is caused by the coupling of the instrument inertia with the elasticity of the sample). As we show also later for colloidal suspensions, the creep ringing data are retained and actually contain useful information on the fluid's LVE properties. Instead the data affected by the motor inertia at time scales shorter than tI (i.e., for ω ≳ 10 rad s−1) cannot be used to determine the viscoelastic moduli. This also implies that, even if the sampling rate tsam is shorter than tI, 1/tsam will not define the largest accessible frequency, which is not the case for step-strain experiments.3 If these initial data affected by inertia are discarded, the two methods show a noteworthy agreement over three decades of frequencies, with a net gain of two decades at low frequencies in favour of i-Rheo, which would be extremely time consuming to achieve with oscillatory measurements. The initial range of creep data to be discarded can be identified by those values of t/γ(t) showing a monotonic decrease at short time scales (i.e., all those data on the left side of the dotted line drawn in the inset of Fig. 5, left). Notice that, as a means of comparison, in Fig. 5 (right) we also report the viscoelastic moduli derived via i-Rheo applied to the entire set of data, including those affected by the instrument inertia; the results endorse the arguments discussed above.
∞ from the terminal (plateau) region of the measurements. Once all the parameters required for the application of eqn (7) have been assigned, then the raw experimental data of both stress and strain functions can be fed to i-Rheo for their conversion into the materials' LVE properties viaeqn (8). The efficacy of i-Rheo is validated by the results reported in both Fig. 4 and 5 (right), where the transformed data are directly compared with conventional oscillatory measurements performed on the same samples prior to performing the creep test. In particular, in the case of PDMS (Fig. 4, right), the two experimental methods agree over a range of frequencies spanning four decades, with a net gain of half decade at frequencies higher than 100 rad s−1 in favour of i-Rheo. In the case of the polyacrylamide solution (Fig. 5, right), it is interesting to highlight the effects of instrument inertia at relatively short time scales (i.e., for t < 1 s in this case), where one could identify a characteristic time tI (dotted lines in Fig. 5, left) before which the instrument is not able to account for the inertia of the electric motor and the strain rapidly increases from zero up to a region where the ‘creep ringing’45,46 phenomenon is observed (which is caused by the coupling of the instrument inertia with the elasticity of the sample). As we show also later for colloidal suspensions, the creep ringing data are retained and actually contain useful information on the fluid's LVE properties. Instead the data affected by the motor inertia at time scales shorter than tI (i.e., for ω ≳ 10 rad s−1) cannot be used to determine the viscoelastic moduli. This also implies that, even if the sampling rate tsam is shorter than tI, 1/tsam will not define the largest accessible frequency, which is not the case for step-strain experiments.3 If these initial data affected by inertia are discarded, the two methods show a noteworthy agreement over three decades of frequencies, with a net gain of two decades at low frequencies in favour of i-Rheo, which would be extremely time consuming to achieve with oscillatory measurements. The initial range of creep data to be discarded can be identified by those values of t/γ(t) showing a monotonic decrease at short time scales (i.e., all those data on the left side of the dotted line drawn in the inset of Fig. 5, left). Notice that, as a means of comparison, in Fig. 5 (right) we also report the viscoelastic moduli derived via i-Rheo applied to the entire set of data, including those affected by the instrument inertia; the results endorse the arguments discussed above.
Moreover, with regards to the lowest accessible frequencies, typically the limiting factor is the signal-to-noise (SNR) ratio of the data measured after a long time. In a creep experiment though, large strain γ values are measured at long times, meaning that the SNR value should be large. This is different from the use of i-Rheo to determine viscoelastic moduli from stress relaxation after a step strain. Indeed, in that case the stress tends to zero at long times and therefore SNR is small. Thus creep tests are in principle a better choice to determine viscoelastic moduli at small frequencies. However, as shown hereafter, the sample behaviour at long times might impose additional constraints.
4.2 Creep experiments on colloidal suspensions
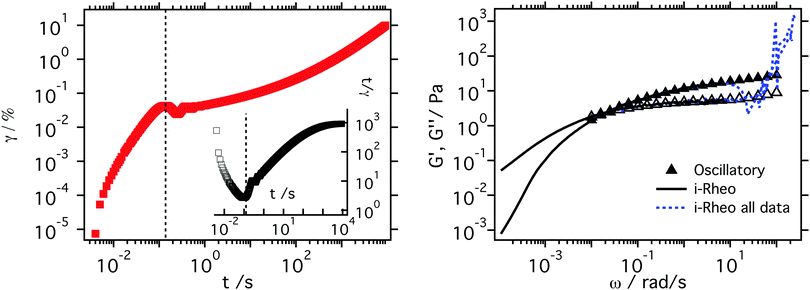
After corroborating the efficacy of i-Rheo for determining the LVE moduli of homogeneous complex fluids, we apply the same approach to concentrated suspensions of hard-sphere like colloids with volume fraction 0.40 ≤ ϕ ≤ 0.60. In these concentrated colloidal suspensions additional complexity is present due to hydrodynamic effects and in particular non-equilibrium effects associated with the glass transition.Hereafter we report the results for a selected sample with ϕ = 0.54 to illustrate the procedure used to determine the linear viscoelastic moduli by means of i-Rheo and investigate the dependence on the applied stress. Then, we report the linear viscoelastic moduli obtained via i-Rheo for all the investigated samples and their comparison with those of conventional DFS.
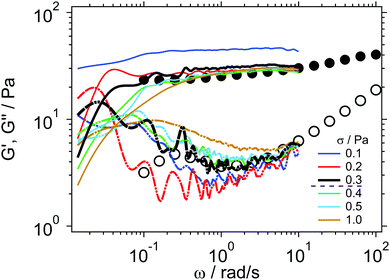
The results of a dynamic strain sweep (DSS) test performed on a sample with ϕ = 0.54 at ω = 1 rad s−1 are reported in Fig. 6. At this frequency, the sample behaves like a viscoelastic solid, with the storage modulus larger than the loss modulus within the material's linear response regime, which extends up to a strain amplitude of γ0 ≈ 1%, with a corresponding oscillatory stress amplitude of circa 0.3 Pa. In the non-linear regime of the material response the moduli cross at γ0 ≈ 12%, which corresponds to a stress amplitude of approximately 1.5 Pa, after which a fluid-like response is observed. This is consistent with recent studies, which indicate the crossing point of the frequency dependent viscoelastic moduli as the yielding point of soft glassy materials.47 We have used the DSS tests to identify for each sample the stress values that fall within the linear and non-linear regimes of the materials. We then selected a series of stresses across the two regimes to investigate the effects of the applied stresses on the frequency-dependent moduli evaluated by means of i-Rheo. Fig. 7 shows the creep measurements performed at different applied stresses (i.e., σ = 0.1, 0.2, 0.3, 0.4, 0.5 and 1 Pa) on a sample having a volume fraction of ϕ = 0.54. As for the polyacrylamide solution, also the response of this system shows inertia effects in the time interval 10−3 < t < 10−1 s, followed by a ‘creep ringing’ regime for 10−1 < t < 1 s. At longer times, all curves show a sub-linear increase of the strain γ(t) with time, which is characteristic of solid-like materials for applied stresses lower than their yield stress σy, which for this system can be estimated from Fig. 6 to be σy ≅ 1.5 Pa. Moreover, from Fig. 7 it can be seen that the measured strain increases with the increase of the applied stress, as expected.
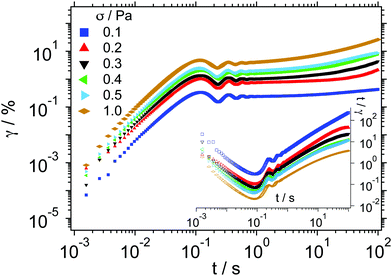 | ||
| Fig. 7 Strain γ(t) as a function of time t obtained from creep measurements performed with different applied stresses on a sample with ϕ = 0.54. Inset: t/γ as a function of t. | ||
4.3 Results of i-Rheo for different applied stresses
In Fig. 8 we report the comparison between the frequency-dependent linear viscoelastic moduli obtained by means of i-Rheo applied to the creep measurements shown in Fig. 7 (lines) and those obtained from a DFS (symbols). In particular, it can be seen that for the smallest applied stress of σ = 0.1 Pa the moduli obtained from i-Rheo overestimate the solid-like behaviour of the material, with a higher G′(ω) and a lower G′′(ω) than those measured with a DFS, whereas, for σ = 0.2 Pa, while the storage modulus shows a good agreement with that obtained from the DFS measurement, G′′(ω) still shows a significant deviation. Interestingly, for σ = 0.3 Pa the agreement between the two methods is very good for both moduli, especially in the frequency range of 0.1 < ω < 10 rad s−1. Notably, this value of the applied stress is very close to the limit of the material's linear response, see Fig. 6. For larger values of the applied stress we observed a detrimental effect on the agreement between the two methods. This is expected as i-Rheo assumes a linear relation between stress and strain, which of course does not hold in the materials' non-linear regime. Therefore, the onset of deviations between the moduli obtained by i-Rheo and those obtained by conventional oscillatory measurements could be used to estimate the onset of the materials' non-linear response. In particular, the moduli derived by means of i-Rheo increasingly deviate from the expected values at small frequencies (i.e. long relaxation times), with a crossover of the moduli that shifts towards increasingly larger frequency values. This is consistent with the progressive shortening of the structural relaxation time of the sample associated with the structural rearrangements induced by the shear deformation, which leads to yielding and fluidisation of the sample when the applied stress falls in the materials' non-linear response regime. It is interesting to notice that, of the two moduli G′(ω) is less sensitive than G′′(ω) to the variations of the applied stress. A similar behaviour has been observed for all samples investigated in this work. Specifically, we found that the best agreement between the two approaches was obtained for stress values that were closely approaching from the bottom the upper limit of the materials' linear response regime. This might be due to the fact that noise contributions are smaller for larger stress, i.e. for stresses close to the limit of the materials' linear response regime the signal to noise ratio is close to its maximum value, but yet within the materials' LVE regime, where the effects of shear-induced structural changes are not observed.4.4 Comparison between i-Rheo and DFS for different ϕ values
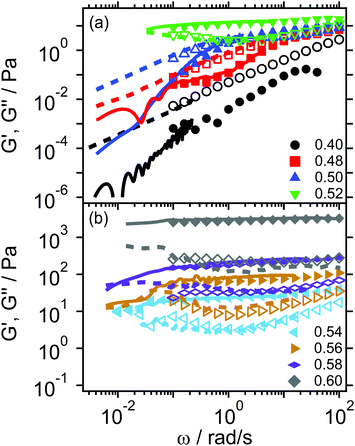
In Fig. 9 we report the comparison between the frequency-dependent linear viscoelastic moduli obtained by means of i-Rheo (lines) by converting creep measurements (see Fig. 10) and those obtained from DFS (symbols) for different colloidal volume fractions, ranging from the fluid state at ϕ = 0.40 to the glass state at ϕ = 0.60. Notably, for all the investigated samples the agreement between the two experimental procedures is very good, confirming the effectiveness of i-Rheo. It must be noted that, while all the creep measurements were performed over the same experimental time window, the related viscoelastic moduli were computed over different frequency ranges, depending on the values of ϕ, because of the instrument inertia45,46 as already discussed earlier. In particular, for ϕ = 0.40 the instrument inertia was affecting the measurement up to a time of t1 ≈ 1.5 s (Fig. 10), which implies a maximum frequency of ω ≈ 5 × 10−1 rad s−1. For ϕ = 0.48, 0.50 and 0.52 the influence of the inertia is less detrimental than the previous case (Fig. 10), and data were truncated at a time of t2 ≈ 1.5 × 10−1 s, which translates into a maximum accessible frequency of the order of 7 rad s−1. For higher volume fractions (or higher material stiffness), i.e. ϕ = 0.54, 0.56 and 0.58 the creep data were discarded (because of inertia) up to a time of t3 ≈ 5 × 10−2 s (Fig. 10) and therefore achieving frequencies up to ω ≈ 20 rad s−1. Finally, for the largest volume fraction ϕ = 0.60 (with the highest stiffness) the maximum frequency was ω ≈ 102 rad s−1. As a preliminary conclusion, we could infer that by increasing the volume fraction of the dispersion we increase the overall stiffness of the material, which mitigates the disruptive effects of instrument inertia on the measurements of the materials' LVE properties via creep tests, as corroborated by the results reported in Fig. 4 and 10. Note that the ringing effects are present for ϕ ≥ 0.50 and become more pronounced with increasing ϕ, in agreement with models describing the coupling between viscoelasticity and inertia.45,46,48–50 It is interesting to mention that the regions of the creep measurements affected by the ringing effects were not discarded during the analysis with i-Rheo; they actually provide output data that are in good agreement with oscillatory measurements, as shown in Fig. 5 and 10, confirming that the ringing regime contains useful information on the LVE properties of materials.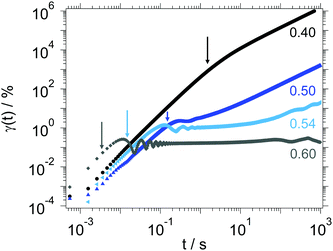 | ||
| Fig. 10 Strain γ(t) as a function of time t obtained in creep experiments for different colloidal volume fractions ϕ, as indicated. The applied stress depends on the sample and corresponds to the value used to obtain the viscoelastic moduli in Fig. 9. Arrows indicate the limit of the response affected by tool inertia effects. | ||
In terms of the lowest accessible frequency, we can argue that it is affected by the physics of the suspension rather than by the technical limitations of the rheometer. Indeed, concentrated colloidal suspensions are often characterised by flow-induced inhomogeneities, such as shear banding, which can affect the response of colloidal dispersions during creep measurements, especially after a long time,30,32 when approaching and/or crossing the glass transition.30–32,51 This was not a problem for the lowest volume fractions explored in this work, i.e. ϕ = 0.40, 0.48 and 0.50, which did not manifest flow inhomogeneities within the measurement time-window (Fig. 10) and therefore the viscoelastic moduli were evaluated down to ω ≈ 4 × 10−3 rad s−1. In the cases of ϕ = 0.40 and 0.48 some oscillations observed in G′′(ω) could be attributed to a low signal and noise of the measurements. Moreover, for all ϕ ≥ 0.52 the samples showed an anomalous behaviour of the strain γ(t) for t ≳ 102 s (Fig. 10), which was limiting the range of the lowest accessible frequencies by means of i-Rheo.
5 Conclusions
In this work we report experimental evidence of the applicability of i-Rheo to the analysis of time-dependent step-stress (creep) measurements for the evaluation of the linear viscoelastic properties of materials. I-Rheo was recently introduced for the analysis of time-dependent step-strain measurements and successfully exploited for the analysis of both molecular dynamics simulations and atomic force microscopy measurements. Here we have validated the applicability of i-Rheo to analyse creep measurements performed on homogeneous complex fluids, and then exploited its effectiveness for the evaluation of the viscoelastic moduli of suspensions of hard sphere-like colloids at different volume fractions, spanning the state diagram from fluids to glasses. For all the explored samples, we found a very good agreement between the outputs obtained by means of i-Rheo and those obtained via conventional oscillatory measurements. We found that the transformation of creep measurements by means of i-Rheo works best for values of the applied stress that are close to the limit of the suspension's linear response regime. By entering the materials' non-linear response regime, we found an increasingly larger deviation from oscillatory measurements, which can be associated with the progressive structural rearrangement of the samples induced by the shear flow. The range of accessible frequencies for the systems investigated in this work was limited by two factors: at high frequencies, by the inertia of the instrument, which becomes less important with increasing the sample stiffness (or increasing ϕ); and at low frequencies, by physical phenomena occurring due to the nature of the samples, such as shear banding. For values of the volume fraction approaching and crossing the glass transition, shear induced inhomogeneities appearing at long times (revealed by an irregular behaviour of the time-dependent strain γ(t)) limited the lowest accessible frequency. Nonetheless, we confirm the effectiveness of i-Rheo for gathering valuable information on the materials' linear viscoelastic properties even from ‘creep ringing’ data, confirming its potency and general validity as an accurate method for determining the material's rheological behaviour for a variety of complex systems. Indeed, we anticipate the use of i-Rheo for the rheological investigation of novel and more complex colloidal systems, with particular attention to the system-specific limitations for the evaluation of the low frequency linear viscoelastic properties. Moreover, besides obvious differences in the experimental protocols, i-Rheo could be successfully used to determine the viscoelastic properties of harder materials, such as for example metallic glasses.52Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. R. B. and M. L. acknowledge support from Consejo Nacional de Ciencias y Tecnologia (CONACYT, Mexico) through grant No. LANIMFE-279887-2017 and CB-2015-01-257636. M. T. acknowledges support via EPSRC grants (EP/R035067/1, EP/R035563/1, and EP/R035156/1).Notes and references
- R. Larson, The structure and rheology of complex fluids, Oxford University Press, New York, 1999 Search PubMed.
- C. W. Macosko, Rheology: Principles, Measurements, and Applications, Wiley-VCH, 1994 Search PubMed.
- M. Tassieri, M. Laurati, D. J. Curtis, D. W. Auhl, S. Coppola, A. Scalfati, K. Hawkins, P. R. Williams and J. M. Cooper, J. Rheol., 2016, 60, 649–660 CrossRef CAS.
- R. M. L. Evans, M. Tassieri, D. Auhl and T. A. Waigh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 012501 CrossRef CAS PubMed.
- Y. H. Chim, L. M. Mason, N. Rath, M. F. Olson, M. Tassieri and H. Yin, Sci. Rep., 2018, 8, 14462 CrossRef PubMed.
- J. A. Moreno-Guerra, I. C. Romero-Sánchez, A. Martinez-Borquez, M. Tassieri, E. Stiakakis and M. Laurati, Small, 2019, 1904136 CrossRef CAS PubMed.
- M. Tassieri, J. Ramrez, N. C. Karayiannis, S. K. Sukumaran and Y. Masubuchi, Macromolecules, 2018, 51, 5055–5068 CrossRef CAS.
- J. Mewis and N. J. Wagner, Colloidal Suspension Rheology, Cambridge University Press, New York, 2012 Search PubMed.
- P. Pusey, Liquids, freezing and the glass transition, North-Holland, Amsterdam, 1991 Search PubMed.
- P. N. Pusey and W. van Megen, Nature, 1986, 320, 340–342 CrossRef CAS.
- W. van Megen and S. M. Underwood, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1994, 49, 4206–4220 CrossRef CAS PubMed.
- D. Heckendorf, K. J. Mutch, S. U. Egelhaaf and M. Laurati, Phys. Rev. Lett., 2017, 119, 048003 CrossRef CAS PubMed.
- P. N. Pusey, J. Phys., 1987, 48, 709–712 CrossRef CAS.
- T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 75, 2770–2773 CrossRef CAS PubMed.
- N. Koumakis, A. Pamvouxoglou, A. S. Poulos and G. Petekidis, Soft Matter, 2012, 8, 4271–4284 RSC.
- M. Siebenbuerger, M. Fuchs, H. H. Winter and M. Ballauff, J. Rheol., 2009, 53, 707–726 CrossRef.
- P. D'Haene, PhD thesis, Katholieke Universiteit Leuven, 1992.
- S. P. Meeker, W. C. K. Poon and P. N. Pusey, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1997, 55, 5718–5722 CrossRef CAS.
- Z. Cheng, J. Zhu, P. M. Chaikin, S.-E. Phan and W. B. Russel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 041405 CrossRef PubMed.
- B. J. Maranzano and N. J. Wagner, J. Chem. Phys., 2002, 117, 10291–10302 CrossRef CAS.
- T. Sentjabrskaja, M. Laurati and S. U. Egelhaaf, Eur. Phys. J.: Spec. Top., 2017, 226, 3023–3037 CAS.
- M. Laurati, P. Masshoff, K. J. Mutch, S. U. Egelhaaf and A. Zaccone, Phys. Rev. Lett., 2017, 118, 018002 CrossRef CAS PubMed.
- N. Koumakis, M. Laurati, A. R. Jacob, K. J. Mutch, A. Abdellali, A. B. Schofield, S. U. Egelhaaf, J. F. Brady and G. Petekidis, J. Rheol., 2016, 60, 603–623 CrossRef CAS.
- C. P. Amann, D. Denisov, M. T. Dang, B. Struth, P. Schall and M. Fuchs, J. Chem. Phys., 2015, 143, 034505 CrossRef PubMed.
- T. Sentjabrskaja, M. Hermes, W. C. K. Poon, C. D. Estrada, R. Castaneda-Priego, S. U. Egelhaaf and M. Laurati, Soft Matter, 2014, 10, 6546–6555 RSC.
- K. J. Mutch, M. Laurati, C. P. Amann, M. Fuchs and S. U. Egelhaaf, Eur. Phys. J.-Spec. Top., 2013, 222, 2803–2817 CrossRef.
- N. Koumakis, M. Laurati, S. U. Egelhaaf, J. F. Brady and G. Petekidis, Phys. Rev. Lett., 2012, 108, 098303 CrossRef CAS PubMed.
- J. Zausch and J. Horbach, Europhys. Lett., 2009, 88, 60001 CrossRef.
- R. Besseling, L. Isa, P. Ballesta, G. Petekidis, M. E. Cates and W. C. K. Poon, Phys. Rev. Lett., 2010, 105, 268301 CrossRef CAS PubMed.
- P. Ballesta and G. Petekidis, Phys. Rev. E, 2016, 93, 042613 CrossRef CAS PubMed.
- S. M. Fielding, J. Rheol., 2016, 60, 821–834 CrossRef CAS.
- D. Bonn, M. M. Denn, L. Berthier, T. Divoux and S. Manneville, Rev. Mod. Phys., 2017, 89, 035005 CrossRef.
- L. Perez-Ocampo, A. Zaccone and M. Laurati, J. Rheol., 2018, 62, 197–207 CrossRef CAS.
- J. D. Ferry, Viscoelastic properties of polymers, Wiley, 3rd edn, 1980 Search PubMed.
- M. Mours and H. Winter, Proceedings of the XIITH International Congress on Rheology, 1996, pp. 737–738 Search PubMed.
- R. M. L. Evans, British Society of Rheology, Rheol. Bull., 2009, 50, 76 Search PubMed.
- R. M. L. Evans, M. Tassieri, D. Auhl and T. A. Waigh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 012501 CrossRef CAS PubMed.
- M. Tassieri, R. Evans, R. L. Warren, N. J. Bailey and J. M. Cooper, New J. Phys., 2012, 14, 115032 CrossRef.
- B. Lathi, Linear Systems and Signals, Oxford University Press, USA, 2004 Search PubMed.
- L. Antl, J. W. Goodwin, R. D. Hill, R. H. Ottewill, S. M. Owens, S. Papworth and J. A. Waters, Colloids Surf., 1986, 17, 67–78 CrossRef CAS.
- C. P. Royall, W. C. K. Poon and E. R. Weeks, Soft Matter, 2013, 9, 17–27 RSC.
- W. Schaertl and H. Sillescu, J. Stat. Phys., 1994, 77, 1007–1025 CrossRef.
- K. W. Desmond and E. R. Weeks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022204 CrossRef PubMed.
- A. Santos, S. B. Yuste, M. López de Haro, G. Odriozola and V. Ogarko, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 040302 CrossRef PubMed.
- R. H. Ewoldt and G. H. McKinley, Rheol. Bull., 2007, 76, 4–6 Search PubMed.
- M. Kim, J.-E. Bae, N. Kang and K. Soo Cho, J. Rheol., 2015, 59, 237–252 CrossRef CAS.
- D. V. Denisov, M. T. Dang, B. Struth, A. Zaccone, G. H. Wegdam and P. Schall, Sci. Rep., 2015, 5, 14359 CrossRef CAS PubMed.
- L. C. E. Struik, Rheol. Acta, 1967, 6, 119–129 CrossRef CAS.
- C. Baravian and D. Quemada, Rheol. Acta, 1998, 37, 223–233 CrossRef CAS.
- A. Jaishankar, V. Sharma and G. H. McKinley, Soft Matter, 2011, 7, 7623–7634 RSC.
- T. Sentjabrskaja, P. Chaudhuri, M. Hermes, W. C. K. Poon, J. Horbach, S. U. Egelhaaf and M. Laurati, Sci. Rep., 2015, 5, 11884 CrossRef CAS PubMed.
- B. Cui, J. Yang, J. Qiao, M. Jiang, L. Dai, Y.-J. Wang and A. Zaccone, Phys. Rev. B, 2017, 96, 094203 CrossRef.
| This journal is © the Owner Societies 2020 |