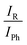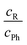Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Three-dimensional docking of alcohols to ketones: an experimental benchmark based on acetophenone solvation energy balances†
C.
Zimmermann
 ,
H. C.
Gottschalk
,
H. C.
Gottschalk
 and
M. A.
Suhm
and
M. A.
Suhm
 *
*
Georg-August-Universität Göttingen, Tammannstraße 6, 37077 Göttingen, Germany. E-mail: msuhm@gwdg.de
First published on 2nd January 2020
Abstract
The two hydrogen bond solvation sites exhibited by the carbonyl group in acetophenone are influenced by alkylation of the methyl group in both the acetophenone and in the prototype solvent methanol, largely due to London dispersion forces. Phenyl docking and alkyl docking preferences can be realized at will by appropriate substitution. In particular, cyclopropylation helps to stabilize the opposite phenyl docking site. In all cases, the energy gap is small enough to allow for a simultaneous detection even under low temperature conditions. This density functional prediction is checked experimentally by jet FTIR spectroscopy and largely confirmed. A spurious out-of-plane solvation preference predicted for cyclopropylphenylketone with tert-butyl alcohol by B3LYP-D3 calculations is not confirmed experimentally. It is unlikely that this discrepancy is due to zero-point energy effects. Instead, the second most stable alkyl-side solvation motif predicted with a more in-plane coordination is found in the jet expansion. Overall, the ability of carbonyl solvation balances to benchmark subtle electronic structure effects for non-covalent interactions without major nuclear motion corrections is supported.
1 Introduction
Hydrogen bonding to![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups1 reflects one of the most important structural design elements of nature, because it provides essential connectivities between chain segments of proteins2 and other biopolymers.3 Quantum chemical and mechanical models used in the life sciences should be able to describe this interaction accurately and without erratic, as opposed to systematic, error cancellation. This can be tested by structural or vibrational spectroscopy of molecular complexes, by preference in the cold gas phase where error compensation from the environment and by thermal effects can be ruled out.4,5 A model which successfully reproduces local structural and vibrational properties of hydrogen bonds to C
O groups1 reflects one of the most important structural design elements of nature, because it provides essential connectivities between chain segments of proteins2 and other biopolymers.3 Quantum chemical and mechanical models used in the life sciences should be able to describe this interaction accurately and without erratic, as opposed to systematic, error cancellation. This can be tested by structural or vibrational spectroscopy of molecular complexes, by preference in the cold gas phase where error compensation from the environment and by thermal effects can be ruled out.4,5 A model which successfully reproduces local structural and vibrational properties of hydrogen bonds to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups may still predict the wrong energy sequence among different conformations, because the latter is a global quantity which heavily involves short and long range secondary contacts described by Pauli and London forces in addition to the primary hydrogen bond. Hence, it is important to develop experimental techniques which probe relative energies of different hydrogen bond arrangements, along with vibrational or rotational spectra. This is the idea behind the concept of intermolecular energy balances.6
O groups may still predict the wrong energy sequence among different conformations, because the latter is a global quantity which heavily involves short and long range secondary contacts described by Pauli and London forces in addition to the primary hydrogen bond. Hence, it is important to develop experimental techniques which probe relative energies of different hydrogen bond arrangements, along with vibrational or rotational spectra. This is the idea behind the concept of intermolecular energy balances.6
An intermolecular energy balance for carbonyl groups exploits the intrinsic similarity between the two lone electron pairs at the oxygen atom as hydrogen bond acceptors. The separation of these two lone pairs is more pronounced than in ethers.7 This provides a balanced bimodal distribution of donors, which can be modulated by donor and acceptor substituents (see Fig. 1).
 | ||
| Fig. 1 Schematic illustration of the two docking sites 4, 4′ for alcohols R′OH on the alkyl (R, with greek acronyms M, Λ and Δ) and phenyl (Ph) sides of the acetophenone. | ||
The barrier between the two docking sites is typically rather low, on the order of a few kJ mol−1. Therefore, complexation of an unsymmetric ketone with a hydrogen bond donor such as an alcohol in a supersonic jet environment may start statistically, but collisional cooling in the expansion allows for some degree of equilibration between the two sites and thus probes their relative energy. This is true down to some effective conformational freezing temperature Tc, below which the lone pairs trap the hydrogen bond donor irrespective of its docking energy because the expansion runs out of energetic collisions. It has been found in previous work that Tc is typically on the order of 150 K or less for molecular complexes, if the conformational interconversion barrier is in the 1 to 5 kJ mol−1 energy range and sufficiently narrow.6,8,9
The concept of intermolecular balances is most easily applied to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes between a solute and a solvent. While cooperativity is important for hydrogen-bonded solvents, 1
1 complexes between a solute and a solvent. While cooperativity is important for hydrogen-bonded solvents, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n complexes would introduce too many isomers for a straightforward Boltzmann analysis. The stronger hydrogen bonds would amplify anharmonic effects and increase the interconversion barriers. Therefore, our focus is on the first microsolvation step for ketones. In the present work, we start with the model complex of methanol with acetophenone,6 where the hydrogen bond coordination happens largely in the plane of the ketone, either on the phenyl side (Ph) or on the alkyl side (R). We then modulate the alkyl side of the accepting ketone by replacing methyl (M) by isopropyl (Λ) and cyclopropyl (Δ), whereas the methanol is optionally replaced by tert-butyl alcohol as the donor R′OH (Fig. 1). This provides six closely related systems, for which the preference of docking to the phenyl or the alkyl side of the ketone can be experimentally determined. The latter is possible because of the pronounced sensitivity of the OH stretching frequency to the in plane C
n complexes would introduce too many isomers for a straightforward Boltzmann analysis. The stronger hydrogen bonds would amplify anharmonic effects and increase the interconversion barriers. Therefore, our focus is on the first microsolvation step for ketones. In the present work, we start with the model complex of methanol with acetophenone,6 where the hydrogen bond coordination happens largely in the plane of the ketone, either on the phenyl side (Ph) or on the alkyl side (R). We then modulate the alkyl side of the accepting ketone by replacing methyl (M) by isopropyl (Λ) and cyclopropyl (Δ), whereas the methanol is optionally replaced by tert-butyl alcohol as the donor R′OH (Fig. 1). This provides six closely related systems, for which the preference of docking to the phenyl or the alkyl side of the ketone can be experimentally determined. The latter is possible because of the pronounced sensitivity of the OH stretching frequency to the in plane C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H angle α. We need theory to predict this dependence and also the angular dependence of the IR activity. If these spectral parameters can be estimated robustly across several quantum chemical levels, they provide a firm assignment of the observed spectral signals for the two docking sites. Then, the line of argument can be inverted and the different theoretical models can be judged in terms of their ability to correctly predict the subtle energy preference between the two docking sites.6 It turns out that for a proper analysis, the torsion τ of the docking H (atom 4 or 4′ in Fig. 1) out of the phenyl C–C
O⋯H angle α. We need theory to predict this dependence and also the angular dependence of the IR activity. If these spectral parameters can be estimated robustly across several quantum chemical levels, they provide a firm assignment of the observed spectral signals for the two docking sites. Then, the line of argument can be inverted and the different theoretical models can be judged in terms of their ability to correctly predict the subtle energy preference between the two docking sites.6 It turns out that for a proper analysis, the torsion τ of the docking H (atom 4 or 4′ in Fig. 1) out of the phenyl C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O plane becomes important, once the substituents are more bulky, although out-of-plane coordination of ketones by more than 15° is not very frequent.7 The spectral signature depends strongly on this angle τ, thus assisting the proper assignment. The robust prediction of spectral assignments across several density functionals empowers jet spectroscopy to judge between different energetical predictions which are more subtle and less uniform.
O plane becomes important, once the substituents are more bulky, although out-of-plane coordination of ketones by more than 15° is not very frequent.7 The spectral signature depends strongly on this angle τ, thus assisting the proper assignment. The robust prediction of spectral assignments across several density functionals empowers jet spectroscopy to judge between different energetical predictions which are more subtle and less uniform.
An important advantage of carbonyl balances over previously investigated O/π balances8 is the expected near-perfect cancellation of anharmonic zero-point energy contributions. The local environment of the two OH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) docking sides is so similar that even the harmonic zero-point energy generated by the docking process is almost the same on both sides, unless one of the sides offers a directional secondary binding site. Furthermore, the hydrogen bonds are sufficiently weak to avoid resonances with other modes and the binding partners are sufficiently rigid to avoid major tunnelling effects on the band centers. This means that any experimentally derived preference for one of the two sides typically provides a realistic statement about the electronic structure preference. This is very valuable because anharmonic zero-point energy corrections are difficult to compute robustly for supramolecular systems of this size.9 We nevertheless include harmonic zero-point correction in our analysis, but we point out the similarity to electronic energy predictions. The docking preference is determined by the interaction of R with R′ in comparison to Ph with R′ (Fig. 1). A systematic offset caused by the ortho-phenyl Cβ–H group, which provides a more repulsive interaction with the alcohol oxygen than a methyl C–H, is superimposed on the long range attraction between R, Ph and R′ and actually facilitates the spectral distinction of the two docking sites.6
docking sides is so similar that even the harmonic zero-point energy generated by the docking process is almost the same on both sides, unless one of the sides offers a directional secondary binding site. Furthermore, the hydrogen bonds are sufficiently weak to avoid resonances with other modes and the binding partners are sufficiently rigid to avoid major tunnelling effects on the band centers. This means that any experimentally derived preference for one of the two sides typically provides a realistic statement about the electronic structure preference. This is very valuable because anharmonic zero-point energy corrections are difficult to compute robustly for supramolecular systems of this size.9 We nevertheless include harmonic zero-point correction in our analysis, but we point out the similarity to electronic energy predictions. The docking preference is determined by the interaction of R with R′ in comparison to Ph with R′ (Fig. 1). A systematic offset caused by the ortho-phenyl Cβ–H group, which provides a more repulsive interaction with the alcohol oxygen than a methyl C–H, is superimposed on the long range attraction between R, Ph and R′ and actually facilitates the spectral distinction of the two docking sites.6
In this work we show that cyclopropylation of the ketone tips the docking balance from the alkyl side towards the phenyl side for methanol as the solvating molecule. For t-butyl alcohol, only the isopropyl ketone strongly favours the alcohol on the alkyl side. As will be shown, density functionals describe these alkyl-modulated docking preferences with reasonable success. Only for the cyclopropyl/tert-butyl alcohol pairing, there are significant inconsistencies with respect to the structure, energetics and spectra, which are sensitive to details of the calculation. These inconsistencies are discussed and a plausible final assignment is presented.
2 Experimental methods
Acetophenone (Sigma-Aldrich, 99%), isobutyrophenone (Sigma-Aldrich, 97%) or cyclopropylphenylketone (Alfa Aesar, 97%) was mixed with methanol (Roth, 99.99%) or tert-butyl alcohol (Roth, 99.9%) in a large excess of helium (Linde, 99.996%) in a temperature- and time-controlled pulsed flow system and collected in a reservoir at a pressure of 0.75 bar. From there, the gas mixture was dosed through six magnetic valves into a pre-expansion chamber which is terminated by a 600 mm long and 0.2 mm wide slit. Vacuum on the low pressure side of this slit nozzle was kept up during the gas pulse by a large buffer chamber and by continuous pumping at 500 to 2000 m3 h−1. Bruker 66v/S FTIR interferometer scans at 2 cm−1 resolution were synchronized with the gas pulse, detected by a cooled InSb detector and co-averaged over 250–425 pulses to yield OH/CH stretching spectra. By varying the concentrations, mixed complex signals can be differentiated from alcohol monomers. Alcohol dimers and mixed oligomers are minimized by sufficiently dilute expansions. More details may be found elsewhere.10 In none of the examples studied in this work was any evidence found for more than two isomers of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex.
1 complex.
An automated statistical evaluation of band integral ratios was used.11 The main parameters entering this evaluation are the positions of the band maxima and – particularly important in the case of spectral overlap – a uniform but statistically varied bandwidth for such absorption signals (here chosen at (3.0 ± 0.5) cm−1). By adding synthetic noise of similar characteristics as in the experimental spectrum, it provides statistical error bars for the band integral ratios IR/IPh, which are converted into phenyl docking fractions xPh. Where spectral band overlap of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes with alcohol dimers is observed (in 2 out of 6 cases), the method is independently applied to uncorrected and dimer-subtracted spectra, combining the two resulting error margins to a single one.
1 complexes with alcohol dimers is observed (in 2 out of 6 cases), the method is independently applied to uncorrected and dimer-subtracted spectra, combining the two resulting error margins to a single one.
3 Computational methods
This is an experimental study, which uses quantum chemical methods including structure optimization and evaluation of the Hessian for assignment purposes. It is meant to invite others to test their own favourite methods. In our hands, most correlated wavefunction methods are too expensive for consistent use in systems of this size and we therefore resort to density functional theory. Predictions are based on three different density functionals. B3LYP-D3/def2-TZVP12–15 as a dispersion-corrected16 hybrid functional (also used for the initial structural isomer search), M06-2X/def2-TZVP15,17 as a global hybrid functional, and TPSS-D3/def2-TZVP15,18 as a dispersion corrected meta-GGA functional. D3 dispersion correction includes Becke–Johnson damping19–22 and a three body term16 (ESI,† Table S1). Reference values for the inexpensive functionals PBEh-3c23 and B97-3c24 are included in the ESI† for comparison. Single point energies for some of the isomer structures were obtained with the lager basis set def2-QZVP15 on B3LYP-D3 level and also using DLPNO-CCSD(T)25–27 with appropriate basis sets (see ESI,† Table S1). Structure optimizations would be desirable at these two levels, but are computationally currently somewhat too demanding for the largest systems under investigation. For the D3-corrected functionals, Orca version 4.0.1.228 and for the DLPNO calculations ORCA version 4.1.129 was used, for M06-2X Gaussian09, Rev. E.0130 was chosen. Details of the employed keywords and numerical choices are tabulated in the ESI.† This is particularly important for the M06-2X functional due to its grid sensitivity.31,32 Thermal corrections were neglected, given the very low (approx. 10 K) rotational temperature, the mode-dependent vibrational temperatures and a conformational temperature on the order of 100 K. The zero-point vibrational energy (ZPVE) was treated harmonically. Taking methanol–acetophenone as an example, the total harmonic ZPVE of the complex is 500 kJ mol−1, 1% more than the sum of the monomers. The two docking isomers differ by about 0.1 kJ mol−1 in harmonic B3LYP-D3 ZPVE, which is about 0.02% of the total ZPVE. Together with the similar bonding environment, this makes sizeable anharmonic ZPVE corrections rather unlikely, whereas the structure optimization and harmonic evaluation must be well converged to minimize numerical error. Vibrational wavenumbers and intensities were thus obtained in the double harmonic approximation. Scaling to the experimental alcohol OH stretching wavenumber removes most of the diagonal anharmonicity and some electronic structure deficiency. More importantly, the wavenumber differences between docking isomers relevant for this work should not depend strongly on anharmonicity, as they involve a very similar environment. This is further validated by deuteration (see Fig. S3 in the ESI†). We note that it is important to reproduce the experimental OH stretching shift between the docking structures as closely as possible for two reasons. It assists the spectral assignment and it contributes importantly to the ZPVE difference. An error of 20 cm−1 in this shift already amounts to 0.12 kJ mol−1 and thus approaches the predicted total B3LYP-D3 ZPVE difference between the docking isomers for methanol–acetophenone.No low-lying isomers where the alcohol OH group interacts with the aromatic π system were found, but some of the O-docking isomers probe part of the π system of the ketone group by moving out of its plane. Fig. S2 in the ESI† supports the important working assumption that the monomeric ketones do not generate torsional isomerism due to insurmountable barriers between thermally populated rotamers and the preferred monomer structure. Thus, the investigated systems involve essentially binary docking decisions which are ideal for a comparison between theory and experiment. Transition state searches between these docking variants were carried out using Woelfling (Turbomole33,34) followed by a transition state optimization with Orca version 4.0.1.2.28
4 Results
4.1 Nomenclature and theoretical predictions
The studied ketones are abbreviated M (for the methyl group in acetophenone), Λ (for the isopropyl group in isobutyrophenone) and Δ (for the cyclopropyl group in cyclopropylphenylketone). The solvating alcohols MeOH (for methanol) and tBuOH (for tert-butyl alcohol) are listed before the ketone acronym. The structures are described by two angles α and τ. 0 ≤ α ≤ 180° denotes the angle between the hydrogen-bonded H and the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C group. The torsion angle τ between H and O
C group. The torsion angle τ between H and O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C(phenyl) determines the degree of out-of-plane twisting and distinguishes between phenyl side docking (closer to 0°) and alkyl side docking (closer to 180°). In graphs, values for the MeOH complexes are denoted as triangles (upright for M, upside-down for Λ, sideways for Δ) and the tBuOH complexes by squares (M), diamonds (Λ) and stars (for the metastable prediction found in tBuOH′-Δ) or circles (for the most stable prediction made for tBuOH-Δ). Where a property refers to the alkyl docking isomer, the symbols are filled, otherwise they are empty.
C–C(phenyl) determines the degree of out-of-plane twisting and distinguishes between phenyl side docking (closer to 0°) and alkyl side docking (closer to 180°). In graphs, values for the MeOH complexes are denoted as triangles (upright for M, upside-down for Λ, sideways for Δ) and the tBuOH complexes by squares (M), diamonds (Λ) and stars (for the metastable prediction found in tBuOH′-Δ) or circles (for the most stable prediction made for tBuOH-Δ). Where a property refers to the alkyl docking isomer, the symbols are filled, otherwise they are empty.
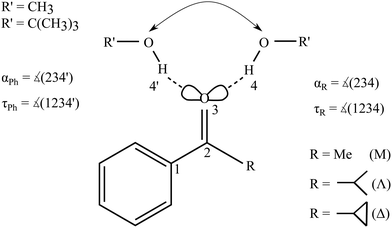
Fig. 2 summarizes the structural predictions in terms of α and τ for all six combinations and their docking isomers for the B3LYP calculations (for detailed structures see ESI,† Fig. S1). To reduce crowding, the MeOH and tBuOH results are split into an upper and lower part, respectively. On the phenyl side (empty symbols), all systems prefer a rather uniform in plane (τ ≈ 0°) hydrogen bond with a systematic distortion relative to sp2 trigonal symmetry (α = 120°) to α ≈ 140°, possibly due to steric Cβ−H⋯O hindrance. The hindrance is evidently small enough to keep the hydrogen bond in plane. On the alkyl side (filled symbols), variation of R introduces more structural scatter. Methyl and isopropyl groups allow for α ≈ 120° by avoiding in-plane Cβ contacts with the alcohol O atom, but the isopropyl group couples this with an out-of-plane displacement of the docking alcohol. Cyclopropyl (Δ) either enforces a larger hydrogen bond angle approaching that of phenyl or (in the case of tBuOH marked without an apostrophe (′) and with a filled circle in Fig. 2) adopts a significantly out-of-plane coordination of the alcohol at a smaller α. This almost isoenergetic bifurcation on the cycloalkyl side will be discussed in more detail below. Overall, except for the parent compound acetophenone, bulkiness of R and R′ tends to favour out-of-plane coordination which could be due to attractive or repulsive effects.35 The phenyl-to-alkyl docking transition states (+) also fall in two categories, either increasing α (more over the top in the case of non-cyclic bulky groups) or lowering α (more escaping out of the carbonyl plane).
 | ||
| Fig. 2 B3LYP structural predictions for the phenyl-to-alkyl (Ph-to-R, left-to-right) docking switch (arrow in Fig. 1) in terms of hydrogen bond angle α and out-of-plane twist τ for the combinations of ketone and methanol (upper panel) or tBuOH (lower panel, including a second isomer on the cyclopropyl side), respectively. Transition state barriers from the phenyl side in kJ mol−1 are placed near their location (+). | ||
Fig. S4 and S5 in the ESI† show the variation of these structural predictions when changing the density functional. For TPSS (Fig. S4, ESI†), the changes are minor, with the exception of phenyl docking for tBuOH to Δ, which is now relaxed out of the plane resulting in a smaller α value. For M06-2X (Fig. S5, ESI†), transition structures are omitted.
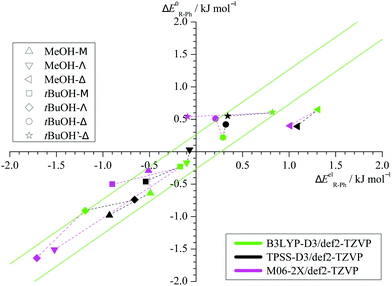
Taking the energy of the phenyl docking site as a reference, Fig. 3 plots the harmonically ZPVE-corrected relative energy of the alkyl docking site against the corresponding electronic value for the three functionals (Table S2 in the ESI† provides the energy differences). One can see that the ZPVE effects are quite subtle and most data points fall almost randomly in a narrow corridor of ±0.2 kJ mol−1 along the diagonal (illustrated by 2 parallel green lines). Only the Δ coordination by methanol is significantly favoured by ZPVE and M06-2X shows a few other small outliers. In contrast, the variations among the functionals (illustrated by connecting dashed lines from B3LYP to the other two functionals) are often larger. This suggests that the energy benchmarking potential of the present study for different functionals is not significantly affected by (an)harmonic effects, which was a design feature.6 Furthermore, the plot shows that the benchmarking dataset is sufficiently balanced, with almost as many (8) cases of predicted phenyl docking preference as for alkyl docking (10) and less (3) undecided cases (<0.2 kJ mol−1 before and after ZPVE correction). The total energy spread is close to 3 kJ mol−1, which demands for supersonic jet cooling and low barriers.
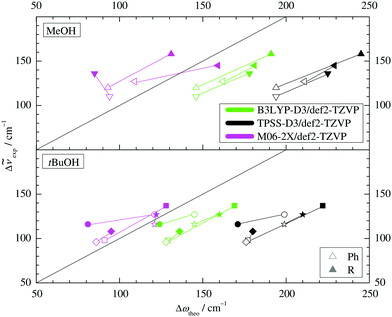
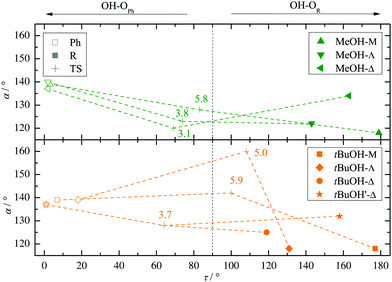
Two other important features of a successful intermolecular energy balance study are a high spectral discrimination of the docking sites and a high robustness with respect to the employed functional in terms of spectral predictions, because this is essential for a correct assignment. Fig. 4 correlates the TPSS predictions (black) and the M06-2X predictions (magenta) with the harmonic B3LYP prediction for the shift of the alkyl docking wavenumber relative to the phenyl docking wavenumber (see Table S3 in the ESI† for the actual numbers). For TPSS, the correlation with B3LYP is close and smooth, whereas M06-2X shows two significant outliers. Almost all predictions have the phenyl docking wavenumber higher than the alkyl docking wavenumber, the only exception being an out-of-plane docking of tBuOH to Δ, which will be further discussed in the context of experimental evidence. Inspection of Fig. 3 shows that the three DFT methods differ in their energetic ranking of this isomer (circles). For B3LYP it is the more stable of the alkyl docking variants, for M06-2X it is slightly the less stable (at least electronically) and for TPSS it is isoenergetic with the more in-plane coordination site (stars). Thus, we have a favourable situation where experiment should be able to discriminate particularly clearly between different functionals. Fig. S6 in the ESI† further suggests that the IR band strength ratio predictions for the docking alternatives are largely uniform across the theoretical methods, thus indicating a reliable conversion into relative abundances.
 | ||
| Fig. 4 B3LYP predicted shifts of the alkyl (R) docking wavenumber relative to the phenyl (Ph) docking wavenumber, plotted against shifts obtained from TPSS and M06-2X calculations. | ||
After having cross-validated three functionals in terms of their ability to predict spectral, structural and energetic differences in carbonyl docking, one can move to the experimental comparison.
4.2 Experimental docking preferences
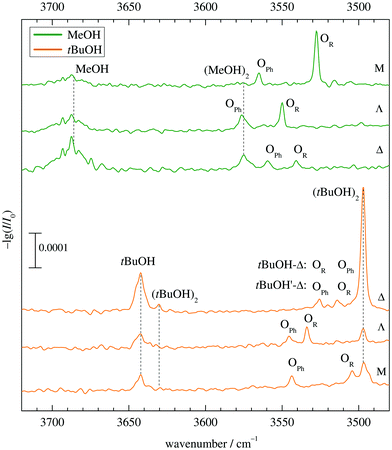
Fig. 5 shows the infrared spectra obtained when combining MeOH (top) and tBuOH (bottom) with M, Λ and Δ. One can see the alcohol monomer OH stretching signals (MeOH, tBuOH) and variable amounts of their down-shifted dimers (MeOH)2, (tBuOH)2. Their signals are connected with dashed vertical lines for better identification. There are always two additional bands OPh, OR corresponding to mixed complexes, in two cases affected by overlap with alcohol dimer bands. For MeOH, they are spectrally further downshifted than the alcohol dimer (or very slightly upshifted in the case of Λ), for tBuOH, they are further upshifted. Based on a very robust computational trend for all MeOH complexes (see Fig. 4 and Table S3 in the ESI†), the most downshifted band is due to alkyl docking, which allows for a more favourable coordination angle of the solvent in most cases (Fig. 2). For Δ, where this is not the case, the experiment rewardingly shows a particularly weak alkyl docking signal and a particularly small spectral splitting. On the other side, the phenyl CH always pushes the alcohol away from the ideal α angle, reducing the hydrogen bond strength and thus upshifting the OH stretching frequency.6 The MeOH complex assignments are therefore unproblematic and nicely correlate experimental shifts with harmonically predicted ones.For tBuOH, the assignment is less straightforward, because the combined sterical demand of the alcohol and ketone enforces out of plane coordination. This leads to a reduced splitting, by a factor of more than 3 when moving from M to Λ (Fig. 5). It brings alkyl coordination in close spectral vicinity to phenyl coordination and requires further scrutiny for the docking assignment in Δ (top trace in the lower part of Fig. 5). As in the MeOH case, the downshift of the Δ complexes increases compared to Λ, indicating a different kind of interaction for the strained ring compound. The closeness of the two spectral features requires a careful assignment to the docking variants.
For this purpose, the upper part of Fig. 6 establishes a correlation between the theoretical harmonic OH stretching wavenumber shift from the monomer and the experimental anharmonic wavenumber shift for MeOH. Due to various anharmonicity contributions, no perfect match (diagonal line) can be expected but a shifted correlation is often observed. This is indeed the case for the B3LYP predictions which are uniformly shifted by about 35 cm−1. A similar correlation with a shift of about 85 cm−1 is found for TPSS. The M06-2X predictions are much less shifted (suggesting negligible anharmonicity, which is unexpected but not impossible due to counteracting diagonal and off-diagonal contributions) but also less systematic, hence less useful for assignment purposes.
Building on this systematic performance for MeOH, the lower part of Fig. 6 with the tBuOH values makes a clear prediction for the actual isomer observed for the tBuOH-Δ system. Alkyl docking is either predicted to have a reduced shift (most stable structure, more out-of-plane coordination, circles) or an increased shift compared to phenyl docking, as in all other five cases (less stable tBuOH′-Δ structure, less out-of-plane coordination, stars). Clearly, the latter provides the more systematic correlation and is thus preferentially assigned. We also note that the TPSS shift prediction shows the largest overestimation, as for MeOH. Thus, B3LYP is seen to provide the most reliable and systematic predictions, if one accepts a consistent and moderate overestimation of hydrogen bond shifts.
After having secured the spectral assignments, an analysis of the predicted energy differences between alkyl and phenyl docking in comparison to the experimental abundances is possible. Table 1 derives the experimental phenyl docking fraction xPh from experimental intensity ratios in combination with predicted B3LYP IR absorption cross sections. Based on this, methanol prefers to dock on the alkyl side except for Δ. tBuOH prefers to dock on the phenyl side except for Λ. However, this docking preference is only pronounced for three out of the six combinations, whereas for the other three the error bar encloses or touches an undecided situation.
The qualitative experimental docking preference is uniformly met by all three DFT levels, if a ZPVE error bar of ±0.2 kJ mol−1 is added to the energy difference predictions (ESI,† Table S2). This is remarkable if one considers that the energy imbalance of the docking alternatives is typically well below 5% of the total binding energy (ESI,† Table S7). The only mismatch is the docking of tBuOH to M, where all three DFT predictions prefer the alkyl side, whereas experiment slightly prefers phenyl docking. It should however be emphasized that this is a case of partial spectral overlap with the alcohol dimer (lowest trace in Fig. 5), where the IR integration procedure may underestimate the error. Therefore, one should not give too much weight to this slight discrepancy. We also note that the discrepancy is particularly small for the B3LYP prediction. This is shown in Fig. 7, where the experimentally derived phenyl docking abundance is plotted against the theoretical energy preference. Areas which are inconsistent between experiment and theory (within the anharmonicity and cross section assumptions) are greyed out. One can see that all data points except for the borderline tBuOH-M case fall in the white area. Corresponding figures for TPSS and M06-2X are shown in the ESI† (Fig. S7 and S8) and show slightly inferior, but qualitatively consistent behaviour. While this does not allow to discriminate between different DFT levels as was the case for methanol docking on substituted anisoles,8 it provides further confidence in the correct assignment of the spectra. The remarkable conclusion is that dispersion-corrected DFT functionals are able to predict relative docking preferences of small and more bulky alcohols at the two sides of a carbonyl group in small and more bulky ketones with sub-kJ mol−1 accuracy, despite slight deficiencies in detail. Perhaps the most significant challenge is the correct prediction of the out-of-plane tendency in docking, for which the right balance between dispersion interactions and anisotropy of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O electron density for the directional hydrogen bond has to be met. The OH vibrational frequency is quite sensitive to the latter and it appears that B3LYP slightly overestimates the out-of-plane tendency when cyclopropyl- and tert-butyl-groups interact, at least for the affordable def2-TZVP basis set.
O electron density for the directional hydrogen bond has to be met. The OH vibrational frequency is quite sensitive to the latter and it appears that B3LYP slightly overestimates the out-of-plane tendency when cyclopropyl- and tert-butyl-groups interact, at least for the affordable def2-TZVP basis set.
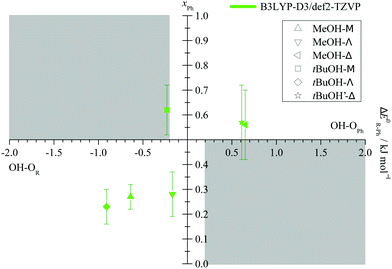 | ||
| Fig. 7 Experimental fraction of phenyl docking xPh = cPh/(cR + cPh) plotted against the predicted ZPV corrected energy advantage for phenyl docking ΔE0R–Ph. Allowing for an estimated error of the ZPV correction of ±0.2 kJ mol−1 (see Fig. 3), grey areas should not fully contain data points within their indicated experimental integration error bar, if relative absorption cross sections calculated at the same level are reliable. | ||
This subtle but spectroscopically rather clear deficiency deserves further analysis. Why is theory so ambivalent concerning two docking variants of a bulky alcohol to the cyclopropyl end of the ketone in competition to the phenyl end? Apparently, the out-of-plane variant realises a compromise between hydrogen bonding to the cyclopropyl side and long range interaction with the phenyl side, whereas the experimentally observed structure focuses on the undistorted hydrogen bond. This can be qualitatively understood by analyzing the difference in D3 dispersion contribution between phenyl and alkyl docking at B3LYP level (see ESI,† Table S4, also for an analogous TPSS analysis) and alternatively by applying a LED36,37 analysis at B3LYP and TPSS structures (see ESI,† Table S5). Rewardingly, all four analyses provide similar results. For almost all pairings, the alkyl docking variant has a dispersion attraction which is 0 to 2 kJ mol−1 smaller than for phenyl docking (after rounding to integer values). This is understandable, as the phenyl ring offers a larger London dispersion interaction area and it is confirmed at TPSS level. There are two marked exceptions: tBuOH-Λ (and in one case also MeOH-Λ) has a dispersion advantage of 1 to 2 kJ mol−1 for alkyl docking. Its markedly out-of-plane alkyl docking structure (ESI,† Fig. S1) maximizes dispersion interaction with both sides of the ketone, whereas in-plane phenyl docking only offers interaction with the phenyl side. London dispersion tends to favour such compromise structures, which can be recognized spectroscopically due to their reduced hydrogen bond downshift. The other exception is the elusive out-of-plane tBuOH-Δ structure, where the dispersion difference between the docking structures is small and undecided. Instead, the observed tBuOH′-Δ alkyl docking structure has a very large (3 to 5 kJ mol−1) predicted dispersion disadvantage compared to phenyl docking and is therefore predicted to be slightly less stable. Already a 5 to 10% reduction of this disadvantage, e.g. by a more complete basis set, would bring tBuOH′-Δ below tBuOH-Δ in energy and thus match the experimental observation. Based on this analysis, it is not surprising that a dispersion correction or other electronic structure effect may fail for such a subtle balance between hydrogen bonding and dispersion.
To check whether this DFT/def2-TZVP-based analysis is plausible, a number of higher level calculations have been carried out (Tables S6 and S8 in the ESI†). Single point calculations at def2-QZVP level contribute 0.1 to 0.2 kJ mol−1 to the stabilization of tBuOH′-Δ relative to tBuOH-Δ at B3LYP and TPSS level. DLPNO-CCSD(T) (with tightPNO settings and aug-cc-pVQZ38 basis set) adds another 0.1 to 0.2 kJ mol−1. In summary, this predicts tBuOH′-Δ to win slightly over tBuOH-Δ for TPSS-based calculations, whereas the B3LYP-based prediction is still slightly off. Because the experimental preference for tBuOH′-Δ is rather unambiguous, this system represents a very subtle test for the quality of relative energy predictions and a correct description of London dispersion has a high leverage on this energy sequence. Once the tBuOH′-Δ alkyl docking structure is predicted to be more stable than the out-of-plane arrangement in tBuOH-Δ, it is quite plausible that the latter will convert efficiently into it during jet expansion, given an almost negligible barrier, which could not be quantified by transition state searches.
For comparison, the inexpensive functionals B97-3c and PBEh-3c have also been tested in their ability to predict the correct energy ranking (Table S2 in the ESI†). They show some more significant outliers (Fig. S9 and S10 in the ESI†), in particular PBEh-3c. This is not surprising, as they have been developed for fast structure searches, rather than final results. Their spectral predictions are also somewhat less reliable. We note that they do not predict the existence of the experimentally supported tBuOH′-Δ structure on the alkyl docking side at all, which is needed to predict the correct spectral phenyl/alkyl sequence.
In summary, the prediction of a spectrally downshifted complex of tBuOH′-Δ with the cyclopropyl side of cyclopropylphenylketone in competition with a more stable and more upshifted complex on the phenyl side is a challenge not only for B97-3c or PBEh-3c, but also for TPSS-D3 and B3LYP-D3 predictions, at least for a def2-TZVP basis set. Because the other five docking pairs investigated in this work are described satisfactorily and zero-point energy effects should be minor by construction, this represents a useful test case for the correct balance of hydrogen bonding and London dispersion on the potential energy hypersurface of such medium-sized complexes. It would be interesting to verify this vibrational diagnosis by structural spectroscopy.
5 Conclusions
We have shown that it is possible to use a range of quantum chemical methods to assign the infrared spectra of a set of alcohol–ketone complexes and then to use these assignments to judge the same methods in their ability to predict the relative energy of the hydrogen bond docking sites. Because of the local similarity of the two sites, zero-point energy differences between the two docking wells should largely cancel. Therefore, the set of experimental data directly probes the ability of quantum chemical methods to predict the relative electronic energy of the competing arrangements. It is shown that in one bulky case B3LYP and to a lesser extent TPSS with a def2-TZVP basis set are slightly biased towards out-of-plane coordination involving the π electron density of the carbonyl group and a maximized dispersion interaction, where experiment finds a more in plane lone pair coordination with much less London dispersion and more directional hydrogen bonding. Otherwise, their performance is quite satisfactory, whereas M06-2X, PBEh-3c and B97-3c show more outliers with clear discrepancies to experiment. Once extended to further ketone substituents such as cyclohexyl39 and to other alcohols such as phenol,40 the intermolecular energy balance strategy promises to provide useful experimental benchmarks for the quantum-chemical description of hydrogen bonding to carbonyl groups in three dimensions.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 271107160/SPP1807. We acknowledge computer time on the local chemistry cluster – 405832858/INST 186/1294-1 FUGG and the GWDG computer center and the workshops of the department for their valuable technical support.References
- J. P. M. Lommerse, S. L. Price and R. Taylor, J. Comput. Chem., 1997, 18, 757–774 CrossRef CAS.
- P.-S. Huang, S. E. Boyken and D. Baker, Nature, 2016, 537, 320 CrossRef CAS PubMed.
- G. A. Jeffrey and W. Saenger, Hydrogen Bonding in Biological Structures, Springer Verlag, 1991 Search PubMed.
- K. Schwing and M. Gerhards, Int. Rev. Phys. Chem., 2016, 35, 569–677 Search PubMed.
- S. T. Shipman, J. L. Neill, R. D. Suenram, M. T. Muckle and B. H. Pate, J. Phys. Chem. Lett., 2011, 2, 443–448 Search PubMed.
- A. Poblotzki, H. C. Gottschalk and M. A. Suhm, J. Phys. Chem. Lett., 2017, 8, 5656–5665 Search PubMed.
- M. Ahmed, C. Jelsch, B. Guillot, C. Lecomte and S. Domagała, Cryst. Growth Des., 2013, 13, 315–325 CrossRef CAS.
- H. C. Gottschalk, J. Altnöder, M. Heger and M. A. Suhm, Angew. Chem., Int. Ed., 2016, 55, 1921–1924 CrossRef CAS PubMed.
- H. C. Gottschalk, A. Poblotzki, M. A. Suhm, M. M. Al-Mogren, J. Antony, A. A. Auer, L. Baptista, D. M. Benoit, G. Bistoni, F. Bohle, R. Dahmani, D. Firaha, S. Grimme, A. Hansen, M. E. Harding, M. Hochlaf, C. Holzer, G. Jansen, W. Klopper, W. A. Kopp, L. C. Kröger, K. Leonhard, H. Mouhib, F. Neese, M. N. Pereira, I. S. Ulusoy, A. Wuttke and R. A. Mata, J. Chem. Phys., 2018, 148, 014301 CrossRef PubMed.
- M. A. Suhm and F. Kollipost, Phys. Chem. Chem. Phys., 2013, 15, 10702–10721 RSC.
- G. Karir, N. O. B. Lüttschwager and M. A. Suhm, Phys. Chem. Chem. Phys., 2019, 21, 7831–7840 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef PubMed.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104 CrossRef PubMed.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- F. Neese, WIREs Comput. Mol. Sci., 2018, 8, e1327 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- S. E. Wheeler and K. N. Houk, J. Chem. Theory Comput., 2010, 6, 395–404 CrossRef CAS.
- K. A. E. Meyer and M. A. Suhm, Chem. Sci., 2019, 10, 6285–6294 RSC.
- TURBOMOLE V7.3 2018, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, 2007, available from http://www.turbomole.com Search PubMed.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, WIREs Comput. Mol. Sci., 2014, 4, 91–100 CrossRef CAS.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296 CrossRef CAS PubMed.
- A. Altun, F. Neese and G. Bistoni, Beilstein J. Org. Chem., 2018, 14, 919–929 CrossRef CAS PubMed.
- W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2016, 12, 4778–4792 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- F. D. Lewis, R. W. Johnson and D. E. Johnson, J. Am. Chem. Soc., 1974, 96, 6090–6099 CrossRef CAS.
- T. Ebata, A. Fujii and N. Mikami, Int. Rev. Phys. Chem., 1998, 17, 331–361 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Keywords, structures, energies, spectral details and performance analyses. See DOI: 10.1039/c9cp06128b |
| This journal is © the Owner Societies 2020 |