 Open Access Article
Open Access ArticleThe N(4S) + O2(X3Σ−g) ↔ O(3P) + NO(X2Π) reaction: thermal and vibrational relaxation rates for the 2A′, 4A′ and 2A′′ states†
Juan Carlos
San Vicente Veliz
 a,
Debasish
Koner
a,
Debasish
Koner
 a,
Max
Schwilk
a,
Raymond J.
Bemish
b and
Markus
Meuwly
a,
Max
Schwilk
a,
Raymond J.
Bemish
b and
Markus
Meuwly
 *a
*a
aDepartment of Chemistry, University of Basel, Klingelbergstrasse 80, CH-4056 Basel, Switzerland. E-mail: m.meuwly@unibas.ch
bAir Force Research Laboratory, Space Vehicles Directorate, Kirtland AFB, New Mexico 87117, USA
First published on 20th January 2020
Abstract
The kinetics and vibrational relaxation of the N(4S) + O2(X3Σ−g) ↔ O(3P) + NO(X2Π) reaction is investigated over a wide temperature range based on quasiclassical trajectory simulations on 3-dimensional potential energy surfaces (PESs) for the lowest three electronic states. Reference energies at the multi reference configuration interaction level are represented as a reproducing kernel and the topology of the PESs is rationalized by analyzing the CASSCF wavefunction of the relevant states. The forward rate matches one measurement at 1575 K and is somewhat lower than the high-temperature measurement at 2880 K whereas for the reverse rate the computations are in good agreement for temperatures between 3000 and 4100 K. The temperature-dependent equilibrium rates are consistent with results from JANAF and CEA results. Vibrational relaxation rates for O + NO(ν = 1) → O + NO(ν = 0) are consistent with a wide range of experiments. This process is dominated by the dynamics on the 2A′ and 4A′ surfaces which both contribute similarly up to temperatures T ∼ 3000 K, and it is found that vibrationally relaxing and non-relaxing trajectories probe different parts of the potential energy surface. The total cross section depending on the final vibrational state monotonically decreases which is consistent with early experiments and previous simulations but at variance with other recent experiments which reported an oscillatory cross section.
1 Introduction
Reactions involving nitrogen and oxygen play important roles in combustion, supersonic expansions, hypersonics, and in atmospheric processes. A particularly relevant process, which is part of the so-called Zeldovich process1 are the (NO + O/O2 + N) and (NO + N/N2 + O) reactions2,3 that describe the oxidation of nitrogen. In the forward direction, the reaction also generates reactive atomic oxygen. These reactions, together with a range of other atom plus diatom and diatom plus diatom reactions form the core of the 5- and 11-species model used in hypersonics.4 At high temperatures (∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K), as present in thin regions of shock layers created at hypersonic speed flight,5 the reactive chemical processes can become very complex. This complexity is in part due to a significant degree of non-equilibrium. The lack of experimental information on the kinetics at these high temperatures makes numerical simulations for reaction cross sections as well as reaction and vibrational relaxation rates a very valuable source of information for characterizing hypersonic flow.
000 K), as present in thin regions of shock layers created at hypersonic speed flight,5 the reactive chemical processes can become very complex. This complexity is in part due to a significant degree of non-equilibrium. The lack of experimental information on the kinetics at these high temperatures makes numerical simulations for reaction cross sections as well as reaction and vibrational relaxation rates a very valuable source of information for characterizing hypersonic flow.
There is also much interest in correctly describing the vibrational distribution of the NO molecules after reactive or nonreactive collisions with atomic oxygen for atmospheric processes. The infrared emission of nitric oxide is one of the main tracers to follow and characterize the energy budget in the upper atmosphere.6 This emission arises from relaxation of vibrationally excited NO after collisional excitation with atomic oxygen. This relaxation process has also been implicated in nighttime cooling of the thermosphere, above ∼100 km. Furthermore, nitric oxide is also formed in situ and used as a tracer for combustion and in hypersonic flows where it is commonly observed by Laser Induced Fluorescence (LIF).
Previous studies included experimental and computational characterizations of the reaction dynamics and final state distributions of the products. Using a pulsed beam of energetic nitrogen atoms at 8 km s−1 interacting with thermal oxygen under single collision conditions to mimic velocities seen in low earth orbit, the distribution of vibrationally excited NO and state specific reaction cross sections for N + O2 → NO + O were determined.7 The analysis showed an oscillatory behaviour of the cross section with increasing final vibrational state, with minima at ν = 3 and ν = 6, with an uncertainty of a factor of two. An even earlier experiment,8 using saturated multiphoton ionization spectroscopy, measured the NO product ground-state distribution, reporting a difference in the cross sections between odd (ν = 1, 3, 5) and even (ν = 0, 2, 4, 6) final vibrational levels.
From the perspective of computer based simulations9–11 the vibrational state-dependent cross sections have been calculated using a variety of potential energy surfaces (PESs). In all of these computational studies, the maximum of the final state vibrational cross section is found to be at ν = 19 or at ν = 210,11 with no notable oscillation. One PES for the 2A′ state used a fit10 to electronic structure calculations at the complete active space SCF (CASSCF) level followed by multireference contracted configuration interaction and a modified Duijneveldt (11s6p) basis set.12 Another PES was based on 1250 (for the 2A′) and 910 (4A′) CASPT2 calculations and fitted to an analytical function.13 Such an approach was also used for the 2A′′ state.14 This was followed by a PESs for the 2A′ state using a diatomics in molecules (DIM) expansion with the two-body terms based on extended Hartree–Fock calculations.15 Then, a 2-dimensional PES with the NO bond length fixed at its equilibrium value of 2.176 a0 was determined at the icMRCI+Q/cc-pVQZ level of theory and represented as a cubic spline.16 This work also presented a PES for the 2A′′ state. More recently, a double many body expansion fit to 1700 points at the MRCI/aug-cc-VQZ level of theory for the 2A′′ state was carried out.17 In addition, quasi classical trajectory (QCT) calculations2,9,13,18 have been reported for the temperature dependent rate for the N(4S) + O2 → NO + O and its reverse reaction using different PESs.
Another important process is the energy transfer following the collision of vibrationally excited NO with oxygen atoms (OA + NOB → OA + NOB) or (OA + NOB → OB + NOA) to yield NO in its ground vibrational state. Using 355 nm laser photolysis of a dilute mixture of NO2 in argon, the experiment3 reports a vibrational relaxation rate of: kν=1→0 = 2.4 ± 0.5(10−11) cm3 s−1 at a temperature of T = 298 K. Later, QCT simulations19 reported a value of kν=1→0 = 2.124 ± 0.73(10−11) cm3 s−1 at T = 298 K which is close to the experimentally reported rate. Another experiment20 used a continuous wave microwave source to form O atoms combined with photolysis of trace amounts of added NO2 to generate vibrationally excited NO. This experiment found a rate of kν=1→0 = 4.2 ± 0.7(10−11) cm3 s−1 at T = 295 K which is larger by 75% compared with the earlier experiments.3 Quite recent QCT simulations using again the DIM-based PES15 mentioned above reported a rate of kν=1→0 = 4.34 ± 0.7(10−11) cm3 s−1 at T = 298 K from QCT simulations21 which used the empirical DIM PES for the 2A′ ground state15 and a more recent, MRCI-based fitted PES for the 2A′′ state.17
Given the rather heterogeneous situation for the quality of the existing PESs for studying the N(4S) + O2(X3Σ−g) reaction and the vibrational relaxation of NO, the present work determines fully dimensional PESs using a consistent methodology to represent the 3 lowest electronic states, 2,4A′ and 2A′′ as well as to evaluate the cross sections for the (forward)
| N(4S) + O2(X3Σ−g) → O(3P) + NO(X2Π) | (1) |
| O(3P) + NO(X2Π) → N(4S) + O2(X3Σ−g) | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. Experimentally, cross sections and rates for the forward and reverse reactions have been measured and experimental data for vibrational relaxation rates for temperatures up to ∼3000 K are available3,7,8,20,22,23 which serve as benchmarks for the present work.
000 K. Experimentally, cross sections and rates for the forward and reverse reactions have been measured and experimental data for vibrational relaxation rates for temperatures up to ∼3000 K are available3,7,8,20,22,23 which serve as benchmarks for the present work.
In the following, the calculation and representation of the asymptotic PESs for the three electronic states and the two channels are described. These are combined to a set of fully-dimensional, reactive PESs which are suitable for quasiclassical trajectory simulations from which cross sections, reaction rates and rates for vibrational relaxation can be determined. The results of the simulations are discussed in the context of the limits of errors in the simulations and comparisons with available experimental data. Finally, the basis of the observables is discussed at an atomistic level, based on analyzing the trajectories.
2 Computational methods
This section presents the generation and representation of the potential energy surfaces and the methodologies for the quasiclassical trajectory (QCT) simulations and their analysis. All PESs are computed at the multi reference CI (MRCI) level of theory together with large basis sets. These are then exactly represented using the reproducing kernel Hilbert space (RKHS) approach. The quality of the representation is then checked using additional MRCI calculated points.2.1 The 2A′, 2A′′ and 4A′ potential energy surfaces
Ab initio energy calculations were carried out for the 2A′, 2A′′ and 4A′ states and a correlation diagram with the asymptotic dissociation states is provided in Fig. S1(ESI†). The energies were computed on a grid defined by Jacobi coordinates (r,R,θ) where r is the separation of the diatomic, R is the distance between the atom and the center of mass of the diatomic and θ is the angle between the two unit vectors![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and
and ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) . For R the grid included 28 points between 1.4 and 12.0 a0, the distance r was covered by 20 points between 1.5 and 4.0 a0 and the angular grid contained 13 angles from a Gauss–Legendre quadrature (169.796°, 156.577°, 143.281°, 129.967°, 116.647°, 103.324°, 90.100°, 76.676°, 63.353°, 50.033°, 36.719°, 23.423°, 10.204°). Such a grid is advantageous for quantum bound state and scattering calculations for which highly accurate angular integrals are required. In the RKHS scheme, the angular grid ∈ [0,180°] is mapped onto the interval [0,1], see below. This transformation leads to a denser grid near the end points (i.e. 0° or 180°) and evenly spaced in between. Thus, with this grid RKHS also performs well near 0° or 180° in the present work as demonstrated below.
. For R the grid included 28 points between 1.4 and 12.0 a0, the distance r was covered by 20 points between 1.5 and 4.0 a0 and the angular grid contained 13 angles from a Gauss–Legendre quadrature (169.796°, 156.577°, 143.281°, 129.967°, 116.647°, 103.324°, 90.100°, 76.676°, 63.353°, 50.033°, 36.719°, 23.423°, 10.204°). Such a grid is advantageous for quantum bound state and scattering calculations for which highly accurate angular integrals are required. In the RKHS scheme, the angular grid ∈ [0,180°] is mapped onto the interval [0,1], see below. This transformation leads to a denser grid near the end points (i.e. 0° or 180°) and evenly spaced in between. Thus, with this grid RKHS also performs well near 0° or 180° in the present work as demonstrated below.
In order to consistently describe all relevant states and avoid numerical instabilities due to closely-lying states of the same symmetry, state-averaged CASSCF24–27 calculations including the two lowest states of each symmetry (two spin symmetries and two spatial symmetries) were carried out. For this, the full valence orbital space was included in the active space. A subsequent internally contracted MRCISD28,29 (referred to as MRCI+Q in the following) calculation including Davidson correction30 of the lowest state for each symmetry then was used to include dynamical electron correlation contributions at a high order level. The augmented Dunning-type correlation consistent polarize triple zeta (aug-cc-pVTZ)31 basis set is used in this work. All electronic structure calculations are done with the Molpro-2019.132 software package. For each of the electronic states, ab initio energy calculations have been performed for total 7280 points for the NO + O channel and 3920 (including symmetry) points for the OO + N channel, i.e. overall ∼11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points which is more than 5 times more reference calculations compared with previous efforts for the same system and at a similar level of theory. It is to be noted that electronic structure calculations for a fraction of the geometries at large R and/or r converged to excited states. Those points were excluded from the training energy data set.
000 points which is more than 5 times more reference calculations compared with previous efforts for the same system and at a similar level of theory. It is to be noted that electronic structure calculations for a fraction of the geometries at large R and/or r converged to excited states. Those points were excluded from the training energy data set.
For certain geometries (<0.5%) far from the strong interaction region the CASSCF or MRCI calculations did not converge. In these cases, the missing grid points were reconstructed using a 2-dimensional reproducing kernel (R,r) for each θ. This procedure of discriminating possible outliers was necessary before constructing the full dimensional RKHS representation of the PES. The 3-dimensional PES for each channel V(R,r,θ), is constructed using a reciprocal power decay kernel with n = 2 and m = 6 for the two radial coordinates and a Taylor spline kernel with n = 2 for the angular part.33 The regularization parameter used was λ = 10−18. It should be noted that in the present work a regularly spaced grid was used for efficiency reasons but that RKHSs can also be constructed for unstructured grids.33
The global, reactive 3D PES V(r1,r2,r3) for an electronic state is constructed by summing the individual PESs for each channel
 | (3) |
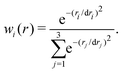 | (4) |
The global, local minima and transition states between the minima and/or entrance channels supported by the PESs were determined using BFGS minimization and the nudged elastic band method34 as implemented in the atomic simulation environment (ASE).35
The two possible ionic channels for the O + NO product are (i) O+ + NO− and (ii) O− + NO+. To determine their asymptotic energetics relative to the neutral state, energies have been calculated for the equilibrium geometry of the diatomic ions at the MRCI+Q/aug-cc-pVTZ level of theory. The ionization energy and the electron affinity for the oxygen atom are36,37 13.61806 eV and36,38 −1.4610 eV, respectively. Hence, the two ionic dissociation channels are then 13.79 and 7.66 eV above the neutral O + NO channel, respectively.
2.2 Quasi-classical trajectory simulations
The QCT simulations used in the present work have been extensively described in the literature.39–42 Here, Hamilton's equations of motion are solved using a fourth-order Runge–Kutta numerical method. The time step was Δt = 0.05 fs which guarantees conservation of the total energy and angular momentum. Initial conditions for the trajectories are sampled using standard Monte Carlo sampling method.39 The reactant and product ro-vibrational states are determined following semiclassical quantization. Since the ro-vibrational states of the product diatom are continuous numbers, the states are assigned by rounding to integer values. Two schemes were used (1) histogram binning (HB), i.e. rounding values to the nearest integers, or (2) Gaussian binning (GB), which weights each trajectory with a Gaussian shaped function (with a full width at half maximum of 0.1) centered on the integer values.41,43,44 Here, both schemes were tested and found to yield comparable results. Therefore results obtained from GB are reported in the following.The state-to-state reaction cross section at fixed collision energy Ec is  . This integral can be evaluated using Monte Carlo sampling39 which yields
. This integral can be evaluated using Monte Carlo sampling39 which yields
 | (5) |
The thermal rate for an electronic state (i) at a given temperature (T) is then obtained from
 | (6) |
For the forward reaction (N(4S) + O2(X3Σ−g) → O(3P) + NO(X2Π)) the rate k+(T) is calculated using degeneracies of 1/6 and 1/3 for the 2A′ and 4A′ states, respectively, whereas for the reverse reaction (O(3P) + NO(X2Π) → N(4S) + O2(X3Σ−g)) the degeneracies are
 | (7) |
 | (8) |
The terms in eqn (7) and (8) are the degeneracies of the J or spin states and the exponential parameters 227.8, 326.6 and 177.1 are the energy differences (in units of K) between two neighboring states. The equilibrium constant is then
 | (9) |
3 Results
3.1 The potential energy surfaces
An overview of the PESs, see Fig. 1, Fig. S2, and Table 1, for all three states investigated (2A′, 4A′, and 2A′′ from bottom to top) is given as 2-dimensional projections with the two asymptotes (N + OO and O + NO) on the left and right columns in Fig. 1, respectively. It should be noted that these representations are all for diatomic separations (O2 and NO, respectively) at values of critical points (see Fig. S3–S5, ESI†) and therefore do not exhibit all features of the full 3-dimensional PES. | ||
| Fig. 1 Two-dimensional cuts through the 3-d PES for the OO + N (left) and the NO + O (right) channels. The OO and NO diatomics are at their equilibrium bond lengths of the respective states, see Fig. S3–S5 (ESI†). They are R(OO) = 2.33 Å, R(OO) = 2.39 Å, R(OO) = 2.30 Å, and R(NO) = 2.26 Å, R(NO) = 2.36 Å, R(NO) = 2.28 Å for the 2A′, 4A′, and 2A′′ states, respectively, from bottom to top. Specific contours with energies in eV are indicated. The zero of energy is for dissociation into atomic fragments O(3P) + O(3P) + N(4S). The symbols indicate the minima discussed in the text and the definition of the coordinates is given on top of the figure. For the NO + O asymptote the OON geometry corresponds to θ = 0 whereas ONO has θ = 180°. | ||
| 2A′ | R (NO)e | R OOe | ∠NOO | ΔE1 | ΔE2 | ΔE213 |
|---|---|---|---|---|---|---|
| MIN1 | 2.27 | 2.58 | 130.4 | −5.78 | −18.34 | −28.50 |
| TS1 | 3.46 | 2.33 | 112.1 | −4.64 | 8.07 | 6.87 |
| TS2 | 2.20 | 2.86 | 134.1 | −5.71 | −16.82 | −27.42 |
| TS3 | 2.19 | 4.63 | 90.7 | −6.29 | −30.12 | −34.26 |
| MIN2 | 2.18 | 4.51 | 121.1 | −6.33 | −31.10 | −37.64 |
| MIN3 | 2.26 | 4.17 | 22.9 | −9.46 | −103.20 | −108.68 |
| 4A′ | R (NO)e | R OOe | ∠NOO | ΔE1 | ΔE2 | ΔE213 |
|---|---|---|---|---|---|---|
| MIN1 | 2.65 | 2.60 | 104.0 | −4.69 | 6.67 | 5.43 |
| TS1 | 3.26 | 2.39 | 108.0 | −4.33 | 15.01 | 12.74 |
| TS2 | 2.36 | 3.07 | 103.0 | −4.68 | 8.75 | 7.81 |
| 2A′′ | R (NO)e | R OOe | ∠NOO | ΔE1 | ΔE2 | ΔE217 |
|---|---|---|---|---|---|---|
| MIN2 | 2.23 | 4.06 | 107.5a | −7.37 | −111.79 | −113.95 |
| TS1 | 3.96 | 2.30 | 111.7 | −2.48 | 0.93 | 0.63 |
| TS2 | 4.35 | 2.31 | 30.8a | −2.44 | 1.95 | 2.07 |
| TS3 | 2.57 | 4.35 | 80.2a | −5.54 | −69.61 | −77.81 |
| TS4 | 2.42 | 3.99 | 109.4a | −7.22 | −108.34 | −113.14 |
| TS5 | 2.39 | 4.31 | 130.2a | −6.78 | 18.60b | 32.25b |
| MIN1 | 2.61 | 2.88 | 67.1a | −6.16 | −83.93 | −85.59 |
| MIN3 | 2.28 | 4.56 | 180.0a | −7.58 | −29.06c | −38.41c |
All PESs for OO + N are symmetric with respect to θ = 90°, as expected. For the 2A′ state and the O2 + N dissociation limit the 2d-PES was generated for TS1 in Fig. S3 (ESI†), i.e. for R(OO) = 2.33 a0. The two symmetry related minima are at R(NO)e = 3.23 a0 and θ = 34° and θ = 146°, respectively. For the NO + O dissociation limit the PES with R(NO) = 2.26 a0 (corresponding to MIN3 in Fig. S3, ESI†) displays two minima. They are at (R(OO) = 3.38 a0, θ = 35°) and (R(OO) = 3.22 a0, θ = 150°).
For the 4A′ state the surface for the O2 + N dissociation limit has R(OO) = 2.39 a0 for TS1 in Fig. S4 (ESI†) and the 2-dimensional PES in Fig. 1 has the minimum at R(NO) = 3.19 a0 with θ = 56° and θ = 124°, respectively. Conversely, at the NO + O asymptote, the PES is almost purely repulsive for R(NO) = 2.36 a0 (TS2 in Fig. S4, ESI†). In Jacobi coordinates, a faint minimum is at (R(OO) = 3.48 a0, θ = 146°).
Finally, for the 2A′′ state the 2-dimensional PES is reported for R(OO) = 2.30 a0 in the OO + N channel (TS1 in Fig. S5, ESI†). It exhibits two minima at (R(NO) = 2.36 a0, θ = 90°), and (R(NO) = 3.55 a0, θ = (0,180)°). At the NO + O asymptote the PES has multiple minima, see Fig. 1. For R(NO) = 2.28 a0 they are at (R(OO) = 3.69 a0, θ = 0°), (R(OO) = 2.53 a0, θ = 95°), (R(OO) = 3.28 a0, θ = 128°), and (R(OO) = 3.50 a0, θ = 180°).
All minima and transition states together with their connectivities on the 3d PES are given in the ESI,† see Fig. S3–S5 and the geometries and relative energies of the stationary and transition states are summarized in Table 1. All these geometries were determined on the mixed PESs. For comparison, the minima were also determined on the 2A′′ PES for the NO + O asymptote. The three minima on the unmixed PES are at (MIN1: rOO = 2.88 a0, rNO = 2.61 a0, and an angle 66.8°) with an energy difference of ΔE = 0.62 kcal mol−1, (MIN2: rOO = 4.09 a0, rNO = 2.21 a0, and an angle 107.3°, ΔE = 0.55 kcal mol−1), and (MIN3: rOO = 4.56 a0, rNO = 2.28 a0, and an angle 180°, ΔE = 0.005 kcal mol−1). Several paths which include a number of minima and transition states can be found on the 2A′ and 2A′′ PESs for the forward and reverse reaction while both reactions follow rather simple paths on the 4A′ PES. It is worthwhile to note that there are no crossings between the 2A′ and 2A′′ PESs as well as between 2A′ and 4A′ electronic states which differs from, e.g., the [CNO]-system.42 For collinear geometries they are, however, degenerate from which a Renner–Teller (rovibronic) coupling may potentially arise but is expected to be of minor significance.
One-dimensional cuts along the O2 + N and NO + O coordinates for constant angle θ for the three different electronic states are reported in Fig. 2. All angular cuts correspond to off-grid points, i.e. data not explicitly used in generating the RKHS. Therefore, the RKHS energies (solid lines) are predictions and are found to compare well with the true energies calculated at the MRCI+Q/aug-cc-pVTZ level of theory. Nevertheless, for a few points on the θ = 175.0° cut around R ∼ 4 a0 for the 2A′ state (see Fig. 2A) the RKHS-predicted energies differ slightly from the true energies.
The quality of all three PESs for both, on- and off-grid points is reported in Fig. S6 (ESI†) as correlation plots. The correlation between the reference (ab initio energies) and RKHS energies ranges from R2 = 0.9996 to 0.9999 for grid points and from R2 = 0.9992 to 0.9997 for off-grid points for the three electronic states. The corresponding root mean squared errors for the on-grid points range from 0.022 to 0.043 eV and off-grid points from 0.033 to 0.057 eV. It should be noted that all the RKHS energies are evaluated on the mixed, fully reactive PES, see eqn (3). The agreement between reference and RKHS energies is even better if the channels are considered separately.
To rationalize the observed topology of the NO + O channel of the MRCI+Q PES (Fig. 1 panels B, D, and F), the orbital diagram of the natural orbitals as obtained from the CASSCF calculations are analyzed. Fig. 3 shows the evolution of the natural orbitals and the energies for R = 3.4 a0 and rNO = 2.183 a0 (equilibrium NO separation) with varying values of θ. Only natural orbitals with significant change in occupation number are shown along the path. Fig. S8 (ESI†) shows a complete MO diagram of the valence space. The dominant configurations for the lowest 2A′ and 2A′′ states are indicated in the MO diagrams, and an illustration of all main configurations along the path is given in Fig. S7 (ESI†). The cut qualitatively includes most of the stationary states of the 2-dimensional PESs of the NO + O channel (see Fig. 1 and Fig. S6, ESI†). For the linear structures (Fig. 3A) two perpendicular π3-systems arise with one electron in an antibonding π3* orbital. The bonding orbital of the π-system shows a more equal contribution from all three atomic centers for the linear ONO structure than for the linear OON structure, making the bonding situation more stable in this case (see Fig. S8, ESI†). Bending of the linear structures leads to a transformation of the in-plane antibonding orbitals of the π-system (“a” in Fig. 3A) into a non-bonding p-orbital on the oxygen at θ = 90°. The two non-bonding orbitals of the linear π-systems transform also into p-orbitals on the oxygen. Hence, at θ = 90° three natural orbitals close in energy with mostly p-orbital contribution on the oxygen atom arise. Their energy fine-ordering depends on the amount of residual antibonding character they bear. However, the out-of-plane antibonding orbital of the linear π-systems (b in Fig. 3A) transforms into an antibonding π* NO-orbital upon bending. Finally, the antibonding orbital with dominant σ*-character for the linear structures (“c” in Fig. 3A) also transforms into an antibonding π* NO-orbital at 90°, considerably lowering its orbital energy. The fine-ordering of the two π* NO-orbitals again depends upon their remaining additional antibonding character. Thus, for a T-shaped structure (θ = 90°) the quasi-degeneracies lead to a large number of configurations with similar energy and lead to small energy differences for the eight states included in the CASSCF wavefunction (see Fig. 3B).
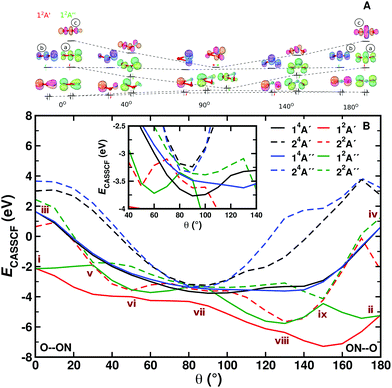 | ||
| Fig. 3 Panel A: MO diagram of NO2 for the doublet ground state for varying values of θ. The dominant configurations at selected angles are shown for the lowest 2A′ and 2A′′ states (in black occupations occurring for both states, state-specific orbital occupations are colour-coded). An asterisk indicates significant (additional) occupation of an orbital due to strong electron correlation. Details for each of the states are provided in Fig. S7 (ESI†). Panel B: CASSCF energies in eV relative to separated atoms. The inset shows details of the states around the T-shaped geometry. Features i through ix are discussed in the text. See also Fig. S9 (ESI†) for MRCI energies. Orbital visulaization was done with IboView.47 | ||
Two additional interesting observations on the NO + O channel can be made from the MO diagram: (1) No stable covalent bonding between the oxygen and the N–O fragment in the T-shaped structure is observed at the CASSCF level of theory. This explains the almost fully repulsive character of the NO + O channel along R for θ close to 90° (cf.Fig. 2). (2) Upon bending, the in-plane π3* orbital (“a” in Fig. 3A) significantly lowers its energy. As the π3* orbitals are partially occupied for the linear structures, bending makes lower energy configurations accessible, yielding minima on the PESs of the NO + O channel for slightly bent structures (cf.Fig. 1). This classifies as a Jahn–Teller distortion.
The CASSCF energies for the eight states along the bending coordinate are shown in Fig. 3B. In the following significant features (i to ix) of the PESs are discussed. For the linear structures (OON (θ = 0) and ONO (θ = 180°)) the orbital degeneracy leads to 2,4A′ and 2,4A′′ lowest states of equal energy (see points i to iv in Fig. 3B). These conical intersections are symmetry-required and go along with Jahn–Teller distortions. The angle θ is the only degree of freedom that lifts the degeneracy. Bending away from the linear geometry leads to an approach and avoided crossing of the 12A′′ and 22A′′ states (θ = 30°, point v), each of which is described by one dominant configuration outside the crossing region. A similar observation is made for the 12A′ and 22A′ states (θ = 50°, point vi). The 12A′ state has a strong multi-reference character with various configurations contributing in an extended region 50° ≤ θ ≤ 100°. As indicated in Fig. 3A, the quasi degeneracies in the T-shaped structures gives rise to a large number of configurations with similar energies and to seven states within 0.9 eV for θ = 90° (point vii). The characteristics of points vii and ix can be described along the same lines as for points vi and v, respectively. The full and detailed analysis of changes in configurations of the states along the path is given in Fig. S7 (ESI†). It is noted that the two lowest 4A states do not show an avoided crossing and have each one dominant configuration along θ. This explains the rather simple topology of the 14A′ PES in Fig. 1. The inset in Fig. 3 amplifies the subtle changes in state order around θ = 90°. Various additional avoided crossings can be observed (their analysis is given in Fig. S7, ESI†).
For the production calculations eight states are included in the CASSCF reference wave function. Exploratory calculations were also run with 12 states in the state-averaging. For the three lowest states (2,4A′ and 2A′′) using 8 or 12 states leads to the same bending curves, see Fig. S9 (ESI†). Also, the topography of the bending curves is very similar from CASSCF and MRCI+Q calculations (Fig. S10, ESI†). The sextet states were not included as they are expected to be repulsive (see Fig. S1, ESI†) which is of little relevance to the thermal and vibrational relaxation rates considered next.
3.2 Thermal rates and reaction cross sections
Thermal rates for the forward (N(4S) + O2(X3Σ−g) → O(3P) + NO(X2Π)) and reverse (O(3P) + NO(X2Π) → N(4S) + O2(X3Σ−g)) reactions are determined between 300 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. A total of 50
000 K. A total of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories was calculated at each temperature for each reaction on each electronic states. The individual contributions of the 2A′ and 4A′ states are reported in Fig. 4 panels A and B. The forward rates are about one order of magnitude higher than the reverse rates for both electronic states. Comparison with previous calculations13 (see Fig. S11, ESI†) shows that for both states and both directions they differ by a factor of ∼2 for high temperature. For lower temperature they rather differ by a factor of ∼5.
000 trajectories was calculated at each temperature for each reaction on each electronic states. The individual contributions of the 2A′ and 4A′ states are reported in Fig. 4 panels A and B. The forward rates are about one order of magnitude higher than the reverse rates for both electronic states. Comparison with previous calculations13 (see Fig. S11, ESI†) shows that for both states and both directions they differ by a factor of ∼2 for high temperature. For lower temperature they rather differ by a factor of ∼5.
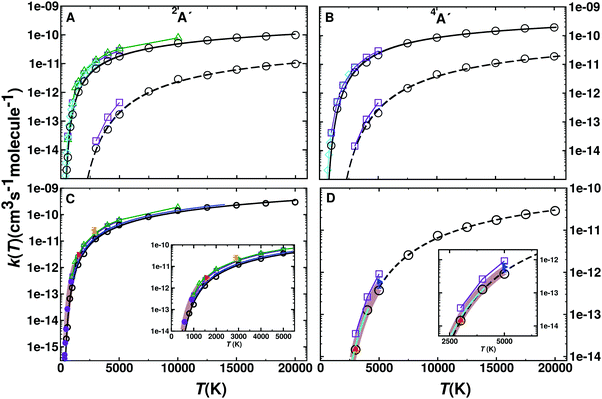 | ||
| Fig. 4 (top) Rate coefficients for the forward (N(4S) + O2(X3Σ−g) → O(3P) + NO(X2Π)) and reverse (O(3P) + NO(X2Π) → N(4S) + O2(X3Σ−g)) reaction for the 2A′ (panel A) and 4A′ (panel B) states. Rates for the forward (open circles and solid black line) and reverse (open circles and dashed lines) reaction are given separately. Results from previous computations based on VTST (green open triangle),9 ICVT (violet open square)13 and quantum treatments (cyan open diamond)48 are also shown for comparison. (Bottom) Total rates k(T) for the forward (panel C) and reverse (panel D) reaction from GB (black open circles) and a fit to a 3-parameter Arrhenius model (solid black line, for parameters see Table 2). Results from VTST (green open triangle up),9 ICVT (violet open square),13 quantum (cyan open diamond)48 and evaluation (blue solid line).2 Experimental values are also reported in Panel C ((red solid right triangle),49 (magenta solid circle),50 (orange solid left triangle)51) and Panel D ((blue solid right triangle),52 (red solid triangle up),53 (blue cyan line)54) together with fits to experiment with errors (brown shaded areas in panels C55 and D56). | ||
Fig. 4C and D show the total rate k(T) for the forward and reverse reaction. The total rate is calculated as the weighted contribution of the 2A′ and 4A′ surfaces, see eqn (6)–(8). For practical applications, such as “Direct Simulation Monte Carlo” (DSMC) simulations,57 it is also useful to fit the data to an empirical, modified Arrhenius relationship.
 | (10) |
The fitted parameters are given in Table 2. Additional fits for N + O2 on the 4A′ state yield9A = 1.41 × 10−14 cm3 per (s molecule), n = 1.04, B = 6112 K based on VTST data.13 Fitting of earlier QCT data2 yields remarkably similar values to the present results, see Table 2 and blue trace in Fig. 4C, which, however, differ both substantially from a more recent study.13 Experimental rates at higher temperatures are rare. One study was carried out at 1575 K49 which is in quite good agreement within typical56 uncertainties of 25% with the present simulations (Fig. 4C) whereas the rate from an experiment at higher temperature (2880 K)51 is larger than the rate from the present and earlier2 simulations by about a factor of two. One possible explanation is that for experiments above T ∼ 2000 K there is interference between the O + N2 and N + O2 reactions and the analysis required a reaction network both of which introduce uncertainties in the rate.51 For the reverse rate the present simulations accurately describe those measured experimentally.52,53,56
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K for the forward (N(4S) + O2(X3Σ−g) → O(3P) + NO(X2Π)) and reverse (O(3P) + NO(X2Π) → N(4S) + O2(X3Σ−g)) reaction. A in units of 10−14 cm3 per (s molecule)
000 K for the forward (N(4S) + O2(X3Σ−g) → O(3P) + NO(X2Π)) and reverse (O(3P) + NO(X2Π) → N(4S) + O2(X3Σ−g)) reaction. A in units of 10−14 cm3 per (s molecule)
The reverse rate (O + NO) in ref. 9 was not determined from QCT simulations but rather by first computing the equilibrium constant Keq(T) according to statistical mechanics and then using k−(T) = k+(T)/Keq(T). The Arrhenius values from ref. 9 are A = 0.114 × 10−14 cm3 per (s molecule), n = 1.13, and B = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 K. To the best of our knowledge the present work determined k−(T) for the first time from QCT simulations.
200 K. To the best of our knowledge the present work determined k−(T) for the first time from QCT simulations.
In addition, the equilibrium constant Keq(T) as defined in eqn (9) is also calculated (see Fig. 5) as it can be compared directly with experimental work. For Keq(T) the present calculations agree favourably with the JANAF and CEA values over the entire temperature range, as can be expected since Keq is also determined from the difference in Gibbs free energy between the initial and final states.
 | ||
Fig. 5 Equilibrium constant Keq(T). QCT results calculated in this work (circles), fit to a modified Arrhenius model (solid lines) for temperatures between 1000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. Previous QCT,58 JANAF tables23 and Chemical Equilibrium with Application (CEA) results22 are also included for comparison. The inset shows an enlarged view for lower temperatures. 000 K. Previous QCT,58 JANAF tables23 and Chemical Equilibrium with Application (CEA) results22 are also included for comparison. The inset shows an enlarged view for lower temperatures. | ||
To determine the cross sections depending on the final vibrational state ν′, additional simulations were carried out. For this 2 × 105 independent trajectories on each of the three electronic states were run starting from the N + O2 asymptote with a distribution of O2 internal (ν,j) states at 1000 K to follow N(4S) + O2(X3Σ−g) → O(3P) + NO(X2Π)(ν′,j). Then, total reaction cross sections for the individual final vibrational states (ν′,j) were determined. The cross section as a function of the vibrational level (ν′) is reported in Table 3 and compared with previous experimental7 and theoretical9 work. Of particular interest is the dependence of σ on the final vibrational state ν′ of NO because experimentally, an oscillating total cross section had been found with minima at ν′ = 3 and ν′ = 5.7 However, earlier experiments59,60 report the rate constant for formation of NO for the N + O2 → NO + O reaction for vibrational levels ν = 2–7. Using eqn (6) these rates were converted into cross sections which are monotonically decreasing with ν except for ν = 2.59 Rates for ν = 0 and ν = 1 were reported to be larger compared to ν ≥ 2.59 A comprehensive comparison of the present results for the cross sections is given in Table 3.
| State ν′ | Exp.61 | Exp.59 | 2A′ | 4A′ | Total | Lit.10 | Lit.11 | Lit.9 |
|---|---|---|---|---|---|---|---|---|
| 0 | — | — | 0.17 | 0.67 | 0.84 | — | 0.28 | 0.50 |
| 1 | 0.49 | — | 0.16 | 0.48 | 0.64 | 0.37 | 0.41 | 0.53 |
| 2 | 0.65 | 0.37 | 0.14 | 0.31 | 0.45 | 0.42 | 0.46 | 0.48 |
| 3 | 0.20 | 0.39 | 0.14 | 0.22 | 0.36 | 0.39 | 0.44 | 0.43 |
| 4 | 0.69 | 0.22 | 0.12 | 0.16 | 0.28 | 0.36 | 0.37 | 0.32 |
| 5 | 0.37 | 0.16 | 0.10 | 0.10 | 0.20 | 0.31 | 0.32 | 0.26 |
| 6 | 0.20 | 0.04 | 0.09 | 0.07 | 0.16 | 0.27 | 0.28 | 0.20 |
| 7 | 0.25 | 0.03 | 0.07 | 0.05 | 0.12 | 0.23 | 0.24 | 0.18 |
No oscillating behaviour of the cross section was found from the present simulations, see Fig. 6. This finding agrees with previous simulations9 based on a DIM PES for the 2A′ state15 and a fitted MBE to CASPT2 calculations for the 4A′ state.13 The present calculations find a decaying cross section with higher vibrational state. The individual contributions of the (2A′) and (4A′) state are calculated in addition to the total contribution which is the weighted sum of the individual states. The previous computational work9 also used the contribution of both the 2A′ and 4A′ states and found a small population inversion peaking at ν′ = 1. But overall, the findings from both simulation studies are consistent and suggest that the experimental findings7 should be reconsidered.
 | ||
| Fig. 6 Vibrational state-dependent, total cross sections (in Å2) for the N + O2(ν) → NO(ν′) + O process as a function of the final ν′. Total contribution (2A′ + 4A′) (open circles and black line) compared with previous computations (turquoise line)9 and experiment (black solid circles)7 with error region (brown shaded area) results. The inset reports the individual contributions from the present work for the 2A′ (red) and 4A′ (green), together with the total cross section. | ||
3.3 Vibrational relaxation
As a third observable reactive (oxygen exchange) and non-reactive vibrational relaxation of O + NO(ν = 1) → O + NO(ν = 0) was studied on the RKHS PESs for all three electronic states as a function of temperature. As has also been noted in previous work, there are a total of 36 states that can potentially participate in the vibrational relaxation dynamics.21,62 However, only energetically low-lying states of 2A′ and 2A′′ symmetry have attractive wells. As the efficiency of vibrational relaxation depends on the contact time between the diatomic and the collision partner, only these two states are deemed to be relevant at the temperature considered in this section, which is T ≤ 3000 K. Such a treatment is also consistent with previous investigations.21,62 Nevertheless, simulations were also carried out for the 4A′ state.An early experiment3 determined the rate for NO(ν = 1) vibrational relaxation by O atoms at room temperature. The vibrationally excited NO and relaxer O atoms were formed using 355 nm laser photolysis of a dilute mixture of NO2 in an argon bath gas. The reported total rate was kν=1→0 = 2.4 ± 0.5(10−11) cm3 s−1 at T = 298 K. It was argued that this value is 2 to 3 times lower than the generally accepted value of K used in atmospheric modeling.63,64 Subsequent QCT simulations19 on the 2A′ and 2A′′ states, find a value of kν=1→0(T = 298 K) = 2.124 ± 0.73(10−11) cm3 s−1. It should be noted that the PESs for these two states are based on different approaches. For the 2A′ PES it is based on a DIM ansatz15 whereas the 2A′′ PES is a MBE fit to CASPT2 calculations.14 Even earlier calculations using the 2A′ PES obtained a somewhat smaller rate of kν=1→0(T = 298 K) = 1.7(10−11) cm3 s−1.65
A more recent experiment20 used a continuous wave microwave source to generate oxygen atoms, combined with photolysis of trace amounts of added NO2 to produce vibrationally excited NO. The rate for vibrational relaxation is kν=1→0(T = 295 K) = 4.2 ± 0.7(10−11) cm3 s−1 which is an increase by 75% compared with the earlier results.3 Later QCT simulations21 based on the DIM PES for the 2A′ state15 and a fitted DMBE PES based on 1681 MRCI/AVQZ calculations for the 2A′′ state17 report a value of kν=1→0(T = 298 K) = 4.34 ± 0.7(10−11) cm3 s−1. Another computational study62 reported a value of kν=1→0(T = 300 K) ∼ 5(10−11) cm3 s−1.
As to compare with the more recent experiments20 the individual contributions of the 2A′, 4A′, and 2A′′ states towards vibrational relaxation of O + NO(ν = 1) → O + NO(ν = 0) were determined here. Additionally, the total rate is compared with previous theoretical19,21 and experimental3,20 results, see Fig. 7. In particular for low temperature the agreement with the more recent20 experiments and the only high-temperature experiment (at 2700 K)66 is noteworthy. The results from the simulations based on high-level, 2-dimensional PESs16 for the 2A′ and 2A′′ states are also in good agreement with the experiments and the present simulations.
 | ||
| Fig. 7 Total vibrational relaxation rate for O + NO(ν = 1) → O + NO(ν = 0). The individual contributions of the 2A′, 4A′, and 2A′′ states are provided in Fig. S12 (ESI†). Present data from Gaussian binning are open black circles and literature values are the symbols as indicated.3,16,19–21,63,66–68 | ||
As can be seen in Fig. S12 (ESI†) and Table 4, trajectories run on the 2A′ state contribute most to the vibrationally relaxing (VR) rates. Hence, to explore whether and how the process of vibrational relaxation (O + NO(ν = 1) → O + NO(ν′ = 0)) and sampling of the underlying PES are related, another 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 independent trajectories were run for the 2A′ state at 530 K. Out of those, 5722 relaxed to ν′ = 0 whereas for 13
000 independent trajectories were run for the 2A′ state at 530 K. Out of those, 5722 relaxed to ν′ = 0 whereas for 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 trajectories either the internal state of NO was changed to (ν′ ≠ 0,j′) or O2 was produced. For the remaining 5967 (nonreactive) trajectories the initial ro-vibrational state is not changed. All the trajectories were saved and rigorous analysis have been carried out to investigate the relaxation process. The opacity function P(b) for relaxing trajectories computed on 2A′ PES is reported in Fig. S13 (ESI†).
311 trajectories either the internal state of NO was changed to (ν′ ≠ 0,j′) or O2 was produced. For the remaining 5967 (nonreactive) trajectories the initial ro-vibrational state is not changed. All the trajectories were saved and rigorous analysis have been carried out to investigate the relaxation process. The opacity function P(b) for relaxing trajectories computed on 2A′ PES is reported in Fig. S13 (ESI†).
| 298 K | 530 K | 640 K | 825 K | 1500 K | 2700 K | 3000 K | |
|---|---|---|---|---|---|---|---|
| 2A′′ | 2.21 | 1.98 | 1.82 | 1.63 | 1.42 | 1.13 | 1.16 |
| 4A′ | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.08 | 0.12 |
| 2A′ | 2.43 | 2.28 | 2.32 | 2.15 | 1.98 | 1.80 | 1.66 |
| Total | 4.64 | 4.26 | 4.14 | 3.77 | 3.41 | 3.00 | 2.94 |
| Exp.20 | 4.2 ± 0.7 | 4.4 ± 0.7 | 4.1 ± 1.2 | 3.1 ± 1.0 | — | — | — |
The probability distributions of different O + NO configurations for different types of trajectories have been computed in (R,θ) space. Structures are included in the computation only if any of the NO bond is within 2.03 to 2.39 a0 (the turning points for the ν = 1 state of NO are rmin = 2.046 a0 and rmax = 2.370 a0). Gaussian binning with bin size ΔR = 0.1 a0 and Δθ = 3° was used and contributions from 2.03 a0 < rNO < 2.39 a0 are excluded. Individually normalized distributions for relaxing (Fig. 8A) and nonrelaxing (Fig. 8B) trajectories are then projected on an r-relaxed 2D PES. This PES was computed by determining the minimum energy for given (R,θ) with r ∈ [2.03,2.39]. Such an r-relaxed PES is a more realistic way for this comparison as it also incorporates the varying NO bond length during the dynamics instead of restricting it to one specified value.
Fig. 8 demonstrates that the two families of trajectories sample distinct regions of the interaction potential. The VR trajectories have a high density in the deep potential well area (dark blue) of the PES and sample mostly θ > 90° region. This suggests formation of a long lived, tightly bound collision complex. However, the non-relaxing (NR) trajectories spend less time in the potential well region and the density map is rather flat, more uniformly distributed along the angular coordinate with slightly larger sampling in the low-θ region.
To check the initial (before collision) angular dependence of the trajectories and role of long-range anisotropic interactions between the atomic collider and the diatomic target, similar density maps like Fig. 8 have been computed for the VR and NR trajectories only up to the time satisfying the criterion that the sum of the three inter-nuclear distances is less than 9.5 a0. Those are shown for the NR trajectories in Fig. S14 and for the relaxing in Fig. S15 (ESI†). It can be seen that at a separation of ∼8.5 a0 the distribution P(θ) already has “structure” for the NR trajectories and in that a large fraction samples the range θ ∼ 50° while the NR trajectories scarcely sample the high-θ region. However, for the relaxing trajectories the distribution is much more even and lacks a specific high-probability characteristic for a particular angle. Since the low-θ region of the PES is repulsive, most of the trajectories are reflected with only changing the rotational state of the NO and resulting NR events. A large fraction of those NR trajectories could not even visit the short-range interaction region (R < 6.0 a0) and they fly by from the target contributing twice (incoming and outgoing trajectories) more in the density map which is obvious in Fig. S14 (ESI†).
In Fig. S16 (ESI†), ten randomly selected VR (red) and NR (black) trajectories from each of the data set plotted in Fig. S14 and S15 (ESI†) are projected on similar 2D PES as in Fig. 8. The dashed lines represent the reactive (oxygen exchange or O2 formation) trajectories. It can be seen that all VR trajectories sample the potential well region which supports a collision complex. Out of the 10 VR trajectories 3 involve a reactive, oxygen exchange event. The ratio 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 is representative of all trajectories (3890
3 is representative of all trajectories (3890![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1832, for relaxing non reactive vs. relaxing reactive trajectories). Thus, oxygen exchange events contribute almost one third to VR. On the other-hand, among the NR trajectories a certain fraction accesses the global minimum of the PES but most of them do not continue beyond R < 6.0 a0 but are reflected at longer R.
1832, for relaxing non reactive vs. relaxing reactive trajectories). Thus, oxygen exchange events contribute almost one third to VR. On the other-hand, among the NR trajectories a certain fraction accesses the global minimum of the PES but most of them do not continue beyond R < 6.0 a0 but are reflected at longer R.
The results above suggest that relaxing and non-relaxing trajectories probe different parts of the PES. Hence, in order to be able to realistically describe vibrational relaxation the relevant regions, especially the potential well of the PES, have to be described sufficiently accurately. Fig. S17 (ESI†) reports the same PES together with the positions in (R,θ) for which MRCI+Q calculations were carried out. It can be seen that the relevant regions sampled by vibrationally relaxing and non-relaxing trajectories are covered by the electronic structure calculations. Thus the current PES is expected to provide an accurate description of the interaction potential for relaxation dynamics, which is also supported when comparing the computed rates with experiments.
As indicated above, for a complete description of the process, 36 state would need to be included. Most of them are repulsive and as indicated by the results in Table 4, the repulsive 4A′ state only contributes ∼5% to the total relaxation rate at temperatures T ∼ 3000 K. However, at higher collision energies it is likely that this contribution increases and additional states need to be included. However, as long as the shape of the PESs is not significantly different from that of the 4A′ state, the contributions from all these PESs would enter the total relaxation rate through a statistical factor, similar to the treatment of the thermal rate described in the Methods section.
4 Discussion and conclusions
QCT calculations were carried out on the 2A′, 4A′ and 2A′′ electronic states of NO2 for both, the forward and reverse reaction. The total rates agree favourably with experiment for the forward and reverse reaction (Fig. 4C and D), except for the experiment for the forward rate at 2880 K for which interference with reactions such as N2 + O render the analysis more difficult.51 The T-dependent equilibrium constants are close to those reported in the JANAF tables23 and to those from results reported in Chemical Equilibrium with Application (CEA).22 This latter fact suggests that the forward rate k+(T) is in fact preferred over the single available experimental result at higher temperature (2880 K).51 Vibrational relaxation rates were computed for the O + NO(ν = 1) → O + NO(ν = 0) process. Both states, 2A′ and 2A′′, contribute to vibrational relaxation whereas the contribution from the 4A′ state is small at low temperature (k ≈ 10−14) but increases for higher temperatures (Table 4).For VR to occur, the force on the NO oscillator must act along the chemical bond, not orthogonal to it. Hence, the PES along the θ = 0 and θ = 180° directions are most relevant to convert translational energy of the oxygen atom into relaxation of the vibrational motion of the NO diatomic, see Fig. 8. As around θ = 0 the PES is repulsive it is primarily the region around θ = 180° which VR is sensitive to. The present work highlights that different parts of the PESs are probed depending on the observable considered, which can even be demonstrated explicitly. For example, using the DIM PES for the 2A′ state for computing the N + O2 → O + NO temperature-dependent rate coefficients together with contributions for the 4A′ state from the literature, acceptable agreement with experiment can obtained whereas for the temperature dependent vibrational relaxation the DIM PES finds a T-independent rate (see Fig. 7) which considerably underestimates that reported from experiments.
The fact that different observables provide information about different parts of the PES has already been highlighted for van der Waals complexes. As an example, the morphed PESs for the Ne–HF complex69 demonstrated that observables from high resolution spectroscopy about the lowest stretching and bending states along the van der Waals coordinate provide sensitive information about the linear Ne–HF approach but no information about the antilinear Ne–FH part of the PES. Hence, it will be interesting to relate the space sampled by trajectories leading to particular final states with specific features such as to better understand what parts of a PES are crucial for reliably characterizing experimental observables from high-level computational studies.
It is expected that the temperature dependence of the rates computed in the present work extrapolate more reliably to higher temperature than the experimental data because, as the collision energy increases, the simulations sample the near vertical repulsive wall of the diatomic, determining its size. As this is an exponentially increasing curve, errors in the exponent will make little difference in the radius that is accessible at a given energy.
The present work uses one of the highest affordable levels of theory for the electronic structure calculations (MRCI+Q) and the validity of their representation as a RKHS is thoroughly tested using a large number of off-grid points. The topology of the PESs could be fully rationalized with an analysis of the CASSCF wave function of the different states. Being the reference wave function of the MRCI+Q calculation, CASSCF gives a qualitatively correct picture of the relevant wave function characteristics. Investigating the effect of nonadiabatic transitions – as has recently been done for the [CNO] system – will provide additional valuable information in future work.
In summary, the reactive dynamics, thermal rates and vibrational relaxation for the N(4S) + O2(X3Σ−g) ↔ O(3P) + NO(X2Π) reaction on the three lowest potential energy surfaces was studied based on QCT simulations. The results are consistent with most of the available experiments. This provides a solid basis for a molecularly refined picture of vibrational relaxation and extrapolation of thermal rates to higher temperatures relevant at the hypersonic flight regime which can be used for more coarse grained studies such as DSMC simulations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Part of this work was supported by the United State Department of the Air Force which is gratefully acknowledged (to MM). Support by the Swiss National Science Foundation through grants 200021-117810, 200020-188724, the NCCR MUST (to MM), the sciCORE cluster and the University of Basel is also acknowledged. The authors also thank Prof. M. González for providing his NO2 potential energy surface.References
- Y. Zeldovich, The Oxidation of Nitrogen in Combustion Explosions, Acta Physicochimica U.S.S.R, 1946, 21, 577–628 CAS.
- D. Bose and G. V. Candler, Thermal rate constants of the O2 + N → NO + O reaction based on the 2A′ and 4A′ potential-energy surfaces, J. Chem. Phys., 1997, 107, 6136–6145 CrossRef CAS.
- J. A. Dodd, R. B. Lockwood, E. S. Hwang, S. M. Miller and S. J. Lipson, Vibrational relaxation of NO(v = 1) by oxygen atoms, J. Chem. Phys., 1999, 111, 3498–3507 CrossRef CAS.
- R. Gupta, J. Yos, R. Thompson and K. Lee, A Review of Reaction Rates and Thermodynamic and Transport Properties for an 11-Species Air Model for Cheical and Thermal Nonequilibrium Calculations to 30000 K, Acta Physicochimica U.S.S.R, 1946, 21, 577–628 Search PubMed.
- C. Park, Review of chemical-kinetic problems of future NASA missions. I-Earth entries, J. Thermophys. Heat Transfer, 1993, 7, 385–398 CrossRef CAS.
- K. Venkataramani, J. D. Yonker and S. M. Bailey, Contribution of chemical processes to infrared emissions from nitric oxide in the thermosphere, J. Geophys. Res. - Space Phys, 2016, 121, 2450–2461 CAS.
- G. Caledonia, R. Krech, D. Oakes, S. Lipson and W. Blumberg, Products of the reaction of 8 km s−1 N(4S) and O2, J. Geophys. Res.: Space Phys., 2000, 105, 12833–12837 CrossRef CAS.
- I. Winkler, R. A. Stachnik, J. I. Steinfeld and S. M. Miller, Determination of NO (ν = 07) product distribution from the N(4S) + O2 reaction using twophoton ionization, J. Chem. Phys., 1986, 85, 890–899 CrossRef CAS.
- P. J. B. S. Caridade and A. J. C. Varandas, Dynamics Study of the N(4S) + O2 Reaction and Its Reverse, J. Phys. Chem. A, 2004, 108, 3556–3564 CrossRef CAS.
- J. W. Duff, F. Bien and D. E. Paulsen, Classical dynamics of the N(4S) + O2 (X3Σ−g) + NO(X2Π) + O(3P) reaction, Geophys. Res. Lett., 1994, 21, 2043–2046 CrossRef CAS.
- B. Ramachandran, N. Balakrishnan and A. Dalgarno, Vibrational rotational distributions of NO formed from N + O2 reactive collisions, Chem. Phys. Lett., 2000, 332, 562–568 CrossRef CAS.
- S. Walch and R. Jaffe, Calculated potential surfaces for the reactions: O + N2 → NO + N and N + O2 rightarrow NO + O, J. Chem. Phys., 1987, 86, 6946–6956 CrossRef CAS.
- R. Sayós, C. Oliva and M. González, New analytical (2A′, 4A′) surfaces and theoretical rate constants for the N(4S) + O2 reaction, J. Chem. Phys., 2002, 117, 670–679 CrossRef.
- M. González, I. Miquel and R. Sayós, Ab initio, VTST, and QCT study of the 12A′′ potential energy surface of the N(2D) + O2(X3Σg) → O(3P) + NO(X2Π) reaction, J. Chem. Phys., 2001, 115, 8838–8851 CrossRef.
- A. Varandas, A realistic multi-sheeted potential energy surface for NO2(2A′) from the double many-body expansion method and a novel multiple energy-switching scheme, J. Chem. Phys., 2003, 119, 2596–2613 CrossRef CAS.
- M. V. Ivanov, H. Zhu and R. Schinke, Theoretical investigation of exchange and recombination reactions in O(3P) + NO(2Π) collisions, J. Chem. Phys., 2007, 126, 054304 CrossRef CAS PubMed.
- V. C. Mota, P. J. S. B. Caridade and A. J. C. Varandas, Ab Initio-Based Global Double Many-Body Expansion Potential Energy Surface for the First 2A′′ Electronic State of NO2, J. Phys. Chem. A, 2012, 116, 3023–3034 CrossRef CAS PubMed.
- J. C. Castro-Palacio, T. Nagy, R. J. Bemish and M. Meuwly, Computational study of collisions between O(3P) and NO(2Π) at temperatures relevant to the hypersonic flight regime, J. Chem. Phys., 2014, 141, 164319 CrossRef PubMed.
- P. J. S. B. Caridade, V. C. Mota, J. R. Mohallem and A. J. C. Varandas, A Theoretical Study of Rate Coefficients for the O + NO Vibrational Relaxation, J. Phys. Chem. A, 2008, 112, 960–965 CrossRef CAS PubMed.
- E. S. Hwang, K. J. Castle and J. A. Dodd, Vibrational relaxation of NO(ν = 1) by oxygen atoms between 295 and 825 K, J. Geophys. Res., 2003, 108, 1109 CrossRef.
- P. J. S. B. Caridade, J. Li, V. C. Mota and A. J. C. Varandas, The O + NO(v) Vibrational Relaxation Processes Revisited, J. Phys. Chem. A, 2018, 122, 5299–5310 CrossRef CAS PubMed.
- S. Gordon and J. McBride, Computer program for calculation of complex chemical equilibrium compositions and applications. I: Analysis, NASA Ref. Pub., 1996, 19, 1311 Search PubMed.
- M. W. Chase, J. L. Curnutt, J. R. Downey, R. A. McDonald, A. N. Syverud and E. A. Valenzuela, JANAF Thermochemical Tables, 1982 Supplement, J. Phys. Chem. Ref. Data, 1982, 11, 695–940 CrossRef CAS.
- H. Werner and P. J. Knowles, A second order multiconfiguration SCF procedure with optimum convergence, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, An efficient second-order MC SCF method for long configuration expansions, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- H. Werner and W. Meyer, A quadratically convergent multiconfiguration selfconsistent field method with simultaneous optimization of orbitals and CI coefficients, J. Chem. Phys., 1980, 73, 2342–2356 CrossRef CAS.
- D. A. Kreplin, P. J. Knowles and H.-J. Werner, Second-order MCSCF optimization revisited. I. Improved algorithms for fast and robust second-order CASSCF convergence, J. Chem. Phys., 2019, 150, 194106 CrossRef PubMed.
- H. Werner and P. J. Knowles, An efficient internally contracted multiconfiguration reference configuration interaction method, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, An efficient method for the evaluation of coupling coefficients in configuration interaction calculations, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS.
- S. Langhoff and E. Davidson, Configuration Interaction Calculations on Nitrogen Molecule, Int. J. Quantum Chem., 1974, 8, 61–72 CrossRef CAS.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- H. J. Werner, P. J. Knowles, G. Knizia and F. R. Manby, et al., M. S. MOLPRO, version 2019.1, a package of ab initio programs. 2019.
- O. T. Unke and M. Meuwly, Toolkit for the Construction of Reproducing Kernel-Based Representations of Data: Application to Multidimensional Potential Energy Surfaces, J. Chem. Inf. Model., 2017, 57, 1923–1931 CrossRef CAS PubMed.
- G. Henkelman, B. Uberuaga and H. Jonsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- A. H. Larsen and J. J. Mortensen, The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- J. E. Bartmess, Negative Ion Energetics Data; NIST Chemistry Webbok, NIST Standard Reference Database Number 69, ed. P. J. Lindstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburgh MD, 20899, 2001, http://webbook.nist.gov Search PubMed.
- D. R. Lide, Handbook of Chemistry and Physics, Springer, US, 1992, pp. 10–211 Search PubMed.
- S. J. Cavanagh, S. T. Gibson, M. N. Gale, C. J. Dedman, E. H. Roberts and B. R. Lewis, High-resolution velocity-map-imaging photoelectron spectroscopy of the O(−) photodetachment fine-structure transitions, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 052708 CrossRef.
- D. G. Truhlar and J. T. Muckerman, Atom – Molecule Collision Theory, ed. R. B. Bernstein, Springer, US, 1979, pp. 505–566 Search PubMed.
- N. E. Henriksen and F. Y. Hansen, Theories of Molecular Reaction Dynamics, Oxford, 2011 Search PubMed.
- D. Koner, L. Barrios, T. González-Lezana and A. N. Panda, State-to-State Dynamics of the Ne + HeH+(ν = 0,j = 0) → NeH+(ν′,j′) + He Reaction, J. Phys. Chem. A, 2016, 120, 4731–4741 CrossRef CAS PubMed.
- D. Koner, R. J. Bemish and M. Meuwly, The C(3P) + NO(X2Π) → O(3P) + CN(X2Σ+), N(2D)/N(4S) + CO(X1Σ+) reaction: Rates, branching ratios, and final states from 15 K to 20
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, J. Chem. Phys., 2018, 149, 094305 CrossRef PubMed.
000 K, J. Chem. Phys., 2018, 149, 094305 CrossRef PubMed. - L. Bonnet and J.-C. Rayez, Quasiclassical Trajectory Method for Molecular Scattering Processes: Necessity of a Weighted Binning Approach, Chem. Phys. Lett., 1997, 277, 183–190 CrossRef CAS.
- L. Bonnet and J.-C. Rayez, Gaussian Weighting in the Quasiclassical Trajectory Method, Chem. Phys. Lett., 2004, 397, 106–109 CrossRef CAS.
- J. D. Bender, P. Valentini, I. Nompelis, Y. Paukku, Z. Varga, D. G. Truhlar, T. Schwartzentruber and G. V. Candler, J. Chem. Phys., 2015, 143, 054304 CrossRef PubMed.
- E. L. Kolsbjerg, M. N. Groves and B. Hammer, An automated nudged elastic band method, J. Chem. Phys., 2016, 145, 094107 CrossRef PubMed.
- G. Knizia IboView: A program for chemical analysis, 2013.
- R. A. Sultanov and N. Balakrishnan, Quantum mechanical investigations of the N(4S) + O2(X3Σ−g) → NO(X2Π) + O(3P) reaction, J. Chem. Phys., 2006, 124, 124321 CrossRef PubMed.
- F. Kaufman and L. J. Decker 7th Symp. (Int.) Combustion 1959, 57.
- W. Wilson, Rate constant for the reaction N + O2 → NO+ O, J. Chem. Phys., 1967, 46, 2017–2018 CrossRef CAS.
- J. B. Livesey, A. L. Roberts and A. Williams, The Formation of Oxides of Nitrogen in some Oxy-Propane Flames, Combust. Sci. Technol., 1971, 4, 9–15 CrossRef CAS.
- K. L. Wray and J. D. Teare, ShockTube Study of the Kinetics of Nitric Oxide at High Temperatures, J. Chem. Phys., 1962, 36, 2582–2596 CrossRef CAS.
- T. C. Clark, S. H. Garnett and G. B. Kistiakowsky, Reaction of Carbon Dioxide with Atomic Oxygen and the Dissociation of Carbon Dioxide in Shock Waves, J. Chem. Phys., 1969, 51, 2885–2891 CrossRef CAS.
- R. K. Hanson, W. L. Flower and C. H. Kruger, Determination of the Rate Constant for the Reaction O + NO → N + O2, Combust. Sci. Technol., 1974, 9, 79–86 CrossRef CAS.
- A. Fernandez, A. Goumri and A. Fontijn, Kinetics of the Reactions of N(4S) Atoms with O2 and CO2 over Wide Temperatures Ranges, J. Phys. Chem. A, 1998, 102, 168–172 CrossRef CAS.
- R. K. Hansen and S. Salimian, in Combustion Chemistry, ed. W. C. Gardiner Jr., Springer, New York, NY, 1984, pp. 361–421 Search PubMed.
- I. D. Boyd and T. E. Schwartzentruber, Nonequilibrium Gas Dynamics and Molecular Simulation, Cambridge University Press, 2017 Search PubMed.
- J. C. Castro-Palacio, R. J. Bemish and M. Meuwly, Communication: Equilibrium rate coefficients from atomistic simulations: The O(3P) + NO(2Π) → O2(X3Σ−g) + N(4S) reaction at temperatures relevant to the hypersonic flight regime, J. Chem. Phys., 2015, 142, 091104 CrossRef PubMed.
- A. Rahbee and J. J. Gibson, Rate constants for formation of NO in vibrational levels ν = 2 through 7 from the reaction N(4S) + O2 → NO++ + O, J. Chem. Phys., 1981, 74, 5143–5148 CrossRef CAS.
- R. R. Herm, B. J. Sullivan and M. E. Whitson, Nitric oxide vibrational excitation from the N(4S) + O2 reaction, J. Chem. Phys., 1983, 79, 2221–2230 CrossRef CAS.
- G. E. Caledonia, R. H. Krech, D. B. Oakes, S. J. Lipson and W. A. M. Blumberg, Products of the reaction of 8 km s−1 N(4S) and O2, J. Geophys. Res., 2000, 105, 12833–12837 CrossRef CAS.
- M. V. Ivanov, R. Schinke and G. C. Mcbane, Theoretical investigation of vibrational relaxation of NO (2Π), O2(3Σ−g), and N2(1Σ+g) in collisions with O(3P), Mol. Phys., 2007, 105, 1183–1191 CrossRef CAS.
- R. P. Fernando and I. W. Smith, Vibrational relaxations of NO by atomic oxygen, Chem. Phys. Lett., 1979, 66, 218–222 CrossRef CAS.
- R. D. Sharma and R. G. Roble, Impact of the new rate coefficients for the O atom vibrational deactivation and photodissociation of NO on the temperature and density structure of the terrestrial atmosphere, J. Geophys. Res.: Space Phys., 2001, 106, 21343–21350 CrossRef CAS.
- M. Quack and J. Troe, Complex Formation in Reactive and Inelastic Scattering: Statistical Adiabatic Channel Model of Unimolecular Processes III, Ber. Bunsenges. Phys. Chem., 1975, 79, 170–183 CrossRef CAS.
- K. Glänzer and J. Troe, Vibrational relaxation of NO in collisions with atomic oxygen and chlorine, J. Chem. Phys., 1975, 63, 4352–4357 CrossRef.
- H. V. Lilenfeld, Deactivation of vibrationally excited NO and CO2 by atoms, Phillips Laboratory, Hanscom Air Force Base, Mass, 1994, PLTR942180, p. 24 Search PubMed.
- S. M. Anderson, F. S. Klein and F. Kaufman, Kinetics of the isotope exchange reaction of 18O with NO and O2 at 298 K, J. Chem. Phys., 1985, 83, 1648–1656 CrossRef CAS.
- M. Meuwly and J. Hutson, Morphing ab initio potentials: A systematic study of Ne-HF, J. Chem. Phys., 1999, 110, 8338–8347 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp06085e |
| This journal is © the Owner Societies 2020 |


