Experimental observation of nanophase segregation in aqueous salt solutions around the predicted liquid–liquid transition in water

Abstract

The liquid–liquid transition in supercooled liquid water, predicted to occur around 220 K, is controversial due to the difficulty of studying it caused by competition from ice crystallization (the so-called “no man's land”). In aqueous solutions, it has been predicted to give rise to phase separation on a nanometer scale between a solute-rich high-density phase and a water-rich low-density phase. Here we report direct experimental evidence for the formation of a nanosegregated phase in eutectic aqueous solutions of LiCl and LiSCN where the presence of crystalline water can be experimentally excluded. Femtosecond infrared and Raman spectroscopies are used to determine the temperature-dependent structuring of water, the solvation of the SCN⁻ anion, and the size of the phase segregated domains.

---

Introduction

Liquid water has many anomalous properties such as a density maximum at 4 °C and a rapid increase in heat capacity on supercooling.^1–3 These anomalies can be explained by the presence of a liquid–liquid critical point that is predicted to occur at positive pressure and a temperature of about 220 K. This critical point would terminate a coexistence line separating a high-density (liquid like) amorphous phase from a low-density (ice like) amorphous phase with increased tetrahedral ordering. Supercooling liquid water should then give rise to a liquid–liquid transition on crossing the Widom line at about 220 K.^4–7

Whether one can observe phase separation due to the liquid–liquid transition depends on the relative rates of coarsening of crystalline domains vs. that of low and high-density water domains. In pure liquid water, homogeneous nucleation of ice is much faster than phase separation, making it impossible to observe the liquid–liquid transition.⁸ One method to delay the onset of crystal nucleation is the addition of solutes that lower the liquidus temperature. In hyperquenched (glassy) dilute LiCl solutions, there is experimental evidence for a polyamorphic transition between two glassy states⁹ and for phase separation having occurred.¹⁰ Macroscopic phase separation has been reported for mixtures of water and glycerol¹¹ but this was subsequently shown to be caused by ice formation.^12,13 Recent work has shown that a water-rich hydrazinium trifluoroacetate solution prevents crystallization and undergoes a reversible phase transition between two homogeneous liquid states.¹⁴

The low-density structured phase of water is relatively solutophobic, readily expelling solutes.¹⁵ Computer simulations¹⁶ predict that homogenous salt solutions, such as that of LiCl in water, form a nanosegregated glass on cooling driven by the expulsion of ions from four-coordinated water to form a solute-rich phase. The characteristic dimension of phase segregation is predicted to be 4–5 nm.

In an attempt to observe phase separation, we have chosen eutectic mixtures of water with LiCl and LiSCN. These eutectic mixtures have a greatly reduced liquidus temperature compared to pure water (nearly 100 K reduction) and as a result the viscosity near this temperature is high, reducing the probability of ice formation. Furthermore, it is easy to turn such samples into glasses by cooling to 140 K.⁶ Studies into the behavior of water in such systems have established that the remaining water participates in enough hydrogen bonds to be thought of as “bulk-like”.¹⁴ In particular, depolarized Raman spectroscopy¹⁷ has shown that the characteristic TA and LA phonon modes of water, arising from vibrations of the hydrogen-bonded liquid water structure, are maintained at low temperature.

Aqueous solutions of lithium chloride and thiocyanate behave similarly, having eutectic temperatures of 193 K and 181 K respectively.^18,19 However, the SCN⁻ ion is a powerful experimental probe: it has a strongly IR-active ν_CN stretch mode at 2040–2200 cm⁻¹ that is sensitive to electrostatic interactions²⁰ and a large anisotropic molecular polarizability, resulting in strong depolarized Raman scattering. In this work, we use D₂O doped solutions of LiCl at the eutectic composition of 7 water molecules per ion pair, within which 6% of chloride ions are substituted for the thiocyanate probe (LiCl-SCN:7H₂O). Yuan et al. used a similar approach to use methyl thiocyanate as a probe of room temperature aqueous LiCl solutions.^21,22 Fourier-transform infrared spectroscopy (FTIR) and femtosecond infrared pump–probe spectroscopy^23,24 were used to measure the temperature-dependent IR spectrum and the vibrational excited-state lifetimes. Ultrafast optical Kerr-effect (OKE) spectroscopy^25–28 was used to measure the temperature-dependent depolarized Raman spectrum of a eutectic solution of LiSCN in water (LiSCN:5.8H₂O).

Materials and methods

Samples for IR spectroscopy

A eutectic solution (6.76 M) of LiCl was prepared by dissolving anhydrous LiCl (Sigma-Aldrich) in distilled water. To allow use of SCN⁻ as an IR-sensitive probe, the LiCl concentration was reduced to 6.36 M and 0.4 M of LiSCN added to maintain the ionic concentration of the eutectic mixture. As both LiSCN and LiCl are hygroscopic, the solutions were prepared under 1 atm N₂ to minimize the absorption of water before and during weighing. A Volhard titration was performed to allow the amount of water absorbed by the LiCl and LiSCN to be accurately determined, this was then taken into account when preparing the solutions. In some cases, 9% D₂O was added to the H₂O solvent (keeping concentrations constant) in order to allow visualization of the OD stretching vibration. The OH-stretching band of water was saturated under normal conditions, prohibiting direct observation of this transition.

Non-eutectic samples were prepared by keeping the SCN⁻ concentration constant at 0.4 M and changing the LiCl concentration.

Samples for OKE spectroscopy

An aqueous eutectic solution (38.27 ± 0.5 wt%) of LiSCN was prepared by diluting a concentrated aqueous LiSCN stock solution with HPLC gradient grade water (Fisher). The stock solution was prepared by dissolving lithium thiocyanate hydrate (Sigma-Aldrich) in HPLC grade water (Fisher). The concentration was determined by flame photometry. The eutectic LiSCN solution was then filtered with a 20 μm hydrophilic PTFE filter (Millex), transferred to a quartz cuvette (Starna) and degassed for 5 minutes in an ultrasound bath.

IR absorption spectroscopy

For all IR measurements, the samples were loaded between two CaF₂ windows separated by a poly-tetrafluoroethylene (PTFE) spacer of 25 μm thickness. For the room temperature measurements, this was housed in a standard transmission cell. For low temperature measurements, the samples were loaded into a cryostat (Oxford Instruments) in which the sample space had been evacuated to less than 10⁻⁶ mbar, before being purged with a 0.2 bar overpressure of dry N₂ for a period of 15 minutes before the sample was inserted. This purge was maintained throughout the experiment. The sample was then adjusted to the required temperature and it was ascertained that the results for the eutectic solution were consistent irrespective of whether the sample was simply cooled to a given temperature or first cooled to 90 K and subsequently heated to the required temperature. Once the temperature had stabilized the sample was held at this temperature for a further 10 minutes before measurements began.

All IR absorption spectra were acquired using a Bruker Vertex 70 Fourier Transform (FT)-IR spectrometer operating in the range of 800–4000 cm⁻¹ with a resolution of 1.0 cm⁻¹. The average of three measurements, each consisting of 20 scans was used for all data shown.

Time-domain infrared spectroscopy

Ultrafast infrared pump–probe and 2D-IR measurements were performed using the spectrometer described previously.^23,24 Briefly, a regeneratively-amplified Ti:sapphire laser system was used to pump an optical parametric amplifier (OPA) equipped with difference-frequency mixing of signal and idler beams. This resulted in the production of mid-IR pulses of ∼100 fs duration with a center frequency 2083 cm⁻¹ and a bandwidth of ∼250 cm⁻¹ at a repetition rate of 1 kHz.

Ultrafast IR pump–probe measurements were performed by splitting the output of the OPA into pump (95% intensity) and probe beams. The pump beam was routed through an optical delay stage in order to control the pump–probe time delay before being overlapped with the probe in the sample. Pump–probe measurements were recorded with parallel and perpendicular polarization of the pump beam with respect to the probe beam. These results were used to calculate the magic angle response, which serves to suppress the effects of molecular rotation in the data recovered.

2D-IR measurements were performed using the FT-2D-IR method described in detail elsewhere.²⁹ This employs a Mach–Zehnder interferometer to create two collinear pump pulses that were subsequently spatially overlapped at the sample with a third, probe pulse in a pseudo pump–probe geometry. The two pump pulses were separated by a variable delay time τ, controlled by the interferometer. The probe pulse was temporally delayed with respect to the second pump pulse by the waiting time, T_w, set by an optical delay line. As the measured signals for the samples studied were relatively small, all 2D-IR measurements were performed with the polarizations of the pulses parallel to each other. After passing through the sample, the probe pulse was dispersed in a spectrometer and detected using a 64-channel mercury–cadmium–telluride (MCT) detector to give the probe frequency axis of the 2D-IR spectrum. The data were collected as a function of τ and a Fourier transformation used to recover the pump frequency axis of the spectrum. A second MCT detector was used to collect the field-autocorrelation signal of the two pump pulses, which informed the accurate determination of the time the pump pulse pair were incident upon the sample. The residual pump–probe signal was removed using a chopper set to half of the laser repetition rate positioned in the fixed arm of the interferometer.

Optical Kerr-effect spectroscopy

The optical Kerr-effect (OKE) spectroscopy data were recorded in a standard time-domain step-scan pump–probe configuration and Fourier transformed to obtain the frequency-domain reduced depolarized Raman spectrum as described previously.^17,25–28 A laser oscillator (Coherent Micra) provided ∼10 nJ pulses (0.8 W average power) with a nominal wavelength of 800 nm at a repetition rate of 82 MHz providing a 30 fs pulse width in the sample. For the longer-timescale relaxation measurements, a second set of data was taken in a similar configuration using a higher pulse energy of, typically, 1 μJ provided by a regeneratively-amplified laser (Coherent Legend Elite USX) at a repetition rate of 1 kHz with a pulse duration stretched to ∼0.5 ps. Stretching the pulse enables a higher energy to be used without nonlinear effects and reduces the upper bandwidth limit allowing large step size scanning without introducing undersampling artefacts. Pump–probe OKE experiments were carried out with delay times from a few femtoseconds to a maximum of 1 to 7 ns, resulting in a spectral resolution (after Fourier transformation) of better than 1 GHz (<0.033 cm⁻¹). The sample was contained in a rectangular quartz cuvette (Starna, thickness: 2 mm) held under a dry nitrogen atmosphere in a liquid nitrogen-cooled cryostat (Oxford Instruments) with a temperature precision of ±0.1 K.

The measurements using the Coherent Micra were done subsequently at 300, 275, 250, 220, 200, 180, 150, and 90 K. Each measurement consisted of at least 33 traces up to 1 ns and lasted for 30 minutes to 1 hour.

For the measurements using the Coherent Legend Elite USX subsequent measurements were done at 90, 150, 180, 200, 220, 250, 275, and 300 K, with the sample held at a given temperature for 20 minutes before measuring. Each measurement consisted of at least 46 traces up to 7 ns and lasted for 1.5 to 2 hours.

Results

Infrared spectroscopy

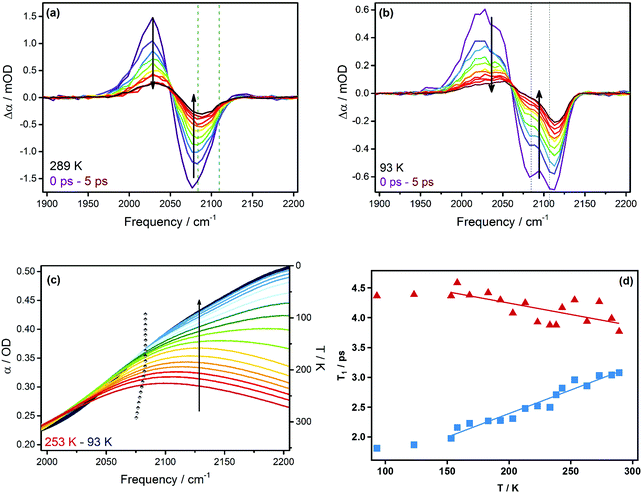
Fig. 1(a) shows the temperature dependence of the IR absorption spectrum of a eutectic mixture (LiCl-SCN:7H₂O doped with D₂O) in the 2000–2600 cm⁻¹ region. Three main features are visible: the ν_CN stretch mode of the SCN⁻ ion at ∼2080 cm⁻¹; a broad peak near 2200 cm⁻¹ due to the H₂O combination band (δ_HOH + ν_lib) involving excitation of both the H–O–H bend (δ_HOH) and a low frequency librational mode (ν_lib); and the ν_OD stretching mode near 2500 cm⁻¹.

Fig. 1 IR spectra of LiCl-SCN:7H₂O doped with D₂O between 253 and 93 K (in direction of arrows). (a) Raw absorbance spectrum showing the ν_CN asymmetric stretch (∼2080 cm⁻¹), H₂O combination band of the H–O–H bend and the librational mode (δ_HOH + ν_lib, ∼2200 cm⁻¹), and the ν_OD stretching mode (∼2500 cm⁻¹). An additional feature visible near 2350 cm⁻¹ is due to a vibrational mode of atmospheric CO₂. (b) The ν_CN stretch mode spectrum extracted from (a) by baseline fitting. (c) Normalized change in absorbance (Δα_norm.) of the shoulder in the ν_CN stretch band (○), the δ_HOH + ν_lib combination band (□), and the ν_OD stretch (△) as well as the frequency of the ν_CN stretch (●), and the ν_OD stretch (■).

The temperature-dependent behavior of the water component in the eutectic solution is indicated by the δ_HOH + ν_lib band and the ν_OD stretching mode. Decreasing temperature causes the former to shift to higher and the latter to lower frequencies, while both increase in amplitude (see arrows in Fig. 1(a)). These trends continue until the glass-transition temperature is reached at ∼140 K (see Fig. 1(c)).³⁰

The temperature-dependence of the ν_CN stretch-mode band in the eutectic solution was extracted by fitting the water combination band to Gaussian lineshape functions to allow subtraction in order to isolate the ν_CN stretch band shown in Fig. 1(b). At room temperature, this band is dominated by a single broad feature that shifts linearly to higher frequency upon lowering the temperature (see Fig. 1(c)). In contrast to the water bands, this behavior stops at ∼180 K and a shoulder at 2105 cm⁻¹ dramatically increases in amplitude down to 140 K.

Similar experiments were carried out on non-eutectic mixtures. For example, Fig. 2 shows the spectra for LiCl-SCN:9H₂O solution, which exhibit the same spectral features but an additional sharp ν_OD stretching band at 2430 cm⁻¹, which vanishes at 233 K upon heating. This temperature corresponds well to the liquidus temperature of the non-eutectic solution^18,19 and the sharp feature continuously changes even at temperatures approaching the glass transition.

Fig. 2 IR spectra of the non-eutectic LiCl-SCN:9H₂O solution doped with D₂O measured from 83 to 253 K. Raw spectrum showing the ν_CN asymmetric stretch (∼2080 cm⁻¹), H₂O combination band of the H–O–H bend and librational mode (δ_HOH + ν_lib, ∼2200 cm⁻¹), and the ν_OD stretching mode of ice (2430 cm⁻¹) and the ν_OD mode of liquid water (∼2500 cm⁻¹).

Temperature-dependent IR pump–probe experiments

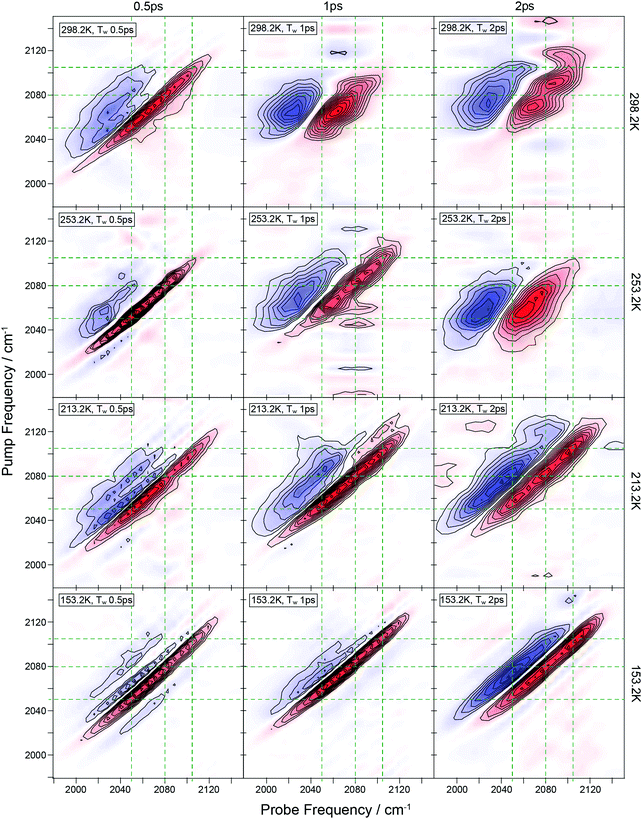
The results of temperature-dependent IR pump–probe experiments on the ν_CN stretch mode of the eutectic mixture are shown in Fig. 3. At room temperature, the spectra show a straightforward lineshape consisting of a negative peak attributable to bleaching/stimulated emission associated with the v = 0–1 transition of the ν_CN stretch mode and a positive feature, shifted to lower frequency, which is assigned to the accompanying v = 1–2 transition. At temperatures below 200 K, a second set of features appeared (Fig. 3(b)), consistent with the observation of the shoulder in the absorption spectra (Fig. 1(b)). Fitting these peaks to Gaussian lineshape functions showed that they decrease in amplitude with increasing pump–probe delay time in a manner that is well-represented by a single exponential decay, from which the vibrational relaxation time (T₁) was extracted. On cooling it was observed that the vibrational lifetime (T₁) of the main ν_CN stretch peak decreases linearly until the glass transition temperature (blue points (Fig. 3(d))), while that of the high-frequency shoulder increases (red points (Fig. 3(d))).

Fig. 3 Results of IR pump–probe experiments. Infrared pump–probe spectra of LiCl-SCN:7H₂O at pump–probe time delays between 0 and 5 ps (in direction of arrows) at (a) 289 K and (b) 93 K. (c) Variation of the δ_HOH + ν_lib combination band of H₂O as a function of temperature. Right hand axis and points show the corresponding position of the ν_CN stretch mode of SCN⁻. The increase in spectral density of the H₂O band at lower temperature is clear and this results in a reduction in the T₁ relaxation time observed for SCN⁻ in IR pump–probe measurements. (d) Temperature-dependent excited vibrational state lifetimes in eutectic LiCl-SCN solution for the ν_CN stretch band (■) and the shoulder (▲) the lines are linear fits to the data for temperatures above 153 K.

Ultrafast 2D-IR spectra were obtained at 293 K, 253 K, 213 K, and 153 K (Fig. 4). The room temperature data were obtained using both the cryostat and a standard absorption cell. Aside from the standard absorption cell allowing a greater throughput of IR radiation and hence giving a better signal to noise ratio than the cryostat, the effects of the cell were not significant. The room temperature 2D-IR data show two main features at short waiting times. A negative feature is present along the spectrum diagonal, this is elongated along the diagonal extending from pump–probe frequencies of around 2040 to 2090 cm⁻¹. This is consistent with the v = 0–1 transition of the components observed in the IR spectrum near 2050 and 2075 cm⁻¹. The two components are not clearly resolved because of the broadened lineshapes as in the FT-IR data. The higher frequency component near 2105 cm⁻¹ is not clearly observed at room temperature due to its small amplitude at this temperature, although the spectra show weak indications of its presence. Accompanying the negative peaks are positive features shifted to lower probe frequency, which correspond to the v = 1–2 transitions as shown in the pump probe spectra.

Fig. 4 2D-IR spectra of LiCl-SCN:7H₂O in H₂O as a function of temperature and waiting time.

As the waiting time is increased, the 2D-IR lineshapes of the room temperature sample were observed to broaden considerably in the anti-diagonal direction, becoming near circular by 2 ps. This effect is attributable to the spectral diffusion and shows that the lineshapes in the FT-IR spectrum are inhomogeneously broadened. This is consistent with solutes in aqueous solutions, where the orientational motion of water leads to a continuum of different environments and hence absorption frequencies for the solutes. At short waiting times, the delay between the excitation and detection events producing the 2D-IR signal is short on the timescale of these water dynamics, such that the environment (and hence frequency) of the solute molecule does not evolve during the experiment leading to a diagonally elongated lineshape. At longer waiting times the timescale for the water molecule dynamics is similar to the waiting time and so the frequency of an excited solute molecule evolves during the experiment, leading to a detection frequency that is different to the excitation frequency. Thus, a lineshape contribution occurs in the off-diagonal region of the spectrum that is manifested as anti-diagonal broadening of the lineshape when averaged over the ensemble of solute molecules.

When considering the effect of reduced temperature on the 2D-IR spectra, the most striking observation is that the spectra extend much further along the diagonal towards higher frequencies as the 2105 cm⁻¹ component of the lineshape becomes more prominent at lower temperatures. This diagonal elongation of the lineshape is more marked at early waiting times, largely as a result of this feature becoming observable. The measured anti-diagonal width at 2075 cm⁻¹ and 500 fs was found to be consistent at all temperatures. As the waiting time increased the anti-diagonal broadening was observed at all temperatures, although the effect is much less apparent than at room temperature. At a waiting time of 2 ps, there is still significant correlation of the excitation and detection frequencies remaining at 253 K, and this is true to a greater extent at lower temperatures and by 153 K the lineshape evolution at 2 ps is minimal. The data therefore indicate a dramatic slowing down of the spectral diffusion processes as the temperature is reduced.

OKE experiments

The room-temperature OKE spectrum of a eutectic LiSCN solution (see Fig. 5(a)) shows the standard pattern of an orientational-diffusion (or α-relaxation) band peaking at ∼20 GHz, intermediate relaxation around 100 GHz, and a librational band peaking at 2 THz. On cooling, the α-relaxation slows down until it is too slow to measure in this experiment. The librational band shifts to higher frequencies on cooling, while the number of functions needed to model the librational band increases from two to four at 200 K. A population fraction for each of the librational modes was extracted (see Fig. 5(b)). The population fraction of the high frequency shoulder shows a linear decrease on cooling, while the three lower frequency librational modes follow a sigmoidal temperature change with a halfway point at 180 K. On careful examination of Fig. 5, one can see a band peaking at 144 GHz that only develops at low temperature (<180 K) and remains in the same position even at 90 K, indicating a non-diffusive mode. These measurements were performed using a eutectic solution of LiSCN in order to obtain good signal-to-noise for the measurements of this feature.

Fig. 5 Temperature-dependent OKE spectra. (a) OKE spectra of LiSCN:5.8H₂O solution taken at 300, 275, 250, 220, 200, 180, 150, and 90 K (in the direction of the arrow). (b) Analysis of the low frequency part of the OKE spectrum at 150 K with a logarithmic vertical scale. The raw data are shown as a solid line while the fit is shown as a dashed line. Noise starts to dominate at lower frequencies. (inset) Temperature dependent changes in the population fraction associated with each peak with confidence intervals (dashed).

Discussion

The IR experiments demonstrate the behavior of water in the eutectic and non-eutectic mixtures. The red-shift of the ν_OD stretch is consistent with stronger hydrogen bonding of water molecules at lower temperatures. This is further supported by the blue-shift of the δ_HOH + ν_lib combination band owing to stronger hydrogen-bonding interactions stiffening the intermolecular potential concomitantly, thereby increasing the librational frequency.^31–33 In contrast, only the non-eutectic mixture develops the sharp, red-shifted peak in the ν_OD stretch region attributable to ice formation. From these experiments, it is clear that the eutectic mixture supercools and vitrifies into a glass at the known glass-transition temperature 140 K.³⁰ This is demonstrated by the continuous changes in the water (ice) lineshape (Fig. 2) and the absence of the prominent spectral features indicative of the microcrystallization reported in LiCl:nH₂O solutions of n > 6.^34–36 The temperature of the water (ice) lineshape in Fig. 2 closely follows the predictions of the LiCl/H₂O phase diagram.^18,19 Thus we conclude that the addition of SCN⁻ and D₂O does not significantly perturb the thermodynamics of the system. Furthermore, the formation of ice in the eutectic samples can be ruled out experimentally.

The ν_CN stretch mode of SCN⁻ has been shown to be a sensitive probe of its environment.^{20,32,37–41} At room temperature the ν_CN stretch band in LiCl-SCN mixtures peaks at 2070 cm⁻¹ rather than at the 2055 cm⁻¹ observed in fully water-solvated anions. This is consistent with the formation of Li⁺NCS⁻ contact ion pairs (CIPs) as expected in solutions at high concentration.^20,42 On cooling, the CIP band shifts to higher frequency consistent with an environment of increased hydrogen-bonding strength.²⁰

However, a dramatic change occurs below ∼180 K, when the blue shifting of the ν_CN CIP band stops, accompanied by the rapid increase in intensity of the shoulder at 2105 cm⁻¹. This peak in SCN⁻ has been previously been identified with “aggregates”.^20,42 SCN⁻ exists in dynamic equilibrium between solvated ions, CIPs, as well as aggregates, and this apparent equilibrium shift therefore shows a segregation of an LiSCN/Cl-rich components. (This type of clustering behavior has also been predicted for SCN⁻ near its solubility limit using molecular dynamics simulations, see ref. 43) It is not consistent with the spectrum of the crystalline form of LiSCN,⁴⁴ demonstrating that the new component is an aqueous and salt-rich phase.

The observations in non-eutectic mixtures are consistent with the formation of crystalline water on reaching the liquidus temperature in tandem with enrichment of the remaining brine, until the eutectic composition is reached. The remaining solution then behaves like the eutectic as expected.

Pump–probe experiments on the ν_CN CIP band show that the ν_CN stretch excited-state lifetime decreases on lowering the temperature. This is contrary to expectations of slower vibrational relaxation rates at lower temperature. However, it has been shown that the mechanism of ν_CN stretch mode relaxation is via energy transfer to the δ_HOH + ν_lib combination band of water with which it overlaps significantly.^32,37 A Fermi Golden rule analysis shows that the temperature-induced shift in the H₂O combination band increases this spectral overlap as the temperature is lowered, leading to the observed faster relaxation consistent with our observations (see Fig. 3(c)).³² This behavior supports our observation of the presence of ‘hydrated SCN’ in a salt-rich phase.

These observations contrast sharply with the weak temperature dependence of the excited-state lifetime of the high-frequency shoulder in the ν_CN CIP band. This is strongly suggestive of a different relaxation mechanism that does not involve interaction with or energy transfer to bulk-like water molecules. As such it is again consistent with the formation of aggregated species featuring reduced engagement with water.

Confidence in the proposed assignments is bolstered by the 2D-IR spectral diffusion measurements on the ν_CN CIP band as a function of temperature (see Fig. 4). These show that, at 253 K, the ν_CN stretch band in the 2D-IR spectrum evolves from diagonally elongated to circular in profile as the waiting time of the experiment increases. This behavior is characteristic of aqueous solutions where hydrogen bonding induces dynamic inhomogeneous broadening of solute vibrational modes. This manifests itself as spectral diffusion or lineshape evolution as the waiting time approaches the time-scale for hydrogen-bond fluctuation.^45,46 Quantification of the lineshape evolution using the ellipticity of the lineshape⁴⁵ indicates a timescale of ∼500 fs, this timescale is similar to the value obtained at room temperature for methyl thiocyanate by Yuan et al.^21,22 Such subpicosecond dynamics are consistent with previous 2D-IR studies on hydrated ionic systems.⁴⁶ In addition, a contribution from longer timescale dynamics is also evident from the fact that the lineshape evolution is not complete even at waiting times of 2 ps. This has been previously attributed to restricted motion of water molecules at high ion concentrations.⁴⁶ At lower temperatures the spectral diffusion rate slows dramatically, as would be expected for a highly viscous salt-rich phase.

The OKE data show the α-relaxation slowing down and then freezing out at lower temperatures, consistent with the formation of a glass. The terahertz librational band is found to be complex and can only be modeled at all temperatures by four Gaussian functions (Fig. 5(b)). These Gaussians do not appreciably change in frequency or width on cooling. Their relative amplitudes, however, do change as can be seen in the inset of Fig. 5(b). The rapid change in amplitude around 180 K is consistent with a change in environment (and therefore intermolecular forces) associated with desolvation from a solvated CIP to a salt-rich aggregate. The new band developing at 144 GHz is similar to one that has been seen previously in OKE experiments on low-temperature eutectic aqueous LiCl solutions,¹⁷ where it was associated with anomalous diffusion of a percolating ion–water network.⁴⁷ However, here the band is shown to be non-Arrhenius (negligible dependence of the peak position on temperature), which is inconsistent with a diffusive process and indicates a coherent phonon-like process.

There have been previous attempts to show that the liquid–liquid transition in water will give rise to domains of high-density (more disordered) and low-density (more tetrahedrally ordered) water that can desolvate other liquids and solutes.¹¹ However, the validity of such experiments has been called into question because of the formation of crystalline water.^12,13 The liquid–liquid immiscibility of aqueous LiCl solutions have been observed for concentrations of LiCl:nH₂O for n > 9,¹⁵ and phase separation occurs at concentrations in the range of n ∼ 9 to ∼100.^10,48 The eutectic value of n = 7 used here represents a higher salt concentration than those used in previous studies.

Our samples do not scatter light yet show the effects of phase separation in their IR and OKE spectra. This is consistent with predictions of molecular dynamics simulations, which showed nanosegregation with ∼4–5 nm domains.¹⁶ The absence of scattered light from the sample rules out the formation of crystals such as crystalline LiSCN or LiSCN hydrate, which would also give rise to phonon modes in the OKE spectra, of which none are observed.

In the OKE spectrum, a non-diffusive phonon-like mode peaking at 144 GHz becomes visible in the temperature region where nanosegregation occurs. Using a speed of sound of 1.9 km s⁻¹ (appropriate for aqueous salt solutions⁴⁹), this corresponds to a wavelength of ∼4 nm, remarkably close to the theoretically predicted nanosegregation domain size.¹⁶ This suggests that the 144 GHz mode corresponds to an acoustic phonon localized in these domains.

Many of the results observed here are consistent with the predicted behaviors of nanophase segregation caused by the desolvation of a solute, as a result of crossing a Widom line associated with a liquid–liquid transition in water. These effects would suggest a transition temperature of 180 K well below the 220 K predicated for pure water and well above the glass transition temperature of 140 K,³⁰ but consistent with recent experiments showing a reversible phase transition.¹⁴ The temperature of a liquid–liquid phase transition in aqueous NaCl solutions is predicted by molecular dynamics studies to be higher than that for pure water.^50,51 We do not observe any change in the OD stretching mode indicating a change to a more tetrahedral water structure which would be definitive evidence of a water liquid–liquid transition.

Without the definitive evidence of a water liquid–liquid transition obtained via the OD stretching mode, we must look at alternative explanations for these results. For high concentrations of salt the water hydrogen bonding structures are significantly altered with much lower numbers of hydrogen bonded water molecules per water molecule, ions cannot be fully hydrated in these high salt concentrated solutions so ions tend to form aggregates.⁴³ These aggregates are predicted to be different for chaotropic and kosmotropic salts, highly concentrated solutions (approaching the solubility limit) of ions such as Na⁺ and Cl⁻ form large aggregate clusters in fairly compact and molten salt or crystal-like ion clusters that exclude water,⁵² while concentrated solutions of K⁺ and SCN⁻ ions tend to form spatially extended networks, that intertwine with the surrounding hydrogen bonding water network which helps to stabilize it. Results of Bian et al.⁵³ show evidence that thiocyanate solutions form clusters in unsaturated solutions in which almost all anions form clusters suggesting water/ion microphase separations. Lim et al. have shown that these water networks can act as wires for fast ion transport.⁵⁴ Regardless of the ion aggregate structures the water hydrogen bonding at such high concentrations are significantly different from those in pure liquid water.⁴³ This different nature of the hydrogen bonded water network with lower water coordination could explain why we do not observe a more tetrahedral water structure that would be associated with a water liquid–liquid transition.

As our solutions are made up of primarily LiCl, we expect these large aggregate clusters to dominate the structure with the SCN⁻ ions acting as a probe of these environments, rather than the system forming the long range intertwined ion and water networks seen in aqueous thiocyanate solutions. Recent work by Jiang et al. has predicted the existence of a hidden (metastable) liquid–liquid critical point for aqueous NaCl solutions,⁵⁵ if a similar point exists for LiCl close to the eutectic point the sample would start to show critical fluctuations resulting in aggregation. Simulations by Choi et al.⁵² observed that for aqueous NaCl solutions as one might expect the free ion concentration decreases rapidly as salt concentration increases, while the mole fraction of ion pairs increases with concentration up to 3 M, beyond which increasing the concentration up to the solubility limit the fraction remains constant. Our observations of the ν_CN stretch are consistent with this; we see no resolvable signal around 2050 cm⁻¹ where we expect to see the contribution from free ions, the amplitude of the feature at ∼2075 cm⁻¹ associated with CIPs remains largely unchanged as the temperature decreases and hence the solubility limit is lowered. At the same time the feature at 2105 cm⁻¹, attributed to aggregates or clusters increases in amplitude. It is likely that the increase in amplitude of this feature is due to a greater proportion of the ions aggregating as the temperature is reduced and the solubility limit is approached.

Conclusion

In conclusion we observed a number of effects that one might associate with a liquid–liquid phase transition in water, ultimately however these effects can also be associated with the aggregation or segregation which occurs in aqueous salt solutions, the presence of concentrations of salt required to suppress the freezing point of water is also sufficient to alter the hydrogen-bonding water network so as to make it impossible to see such a transition in this system. Our method however could be used to experimentally probe these salt aggregates.

Data availability

The data that support the findings of this study are available in Enlighten: Research Data Repository (University of Glasgow) with the identifier: http://dx.doi.org/10.5525/gla.researchdata.1001.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

We thank the Engineering and Physical Sciences Research Council (EPSRC) for support through grants EP/J009733/1, EP/J00975X/1, EP/K034995/1, and EP/N007417/1. This work was part funded by Leverhulme Trust Research Project Grant RPG-2018-350 and received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement No. 832703).

References

1. P. Gallo, K. Amann-Winkel, C. A. Angell, M. A. Anisimov, F. Caupin, C. Chakravarty, E. Lascaris, T. Loerting, A. Z. Panagiotopoulos, J. Russo, J. A. Sellberg, H. E. Stanley, H. Tanaka, C. Vega, L. Xu and L. G. M. Pettersson, Chem. Rev., 2016, 116, 7463–7500.
2. K. Amann-Winkel, R. Böhmer, F. Fujara, C. Gainaru, B. Geil and T. Loerting, Rev. Mod. Phys., 2016, 88, 011002.
3. E. Brini, C. J. Fennell, M. Fernandez-Serra, B. Hribar-Lee, M. Lukšič and K. A. Dill, Chem. Rev., 2017, 117, 12385–12414.
4. O. Mishima and H. E. Stanley, Nature, 1998, 396, 329–335.
5. P. H. Handle, T. Loerting and F. Sciortino, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13336–13344.
6. C. A. Angell, Science, 2008, 319, 582–587.
7. K. H. Kim, A. Späh, H. Pathak, F. Perakis, D. Mariedahl, K. Amann-Winkel, J. A. Sellberg, J. H. Lee, S. Kim, J. Park, K. H. Nam, T. Katayama and A. Nilsson, Science, 2017, 358, 1589–1593.
8. E. B. Moore and V. Molinero, Nature, 2011, 479, 506–508.
9. O. Mishima, J. Chem. Phys., 2007, 126, 244507.
10. Y. Suzuki and O. Mishima, Phys. Rev. Lett., 2000, 85, 1322–1325.
11. K.-I. Murata and H. Tanaka, Nat. Mater., 2012, 11, 436–443.
12. I. Popov, A. Greenbaum (Gutina), A. P. Skolov and Y. Feldman, Phys. Chem. Chem. Phys., 2015, 17, 18063–18071.
13. J. R. Bruijn, T. H. van der Loop and S. Woutersen, J. Phys. Chem. Lett., 2016, 7, 795–799.
14. S. Woutersen, B. Ensing, M. Hilbers, Z. Zhao and C. A. Angell, Science, 2018, 359, 1127–1131.
15. C. A. Angell and E. J. Sare, J. Chem. Phys., 1968, 49, 4713–4714.
16. L. Le and V. Molinero, J. Phys. Chem. A, 2011, 115, 5900–5907.
17. D. A. Turton, C. Corsaro, D. F. Martin, F. Mallamace and K. Wynne, Phys. Chem. Chem. Phys., 2012, 14, 8067–8073.
18. C. Monnin, M. Dubois, N. Papaiconomou and J.-P. Simonin, J. Chem. Eng. Data, 2002, 47, 1331–1336.
19. F. A. Schimmel, J. Chem. Eng. Data, 1960, 5, 519–520.
20. P. W. Schultz, G. E. Leroi and A. I. Popov, J. Am. Chem. Soc., 1996, 118, 10617–10625.
21. R. Yuan and M. D. Fayer, J. Phys. Chem. B, 2019, 123, 7628–7639.
22. R. Yuan, C. Yan and M. Fayer, J. Phys. Chem. B, 2018, 122, 10582–10592.
23. R. Fritzsch, O. Brady, E. Adair, J. A. Wright, C. J. Pickett and N. T. Hunt, J. Phys. Chem. Lett., 2016, 7, 2838–2843.
24. G. Hithell, M. González-Jiménez, G. M. Greetham, P. M. Donaldson, M. Towrie, A. W. Parker, G. A. Burley, K. Wynne and N. T. Hunt, Phys. Chem. Chem. Phys., 2017, 19, 10333–10342.
25. M. González-Jiménez, G. Ramakrishnan, T. Harwood, A. J. Lapthorn, S. M. Kelly, E. M. Ellis and K. Wynne, Nat. Commun., 2016, 7, 11799.
26. G. Ramakrishnan, M. González-Jiménez, A. J. Lapthorn and K. Wynne, J. Phys. Chem. Lett., 2017, 8, 2964–2970.
27. J. Reichenbach, S. A. Ruddell, M. González-Jiménez, J. Lemes, D. A. Turton, D. J. France and K. Wynne, J. Am. Chem. Soc., 2017, 139, 7160–7163.
28. J. Reichenbach and K. Wynne, J. Phys. Chem. B, 2018, 122, 7590–7596.
29. L. P. DeFlores, R. A. Nicodemus and A. Tokmakoff, Opt. Lett., 2007, 32, 2966–2968.
30. M. Kobayashi and H. Tanaka, Phys. Rev. Lett., 2011, 106, 125703.
31. T. Tassaing, Y. Danten and M. Besnard, J. Mol. Liq., 2002, 101, 149–158.
32. D. Czurlok, J. Gleim, J. Lindner and P. Vöhringer, J. Phys. Chem. Lett., 2014, 5, 3373–3379.
33. P. K. Verma, A. Kundu, M. S. Puretz, C. Dhoonmoon, O. S. Chegwidden, C. H. Londergan and M. Cho, J. Phys. Chem. B, 2018, 122, 2587–2599.
34. M. E. Gallina, L. Bove, C. Dreyfus, A. Polian, B. Bonello, R. Cucini, A. Taschin, R. Torre and R. M. Pick, J. Chem. Phys., 2009, 131, 124504.
35. L. E. Bove, C. Dreyfus, R. Torre and R. M. Pick, J. Chem. Phys., 2013, 139, 044501.
36. A. Elarby-Aouizerat, J.-F. Jal, P. Chieux, J. M. Letoffé, P. Claudy and J. Dupuy, J. Non-Cryst. Solids, 1988, 104, 203–210.
37. V. Lenchenkov, C. She and T. Lian, J. Phys. Chem. B, 2006, 110, 19990–19997.
38. Z. Ren, T. Brinzer, S. Dutta and S. Garrett-Roe, J. Phys. Chem. B, 2015, 119, 4699–4712.
39. Q. Zhong, A. P. Baronavski and J. C. Owrutsky, J. Chem. Phys., 2003, 119, 9171–9177.
40. K.-I. Oh, J.-H. Choi, J.-H. Lee, J.-B. Han, H. Lee and M. Cho, J. Chem. Phys., 2008, 128, 154504.
41. M. Li, J. Owrutsky, M. Sarisky, J. P. Culver, A. Yodh and R. M. Hochstrasser, J. Chem. Phys., 1993, 98, 5499–5507.
42. S. Park, M. Ji and K. J. Gaffney, J. Phys. Chem. B, 2010, 114, 6693–6702.
43. J.-H. Choi, H. Kim, S. Kim, S. Lim, B. Chon and M. Cho, J. Chem. Phys., 2015, 142, 204102.
44. M. M. Gafurov, A. R. Aliev and I. R. Akhmedov, Spectrochim. Acta, Part A, 2002, 58, 2683–2692.
45. J. J. Loparo, S. T. Roberts and A. Tokmakoff, J. Chem. Phys., 2006, 125, 194521.
46. S. Park and M. D. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 16731–16738.
47. C. A. Angell and R. D. Bressel, J. Phys. Chem., 1972, 76, 3244–3253.
48. Y. Suzuki and O. Mishima, J. Chem. Phys., 2013, 138, 084507.
49. S. J. Kleis and L. A. Sanchez, Sol. Energy, 1990, 45, 201–206.
50. D. Corrandini and P. Gallo, J. Phys. Chem. B, 2011, 115, 14161–14166.
51. T. Yagasaki, M. Matsumoto and H. Tanaka, J. Chem. Phys., 2019, 150, 214506.
52. J.-H. Choi and M. Cho, J. Chem. Phys., 2014, 141, 154502.
53. H. Bian, X. Wen, J. Li, H. Chen, S. Han, X. Sun, J. Song, W. Zhuang and J. Zheng, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4737–4742.
54. J. Lim, K. Park, H. Lee, J. Kim, K. Kwak and M. Cho, J. Am. Chem. Soc., 2018, 140, 15661–15667.
55. H. Jiang, P. G. Debenedetti and A. Z. Panagiotopoulos, J. Chem. Phys., 2019, 150, 124502.

---