Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hydrophilic and hydrophobic interactions in concentrated aqueous imidazole solutions: a neutron diffraction and total X-ray scattering study†
Laila H.
Al-Madhagi
 ab,
Samantha K.
Callear
c and
Sven L. M.
Schroeder
ab,
Samantha K.
Callear
c and
Sven L. M.
Schroeder
 *abd
*abd
aSchool of Chemical and Process Engineering, University of Leeds, Leeds LS2 9JT, UK. E-mail: S.L.M.Schroeder@leeds.ac.uk
bDiamond Light Source Ltd., Didcot, Oxfordshire, OX11 0DE, UK
cISIS Facility, STFC Rutherford Appleton Laboratory, Didcot, Oxfordshire, OX11 0QX, UK
dResearch Complex at Harwell, Didcot, Oxfordshire, OX11 0DE, UK
First published on 18th February 2020
Abstract
The intermolecular interactions in concentrated (5 M) aqueous imidazole solutions have been investigated by combining neutron diffraction with isotopic substitution, total X-ray scattering and empirical potential structure refinement (EPSR) simulations using a box containing 5530 water and 500 imidazole molecules. The structural model with the best fit was used to generate radial distribution functions and spatial density functions. The local volume surrounding imidazole molecules is dominated by water, due to strong hydrogen-bonding between the nitrogen moieties of imidazole and water molecules; within a radius of 6.4 Å from the central imidazole molecule there are, on average, 17 water and only 3 imidazole molecules. Even though imidazole interacts with water it appears to disrupt hydrogen bonding in the surrounding water network only minimally. Hydrogen-bonding between imidazole molecules is negligible. The most probable positions of imidazole nearest-neighbours are above and below the plane of the aromatic ring. At low distances (up to ∼3.5–3.8 Å) these nearest neighbours were found to prefer parallel orientation of the molecular planes, indicating hydrophobic (π–π) stacking. At longer distances (up to ∼5 Å), imidazole neighbours assume both parallel and edge-to-face orientations. Overall, hydrated imidazole molecules are the most probable structural motif in aqueous solutions, with very few direct imidazole–imidazole interactions.
Introduction
The solvation of organic molecules in aqueous systems influences virtually all biological processes. Water forms hydration shells around soluble organic molecules and hydrophilic functional groups that may be at the surface of organelles or in dispersed phases. Likewise, when molecules aggregate or, in the case of biological macromolecules, when enzymes or substrates (e.g. drugs) interact with solvated molecules, desolvation takes place, i.e., water molecules are expelled from the hydration shell. These hydration and dehydration processes are mainly governed by the competitive breaking and forming of hydrogen bonds in solvent–solvent, solute–solvent and solute–solute pairs. Unravelling the structure and dynamics of these hydrogen-bonding networks in multi-component and macromolecular systems is not trivial with conventional spectroscopic and diffraction techniques. However, examining the hydrogen-bonding of models for the constituent functional groups, for example in aqueous solutions, can provide structural information that can be extrapolated to more complex macromolecular systems.Imidazole is a five-membered heterocycle that exhibits both aromatic and basic character. Understanding the solvation of imidazole in aqueous environments, including solute–solvent and solute–solute interactions, is of special interest due to its biological and pharmaceutical relevance. Imidazole is the side chain of histidine, one of the 20 naturally occurring amino acids, where it plays an important role in enzyme catalysis1 and as a metal binding ligand.2–8 It is also one of the two constituents in purine nucleobases, which are the building blocks for RNA and DNA. Derivatives of imidazole are part of antibacterial, antifungal, antiprotozoal and anthelmintic medications,9,10 and are also potential anticancer agents.11
The intermolecular interactions in aqueous imidazole solutions have been investigated since the 1940s and evidence for self-association of imidazole molecules at concentrations above 10−4 mol L−1 has been established.12 Ultraviolet spectroscopy13 and energy dispersive X-ray diffraction14 have been used to probe self-association of imidazole in aqueous solutions, which indicated that stacked π–π assemblies of imidazole molecules were formed. The binding preference of water molecules to imidazole has been investigated by supersonic jet FTIR with O18 substitution and it was found that the water molecules prefer to act as hydrogen-bond donors (O–H⋯N).15 Nuclear magnetic resonance (NMR) has been extensively used to elucidate the structural properties of imidazole and imidazole containing molecules as well as the proton transfer mechanism.16–21 However, the signal from the two pseudoequivalent nitrogen atoms in imidazole is not distinguishable by 15N NMR16–18 due to the low time resolution (10−5 seconds) of NMR, which cannot capture the rapid tautomeric exchange between the nitrogen moieties (picoseconds). X-ray spectroscopic techniques have also been utilised to examine the local environment around imidazole in aqueous solutions and to probe the changes induced by phase transition,22,23 solvation,22–24 and protonation.25,26
Spectroscopic, scattering and diffraction techniques have so far provided limited molecular level information, or they only provide qualitative information on intermolecular interactions. A particular problem is the insensitivity of X-ray scattering and X-ray spectroscopy techniques to hydrogen atoms. Quantitative structural analysis has therefore been attempted through electronic structure calculations, to identify structural models representative of the interactions present in the solution. Theoretical DFT studies using explicit and implicit solvation models gave poor representation of the intermolecular interactions in aqueous imidazole solutions.22–24 This is because of the difficulty associated with the construction of an appropriate solvation model, particularly for complex systems or for systems with complex electronic structure. Other simulation approaches such as molecular dynamics (MD) have been utilised to probe the structural and dynamic properties of imidazole in aqueous solutions.27,28 In MD simulations, the atomic configurations are generated by integration of the classical Newtonian equations of motion and empirical potential functions (i.e. force fields) are used to provide the interatomic forces required for such calculations. Quantitative and qualitative differences in the predicted local structures by MD simulations arise from differences in the description of the force fields used.27,28 Moreover, it is challenging to construct these empirical potential functions in the first place; especially for complex systems.
This raises the need for an alternative approach to unravelling the solute–solute and solute–solvent interactions in aqueous solutions of imidazole and to obtain experimentally determined structural models that are more representative of the molecular structure in solution than models generated from electronic structure calculations or MD simulations. Neutron diffraction is sensitive to scattering from all constituent atoms, C, N, O and H, and by measuring different isotopes one can create contrast that allows determination of the structure and coordination around different atomic species in the solution. However, due to the limited availability of isotopes, obtaining all site–site correlations for multicomponent systems is usually not feasible. Empirical potential structure refinement (EPSR), a reverse Monte Carlo computational method, can be used to model the experimental diffraction data29,30 and refine the structural model against the data. Neutron diffraction augmented by isotopic substitution and combined with EPSR simulations has thus been extensively used to probe the structure of water30–33 and the intermolecular interactions in aqueous solutions.34–42 We have now used this technique to examine the solvation structure and the nature of the intermolecular interactions of 5 M aqueous imidazole solutions.
Experimental
Neutron diffraction with isotopic substitution
The differential cross section, , is the quantity obtained by neutron diffraction after the relevant corrections are applied to experimental data.43 It is the sum of single atom cross section and interference differential cross section (eqn (1)).43 The first term in eqn (1) arises from interferences between waves from the same atom while the second involves interferences of waves between different atoms.
, is the quantity obtained by neutron diffraction after the relevant corrections are applied to experimental data.43 It is the sum of single atom cross section and interference differential cross section (eqn (1)).43 The first term in eqn (1) arises from interferences between waves from the same atom while the second involves interferences of waves between different atoms. | (1) |
 | (2) |
![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) α
α![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) β is the neutron scattering length weightings for the atom-pair correlations where α and β are the atomic pair of interest, c is atomic fraction and b is neutron diffraction length of the atoms.
β is the neutron scattering length weightings for the atom-pair correlations where α and β are the atomic pair of interest, c is atomic fraction and b is neutron diffraction length of the atoms. | (3) |
5 M aqueous solutions of imidazole were prepared with a series of H/D isotopomeric contrasts (see Table 1 for the isotopic composition of measured samples). The concentration was chosen to enable isotopic substitution of the imidazole.44 D2O (98% purity D) and H-imidazole (puriss >99.5%) were obtained from Sigma-Aldrich and imidazole-d4 was obtained from QMX Laboratories Ltd. Neutron diffraction data were collected for the seven samples (listed in Table 1) using NIMROD at the ISIS neutron spallation source, Rutherford Appleton Laboratory (UK), which is ideally suited to measurement of hydrogen containing liquids owing to the forward scattering arrangement of its detectors. The H/D isotopic substitution technique was employed in order to constrain the solvent diffraction contributions to the EPSR model as much as possible.45,46 The solutions were loaded into TiZr cells with a 1 mm path length and data were collected at 25 °C across the range 0.05 < Q < 50 Å−1. In order to produce F(Q) for each isotopic substitution of the solution, the raw data were normalised to a vanadium niobium plate and corrected for instrumental and TiZr cell backgrounds, absorption, multiple scattering and the effect of the incoherent scattering from hydrogen using GudrunN.47
| Sample number | Imidazole | Water |
|---|---|---|
| 1 | D | D |
| 2 | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 H/D 50 H/D |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 H/D 50 H/D |
| 3 | H | H |
| 4 | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 H/D 50 H/D |
D |
| 5 | H | D |
| 6 | D | H |
| 7 | D | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 H/D 50 H/D |
Total X-ray scattering
Total X-ray scattering also provides a measure of F(Q) and the partial structure factors, Sαβ(Q), but these are weighted by both the atomic concentration and the form factor because unlike neutrons, X-rays do not scatter from the point-like atomic nuclei but the electron density distribution.43 For simple analysis, zero-Q limit of the X-ray form factor is used and it is the atomic number of the element of interest. However, for an accurate analysis, the full-Q dependent form factors should be used as in the EPSR simulation.While the electron density at atoms and hence the X-ray scattering cross sections generally increase with atomic number, there are considerable variations of neutron scattering cross sections across the periodic table due to their more complex dependence on nuclear properties. Hence, the two techniques can be used complementarily and their combination can increase the contrast between the measured F(Q) in the determination of the partial structure factors Sαβ(Q).43
Total X-ray scattering data were collected for a 5 M aqueous imidazole solution using the PANalytical X’Pert Pro Diffractometer at ISIS, Harwell Oxford (UK), equipped with an Ag source. Data were collected in capillary mode, with the sample held in 2 mm inner diameter sealed quartz capillary. Data were collected across the range 0.03 < Q < 18 Å−1. The raw data were corrected for instrument and quartz capillary backgrounds, absorption, multiple scattering and Compton scattering using GudrunX.48
Empirical potential structure refinement (EPSR)
A cubic box with side length of 60.916 Å was constructed with 5530 water molecules and 500 imidazole molecules, with an atomic number density of 0.093 atoms per Å3. The water molecules were constructed according to Soper32 and imidazole molecules were constructed in J mol, with the intramolecular structure minimised using MOPAC7 (PM3 calculation).49 Bond and angle restraints were employed, as well as torsional restraints for the imidazole molecule. However, the molecular conformations were not held rigid during the EPSR simulation, in order to reproduce the experimental diffraction data.30 The intramolecular distances, angles and torsional parameters for the imidazole molecule are listed in Table 2.| Atom pair | Bond length (Å) | Intramolecular angle | Bond angle (°) | Dihedral | Angle (°) |
|---|---|---|---|---|---|
| N1–C2 | 1.403 | ∠ H1 N1 C2 | 125 | ∠H1 N1 C2 C3 | 180 |
| N1–H1 | 0.987 | ∠C1 N1 C2 | 109 | ∠H1 N1 C2 H2 | 0 |
| N1–C1 | 1.393 | ∠H1 N1 C1 | 126 | ∠C1 N1 C2 C3 | −0 |
| C2–C3 | 1.385 | ∠N1 C2 C3 | 106 | ∠C1 N1 C2 H2 | 180 |
| C2–H2 | 1.089 | ∠N1 C2 H2 | 124 | ∠C2 N1 C1 H2 | 0 |
| C1–H2 | 1.092 | ∠C3 C2 H2 | 130 | ∠C2 N1 C1 N2 | −180 |
| C1–N2 | 1.348 | ∠N1 C1 H2 | 127 | ∠H1 N1 C1 H2 | −180 |
| N2–C3 | 1.393 | ∠N1 C1 N2 | 108 | ∠H1 N1 C1 N2 | −0 |
| C3–H2 | 1.089 | ∠N2 C1 H2 | 125 | ∠N1 C2 C3 H2 | 0 |
| ∠N2 C3 C2 | 109 | ∠N1 C2 C3 H2 | −180 | ||
| ∠N2 C3 H2 | 122 | ∠H2 C2 C3 H2 | −180 | ||
| ∠C2 C3 H2 | 130 | ∠H2 C2 C3 H2 | −0 | ||
| ∠C1 N2 C3 | 109 | ∠N1 C1 H2 C3 | −0 | ||
| ∠N2 C1 H2 C3 | 180 | ||||
| ∠C2 C3 H2 C1 | −0 | ||||
| ∠H2 C3 H2 C1 | −180 |
The initial reference potential used by EPSR for each atom within the 3-dimensional model comprises of a Lennard-Jones potential together with a Coulomb charge to define the intermolecular interactions (Table 3). The parameters for water were obtained from the SPC/E model50 and those for imidazole were taken from the OPLS.51 The reference potential is utilised by EPSR to generate the initial configuration of atoms using a standard Monte Carlo simulation. After equilibration, an additional empirical potential is refined iteratively by perturbation of the reference potential and F(Q) is calculated for each new atomic configuration. The atomic configuration is either accepted or discarded according to the goodness of the agreement between the experimental and calculated F(Q). Finally radial, spatial and angular distribution of atomic and molecular pairs were calculated using routines within EPSR and Dlputils.52
| Atom | ε/kJ mol−1 | σ/Å | Charge/e− |
|---|---|---|---|
| Ow | 0.650 | 3.166 | −0.848 |
| Hw | 0.000 | 0.000 | 0.424 |
| N1 | 0.711 | 3.250 | −0.570 |
| C2 | 0.293 | 3.550 | −0.015 |
| H1 | 0.000 | 0.000 | 0.420 |
| C1 | 0.293 | 3.550 | 0.015 |
| C3 | 0.293 | 3.550 | 0.295 |
| H2 | 0.126 | 2.420 | 0.115 |
| N2 | 0.711 | 3.250 | −0.490 |
Results and discussion
The interference differential cross section (F(Q)) values obtained from the neutron diffraction and the total X-ray scattering data (i.e. the experimental data) and from the EPSR structural model (i.e. the calculated data) are shown in Fig. 2 alongside the differences between the experimental and calculated values. The uncertainty of the method arises from how well the calculated structure factors (from the EPSR simulations) represent the experimental data. For all the datasets, the calculated F(Q) values from the EPSR fits well with the experimental data, with small discrepancies at the low Q values (<2.5 Å−1) where the background and the inelasticity corrections are hardest to remove due to the hydrogen presence.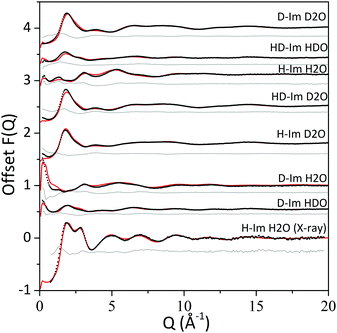 | ||
| Fig. 2 F(Q) values from experimental data (black dots) and EPSR model (red line) and the difference between the two (grey line). | ||
Distribution functions are used to describe disordered systems, such as the system studied here. When conducting refinement by conventional molecular simulations (e.g. reverse Monte Carlo methods), multiple specific configurations can produce distribution functions with structure factors consistent with the experimental functions. However, in EPSR the number of possible satisfactory configurations is strongly limited because the aqueous imidazole solution system is made up of molecules with defined intramolecular interaction parameters.
It might be useful to note that the S0(Q) limit in the measured F(Q) data (Fig. 2) is not large enough to represent SANS signal. The neutron scattering data were measured in absolute units of barn per steradian per atoms and signal attributed to assembled imidazole molecules would arise from fluctuations on the level of one to two atoms per ensemble of many hundreds of atoms in the system. Hence, the deviations observed at the low Q range are too small to be attributed to a large number of assembled imidazole molecules; for example, dimeric imidazole ensembles.
Water–water interactions
The radial distribution functions (RDFs) for water–water atomic pairs in the imidazole solution are similar to those of pure water (Fig. 3). There is a slight increase in the intensity of the RDF peaks from the imidazole solution when compared to pure water, which could be attributed to the excluded volume effect.53 In solutions, the presence of the solute increases the local water density, resulting in a higher average density over the whole volume. Comparison of the coordination numbers for the water–water atomic pairs in the imidazole solution (listed in Table 3) reveals that they are lower than those reported for pure water.32 This deviation from pure water can be attributed to the larger volume of imidazole molecule compared to water and to the fact that the solution is fairly concentrated, with an imidazole![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water ratio of 1
water ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10.
10.
 | ||
| Fig. 3 The radial distribution functions (RDFs) for water atomic pairs in 5 M aqueous imidazole solution (red) and pure water (black). RDFs of pure water were obtained from ref. 32. | ||
The positions of first and second peaks in the RDFs for the imidazole solution are almost identical to those in pure water. This indicates that upon solvation, imidazole minimally disrupts the hydrogen-bond network of water. Such absence of disruption to the bulk water network has also been reported for other organic molecules, such as proline35 and acetylcholine.34 Note, however, the limitations of diffraction analysis and associated modelling in determining the water structure, which have been highlighted through inconsistencies between RDFs of water atomic pairs determined by EPSR and molecular dynamics for DMSO solutions.36,54 Likewise, discrepancies have been observed when comparing experimental X-ray absorption (XA) spectra with calculated spectra that were based on diffraction data and the associated EPSR simulations.55 Other techniques such as FTIR can then be helpful to provide complementary information on the effect of solute molecules on the hydrogen-bond network of water. A recent FTIR study highlighted the combined bend and libration band (centred at 2130 cm−1) as a reporter on the dynamic structure of water and the rigidity of the hydrogen-bond network in the presence of salts, denaturants and osmolytes.56
Imidazole–water interactions
Although there appears to be minimal disruption to the water network by imidazole, significant interaction between imidazole and water is expected, since imidazole has high solubility in water (11 mol L−1 at 25 °C).57 Imidazole can act as both a hydrogen-bond donor (via the pyrrolic N1–H moiety) and acceptor (via the pyridinic N2). Indeed, the radial distribution functions (RDFs) for hydrogen-bonding pairs between the nitrogen moieties in the imidazole molecule and water (Fig. 4) and the coordination numbers at the minima after the first RDF peak (Table 4) confirm that hydrogen-bonding takes place between the nitrogen moieties (N1 and N2) and water molecules. The difference of ∼1 Å between the N2⋯Ow and N2⋯Hw and between N1⋯Ow and H1⋯Ow indicates collinear N–H–O hydrogen-bonding.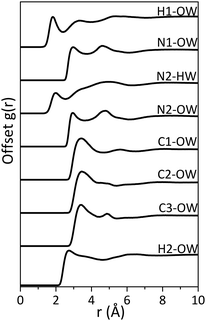 | ||
| Fig. 4 The radial distribution functions (RDFs) for hydrogen-bonded imidazole–water pairs in 5 M aqueous imidazole solution. | ||
Our analysis shows that the minima around the first peak in the RDF of imidazole–water bonding pairs do not go to zero, which indicates significant disorder around the centroid distances of the first hydration shell. The second peak in the N1⋯Ow RDF (at ∼4.70 Å) corresponds to correlation involving water molecules bound to the N2 site of the imidazole ring. Similarly, the second peak in the N2⋯Ow corresponds to correlation with water molecules at the N1 site. The C⋯Ow RDFs show a broad peak at ∼3.50 Å, which is attributed to the distance between carbon atoms in the imidazole ring and water molecules bonded to the nitrogen moieties. The difference between the H2⋯Ow and the C⋯Ow is less than 1 Å (as seen in Fig. 4), which eliminates the probability of hydrogen bonding between the hydrophobic carbon moieties in imidazole and water.
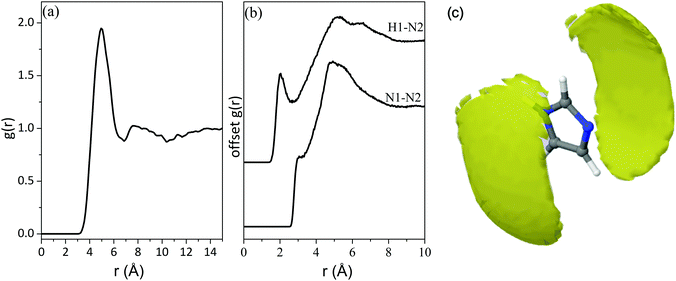
Applying a cut-off radius of 2.40 Å and 2.50 Å, the coordination numbers of Ow around H1 and Hw around N2 are 0.75 and 1.30 respectively (Table 4). This indicates that there is approximately one water molecule per nitrogen atom in the first hydration shell. At a cut-off radius that is ∼1.3/1.2 Å longer, the presence of three water molecules per nitrogen atom is predicted, as seen in Table 4. This could indicate the presence of water molecules in locations that are not collinear to the nitrogen moieties. This is further illustrated by the RDF of the water centre of geometry (cog) around the imidazole cog, which has an intense peak at ∼4 Å with a slight shoulder at ∼3 Å (Fig. 5(a)). The water molecules bonded to the nitrogen atoms seem further away (at ∼4 Å) than in the atomic pair RDFs (∼2.4/2.5 Å) because the radial distribution here is determined from the centre of geometry of the two molecules. The shoulder at 3 Å is attributed to water molecules over and below the plane of the imidazole ring.
The spatial density function (SDF) of Ow and Hw around imidazole (Fig. 5(b)) confirms the structural characteristics obtained from the RDFs. It shows that the most common location of water molecules for distances up to 3.4 Å and 4.4 Å (which are the minima after the first peaks in the RDFs of N2⋯Hw and N1⋯Ow/N2⋯Ow respectively shown in Fig. 4) is adjacent to the N1–H1 and N2 moieties of the imidazole ring, as well as above and below the plane of the imidazole ring, with no water molecules adjacent to the hydrophobic C–H moieties. Water molecules prefer the formation of a collinear Ow–H1–N1 bond in the plane of the aromatic ring, while hydrogen-bonds to the N2 site have a wider angular distribution with a significant out-of-plane population. The higher mobility of the water molecules around the N2 side of the imidazole ring is indicated by the featureless correlation in the N2⋯Hw RDF between 3–6 Å, which hints towards non-directional hydrogen-bonding. The reason for this is probably that hydrogen bonds to N2 are formed with its lone pair of electrons, resulting in partial sp3 character of the nitrogen centre, which imparts out-of-plane positions. Due to the mirror symmetry of the molecule such bonds are formed with equal likelihood above and below the aromatic ring plane, and this is evident through a symmetric angular distribution of water positions relative to N2. These observations about the positions of hydrate molecules are in line with previous studies combining molecular dynamics modelling with neutron and X-ray scattering results, including neutral and protonated imidazole,58 and the related solutes pyrazole59 and pyridine60 in aqueous solutions. Recent MD simulation studies of aqueous solutions of imidazole at different concentrations came to similar conclusions.27,28
Imidazole–imidazole interactions
The peak at ∼5 Å in the RDF of the imidazole cog around imidazole cog (Fig. 6(a)) is comparable to the intermolecular distances between the imidazole molecules in the crystal structure61,62 associated with hydrogen-bonded chains (HB) and π–π stacks (parallel displaced (PD) or edge-to-face (EF)) (Fig. 7). More insight is provided by the RDFs of intermolecular bonding pairs of imidazole Fig. 6(b) where the sharp peak in the H1⋯N2 and N1⋯N2 pair correlations at about 2 Å and 3 Å, respectively, is associated with intermolecular hydrogen-bonded imidazole chains. The difference of ∼1 Å is in line with the distance in the collinear N1–H⋯N2 hydrogen-bond. However, the fraction of imidazole molecules exhibiting such intermolecular hydrogen-bonds is low, as indicated by the low coordination number (0.08) for N1 around N2, below a cut-off radius of 3.3 Å (Table 4). In line with this, the imidazole–imidazole spatial density function (SDF) (Fig. 6(c)) reveals that (for distances up to 6.4 Å) the nearest imidazole neighbours are most likely positioned above and below the plane of the imidazole ring. This suggests self-association through hydrophobic interactions, such as π–π stacking, which has previously been evident in ultraviolet spectroscopy and energy dispersive X-ray diffraction data.13,14 | ||
| Fig. 7 Hydrogen-bonded (HB), parallel displaced (PD) and edge to face (EF) assemblies with annotated ring⋯ring centroid distances from crystal structure.61,62 | ||
The broad maxima centred at ∼5 Å in the intermolecular H1⋯N2 and N1⋯N2 RDFs and the peak at ∼6.5 Å in the H1⋯N2 RDF (Fig. 6(b)) indicate that at these distances the imidazole molecules are assembled such that N2 is either at the same distance from N1 as from H1 or is closer to N1 than H1. These arrangements indicate stacked assemblies; such as parallel displaced (PD) or edge-to-face (EF) stacks. The orientation of the imidazole molecules within the stack was investigated by determining the angular radial distribution function (ARDF) between the z-axes of the imidazole molecules (Fig. 8). The z-axis is defined as perpendicular to the lines passing through the two nitrogen atoms (x-axis) and the C1 atom (y-axis). The plot shows that at short distances (3.5–3.8 Å) there is a high probability for finding parallel π–π stacked imidazole molecules. At longer distances (up to ∼5 Å) the likelihood of observing both parallel and edge-to-face stacked molecules becomes equal, suggesting that the influence of π–π stacking does not extend beyond the first imidazole neighbours (Fig. 8). It is interesting to note here that previous studies on π–π stacking in aromatic liquids63 and in amino acids with cyclic side chains (e.g. histidine)64 likewise suggested parallel stacking at smaller separations and edge-to-face stacking at larger distances.
A molecular dynamics simulation utilising a multipolar electrostatic potential derived from quantum chemical topology predicted a higher probability for the presence of hydrogen-bonded imidazole ‘chain’ dimers over stacked assemblies in aqueous solutions.27 The discrepancy between the predicted self-assembly structures of imidazole in the higher rank MD simulation and our study might indicate that hydrogen-bonded assemblies are localised and perhaps transient features which are not as significant within the average structure of the solution. A recent neutron diffraction and isotopic substitution study on imidazolium protic ionic liquids (PILs) attributed the absence of NH⋯N correlations to the fact that only the average ring position can be identified, while the short-lived NH⋯N correlations responsible for the rapid proton exchange are averaged out and not picked up by neutron diffraction.65 The pre-defined geometrical parameters for the stacked dimers in the abovementioned MD simulation could be another reason for the discrepancy between their results and our experimental findings. The distance between the stacked imidazole molecules in the MD simulation was limited to 3.8 Å,27 which is shorter than any π–π stack distances in the crystal structure and also shorter than the distances suggested by the experimental RDFs presented here. The presence of edge to face assemblies in aqueous imidazole solutions was not investigated in the high rank MD study.27 These dimeric assemblies, which are predicted in this work, were proven to be the most abundant structure in another MD simulation study.28
Finally, the first peak in the RDF of the imidazole⋯imidazole cog is centred at 5 Å (Fig. 6(a)), which is at a longer radius than the centre of the first peak in the imidazole⋯water cog RDF (Fig. 5(a)). The coordination number of Ow around imidazole (cog) is 17 at a cut-off radius of 5.8 Å, while the coordination number of imidazole⋯imidazole (cog) is merely ∼3 at a cut-off radius of 6.4 Å. These observations suggest that the imidazole in 5 M aqueous solution is predominantly hydrogen-bonded to water, with water molecules forming a hydration shell around the imidazole molecule. Direct hydrogen-bonding between the imidazole molecules is minimal. These results are in line with conclusions drawn in a recent X-ray Raman Scattering study of the N K-edges of imidazole.23 The ultrafast nature of the K-edge core level excitations probes the local electronic structure at the two inequivalent nitrogen centres and can thus be used to distinguish hydrated imidazole molecules from molecules in the crystal structure. Probing the structural evolution of imidazole during cooling crystallisation from water,23 the study concluded that hydrated imidazole clusters with minimal imidazole–imidazole hydrogen-bonding is the most probable structural motif in the solution, as the N K-edge exhibited minimal variation during cooling, and an instantaneous change was picked up upon crystal formation. It was concluded that desolvation is the rate-limiting step in the crystallisation of imidazole from aqueous solutions, in line with the finding of the present study that imidazole–water hydrogen-bonding is a much more prevalent structural motif than hydrogen-bonded imidazole molecules.
Conclusions
The results of a combined study with neutron diffraction augmented with isotopic substitution, total X-ray scattering and EPSR simulations strongly indicates the dominance of hydrogen-bonding between imidazole and water molecules in aqueous solution, rather than hydrogen-bonding between imidazole molecules. The solvent molecules prefer to bind through a collinear Ow⋯H1–N1 bond and a more angularly dispersed distribution around the pyridine-like N2 moiety. The presence of imidazole in the aqueous solution appears to cause minimal disruption to the water structure, as the peak positions in the water–water RDF for the aqueous imidazole solution were identical to those of pure water. No evidence for hydrogen-bonded imidazole assemblies was found. The imidazole–imidazole spatial density function indicated strongly that the most probable positions of the nearest imidazole neighbours are above and below the plane of the ring, in line with the presence of hydrophobic π–π stacking. The orientation of imidazole molecules in these stacks was investigated through analysing their angular distribution, which indicated the presence of parallel π–π stacking at short distances (up to ∼3.5–3.8 Å) and both parallel and edge-to-face stacking at longer distances (∼5 Å). The coordination number of water around imidazole (∼17 within a distance of ∼5.8 Å) was found to be much higher than for imidazole around imidazole (∼3 within 6.4 Å distance) which indicates that the most probable structural motif is hydrated imidazole molecules with minimal direct solute–solute interactions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The neutron diffraction experiment at ISIS was supported by EPSRC grant EP/L015285/1. LHA gratefully acknowledges financial support by the University of Leeds and Diamond Light Source through a PhD studentship. SLMS thanks the Royal Academy of Engineering, Diamond Light Source Ltd and Infineum UK for support of the Bragg Centenary Chair. Our research has been performed with the use of laboratory facilities at the Research Complex at Harwell, with financial support from the Future Continuous Manufacturing and Advanced Crystallisation (CMAC) Hub (EPSRC Grant EP/P006965/1). The authors thank Daniel Bowron for his support and advice. All data supporting this study are provided either in the results section of this paper or in the ESI† accompanying it.Notes and references
- G. L. Holliday, J. B. O. Mitchell and J. M. Thornton, J. Mol. Biol., 2009, 390, 560–577 CrossRef CAS.
- L. J. C. Jeuken, P. van Vliet, M. P. Verbeet, R. Camba, J. P. McEvoy, F. A. Armstrong and G. W. Canters, J. Am. Chem. Soc., 2000, 122, 12186–12194 CrossRef CAS.
- S. R. Smith, K. Z. Bencze, K. A. Russ, K. Wasiukanis, M. Benore-Parsons and T. L. Stemmler, Inorg. Chem., 2008, 47, 6867–6872 CrossRef CAS PubMed.
- M. J. Haydon and C. S. Cobbett, New Phytol., 2007, 174, 499–506 CrossRef CAS.
- D. L. Callahan, A. J. M. Baker, S. D. Kolev and A. G. Wedd, J. Biol. Inorg. Chem., 2006, 11, 2–12 CrossRef CAS PubMed.
- I. L. Alberts, K. Nadassy and S. J. Wodak, Protein Sci., 1998, 7, 1700–1716 CrossRef CAS PubMed.
- R. Sankararamakrishnan, S. Verma and S. Kumar, Proteins: Struct., Funct., Bioinf., 2005, 58, 211–221 CrossRef CAS PubMed.
- H. R. Li, D. T. Mapolelo, N. N. Dingra, G. Keller, P. J. Riggs-Gelasco, D. R. Winge, M. K. Johnson and C. E. Outten, J. Biol. Chem., 2011, 286, 867–876 CrossRef CAS PubMed.
- L. De Luca, Curr. Med. Chem., 2006, 13, 1–23 CAS.
- A. R. Katritzky and A. F. Pozharskii, Handbook of heterocyclic chemistry, Pergamon Press, Amsterdam, Lausanne, New York, 2000 Search PubMed.
- G. Zhao and H. Lin, Curr. Med. Chem. Anticancer Agents, 2005, 5, 137–147 CrossRef CAS PubMed.
- W. Hückel, J. Datow and E. Simmersbach, Z. Phys. Chem., Abt. A, 1940, 186, 129 Search PubMed.
- F. Peral and E. Gallego, J. Mol. Struct., 1997, 415, 187–196 CrossRef CAS.
- L. Gontrani, R. Caminiti, L. Bencivenni and C. Sadun, Chem. Phys. Lett., 1999, 301, 131–137 CrossRef CAS.
- J. Zischang, J. J. Lee and M. A. Suhm, J. Chem. Phys., 2011, 135, 061102 CrossRef PubMed.
- M. Munowitz, W. W. Bachovchin, J. Herzfeld, C. M. Dobson and R. G. Griffin, J. Am. Chem. Soc., 1982, 104, 1192–1196 CrossRef CAS.
- W. W. Bachovchin and J. D. Roberts, J. Am. Chem. Soc., 1978, 100, 8041–8047 CrossRef CAS.
- B. S. Hickman, M. Mascal, J. J. Titman and I. G. Wood, J. Am. Chem. Soc., 1999, 121, 11486–11490 CrossRef CAS.
- A. N. Nesmeyanov, E. B. Zavelovich, V. N. Babin, N. S. Kochetkova and E. I. Fedin, Tetrahedron, 1975, 31, 1461–1462 CrossRef CAS.
- G. R. Goward, M. F. H. Schuster, D. Sebastiani, I. Schnell and H. W. Spiess, J. Phys. Chem. B, 2002, 106, 9322–9334 CrossRef CAS.
- K. C. Chang and E. Grunwald, J. Am. Chem. Soc., 1976, 98, 3737–3738 CrossRef CAS.
- M. J. Thomason, C. R. Seabourne, B. M. Sattelle, G. A. Hembury, J. S. Stevens, A. J. Scott, E. F. Aziz and S. L. M. Schroeder, Faraday Discuss., 2015, 179, 269–289 RSC.
- L. H. Al-Madhagi, S.-Y. Chang, M. Balasubramanian, A. B. Kroner, E. J. Shotton, E. A. Willneff, B. Mishra and S. L. M. Schroeder, CrystEngComm, 2018, 20, 6871–6884 RSC.
- B. Jagoda-Cwiklik, P. Slavíček, L. Cwiklik, D. Nolting, B. Winter and P. Jungwirth, J. Phys. Chem. A, 2008, 112, 3499–3505 CrossRef CAS PubMed.
- D. Nolting, N. Ottosson, M. Faubel, I. V. Hertel and B. Winter, J. Am. Chem. Soc., 2008, 130, 8150–8151 CrossRef CAS PubMed.
- F. Meyer, M. Blum, A. Benkert, D. Hauschild, Y. L. Jeyachandran, R. G. Wilks, W. Yang, M. Bar, F. Reinert, C. Heske, M. Zharnikov and L. Weinhardt, Phys. Chem. Chem. Phys., 2018, 20, 8302–8310 RSC.
- S. Y. Liem, M. S. Shaik and P. L. A. Popelier, J. Phys. Chem. B, 2011, 115, 11389–11398 CrossRef CAS PubMed.
- M. Pagliai, G. Funghi, D. Vassetti, P. Procacci, R. Chelli and G. Cardini, J. Phys. Chem. B, 2019, 123, 4055–4064 CrossRef CAS PubMed.
- A. K. Soper, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104204 CrossRef.
- A. K. Soper, Mol. Phys., 2001, 99, 1503–1516 CrossRef CAS.
- A. K. Soper, J. Phys.: Condens. Matter, 2007, 19, 335206 CrossRef CAS PubMed.
- A. K. Soper, ISRN Phys. Chem., 2013, 2013, 279463 Search PubMed.
- A. K. Soper, Chem. Phys., 2000, 258, 121–137 CrossRef CAS.
- E. C. Hulme, A. K. Soper, S. E. McLain and J. L. Finney, Biophys. J., 2006, 91, 2371–2380 CrossRef CAS PubMed.
- S. E. McLain, A. K. Soper, A. E. Terry and A. Watts, J. Phys. Chem. B, 2007, 111, 4568–4580 CrossRef CAS PubMed.
- S. E. McLain, A. K. Soper and A. Luzar, J. Chem. Phys., 2007, 127, 174515 CrossRef PubMed.
- A. K. Soper, E. W. Castner and A. Luzar, Biophys. Chem., 2003, 105, 649–666 CrossRef CAS PubMed.
- N. H. Rhys, R. J. Gillams, L. E. Collins, S. K. Callear, M. J. Lawrence and S. E. McLain, J. Chem. Phys., 2016, 145, 224504 CrossRef PubMed.
- F. Meersman, D. Bowron, A. K. Soper and M. H. J. Koch, Phys. Chem. Chem. Phys., 2011, 13, 13765–13771 RSC.
- R. C. Burton, E. S. Ferrari, R. J. Davey, J. Hopwood, M. J. Quayle, J. L. Finney and D. T. Bowron, Cryst. Growth Des., 2008, 8, 1559–1565 CrossRef CAS.
- A. J. Johnston, S. Busch, L. C. Pardo, S. K. Callear, P. C. Biggin and S. E. McLain, Phys. Chem. Chem. Phys., 2016, 18, 991–999 RSC.
- S. K. Callear, A. Johnston, S. E. McLain and S. Imberti, J. Chem. Phys., 2015, 142, 014502 CrossRef.
- H. E. Fischer, A. C. Barnes and P. S. Salmon, Rep. Prog. Phys., 2006, 69, 233–299 CrossRef CAS.
- J. L. Finney and A. K. Soper, Chem. Soc. Rev., 1994, 23, 1–10 RSC.
- J. E. Enderby, Chem. Soc. Rev., 1995, 24, 159–168 RSC.
- D. T. Bowron, J. L. Finney and A. K. Soper, J. Phys. Chem. B, 1998, 102, 3551–3563 CrossRef CAS.
- A. K. Soper, RAL Technical Reports.
- A. C. Hannon, W. S. Howells and A. K. Soper, Inst. Phys. Conf. Ser., 1990, 193–211 Search PubMed.
- J. J. P. Stewart, J. Comput.-Aided Mol. Des., 1990, 4, 1–45 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- T. G. A. Youngs, Dlputils, https://www.projectaten.com/dlputils.
- A. K. Soper, J. Phys.: Condens. Matter, 1997, 9, 2399–2410 CrossRef CAS.
- A. Luzar and D. Chandler, J. Chem. Phys., 1993, 98, 8160–8173 CrossRef CAS.
- M. Leetmaa, M. Ljungberg, H. Ogasawara, M. Odelius, L. A. Naslund, A. Nilsson and L. G. M. Pettersson, J. Chem. Phys., 2006, 125, 244510 CrossRef PubMed.
- P. K. Verma, A. Kundu, M. S. Puretz, C. Dhoonmoon, O. S. Chegwidden, C. H. Londergan and M. Cho, J. Phys. Chem. B, 2018, 122, 2587–2599 CrossRef CAS PubMed.
- U. Domańska, M. K. Kozłowska and M. Rogalski, J. Chem. Eng. Data, 2002, 47, 456–466 CrossRef.
- E. Duboue-Dijon, P. E. Mason, H. E. Fischer and P. Jungwirth, J. Chem. Phys., 2017, 146, 185102 CrossRef.
- F. Ramondo, L. Tanzi, M. Campetella, L. Gontrani, G. Mancini, A. Pieretti and C. Sadun, Phys. Chem. Chem. Phys., 2009, 11, 9431–9439 RSC.
- P. E. Mason, G. W. Neilson, C. E. Dempsey, D. L. Price, M. L. Saboungi and J. W. Brady, J. Phys. Chem. B, 2010, 114(6), 5412–5419 CrossRef CAS.
- G. Will, Z. Kristallogr. – Cryst. Mater., 1969, 129, 211 CrossRef CAS.
- B. M. Craven, R. K. McMullan, J. D. Bell and H. C. Freeman, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 2585–2589 CrossRef.
- T. F. Headen, C. A. Howard, N. T. Skipper, M. A. Wilkinson, D. T. Bowron and A. K. Soper, J. Am. Chem. Soc., 2010, 132, 5735–5742 CrossRef CAS.
- M. Chourasia, G. M. Sastry and G. N. Sastry, Int. J. Biol. Macromol., 2011, 48, 540–552 CrossRef CAS PubMed.
- A. H. Turner, S. Imberti, M. Swadzba-Kwasny and J. D. Holbrey, Faraday Discuss., 2018, 206, 247–263 RSC.
Footnote |
| † Electronic supplementary information is available from: http://www.doi.org/10.5281/zenodo.3609288 |
| This journal is © the Owner Societies 2020 |