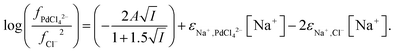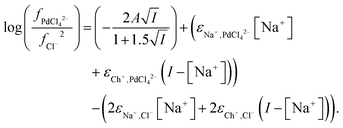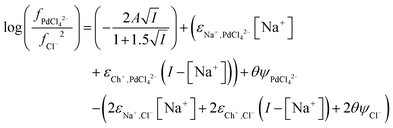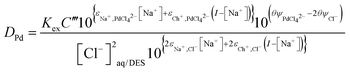Metal extraction from a deep eutectic solvent, an insight into activities†
Received
3rd November 2019
, Accepted 27th April 2020
First published on 28th April 2020
Abstract
The solvent extraction of gold, palladium, technetium, indium and rhenium from both mixtures of a deep eutectic solvent with aqueous salt solutions and of two different aqueous salt solutions has been performed. Initially using gold and then the other metals the solvent extraction results were interpreted using an activity coefficient/function equation (specific ion interaction theory). The most important presented result is the addition of a new term to the specific ion interaction theory equation. Using the new model it will be possible to make predictions of the behaviour of a solvent extraction system where one of the liquid phases is a mixture of aqueous salts and the deep eutectic solvent.
Introduction
The liquid–liquid extraction (solvent extraction) of metals is an important method for waste management1 and the purification of high value metals in industry.2 It also has important applications on the small scale in laboratories where it is used for analytical purposes3 and to gather thermodynamic information.4 Traditionally solvent extraction has been done using conventional solvents, for example for the collection of thermodynamic data, organic phases based on benzene have been used.5 As part of the effort to move to more sustainable methods for performing chemical operations we have an interest in solvent extraction in novel media. Ourselves6 and others7 have been performing experiments in which solvent extraction experiments are conducted using less conventional liquids. This has included experiments in which deep eutectic solvents are used.
The ionic liquids have been the subject of considerable industrial8 and academic interest. Sadly many of the ionic liquids are expensive and are often toxic.9 While the lack of vapour pressure might eliminate the threat due to inhalation of vapour it is still possible to inhale an aerosol of liquid droplets, and many of the cations (such as imidazoliums) are toxic to aquatic organisms.10 Many of the anions used in the butyl methyl imidazolium ionic liquids are toxic to bacteria.11 A less toxic and inexpensive alternative to the ionic liquids are deep eutectic solvents (DES) formed from choline chloride, these were developed at Leicester in recent times.12 In common with the ionic liquids the deep eutectic solvents have high ionic strengths and low melting points, but often it is possible to form deep eutectic solvents from inexpensive and relatively harmless chemicals. Many of these solvents are formed from choline chloride (Fig. 1), which is a vitamin needed in large amounts as a food additive for farm animals,13 together with a hydrogen bonding agent such as glycerol. We have been attempting to develop deep eutectic solvent based recycling methods for metals which uses solvent extraction to separate and purify the metals,14 as a result it was recognised that a deeper insight into activity issues in these new liquids is needed. We suspect that this better understanding is needed both to enable the rational design of new processes and to enable us to understand the results of our experiments.
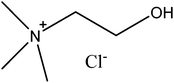 |
| | Fig. 1 The structure of choline chloride. | |
To be able to understand the results of solvent extraction experiments it is often important to know that the activities of the species in the two layers change as the experimental conditions are altered. Concentration and activity in chemistry are clearly not the same. Concentration is the amount in a volume or mass of solvent, while activity relates to the ability of a substance to act in a chemical or physical reaction. The activity (relative) is defined in the IUPAC gold book in relation to the deviation of the chemical potential (μ) of a species away from the value it has under standard conditions (μ0). This is expressed in eqn (1).
| | 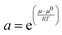 | (1) |
The activity coefficient (γ) of a species is the dimensionless number obtained by division of the activity of the species by its molality15 while the activity function (f) is the dimensionless number obtained by division of the activity of the species by its concentration. The determination of activity coefficients of neutral organic compounds in ionic liquids has been measured by inverse gas chromatography by numerous workers.16–19 Some other volatile or semi volatile neutral organic compounds have been investigated using a transpiration method20 which is similar in principle to inverse gas chromatography. Equally using liquid–liquid extraction the distribution of thiophene21 and linalool22 between organic phases and these high ionic strength media has been reported. The activity coefficients of ionic liquids dissolved in water has been considered by some workers23,24 but very little research has been done on the activity coefficients of ions inside deep eutectic solvents.
We reason that a knowledge of activity functions in deep eutectic solvents will increase our ability to use these substances. Rather than designing industrial processes and laboratory applications for these liquids by trial and error we could be able to make a faster and more rational approach to the design process. If one phase is kept constant during an experiment it is often reasonable to assume that the activity coefficients in it are constant, but a solvent extraction experiment in which both phases and all conditions remain constant is of limited value. If we change a conventional aqueous layer then it is often possible to use Pitzer equations or specific ion interaction theory (SIT) to model the change in the activity coefficients in the aqueous phase. However for mixtures of ionic liquids or deep eutectic solvents these methods have not been applied so far. It is possible to use the Pitzer equations to model salts in water/methanol mixtures25 but so far it has not been used to consider the deep eutectic solvents. While some determinations of activity coefficients in ionic liquids systems have been performed,26 less work has been done on the deep eutectic solvents. In this work we present our first determinations of parameters allowing the use of SIT for a deep eutectic solvent. While it could be possible to determine activity coefficients from kinetics experiments similar to those reported by Welton et al.27 we have chosen to use measurements of systems which are at equilibrium.
We had a choice between solid–liquid and liquid–liquid extraction experiments. The replacement of water with another polar solvent can alter the distribution of a metal between two phases.28,29 This is because the partial replacement of water with another solvent alters the swelling of the resin changes as a function of the water to cosolvent ratio in the liquid phase,30 hence in the ion exchange resin experiments both phases are changing when the water is replaced with a cosolvent. As a result of this complication we sought a liquid–liquid extraction system in which the organic phase composition and properties will remain constant as the denser phase is changed. Both water and ethylene glycol have low mutual solubilities with the diluent which makes up the majority of the organic phase. Our standard aliphatic kerosene (solvent 70) is a mixture of alkanes with between 11 and 14 carbon atoms. As it is known that octane, dodecane and hexadecane have very low mutual solubilities with both water and ethylene glycol,31 we were confident that the composition of the organic phase would change little as the water in the denser phase is replaced with ethylene glycol.
In solvent extraction two things have an influence on the metal distribution ratio at equilibrium these are the physical equilibria which partition substances between the two liquid phases and the chemical equilibria. Chemical equilibria can operate in one or both of the liquid layers, these interconvert solutes between different chemical forms which can partition differently between the two layers. Berthelot and Jungfleisch demonstrated that when elemental iodine solutions in either water or carbon disulfide were shaken with either carbon disulfide or water then that at a constant temperature the ratio of the concentrations in the two phases is independent of concentration‡ of the iodine.32 This distribution law is only true for ideal dilute solutions, when the concentration of a solute is sufficiently high to alter the properties of one or more of the liquid layers then the system will deviate. For example the distribution ratio for toluene between sulfolane and heptane changes as a function of the toluene concentration in the heptane layer.33 Hence in our experiments we endeavour to use as low concentrations of the extractable metals as possible. An important assumption has been made in this work, the first is that the distribution constants (Kd) for relevant species (neutral metal chloride, the extractant and the metal chloride complexes of the extractant) remain the same no matter what the composition of the denser phase is.
Experimental
The distribution ratio of a metal (DM) is defined as the total metal concentration in the organic (upper) phase divided by the metal concentration in the lower (aqueous or DES) phase. The solvent extraction experiments (Section A of the ESI†) were performed using the general method described already in the article in Cogent Chemistry,34 with the modification that Inductively Coupled Plasma Mass Spectroscopy (ICPMS) was used in place of ICPOES for the measurement of all stable metals other than silver and yttrium. Technetium was determined by measurement of the emission of gamma photons from a metastable state (99mTc) using a spectrometer containing a high purity germanium crystal (for details of the radioactive work see Section B of the ESI†). Solutions of aliquat 336 in ethyl benzene and tetra-(2-ethylhexyl) malonamides in solvent 70 (aliphatic kerosene) were used for the extraction experiments. The chloride content of the starting solutions for the extraction of palladium and rhenium with aliquat 336 were measured and was on average 3.92 M with a standard deviation of 0.07 M (Section C of the ESI†). The use of ethyl benzene in a paper on green chemistry might be surprising, as it is well known that an aromatic diluent35 is required to maintain a stable organic phase using a single diluent and the use of ethyl benzene is not part of a proposed metal recovery process. Instead it was used in solvent extraction experiments designed to increase our understanding of the deep eutectic solvents and other novel high ionic strength liquids. It is possible to use aliquat 336 in mixtures of aliphatic kerosene and long chain alcohols such as octanol,36 but the use of mixtures of diluents will undermine any attempt to gather data.§
WARNING: Technetium-99m (99mTc) is a radionuclide which emits 141 keV gamma photons. It should only be used by a suitably trained and equipped radioactivity worker in a radiochemical facility. See Section B of the ESI† for further details.
Results and discussion
We decided to investigate the deep eutectic formed from choline chloride and ethylene glycol (ethaline) because it has chemistry which is more simple than the choline chloride/lactic acid eutectic. We did so because ethylene glycol is less able to bind to metals than the lactate anions formed by the deprotonation of lactic acid. During constant ionic strength experiments with a choline chloride/lactic acid deep eutectic it was noticed that cadmium and zinc distribution ratios changed exponentially as DES was replaced with sodium chloride,37 in retrospect this observation can be explained as being due to changes in activity functions. In a further study it was shown that identical behaviour was exhibited with a series of three¶ very different solvent extraction systems.38 At the start of our experimental work we attempted to measure data for a grid of four metals with three extraction reagents. We choose to use two “solvating” extraction agents which act as Lewis bases (cyanex 923 and the malonamides) and a dilute solution of an ionic liquid (aliquat 336) in an aromatic solvent. As the phosphine oxide cyanex 923 is known to strongly extract gold(III) from hydrochloric acid39 we chose to use tetra(2-ethylhexyl) malonamide (Fig. 2) as it is a poor extraction agent for lanthanides40 in an attempt to reduce the distribution ratios to those which can be measured precisely.|| The dense phases for these experiments were a mixture of gold(III), indium(III), palladium(II) and rhenium(VII) in mixtures of aqueous sodium chloride, aqueous choline chloride and the deep eutectic solvent. In all these experiments the total chloride concentration was kept constant. The results of the study are summarised in Table 1. It is very difficult to accurately measure a distribution ratio which is either greater than 100 or below 0.01, thus where the majority of the distribution ratios obtained with a system were outside the range 0.01 to 100 they were judged to be either “too little” or “excessive”. For six of the combinations the distribution ratios are in a range which is suitable for our purposes.
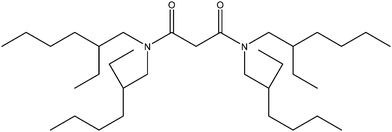 |
| | Fig. 2 Tetra(2-ethylhexyl) malonamide. | |
Table 1 Summary of the results of the initial solvent extraction experiments
| Extraction system |
Metal |
| Palladium |
Indium |
Rhenium |
Gold |
| 30% aliquat 336 |
Moderate |
Moderate |
Moderate |
Excessive |
| 30% cyanex 923 |
Too little |
Excessive |
Moderate |
Excessive |
| 10% malonamide |
Excessive |
Too little |
Moderate |
Moderate |
In the past our attempts to study the solvent extraction of gold had been stymied by a strong memory effect in our inductively coupled plasma mass spectrometer (ICPMS), so before we performed the scientific work with gold, some technical development work was needed. To reduce the memory effect we decided to add a water soluble ligand which would form a strong hydrophilic complex with gold. We selected methionine as others had found that thiourea41 greatly mitigates the memory effect caused by the reversible adsorption of gold onto the surfaces inside the sample introduction system of the ICPMS. Sadly thiourea is carcinogenic,42 so in the interests of workplace safety it was replaced with the non-toxic amino acid (methionine). With methionine present in the aqueous acid fed to the ICPMS the memory effect was so small that the second blank always gave at least a 4000 times lower response for gold than the starting solution (50 ppb). See Section D of the ESI† of details of the ICPMS method development work for gold.
The rhenium with cyanex 923 and the malonamides might be extracted by ion pairing of the protonated extractant with the perrhenate anion, as the extraction mechanisms were unclear these two combinations were excluded from the rest of this study.
Gold and indium extraction
Gold(III) in moderately acidic chloride (3 to 4 M) media should be almost exclusively as the neutral AuCl3 and anionic AuCl4− complexes. As lipophilic Lewis acids can form Lewis acid/base complexes which can enter the organic phase it can be reasoned that the extraction of gold can be used to investigate the properties of DES.
Using a 30% solution of tetra-(2-ethylhexyl) malonamide in a nontoxic diluent (solvent 70)43 a series of solvent extraction experiments were conducted at 30 °C using a dilute solution of gold(III) chloride in mixtures of sodium and choline chlorides (total chloride concentration maintained at 3.87 M). Solvent extraction experiments were also performed using solutions of gold chloride in mixtures of ethaline and either aqueous sodium chloride or aqueous choline chloride. It was found that the gold distribution ratio changed as one denser phase was replaced with another. These results are summarised in Fig. 3.
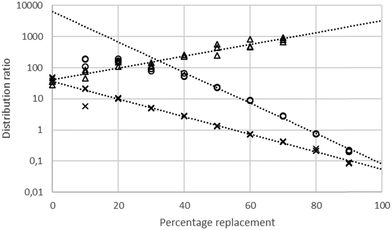 |
| | Fig. 3 A graph of the distribution ratios** of gold with combinations of (1) Aqueous sodium and choline chlorides. (2) Aqueous sodium chloride and DES. (3) Aqueous choline chloride and DES. Key: crosses choline chloride solution (on the left) being replaced with the deep eutectic solvent, circles sodium chloride (on the left) being replaced with the deep eutectic solvent and triangles choline chloride solution (on the left) being replaced with sodium chloride. | |
When either sodium or choline chloride was replaced with the deep eutectic solvent the gold distribution ratio decreased. Equally, when aqueous sodium chloride was replaced with choline chloride the gold distribution ratio decreased. While the last of the three series did not include ethaline we choose to consider it first. Before going any further we tested the null hypothesis that the distribution ratio was independent of the sodium to choline ratio in the aqueous phase. It was clear that it was impossible to find a value on the y axis which was within two estimated standard deviations of the means of the distribution ratios measured with the different aqueous layers.
Using the data of Chateau et al. it can be predicted that in a 3 mole per litre chloride solution if all activity coefficients are one then more than 99.999% of the gold(III) is in the form of AuCl4− so we reasoned that the extraction can be described using the following three eqn (2)–(4) where tetra-2-ethylhexyl malonamide is TEHM.††
| | 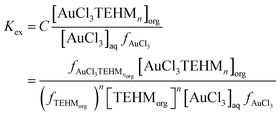 | (2) |
where all activity factors
‡‡ are denoted by
f and
C is equal to the activity factor of the gold malonamide complex in the organic phase divided by the activity of the malonamide in the organic phase ([TEHM]
fTEHM,org) raised to the power of
n. A third assumption was made, this is that the activity of a neutral solute is equal to its concentration. Many systems exist in which the activity coefficient of a neutral solute changes as a function of its environment (solvent). For example from measurements of the vapour/liquid equilibrium for the ethanol/toluene system it is clear that as the ethanol content of the liquid is changed the activity coefficients of both ethanol and toluene change resulting in the observation of an azeotrope. However, in an attempt to enable progress to be made and to reduce the complexity of our algebra we choose to make the assumption that as the gold trichloro complex is neutral its activity is equal to the concentration. The creation of the equations used to consider the gold system is shown in full detail together with the solvent extraction theory behind it in the ESI
† in Section E.
The stability constant for the formation of AuCl4− from AuCl3 and a chloride ion (K4) is known, so we can write an equation which explains how as the ratio of activity functions change the distribution ratio will vary as the activity functions of the chloride and tetrachloroaurate anion change relative to each other. Eqn (2) can be rearranged to provide eqn (3) which offers a means of obtaining ratio S which is the chloride activity function divided by the tetrachloroaurate function. A considerable uncertainty exists in the value of K4 as pointed out by Ben Goldacre44 by combining data from multiple studies it is possible to obtain an estimate with a smaller uncertainty. In our case it is possible to make a slight reduction in the uncertainty in K4 by using the mean of two different studies.45,46 Our estimate of K4 obtained by combining the two studies is 1.31 × 105 with a standard deviation of 3.11 × 104.
| | 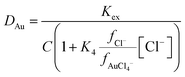 | (3) |
| | 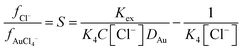 | (4) |
No attempt was made to reconcile the experimental results with the simple Debye–Hückel or Davies equations
47 as the activity function calculated with these equations is valid only for very solutions up to 0.2–0.5 m ionic strength. We have chosen the simpler specific ion interaction (SIT) due to its use in the NEA-TDB project to handle medium effects on complex formation.
48 While the extended Debye–Hückel equation is able to predict activity functions at ionic strengths lower than 0.2 m its predictions deviate more from reality than those made using the Pitzer and specific ion interaction theory (SIT). The Pitzer model is more elaborate and assures a better description of the activity coefficients of conventional electrolytes, but it is difficult to apply it for complex formation reactions because of the lack of accurate single electrolyte activity coefficients for complex ions, from which to extract the three parameters needed for applying Pitzer equations. Within the framework of SIT and related approaches the activity factor of an ion the aqueous media can be written using
eqn (5).
Eqn (5) is very similar to the equation of Guggenheim and Turgeon,
49 in
eqn (5) we used a value of 1.5 for
b while Guggenhaim and Turgeon chose a value of 1. As pointed out before,
50 the use of the 1.5 factor in the denominator of the Debye–Huckel term allows the equation to deal with concentrated salt solutions better.
51| | 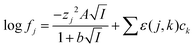 | (5) |
As the Debye–Hückel term in the SIT equation depends only on the medium and the ionic strength (
I,
I = [Na
+] + [Ch
+])
§§ which was kept constant in our experiments we can simplify our equations greatly. We can write
eqn (6).
| | 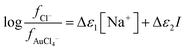 | (6) |
where
| Δε1 = ε(Na+,Cl−) + ε(Ch+,AuCl4−) − ε(Ch+,Cl−) − ε(Na+,AuCl4−) |
and
| Δε2 = ε(Ch+,Cl−) − ε(Ch+,AuCl4−) |
As many of the distribution ratios measured with the sodium chloride/choline chloride system were exceptionally high (>100), we chose to repeat the measurements for this series of denser phases using both 10 and 5% by volume solutions of the malonamide in aliphatic kerosene (solvent 70). The data obtained for all three organic phases obeys the eqn (7).
| | 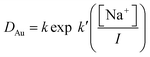 | (7) |
For the 5 and 10% malonamide solution, for which we have trustworthy data, the values of
k′ were 3.127 and 3.304, while for the less trustworthy data obtained with 30% malonamide the value of
k′ was 3.078. When the values of
k were compared with the volume fractions of the malonamide used it was clear that the distribution ratios were proportional to the square of the malonamide concentration. This slope is similar to that reported by Mowafy and Mohamed.
52 When Mowafy and Mohamed performed extraction experiments from a constant ionic strength medium (5 M) in which the ratio of sodium chloride to hydrochloric acid was varied they observed an increase in the gold concentration as the proton concentration increased. They interpreted this result as being evidence for extraction by the mechanism depicted in
eqn (8).
| | | Au3+(aq) + 3Cl−(aq) + HCl(aq) + 2L(org) → HAuCl4L2(org) | (8) |
We reasoned that a better explanation is that their change in distribution ratio is due to a decrease in the chloride activity, as sodium chloride is replaced with hydrochloric acid. While the interaction coefficients (
ε) for sodium and choline cations with chloride anions can be obtained from the literature. The coefficients for the interaction of the anionic gold complex with these cations can only be determined indirectly through equilibrium constant measurements. Using literature osmotic data for sodium and choline chlorides of Bates
et al. it is possible to estimate the SIT parameters for sodium and choline chlorides over the range of 0.01 to 5 moles per kilo.
53 The values of
ε(Na
+,Cl
−) and
ε(Ch
+,Cl
−) are 0.0406 and −0.0074 at the concentration (3.873 M) present in the mixtures of sodium and choline chlorides, using these values with the solver function of excel we were able to make an estimate of the values of Δ
ε1, Δ
ε2,
Kex/
C,
ε(Na
+,AuCl
4−) and
ε(Ch
+,AuCl
4−) to be −0.3763, 0.9973, 1.0859 × 10
9, −0.5804 and −0.9899 respectively using the data for 5% malonamide in solvent 70. Details of the numerical method used are shown in Section F of the ESI.
† It can be seen in the following graph (
Fig. 4) that a good agreement can be found between the experimental data and the calculations.
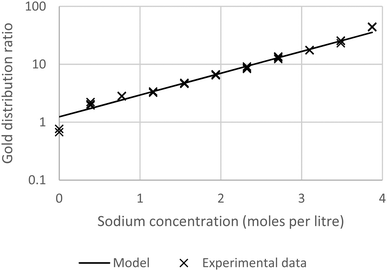 |
| | Fig. 4 A graph showing agreement between the experimental results obtained with 5% malonamide solution and the model based on the SIT theory. | |
An assessment of the effects of the sources of errors when using eqn (3) and (6) to predict a series of gold distribution ratios for a series of mixtures of sodium and choline chlorides, where the total chloride concentration remained constant was made. We wished to discover what effect a change in K4, Kex/C, ε(Na+,AuCl4−) or ε(Ch+,AuCl4−) would have on a graph of the distribution ratio against the sodium concentration. It was found that a change in K4 or Kex/C had no effect on the slope of the graph of the logarithm of the distribution ratio against the sodium concentration, Instead the straight line of that graph was displaced upwards or downwards. Using the calculated data a series of attempts were made to recalculate Kex/C, ε(Na+,AuCl4−) and ε(Ch+,AuCl4−) from the fictional data. It was found that it was possible to obtain multiple solutions using the excel solver. If we assumed that K4 was correct and we allowed Kex/C, ε(Na+,AuCl4−) and ε(Ch+,AuCl4−) to be varied then it was found that when K4, ε(Na+,AuCl4−) and ε(Ch+,AuCl4−) were fixed at 1.31 × 105, 0.0406 and −0.0074 that the following values of Kex/C, ε(Na+,AuCl4−) and ε(Ch+,AuCl4−) in Table 2 below all predict the same line.
Table 2 Computational results from the investigation of the effect of the value of Kex/C on the values of ε(Na+,AuCl4−) and ε(Ch+,AuCl4−)
| Solution |
1 |
2 |
3 |
4 |
5 |
6 |
|
K
ex/C |
1.0859 × 109 |
1 × 106 |
1 × 107 |
1 × 108 |
1 × 109 |
1 × 1010 |
|
ε(Na+,AuCl4−) |
−0.5804 |
0.203432 |
−0.05476 |
−0.31296 |
−0.57116 |
−0.82936 |
|
ε(Ch+,AuCl4−) |
−0.9899 |
−0.20607 |
−0.46426 |
−0.72247 |
−0.98066 |
−1.23886 |
Hence we can conclude that the gold extraction experiment with our current interpretation is not able to determine the values of Kex/C, ε(Na+,AuCl4−) and ε(Ch+,AuCl4−), but it has an ability to determine the difference between ε(Na+,AuCl4−) and ε(Ch+,AuCl4−) as regardless of the value chosen for Kex/C the difference between these two items is the same (0.4095). So the this work would benefit greatly from an independent measurement of the activity function of either sodium tetrachloroaurate or the choline salt. While an isopiestic study but the exceptionally high cost of gold causes such a study to be impossible in our group. Before moving onwards to a better system we considered the likely effect of an error in the slope of the graph of the log on the difference between ε(Na+,AuCl4−) and ε(Ch+,AuCl4−) which is calculated by the method. Using fictional data created using an equation closely related to eqn (7) (eqn (9)) where k, I, Kex, K4, ε(Na+,Cl−) and ε(Ch+,Cl−) were fixed at 0.3352, 3.873, 108, 0.0406 and −0.0074 we used the excel solver to estimate the values of ε(Na+,AuCl4−) and ε(Ch+,AuCl4−) for values of k′ between −1 and 1.
We found that the graph of ε(Na+,AuCl4−) − ε(Ch+,AuCl4−) against k′ was a simple straight line which obeys eqn (10).
| | | {ε(Na+,AuCl4−) − ε(Ch+,AuCl4−)} = (0.443k′) + {ε(Na+,Cl−) − ε(Ch+,Cl−)} | (10) |
As the line of the graph is close to one which would be described by
y =
rx +
s when
s¶¶ is equal to zero, we can reason that the contribution to the error of percentage error in the value of {
ε(Na
+,AuCl
4−) −
ε(Ch
+,AuCl
4−)} made by random errors in the distribution ratios will be the same as the percentage error in
k′. The standard deviation in
u when
u = ln(
v) is given by 0.434 multiplied by the standard deviation of
v divided by
v we can calculate the estimated standard deviations of the natural logarithms of the mean distribution ratios used for the calculation of {
ε(Na
+,AuCl
4−) −
ε(Ch
+,AuCl
4−)}. Using the LINEST command in excel it was clear that the estimated standard deviation on the slope of the line of the graph of the logarithms of the distribution ratios against the sodium concentrations is 2.94%. If we round this error up to 3% then means that the estimated standard deviation on the final value of {
ε(Na
+,AuCl
4−) −
ε(Ch
+,AuCl
4−)} is 3% of value. This means that the value of {
ε(Na
+,AuCl
4−) −
ε(Ch
+,AuCl
4−)} should be regarded as being 0.4095 with a standard deviation of 0.0123.
As the indium distribution ratio obtained with 10% (v/v) of aliquat 336 decreased as sodium chloride was replaced with choline chloride we considered it with a similar method to that applied to the results from the gold experiment. Because the binding constant for the reaction of a chloride anion with the neutral trichloro complex is much lower for indium than it is for gold, two equilibria must be considered for the indium. We considered the hypothesis that the extraction of indium from our chloride media could be described using the eqn (11). The derivation of the equations for the indium system is shown in the ESI† in Section E.
| | 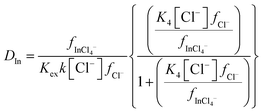 | (11) |
Our next logical step was to use a modified version of eqn (4) to calculate the ratio of the two activity functions. In this equation the two Δε terms are given by.
| Δε1 = ε(Na+,Cl−) + ε(Ch+,InCl4−) − ε(Ch+,Cl−) − ε(Na+,InCl4−) |
and
| Δε2 = ε(Ch+,Cl−) − ε(Ch+,InCl4−) |
In an attempt to estimate the values of
Kexk,
ε(Ch
+,InCl
4−) and
ε(Na
+,InCl
4−) we used our solvent extraction data and a literature value for
K4.
54 Using the solver function of excel we found that when the values of these constants were 0.00168, −0.317 and −0.027 respectively, a match could be obtained between our experimental data and our
eqn (11). So we can state that {
ε(Ch
+,InCl
4−) and
ε(Na
+,InCl
4−)} is equal to 0.29. Our ability to repeat the gold work for indium suggests that our method may be a general method rather than an abnormal result caused by a special feature of gold chemistry.
We desired to obtain a more conventional estimate of the random errors in Kex/C, ε(Na+,AuCl4−) and ε(Ch+,AuCl4−), a step in the process we first selected was to create a graph of S as a function of the composition of the denser phase. During this process our attempts to use eqn (4) resulted in a nonsensical series of values for S. The values of S obtained from eqn (3) were negative, this lead us to question the third assumption that the activity function of the neutral gold trichloride complex was one in the denser phase. By including the activity function for the neutral complex in our algebra we obtained the following new expression (eqn (12)) for the gold distribution ratio.
| | 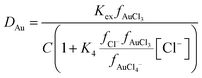 | (12) |
Modelling of gold extraction from the deep eutectic solvent
While it is likely that the model which assumes that the activity function of the neutral gold trichloride complex is constant and equal to one, it is not able to fully describe the system, we chose to develop this model further in an attempt to create a predictive tool. As the distribution ratio of gold decreases in an exponential manner as the volume fraction of ethaline in a mixture of it and aqueous choline chloride increases. We added a new term to the SIT activity function equation. In the new equation (eqn (13)) the fraction of the liquid phase which is made up of ethaline is denoted as theta (θ) while psi (ψ) is a new constant.| | 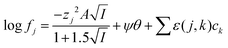 | (13) |
We can write for these metals the following equations. We choose to test the hypothesis that the extraction equilibria of gold metals could be described in mixtures of the deep eutectic solvent (ethaline) and the aqueous chlorides using eqn (14).
| | 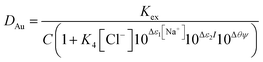 | (14) |
Using a Δ
ψ value of 3 we obtained good agreement between the experimental data for gold for the denser media which were free of sodium which were obtained with the 30% malonamide solutions. It was found that the more trustworthy gold extraction data obtained with the 5 and 10% solutions of the malonamide could be described well by this equation. Using the solver function in Microsoft Excel we were able to fit the extraction data to the model. Here Δ
ψ was 1.50 while for the 5% data
Kex/
C was 1.105 × 10
9 while for the 10% data it was 3.553 × 10
9. The agreement between the predicted distribution ratios and the measured distribution ratios can be seen in
Fig. 5. Using a similar method to that applied to the simple aqueous system for gold, we have estimated that the standard deviation on Δ
Ψ is 4% of its value, thus its value should be regarded as being 1.50 with a standard deviation of 0.06.
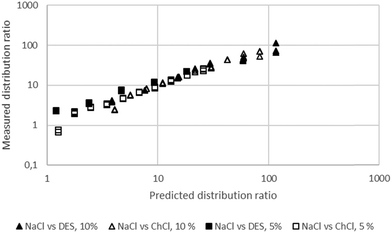 |
| | Fig. 5 The agreement between the predicted and measured gold distribution ratios for four different solvent extraction experiments. A model which is perfectly able to predict the distribution ratios would create a straight line of points which would obey the equation y = x where x is the predicted distribution ratio and y is the measured distribution ratio. | |
For indium we found that the simple use of ψ failed to describe the system well, as the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D against DES volume fraction graph had an appearance similar to the cell survival curves in the Linear-Quadratic (LQ) model used in radiobiology we considered if the eqn (15) with two ψ terms could give a better fit. For the indium data obtained with the choline chloride/deep eutectic solvent mixtures the change in the ratio of the chloride and tetrachloroindium anions is best explained with values of 0.22 and 1.04 for ΔΨ1 and ΔΨ2. Sadly the indium data for the sodium chloride/DES mixtures with between 20 and 80% DES can not be modelled well with our model. A need exists for additional experiments with other metals.
D against DES volume fraction graph had an appearance similar to the cell survival curves in the Linear-Quadratic (LQ) model used in radiobiology we considered if the eqn (15) with two ψ terms could give a better fit. For the indium data obtained with the choline chloride/deep eutectic solvent mixtures the change in the ratio of the chloride and tetrachloroindium anions is best explained with values of 0.22 and 1.04 for ΔΨ1 and ΔΨ2. Sadly the indium data for the sodium chloride/DES mixtures with between 20 and 80% DES can not be modelled well with our model. A need exists for additional experiments with other metals.
| | 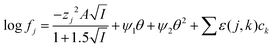 | (15) |
Eqn (12) can be rearranged into eqn (16), if at a future point it is possible to make an estimate of the activity function of the neutral gold trichloride then eqn (16) could be used to obtain the activity function of the tetrachloroaurate complex.
| | | fAuCl4− = DAuCK4[Cl−]fCl− − K4[Cl−]fAuCl3fCl− | (16) |
As the charge on the neutral complex is zero, the SIT equation for the activity function of the neutral complex would not contain a Debye–Huckel term. Instead the SIT equation for the activity function of the neutral species will be the Sechenov equation. Using
eqn (17) for the activity of the neutral gold complex the solver function of excel found a good match between the experimental data and the model described in
eqn (14) when
Kex/
C,
Ks2, Δ
ε1 and Δ
ε2 were 100.41, 0.05405, −0.4332 and −1.1110 when
Ks1 was set at zero.
| | | fAuCl3 = 10(+Ks1I+Ks2[Na+]) | (17) |
For non-polar compounds such as benzene,55 butane56 and hexane,57 their solubilities in water decrease as the sodium chloride concentration is increased, which can be described using Setchenov's equation for the activity function of the hydrocarbon in water. As many things are varied to obtain agreement between theory and experiment we were disappointed and sought a more simple system. While we suspect that our model in which the activity function for the neutral gold complex is equal to one is not perfect we hold the view that the model is able to describe the system.
Palladium, rhenium and technetium extraction
Next we wished to consider a more simple system where no neutral metal complexes are present, this is because fewer variables are present. A system where the ε value for the large anion in sodium chloride could be estimated from literature data. We choose the extraction of rhenium(VII) from mixtures of aqueous choline chloride. aqueous sodium chloride and ethaline by a dilute solution of an ionic liquid (aliquat 336) in ethyl benzene. For perrhenate we can write eqn (18).| | 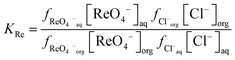 | (18) |
This can be rearranged to give the following expression (eqn (19)) in which C′ is a constant which contains the activity factors in the organic phase, and the chloride concentrations as chloride concentration in both liquid phases was kept constant in our experiments. A similar equation (eqn (20)) can be written for the extraction of palladium as PdCl42−.
| | 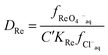 | (19) |
| | 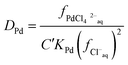 | (20) |
It was found for both palladium and perrhenate that when the aqueous phase was aqueous sodium chloride, that the distribution ratios were so large that they were impossible to measure by shaking tube experiments. By extrapolation of the graphs of the logarithm of the metal distribution ratios against the volume ratio of sodium chloride to ethaline it can be estimated that the distribution ratio would be 9285 and 371 for rhenium for aqueous sodium and choline chloride solutions respectively. The sodium chloride results were confirmed by a radiochemistry experiment using pertectinate, when the aqueous phase was 3.777 M sodium chloride according to gamma spectroscopy the distribution ratio was very high.|||| However when the experiment was repeated with a 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of DES and dilute sodium chloride the distribution ratio was much lower.*** Using the eqn (21) it is possible to determine the ratios of the activity factors of perrhenate in the sodium and choline chloride solutions.
2 mixture of DES and dilute sodium chloride the distribution ratio was much lower.*** Using the eqn (21) it is possible to determine the ratios of the activity factors of perrhenate in the sodium and choline chloride solutions.
| | 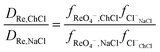 | (21) |
It can be calculated that the ratio of the activity functions of perrhenate and chloride in the choline chloride solution is 25 times lower than that in the sodium chloride solution. If the activity functions of the chloride and perrhenate anions change according to the SIT theory as an aqueous sodium chloride solution is gradually replaced with choline chloride then the rhenium distribution ratio will be given by eqn (22).
The sum of the
k values for lines 2 and 3 are within 0.163 of the
k value for line 1 (
Table 3). Due to the large experimental errors on exceptionally high distribution ratios, it is impossible with our experimental method to measure high (>200) distribution ratios directly. As a compromise it was decided that mixtures of ethaline, sodium chloride and choline chloride solutions would be used in solvent extraction experiments. In these experiments, 50% (v/v) of all the denser phases was the deep eutectic solvent (ethaline).
Table 3 Summary of the rhenium distribution ratio results (lines 1, 2 and 4). Line 3 was obtained by extrapolation
| Line |
Composition |
D
max
|
K
|
|
θ = 0 |
θ = 1 |
| 1 |
Sodium chloride solution |
Pure ethaline |
9285 |
7.748 |
| 2 |
Choline chloride solution |
Pure ethaline |
371 |
4.690 |
| 3 |
Sodium chloride solution |
Choline chloride solution |
9285 |
3.221 |
| 4 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ethaline and sodium chloride 50 ethaline and sodium chloride |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ethaline and choline chloride 50 ethaline and choline chloride |
129 |
1.279 |
If we assume that C′KRe is a constant then it is possible to determine the change in the activity function of perrhenate as a function of the sodium to choline ratio. As a result of concerns about the long lived fission product technetium in the form of pertechtinate, activity data for sodium perrhenate solutions58 and the molar volume of the compound exists in the literature.59 Thus it is possible to estimate the activity functions for solutions of sodium perrhenate. Using the osmotic data of Boyd, it can be predicted that ε(Na+,ReO4−) has a value of −0.0634 over the range of 0.1 to 4 moles per litre of sodium perrhenate. Using a polynomial similar that used in the Pitlzer equation (eqn (23)) it was possible to obtain an equation which describes well how the activity function changes as a function of concentration.†††
| | 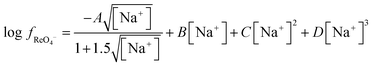 | (23) |
Using this equation the activity function for perrhenate in a 3.873 M sodium solution can be calculated, using this data it can be concluded that if
C and
D are equal to zero then at 3.873 the value of
B should be −0.0478. Using this value and the SIT constants for both sodium and choline cations with chloride anions it is possible to model the extraction of perrhenate using the SIT model by combination of
eqn (19) with
eqn (24).
| | 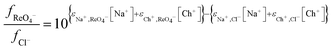 | (24) |
Modelling of extraction by aliquat 336 from the deep eutectic solvent
We have a choice we can write purely descriptive equations or we could attempt to derive from first principles a theory which explains the salt solutions in mixtures of ethylene glycol and water. The glittering prize of a first principles explanation is a goal which we are working towards but so far only eqn (25) which is a descriptive equation exists.| | 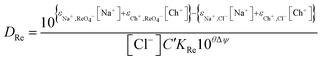 | (25) |
While for the rhenium system in a fitting exercise using distribution ratios which were no higher than 110 a value of 2.04 was obtained for Δψ when data obtained with mixtures containing sodium chloride were included. The constant ψ for the system allows us to by fitting the experimental data against our model we estimated that the value of εCh+,ReO4− to be −0.445. In Fig. 6 it can be seen that a good agreement exists between the experimental results and those predicted by the model.
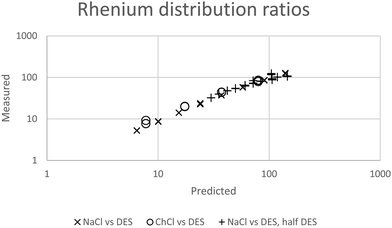 |
| | Fig. 6 The agreement between predicted and measured distribution ratios for rhenium. A model which is perfectly able to predict the distribution ratios would create a straight line of points which would obey the equation y = x where x is the predicted distribution ratio and y is the measured distribution ratio. | |
In a similar way to our consideration of the errors in the gold work we choose to consider the effect of changing ε(Ch+,ReO4−), C′KRe and ΔΨ in eqn (25) on the values of the distribution ratios predicted. Only ΔΨ had an effect on the slope of the graph of the logarithm of the distribution ratio against the DES fraction (θ) of the mixture, so as a result we choose to consider the relationship between the slope of the logarithms of the distribution ratio against the DES content of the lower phase and ΔΨ. Using fictional data it was found that our method based on the solver feature of excel provides a value of ΔΨ which is proportional to the slope of the graph of the logarithm of the distribution ratio against the value of θ. Thus the uncertainty expressed as a percentage in the value of will be equal to the uncertainty as a percentage in the slope of the graph of the logarithm of the distribution ratios against the values of θ. We used the LINEST feature of excel to calculate the estimated standard deviation on the slope of the line in the graph of the logarithms of the rhenium distribution ratios against the DES content (θ) of the denser phase (for the mixtures of DES with aqueous choline chloride). The LINEST feature indicates that the certainty in this slope is 0.9%, so we regard ΔΨ to be equal to 2.04 with a standard deviation of 0.02.
While the distribution ratio for rhenium from the aqueous sodium chloride is so high that it would be impossible to measure using the shaking tube and even the AKUFVE experimental rig.60 If it possible to estimate then by extrapolation of the data from the experiments in which the deep eutectic solvent was gradually replaced with either aqueous sodium or choline solution. By extrapolation it can be reasoned that the rhenium distribution ratio when the aqueous phase is the sodium chloride solution will be 6330 with a standard deviation of 875. When this process was repeated with the solvent extraction experiments performed with mixtures of DES and aqueous choline chloride, it was 278.7 with a standard deviation of 10.3. From eqn (21) we can create the following equation (eqn (26)) we can make an estimate of ε(Ch+,ReO4−) which does not require us to use the solver feature of excel.
| | 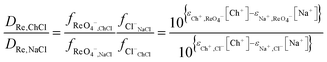 | (26) |
From this equation we can now obtain eqn (27).
| |  | (27) |
If we assume that the ionic strengths of the sodium and choline chloride solutions were identical at 4 M then this estimate for ε(Ch+,ReO4−) is −0.449 with a standard deviation of 0.021. This estimate made using eqn (25) is similar to that produced by the solver function in excel. While the solver feature in excel offers a convenient means of calculating ΔΨ and ε(Ch+,ReO4−) it does not offer a convenient means of estimating the standard deviations in these values. Our solvent extraction experiments could be improved by finding conditions under which the distribution ratios of rhenium are lower, one option is to change fully to technetium and to use lower concentration of aliquat 336. By using 99mTcO4− it would be possible to use even lower chemical concentrations of the metal. By using lower concentrations of the metal it would be possible to use lower concentration of the aliquat 336 without overloading the organic phase. Using the Bateman equations61 it is possible to predict that we could have a chemical concentration of in the 700 μl of the denser phase added to a shaking vial if we were to have 10 kBq of 99mTc present in the tube. Then the chemical concentration of technetium would be 8.36 picomoles per litre if we had milked a technetium cow (99Mo as molybdate on alumina eluted with saline)62 at 8 AM Friday morning before milking a second time at 8 AM Monday before using the Monday morning technetium for the experiment. The w/w concentration of the technetium in the lower phase would be 0.83 ppt. The corresponding concentration of a rhenium solution with the same chemical concentration is 1.55 ppt. As the samples from the shaking tubes must be diluted at least 50 times before feeding them into the ICPMS, this indicates that it would be exceptionally difficult or even impossible to use an ICPMS machine for this experiment using 8.36 picomoles per litre of metal. While one of us has warned how predictions based on Bateman equations can be misleading,63 in this case it is possible to use those equations. A nonradioactive alternative is to change the diluent (organic solvent in which the aliquat 336 is dissolved) to one in which the extractant is less able to extract perrhenate. While often less attention is paid to diluents than extractants, it is often true that by changing the diluent the ability of an extractant to extract metals can be changed.64,65
While we are gratified with our model which rationalises the extraction of gold and rhenium from the deep eutectic, we are aware that the extraction of anions which have multiple charges will be more complex. In both this study and our earlier work we found that metal distribution ratios change as an exponential function of the deep eutectic solvent fraction of the mixture. We considered the question of how valid is our approach of adding the ψ term to the activity function equation, data exists in the literature for sodium bromide in mixtures of water and formamide.66 The literature data was fitted to the SIT model. In this fitting exercise the values of A and B in the following equation were varied in eqn (28) for the aqueous systems.‡‡‡
| | 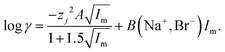 | (28) |
The activity coefficient at 2 moles of sodium bromide per kilo of solvent was reconstructed using this equation. For the literature data for samples with between 0 and 80% formamide by volume a value of 0.301 gave a good agreement between our modified SIT model and the experimental data. When all the data in that paper is used it is possible to obtain a reasonable fit between eqn (29) and the data. Eqn (29) is related to eqn (13).
| | 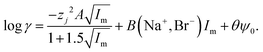 | (29) |
As this paper is about the discovery of new models, we chose to compare
eqn (29) with three other related equations (
eqn (30)–(33)). In this test we attempted to fit all of the data in Hernández-Luis
et al.'s paper to our models. As all our solvent extraction experiments were performed with close to constant ionic strengths we regard their data to be of great interest. The graphs in which our models are compared with the experimental data are shown in the ESI
† at Section G.
| | 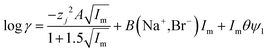 | (30) |
| | 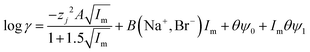 | (31) |
| | 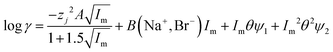 | (32) |
| | 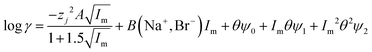 | (33) |
It was found as the equations become more complex, the agreement between them and the experimental data becomes better (Table 4), but as the number of terms in an equation containing a polynomial increases it is important to keep in mind that while the ability of an equation to describe reality increases the equation may have less and less of a theoretical basis. While in the ideal world we would have perfect models, which are both derived from first principles and well able to describe reality, a purely descriptive equation which is able to describe reality has great value during the development of industrial processes.
Table 4 The sodium bromide in formamide/water mixtures modelled with eqn (29)–(33). In this model A is fixed at 0.59159 and B at 0.068535. The predicted activity coefficients were plotted against the measured literature values and in excel a linear trend line was created which passes through the origin. This line is described by the equation y = kx, and the R2 value was recorded. The perfect model would result in both k and R2 being equal to 1
| Equation number |
K
|
R
2
|
Ψ
0
|
Ψ
1
|
Ψ
2
|
|
(29)
|
0.8828 |
0.4946 |
0.2308 |
— |
— |
|
(30)
|
0.9904 |
0.9101 |
— |
0.1083 |
— |
|
(31)
|
0.9962 |
0.9273 |
0.1251 |
0.0732 |
— |
|
(32)
|
1.0042 |
0.9133 |
— |
0.1683 |
−0.0240 |
|
(33)
|
0.9983 |
0.9303 |
0.1164 |
0.0834 |
−0.0030 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 salts
1 salts
If we apply our reasoning and our descriptive equation to the extraction of tetrachloropalladate anions then for the pure sodium system we can write eqn (34).| | 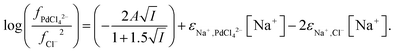 | (34) |
For the aqueous mixed sodium/choline system we can write eqn (35).
| | 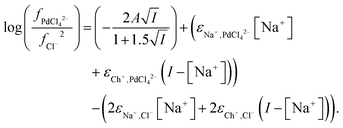 | (35) |
We can add the ψθ terms for the solvent extraction experiments where the denser as is a mixture of an aqueous medium and ethaline, at a fixed ionic strength, thus forming eqn (36).
| | 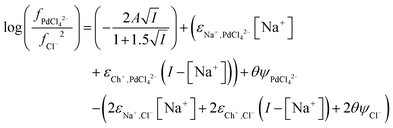 | (36) |
From the data obtained from the mixtures of choline chloride and ethaline it can be determined that ψPdCl42− − 2ψCl− is equal to −2.28. A graph of the logarithms of the palladium distribution ratio against the ethaline fraction of the denser phase is slightly curved. While in the case of the perrhenate the extended Debye–Hückel terms cancel in the case of the palladium they do not in the case of tetrachloropalladate. We reason that as the ethylene glycol and water contents of the lower phase change then the value of A within the Debye–Hückel terms will change, if all the other parameters in the SIT equation were to remain constant this alone would cause the ratio of the activity functions to change if the ions have different charges. If we assume that no thermal expansion occurs on warming a solution from 25 to 30 °C, then the value of A in the term will decrease by 2.5%. Using eqn (18) and our expressions for the activity functions of the anions we can reconcile our experimental data to our model if we assume that the value of A in both the aqueous media and ethaline is the same. For a system where the ionic strength is constant the Debye–Hückel term in eqn (36) will remain constant. We can write eqn (37).
| | 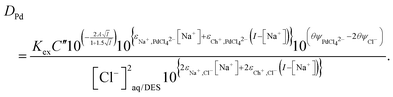 | (37) |
We were gratified to obtain a good agreement between the model and the experimental results as can be seen in Fig. 7. In our final model using the measured sodium and chloride concentrations in the string solutions ψPdCl42− − 2ψCl−, εNa+,PdCl42−, εCh+,PdCl42−, C′′Kex and A are −2.239, −5.31 × 10−5, −0.611, 2.026 × 10−6 and 0.433 respectively. While our method is able to discern the difference between εNa+,PdCl42−, εCh+,PdCl42− it is unable to determine the absolute values of these parameters.
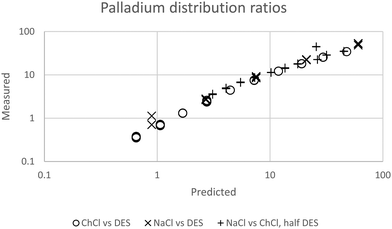 |
| | Fig. 7 The agreement between predicted and measured distribution ratios for palladium. A model which is perfectly able to predict the distribution ratios would create a straight line of points which would obey the equation y = x where x is the predicted distribution ratio and y is the measured distribution ratio. | |
We can make this equation slightly more simple by adsorbing the Debye–Hückel term into a constant C′′′ together with C′′ if we maintain a constant ionic strength. This then allows us to write eqn (38) for this special case.
| | 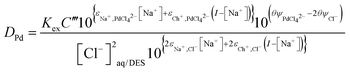 | (38) |
We wish to further explore the topic of activity functions of ions in deep eutectic solvents, hydrophilic ionic liquids and related media, we are conducting experiments to determine how general our observations are. A need exists for measurements of the activity functions of alkali metal salts of chloroanions of the platinum group metals, such data would increase the usefulness of the results in this paper.
Conclusions
A series of relatively simple solvent extraction experiments have been done, the results of these have been considered using the specific ion interaction theory (SIT). We have been able to use the theory to create a model which can be used to describe mathematically the results of the metal extractions, we have been able to explain and rationalise the activity functions of ions in chloride rich deep eutectic solvents. Our work has used two unrelated solvent extraction systems suggesting that our method might be a general method rather than one which only can be applied on a single system. A need exists for further solvent extraction and other types of experiment to determine the limits of our new method. So far we have a purely descriptive model, but the SIT equation with the additional terms can be reconciled with our results and solutions of sodium bromide in mixtures of formamide and water.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We are grateful to the China Scholarship Council for their support in the form of a support from the State Scholarship Fund to Peng Cen (Scholarship number 201806080088). We would like to thank Chelsea M. Foreman and Karl S. Ryder for English language proofreading and for advice about the scientific content of the paper respectively.
References
- A. Kumar, A. Thakur and P. S. Panesar, Rev. Environ. Sci. Bio/Technol., 2019, 18, 153 CrossRef.
- D. Q. Li, J. Rare Earths, 2019, 37, 468 CrossRef CAS.
- V. Carbonell, A. Salvador and M. Delaguardia, Fresenius' J. Anal. Chem., 1992, 342, 529 CrossRef CAS.
- S. Allard and C. Ekberg, J. Solution Chem., 2006, 35, 1173 CrossRef CAS.
- J. Rydberg and Y. Albinsson, Solvent Extr. Ion Exch., 1989, 7, 577 CrossRef CAS.
- F. J. Albler, K. Bica, M. R. S. Foreman, S. Holgersson and M. S. Tyumentsev, J. Cleaner Prod., 2017, 167, 806 CrossRef CAS.
- S. Wellens, B. Thijs, C. Möller and K. Binnemans, Phys. Chem. Chem. Phys., 2013, 15, 9663 RSC.
- N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123 RSC.
- D. B. Zhao, Y. C. Liao and Z. D. Zhang, Clean: Soil, Air, Water, 2007, 35, 42 CAS.
- D. J. Couling, R. J. Bernot, K. M. Docherty, J. K. Dixon and E. J. Maginn, Green Chem., 2006, 8, 82 RSC.
- H. Wang, S. V. Malhotra and A. J. Francis, Chemosphere, 2011, 82, 1597 CrossRef CAS PubMed.
- A. P. Abbott, D. Boothby, G. Capper, D. L. Davies and R. K. Rasheed, J. Am. Chem. Soc., 2004, 126, 9142 CrossRef CAS PubMed.
- A. T. Mudd, C. M. Getty, B. P. Sutton and R. N. Dilger, Nutr. Neurosci., 2016, 19, 425 CrossRef CAS PubMed.
- M. R. St. J. Foreman, Cogent Chem., 2016, 2, 1139289 Search PubMed.
- M. B. Ewing, T. H. Lilley, G. M. Olofsson, M. T. Rätzsch and G. Somsen, Pure Appl. Chem., 1994, 66, 533 CAS.
- T. Shida, Y. Hiraga, T. Sugiyama, Y. Sato, M. Watanabe and R. L. Smith, Fluid Phase Equilib., 2019, 488, 72 CrossRef CAS.
- T. Ban, C. L. Li and Q. Wang, J. Mol. Liq., 2018, 271, 265 CrossRef CAS.
- N. Nkoosi, K. Tumba and S. Ramsuroop, Fluid Phase Equilib., 2018, 462, 31 CrossRef.
- T. M. Lecher and P. Reddy, Fluid Phase Equilib., 2005, 235, 11 CrossRef.
- S. P. Verevkin, T. V. Vasiltsova, E. Bich and A. Heintz, Fluid Phase Equilib., 2004, 218, 165 CrossRef CAS.
- L. Alonso, A. Arce, M. Francisco, O. Rodríguez and A. Soto, J. Chem. Eng. Data, 2007, 52, 1729 CrossRef CAS.
- S. Lago, H. Rodríguez, A. Soto and A. Arce, J. Chem. Eng. Data, 2011, 56, 1273 CrossRef CAS.
- H. Ashassi-Sorkhabi and A. Kazempour, J. Solution Chem., 2017, 46, 1490 CrossRef CAS.
- B. Ghalami-Choobar and M. Shekofteh-Gohari, J. Mol. Liq., 2013, 180, 154 CrossRef CAS.
- D. S. P. Koh, K. H. Khoo and C.-Y. Chan, J. Solution Chem., 1985, 14, 635 CrossRef CAS.
- E. Amado-Gonzalez, M. A. Esteso and W. Gomez-Jaramillo, J. Chem. Eng. Data, 2017, 62, 752 CrossRef CAS.
- N. L. Lancaster, T. Welton and G. B. Young, J. Chem. Soc., Perkin Trans. 2, 2001, 2267 RSC.
- R. Smits, D. L. Massart, J. Juillard and J.-P. Morel, Anal. Chem., 1976, 48, 458 CrossRef CAS.
- N. S. Jayasinghe, F. P. Lucien and T. Tran, Ind. Eng. Chem. Res., 2005, 44, 7496 CrossRef CAS.
- C. W. Davies and B. D. R. Owen, J. Chem. Soc., 1956, 1676 RSC.
- I. Mokbel, C. Lindemann, P. Duchet-Suchaux and J. Jose, Fuel, 2016, 163, 17 CrossRef CAS.
- M. Berthelot and J. Jungfleisch, Ann. Chim. Phys., 1872, 26, 396 Search PubMed.
- G. W. Meindersma, A. J. G. Podt and A. B. de Haan, Fluid Phase Equilib., 2006, 247, 158–168 CrossRef CAS.
- M. R. St. J. Foreman, Cogent Chem., 2016, 2, 1139289 Search PubMed.
- M. J. Hudson, Hydrometallurgy, 1982, 9, 149 CrossRef CAS.
- F. D. M. Fabrega and M. B. Mansur, Hydrometallurgy, 2007, 87, 83 CrossRef CAS.
- M. R. St. J. Foreman, Cogent Chem., 2016, 2, 1139289 Search PubMed.
- M. R. S. Foreman, S. Holgersson, C. McPhee and M. S. Tyumentsev, New J. Chem., 2018, 42, 2006 RSC.
- B. Gupta and I. Singh, Hydrometalurgy, 2013, 134–135, 11 CrossRef CAS.
- M. S. Tyumentsev, M. R. S. Foreman, C. Ekberg, A. V. Matyskin, T. Retegan and B. M. Steenari, Hydrometallurgy, 2016, 164, 24 CrossRef CAS.
- W. Chen, P. Wee and I. D. Brindle, J. Anal. At. Spectrom., 2000, 15, 409 RSC.
- K. Ziegler-Skylakakis, S. Nill, J. F. Pan and U. Andrae, Environ. Mol. Mutagen., 1998, 31, 362 CrossRef CAS PubMed.
- F. J. Albler, K. Bica, M. R. S. Foreman, S. Holgersson and M. S. Tyumentsev, J. Cleaner Prod., 2017, 167, 806 CrossRef CAS.
-
B. Goldacre, Bad Science, Fourth Estate, London, 2008 Search PubMed.
- L. Drougge and L. I. Elding, Inorg. Chem., 1987, 26, 1073 CrossRef.
- I. V. Mironov and E. V. Makotchenko, J. Solution Chem., 2009, 38, 725 CrossRef CAS.
- C. W. Davies, J. Chem. Soc., 1938, 2093 RSC.
-
I. Grenthe, J. Fuger, R. J. M. Konings, R. J. Lemire, A. B. Muller, C. Nguyen-Trung and H. Wanner, Chemical Thermodynamics of Uranium, Appendix B, NEA OCED, Elsevier, 1992, p. 683 Search PubMed.
- E. A. Guggenheim and J. C. Turgeon, Trans. Faraday Soc., 1955, 51, 747 RSC.
-
K. Spahiu, The use of SIT in the NEA TDP project – advantages, drawbacks and comparison with the approaches used in some geochemical codes, In The Use of Thermodynamic Databases in Performance Assessment (NEA TDB International Workshop, Barcelona, Spain, 29–30 May 2001), OCED, Paris, 2002, pp. 61–68.
- G. Scatchard, J. Am. Chem. Soc., 1961, 83, 2636 CrossRef CAS.
- E. A. Mowafy and D. Mohamed, Sep. Purif. Technol., 2016, 167, 146 CrossRef CAS.
- J. B. Macaskill, M. S. Mohan and R. G. Bates, Anal. Chem., 1977, 49, 209 CrossRef CAS PubMed.
- K. A. Kraus, F. Nelson and G. W. Smith, J. Phys. Chem., 1954, 58, 11 CrossRef CAS.
- A. de Visscher, Monatsh. Chem., 2018, 149, 231 CrossRef CAS.
- P. A. Rice, R. P. Gale and A. J. Barduhn, J. Chem. Eng. Data, 1976, 21, 204 CrossRef CAS.
- S. Koroleva, P. Korchak, S. Enders, Y. Dobryakov and A. Victorov, J. Chem. Eng. Data, 2019, 64, 4314 CrossRef CAS.
- G. E. Boyd, J. Solution Chem., 1978, 7, 229 CrossRef CAS.
- R. J. Lemire, P. P. S. Saluja and A. B. Campbell, J. Solution Chem., 1992, 21, 507 CrossRef CAS.
- C. Ekberg, M. Nilsson and P. Brown, Solvent Extr. Ion Exch., 2019, 37, 213 CrossRef CAS.
- H. Bateman, Proc. Cambridge Philos. Soc., 1910, 15, 423 CAS.
- M. Elgarhy, S. Elbayoum and S. Elalfy, Radiochim. Acta, 1967, 7, 163 CAS.
- M. R. St. J. Foreman, Cogent Chem., 2018, 4, 1450944 Search PubMed.
- M. Taube, J. Inorg. Nucl. Chem., 1959, 12, 174 CrossRef CAS.
- M. Nilsson, S. Andersson, F. Drouet, C. Ekberg, M. Foreman, M. Hudson, J. O. Liljenzin, D. Magnusson and G. Skarnemark, Solvent Extr. Ion Exch., 2006, 24, 299 CrossRef CAS.
- F. Hernández-Luis, R. Rodriguex-Raposo and D. Grandoso, J. Chem. Eng. Data, 2011, 56, 3940 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05982b |
| ‡ Between 0.03 and 0.69 M iodine in carbon disulfide. |
| § The distribution ratio is influenced by the nature of the diluent, if a mixture of two diluents with different solubilities in water and/or the deep eutectic solvent is used then the ratio of the two diluents will change each time the organic phase is shaken with an aqueous or deep eutectic phase. |
| ¶ Zinc with a dialkyldithiophosphinic acid, indium with a trialkyl phosphine oxide (cyanex 923), palladium and perrhenate with aliquat 336. |
| || Distribution ratios greater than 100 are difficult to measure as the uncertainties in the metal concentration in the denser phase are so large. Also the effect of even a miniscule contamination of the sample of the denser phase with the lighter phase during the sampling of the denser phase can become very significant when the distribution ratio is very high. The authors recommend that any distribution ratio above 100 be viewed as being uncertain while a distribution ratio of 1000 or more be considered merely as very high. |
| ** DAu, defined as the total gold concentration in the organic (upper) phase divided by the gold concentration in the lower (aqueous or DES) phase. |
| †† A concentration in this paper is indicated by placing a substance in square brackets, for example [Na+] indicates the concentration of sodium ions. |
| ‡‡ Activity coefficients are calculated from molal concentrations (molality) which are an amount of a solute (moles) in a given mass of solvent (1000 g). Activity functions are calculated from molar concentration which is an amount of a solute in a given volume (1 l). The volume is a combination of the solute and the solvent. |
| §§ In the mathematical equations used choline is abbreviated to Ch. |
| ¶¶ While the equation y = mx + c is more well known than y = rx + s, we choose to replace m and c with r and s respectively to avoid reusing a symbol for a different purpose. |
| |||| The distribution ratio for technetium was estimated to be 671 with a standard deviation of 54. This value is too high for reliable measurement in a shaking tube experiment. The estimated standard deviation was 8.1% and the amount of radioactivity recovered from the shaking vials on average within 2.7% of the amount added to the vial. |
| *** The distribution ratio for technetium for 10% aliquat 336 in ethyl benzene when the lower phase was the DES was 2.75(6). The estimated standard deviation was 2.3% and the amount of radioactivity recovered from the shaking vials on average within 2.6% of the amount added to the vial. |
| ††† B = −0.1009, C = 0.01373 and D = 1 × 10−4. |
| ‡‡‡ Note that as eqn (28)–(33) predicts the activity coefficient and is based on molality, thus the symbol is different for one of the terms. |
|
| This journal is © the Owner Societies 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b and
Mark R. St. J.
Foreman
b and
Mark R. St. J.
Foreman
 *b
*b
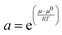

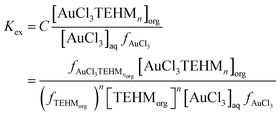
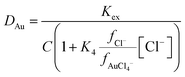
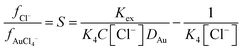
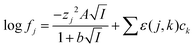
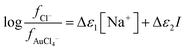
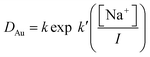


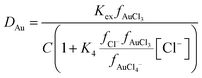
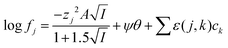
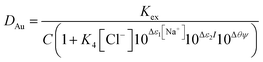
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D against DES volume fraction graph had an appearance similar to the cell survival curves in the Linear-Quadratic (LQ) model used in radiobiology we considered if the eqn (15) with two ψ terms could give a better fit. For the indium data obtained with the choline chloride/deep eutectic solvent mixtures the change in the ratio of the chloride and tetrachloroindium anions is best explained with values of 0.22 and 1.04 for ΔΨ1 and ΔΨ2. Sadly the indium data for the sodium chloride/DES mixtures with between 20 and 80% DES can not be modelled well with our model. A need exists for additional experiments with other metals.
D against DES volume fraction graph had an appearance similar to the cell survival curves in the Linear-Quadratic (LQ) model used in radiobiology we considered if the eqn (15) with two ψ terms could give a better fit. For the indium data obtained with the choline chloride/deep eutectic solvent mixtures the change in the ratio of the chloride and tetrachloroindium anions is best explained with values of 0.22 and 1.04 for ΔΨ1 and ΔΨ2. Sadly the indium data for the sodium chloride/DES mixtures with between 20 and 80% DES can not be modelled well with our model. A need exists for additional experiments with other metals.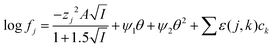
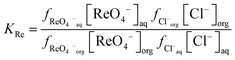
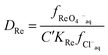
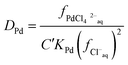
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of DES and dilute sodium chloride the distribution ratio was much lower.*** Using the eqn (21) it is possible to determine the ratios of the activity factors of perrhenate in the sodium and choline chloride solutions.
2 mixture of DES and dilute sodium chloride the distribution ratio was much lower.*** Using the eqn (21) it is possible to determine the ratios of the activity factors of perrhenate in the sodium and choline chloride solutions.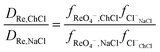
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ethaline and sodium chloride
50 ethaline and sodium chloride![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ethaline and choline chloride
50 ethaline and choline chloride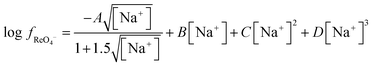
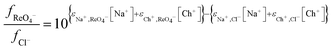
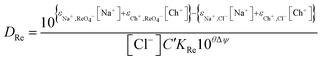
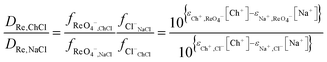

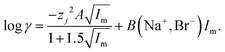
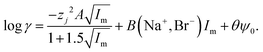
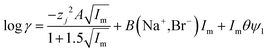
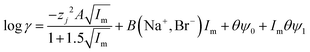
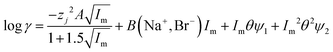
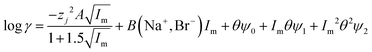
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 salts
1 salts