Understanding ¹²⁵Te NMR chemical shifts in disymmetric organo-telluride compounds from natural chemical shift analysis

Abstract

Organotellurium compounds of general formula X–Te–R display a broad range of chemical shifts that are very sensitive to the X and R substituents. In order to link the ¹²⁵Te chemical shift of a series of perfluoroalkyl aryl tellurides to their electronic structure, the chemical shielding tensors of the ¹²⁵Te nuclei were calculated by density functional theory (DFT) and further analyzed by a decomposition into contributions of natural localized molecular orbitals (NLMOs). The analysis indicated that the variation in ¹²⁵Te chemical shifts in molecules 1–13 is mainly due to the magnetic coupling of the tellurium p-character lone pair with antibonding orbitals perpendicular to it {σ*(Te–X) and σ*(Te–C(Ar))} upon action of an external magnetic field. The strength of the coupling is affected by electronic properties of the X-substituents, polarization of the antibonding orbitals and presence of secondary interactions perturbing the energy of these orbitals. The lower in energy and the more polarized towards tellurium the antibonding orbitals are, the stronger is the coupling and the more deshielded the tellurium nucleus.

---

Introduction

Understanding the electronic origin of NMR chemical shifts is a subject of on-going research in physical, inorganic, and organic chemistry.¹ Examples include both main group element^2–11 and transition metal nuclei.^12–14 Also one of our groups has shown that analysis of chemical shielding tensors of ¹³C and ¹⁷O nuclei can provide valuable insight into the electronic structure of molecules and their reactivity.^15–23 This approach has been used, for example, to understand electronic structures involved in hydrocarbon conversion and oxidation processes.

Tellurium is a main-group element (group 16, period 5) with a broad range of accessible oxidation states (from −II to +VI). Organotellurium compounds were first reported in 1840²⁴ and they have been the subject of fundamental studies regarding their structure and bonding.²⁵ They have also found applications in the functionalizations of carbon–carbon multiple bonds²⁶ or as glutathione mimics.²⁷

Tellurium has two spin 1/2 isotopes, ¹²³Te and ¹²⁵Te, the latter being the isotope of choice due to its higher natural abundance (7%). In fact, ¹²⁵Te displays a particularly large chemical shift window of approximately 5000 ppm,²⁸ indicative of the high sensitivity of Te chemical shift to electronic structure. Although calculations of ¹²⁵Te chemical shifts have been reported,^29–35 so far little is known on the relation between ¹²⁵Te chemical shift and the structural motif of organotellurium compounds.

We became interested in tellurium compounds as structural equivalents of iodine(III) reagents developed and extensively studied in our group. Iodine(III) reagents are widely used as oxidants and in group-transfer reactions.^36,37 Examples include selective oxidation of alcohols to aldehydes,³⁸ as well as the formation of C–X and C–C bonds.³⁹ In the context of tellurium chemistry, disymmetric tellurium(II) compounds carrying one aryl and one fluorinated substituent (type A in Scheme 1; see specific examples in Fig. 1) were conceived and prepared in our laboratory⁴⁰ as isolobal analogues of iodine(III)-centered electrophilic perfluoroalkylating reagents (exemplified by B in Scheme 1).^41,42

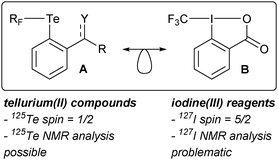Scheme 1 A general structure of a disymmetric telluride considered in this work and an example of a isolobal iodine(III) reagent for trifluoromethylation. R_F = CF₃, CF₂H, C₆F₅; Y = O or NR.

Fig. 1 Tellurium compounds considered in this work.

While the ¹²⁷I nucleus is NMR active, it possesses an extremely large quadrupolar moment and is thus not readily accessible for NMR purposes.⁴³ Consequently, an appreciation of reactivity patterns of iodine-based reagents via the understanding of the underlying electronic structure cannot be obtained using this tool. We addressed this problem by preparing tellurium(II) analogues of type A (Scheme 1). However, these compounds did not show the reactivity of the parent iodine reagents, so their use as models for B and related reagents is limited.

Nevertheless, the obtained compounds A were characterized by ¹²⁵Te NMR spectroscopy. Thus, organotellurium derivatives 1–13 (Fig. 1) display a chemical shift range that varies between 600 and 1700 ppm. We show that a natural chemical shift analysis of the chemical shielding tensors of compounds 1–13 is a valuable approach to understand the electronic structure of these compounds. This also provides a guideline to understand variation of chemical shifts based on a simple localized molecular orbital picture and helps improving our understanding of chemical shifts in general.

Background

Experimentally determined chemical shift (δ, frequency-shifted resonance) is among the most important NMR parameters for the structural characterization of molecules. Its theoretically calculated counterpart, the chemical shielding σ describes the degree of magnetic shielding at a nucleus in a molecule with respect to the bare nucleus. The two parameters are related by eqn (1), where σ_ref is the chemical shielding on the nucleus of choice in an arbitrary reference compound.¹

δ = (σ_ref − σ)/(1 − σ_ref) (1)

Chemical shielding is an anisotropic property described by a second rank tensor with three principal components (convention: σ₁₁ < σ₂₂ < σ₃₃). Computationally, it can be decomposed into diamagnetic (dia), paramagnetic (para) and spin–orbit (SO) contributions. The diamagnetic contributions arise from the electronic ground state of a molecule and leads to a shielding of the nucleus and chemical shift. The paramagnetic contributions arise due to coupling of occupied and vacant orbitals close in energy and perpendicular to each other upon action of the angular momentum operator, induced by the presence of an external magnetic field (Scheme 2).¹ These contributions usually lead to deshielding, even though exceptions to this trend have been pointed out.⁴⁴ Because the strength of the coupling is inversely proportional to the energy difference between these orbitals, major contributions to paramagnetic shielding originate from frontier orbitals. Spin–orbit contributions are of importance for heavy atoms, for which spin–orbit coupling generates non-zero spin density that can be distributed in the molecule by Fermi contact mechanisms. Spin–orbit contributions can be shielding or deshielding, depending on the symmetry and occupation of the involved frontier orbitals.⁴⁵ While the diamagnetic contribution typically remains constant for a certain atom type, paramagnetic and spin–orbit contributions can vary significantly depending on the atom environment.

Scheme 2 Schematic explanation of paramagnetic shielding. A coupling between an occupied and a vacant orbital perpendicular to each other results in deshielding along direction i.

In this work, we calculated chemical shielding of tellurium nuclei in the selected compounds 1–13 and analyzed the different contributions to the chemical shielding in order to identify the major sources of variation. In case of molecule 2, the calculated shielding tensor was benchmarked against an experimental value obtained from a solid state NMR measurement whereby an excellent agreement was observed (see Fig. S2, ESI†). Later, we turned our attention to the anisotropic aspect of the shielding, in particular to the orientation of the principal components of the shielding tensor in a molecule. Since deshielding of a nucleus is expected along the direction i (Scheme 2) if an occupied orbital on this nucleus can be superimposed onto a vacant orbital on the same nucleus upon a 90°-rotation about i, the tensor orientation contains information on orbital interactions relevant for shielding in a given molecule. This analysis was further supported by determination of different orbital contributions to shielding along the three principal directions in a Natural Chemical Shielding (NCS) analysis based on Natural Localized Molecular Orbitals (NLMOs).^46,47 In short, we found that ¹²⁵Te chemical shielding in molecules of general structure A is to a major extent determined by magnetically-induced coupling of a p-character tellurium lone pair and Te-ligand antibonding orbitals. The strength of this coupling is particularly sensitive to the energy of the antibonding orbitals and hence the electronic properties of the ligands on tellurium and the presence of secondary interactions affect the chemical shift.

Computational details

NMR calculations were performed within the GIAO framework using ADF 2014⁴⁸ with the PBE0 functional and Slater-type basis sets of quadruple-ζ (Te) and triple-ζ quality (other atoms). Relativistic effects were treated by the 2 component zeroth order regular approximation (ZORA).^49–53 Analysis of scalar-relativistic natural localized molecular orbitals were done with the NBO 6.0 program.⁵⁴ Polar plots of the shielding tensors in Fig. 4 and 6 were prepared according to ref. 55 and 56. Further details are provided in ESI,† Section 2.

Results and discussion

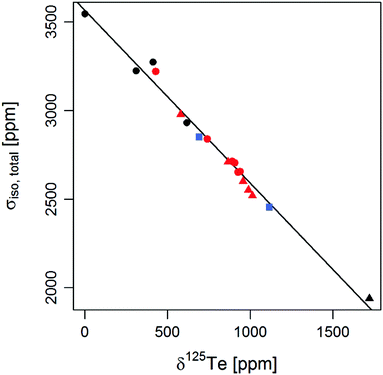
A linear correlation between the isotropic chemical shift measured in solution and calculated total isotropic chemical shielding was obtained for molecules 1–15 (Fig. 2). This linear correlation shows that the trend in ¹²⁵Te NMR chemical shifts can be reproduced by DFT calculations, even without conformational averaging. Dimethyl telluride, used as an external reference for ¹²⁵Te NMR measurements also followed the trend. Additionally, chemical shifts calculated for two previously reported tellurium compounds^57,58 Ph₂Te (16) and 17 were in reasonable agreement with the reported values (blue squares in Fig. 2).

Fig. 2 Chemical shift in solution (experiment) vs. total isotropic chemical shielding (calculation) correlation, all values in ppm. Fluorinated molecules (2–12) are marked in red. Tellurium(II) compounds carrying a carbonyl group (1–6) are represented as triangles while molecules without a carbonyl group (7–15, Me₂Te) are represented as circles. Benchmark compounds Ph₂Te and 16 are marked with blue squares. For ditellurides 14–15, an average value over total isotropic shielding of two tellurium atoms is used. The solid line represents linear regression fit to the data with intercept = 3566 (std. error = 27), slope = −0.98 (std. error = 0.03), multiple R-squared = 0.99, adjusted R-squared = 0.98 on 14 degrees of freedom.

A more detailed analysis of the calculated chemical shielding indicated that among the three contributions, the paramagnetic term varied most between the compounds (Fig. 3 and ESI† Section 5). Diamagnetic and spin–orbit contributions remained virtually constant with exception of ditellurides 14 and 15, for which a small deviation in spin–orbit contributions was observed. Since the ditellurides are structurally distinct from other compounds in this study and were considered only in the context of chemical shielding vs. shift correlation, this deviation was not investigated and further analysis focused on the paramagnetic term in molecules 1–13.

Fig. 3 Overview of contributions to chemical shielding [ppm] in molecules 1–7. For molecules 8–13, see ESI.† Total isotropic shielding (σ_iso), diamagnetic (σ_dia), paramagnetic (σ_para) and spin–orbit (σ_SO) contributions to total isotropic shielding are shown. The paramagnetic contribution is further decomposed to contributions along three principal directions.

A closer look at the three principal components of the paramagnetic shielding tensors revealed that the most deshielded component σ_para,11 and the least deshielded σ_para,33 varied most across the series. Variation in σ_para,22 component was also present, but less significant.

Having established a linear correlation between experimental and theoretical results, we moved to the analysis of the chemical shielding tensor orientation on the tellurium atom in molecules 1–13. Because the chemical shielding in these compounds varies mainly due to the paramagnetic contribution that arises from frontier orbitals coupling upon an action of an external magnetic field, information about these couplings is encoded in the tensor orientation. An occupied and a virtual orbital perpendicular to each other generate deshielding in the direction perpendicular to both (see Introduction and Scheme 2).

In the majority of cases the most deshielded component σ₁₁ is aligned with the Te–C(Ar) bond or slightly tilted away from it (molecules: 3, 4, 5, 7, 8, 9, 11, 12; see Fig. 4 and ESI† Section 6). A more significant tilting is observed in molecules 1, 2, 6, 10, 13. In Me₂Te, σ₁₁ is located in the plane bisecting the C–Te–C angle. Component σ₂₂ is typically perpendicular to Te–C(Ar) and Te–X bonds (X = CF₃, CF₂H, C₆F₅, Cl, CH₂CN), in the direction of a p-character lone pair of tellurium (vide infra). Component σ₃₃ is perpendicular to the other two, which in most cases results in an imperfect alignment with the Te–X bond. In molecules 1 and 3 the orientation of the two less deshielded components is reversed. However, in case of 3 components σ₂₂ and σ₃₃ are similar in magnitude, so only compound 1 is an exception of the generally observed trend.

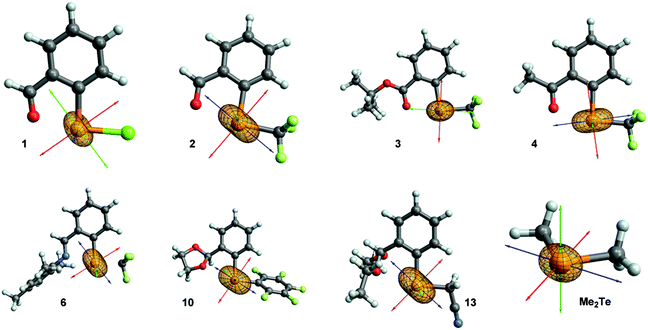Fig. 4 Orientation of total chemical shielding tensor in selected molecules. The principal components are represented as red (σ₁₁), green (σ₂₂) and blue (σ₃₃) arrows.

Orientation of the chemical shielding tensor combined with the knowledge of orbital contributions to shielding allows to determine the origin of chemical shielding for a given atom. Therefore, our next step was to calculate contributions of natural localized molecular orbitals (NLMOs) to principal components of the total shielding tensor using NCS analysis for a representative set of molecules (1, 2, 3, 4, 6, 10 and Me₂Te). The focus of this section is mainly on the most deshielded component σ₁₁, which is also the component that varies most across the series. A comment regarding the other components is provided later and details can be found in ESI.†

In all cases studied, NBO analysis indicated that from the two lone pairs of the tellurium atom, one is an almost pure p-lone pair (>99% p-character, oriented perpendicular to the plane defined by the aromatic ring, further denoted as n(Te)), while the other predominantly displays s-character (approx. 80% s, 20% p, denoted s-n(Te)).

According to the NCS analysis, in all cases the major contribution to the deshielding along σ₁₁ originates from the p-character lone pair on tellurium (n(Te)), while the s-n(Te) orbital contributes only to a minor extent and the contribution is shielding in nature (Fig. 5 and ESI† Section 7). Typically, n(Te) accounts for approx. 80% of the total value of σ₁₁. Among other orbitals, the Te–X bonding orbital contributes most significantly. Consequently, the variation of chemical shielding (and the chemical shift) of tellurium in the set can be explained by the coupling of n(Te) with virtual (unoccupied) orbitals perpendicular to it upon action of an external magnetic field. The identity of the virtual orbitals can be deduced from the orientation of the σ₁₁ component in the molecular frame.

Fig. 5 Orbital contributions to chemical shielding [ppm] along σ₁₁ in selected molecules. Total value (σ₁₁), paramagnetic (σ_para) and diamagnetic (σ_dia) contributions are shown. The paramagnetic contribution is further decomposed to contributions from tellurium p-character lone pair (n(Te)), tellurium s-character lone pair (s-n(Te)), tellurium-substituent single bonds (σ_Te–X and σ_Te–C(Ar)). For X and C(Ar) notation, see main text and Fig. 7.

In the simple example of Me₂Te, the σ₁₁ component is oriented in the plane bisecting the C–Te–C angle (Fig. 6, left). Deshielding in this direction can be considered a vector sum of deshielding along the two Te–C bonds. Since the C–Te–C angle is close to 90 °C in the optimized structure (exact value: 94.9 °C), a coupling of the tellurium lone pair with one σ*(Te–C) antibonding orbital results in deshielding along the other Te–C bond. Because the two Te–C bonds and consequently the σ*(Te–C) antibonding orbitals are equivalent in Me₂Te, both of these interactions are equally pronounced and deshielding along both Te–C bonds is equal in magnitude and the two contributions sum up resulting in the observed orientation of σ₁₁ (in the plane bisecting the C–Te–C angle).

Fig. 6 Schematic rationalization of σ₁₁ orientation in Me₂Te and CF₃TeMe. Top: Orientation of the chemical shielding tensors in the molecules. Middle: Energy levels of orbitals that couple upon action of an external magnetic field and a schematic representation of these orbitals. Bottom: Approx. contributions to deshielding resulting from these couplings. Black arrows represent contributions from each coupling and the length of an arrow illustrates the coupling strength. The red arrow is the vector sum thereof.

When two substituents of different electronic properties are attached to a tellurium atom, the orientation of σ₁₁ changes and in most cases deshielding in the direction of the less electronegative substituent is observed. Molecules shown in Fig. 1 aside, this can be demonstrated on the simpler example of CF₃TeMe, a Me₂Te analogue in which one methyl group is replaced by a more electron withdrawing CF₃ group (Fig. 6, right). Clearly, the vector representing σ₁₁ is tilted towards the methyl substituent in this case. Following the argument above, this indicates a stronger coupling between n(Te) and σ*(Te–CF₃) than between n(Te) and σ*(Te–Me). Since higher electronegativity of the CF₃ group results in lower energy σ*(Te–CF₃) compared to σ*(Te–Me) and the strength of the coupling is inversely proportional to the energy gap between interacting orbitals, the coupling between n(Te) and σ*(Te–CF₃) is stronger and the deshielding along Te–Me bond larger in magnitude, as reflected in the orientation of σ₁₁.

The same argument holds for molecules 2–12, in which the difference in σ*(Te–X) and σ*(Te–C(Ar)) energies is the reason for the tilt of the vector representing σ₁₁ towards the Te–C(Ar). In molecule 13, this vector is oriented similarly as in the Me₂Te case, due to the fact that the two substituents on tellurium have similar electron-withdrawing properties.

In the representative set, approximate energies of σ*(Te–X) and σ*(Te–C(Ar)) are provided by the NBO analysis (ESI† Section 7.3). From the comparison of the calculated values, the energy gap between n(Te) and σ*(Te–X) is smaller by 18–21 kcal mol⁻¹ compared to the n(Te) ↔ σ*(Te–C(Ar)) gap in cases where X = CF₃ (2, 3, 4). For 10, which carry two aryl groups on the tellurium atom, a significantly lower value is obtained (6 kcal mol⁻¹ in favour of the n(Te) ↔ σ*(Te–C(Ar)) interaction) in line with the fact that the tilt of σ₁₁ towards the Te–C(Ar) bond is also smaller. However, NBO energies cannot be used to explain the orientation of σ₁₁ in molecules 1 (almost in the plane bisecting the Cl–Te–C angle) and 6 (tilted towards the Te–CF₃ bond). Clearly, factors different from NBO energies and perturbation effects not considered in NBO energy determination are relevant for chemical shielding of the tellurium atom.

A secondary interaction between tellurium and a proximal heteroatom is most likely one of such factors. This interaction, described as a donation of electron density from the heteroatom lone pair to the Te–X antibonding orbital⁵⁹ (n(Y) → σ*(Te–X)) is known in the literature⁶⁰ and quantitatively equivalent to the 3-centered-4-electron bond in Pimentel–Hach–Rundle model.⁶¹ According to simple MO considerations, its presence raises the energy of σ*(Te–X) (Fig. 7) and hence weakens the n(Te) ↔ σ*(Te–X) coupling and reduces the deshielding along the Te–C(Ar) bond. Among the molecules analysed in the representative set, the interaction is expected to be strongest in case of 1 and 6, due to the high electronegativity of X (1), or the presence of nitrogen in the Y position (6). The high electronegativity of X results in low energy of σ*(Te–X), while the n(Y) energy is lower when Y = N vs. O. Both effects result in strengthening of the secondary interaction, in case of 6 additionally illustrated by shortening of the Y–Te distance in the solid state (Y–Te distance: 2.570(3)Å and 2.481(6) Å in 2 and 6, respectively, the trend is reproduced in the gas phase).

Fig. 7 Secondary interaction between σ* (Te–X) antibonding orbital and a lone pair of a proximal heteroatom. This interaction increases the energy of the vacant orbital.

A quantitative description of the n(Y) → σ*(Te–X) interaction is available from the NBO analysis (ESI† Section 7.3). Indeed, estimation of second order perturbation effects for this interaction in 1 and 6 are 42 and 29 kcal mol⁻¹ respectively, the highest in the representative set. In terms of chemical shielding, this is reflected in the fact that the σ₁₁ vectors are tilted towards Te–X bonds instead of Te–C(Ar) bonds, as the n(Te) ↔ σ*(Te–X) coupling becomes weaker due to increase in the energy gap between these two orbitals. The same argument can also be used to explain the difference in orientation of σ₁₁ in the otherwise very similar molecules 2 and 4 (second order perturbative estimates: 17 kcal mol⁻¹vs. 6 kcal mol⁻¹ for 2 and 4 respectively).

In case of 1, this effect is partially counterbalanced by significant polarization of the σ*(Te–Cl) antibonding orbital towards tellurium (to an extent of 74% vs. approx. 63% in other cases, see ESI†). A coupling of two orbitals is stronger when these orbitals are similar in size. High polarization of the σ*(Te–X) antibonding orbital towards tellurium results in a large orbital coefficient on tellurium and a better overlap with n(Te) upon action of an external magnetic field. Consequently, the coupling between n(Te) and σ*(Te–Cl) is on the one hand disfavoured due to the strong secondary interaction, on the other hand favoured due to polarization of σ*(Te–X) and the orientation of σ₁₁ is between Te–C(Ar) and Te–Cl bonds, quantitatively similar to the Me₂Te case.

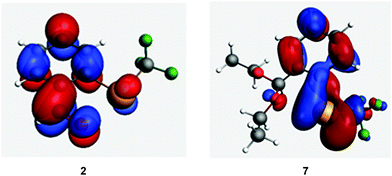
Apart from couplings of the tellurium lone pair, σ(Te–X) bond also contributes to σ₁₁ in the representative examples. This contribution indicates the presence of a low-lying vacant orbital perpendicular to the Te–X bond with a coefficient on the tellurium atom. This vacant orbital could be constructed from the tellurium lone pair and p-character orbitals on carbon atoms in the aromatic ring. In fact, such an orbital was found to be the LUMO of molecules 1–6. In molecules 7–13, the LUMO appears to be a combination of σ*(Te–X), n(Te) and carbon p-orbitals (see Fig. 8 for an example and ESI† Section 8.1 for other molecules).

Fig. 8 LUMO of molecules 2 (left) and 7 (right). Blue and red colors denote the phase of the orbitals. Carbon atoms shown in grey, hydrogen in white, fluorine in green, oxygen in red and tellurium in yellow.

Following the argument presented for σ₁₁, significant variation in σ₃₃ can also be understood. Since the σ₃₃ vector is perpendicular to n(Te) and tilted away from the Te–X bond in the majority of cases, the factors that affect orientation of σ₁₁ will also affect σ₃₃. Moreover, as the paramagnetic shielding is largely due to the coupling of the tellurium lone pair and σ₂₂ is typically pointing in the direction of n(Te), much smaller variation in σ₂₂ values across the series can also be explained.

The variation of tellurium chemical shifts in molecules 1–13 is therefore a result of several factors, including electron-withdrawing properties of substituents on tellurium, presence of secondary bonding interactions and orbital polarisation. This makes prediction of chemical shifts within a group of similar molecules (e.g. molecules with a CF₃ group on tellurium) a complex task. However, general trends in chemical shifts of molecules 1–13 can be rationalized following these considerations. Hence, the highest chemical shift (the largest deshielding) is experimentally observed for compound 1, followed by CF₃ derivatives (2–4, 6–9, 12), CF₂H derivative 11 and C₆F₅ derivatives 5 and 10. This is due to the fact that the electron-withdrawing effect of X-substituent, that influences both orbital energies and polarization decreases in this series. In addition, imine 6 has a lower chemical shift than aldehyde 2, due to the presence of a stronger secondary interaction between the tellurium centre and the proximal heteroatom in the former. This interaction increases the energy of the Te–CF₃ antibonding orbital leading to a weaker coupling with n(Te).

Conclusions

To conclude, the variation in ¹²⁵Te chemical shifts in molecules 1–13 is mainly due to the magnetic coupling of the tellurium p-character lone pair with antibonding Te-Ligand orbitals perpendicular to it upon action of an external magnetic field. The strength of these couplings and consequently the magnitude of the ¹²⁵Te shift is determined by the relative energies and polarization of these antibonding orbitals, with low-energy orbitals polarized towards tellurium yielding the strongest couplings and the highest chemical shifts. The energies of the antibonding orbitals depend on the electron-withdrawing character of the substituents attached to tellurium and are affected by secondary interactions between the tellurium centre and a proximal heteroatom (oxygen vs. nitrogen for instance). Analysis of all three factors (electronic properties of substituents, polarization effects and secondary interactions) is necessary to explain the orientation of the chemical shielding tensor in the molecule and consequently to determine the origin of tellurium chemical shifts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Odile Eisenstein is acknowledged for discussions at the early stage of this project. Christopher P. Gordon thanks the Scholarship Fund of the Swiss Chemical Industry (SSCI) for funding.

Notes and references

1. C. M. Widdifield and R. W. Schurko, Concepts Magn. Reson., Part A, 2009, 34, 91.
2. G. Wu, D. Rovnyak, M. J. A. Johnson, N. C. Zanetti, D. G. Musaev, K. Morokuma, R. R. Schrock, R. G. Griffin and C. C. Cummins, J. Am. Chem. Soc., 1996, 118, 10654.
3. M. Kaupp, V. G. Malkin, O. L. Malkina and D. R. Salahub, Chem. – Eur. J., 1996, 2, 24.
4. D. Auer, M. Kaupp and C. Strohmann, Organometallics, 2004, 23, 3647.
5. E. L. Sceats, J. S. Figueroa, C. C. Cummins, N. M. Loening, P. Van Der Wel and R. G. Griffin, Polyhedron, 2004, 23, 2751.
6. V. Kravchenko, R. Kinjo, A. Sekiguchi, M. Ichinohe, R. West, Y. S. Balazs, A. Schmidt, M. Karni and Y. Apeloig, J. Am. Chem. Soc., 2006, 128, 14472.
7. P. S. Engl, C. B. Santiago, C. P. Gordon, W.-C. Liao, A. Fedorov, C. Copéret, M. S. Sigman and A. Togni, J. Am. Chem. Soc., 2017, 139, 13117.
8. R. V. Viesser, L. C. Ducati, C. F. Tormena and J. Autschbach, Chem. Sci., 2017, 8, 6570.
9. R. V. Viesser, L. C. Ducati, C. F. Tormena and J. Autschbach, Phys. Chem. Chem. Phys., 2018, 20, 11247.
10. S. L. Staun, D.-C. Sergentu, G. Wu, J. Autschbach and T. W. Hayton, Chem. Sci., 2019, 10, 6431.
11. J. D. Epping, S. Yao, M. Karni, Y. Apeloig and M. Driess, J. Am. Chem. Soc., 2010, 132, 5443.
12. J. Autschbach and S. Zheng, Magn. Reson. Chem., 2008, 46, S45.
13. K. Sutter and J. Autschbach, J. Am. Chem. Soc., 2012, 134, 13374.
14. M. Srebro and J. Autschbach, Chem. – Eur. J., 2013, 19, 12018.
15. C. P. Gordon, C. Raynaud, R. A. Andersen, C. Copéret and O. Eisenstein, Acc. Chem. Res., 2019, 52, 2278.
16. C. P. Gordon, R. A. Andersen and C. Copéret, Helv. Chim. Acta, 2019, 102, e1900151.
17. C. Ehinger, C. P. Gordon and C. Copéret, Chem. Sci., 2019, 10, 1786.
18. C. P. Gordon, D. B. Culver, M. P. Conley, O. Eisenstein, R. A. Andersen and C. Copéret, J. Am. Chem. Soc., 2019, 141, 648.
19. C. P. Gordon, K. Yamamoto, K. Searles, S. Shirase, R. A. Andersen, O. Eisenstein and C. Copéret, Chem. Sci., 2018, 9, 1912.
20. L. Foppa, K. Yamamoto, W.-C. Liao, A. Comas-Vives and C. Copéret, J. Phys. Chem. Lett., 2018, 9, 3348.
21. C. P. Gordon, S. Shirase, K. Yamamoto, R. A. Andersen, O. Eisenstein and C. Copéret, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E5867.
22. C. P. Gordon, K. Yamamoto, W.-C. Liao, F. Allouche, R. A. Andersen, C. Copéret, C. Raynaud and O. Eisenstein, ACS Cent. Sci., 2017, 3, 759.
23. S. Halbert, C. Copéret, C. Raynaud and O. Eisenstein, J. Am. Chem. Soc., 2016, 138, 2261.
24. F. Wöhler, Ann. Chem. Pharm., 1840, 35, 111.
25. T. Chivers and R. S. Laitinen, Chem. Soc. Rev., 2015, 44, 1725.
26. Patai's Chemistry of Functional Groups, ed. Z. Rappoport, Wiley, 2012, pp. 891–949.
27. C. W. Nogueira, G. Zeni and J. B. T. Rocha, Chem. Rev., 2004, 104, 6255.
28. H. Duddeck and A. Biallass, Magn. Reson. Chem., 1994, 32, 303.
29. I. L. Rusakova and L. B. Krivdin, Mendeleev Commun., 2018, 28, 1.
30. F. Alkan and C. Dybowski, Solid State Nucl. Magn. Reson., 2018, 95, 6.
31. M. Bortoli, M. Dalla Tiezza, C. Muraro, G. Saielli and L. Orian, Molecules, 2019, 24, 1250.
32. I. L. Rusakova, Y. Y. Rusakov and L. B. Krivdin, J. Phys. Chem. A, 2017, 121, 4793.
33. S. Hayashi, K. Matsuiwa and W. Nakanishi, RSC Adv., 2014, 4, 44795.
34. F. Aquino, N. Govind and J. Autschbach, J. Chem. Theory Comput., 2011, 7, 3278.
35. Y. Ruiz-Morales, G. Schreckenbach and T. Ziegler, J. Phys. Chem. A, 1997, 101, 4121.
36. A. Yoshimura and V. V. Zhdankin, Chem. Rev., 2016, 116, 3328.
37. V. V. Zhdankin, Hypervalent Iodine Chemistry Preparation, Structure and Synthetic Applications of Polyvalent Iodine Compounds, John Wiley & Sons, Ltd, 2014.
38. V. V. Zhdankin, J. Org. Chem., 2011, 76, 1185.
39. Y. Li, D. P. Hari, M. V. Vita and J. Waser, Angew. Chem., Int. Ed., 2016, 55, 4436.
40. E. Pietrasiak and A. Togni, Organometallics, 2017, 36, 3750.
41. J. Charpentier, N. Früh and A. Togni, Chem. Rev., 2015, 115, 650.
42. V. Matoušek, J. Václavík, P. Hájek, J. Charpentier, Z. E. Blastik, E. Pietrasiak, A. Budinská, A. Togni and P. Beier, Chemistry, 2016, 22, 417.
43. C. Hall, Q. Rev., Chem. Soc., 1971, 25, 87.
44. K. B. Wiberg, J. D. Hammer, K. W. Zilm, J. R. Cheeseman and T. A. Keith, J. Phys. Chem. A, 1998, 102, 8766.
45. J. Vícha, S. Komorovsky, M. Repisky, R. Marek and M. Straka, J. Chem. Theory Comput., 2018, 14, 3025.
46. J. A. Bohmann, F. Weinhold and T. C. Farrar, J. Chem. Phys., 1997, 107, 1173.
47. J. Autschbach, J. Chem. Phys., 2008, 128, 164112.
48. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931.
49. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597.
50. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783.
51. E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505.
52. E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Int. J. Quantum Chem., 1996, 57, 281.
53. E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943.
54. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, 2013, http://nbo6.chem.wisc.edu/.
55. J. Autschbach, S. Zheng and R. W. Schurko, Concepts Magn. Reson., Part A, 2010, 36, 84.
56. E. Zurek, C. J. Pickard and J. Autschbach, J. Phys. Chem. C, 2008, 112, 11744.
57. Y. Yamamoto, F. Sato, S. Kodama, A. Nomoto and A. Ogawa, Heteroat. Chem., 2018, 29, e21471.
58. E. Pietrasiak, A. F. Baxter, B. Jelier, N. Santschi and A. Togni, Helv. Chim. Acta, 2019, 102, e1900079.
59. C. Bleiholder, R. Gleiter, D. B. Werz and H. Koeppel, Inorg. Chem., 2007, 46, 2249.
60. R. N. Behera and A. Panda, Comput. Theor. Chem., 2012, 999, 215.
61. G. C. Pimentel, J. Chem. Phys., 1951, 19, 446.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental section, computational details, ssNMR of 2, graphical representations of: correlations, chemical shielding tensors, NCS analysis and selected orbitals; optimized geometries. See DOI: 10.1039/c9cp05934b

---