A DFT and KMC based study on the mechanism of the water gas shift reaction on the Pd(100) surface

Abstract

We present a combined density functional theory (DFT) and Kinetic Monte Carlo (KMC) study of the water gas shift (WGS) reaction on the Pd(100) surface. We propose a mechanism comprising both the redox and the associative pathways for the WGS within a single framework, which consists of seven core elementary steps, which in turn involve splitting of a water molecule followed by the production of an H-atom and an OH-species on the Pd(100) surface. In the following steps, these intermediates then recombine with each other and with CO leading to the evolution of CO₂, and H₂. Seven other elementary steps, involving the diffusion and adsorption of the surface intermediate species are also considered for a complete description of the mechanism. The geometrical and electronic properties of each of the reactants, products, and the transition states of the core elementary steps are presented. We also discuss the analysis of Bader charges and spin densities for the reactants, transition states and the products of these elementary steps. Our study indicates that the WGS reaction progresses simultaneously via the direct oxidation and the carboxyl paths on the Pd(100) surface.

---

1. Introduction

The water gas shift (WGS) reaction plays a crucial role in many industrially important processes as diverse as steam-methane reforming for ammonia and methanol synthesis and direct proton exchange membrane fuel cell applications.^1–24 In the last few years, the mechanism of this reaction has been studied intensively using both theoretical and experimental techniques; it is, however, still extensively debated.²⁵ In previous studies, various reaction pathways have been considered; for example, a study by Huang et al. focused on three different pathways for the WGS reaction on the Fe₂O₃(111) surface using density functional theory with Hubbard correction (DFT+U) i.e. a redox mechanism also known as the regenerative mechanism, the associative or the carboxyl mechanism and the coupling mechanism.^3,20 In the redox mechanism, the water molecule is dissociated into atomic H and O atoms; the dissociated O-atom then interacts with the adsorbed CO molecule to form CO₂. In the associative mechanism, the adsorbed CO interacts with adsorbed OH species obtained by partial dissociation of H₂O, to give a carboxyl intermediate, which then decomposes to CO₂ and an H-atom.²⁶ Finally, in the coupling mechanism, the evolution of CO₂ takes place directly from the reaction of CO and OH species. This study concluded that the redox mechanism is the most favourable pathway for the WGS reaction on the Fe₃O₄(111) surface. In an earlier work, Gokhale et al. studied all the elementary steps of redox and carboxyl mediated mechanisms for the low-temperature WGS reaction on the Cu(111) surface, using density functional theory (DFT) and microkinetic modelling.³ They proposed that the abstraction of H from H₂O is the rate determining step, while in another study Grabow et al. employed DFT, microkinetic modelling and experimental techniques to study the WGS reaction on the Pt(111) surface.¹⁸ They concluded that formate species act as spectators and cannot be formed from CO and OH in a single elementary step. The CO species was identified as the most abundant of the surface intermediates and the carboxyl group (COOH), formed from CO and OH, subsequently combined with OH to form CO₂ and H₂O. While this step was considered to be the favoured CO₂ formation path, due to its low activation energy barrier, their microkinetic modelling study, shows that this reaction is limited by the low OH coverage. They proposed that the direct decomposition step of COOH → CO₂ + H accounts for 75–95% of the total CO₂ production.

Mohsenzadeh et al. recently reported a DFT based study on the effect of three different Ni surfaces i.e., Ni(111), Ni(110) and Ni(100) on the WGS reaction.⁴ They considered nine elementary steps, which included water dissociation, CO oxidation and the formation of hydrogen. Their calculations indicated that water dissociation, formyl formation, formate dissociation and formation of H₂ have the lowest barrier on the Ni(110) surface, CO oxidation has the lowest barrier on the Ni(100) surface. Their analysis showed that the rate limiting step was CO + O → CO₂. The barrier for this reaction decreased in the order of Ni(110) > Ni(111) > Ni(100) surfaces. In another study involving DFT, near-edge X-ray absorption fine structure (NEXAFS) and IR spectroscopy, Senanayake et al. investigated the role of formate, carbonate and carboxyl species as possible intermediates in the WGS reaction on the Au(111) surface.²⁷ They found that for formate, the bidentate is more stable than the monodentate configuration by ∼0.650 eV and it is, therefore, unlikely that formate is a key intermediate in the WGS reaction. They concluded that carbonate species are not present during the reaction of CO with OH on Au(111) at 90–120 K and that carbonate is much less stable on the Au(111) surface than on oxide surfaces. However, we note that that there are reports where the formate species have been observed as intermediates, for example in studies on the reverse WGS reaction by Choi et al. employing in situ FT-IR and DFT techniques on Pd, Ni, Cu and Ag.²⁸

In addition to pristine metallic surfaces, there are also several reports of investigations of the WGS reaction on metals supported on metal oxides.^14,29,30 Song et al. for example, employed DFT+U techniques to understand the mechanism of the WGS reaction on a single Au atom versus Au cluster supported on CeO₂.¹⁴ They concluded that the carboxyl mechanism has a lower energy pathway compared to the redox mechanism. In related studies, the elementary steps involving water splitting, and CO oxidation have also been studied. For instance, Filhol et al. elucidated the electrochemical activation of water over the Pd(111) surface and Peterson et al. investigated low temperature CO oxidation catalysed by atomically dispersed Pd on Al₂O₃.^31,32 We also note that the kinetics of the WGS reaction could be also greatly influenced by catalyst supports. For example, earlier studies by Grenoble et al. performed a detailed study on the Group VIIB, VIII and IB metals supported on Al₂O₃ and showed that the rate per surface metal atom of Pt supported on Al₂O₃ has an higher magnitude as compared to Pt supported on SiO₂.³³

It is clear that despite the wide range of theoretical and experimental studies on the WGS reaction, there are considerable uncertainties regarding the key elementary steps of its reaction mechanism. Therefore, in this study we employ density functional theory (DFT) and Kinetic Monte Carlo (KMC) simulations to understand the mechanism of this important reaction over the Pd(100) surface.

In this study, we focus our study on the Pd surface as Pd-based membranes are known to be able to isolate hydrogen in large quantities and maintain its stability during the water gas shift reaction. For instance, recent studies have demonstrated that the Pd and Pd-based alloy membranes are able to produce H₂ with a high purity of 99.89%.^34,35 The choice of the Pd(100) surface, on the other hand, is largely based on the fact that it is well characterised by a large number of recent experimental studies using in situ methods.³⁶ Furthermore, Zhang et al. using periodic DFT showed that the reaction pathways on the Pd(111) and Pd(110) surfaces display common features despite the fact that they have different surface symmetries.³⁷ Recent, theoretical studies have also shown that the surface energies of the Pd surfaces are in the order Pd(111) < Pd(100) < Pd(110), so the Pd(111) surface is the most stable surface followed by Pd(100) and Pd(110).²⁸ Therefore, we considered the Pd(100) surface to capture the WGS reaction on the surface, which is experimentally well-known, relatively active but sufficiently stable.

In the following sections, we will present first the details of our computational procedures and a description of the proposed reaction mechanism in terms of geometric and electronic properties, which will be followed by the discussions of the results obtained from the DFT calculations and their implementation in the KMC analysis. We show that the water gas shift reaction progresses simultaneously via both direct oxidation and carboxyl pathways, which consist of seven core elementary steps.

2. Computational details

DFT calculations

We employ the Vienna Ab initio Simulation Package (VASP) to perform DFT calculations.^38–41 We used the projector augmented wave (PAW) method and the cut-off energy is set to 450 eV, which gave bulk energies converged to within 10⁻⁵ eV. We chose a convergence criterion of 0.02 eV Å⁻¹ for our structural optimisations and the Perdew–Wang (PW91) version of the generalized gradient approximation (GGA) to carry out total energy calculations and perform geometry optimisations.^42,43 We note that the PW91 functional has been shown to be reliable for such studies.^44,45 For all the calculations an experimental lattice constant of 3.891 Å is used for bulk Pd and the ideal Pd(100) surfaces are modelled by a 3 × 3 supercell with 4 atomic layers respectively from bulk Pd. Of the four layers we have relaxed the top two atomic-layers and fixed the bottom two layers to mimic the bulk of the system. Six equivalent layers of vacuum between two successive metal slabs are used. To determine the minimum energy paths for all the elementary steps, we employed the climbing-image nudged elastic band (CI-NEB) method.^46,47 The transition state of the optimised reaction coordinate was confirmed by calculations of the vibrational frequencies. Since a slab exposes two surfaces (top and the bottom of the slab), placing an adsorbate on one of these generally induces a dipole moment. To eliminate the latter, one can place a second adsorbate symmetrically on the other surface; yet, this increases computational cost and leads to problems when calculating transition states (two imaginary frequencies for symmetrically placed transition state species). To avoid these issues, adsorption is allowed on only one of the two surfaces in all of our calculations. The dipole moment for these calculations, due to the adsorbed species is accounted for using the methods according to the works of Makov et al. and Neugebauer et al.^48,49 as implemented in VASP. A k-point grid of 18 × 18 × 1 was used for all the calculations. The adsorption energy of adsorbates on Pd(100) surface is then calculated using:

E_ad = E_{adsorbate + Pd(100)} − (E_Pd(100) + E_adsorbate), (1)

where, E_ad is the adsorption energy, E_{adsorbate+Pd(100)} is the energy of the system with the adsorbate on Pd surfaces, E_Pd(100) is the energy of pristine surface and E_adsorbate is the energy of the adsorbate. The adsorption energy values include zero-point energy corrections. The charges on various atoms were obtained using the Bader charge analysis as implemented by Henkelman and co-workers.⁵⁰ It is also worth mentioning that previously, Tsuzuki et al. used PW91 exchange and correlation functional to evaluate nonbonding dispersive interactions, and they found that the interaction energies are very close to their CCSD(T) and MP2 results.⁵¹ It has been also reported that PW91 already overestimates the binding energy; therefore, inclusion of additional vdW term does not lead to further improvements.⁵² Further to this, Ortmann et al. also showed that the use of PW91 and PW91 + vdW results in very little difference in lattice parameters, bulk modulus, cohesive energies, vibrational frequencies, bond lengths, of solids and molecules.⁵² Therefore, in this study we have not considered the dispersive effects separately.

Kinetic Monte-Carlo simulations

The KMC simulations were run using the Zacros code^53,54 (http://zacros.org) with the results processed using MATLAB (https://uk.mathworks.com/). During the simulations, the species number and process statistics were sampled every 1 ms and a snapshot of the adlayer was taken every 50 ms. We have used H₂O, CO, CO₂, and the pristine Pd(100) surface as the reference species. Stiffness scaling was used on all the diffusion and water adsorption and desorption steps to prevent these steps from dominating and hampering time progression past a few milliseconds. All the steps were allowed to be reversible, so that the simulation satisfies microscopic reversibility. It was necessary to include 7 extra steps involving diffusion, adsorption and desorption in the proposed mechanism considered for the DFT calculations, in order to simulate an open system and take into account the mobility of the adsorbates on the surface. The pressure and temperature are kept at 1 atm and 600 K respectively, which was selected so that a suitable time could be sampled within available computational resources. The partial pressure ratio of CO and H₂O was varied, ranging from 1 : 1 to a 1000 : 1 ratio of CO and H₂O.⁵⁵ Lateral interactions were calculated by deriving the interaction energies using DFT on two adjacent molecules (both for the same or for different species) on the same surface (see Table S1, ESI†).⁵⁶ Pre-exponential factors were then computed using the vibrational frequencies from the DFT calculations. A detailed discussion on the evaluation of the pre-exponential factors has been given previously by Stamatakis and co-workers in ref. 57.

3. Results and discussion

The overall water gas shift reaction is given by the equation:

CO + H₂O ⇌ CO₂ + H₂

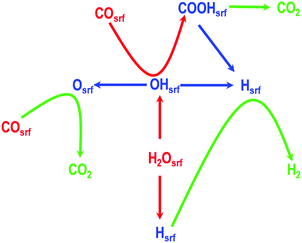
To formulate the mechanism of this reaction, we first consider the key intermediates including H, O, and OH, which can be obtained from H₂O and the reactant CO, and then determine all the other probable intermediates in this reaction. In a recent study, Mohsenzadeh et al. have shown that HCO is an unstable intermediate; similarly, Plauk et al. have shown that the OOH intermediate on Pd(111) and Pd(100) surfaces will readily dissociate to give O and OH intermediates; and as described previously, Grabow et al. reported that the formate species is a spectator species and cannot be formed from CO and OH in a single elementary step.^4,18,44 Therefore, considering all these aspects, we formulated a mechanism consisting of seven core elementary steps involving both redox and carboxyl mechanisms as shown in Fig. 1. We propose that the splitting of the water molecule, gives rise to an adsorbed H-atom and an OH-species on the Pd(100) surface. In the following steps, these intermediate species combine with CO leading to the evolution of CO₂, and H₂. We have also considered the possibility that the CO₂ molecule is formed via another route involving a carboxyl species. It is worth mentioning that the Boudouard reaction, which is 2CO ⇌ C_srf + CO₂, is also one of the probable elementary steps. However, recent studies have shown that the rate of this reaction decreases in presence of H₂O and H₂.⁵⁸ Additionally, the inclusion of this elementary step could lead to another step i.e., C_srf ⇌ C_bulk, as shown by us in our previous studies on palladium carbides, which may greatly affect the mechanism of the water gas shift reaction.^59,60 In this study, to simplify the proposed mechanism we have not included these two steps. For clarity, each of these proposed elementary steps are summarised below (in which the subscript “srf” indicates a surface species):

Fig. 1 A mechanism consisting of seven core elementary steps involving both redox and carboxyl mechanisms for water gas shift reaction. For simplicity the adsorption and desorption steps are not shown.

Step 1: water splitting

(H₂O)_srf ⇌ (OH)_srf + (H)_srf

Step 2: formation of H₂O and adsorption of O

(OH)_srf + (OH)_srf ⇌ (H₂O)_srf + (O)_srf

Step 3: OH splitting

(OH)_srf ⇌ (O)_srf + (H)_srf

Step 4: H₂ evolution from (H)_srf

(H)_srf + (H)_srf ⇌ H₂

Step 5: CO oxidation

(CO)_srf + (O)_srf ⇌ CO₂

Step 6: formation of COOH from CO_srf and (OH)_srf

(CO)_srf + (OH)_srf ⇌ (COOH)_srf

Step 7: CO₂ evolution

(COOH)_srf ⇌ (CO₂)_srf + (H)_srf

In addition to these seven core steps, we have also considered the adsorption and desorption of CO and H₂O and diffusion of CO, H₂O, O, H, OH, and CO₂ for a complete description of the WGS reaction, which we will discuss when we present our KMC studies. The geometric and electronic properties of atomic and/or molecular species involved in reactants, products, and transition states of each of these core elementary steps are described in the next section.

3.1. Adsorption properties of the atomic and molecular species

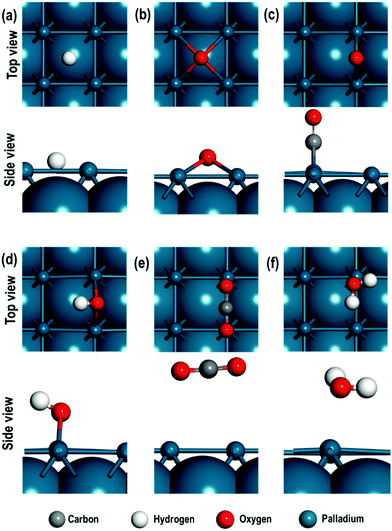
We first consider the adsorption energies of all the adsorbed atomic and molecular species on the Pd(100) surface. The adsorption energies of these species are calculated on top (T) of a Pd atom, in between two Pd atoms i.e. the bridge site (B) and on the four-fold hollow (4f) site. In Table 1, the calculated distances of the atomic and/or molecular species from the Pd(100) surface, their interatomic distance and the adsorption energies for all these adsorbates are given. The top and side views of all the optimised structures for the atomic and molecular species are also shown in Fig. 2(a–f).

Table 1 The geometry and adsorption energies of various adsorbates with zero point energy corrections on the four-fold hollow (4f), bridge (B) and top (T) sites of Pd(100) surface. “A” in the table represents the atoms closer to the Pd(100) surface

Species	Sites	Proximity to Pd	Interatomic distances (Å)		E ad (eV)
			Pd–A	A–B (Å)
H	4f	H	1.981	—	−2.342
	B	H	1.717	—	−2.342
	T	H	1.555	—	−1.906
O	4f	O	2.149	—	−1.221
	B	O	1.933	—	−0.890
	T	O	1.825	—	0.123
CO	4f	C	2.206	1.203	−1.854
	B	C	2.000	1.178	−1.924
	T	C	1.876	1.158	−1.501
OH	4f	O	2.159	0.978	−3.128
	B	O	1.934	0.976	−3.204
	T	O	1.969	0.967	−2.440
CO2 (horizontal)	4f	C, O	—	1.177	0.173
	B	C, O	—	1.176	0.011
	T	C, O	—	1.777	−0.025
H2O	4f	O	2.987	0.975	−0.100
	B	O	2.484	0.973	−0.147
	T	O	2.966	0.980	−0.076

---

Fig. 2 Top and side views of the most stable structures of (a) H atom, (b) O atom, (c) CO molecule, (d) OH species, (e) CO₂ molecule, and (f) H₂O molecule. For clarity the uppermost layer is shown as ball and stick format and for the lower subsurfaces van der Waals representation of the atoms is adopted.

We find that the H-atom displays similar adsorption energies on the four-fold hollow (4f) and the bridge (B) sites and is stable in both these sites. The adsorption energies of the O-atom indicate strongest binding at the 4f site. For the diatomic molecules (or species) such as CO, OH and H₂, we find that the adsorption at the bridge sites is of lower energy. We also note that the adsorbed OH species display an interesting geometrical property after relaxation i.e., the H atom adopts a slanted position with respect to the surface Pd-atom to which O of the OH species is bound. In contrast, CO is bound via the C-atom in a perpendicular configuration. The probable reason for this difference can be investigated using Bader charge analysis. The average charge on the Pd atoms on the surface is 0.034 e and 0.012 e respectively for OH/Pd(100) and CO/Pd(100) systems. However, when we consider the Pd atoms in the immediate neighbourhood surrounding the OH and CO species, we see that they have a residual average negative charge i.e., −0.020 e and −0.053 e for OH/Pd(100) and CO/Pd(100) surfaces respectively. On the other hand, the charge on the H-atom of OH species is 0.595 e and −1.009 e for the O-atom in the CO species, resulting in an electrostatic attraction between the H of OH species and the Pd(100) surface and hence the bent structure. The CO₂ molecule is weakly adsorbed on the top site, while the H₂O molecule is weakly chemisorbed on the “bridge-top” site i.e., after relaxation of the H₂O molecule adsorbed on the bridge site, it migrates closer to the top site and remains tilted towards the surface.

Having established the favoured sites for the adsorbed species, we now explore their geometrical and electronic properties in more detail.

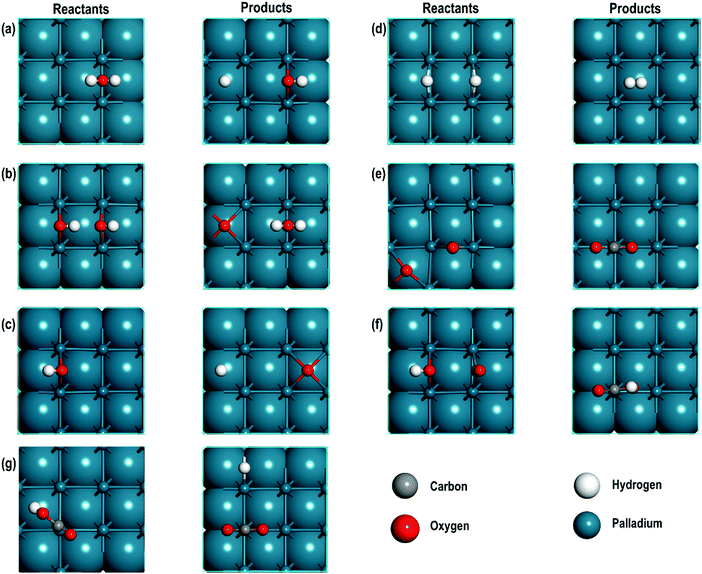
3.2. Geometrical and electronic properties of the reactants, and products

The optimised geometries of all the reactants and the products are reported in Fig. 3(a–f) and summarised in Table 2. Interestingly, the Pd–Pd distances in close proximity to the adsorbed sites involving O-atoms are slightly longer than the average values of 2.729 Å. For example, in Step 1, the Pd–Pd distance is unperturbed around the adsorbed H-atom but it is 2.884 Å around the OH species (i.e., longer by ∼0.152 Å). This difference can be attributed to the strong interaction between the O-containing species bound to the neighbouring Pd atoms. To support these conclusions, we analyse the partial density of states (PDOS) of two Pd atoms close to the O-atom (referred to as Pd_1close and Pd_2close) and another pair of Pd atoms further away from the O-adsorption site (referred to as Pd_3far and Pd_4far). As shown in Fig. 4, the d-orbital signatures completely overlap with each other for both pairs of Pd atoms, showing strong d–d interactions. However, despite their similarities we can see that in the former case the intensity of d-orbital signatures around the Fermi energy (E_F) is lower than with the pair of Pd atoms further away from the O-adsorption site, implying weakening of d–d interactions, which may be related to the polarisation of Pd atoms due to presence of electronegative O-atom leading to the increased Pd–Pd distance. Another interesting point is that, in the former case, we can also see s and d signatures at around −7 eV (Fig. 4(a)), which are missing in the pair of Pd atoms further away from the O-adsorption site. These additional signatures are due to the interaction of the O-atom with the Pd atoms.

Fig. 3 The top view of reactants and products of (a) water splitting, (b) formation of H₂O and adsorption of O, (c) OH splitting, (d) H₂ evolution, (e) CO oxidation, (f) formation of carboxyl species and (g) CO₂ evolution from carboxyl species. For clarity the upper most atomic layer is shown in ball and stick and lower sub-surfaces are shown in van der Waals representation.

Table 2 The Pd–Pd on the surface ((Pd–Pd)_srf) and in proximity ((Pd–Pd)_near) of the interacting species, the distance between the nearest atom (A) of these species with the Pd(100) surface and their Bader charges. The coordinates of all the files have been included in the ESI

Step	Species on Pd	Average interatomic distances (Å)							Bader charges
		(Pd–Pd)srf	(Pd–Pd)near		Pd–A		Pdint		Species
			Distance	Pd close to	Distance	Pd – species
1	H2O	2.749	2.816	O of H2O	2.591	O of H2O	−0.001	PdH2O	−1.232	O of H2O
									0.635	H of H2O
	H + OH	2.750	2.729	H	1.978	H	0.159	PdOH	−1.052	O of OH
									0.651	H of OH
			2.884	O of OH	2.101	O of OH	0.045	PdH	−0.086	H
2	OH + OH	2.729	2.885	O of OH	2.082	O of OH	0.185	PdOH	−1.045	O of OH
			2.891	O of OH	2.135	O of OH			0.635	H of H
	O + H2O	2.754	2.763	O	2.154	O	0.087	PdH2O	−1.266	O of H2O
			2.804	O of H2O	2.613	O of H2O	0.095	PdO	0.654	H of H2O
									−0.760	O
3	OH	2.754	2.877	O of OH	2.104	O of OH	0.168	PdO	−1.005	O of OH
									0.594	H of OH
	O + H	2.754	2.778	H	1.714	H	0.167	PdO	−0.730	O
			2.760	O	2.145	O	0.008	PdH	−0.062	H
4	H + H	2.751	2.785	H	1.715	H	0.020	PdH	−0.086	H
			2.785	H	1.715	H	−0.010	PdH	−0.085	H
	H2	2.751	—	—	—	—	—	—	0.027	H
									−0.039	H
5	CO2	2.749	—	—	—	—	—	—	2.090	C of CO2
									−1.068	O of CO2
	CO + O	2.756	2.778	O	2.168	O	0.135	PdCO	−0.731	O on Pd
			2.747	C of CO	1.998	C of CO	0.188	PdO	−0.976	O of CO
									0.844	C of CO
6	–COOH	2.752	2.759	C of –COOH	1.994	C of –COOH	0.075	PdC	1.407	C of –COOH
									−1.192	OH of –COOH
									−1.094	O of –COOH
									0.688	H of –COOH
	OH + CO	2.756	2.884	O of OH	2.104	O of OH	0.191	PdOH	−1.012	O of OH
									0.629	H of OH
			2.771	C of CO	2.006	C of CO	0.069	PdCO	0.854	C of CO
									−1.047	O of CO
7	H + CO2	2.747	—	CO2	—	CO2	—	—	1.970	C of CO2
									−1.007	O of CO2
			2.780	H	1.717	H	0.012	PdH	−0.087	H on Pd

---

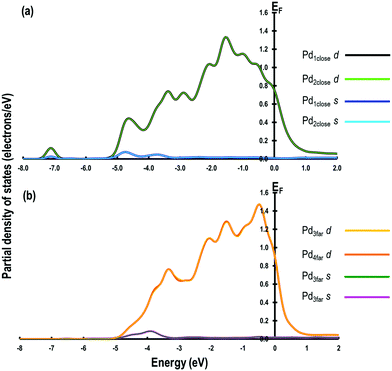Fig. 4 Partial density of states for (a) Pd atoms in close proximity and (b) Pd atoms further away from the adsorbed O-atom.

On closely monitoring the Pd–Pd distances for all the reactants and products, we can, however, see an exception to the above observation in step 5 (see Table 2) i.e., in close proximity to an adsorbed O-atom, the Pd–Pd distance is 2.778 Å, which is similar to the average Pd–Pd distance on the surface. In this case, the adsorbed oxygen atom, in the four-fold hollow site, is shared by four Pd atoms and therefore, the effect of weakening the d–d interactions is minimal.

We further analysed the Bader charges of all the reactants and products adsorbed on the Pd(100) surface, which indicate that the interacting Pd (Pd_int) atoms exhibit mostly positive charges ranging from 0.012 e to 0.188 e, showing that due to the adsorption of various species there is a charge transfer from the Pd surface. In steps 1, and 4 however, we observe that Pd_int has zero charge. The analyses of charges show that O-atoms bonded to H in OH, C in CO or CO₂ and H in H₂O have charges in the range of −0.966 e to −1.232 e and when they are directly adsorbed on the Pd surface they have a charge of −0.730 e. It is interesting to note that the H-atoms are adsorbed on the Pd surface as hydride ions.

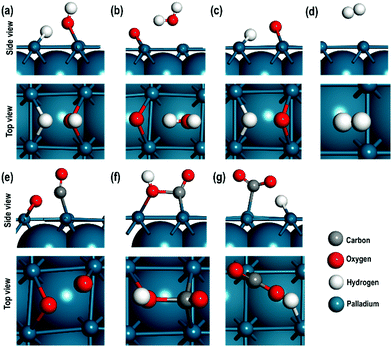
3.3. Geometry, energetics and local electronic properties of the transition states

In this section, we will describe the geometrical and local electronic properties of the transition states with respect to the reactants and products. The side and top views of each of the transition states (TS) for all the steps of the proposed mechanism are shown in Fig. 5.

Fig. 5 Top and side views of (a) TS1, (b) TS2, (c) TS3, (d) TS4, (e) TS5, (f) TS6, and (g) TS7 where, TS represents transition states and 1–7 represents the steps. For clarity the upper most atomic layer is shown in ball and stick and lower sub-surfaces are shown in van der Waals representation.

In the first step, [H₂O ⇌ (OH)_srf + (H)_srf], i.e. water splitting, the energy barrier is 1.320 eV and the reaction is slightly exothermic in nature. Previous high-resolution electron energy loss spectroscopy (HEELS), temperature-programmed desorption (TPD) and time-of-flight (TOF) spectroscopic studies on Pd surface have also revealed reversible water dissociation by forming surface hydroxyl (OH_srf) groups and H atoms adsorbed on the surface.⁶¹ In the transition state, one of the H-atoms is at a distance of 1.460 Å while the other is at a distance of 0.979 Å from the O-atom, i.e. one of the two O–H bonds is stretched (Fig. 5(a)). At this stage, the dissociated H-atom is ∼1.852 Å away from the Pd surface. The Bader charges show that it has a charge of 0.165 e, so it is not very strongly adsorbed to the Pd surface, unlike fully dissociated H-atoms, which are adsorbed as hydride ions. To better understand the charge distribution of the transition state, we compare the spin charge densities of the interacting Pd(100) surface with the pristine Pd(100) surface (see Fig. 5). In the pristine Pd(100) surface, the heights of spin density peaks are uniform and a distortion of these peak heights along with the calculated Bader charges will indicate the nature of the interaction between the TS and Pd(100) surface. The Pd atoms interacting directly with the O-atom (of –OH species) have a shorter peak height due to the electronegative effect of the O-atom. The Bader charge of these two atoms is +0.124 e, i.e. there is charge transfer from the surface to the –OH species. The other Pd atoms interact weakly with the H-atom, which has a charge of +0.016 e. There is a small distortion in the shapes of the peaks, which may be due to the polarising effects of the Pd atom interacting with the –OH species.

In the second step, [(OH)_srf + (OH)_srf ⇌ (H₂O)_srf + (O)_srf], the –OH species formed in the first step may recombine via an exothermic reaction to give H₂O and an adsorbed O-atom, the energy barrier for which is found to be 0.880 eV. In the transition state, the abstraction of one of the H-atoms from the –OH species takes place. The distance of this H-atom from the parent –OH species is 2.000 Å, indicating a weak interaction via a H-bond, and its distance from the other OH species is ∼0.990 Å, which is close to the normal O–H bond distance in a water molecule. The Bader charge on the adsorbed O-atom is −0.755 e and the average charge on the interacting Pd atoms is +0.202 e, indicating a strong interaction between them. In contrast, the charge on the Pd atom close to the water molecule is +0.051 e revealing a weak interaction between the water molecule and the Pd(100) surface, which is also evident in the spin density map shown in Fig. 5c.

In the third step, [(OH)_srf ⇌ (O)_srf + (H)_srf], the –OH obtained from water dissociation (in the first step) can further split to give an adsorbed O-atom and H-atom via an exothermic reaction with an energy barrier of 0.320 eV. In the transition state, the O⋯H distance has increased to 1.689 Å from the normal O–H distance of 0.978 Å. The O-atom has a charge of −0.658 e, and Pd atoms directly interacting with it have an average charge of +0.121 e, showing that there is a strong charge transfer effect between the dissociated O-atom and the surface. In contrast, the dissociated H-atom has a charge of +0.096 e, confirming it to be in the H⁺ state. The charge on the nearest Pd atom is zero. As shown in Fig. 6(d), when we visualise the electron spin densities, we find that the peak heights are smaller for the Pd atoms interacting with the adsorbed O-atom (third column from the left in Fig. 6(d)) as compared with the other Pd atoms. The Pd interacting with H⁺ species also show smaller peak heights, which may be related to the polarizing effects of the Pd atoms directly interacting with the electronegative O-atom.

Fig. 6 Spin densities of the exposed surface in (a) pristine Pd(100) (min = 9.45 × 10⁻⁷ e Å⁻³, max = 4.13 × 10⁻⁵ e Å⁻³) and during the interaction of the transition states in (b) step 1 (min = 7.63 × 10⁻⁷ e Å⁻³, max = 2.79 × 10⁻⁵ e Å⁻³), (c) step 2 (min = 4.44 × 10⁻⁷ e Å⁻³, max = 3.37 × 10⁻⁵ e Å⁻³), (d) step 3 (min = 5.52 × 10⁻⁸ e Å⁻³, max = 1.80 × 10⁻⁵ e Å⁻³), (e) step 4 (min = −1.68 × 10⁻⁷ e Å⁻³, max = 2.74 × 10⁻⁵ e Å⁻³), (f) step 5 (min = −3.22 × 10⁻⁵ e Å⁻³, max = 5.89 × 10⁻³ e Å⁻³), (g) step 6 (min = −7.71 × 10⁻⁸ e Å⁻³, max = 4.69 × 10⁻⁶ e Å⁻³) and (h) step 7 (min = −3.04 × 10⁻⁸ e Å⁻³, max = 1.02 × 10⁻⁵ e Å⁻³).

The fourth step, [(H)_srf + (H)_srf ⇌ H₂], involves the evolution of the H₂ molecule due to the recombination of the adsorbed H-atoms with an energy barrier of 0.810 eV. As shown in Table 2, the adsorbed hydride ions are at a distance of 1.715 Å and in the transition state of this reaction, both the H-atoms are at a distance of approximately 2.748 Å from the nearest Pd atom with an interatomic distance of 0.763 Å, which is close to the H–H bond length in the H₂ molecule (see Fig. 5(d)). The calculation of Bader charges indicates that in the transition state, the H-atoms and the closest Pd atoms have approximately zero charge (Table 3). In the spin charge density contour map, we can, however, observe small charges on these Pd atoms (third column in Fig. 6(e)), which may be due to weak electrostatic interactions between the H⋯H species and the surface.

Table 3 Interatomic distances and Bader charges for the transition states. The coordinates of all the files have been included in the ESI

TS for step	Interatomic distances			Bader charges
	Pd–Pdsrf	Pd – species		Species 1		Species 2		Pdspecies 1	Pdspecies 2
1	2.764	1.846	H	0.165	H	0.585	H of OH	0.016	0.124
		2.200	O of OH			−1.029	O
2	2.766	2.004	O	−0.755	O	−1.275	O of H2O	0.202	0.051
		2.617	O of H2O			0.654	H of H2O
3	2.765	1.766	H	0.096	H	−0.658	O	0.009	0.234
		1.977	O
4	2.753	2.831	H	−0.004	H	0.000	H	0.002	2 Pd near TS (negligible charge)
		2.816	H
5	2.743	2.035	O	−0.710	O	0.999	C of CO	0.185	0.110
		1.947	CO			−1.007	O of CO
6	2.749	2.078	C of OC–OH	1.053	C of OC–OH	−1.060	O of HO–CO	0.097	0.113
		2.331	O of HO–CO	−1.074	O of OC–OH	0.672	H of HO–CO
7	2.755	2.057	C of COO	1.604	C of COO	0.208	H	0.068	−0.005
		1.858	H	−1.008	O of COO

---

The oxidation of CO, [(CO)_srf + (O)_srf ⇌ (CO₂)_srf], takes place in the fifth step with an energy barrier of 0.690 eV. In the transition state (Fig. 5(e)), the Pd–O and Pd–CO distances are slightly shorter than the Pd–O and Pd–CO distances in the reactant (Table 2). The CO has moved from the bridge site towards the adsorbed O-atom in the TS. The Bader charges show that the C in CO in the TS is slightly electropositive as compared to the CO in the reactant, which makes it more feasible for the adsorbed O-atom to combine with the C of CO to give a CO₂ molecule. Furthermore, the charges on the interacting Pd atoms in the reactants decreased from +0.188 e to +0.110 e indicating that the Pd–CO bond is weak. While in the reactant the CO is adsorbed to two Pd atoms, in the transition state it is bonded to only one, which is also clearly seen in the charge spin density contour map for the Pd atom directly interacting with the CO (second column third row from the top in Fig. 6(f)).

Previous studies have suggested that bidentate formate is a spectator species in the WGS reaction and hence the energetically less stable carboxyl group, which is adsorbed to the surface through the C-atom, may play a crucial role.^18,62 Therefore, in addition to the above five steps, we consider two more steps for the WGS reaction, in which the evolution of CO₂ molecule may occur via the formation of a carboxyl species due to the reaction between adsorbed CO_srf with an OH species, which is step 6 [(CO)_srf + (OH)_srf ⇌ (COOH)_srf]. The carboxyl species in step 6 may then decompose to give CO₂ and an adsorbed hydrogen atom in step 7 [(COOH)_srf ⇌CO₂ + (H)_srf].

In step 6, the OH and CO species are originally bonded to two pairs of nearby Pd surface atoms at a distance of 2.884 Å and 2.771 Å respectively. In the transition state (Fig. 5(f)), the OH and the CO species are bonded to only one surface Pd atom with a distance of 2.078 Å and 2.331 Å respectively and the O of OH and C of CO are at a distance of 1.669 Å. A comparison of the charges in the reactants and the products shows that, during the transition state, the charge on carbon changes from +0.793 e to +1.053 e and the charge on the O-atom of the OH species changes from −1.034 e to −1.060 e, indicating that the OH species acts as a nucleophile to form a new C–O bond to give a carboxyl like species. The charge spin densities show significant changes in the peak heights directly interacting with the CO and OH species, which agrees with the calculated charges on these two Pd atoms (see Fig. 6(g) and Table 3). The formation of the carboxyl species is an endothermic reaction with an energy barrier of 0.720 eV.

Finally, in step 7, which is an exothermic reaction, the carboxyl species decomposes to give CO₂ and a hydrogen atom (hydride ion on the surface) with an energy barrier of 0.540 eV (Table 2). In the transition state (Fig. 5(g)), the H-atom is at a distance of 1.465 Å, which is longer than the C–H distance of 1.109 Å in the carboxyl species indicating that the H-atom is abstracted and has a charge of +0.208 e. The Pd atom in the vicinity of the H-atom is almost neutral and in the vicinity of CO₂ species, slightly positive (+0.068 e). The charge spin density maps also show that only one Pd atom has a lower peak height i.e., interacting with the adsorbed CO₂ species (Fig. 6(h)). We also note, as shown in Table 3, that for all the transition states, the measured Pd–Pd interatomic distances are close to those in the pristine surface. For clarity the energy barriers for the forward, reverse reactions and the ΔE_reaction are summarised in Table S2 (ESI†).

3.4. Kinetic Monte Carlo simulation

Using the results of our DFT calculations, we are able to simulate the WGS reaction on Pd(100) using the Kinetic Monte Carlo (KMC) method, in order to gain deeper insight into the kinetics of the mechanism under reaction conditions. To simulate the reaction mechanism, in addition to the core steps discussed in the previous sections, we consider another seven steps relating to the adsorption, desorption and diffusion of CO, CO₂, H₂O, H, and OH. The steps are:

Step 8: CO adsorption

CO + (*)_srf ⇌ (CO)_srf

Step 9: H₂O adsorption

H₂O + (*)_srf ⇌ (H₂O)_srf

Step 10: O diffusion

(O)_srf + (*)_srf ⇌ (*)_srf + (O)_srf

Step 11: H diffusion

(H)_srf + (*)_srf ⇌ (H)_srf + (*)_srf

Step 12: OH diffusion

(OH)_srf + (*)_srf ⇌ (*)_srf + (OH)_srf

Step 13: CO diffusion

(CO)_srf + (*)_srf ⇌ (*)_srf + (CO)_srf

Step 14: CO₂ desorption (see step 7)

(CO₂)_srf ⇌ CO₂ + (*)_srf

For clarity, in the above reactions the surface sites in the diffusion steps are represented by (*)_srf. The CO adsorption, H₂O adsorption, O diffusion and CO₂ desorption have no energy barriers. The energy barriers for H diffusion, OH diffusion and CO diffusions are calculated as 0.017 eV, 0.400 eV and 0.090 eV respectively, which are obtained from the zero-point corrected energy of the DFT results.

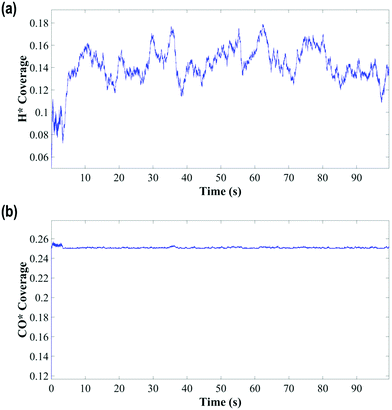
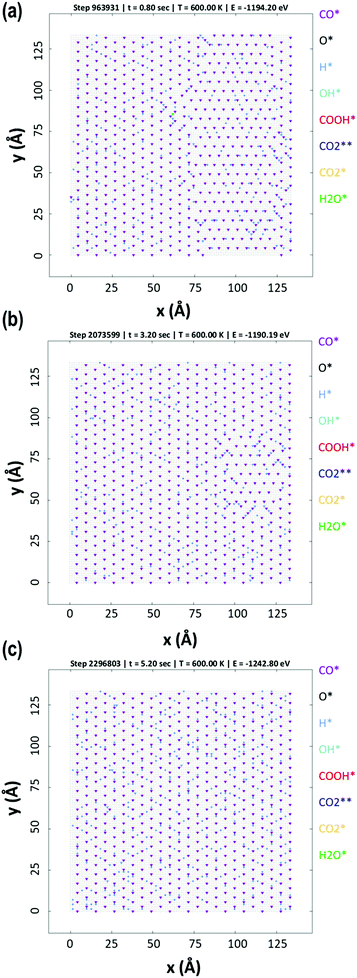
The KMC simulations show that the coverage of H is around 0.15 H atoms per site in a monolayer and as shown in Fig. 7(a and b), the coverage of H exhibited higher fluctuations than that of CO. The H surface coverage is found to reach values as low as 0.04 and as high as 0.18 (Fig. 7a). The KMC simulations further exhibit an average CO coverage of 0.25 molecules per site (monolayers) (see Fig. 7(b)), which does not change significantly during any of the simulations and was found to be almost constant after the initial adsorption of CO. Furthermore, CO forms patterns on the surface due to lateral interactions, as shown in the snapshots in Fig. 8(a–c). Within the first 5 seconds, grain boundaries can be seen between different adsorption patterns, which disappear to form a single adsorption pattern after this time, suggesting an equilibrium period of about 5 s.⁶³ It is also worth noting that only CO and H adsorbates are seen on the surface at any of these snapshots meaning that these are the dominant species and under these conditions the turnover for H₂ production is found to be low. An increase of the turnover is seen with increasing H₂O partial pressure, as shown in Fig. 9, with the overall mechanism remaining the same over the whole range.

Fig. 7 (a) H and (b) CO coverage against time.

Fig. 8 Snapshots for simulation area at (a) 0.8 s, (b) 3.2 s and (c) 5.2 s. All simulation have 1 to 1 ratio for H₂O and CO in the gas phase, under the conditions stated in computational details section.

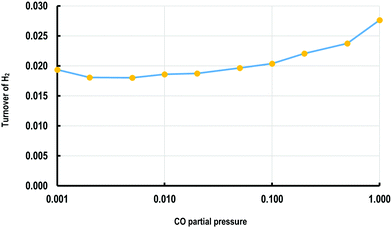Fig. 9 Plot of turnover frequency for H₂ (molecules per site per s) against the ratio of H₂O/CO partial pressure (bar).

When the frequencies of the simulated elementary events, shown in Fig. 10, are examined, it is found that adsorption and diffusion events dominate; therefore, these adsorption and diffusion processes are limited (“throttled”) by a stiffness scaling method.^64–68 The other most common events are H₂O and OH decomposition, which are also seen to be reversible in nature. The OH molecule reacts with the CO molecule to form carboxyl which subsequently generates CO₂; while the OH molecule may break down, thereby producing oxygen which then reacts with CO to form CO₂via direct CO oxidation. The only other reversible step is the –COOH formation. Of the remaining 5 steps i.e., 4, 5, 7 and 14 show that the reactions progress only in one direction and step 2 shows no activity. From the above analysis it can be summarised that WGSR mechanism involves both direct oxidation and carboxyl pathways.

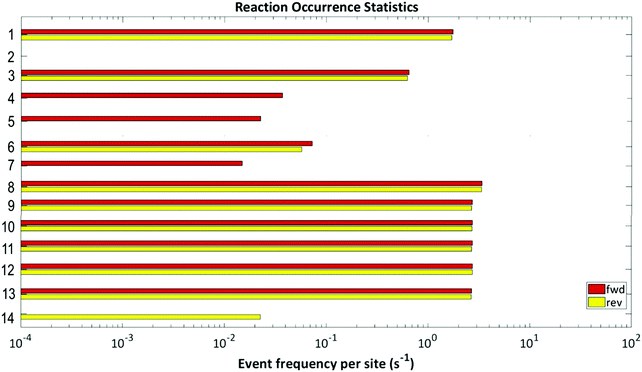Fig. 10 Event frequency per site for each of the elementary steps of the proposed reaction mechanism.

3.5. Summary and conclusions

Our combined DFT and KMC study of the WGS reaction on the Pd(100) surface has allowed us to propose a reaction mechanism in which both redox and associative pathways operate within a single framework, which consists of seven core elementary steps. For the complete description of the WGS chemistry, seven additional steps constituting of adsorption, diffusion and desorption are included in the KMC simulations. Our study on the geometrical changes in each of the reactants, products and the transition states shows that irrespective of the type of species adsorbed on the Pd(100) surface, the average Pd–Pd distance on the surface is always similar except when the adsorbed species are O-atoms. The analysis of electronic properties reveals that this exception is related to the weakening of d–d interactions due to presence of electronegative O-atoms. The calculated energy barriers demonstrate that the splitting of H₂O to give OH and H surface intermediates is the rate determining step. The energy barriers for OH and OH recombination to give H₂O and adsorbed O, and for the hydrogen evolution steps are also high. The KMC study indicates that the H₂O and OH decomposition are the most common events i.e., the OH radical either reacts with the CO molecule to form carboxyl which subsequently generates CO₂; or the radical may break down to oxygen which then reacts with CO to form CO₂via direct CO oxidation. From our study we conclude that the redox-associative mechanism of the water gas shift reaction on Pd(100) progresses via both direct oxidation and carboxyl pathways that occur in parallel, rather than separately, which we consider will lead to a deeper understanding of this important chemical problem on pristine transition metal based catalyst surfaces.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank for resources and support provided via our membership of the UK Catalysis Hub consortium, which is funded by EPSRC (grants EP/K014706/1, EP/K014668/1, EP/K014854/1, EP/K014714/1, EP/M013219/1). Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202) this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk). We acknowledge the use of Athena at HPC Midlands+, which was funded by the EPSRC (grant EP/P020232/1), in this research, via the EPSRC RAP call of spring 2018 and 2019. We also thank Supercomputer Wales for the computing time.

References

1. L. Bollmann, J. L. Ratts, A. M. Joshi, W. D. Williams, J. Pazmino, Y. V. Joshi, J. T. Miller, A. J. Kropf, W. N. Delgass and F. H. Ribeiro, Effect of Zn Addition on the Water–Gas Shift Reaction over Supported Palladium Catalysts, J. Catal., 2008, 257(1), 43–54.
2. T. Bunluesin, R. J. Gorte and G. W. Graham, Studies of the Water–Gas-Shift Reaction on Ceria-Supported Pt, Pd, and Rh: Implications for Oxygen-Storage Properties, Appl. Catal., B, 1998, 15, 107–114.
3. A. A. Gokhale, J. A. Dumesic and M. Mavrikakis, On the Mechanism of Low-Temperature Water Gas Shift Reaction on Copper, J. Am. Chem. Soc., 2008, 130(33), 1402–1414.
4. A. Mohsenzadeh, T. Richards and K. Bolton, DFT Study of the Water Gas Shift Reaction on Ni(111), Ni(100) and Ni(110), Surf. Interface Sci., 2016, 644, 53–63.
5. A. A. Phatak, W. N. Delgass, F. H. Ribeiro and W. F. Schneider, Density Functional Theory Comparison of Water Dissociation Steps on Cu, Au, Ni, Pd, and Pt, J. Phys. Chem. C, 2009, 113, 7269–7276.
6. C. Ratnasamy and J. P. Wagner, Water Gas Shift Catalysis, Catal. Rev., 2009, 51(3), 325–440.
7. J. A. Rodriguez, S. D. Senanayake, D. Stacchiola, P. Liu and J. Hrbek, The Activation of Gold and the Water–Gas Shift Reaction: Insights from Studies with Model Catalysts, Acc. Chem. Res., 2014, 47, 773–782.
8. J. A. Rodriguez, P. Liu, J. Hrbek, J. Evans and M. Perez, Water Gas Shift Reaction on Cu and Au Nanoparticles Supported on CeO₂(111) and ZnO(0001̄): Intrinsic Activity and Importance of Support Interactions, Angew. Chem., Int. Ed., 2007, 119, 1351–1354.
9. J. A. Rodríguez, J. Evans, J. Graciani, J.-B. Park, P. Liu, J. Hrbek and J. F. Sanz, High Water–Gas Shift Activity in TiO₂ (110) Supported Cu and Au Nanoparticles: Role of the Oxide and Metal Particle Size, J. Phys. Chem. C, 2009, 113(17), 7364–7370.
10. E. T. Saw, U. Oemar, X. R. Tan, Y. Du, A. Borgna, K. Hidajat and S. Kawi, Bimetallic Ni–Cu Catalyst Supported on CeO₂ for High-Temperature Water–Gas Shift Reaction: Methane Suppression via Enhanced CO Adsorption, J. Catal., 2014, 314, 32–46.
11. M. Shekhar, J. Wang, W.-S. Lee, W. D. Williams, S. M. Kim, E. A. Stach, J. T. Miller, W. N. Delgass and F. H. Ribeiro, Size and Support Effects for the Water–Gas Shift Catalysis over Gold Nanoparticles Supported on Model Al₂O₃ and TiO₂, J. Am. Chem. Soc., 2012, 134(10), 4700–4708.
12. R. Si and M. Flytzani-Stephanopoulos, Shape and Crystal-Plane Effects of Nanoscale Ceria on the Activity of Au–CeO₂ Catalysts for the Water–Gas Shift Reaction, Angew. Chem., Int. Ed., 2008, 47(15), 2884–2887.
13. M. Flytzani-Stephanopoulos, Gold Atoms Stabilized on Various Supports Catalyze the Water–Gas Shift Reaction, Acc. Chem. Res., 2014, 47(3), 783–792.
14. W. Song and E. J. M. Hensen, Mechanistic Aspects of the Water–Gas Shift Reaction on Isolated and Clustered Au Atoms on CeO₂(110): A Density Functional Theory Study, ACS Catal., 2014, 4(6), 1885–1892.
15. M. Stamatakis, Y. Chen and D. G. Vlachos, First-Principles-Based Kinetic Monte Carlo Simulation of the Structure Sensitivity of the Water–Gas Shift Reaction on Platinum Surfaces, J. Phys. Chem. C, 2011, 115(50), 24750–24762.
16. A. A. Upadhye, I. Ro, X. Zeng, H. J. Kim, I. Tejedor, M. A. Anderson, J. A. Dumesic and G. W. Huber, Plasmon-Enhanced Reverse Water Gas Shift Reaction over Oxide Supported Au Catalysts, Catal. Sci. Technol., 2015, 5(5), 2590–2601.
17. J. Yu, F. J. Tian and C. Z. Li, Novel Water–Gas-Shift Reaction Catalyst from Iron-Loaded Victorian Brown Coal, Energy Fuels, 2007, 21(2), 395–398.
18. L. C. Grabow, A. A. Gokhale, S. T. Evans, J. A. Dumesic and M. Mavrikakis, Mechanism of the Water Gas Shift Reaction on Pt: First Principles, Experiments, and Microkinetic Modeling, J. Phys. Chem. C, 2008, 112(12), 4608–4617.
19. L. Gradisher, B. Dutcher and M. Fan, Catalytic Hydrogen Production from Fossil Fuels via the Water Gas Shift Reaction, Appl. Energy, 2015, 139, 335–349.
20. L. Huang, B. Han, Q. Zhang, M. Fan and H. Cheng, Mechanistic Study on Water Gas Shift Reaction on the Fe₃O₄(111) Reconstructed Surface, J. Phys. Chem. C, 2015, 119(52), 28934–28945.
21. N. Kuriakose, S. Kadam and K. Vanka, A Theoretical Study of Metal–Metal Cooperativity in the Homogeneous Water Gas Shift Reaction, Inorg. Chem., 2012, 51(1), 377–385.
22. J. Lin, A. Wang, B. Qiao, X. Liu, X. Yang, X. Wang, J. Liang, J. Li, J. Liu and T. Zhang, Remarkable Performance of Ir₁/FeO_x Single-Atom Catalyst in Water Gas Shift Reaction, J. Am. Chem. Soc., 2013, 135(41), 15314–15317.
23. C. H. Lin, C. L. Chen and J. H. Wang, Mechanistic Studies of Water–Gas-Shift Reaction on Transition Metals, J. Phys. Chem. C, 2011, 115(38), 18582–18588.
24. A. Herron, J. Scaranto, P. Ferrin, S. Li and M. Mavrikakis, Trends in Formic Acid Decomposition on Model Transition Metal Surfaces: A Density Functional Theory Study, ACS Catal., 2014, 4, 4434–4445.
25. K. Ding, A. Gulec, A. M. Johnson, N. M. Schweitzer, G. D. Stucky, L. D. Marks and P. C. Stair, Identification of Active Sites in CO Oxidation and Water–Gas Shift over Supported Pt Catalysts, Science, 2015, 350(6257), 189–192.
26. E. F. Armstrong and T. P. Hilditch, Interaction of Carbon Monoxide and Steam as Conditioned, Proc. R. Soc. London, Ser. A, 1920, 97(1909), 265–273.
27. S. D. Senanayake, D. Stacchiola, P. Liu, C. B. Mullins and J. Hrbek, Interaction of CO with OH on Au (111): HCOO, CO₃, and HOCO as Key Intermediates in the Water–Gas Shift Reaction, J. Phys. Chem. C, 2009, 113(2), 19536–19544.
28. S. Choi, B. I. Sang, J. Hong, K. J. Yoon, J. W. Son, J. H. Lee, B. K. Kim and H. Kim, Catalytic Behavior of Metal Catalysts in High-Temperature RWGS Reaction: In Situ FT-IR Experiments and First-Principles Calculations, Sci. Rep., 2017, 1–10.
29. D. Tibiletti, A. Amieiro-Fonseca, R. Burch, Y. Chen, J. M. Fisher, A. Goguet, C. Hardacre, P. Hu and D. Thompsett, DFT and In Situ EXAFS Investigation of Gold/Ceria-Zirconia Low-Temperature Water Gas Shift Catalysts: Identification of the Nature of the Active Form of Gold, J. Phys. Chem. B, 2005, 109(47), 22553–22559.
30. A. Goguet, R. Burch, Y. Chen, C. Hardacre, P. Hu, R. W. Joyner, F. C. Meunier, B. S. Mun, D. Thompsett and D. Tibiletti, Deactivation Mechanism of a Au/CeZrO₄ Catalyst During a Low-Temperature Water Gas Shift Reaction, J. Phys. Chem. C, 2007, 111(45), 16927–16933.
31. J. S. Filhol and M. Neurock, Elucidation of the Electrochemical Activation of Water over Pd by First Principles, Angew. Chem., Int. Ed., 2006, 45(3), 403–406.
32. E. J. Peterson, A. T. DeLaRiva, S. Lin, R. S. Johnson, H. Guo, J. T. Miller, J. H. Kwak, C. H. F. Peden, B. Kiefer and L. F. Allard, et al., Low-Temperature Carbon Monoxide Oxidation Catalysed by Regenerable Atomically Dispersed Palladium on Alumina, Nat. Commun., 2014, 5, 1–11.
33. D. C. Grenoble, M. M. Estadt and D. F. Ollis, The Chemistry and Catalysis of the Water Gas Shift Reaction. 1. The Kinetics over Supported Metal Catalysts, J. Catal., 1981, 67(1), 90–102.
34. B. Castro-Dominguez, I. P. Mardilovich, L. C. Ma, R. Ma, A. G. Dixon, N. K. Kazantzis and Y. H. Ma, Integration of Methane Steam Reforming and Water Gas Shift Reaction in a Pd/Au/Pd-Based Catalytic Membrane Reactor for Process Intensification, Membranes, 2016, 6(3), 1–18.
35. I. P. Mardilovich, B. Castro-Dominguez, N. K. Kazantzis, T. Wu and Y. H. Ma, A Comprehensive Performance Assessment Study of Pilot-Scale Pd and Pd/Alloy Membranes under Extended Coal-Derived Syngas Atmosphere Testing, Int. J. Hydrogen Energy, 2015, 40(18), 6107–6117.
36. V. Mehar, M. Kim, M. Shipilin, M. Van Den Bossche, J. Gustafson, L. R. Merte, U. Hejral, H. Grönbeck, E. Lundgren and A. Asthagiri, et al., Understanding the Intrinsic Surface Reactivity of Single-Layer and Multilayer PdO(101) on Pd(100), ACS Catal., 2018, 8(9), 8553–8567.
37. C. J. Zhang and P. Hu, CO Oxidation on Pd(100) and Pd(111): A Comparative Study of Reaction Pathways and Reactivity at Low and Medium Coverages, J. Am. Chem. Soc., 2001, 123(6), 1166–1172.
38. G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561.
39. G. Kresse and J. Hafner, Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal–Amorphous-Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(20), 14251–14269.
40. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186.
41. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979.
42. J. P. Perdew and Y. Wang, Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(23), 13244–13249.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
44. A. Plauck, E. E. Stangland, J. A. Dumesic and M. Mavrikakis, Active Sites and Mechanisms for H₂O₂ Decomposition over Pd Catalysts, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(14), E1973–E1982.
45. J. Xu, S. Guo, F. Hou, J. Li and L. Zhao, Methanol Oxidation on the PtPd(111) Alloy Surface: A Density Functional Theory Study, Int. J. Quantum Chem., 2017, 118(3), e25491.
46. G. Henkelman, B. P. Uberuaga and H. Jónsson, Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113(22), 9901–9904.
47. G. Henkelman and H. Jónsson, Improved Tangent Estimate in the Nudged Elastic Band Method for Finding Minimum Energy Paths and Saddle Points, J. Chem. Phys., 2000, 113(22), 9901–9904.
48. G. Makov and M. Payne, Periodic Boundary Conditions in Ab Initio Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51(7), 4014–4022.
49. J. Neugebauer and M. Scheffler, Adsorbate-Substrate and Adsorbate–Adsorbate Interactions of Na and K Adlayers on Al(111), Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(24), 16067–16080.
50. W. Tang, E. Sanville and G. Henkelman, A Grid-Based Bader Analysis Algorithm without Lattice Bias, J. Phys.: Condens. Matter, 2009, 21(8), 084204.
51. S. Tsuzuki and H. P. Lüthi, Interaction Energies of van der Waals and Hydrogen Bonded Systems Calculated Using Density Functional Theory: Assessing the PW91 Model, J. Chem. Phys., 2001, 114(9), 3949–3957.
52. F. Ortmann, F. Bechstedt and W. G. Schmidt, Semiempirical van der Waals Correction to the Density Functional Description of Solids and Molecular Structures, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(20), 1–10.
53. M. Stamatakis and D. G. Vlachos, A Graph-Theoretical Kinetic Monte Carlo Framework for on-Lattice Chemical Kinetics, J. Chem. Phys., 2011, 134, 21.
54. J. Nielsen, M. D’Avezac, J. Hetherington and M. Stamatakis, Parallel Kinetic Monte Carlo Simulation Framework Incorporating Accurate Models of Adsorbate Lateral Interactions, J. Chem. Phys., 2013, 139(22), 224706.
55. S. Piccinin and M. Stamatakis, CO Oxidation on Pd(111): A First-Principles-Based Kinetic Monte Carlo Study, ACS Catal., 2014, 4(7), 2143–2152.
56. H. Prats, S. Posada-Pérez, J. A. Rodriguez, R. Sayós and F. Illas, Kinetic Monte Carlo Simulations Unveil Synergic Effects at Work on Bifunctional Catalysts, ACS Catal., 2019, 9(10), 9117–9126.
57. J. Nielsen, M. D’Avezac, J. Hetherington and M. Stamatakis, Parallel Kinetic Monte Carlo Simulation Framework Incorporating Accurate Models of Adsorbate Lateral Interactions, J. Chem. Phys., 2013, 139(22), 224706.
58. J. Y. Lim, J. McGregor, A. J. Sederman and J. S. Dennis, The Role of the Boudouard and Water–Gas Shift Reactions in the Methanation of CO or CO₂ over Ni/γ-Al₂O₃ Catalyst, Chem. Eng. Sci., 2016, 152, 754–766.
59. S. M. Rogers, C. R. A. Catlow, C. E. Chan-Thaw, A. Chutia, N. Jian, R. E. Palmer, M. Perdjon, A. Thetford, N. Dimitratos and A. Villa, et al., Tandem Site- and Size-Controlled Pd Nanoparticles for the Directed Hydrogenation of Furfural, ACS Catal., 2017, 7(4), 2266–2274.
60. W. Jones, P. P. Wells, E. K. Gibson, A. Chutia, I. P. Silverwood, C. R. A. Catlow and M. Bowker, Carbidisation of Pd Nanoparticles by Ethene Decomposition with Methane Production, ChemCatChem, 2019, 11(17), 4334–4339.
61. X. Y. Zhu, J. M. White, M. Wolf, E. Hasselbrink and G. Ertl, Photochemical Pathways of Water on Pd(111) at 6.4 eV, J. Phys. Chem., 1991, 95(21), 8393–8402.
62. A. Chutia, I. P. Silverwood, M. R. Farrow, D. O. Scanlon, P. P. Wells, M. Bowker, S. F. Parker and C. R. A. Catlow, Adsorption of Formate Species on Cu(h,k,l) Low Index Surfaces, Surf. Sci., 2016, 653, 45–54.
63. K. G. Papanikolaou, M. T. Darby and M. Stamatakis, Adlayer Structure and Lattice Size Effects on Catalytic Rates Predicted from KMC Simulations: NO Oxidation on Pt(111), J. Chem. Phys., 2018, 149(18), 184701.
64. A. Chatterjee and A. F. Voter, Accurate Acceleration of Kinetic Monte Carlo Simulations through the Modification of Rate Constants, J. Chem. Phys., 2010, 132(19), 194101.
65. M. Stamatakis and D. G. Vlachos, Equivalence of On-Lattice Stochastic Chemical Kinetics with the Well-Mixed Chemical Master Equation in the Limit of Fast Diffusion, Comput. Chem. Eng., 2011, 35(12), 2602–2610.
66. M. Núñez, T. Robie and D. G. Vlachos, Acceleration and Sensitivity Analysis of Lattice Kinetic Monte Carlo Simulations Using Parallel Processing and Rate Constant Rescaling, J. Chem. Phys., 2017, 147(16), 164103.
67. E. C. Dybeck, C. P. Plaisance and M. Neurock, Generalized Temporal Acceleration Scheme for Kinetic Monte Carlo Simulations of Surface Catalytic Processes by Scaling the Rates of Fast Reactions, J. Chem. Theory Comput., 2017, 13(4), 1525–1538.
68. T. Danielson, J. E. Sutton, C. Hin and A. Savara, SQERTSS: Dynamic Rank Based Throttling of Transition Probabilities in Kinetic Monte Carlo Simulations, Comput. Phys. Commun., 2017, 219, 149–163.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05476f

---