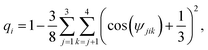Brine rejection and hydrate formation upon freezing of NaCl aqueous solutions

Abstract

Studying the freezing of saltwater on a molecular level is of fundamental importance for improving freeze desalination techniques. In this study, we investigate the freezing process of NaCl solutions using a combination of X-ray diffraction and molecular dynamics simulations (MD) for different salt-water concentrations, ranging from seawater conditions to saturation. A linear superposition model reproduces well the brine rejection due to hexagonal ice Ih formation and allows us to quantify the fraction of ice and brine. Furthermore, upon cooling at T = 233 K, we observe the formation of NaCl·2H₂O hydrates (hydrohalites), which coexist with ice Ih. MD simulations are utilized to model the formation of NaCl crystal hydrates. From the simulations, we estimate that the salinity of the newly produced ice is 0.5% mass percent (m/m) due to ion inclusions, which is within the salinity limits of fresh water. In addition, we show the effect of ions on the local ice structure using the tetrahedrality parameter and follow the crystallite formation using the ion coordination parameter and cluster analysis.

---

1. Introduction

Freeze desalination, also known as cryo-desalination, freezing–melting and freeze–thaw desalination, has been suggested as an energy effective alternative to distillation processes.¹ This is due to the fact that the latent heat of freezing (334 kJ kg⁻¹) is significantly lower than that of evaporation (2257 kJ kg⁻¹).² Despite the myths and misconceptions associated with this method³ there have been several case studies that demonstrate the feasibility of this approach from small freezing units⁴ to single-step desalination plants,⁵ as well as for treating the waste water from reverse osmosis (RO) plants.⁶ The energy consumption of freeze desalination has been estimated to be as low as 41.4 kJ kg⁻¹ (11.5 kW h per 1000 kg of ice produced)⁷ and 26.64 kJ kg⁻¹ (7.4 kW h per 1000 kg of ice produced),⁸ which approaches the specific energy consumption of an RO plant, typically in the order of 7 kJ kg⁻¹ (about 2 kW h m⁻³).^9,10 The challenges and obstacles to scale-up this technology have been recently discussed^11,12 and its combination with liquefied natural gas (LNG) technologies has been considered to be very promising.^13–17 In addition, there have also been several studies examining freeze desalination from a physicochemical perspective, investigating the depletion of ions¹⁸ and the ice impurities and sweating.¹⁹

When the freezing process of salt solutions takes place, the salt ions are expelled from the solid phase, due to the preferential formation of pure ice.²⁰ As a result, the remaining liquid phase turns into brine, which is liquid water saturated with salt.²¹ The salting-out that occurs due to freezing is one of the basic mechanisms in freeze desalination. The main challenge is the ice–brine separation, i.e. the separation of salt from crystalline ice due to the formation of polycrystalline micro-domains upon crystallization.²² Experiments indicate that frozen NaCl aqueous solutions can form different NaCl–water crystal phases.^23,24 In addition, theoretical investigations indicate that on a molecular level, brine rejection progresses through a disordered layer with fluctuating ion density followed by a neat ice layer.²⁵ Recent simulations further indicate that ions are included in the ice lattice as dopants with Cl⁻ ions having a higher probability of inclusion than Na⁺ ions.^26,27 Furthermore, in the case of homogeneous nucleation of saltwater, the nucleation rate decreases with the addition of salt.²⁸

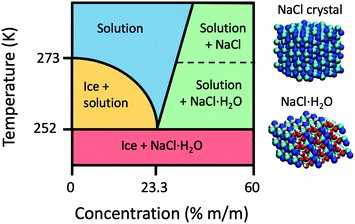
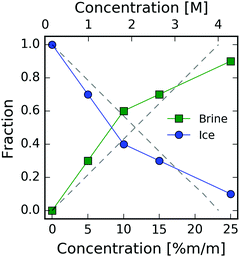
The temperature–concentration phase diagram of the NaCl aqueous solution²⁹ is depicted in Fig. 1. Salt solutions are in the liquid form at temperatures above the melting point and a low concentration of NaCl, whereas an increase in salt concentration beyond saturation initiates the formation of NaCl crystals. Depending on the temperature the resulting crystals can be either pure NaCl or NaCl·2H₂O hydrates (hydrohalites), as shown in the right side of Fig. 1. Upon decreasing the temperature, ice formation occurs, leading to brine rejection, where the brine coexists with the ice crystals. The three phases meet at the eutectic point of NaCl³⁰ located at a concentration of 3.99 M (23.3% m/m) and a temperature of 251.9 K. Upon further cooling, the salt solution crystallizes and consists of a mixture of NaCl·2H₂O hydrates and ice crystals. The phase diagram of NaCl and that of other salt solutions has been investigated previously, and it is important for modeling sea and lake water,³¹ understanding the marine cloud microphysics³² and improving cryobiological applications.³³

Fig. 1 A schematic phase diagram of the NaCl aqueous solution. Above the melting point and at low concentrations of NaCl, the solution is in the liquid phase. At higher concentrations, saturation leads to NaCl crystal or NaCl·2H₂O hydrate formation (shown on the right). Upon decreasing the temperature below the melting point, ice is formed pushing out the salt, in a process called brine rejection. When decreasing the temperature further to below 251.9 K, ice and NaCl·2H₂O crystals coexist.

In this study, we investigate both experimentally and theoretically the crystallization of NaCl aqueous solutions and the brine rejection process using X-ray diffraction (XRD) at different temperatures and NaCl concentrations. A model is devised based on a linear superposition of saltwater, ice and hydrate crystals, which allows us to reproduce the crystalline XRD pattern and quantify the amount of ice, brine and the formation of NaCl·2H₂O hydrates. The analysis is complemented by molecular dynamics (MD) simulations, which allow us to capture evolution of ion concentration as a function of time and estimate the percentage of ions trapped inside the crystal lattice. Furthermore, the resulting structures are analyzed in terms of partial radial distribution functions for the different phases. Finally, we quantify the impact of ions on the ice structure by utilizing the tetrahedrality order parameter, as well as the formation of crystallites using the ion coordination parameter.

2. Materials and methods

2.1. Experimental methods

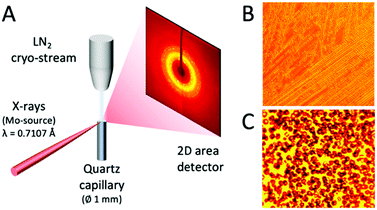
A schematic of the experimental setup is depicted in Fig. 2A. A Bruker D8 VENTURE X-ray diffractometer was used to obtain diffraction data using a Molybdenum source (λ = 0.7107 Å). The temperature was regulated by a liquid nitrogen cryo-stream at the sample position and the cooling rate was set to 5 K min⁻¹. For each temperature, the XRD pattern of the samples was measured sufficiently long as to ensure that equilibrium is reached. Microscope images were taken at different temperatures, as shown in Fig. 2B and C. These images were taken for a solution with 5% m/m NaCl concentration at temperatures of 253 K and 233 K. One can observe the formation of polycrystalline ice domains and upon further cooling the appearance of salt microcrystals. The samples were measured in a quartz capillary (diameter 1 mm, wall thickness 10 μm). The NaCl aqueous solutions were prepared at different concentrations, expressed as the ratio of salt mass to total solution mass (m/m) in percentage. The total sample volume of each solution prepared was 100 mL, whereas the volume illuminated by the beam (diameter 0.1 mm) is estimated in the order of 1 μL. The NaCl solute used was a laboratory-grade reagent purchased from Sigma Aldrich and it was used without further purification in combination with Milli-Q water. An identical protocol was applied for all NaCl solutions measured at several temperatures and concentrations.

Fig. 2 (A) Schematic of the experimental setup used. (B) and (C) show microscope images of the sample at two different temperatures at 5% m/m NaCl concentration, where the frame size is 1 mm. (B) At 253 K, the formation of polycrystalline ice is evident. (C) At 233 K, the appearance of salt microcrystals is observed.

2.2. Molecular dynamics methods

We performed molecular dynamics (MD) simulations using the GROMACS package³⁴ (ver. 5.1.4) to investigate the exclusion of ions from a growing ice crystal. We used the OPLS-AA force field³⁵ for Na⁺ and Cl⁻ ions together with the TIP4P model of water.³⁶ The simulation was run at a temperature of T = 220 K with a total of N_H2O = 13 824 TIP4P molecules and N_Cl⁻ = N_Na⁺ = 100 Na⁺ and Cl⁻ ions, respectively. Ice growth was seeded with an ice block of N_ice = 3456 TIP4P molecules corresponding to a crystal with dimensions of 5.40 nm × 4.65 nm × 4.39 nm. The concentration of the aqueous NaCl solution in contact with the ice block is thus 3% m/m, i.e. 0.53 M (2.3% m/m for the entire simulation box) initially chosen to be representative of the order of magnitude of typical seawater salt concentration. The melting temperature of the TIP4P model of water has previously been determined³⁷ to be T_m = 232 ± 5 K, and the simulation temperature thus corresponds to the temperature difference from the melting point of pure TIP4P water of about ΔT = T − T_m = −12 K at ambient pressure. We have not rescaled the concentration with respect to the saturation concentration of the model (see the Results section for an estimate), which can in fact deviate from the experimental values as indicated from previous detailed comparisons between force fields.^38,39

The simulation was run in the NPT ensemble using the Bussi thermostat⁴⁰ and the Berendsen barostat⁴¹ with semi-isotropic pressure coupling (p_x = p_y ≠ p_z) to set the initial rectangular geometry of the simulation box to about 5.40 nm × 4.65 nm × 17.59 nm. Coulombic interactions were treated using the particle-mesh Ewald method, whereas real space Coulombic and van der Waals interactions were taken smoothly to zero between 0.87 and 0.9 nm. In addition, we used dispersion corrections and the simulation ran for t_sim = 1 μs at a time step of Δt = 2 fs.

3. Results

3.1. Experimental results

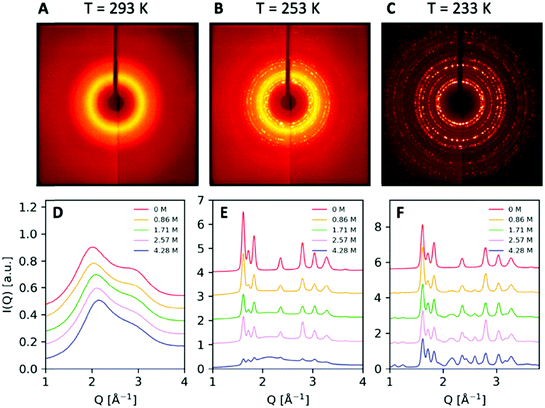
X-ray diffraction scattering patterns were obtained for a series of salt solutions, as well as for pure water and pure NaCl crystals. The XRD patterns recorded at temperatures T = 293 K, T = 253 K and T = 233 K and concentration 0.86 M (5% m/m) are shown in Fig. 3. At T = 293 K, the scattering pattern is uniform and broad, indicative of the sample being in the liquid form, i.e. saltwater. At T = 233 K, the appearance of sharp Bragg peaks indicates a polycrystalline structure arising from ice Ih and salt crystals. At the intermediate temperature T = 253 K, the scattering pattern exhibits the coexistence of the liquid and crystalline forms manifested during the brine exclusion process. These three distinct structures observed correspond to different areas of the phase diagram presented in Fig. 1.

Fig. 3 X-ray scattering patterns of NaCl solutions at 0.86 M (5% m/m) and temperatures (A) T = 293 K, (B) T = 253 K and (C) T = 233 K. (D) Angularly integrated scattering intensity I(Q) of NaCl solutions at various concentrations indicated in the legend and at temperature T = 293 K, (E) T = 253 K and (F) and T = 233 K.

The angularly integrated scattering intensity I(Q) obtained for different salt concentrations, 0.86 M, 1.71 M, 2.57 M, and 4.28 M (5% m/m, 10% m/m, 15% m/m, and 25% m/m, respectively), is shown in Fig. 3. Upon increasing concentration in the liquid at 293 K as shown in Fig. 3D, the first diffraction peak shifts and becomes less structured, in agreement with previous investigations.^42,43 This change in the scattering pattern is indicative of the influence of salt on the structure of the hydrogen bond network of water, seen also by X-ray absorption spectroscopy⁴⁴ and small-angle X-ray scattering.⁴⁵ The scattering intensity at T = 253 K shown in Fig. 3E corresponds to ice Ih coexisting with brine. In this condition, it is evident that the intensity of the peaks depends strongly on the concentration of salt and one can observe a decrease in the peak intensity with increasing salt concentration. This is due to the fact that by changing the amount of salt present in the solution, one effectively changes the relative ratio of ice and brine. For lower salt concentrations, the solution consists mainly of ice Ih and results in sharp Bragg peaks.

For T = 233 K, the sample crystallizes completely and consists largely of a mixture of ice Ih and salt crystals, as shown in Fig. 3F for different salt concentrations. Interestingly, upon increasing concentration, we observe the appearance of two new peaks at the lower momentum transfer region Q = 1.11 Å⁻¹ and Q = 1.278 Å⁻¹. The scattering pattern exhibits sharp Bragg peaks at this length scale, which are distinct from those present in the crystalline structure of ice Ih and the NaCl crystals and are a signature of the presence of NaCl·2H₂O hydrate formation.

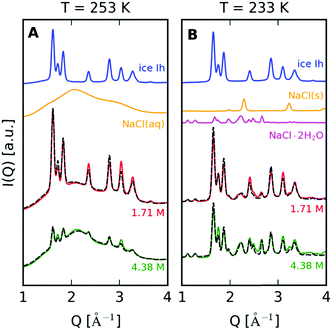
In order to quantify the underlying contributions to the XRD diffraction pattern, we construct a model comprising a linear combination of the different components depending on temperature and concentration. Fig. 4A shows such an analysis for T = 253 K, where we observe the coexistence of brine and ice Ih. The model utilizes two components shown in the upper row, where an offset has been introduced to facilitate the comparison. In this study, the two components utilized are pure ice Ih measured at 250 K (blue solid line) and NaCl aqueous solution at T = 293 K with a concentration of 4.28 M (25% m/m) to model the saturated brine solution (orange solid line). The linear superposition of these two components is indicated with a dashed line. When comparing this model with the data obtained at T = 253 K and concentrations of 1.71 M (red solid line) and 4.28 M (green solid line), we observe good agreement with the experimental results.

Fig. 4 (A) A model based on linear superposition of the different components is used to analyse the I(Q). The brine and ice coexistence at T = 253 K is modelled by combining ice Ih (blue solid line) with the NaCl aqueous solution at 4.28 M (orange solid line). The linear combination model (dashed line) is compared to the data at T = 253 K with concentration 1.71 M (10% m/m) and 4.28 M (25% m/m). (B) The same analysis for T = 233 K, where the components in this case are ice Ih (blue solid line), NaCl·2H₂O (magenta solid line) and NaCl crystals (orange solid line). The model (dashed line) is compared with the data recorded at concentrations of 1.71 M (10% m/m) and 4.28 M (25% m/m).

From the model described in Fig. 4, we estimate the fraction of ice and brine at each concentration, as shown in Fig. 5. This fraction is calculated from the relative weights used to reproduce the experimental scattering intensities. The results from the linear superposition model are compared to the ice/brine fraction determined from the phase diagram (dashed lines) using the Lever rule.^33,46 More specifically, this rule states that the volume fraction of two phases in equilibrium is proportional to the difference between the overall mass fraction of the two components at a given temperature. We observe that at concentrations 5–15% m/m, the model yields lower ice volume fractions than those obtained from the phase diagram, which can be attributed to the presence of ions in the ice lattice. Furthermore, one of the limitations of the model is that we use the NaCl aqueous solution at T = 293 K, whereas the data are taken at T = 253 K, which can introduce a shift in the first diffraction peak. An additional restriction of this approach is that this model does not include any interference (cross-terms) between the ice Ih and the brine, as the XRD pattern is the linear superposition of contributions arising from the two components.

Fig. 5 The volume fraction of ice (blue circles) and brine (green squares) at T = 253 K, as a function of concentration indicated in both M (top axis) and mass percent m/m (lower axis). The dashed lines are the estimates from the phase diagram.

A similar approach is used for the data at T = 233 K. The model consists of NaCl crystals (Fig. 4B – orange solid line), NaCl·2H₂O (Fig. 4B – magenta solid line) and ice Ih recorded at T = 233 K (Fig. 4B – blue solid line). The dihydrate diffraction pattern is modeled as described in the ESI.† In this case, the model (dashed line) again exhibits quantitative agreement with the measured XRD pattern and indicates that the scattering intensity is mostly due to the formation of NaCl dihydrates, which is consistent with previous observations.³²

3.2. Simulation results

Snapshots of the MD at different timescales of the trajectory at T = 220 K are shown in Fig. 6. The Na⁺ ions are denoted by dark blue spheres and Cl⁻ ions by turquoise spheres. Initially, the simulation was seeded with a block of pure ice Ih with the basal plane exposed to the NaCl liquid solution (t = 0). Upon crystallization the majority of the ions is expelled into the liquid form. However, there is a small fraction of ions trapped in the ice lattice, consistent with previous MD simulations,²⁶ where it was seen that more Cl⁻ is incorporated in the lattice than Na⁺.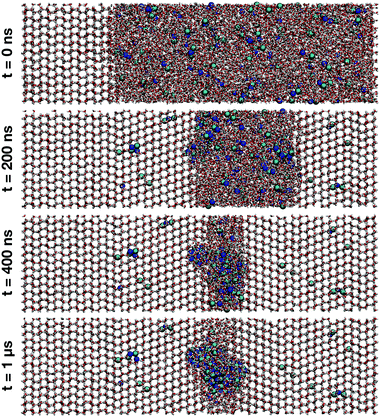

Fig. 6 Snapshots obtained from MD simulations at T = 220 K showing ice crystal growth at simulation times t = 0, 200 ns, 400 ns and 1 μs. A small fraction of ions get trapped within the ice structure while the majority of ions are expelled into the solution phase of increasing salt concentration. Na⁺ ions are represented by dark blue, and Cl⁻ ions by turquoise spheres. The snapshots were rendered with VMD.⁴⁷

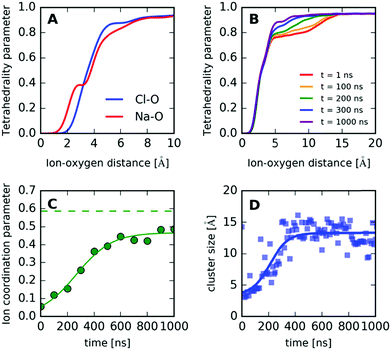
The concentrations of ions in ice and in brine are shown as a function of time in Fig. 7 (see also the ESI†). The increase in concentration coincides with the potential energy decrease due to freezing, shown in gray (right-hand side y-axis). The potential energy of the system (Fig. 7) decreases rapidly upon ice growth and the decrease at about 200 ns, when we observe the formation of small salt crystallites in the remaining brine liquid (see cluster analysis below). The minor increase in ion concentration in ice to about 0.5% m/m is due to ion inclusion in the ice lattice. This value is significantly reduced from the initial concentration of 3% m/m, and near the standard salinity limit of fresh water, typically 0.1% m/m for drinking water and 0.5% m/m for agricultural use.

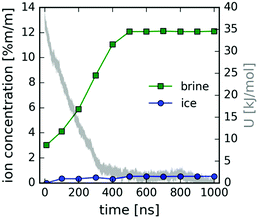Fig. 7 Ion concentration (left y-axis) in ice (blue circles) and brine (green squares) and the potential energy in the MD simulation (gray line – right y-axis) as a function of time.

We note here that the simulation using OPLS-AA parameters for the ions together with the TIP4P water potential underestimates the experimental solubility and saturation concentration, which is 6.14 mol kg⁻¹ (0.599 M) at T = 273 K.⁴⁸ From the concentration at the time of the onset of heterogeneous crystallite formation around 200 ns, we estimate the saturation concentration for the OPLS-AA/TIP4P combination to be roughly 1 M at T = 220 K. This is consistent with similar force field combinations, e.g. AMBER-99 or OPLS-AA ion parameters with TIP3P water, which also yield solubility values between 1 and 2 mol kg^−1 39 (corresponding to roughly 1–2 M). Furthermore, this issue has been potentially improved in relatively recent force field parameters for NaCl ions,⁴⁹ as salt crystal formation was not observed in the brine phase under similar conditions.²⁶

In order to investigate the formation and local structure of the NaCl dihydrate crystals encapsulated in ice Ih, we calculate the radial distribution function g(r) shown in Fig. 8. Fig. 8A shows the total g(r) as a function of simulation time, where the changes observed are mainly due to freezing. Fig. 8B shows the O–O contribution comparing the various components, such as the crystalline (s) and the aqueous environment (aq). A distinction is made between the self-correlations of the different atoms, such as the O–O, Cl–Cl and Na–Na, with the corresponding cross-correlations, such as Na–Cl, O–Cl and O–Na. The O–O radial distribution function g(r) of the crystal (solid line) resembles that of ice Ih, with the addition of disorder due to the water–brine interaction. The corresponding brine at the beginning of the trajectory in the liquid phase is depicted as the dashed line. Both the Cl–Cl and Na–Na correlations exhibit a peak at r = 4 Å, which is consistent with the atomic spacing in NaCl crystals where the FCC lattice spacing is d = 5.64 Å, and the shortest Cl–Cl and Na–Na distance is 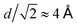. The Na–Cl correlation contains a dominating peak at r = 2.8 Å and in addition two peaks at r = 4.9 Å and 6.35 Å, which correspond to Na–Cl spacing in the salt crystal lattice. This is an indication of near ion–ion ordering that resembles the crystal locally.

Fig. 8 The radial distribution function g(r) obtained from the MD simulations. (A) The time evolution of the total g(r), (B) the O–O of the crystalline (s) and aqueous (aq) components and (C) Cl–Cl, Na–Na as well as the cross-correlations between Na–Cl and (D) O–Cl, O–Na for both crystalline (s) and aqueous (aq) components.

The ion–oxygen cross-correlations in the radial distribution function g(r) (Fig. 8D) contains information about the O–Cl and O–Na components in the crystal (s), which partially resembles the radial distribution of ions in liquid NaCl aqueous solutions (aq).^50,51 These contributions arise from an ion (Na⁺ or Cl⁻) surrounded by water molecules, occurring within the hydrates and at the boundaries of the NaCl crystallite with water. The first peak reveals the first neighboring water molecules around the ion, which in the case of Na–O correlation corresponds to distances of r = 2.45 Å and for Cl–O of r = 3.18 Å. This difference is due to the influence of the positive charge of the Na⁺ which attracts the oxygen, whereas in the case of Cl⁻ negative charge attracts the hydrogen and results in larger O–Cl distances. Interestingly, the O–Cl correlation features an additional peak at around 3.75 Å, which is attributed to the hydrate formation (see the ESI† for the g(r) of the dihydrate).

We quantify the effect of ions on the local ice structure by calculating the tetrahedrality parameter,⁵² which enables us to quantify the orientational order of the water molecules in the simulation as a function of distance to the closest ion. The tetrahedrality parameter is defined as follows:

where ψ_jik is the angle formed by the lines joining the oxygen atom of a given molecule and those of its nearest neighbors j and k (≤4). This analysis, shown in Fig. 9A, reveals a high average tetrahedrality parameter of about 〈q_i〉 ≈ 0.94 for molecules that are part of the ice, whereas we see a difference between the Cl–O and Na–O, consistent with the corresponding radial cross-correlations in the radial distribution function. Furthermore, from the time evolution of the tetrahedral parameter (Fig. 9B), we note that the major changes occur in the range 0.7 < 〈q_i〉 < 0.9 for O–ion distances in the interval of 4–15 Å and at early simulation timescales. In this intermediate distance range interval, 〈q_i〉 increases over time indicating that the molecules less affected by ions become part of the ice phase.

Fig. 9 (A) Tetrahedrality parameter as a function of distance between the water's oxygen and the closest ion, for Cl–O and Na–O. (B) The tetrahedrality parameter for different simulation times, indicated in the legend. (C) Ion coordination parameter as a function of time (green circles) and the same parameter calculated for a NaCl·2H₂O crystal (dashed line). (D) The crystallite size quantified by cluster analysis as a function of simulation time.

Furthermore, in order to quantify the formation of the crystallites and understand the underlying mechanism, we define a simple “ion coordination parameter” 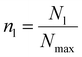as the number of neighbor ions N_l within a cutoff distance of d_c = 3.4 Å and divide by the maximum number N_max of counterions within this distance for the ideal ionic crystal of cubic symmetry, i.e. N_max = 6. The aforementioned parameter does not directly probe the local symmetry; yet due to strong Coulombic interactions, this simple approach can be justified. The so-defined parameter takes average values close to unity for a NaCl crystal and average values close to zero for dissociated ions in solution where only temporary ion pairing is expected to make this number slightly larger than zero. Intermediate values of 〈n_l〉 indicate that there are ions in contact with their counterions, yet there is no complete coordination as compared to coordination in the cubic symmetry. For a NaCl·2H₂O crystal, the coordination parameter is n_l = 0.586, whereas in the case of the simulation we observe that n_l levels off at n_l = 0.467 after 400 ns approaching the hydrate value. Any deviation here is attributed to ions in the surface of the crystal, which will have smaller ion coordination numbers.

In addition, we calculate the crystal size by performing cluster analysis^53,54 (see the ESI†). The cluster size as a function of time is shown in Fig. 9D, which reaches a constant value on a similar time scale as the ion coordination parameter, indicating the formation of ion clusters with an average size of roughly 13 Å.

4. Conclusion

In summary, we have investigated the crystallization of NaCl aqueous solutions using XRD for different temperatures (293 K, 253 K, and 233 K) and NaCl concentrations (0.86 M, 1.71 M, 2.57 M, and 4.28 M). The brine rejection mechanism was discussed and we observe that a model consisting of a linear combination of the X-ray diffraction intensity of ice Ih crystals and NaCl aqueous solution reproduces well the experimental data and allows us to quantify the fraction of recovered ice and brine under each condition, which is indicative of the freeze desalination efficiency. In addition, the regime where ice Ih coexists with NaCl crystals is analyzed. In this case, a model consisting of two components, ice Ih and NaCl dihydrate crystals, reproduces well the observed diffraction pattern and helps us identify the signature of hydrate formation in the scattering intensity.

In order to model the salt-exclusion and formation of NaCl dihydrates, we performed MD simulations of the NaCl aqueous solution crystallization process. The simulation results were analyzed in terms of radial distribution functions for oxygen–oxygen, oxygen–ion and ion–ion correlations. We observe signatures of hydrate formation in the O–Cl correlation. Furthermore, we quantify the impact of ions on the ice structure by calculating the tetrahedrality parameter as a function of ion–oxygen distance. The structure of the resulting crystallite is analyzed using the ion coordination parameter and cluster analysis, which indicates that hydrate formation takes place within 400 ns. From the simulations, we can estimate the concentration of ions trapped inside the ice, which is approximately 0.5% m/m. This value is reduced significantly from the initial NaCl concentration 3% m/m and is on the fresh water salinity limit, which is typically on the order of 0.1% m/m for drinking water and 0.5% m/m for agriculture.

The present investigation provides a valuable insight into the limitations of freeze desalination by utilizing an X-ray-based detection method of the ions trapped inside ice in the form of crystal impurities. This study sets the stage for future investigations using ultrafast X-ray scattering at X-ray free-electron lasers that would allow to follow the brine rejection in situ with nanosecond resolution. It will also be interesting to resolve spatially the formation of hydrates by utilizing the new diffraction-limited synchrotron sources, where a nano-focus X-ray beam would allow one to quantify experimentally the size of the salt crystallites.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge financial support from the Swedish Research Council (VR starting grant under project no. 2019-05542) and from the European Research Council (ERC advanced grant WATER under project no. 667205). This research is part of the MaxWater initiative of the Max-Planck Society. We would like to thank L. G. M. Pettersson, T. J. Lane and K. Amann-Winkel for their useful comments on the manuscript. I.T. was additionally supported by the Erasmus+ program of the European Union. The simulations were performed using resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre (NSC) and the High-Performance Computing Centre North (HPC2N).

References

1. J. Fournier, J. L. Grange and S. Vergara, Water desalination by natural freezing, Desalination, 1974, 15, 4.
2. P. V. Hobbs, Ice Physics, Oxford University Press, Oxford, New York, 2010.
3. H. F. Wiegandt and R. L. Von Berg, Myths about freeze desalting, Desalination, 1980, 33, 287–297.
4. A. F. Abdul-Fattah, Use of low grade in driving small freezing units for desalination, Desalination, 1987, 61, 169–183.
5. L. Erlbeck, D. Wössner, T. Kunz, M. Rädle and F.-J. Methner, Investigation of freeze crystallization and ice pressing in a semi-batch process for the development of a novel single-step desalination plant, Desalination, 2018, 448, 76–86.
6. D. G. Randall, J. Nathoo and A. E. Lewis, A case study for treating a reverse osmosis brine using Eutectic Freeze Crystallization—Approaching a zero waste process, Desalination, 2011, 266, 256–262.
7. A. Zambrano, Y. Ruiz, E. Hernández, M. Raventós and F. L. Moreno, Freeze desalination by the integration of falling film and block freeze-concentration techniques, Desalination, 2018, 436, 56–62.
8. T. Mtombeni, J. P. Maree, C. M. Zvinowanda, J. K. O. Asante, F. S. Oosthuizen and W. J. Louw, Evaluation of the performance of a new freeze desalination technology, Int. J. Environ. Sci. Technol., 2013, 10, 545–550.
9. M. Sarai Atab, A. J. Smallbone and A. P. Roskilly, An operational and economic study of a reverse osmosis desalination system for potable water and land irrigation, Desalination, 2016, 397, 174–184.
10. A. J. Karabelas, C. P. Koutsou, M. Kostoglou and D. C. Sioutopoulos, Analysis of specific energy consumption in reverse osmosis desalination processes, Desalination, 2018, 431, 15–21.
11. P. M. Williams, M. Ahmad, B. S. Connolly and D. L. Oatley-Radcliffe, Technology for freeze concentration in the desalination industry, Desalination, 2015, 356, 314–327.
12. B. Kalista, H. Shin, J. Cho and A. Jang, Current development and future prospect review of freeze desalination, Desalination, 2018, 447, 167–181.
13. P. J. Schroeder, Freezing processes—The standard of the future—An update, Desalination, 1980, 33, 299–310.
14. W. Lin, M. Huang and A. Gu, A seawater freeze desalination prototype system utilizing LNG cold energy, Int. J. Hydrogen Energy, 2017, 42, 18691–18698.
15. C. Xie, L. Zhang, Y. Liu, Q. Lv, G. Ruan and S. S. Hosseini, A direct contact type ice generator for seawater freezing desalination using LNG cold energy, Desalination, 2018, 435, 293–300.
16. Z. R. Chong, T. He, P. Babu, J. Zheng and P. Linga, Economic evaluation of energy efficient hydrate based desalination utilizing cold energy from liquefied natural gas (LNG), Desalination, 2019, 463, 69–80.
17. J. Chang, J. Zuo, K.-J. Lu and T.-S. Chung, Membrane development and energy analysis of freeze desalination-vacuum membrane distillation hybrid systems powered by LNG regasification and solar energy, Desalination, 2019, 449, 16–25.
18. L. Erlbeck, M. Rädle, R. Nessel, F. Illner, W. Müller, K. Rudolph, T. Kunz and F.-J. Methner, Investigation of the depletion of ions through freeze desalination, Desalination, 2017, 407, 93–102.
19. Y. Mandri, A. Rich, D. Mangin, S. Abderafi, C. Bebon, N. Semlali, J.-P. Klein, T. Bounahmidi and A. Bouhaouss, Parametric study of the sweating step in the seawater desalination process by indirect freezing, Desalination, 2011, 269, 142–147.
20. G. L. Stepakoff, D. Siegelman, R. Johnson and W. Gibson, Development of a eutectic freezing process for brine disposal, Desalination, 1974, 15, 25–38.
21. P. K. Rohatgi and C. M. Adams, Ice–Brine Dendritic Aggregate formed on Freezing of Aqueous Solutions, J. Glaciol., 1967, 6, 663–679.
22. D. N. Thomas and G. S. Dieckmann, Sea Ice 2nd Edition, Blackwell, Oxford U.K., 2010.
23. A. Křepelová, T. Huthwelker, H. Bluhm and M. Ammann, Surface Chemical Properties of Eutectic and Frozen NaCl Solutions Probed by XPS and NEXAFS, ChemPhysChem, 2010, 11, 3859–3866.
24. T. Bartels-Rausch, H.-W. Jacobi, T. F. Kahan, J. L. Thomas, E. S. Thomson, J. P. D. Abbatt, M. Ammann, J. R. Blackford, H. Bluhm, C. Boxe, F. Domine, M. M. Frey, I. Gladich, M. I. Guzmán, D. Heger, T. Huthwelker, P. Klán, W. F. Kuhs, M. H. Kuo, S. Maus, S. G. Moussa, V. F. McNeill, J. T. Newberg, J. B. C. Pettersson, M. Roeselová and J. R. Sodeau, A review of air–ice chemical and physical interactions (AICI): liquids, quasi-liquids, and solids in snow, Atmos. Chem. Phys., 2014, 14, 1587–1633.
25. L. Vrbka and P. Jungwirth, Brine rejection from freezing salt solutions: a molecular dynamics study, Phys. Rev. Lett., 2005, 95, 148501.
26. M. M. Conde, M. Rovere and P. Gallo, Spontaneous NaCl-doped ice at seawater conditions: focus on the mechanisms of ion inclusion, Phys. Chem. Chem. Phys., 2017, 19, 9566–9574.
27. J. S. Kim and A. Yethiraj, The effect of salt on the melting of ice: a molecular dynamics simulation study, J. Chem. Phys., 2008, 129, 124504.
28. G. D. Soria, J. R. Espinosa, J. Ramirez, C. Valeriani, C. Vega and E. Sanz, A simulation study of homogeneous ice nucleation in supercooled salty water, J. Chem. Phys., 2018, 148, 222811.
29. O. Braitsch, in Salt Deposits Their Origin and Composition, ed. O. Braitsch, Springer, Berlin, Heidelberg, 1971, pp. 27–83.
30. R. E. Dickerson, Molecular Thermodynamics, W. A. Benjamin, Pasadena, 1969.
31. D. Li, D. Zeng, X. Yin, H. Han, L. Guo and Y. Yao, Phase diagrams and thermochemical modeling of salt lake brine systems. II. NaCl + H₂O, KCl + H₂O, MgCl₂ + H₂O and CaCl₂ + H₂O systems, Calphad, 2016, 53, 78–89.
32. A. Peckhaus, A. Kiselev, R. Wagner, D. Duft and T. Leisner, Temperature-dependent formation of NaCl dihydrate in levitated NaCl and sea salt aerosol particles, J. Chem. Phys., 2016, 145, 244503.
33. B. Han, J. H. Choi, J. A. Dantzig and J. C. Bischof, A quantitative analysis on latent heat of an aqueous binary mixture, Cryobiology, 2006, 52, 146–151.
34. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25.
35. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236.
36. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935.
37. C. Vega, E. Sanz and J. L. F. Abascal, The melting temperature of the most common models of water, J. Chem. Phys., 2005, 122, 114507.
38. A. L. Benavides, J. L. Aragones and C. Vega, Consensus on the solubility of NaCl in water from computer simulations using the chemical potential route, J. Chem. Phys., 2016, 144, 124504.
39. A. K. Giri and E. Spohr, Cluster formation of NaCl in bulk solutions: arithmetic vs. geometric combination rules, J. Mol. Liq., 2017, 228, 63–70.
40. G. Bussi, T. Zykova-Timan and M. Parrinello, Isothermal-isobaric molecular dynamics using stochastic velocity rescaling, J. Chem. Phys., 2009, 130, 074101.
41. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690.
42. S. Bouazizi, S. Nasr, N. Jaîdane and M.-C. Bellissent-Funel, Local Order in Aqueous NaCl Solutions and Pure Water: X-ray Scattering and Molecular Dynamics Simulations Study, J. Phys. Chem. B, 2006, 110, 23515–23523.
43. R. Mancinelli, A. Botti, F. Bruni, M. A. Ricci and A. K. Soper, Perturbation of water structure due to monovalent ions in solution, Phys. Chem. Chem. Phys., 2007, 9, 2959–2967.
44. I. Waluyo, D. Nordlund, U. Bergmann, D. Schlesinger, L. G. M. Pettersson and A. Nilsson, A different view of structure-making and structure-breaking in alkali halide aqueous solutions through x-ray absorption spectroscopy, J. Chem. Phys., 2014, 140, 244506.
45. C. Chen, C. Huang, I. Waluyo, T. Weiss, L. G. M. Pettersson and A. Nilsson, Long-range ion–water and ion–ion interactions in aqueous solutions, Phys. Chem. Chem. Phys., 2015, 17, 8427–8430.
46. S. A. Morse, Binary Solutions and the Level Rule Revisited, J. Geol., 1997, 105, 471–482.
47. W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38.
48. B. S. Krumgalz, Temperature Dependence of Mineral Solubility in Water. Part I. Alkaline and Alkaline Earth Chlorides, J. Phys. Chem. Ref. Data, 2017, 46, 043101.
49. A. L. Benavides, M. A. Portillo, V. C. Chamorro, J. R. Espinosa, J. L. F. Abascal and C. Vega, A potential model for sodium chloride solutions based on the TIP4P/2005 water model, J. Chem. Phys., 2017, 147, 104501.
50. D. Corradini, M. Rovere and P. Gallo, Structural Properties of High and Low Density Water in a Supercooled Aqueous Solution of Salt, J. Phys. Chem. B, 2011, 115, 1461–1468.
51. Y. Ding, A. A. Hassanali and M. Parrinello, Anomalous water diffusion in salt solutions, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3310–3315.
52. J. R. Errington and P. G. Debenedetti, Relationship between structural order and the anomalies of liquid water, Nature, 2001, 409, 318–321.
53. F. H. Stillinger, Rigorous Basis of the Frenkel-Band Theory of Association Equilibrium, J. Chem. Phys., 1963, 38, 1486–1494.
54. L. A. Patel and J. T. Kindt, Simulations of NaCl Aggregation from Solution: Solvent Determines Topography of Free Energy Landscape, J. Comput. Chem., 2019, 40, 135–147.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05436g

‡ These authors contributed equally to this work.

---