Synchronously voltage-manipulable spin reversing and selecting assisted by exchange coupling in a monomeric dimer with magnetic interface
Abstract
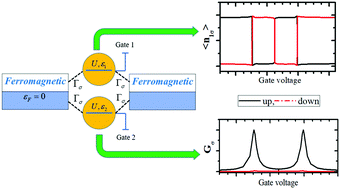
The use of the molecular spin state as a quantum of next-generation information technology is receiving impressive research attention, within which the fundamental issues include manipulating the phase transition between the spin-up and -down states and generating spin polarized current. The spinterface between ferromagnetic electrodes and a molecular bridge represents one of the most intriguing elements in this context. Herein, by means of the celebrated numerical renormalization group technique, we present an original way to realize spin reversal in a monomeric dimer. Our scheme is based on the exchange interactions between electronic spins on one monomer and those on the other one or on the electrodes, which could be easily controlled through purely electronic technology. Through a careful engineering of the interfacial parameters, one of the monomers is devoted to the spin reversing, whereas the other one contributes to the spin selecting. The charge numbers of spin-up and -down electrons swap their respective occupancies at some particular points, indicating charge sensing between different spins. The competition between the spinterface and the molecular energy level results in charge oscillating in a single spin channel, which is unfavorable to the spin selecting. The observation may provide a prospective example for a multifunctional magnetoelectronics molecular device, which works without any external magnetic field.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...