Open Access Article
Open Access ArticleCalculations on the unimolecular decomposition of the nerve agent VX†
Xiao
Shan
 *a,
Mark R.
Sambrook
*a,
Mark R.
Sambrook
 b and
David C.
Clary
b and
David C.
Clary
 *a
*a
aPhysical and Theoretical Chemistry Laboratory, Department of Chemistry, University of Oxford, South Parks Road, Oxford, OX1 3QZ, UK. E-mail: xiao.shan@chem.ox.ac.uk; david.clary@chem.ox.ac.uk
bCBR Division, Defence Science and Technology Laboratory (Dstl), Porton Down, Salisbury, SP4 0JQ, UK
First published on 17th December 2019
Abstract
It is very difficult to perform experiments on the physical parameters for the thermal decomposition of chemical nerve agents such as VX and computations, therefore, are useful. The reaction dynamics of the gas-phase pericyclic hydrogen transfer of the nerve agent VX is studied computationally. The geometries of the stationary structures are calculated at M06-2X/jul-cc-pVTZ level of theory. Single point energy calculations are carried out at the CBS/QB3 level to correct the energy barriers. Canonical reaction rate constants are calculated as a function of temperature. The one-dimensional semiclassical transition state theory is used to analyse the quantum tunneling effects. A reduced-dimensional hindered rotor model is proposed, tested, and applied to calculate the vibrational partition functions. It is found that the ester (O-side) and thioester (S-side) side chains of VX undergo pericyclic H-transfer reactions that result in decomposition of the molecule. The S-side reaction is favoured both kinetically and thermodynamically and dominates the pyrolysis over the temperature range from 600 K to 1000 K. It is predicted that VX completely decomposes in 2 s at temperatures above 750 K.
1 Introduction
The V-series of organophosphorus (OP) nerve agents are highly toxic to organisms including humans due to inhibition of the acetycholinesterase enzyme.1–3 Various V-series agents were developed into chemical warfare agents (CWAs).1,3 It is, therefore, important to study and mitigate against such synthetic toxic molecules. Numerous researches have been devoted to investigate different methods to degrade V-series agents including, among others, surface sorption,4–7 hydrolysis,8–12 perhydrolysis,13 novel catalysts,14–18 binding to metal ions,19 and incineration. In recent studies, the thermally activated pericyclic H-transfer reaction in gas-phase via a 6-membered-ring transition state (TS) has been investigated for the G-series OP nerve agent sarin (GB),20,21 and for VX simulants.22 Note that this mechanism is only possible for gas-phase reactions; in the solution state this is not a feasible degradation pathway.1,3 In combination with earlier studies,23 the results for unimolecular decomposition showed that the 6-membered-ring TS is energetically favoured with a second most stable TS somewhere over 100 kJ mol−1 higher on the potential energy surface (PES). The structure of VX allows such calculations to be carried out on both the ester and thioester side chains. In our previous work,22 we studied the reaction mechanism of VX using a series of simulant molecules. We found that in the simulant molecule where both ester and thioester side chains are present, the thioester side reaction has a lower forward barrier and smaller endothermicity. The thioester side reaction is therefore favoured both kinetically and thermodynamically. In the current paper, we extend this work to study the reaction of VX itself. To the best of our knowledge, this study is the first attempt on calculating reaction rate constants, especially quantum tunneling contribution to rate constants for gas-phase VX thermal decompositions via the pericyclic H transfer route. The major difficulties in performing such calculation is the computational costs due to the size of the molecule, which for VX is 42 atoms. The challenge comes in two folds. On one hand the ab initio quantum chemistry calculations performed for a single geometry point on the PES for these relatively large systems are already expensive, on the other hand, in order to construct a reasonable representation of the PES to analyse the quantum tunneling effect adds another dimension into the cost.In order to overcome these challenges, we first employ density functional theory (DFT) for the quantum chemistry calculations. In our previous studies,21,22 we tested the performance of various combinations of DFT functionals and basis sets on calculating the quantum tunneling contribution to reaction rate constants of H-transfer reactions of VX simulants. In the current study, we use the functional with the best performance, M06-2X,24 and the basis set jul-cc-pVTZ25 in the calculation. The quantum tunneling contribution to the reaction rate constants is calculated using the semiclassical transition state theory (SCTST) developed by Miller and co-workers.26–31 The SCTST calculates the overall quantum tunneling probability by summing over a series of TS vibrational configuration-dependent tunneling probabilities. The shape of each individual configuration-dependent potential energy barrier is determined by the vibrational frequencies and anharmonic constants of the TS.30,32–35 Obtaining the anharmonic constants30 and number/density of states32 of the TS are the two main computational costs in a full-dimensional (FD) SCTST calculation. These costs increase dramatically as the number of atoms in a system increases.36–38 In addition, because of the size of the molecule, a great number of vibrations do not directly contribute to the reaction, and the coupling anharmonic constants between these modes and the reaction mode are very small. In practice, the numerical computations of these anharmonic constants can introduce unnecessary error in a FD calculation. In the current study, we employ the one-dimensional (1D) SCTST,21,36,39–41 which is a much less expensive and yet sufficiently accurate approximation to the FD SCTST. We have used the 1D SCTST in a combined experimental and theoretical study of a pericyclic H-transfer reaction of sarin,21 similar to the title reactions, and found excellent agreement between the two.
An additional computational challenge one faces when working with relatively large molecules is the treatment of the partition functions of the internal rotational degrees of freedom (DoFs).42–46 These DoFs are often referred to as the hindered rotors (HRs), because they behave similarly to a normal vibrational mode at low temperature, while at high temperature they should be treated as a rotation. It has been shown that one could solve the Schrödinger equation for one43,47–49 to two50,51 dimensional HRs provided that the relative PES is known. Recently, this approach has been extended by Truhlar and co-workers to deal with the multi-dimensional (MD) HRs cases,52 where the HR modes are treated as pair-wise coupled. All of the above methods are applicable at a great computational cost especially for systems as large as VX. Alternatively, a relatively more cost efficient method proposed by Truhlar and co-workers,43–46,53 the multi-structure all-structure (MS-T) method, can be easily adapted into the SCTST rate constant calculation.21,22
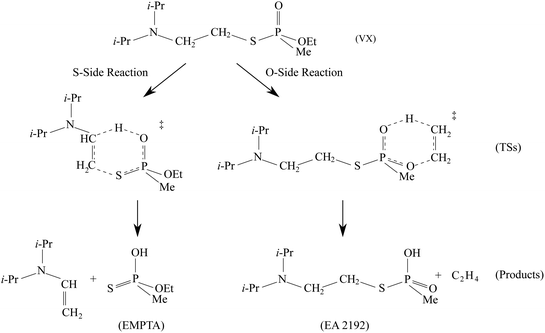
The predicted full two-step mechanism of VX thermal decomposition through pericyclic H transfer reaction has been shown in ref. 22. The current study is focused on the first step reactions; a schematic illustration of the mechanism is shown in Fig. 1. The S- and O-side reactions yield O-ethyl methylphosphonothioic acid (EMPTA) and EA 2192, respectively. EA 2192 is also a possible product of VX hydrolysis,8–12 however, EMPTA can only be formed via pericyclic H transfer of VX. Although the decomposition of VX via pericyclic H transfer is somewhat similar to the hydrolysis, especially for the products, it should be noted that the two types of reactions are fundamentally different in the position of the bond cleavage. In hydrolysis, the PO–X (X = O or S) bond is broken forming an alcohol or thioalcohol leaving group, while in pericyclic H transfer, the POX–CH2 (X = O or S) bond is broken forming an alkene. EA 2192 formed in the hydrolysis of VX can have either S or R chirality, while the pericyclic H transfer can only product one specific enantiomer. R- and S-VX can yield only S- and R-EA 2192, respectively.
The remainder of the paper is organised in the following way. In Section 2, we briefly discuss the theoretical derivation of 1D SCTST and the implementation of the reduced-dimensional hindered rotor method. The details of computational and experimental methods employed in the current study are given in Section 3. Results and discussions of our measurements and calculations of the IR spectra, as well as calculated stationary point geometries, reaction energetics, reaction rate constants, and the survival percentage of VX are given in Section 4. Our key findings in this study are summarised in Section 5.
2 Theory background
2.1 One-dimensional semiclassical transition state theory
In this study, we use one-dimensional semiclassical transition state theory (1D SCTST)36,54 to calculate the canonical rate constants, k(T), at high pressure limit. We showed in a previous study21 that our method is also applicable to the calculation of the microcanonical rate constant, k(E). Recent developments of SCTST, including the 1D approximation can be found in ref. 55. Here we only give a short outline of the method. In 1D SCTST, k(T) is given by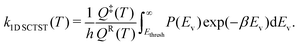 | (1) |
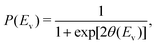 | (2) |
The vibrational perturbation theory (VPTn) to the second order is commonly used for this expression.27–29,32,35,54,56,57 Recently, Stanton et al.58 showed that it is also possible to apply the VPT4 in a 1D analysis. The VPT4 requires up to 6th order derivatives of the potential energy surface with respect to the vibrational modes, however it does not improve the VPT2 results by a great deal58 especially in a high temperature situation such as the pericyclic H transfer. In addition, for systems as large as VX, the computational cost must be taken into consideration. We therefore use the expression of θ(Ev) based on the VPT2 calculation, it is given by
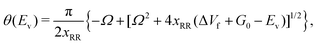 | (3) |
| Ω = Im(ħωR), |
Here, the subscript “R” denotes the reaction vibrational mode, and f3 and f4 are the third and fourth order derivatives of the potential energy with respect to this vibrational mode. To obtain the values of f3 and f4, one can perform numerical differentiation using either the Hessian matrix elements at 2 displaced geometries or single point energies at 4 displaced geometries. In previous studies,21,22,36 the Richardson extrapolation59–61 was used to improve the accuracy of the numerical derivatives. However, as our recent study of the reactions with simulant molecules22 showed that these reactions are strongly asymmetric, it is possible that the Richardson extrapolation fails to produce the correct derivatives. In the current study, we therefore use both the second order Richardson extrapolation and fitting a fourth order function to the energies at displacement geometries to calculate the higher order derivatives.
It is known that this VPT2 expression of θ(Ev) is inaccurate for reactant or product asymptotes known as the deep tunneling (DT) region.62 In the DT correction proposed by Wagner et al.62eqn (3) is replaced by a piece-wise continuous asymmetric Eckart barrier model. It improves the results at temperatures typically lower than 500 K.21,36,39–41,54 The additional computational cost of constructing the DT barrier is only the reverse barrier height.
2.2 Approximated hindered rotor treatment
In large molecular systems, hindered rotor (HR) vibrations become a prominent feature. It has been shown that it is incorrect to treat them using harmonic oscillator models.42–45 Although it is possible to calculate the exact 1D21,40,43 or 2D50,51 HR partition functions, the treatment to multi-dimensional (MD) HR remains a challenge. For large molecules, the challenge comes from both the computational cost of constructing the MD HR potential energy surface as well as solving the MD HR Schrödinger equation. The multi-structural all structure (MS-T) method developed by Truhlar and co-workers45 provides a relatively inexpensive yet sufficiently accurate solution to the problem. Using the MS-T method, the 1D SCTST rate constant can then be written as | (4) |
For a system that consists a total of J torsional conformers, the conformational rovibrational partition function, Qcon-rovib(T), is given by
 | (5) |
To carry out the MS-T treatment, the information of the Hessian matrix at each of the torsional conformers of a molecule is required. The number of calculations scales up very quickly as the number of HR modes in a molecule increases. For molecules of the size of VX, there are a total of 12 HR modes in VX. Four of them are CH3 group rotation and can be approximated as having a C3 symmetry, we then have 8 hindered rotors each have 2–3 conformer geometries to analyse, which translates to between 128 (= 28) and 6561 (= 38) geometries. In our previous study of decomposition of GB,21 we employed a single structure approximation to the MS-T treatment. In the following test study, this method is referred to as the single-structure (SS)-HR. In the SS-HR, instead of calculating all of the torsional conformers, only the lowest energy conformer is considered in the treatment. In practice, it is impossible to find the lowest energy conformer without computing the energies for all conformers. However, the multi-structure reference-structure (MS-RS) method45 can usually find a low energy conformer close to the lowest energy one.
In the current study, adapting the reduced dimensionality framework,63–65 we propose a method that is somewhat in between SS-HR and MS-T. Before we going into details of this method, it is helpful to discuss the locality of a vibrational mode.41,66 For a particular vibrational mode, Q, it is given by
 | (6) |
 | (7) |
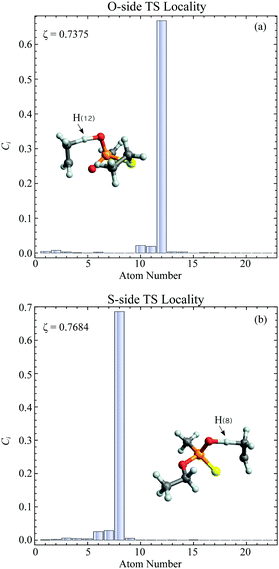
In general, higher ζ value suggest greater single atom movement in the vibrational mode. Taking a simulant molecule, O,S-diethyl methylphosphonothiolate, as an example, there are two possible pericyclic H-transfer sites from the CH3 group on either the ester or the thioester side chain. We show the calculation results for the atomic locality of the reaction mode for the two TSs in Fig. 2. It can be seen that in either cases, the movement of the atoms in this vibrational mode is dominated by the H atom transferring from the attached C atom to the O atom.
Based on this observation, we propose a computationally less expensive HR treatment, the reduced-dimensional HR (RD-HR) method. In this method, only the HR modes in the reactant that change the relative position of the transferring H atom are treated explicitly as in the MS-T method. These set of HR modes are referred to as the active HR modes. At each of the conformers resulting from an active HR mode rotation, the rest of HR modes, (the spectator HR modes) are treated the same as in a simple SS-HR method. In Fig. 3, we illustrated the RD-HR treatment to the O-side TS for the reaction of O,S-diethyl methylphosphonothiolate. The active and spectator HR modes are marked as the red and blue arrows, respectively. For this reaction, using the RD-HR method, the rotations related to the thioester group as well as the CH3 group attached to the P-atom are not active. In this way, the number of conformers for the reactant and TS of the reaction is reduced from 16 to 2 and from 6 to 1, respectively. The same can be applied to the S-side reaction yielding 6 and 1 conformers for the reactant and TS, respectively.
Recently, Wu et al.67 proposed and tested a multi-structural 2-dimensional torsion (MS-2DT) method to compute accurate partition functions at a smaller computational cost than the MS-T method on C6–C8 alkanes. Although it is possible to extend the application to VX, it is still more expensive than our method. For a 5 three-fold rotatable torsions, the MS-2DT method requires 90 initial conformers,67 while the RD-HR method based on the MS-RS method would require scanning through only 15 conformer. It should be noted that the goal of our RD-HR method is to sufficiently accurately and efficiently estimating the rate constant of reactions with presence of multiple hindered rotors affecting the mechanism, it should not be used to reproduce accurate MS-T partition functions.
We show in Fig. 4 the comparison between the RD-HR method and MS-T results for both reactions presented in Fig. 2. We also included the results calculated using the SS-HR method and purely harmonic oscillator (HO) models using the reactant and TS conformers of the lowest energy. Details of their structures and energies can be found in ref. 22. Note that in the logarithmic scale, a deviation of 1.0 is 10 times over- or underestimation of the rate constant. It can be seen that the RD-HR has a good agreement to the MS-T results (note that the MS-T results are simply the x-axes of the plots) for temperature typically lower than 1000 K, yielding a rate constant that is within ∼25% when comparing to the MS-T. On the other hand, both the SS-HR and the HO results are much worse comparing to the RD-HR ones. Therefore, in the following study of VX reactions, only the RD-HR method is used.
 | ||
| Fig. 4 Comparison of rate constants for (a) O-side and (b) S-side pericyclic H transfer reaction for O,S-diethyl methylphosphonothiolate calculated using various approximated hindered rotor models. The rate constants for the MS-T results, as well as the geometries, relative energies, vibrational frequencies and anharmonic constants of reactant and TS's can be found in ref. 22. | ||
3 Practical details
3.1 Computational details
In this study, we used Gaussian09 software68 for the quantum chemistry calculations. The geometry optimizations and vibrational analyses were performed using the DFT method M06-2X.24 The jul-cc-pVTZ basis set, developed by Truhlar and co-workers,25 was used. We used an ultrafine integration grid and the “tight” option in Gaussian09 as the optimization condition. The starting low energy conformer geometry was found using the MS-RS method.45 Single point energy calculations were then carried out at each of the optimized geometries at the CBS/QB369,70 level. Note that we set the geometry optimization threshold to a high value in the CBS/QB3 input to avoid reoptimization of the input geometry that is usually carried out by this method at B3LYP level; and only the resulting single point energy values were used in our calculation. The anharmonic constant calculations for the reaction vibrational mode in the TS were carried out using second order vibrational perturbation theory (VPT2),29 with the information of the third and fourth order derivatives of the potential energy surface with respect to the reaction mode. These higher order derivatives were calculated by numerically differentiating the single point energies obtained at displaced geometries at M06-2X/jul-cc-pVTZ level of theory. A total of 8 displacement geometries for each TS were used in the anharmonic constant calculation, and a step-size of 0.03a0Da0.5 was chosen.3.2 Experimental details for IR spectra of VX
The IR spectrum of VX liquid (ca. 2 μL; >80% purity) was collected on a commercially available spectrometer in ATR mode at room temperature.4 Results and discussions
4.1 Structures and energetics
We show in Fig. 5 the optimized geometries of the stationary structures of the VX reactions. Similar to our findings in previous studies on selected simulants of VX,22 the TSs of both the S-side and the O-side reaction consist of 6-membered-ring structures. Key bond lengths and bond angles are reported in Table 1, they are also very similar to what we have found in the simulant molecules.22 One main difference between the VX and the simulants is that the TS for the S-side reaction, in addition to the P atom, has a chiral centre on the secondary C atom on the thioester chain, where the H is transferred from (shown on Fig. 5). Therefore there are two stereoisomers of the S-side TS, similar to the TS for the pericyclic reaction of sarin.21 It is worth noting that these two TSs will result in the same products. The more stable stereoisomer is shown in Fig. 5.In Table 2, we report the adiabatic barrier heights for the forward and reverse reactions. The reactions for both sides have significant forward barrier heights over 176 kJ mol−1, approximately 10 kJ mol−1 higher than the barrier for the sarin reaction.21 Similar to sarin and VX simulants,21,22 both reactions are endothermic. The S-side reaction is favoured both kinetically and thermodynamically by having a lower forward barrier height by ∼14 kJ mol−1 and a smaller endothermicity by ∼20 kJ mol−1. It should be noted that, unlike in the sarin case,21 the two stereoisomers of the S-side TS are very different in energy due to steric hindrance. The corresponding reactions should be treated independently. In addition, due to the existence of the chiral C atom in the TS, the two H atoms attached to it should be treated as in different chemical environments in the reactant partition function calculation especially for treating the HR modes. We also report the relative RD-HR reactant conformer energies in Table 2. We can see that the S-side reaction has more conformers than the O-side, although the two sides have the same number of active HR modes. The rotation of CH3 on the O-side ester can be treated as a simple three-fold symmetric top, and hence only the conformers of the other two active HR modes are needed in the calculation. On the other hand, all the possible conformers of the equivalent rotation on the S-side have to be treated individually. Note that this does not increase the number of reactant conformers for the S-side reaction by a great deal due to the steric hindrance of the (i-Pr)2NCH2CH2– group.
| S-side | O-side | |
|---|---|---|
| ΔVf | 176.24 (186.19) | 190.64 |
| ΔVr | 127.95 (137.90) | 112.52 |
| conf1 | 0.00 | 0.00 |
| conf2 | 0.3403 | 0.2281 |
| conf3 | 10.23 | 3.954 |
| conf4 | 13.36 | 13.09 |
| conf5 | 2.799 | 14.13 |
| conf6 | 17.34 | — |
| conf7 | 11.50 | — |
4.2 Vibrational analysis
Our calculated IR spectrum of VX is compared to experimental data in Fig. 6. A scaling factor of 0.97171 is used to correct the M06-2X/jul-cc-pVTZ frequencies. Overall a good agreement is found between the two spectra. Note that the calculation results include hindered rotor modes at a frequency typically below 600 cm−1 and these modes are not shown in the experimental spectrum. The two spectra have the best agreement for vibrations between ∼700 cm−1 to ∼1500 cm−1, where we can see that the calculation manages to catch almost all the peaks in the experimental results in terms of both peak position and relative intensity. However, for the H-containing bond stretching modes, for which the frequencies are around 300 cm−1, it can be seen that the calculation overestimates by ∼50 cm−1. | ||
| Fig. 6 Comparison between calculated IR spectrum of VX and experimental results, ©Crown Copyright (2019), Dstl. | ||
The values of the third and fourth order derivatives of the reaction mode calculated numerically with Richardson extrapolation up to the 2nd order are reported in Table 3. We can see that for the two third order derivatives, the extrapolation does not converge. In addition, large deviation can be found for the 0th order extrapolation results, this is because the barriers for both reactions are significantly asymmetric. As shown in Table 2, for instance, the forward barrier of the O-side reaction is approximately twice as large as the reverse barrier. As the displacement geometry moving further away from the TS, the calculated energies used in the numerical differentiation would have a more realistic representation of the shape of the overall PES. In other words, the Richardson extrapolation intended to improve the value calculated at the smallest displacements would no longer provide a sufficiently accurate result. Therefore, in the current study, we fitted the single point energies calculated at a total of eight displacement geometries with a fourth order polynomial to obtain the higher order derivatives. The results are reported in Table 3. We can see that these higher order derivatives from polynomial fitting for either reaction sides are quite different from the highest order Richardson extrapolated results. The residual sum of squares (RSS) of the fittings are also shown in Table 3, we can see the fittings are very good.
| S-side TS | ||||
|---|---|---|---|---|
| ΔQ | Richardson extrapolation order | Polynomial fitting | ||
| 0 | 1 | 2 | ||
| f 3,R × 107 | ||||
| 0.03 | 5.737 | 6.244 | 6.388 | |
| (−7.147) | (−7.260) | (−7.323) | ||
| 0.06 | 4.216 | 4.084 | — | 4.590 |
| (−6.807) | (−6.320) | — | (−8.320) | |
| 0.12 | 4.613 | — | — | |
| (−8.268) | — | — | ||
| f 4,R × 107 | ||||
| 0.03 | 3.528 | 3.479 | 3.477 | |
| (0.6789) | (0.1280) | (0.02173) | ||
| 0.06 | 3.674 | 3.508 | — | 4.180 |
| (2.332) | (1.722) | — | (4.238) | |
| 0.12 | 4.173 | — | — | |
| (4.160) | — | — | ||
| O-side TS | ||||
|---|---|---|---|---|
| ΔQ | Richardson extrapolation order | Polynomial fitting | ||
| 0 | 1 | 2 | ||
| f 3,R × 107 | ||||
| 0.03 | 6.838 | 7.202 | 7.277 | |
| 0.06 | 5.746 | 6.078 | — | 4.826 |
| 0.12 | 4.750 | — | — | |
| f 4,R × 107 | ||||
| 0.03 | 2.417 | 2.354 | 2.349 | |
| 0.06 | 2.608 | 2.427 | — | 3.156 |
| 0.12 | 3.149 | — | — | |
The calculated vibrational frequencies (ωR) and anharmonic constants (xRR) for the reaction mode vibration and the anharmonic correction (G0) to the PES are presented in Table 4. We show results from both the Richardson extrapolation and fitted polynomial data. It can be seen that for both the S- and O-side reactions, compared to the barrier heights reported in Table 2, the effect of G0 on reaction rate constant is negligible. The error in the calculation of G0 from using in the Richardson extrapolated higher order derivatives is therefore not significant. However, the errors in xRR are more noticeable. For both reactions, the xRR from the extrapolated derivatives are ∼20% smaller in absolute value comparing to the ones from the fitted derivatives, resulting in a narrower barrier and an overestimated tunneling probability. Therefore, for the remainder of the paper, our results will be based on the higher order derivatives obtained from polynomial fitting.
| S-side TS | ||
|---|---|---|
| ω R | 1457.1i | |
| (1452.4i) | ||
| x RR | Extrapolation | Fitting |
| −113.02 | −132.57 | |
| (−7.0731) | (−139.10) | |
| G 0 | Extrapolation | Fitting |
| −0.3285 | −0.3915 | |
| (−8.408 × 10−4) | (−0.4002) | |
| O-side TS | ||
|---|---|---|
| ω R | 1418.1i | |
| x RR | Extrapolation | Fitting |
| −84.12 | −106.77 | |
| G 0 | Extrapolation | Fitting |
| −0.2377 | −0.3130 | |
4.3 Rate constants
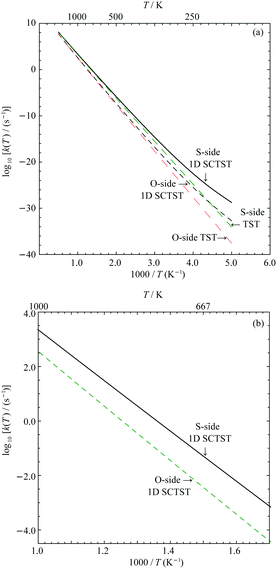
In Fig. 7(a), the logarithmic plots of the reaction rate constants for both the S- and O-sides are presented. All rate constant data used to construct the plots are given in the Supporting Information. We can see for either reaction sides, the corresponding 1D SCTST and TST rate constants converge at high temperature as expected. At low temperatures, typically below 300 K, we can see significant quantum tunneling contributions. We take the S-side reaction as an example. At 300 K, the 1D SCTST rate constant is ∼17.4 times larger than the corresponding TST result. At temperatures ranged from 400 K to 1000 K, the ratio between 1D SCTST and TST calculated reaction constant reduces from ∼3.89 to ∼1.24. These results show that quantum tunneling still plays an important role in the reaction mechanism. As seen in our previous work on sarin,21 only when the quantum tunneling contributions at relatively high temperatures are accounted for, the resulting %survival rate of the molecule agrees with experimental data. A similar quantum tunneling effect can also be found for the O-side reaction. We compare the rate constants for the two reactions between 700 K and 1000 K in Fig. 7(b). The rate constant of the S-side reaction is ∼10.03 times greater than the O-side one at 1000 K and becomes greater as temperature decreases. At 700 K, it is ∼22.49 times greater. This is expected due to the smaller forward barrier for the S-side reaction.Since both the S-side and O-side reactions are unimolecular, it is easy to calculate the percentage survival of VX (VX %survival) as a function of temperature and reaction time using the following equation:
 | (8) |
We plot in Fig. 8(a) the total VX %survival as a function of temperature, where we have k(T) = kS-side(T) + kO-side(T). The results of a total of four different reaction times are presented. From observing each individual curve, we can see that the longer the reaction the lower temperature required for complete decomposition. Alternatively, we can also measure the decomposition completeness at a particular temperature after different reaction times. For instance, at 725 K, there are ∼30% and ∼8.8% of VX left after 1 s and 2 s reaction time, respectively. The inset of Fig. 8(a) shows a comparison between the 1D SCTST (solid black curve) and TST (dashed red curve) results after 2 s reaction time. The 1D SCTST estimated rate constants are ∼1.5 times greater than the TST ones in the temperature range shown, and the quantum tunneling effects still have contributions to the reaction. Note that similar results were found for the sarin pericyclic H-transfer reaction,21 where the 1D SCTST results had excellent agreement to the experimental data.
 | ||
| Fig. 8 Percentage survival of VX at various temperatures and reaction times for the (a) total reaction after various reaction times and comparison between the TST and 1D SCTST in the inset and (b) comparison between the S-side and O-side reaction and their contribution to the total reaction. The %survival of GB after 2 s calculated using the rate constants reported previously.21 | ||
In Fig. 8(b), we show the VX %survival after 2 s reaction calculated using the total reaction rate constant. The GB %survival estimated based on the rate constant reported in ref. 21 are also shown for comparison. To achieve the same percentage of decomposition VX in general requires a temperature that is ∼ 50 to ∼60 K higher than GB. This agrees with the finding that the smallest barrier found in the VX reactions, 176.24 kJ mol−1, is approximately 10 kJ mol−1 higher than the barrier of the GB reaction, which is 166 kJ mol−1.21
In addition, we show the VX %survival after 2 s of the S-side and O-side reaction in Fig. 8(b). Comparing to the total %survival, the reaction is dominated by the S-side reaction, which yields O-ethyl methylphosphonothiolate (EMPTA). Although EMPTA is a VX precursor,72 its toxicity is considered to be low. Conversely, cleavage of the ester side-chain furnishes the breakdown product EA 2192, which is considered to be nearly as toxic as VX and to be relatively stable to, for example, hydrolysis.1,3 It should also be noted that hydrolysis of VX can proceed via either O-side or S-side chain cleavage, with the ratio of the products formed dependent on the solution pH. For example, Munro et al.9 described hydrolysis at pH < 6 and >10 as dominated by P–S cleavage, while pH 7–10 by P–O cleavage. The thermal degradation, presented in the current study, on the other hand shows that the S-side reaction is much more strongly favoured than the O-side, in agreement with results presented by Riches and co-workers73 on the treatment of VX-contaminated soil using accelerant-based fires. In addition, it is possible that under the pyrolysis condition both EMPTA and EA 2192 can further breakdown via pericyclic H-transfer reaction to form methylphosphonothioic S-acid and methylphosphonothioic acid, respectively,22 while it is difficult to perform further hydrolysis of EA 2192.3
5 Conclusions
In this work, we investigated theoretically the thermal decomposition of the nerve agent VX. The canonical reaction rate constants over a wide range of temperatures were calculated. Quantum tunneling effects were included in the calculation using the one-dimensional semiclassical transition state theory (1D SCTST). A large number of hindered rotor (HR) vibrational modes were observed in VX. In order to study these reactions efficiently while maintaining sufficient accuracy, we developed the reduced-dimensional (RD)-HR method. In this method, only a subset of the HRs, which directly affects the position of the reacting H atom are treated explicitly. In this study, we tested the RD-HR method on a simulant molecule then applied it to VX.Both the ester (O-side) and thioester (S-side) side chains can carry out pericyclic H-transfer reactions that results in breaking down of the VX molecule. The S-side reaction was favoured both kinetically and thermodynamically and dominated the reaction mechanism in the temperature range of pyrolysis (∼600 K to ∼1000 K). We examined the %survival of the molecules as a function of time and temperature based on the 1D SCTST rate constant. In the gas-phase high pressure limit, at temperature above 750 K, VX would completely decompose after 2 s. It should be noted that the P-atom containing products of all the reactions can carry out further pericyclic H-transfer reactions and decompose to smaller less toxic compounds. The mechanisms and reaction rate constants of some of these decompositions have been reported previously.22
Conflicts of interest
There are no conflicts to declare.Acknowledgements
X. S. acknowledges the use of the University of Oxford Advanced Research Computing (ARC) facility in carrying out the theoretical studies in this work. X. S. and D. C. C. acknowledge support from DSTL Grant No. R1000121682. M. R. S. thanks Dr Linda Lee and the Chemical Sensing team at Dstl (CBR Division) for the provision of spectral data. Content includes material subject to Crown copyright (2018), Dstl. This material is licensed under the terms of the Open Government Licence except where otherwise stated. To view this licence, visit http://www.nationalarchives.gov.uk/doc/open-government-licence/version/3 or write to the Information Policy Team, The National Archives, Kew, London, TW9 4DU, or email psi@nationalarchives.gsi.gov.uk.References
- K. Kim, O. G. Tsay, D. A. Atwood and D. G. Churchill, Chem. Rev., 2011, 111, 5345–5403 CrossRef CAS.
- H. Rice, C. H. Dalton, M. E. Price, S. J. Graham, A. C. Green, J. Jenner, H. J. Groombridge and C. M. Timperley, Proc. R. Soc. A, 2015, 471, 20140891 CrossRef PubMed.
- Y. J. Jang, K. Kim, O. G. Tsay, D. A. Atwood and D. G. Churchill, Chem. Rev., 2015, 115, PR1–PR76 CrossRef PubMed.
- A. R. Wilmsmeyer, W. O. Gordon, E. D. Davis, D. Troya, B. A. Mantooth, T. A. Lalain and J. R. Morris, J. Phys. Chem. C, 2013, 117, 15685–15697 CrossRef CAS.
- D. E. Taylor, K. Runge, M. G. Cory, D. S. Burns, J. L. Vasey, J. D. Hearn, K. Griffith and M. V. Henley, J. Phys. Chem. C, 2013, 117, 2699–2708 CrossRef CAS.
- B. N. Papas, I. D. Petsalakis, G. Theodorakopoulos and J. L. Whitten, J. Phys. Chem. C, 2014, 118, 23042–23048 CrossRef CAS.
- N. Q. Le, C. E. Ekuma, B. I. Dunlap and D. Gunlycke, J. Phys. Chem. C, 2018, 122, 2832–2839 CrossRef CAS.
- Y.-C. Yang, Acc. Chem. Res., 1999, 32, 109–115 CrossRef CAS.
- N. B. Munro, S. S. Talmage, G. D. Griffin, L. C. Waters, A. P. Watson, J. F. King and V. Hauschild, Environ. Health Perspect., 1999, 107, 933–974 CrossRef CAS PubMed.
- J. J. Kiddle and S. P. Mezyk, J. Phys. Chem. B, 2004, 108, 9568–9570 CrossRef CAS.
- E. Gershonov, I. Columbus and Y. Zafrani, J. Org. Chem., 2009, 74, 329–338 CrossRef CAS PubMed.
- G. O. Bizzigotti, H. Castelly, A. M. Hafez, W. H. B. Smith and M. T. Whitmire, Chem. Rev., 2009, 109, 236–256 CrossRef CAS PubMed.
- G. W. Wagner and Y.-C. Yang, Ind. Eng. Chem. Res., 2002, 41, 1925–1928 CrossRef CAS.
- R. Zboril, M. Andrle, F. Oplustil, L. Machala, J. Tucek, J. Filp, Z. Marusak and V. K. Sharma, J. Hazard. Mater., 2012, 211–212, 126–130 CrossRef CAS PubMed.
- G. W. Peterson and G. W. Wagner, J. Porous Mater., 2014, 21, 121–126 CrossRef.
- L. Bromberg, W. R. Creasy, D. J. McGarvey, E. Wilusz and T. A. Hatton, ACS Appl. Mater. Interfaces, 2016, 7, 22001–22011 CrossRef PubMed.
- J. Zhao, D. T. Lee, R. W. Yaga, M. G. Hall, H. F. Barton, I. R. Woodward, C. J. Oldham, H. J. Walls, G. W. Peterson and G. N. Parsons, Angew. Chem., Int. Ed., 2016, 55, 13224–13228 CrossRef CAS PubMed.
- R. Gil-Sam-Millan, E. López-Maya, M. Hall, N. M. Padial, G. W. Peterson, J. B. DeCoste, L. M. Rodríguez-Albelo, J. E. Oltra, E. Barea and J. A. R. Navarro, ACS Appl. Mater. Interfaces, 2017, 9, 23967–23973 CrossRef PubMed.
- I. Bandyopdhyay, M. J. Kim, Y. S. Lee and D. G. Churchill, J. Phys. Chem. A, 2006, 110, 3655–3661 CrossRef PubMed.
- T. Ash, T. Debnath, T. Banu and A. K. Das, Chem. Res. Toxicol., 2016, 29, 1439–1457 Search PubMed.
- X. Shan, J. C. Vincent, S. Kirkpatrick, M. D. Walker, M. R. Sambrook and D. C. Clary, J. Phys. Chem. A, 2017, 121, 6200–6210 CrossRef CAS PubMed.
- X. Shan, M. R. Sambrook and D. C. Clary, J. Phys. Chem. A, 2019, 123, 59–72 CrossRef CAS PubMed.
- L. Yang, R. M. Shroll, J. Zhang, U. Lourderaj and W. L. Hase, J. Phys. Chem. A, 2009, 113, 13762–13771 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034 CrossRef CAS PubMed.
- W. H. Miller, J. Chem. Phys., 1975, 62, 1899 CrossRef CAS.
- W. H. Miller, Faraday Discuss. Chem. Soc., 1977, 62, 40–46 RSC.
- W. H. Miller, Annu. Rev. Phys. Chem., 1990, 41, 245–281 CrossRef CAS.
- W. H. Miller, R. Hernandez, N. C. Handy, D. Jayatilaka and A. Willetts, Chem. Phys. Lett., 1990, 172, 62–68 CrossRef CAS.
- M. J. Cohen, N. C. Handy, R. Hernandez and W. H. Miller, Chem. Phys. Lett., 1992, 192, 407–416 CrossRef CAS.
- R. Hernandez and W. H. Miller, Chem. Phys. Lett., 1993, 214, 129–136 CrossRef CAS.
- T. L. Nguyen, J. F. Stanton and J. R. Barker, J. Phys. Chem. A, 2011, 115, 5118–5126 CrossRef CAS PubMed.
- J. R. Barker, T. L. Nguyen and J. F. Stanton, J. Phys. Chem. A, 2012, 116, 6408–6419 CrossRef CAS PubMed.
- R. E. Weston, Jr., T. L. Nguyen, J. F. Stanton and J. R. Barker, J. Phys. Chem. A, 2013, 117, 821–835 CrossRef PubMed.
- T. L. Nguyen and J. F. Stanton, J. Chem. Phys., 2017, 147, 152704 CrossRef PubMed.
- S. M. Greene, X. Shan and D. C. Clary, J. Chem. Phys., 2016, 144, 244116 CrossRef PubMed.
- C. Aieta, F. Gabas and M. Ceotto, J. Phys. Chem. A, 2016, 120, 4853–4862 CrossRef CAS PubMed.
- C. Aieta, F. Gabas and M. Ceotto, J. Chem. Theory Comput., 2019, 15, 2142–2153 CrossRef CAS PubMed.
- X. Shan and D. C. Clary, Philos. Trans. R. Soc., A, 2017, 376, 20170147 CrossRef PubMed.
- T. A. H. Burd, X. Shan and D. C. Clary, Chem. Phys. Lett., 2018, 693, 88–94 CrossRef CAS.
- T. A. H. Burd, X. Shan and D. C. Clary, Phys. Chem. Chem. Phys., 2018, 20, 25224 RSC.
- Y.-Y. Chuang and D. G. Truhlar, J. Chem. Phys., 2000, 112, 1221–1228 CrossRef CAS.
- B. A. Ellingson, V. A. Lynch, S. L. Mielke and D. G. Truhlar, J. Chem. Phys., 2006, 125, 084305 CrossRef PubMed.
- J. Zheng and D. G. Truhlar, Phys. Chem. Chem. Phys., 2010, 12, 7782–7793 RSC.
- J. Zheng, T. Yu, E. Papajak, I. M. Alecu, S. L. Mielke and D. G. Truhlar, Phys. Chem. Chem. Phys., 2011, 13, 10885–10907 RSC.
- J. Zheng and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 1356–1367 CrossRef CAS PubMed.
- K. S. Pitzer and W. D. Gwinn, J. Chem. Phys., 1942, 10, 428–440 CrossRef CAS.
- K. S. Pitzer, J. Chem. Phys., 1946, 14, 239–243 CrossRef CAS.
- J. E. Kilpatrick and K. S. Pitzer, J. Chem. Phys., 1949, 17, 1064–1075 CrossRef CAS.
- A. Fernández-Ramos, J. Chem. Phys., 2013, 138, 134112 CrossRef PubMed.
- L. Simón-Carballido and A. Fernández-Ramos, J. Mol. Model., 2014, 20, 2190 CrossRef PubMed.
- L. Simón-Carballido, J. L. Bao, T. V. Alves, R. Meana-Pañeda, D. G. Truhlar and A. Fernández-Ramos, J. Chem. Theory Comput., 2017, 13, 3478–3492 CrossRef PubMed.
- J. Zheng, S. L. Mielke, K. L. Clarkson and D. G. Truhlar, Comput. Phys. Commun., 2012, 183, 1803–1812 CrossRef CAS.
- S. M. Greene, X. Shan and D. C. Clary, J. Chem. Phys., 2016, 144, 084113 CrossRef PubMed.
- X. Shan, T. A. H. Burd and D. C. Clary, J. Phys. Chem. A, 2019, 123, 4639–4657 CrossRef CAS PubMed.
- T. L. Nguyen and J. R. Barker, J. Phys. Chem. A, 2010, 114, 3718–3730 CrossRef CAS PubMed.
- S. M. Greene, X. Shan and D. C. Clary, J. Phys. Chem. A, 2015, 119, 12015–12027 CrossRef CAS PubMed.
- J. F. Stanton, J. Phys. Chem. Lett., 2016, 7, 2708–2713 CrossRef CAS.
- L. F. Richardson and J. A. Gaunt, Philos. Trans. R. Soc., A, 1927, 226, 299–361 CrossRef.
- C. Ridders, Adv. Eng. Software, 1982, 4, 75–76 CrossRef.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in C: The Art of Scientific Computing, Cambridge University Press, Cambridge, 2nd edn, 1992 Search PubMed.
- A. F. Wagner, J. Phys. Chem. A, 2013, 117, 13089–13100 CrossRef CAS PubMed.
- J. M. Bowman, Adv. Chem. Phys., 1985, 61, 115–167 CAS.
- J. M. Bowman, J. Phys. Chem., 1991, 95, 4960–4968 CrossRef CAS.
- J. M. Bowman, Theor. Chem. Acc., 2002, 108, 125–133 Search PubMed.
- P. T. Panek and C. R. Jacob, J. Chem. Phys., 2016, 144, 164111 CrossRef.
- J. Wu, H. Ning, X. Xu and W. Ren, Phys. Chem. Chem. Phys., 2019, 21, 10003–10010 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- J. A. Montgomery, Jr., M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822–2827 CrossRef.
- J. A. Montgomery, Jr., M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532–6542 CrossRef.
- H. Zhang, X. Zhang, D. G. Truhlar and X. Xu, J. Phys. Chem. A, 2017, 47, 9033–9044 CrossRef PubMed.
- R. M. Black and J. M. Harrison, in The Chemistry of Organophosphorus Chemical Warfare Agents, ed. F. R. Hartley, John Wiley & Sons, Ltd, 2006, vol. 4, ch. 10, pp. 781–840 Search PubMed.
- M. R. Gravett, F. B. Hopkins, A. J. Self, A. J. Webb, C. M. Timperley and J. R. Riches, Anal. Bioanal. Chem., 2014, 406, 5121–5135 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05109k |
| This journal is © the Owner Societies 2020 |

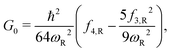
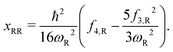
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O
O