Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermodynamics of the formation of surface PtO2 stripes on Pt(111) in the absence of subsurface oxygen†
Selwyn
Hanselman
a,
Ian T.
McCrum
a,
Marcel J.
Rost
b and
Marc T. M.
Koper
 *a
*a
aLeiden Institute of Chemistry, Leiden University, P.O. Box 9502, 2300 RA Leiden, The Netherlands. E-mail: m.koper@chem.leidenuniv.nl
bHuygens-Kamerlingh Onnes Laboratory, Leiden University, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands
First published on 30th October 2019
Abstract
This paper examines the thermodynamics of PtO2 stripes formed as intermediates of Pt(111) surface oxidation as a function of the degree of dilation parallel to the stripes, using density functional theory and atomistic thermodynamics. Internal energy calculations predict 7/8 and 8/9 stripe structures to dominate at standard temperature and pressure, which contain 7 or 8 elevated PtO2 units per 8 or 9 supporting surface Pt atoms, respectively. Moreover, we found a thermodynamic optimum with respect to mean in-stripe Pt–Pt spacing close to that of α-PtO2. Vibrational zero point energies, including bulk layer contributions, make a small but significant contribution to the stripe free energies, leading to the 6/7 stripe being most stable, although the 7/8 structure is still close in free energy. These findings correspond closely to experimental observations, providing insight into the driving force for oxide stripe formation and structure as the initial intermediate of platinum surface oxidation, and aiding our understanding of platinum catalysts and surface roughening under oxidative conditions.
1. Introduction
Surface oxidation, which happens both in gas-phase catalysis and in electrochemical environments, impacts profoundly the selectivity, activity and stability of (electro)catalysts.1,2 A commonly-used electrocatalyst material, platinum, has long been known to undergo surface oxidation during catalyst operation.1–4 Whether as an electrocatalyst or as a gas-phase heterogeneous catalyst, the metal surface is exposed to oxygen species, which may lead to surface reconstruction, or in the case of aqueous media, dissolution.5 Dissolution,6–8 and reduction of surface oxides,9 drive further reconstruction and (irreversible) roughening of the surface.4,8,10,11 In order to mitigate any deleterious effects and improve our understanding of oxygen-induced surface roughening, we need to know the adsorption patterns of oxygen on – and in – platinum.There is ample evidence for more complicated oxygenation of Pt(111) than simple on-surface adsorption. At low oxygen coverages generated under ultrahigh vacuum (UHV) conditions, Devarajan et al. observed this on-surface adsorption of oxygen in fcc hollow sites using temperature programmed desorption and scanning-tunneling microscopy (STM) experiments.12 Yet for oxygen coverages greater than 0.40 ML, some Pt atoms are elevated, forming PtOx stripe segments and (above 0.71 ML) honeycombs. Density functional theory (DFT) calculations by Hawkins et al. and force field simulations by Farkas et al. corroborated part of these findings by finding stripe segments at coverages equivalent to 0.75 ML and stable PtO2 stripes for 1 ML coverage; all these structures were supported by subsurface oxygen.13,14 Holby et al., on the other hand, indicated that it is not necessary to incorporate subsurface oxygen: they found striped structures alternating between flat and buckled stripes.15
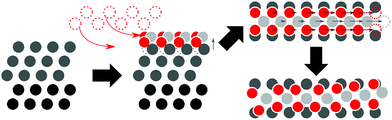
In practice, platinum catalysts are usually operated under standard or elevated pressures and close to standard temperature in the presence of O2, as opposed to UHV and high-temperature conditions using more strongly oxygenating reagents. Luo et al. found that for platinum films, exposure to either pure O2 or mixtures of O2 and water vapor led to near-monolayer oxygen coverage.16 In an in situ STM study of oxygenation patterns, Van Spronsen et al. exposed Pt(111) to O2 at pressures ranging from 1–5 bar and at temperatures between 300–538 K.17 During O2 exposure at 1 bar, a spokewheel structure is observed, above 2.2 bar accompanied by stripes as illustrated in Fig. 1.17 The linear segments, or spokes of the spokewheel, are PtO2 stripe structures which are platinum deficient relative to the underlying surface, causing a ∼14% lattice mismatch of PtO2 structures relative to the pristine surface lattice vectors. In other terms, these structures contain 7/8 PtO2 units per Pt atom partaking in the reaction.
 | ||
| Fig. 1 Artist's impression of spokewheel (a) and stripe (b) models adapted from Van Spronsen et al.17 | ||
This lattice mismatch appears to be mirrored in sub-monolayer PtOx structures studied by Hawkins et al., who found non-contiguous PtOx clusters supported by subsurface oxygen to be dilated relative to the underlying platinum bulk lattice parameter.13 The presence of subsurface oxygen supporting Pt atoms corresponds to the concept of place exchange, which was first proposed by Reddy et al. for electrochemical oxidation of platinum,18 and later supported by a kinetic study by Conway et al. and X-ray measurements by You et al.19–21 The traditional definition of place-exchange, as mentioned by Drnec et al., involves switching one platinum atom in the surface by one oxygen atom, lifting the former from the surface and integrating the latter into it. Yet, platinum atoms in Van Spronsen et al.'s study appear to be elevated in continuous stretches, and the oxygen coverage is twice the fraction of surface platinum atoms in the stripes, which are lifted through oxidation. This suggests that contrary to Hawkins et al.'s PtOx structures, Van Spronsen's structures on average consist of PtO2 units even below 1 ML oxygen coverage. All these lifted atoms are found to be adjacent in spokewheel structures, which one would not expect if buckled stripes play a major role as in the model proposed by Holby et al.15 XPS measurements on stripe structures by Van Spronsen show 0.88 ML O coverage, indicating regular 7/8 dilation, yet could not be elucidated using STM imaging. Additionally, platinum atoms are expelled from the pristine surface domain on which these stripes are formed, an effect not taken into account by Hawkins et al.13 This may in turn aid the formation of serpentine islands otherwise attributed to adsorbate-induced strain by Van Spronsen et al. Most strikingly, Van Spronsen et al.'s results indicate that subsurface oxygen is not necessary to stabilize PtO2 surface structures under (near-)standard oxidizing conditions.
Apart from their role in gas-phase Pt oxidation, PtO2 stripes may also be first intermediates in the electrochemical oxidation of Pt electrodes. Furuya et al. detected oxidized platinum atoms exposed on-surface under electrochemical conditions at ∼1.05–1.20 V, suggesting the formation of surface PtOx in a so-called quasi-3D structure as in gas-phase Pt oxidation.5In situ electrochemical STM measurements by Jacobse et al. show that cycling of Pt(111) through relatively mild oxidative potentials of 1.35 V initially causes island formation, and subsequently irreversibly roughens the surface during multiple oxidation–reduction cycles,11 in agreement with X-ray spectroscopy measurements by Ruge et al.22 Lifting of Pt atoms from the surface has been observed through in situ X-ray observations of electrochemical Pt oxidation and assumed to involve place exchange;4,23 Drnec et al., however, noted that their measurements do not show either an ordered overlayer with a different lattice parameter, nor an amorphous oxide structure, but they cannot exclude the possibility of (long-range) oxide chain formation.4 Together, these findings suggest a role for a PtOx based intermediate not supported by subsurface oxygen under electrochemical conditions, both regarding reactivity of Pt electrodes at high potentials and the surface transformation as a result of oxidation–reduction cycles.
In this study, we investigate the formation energies of subsurface oxygen-free PtO2 stripes as proposed by Van Spronsen, and attempt to reproduce their structures, using DFT methods. In the process, we compare various stripe PtO2/Pt(displaced) ratios, calculate their energies as a function of oxygen chemical potential and electrochemical potential, and discuss their similarity to the ordering of the spokewheel segments, and how these energies are related to PtO2 geometries and bulk platinum properties.
2. Density functional theory methods and initial structure generation
All calculations on Pt(111) and oxidized Pt(111) were performed using density functional theory (DFT) in the Vienna Ab Initio Simulation Package,24 with the spin-restricted Perdew–Burke–Ernzerhof (PBE) exchange correlation functional.25 All plane-wave cutoffs are equal to 450 eV, while ionic cores are described using plane augmented wave (PAW) pseudopotentials for PBE supplied in the VASP 5.2 distribution.24 Orbital occupancies in slab systems and bulk solids are subject to 0.20 eV first order Methfessel–Paxton smearing,26 whereas gas-phase molecules are subject to 0.0001 eV Gaussian smearing.27 The bulk Pt lattice parameter a was found to be equal to 3.9754 Å through minimization of internal energy of a single atom fcc bulk cell under variation of lattice vector lengths. Computational details pertaining to gas phase molecules (H2(g), H2O(g)) are listed in Section 3 of the ESI.†We defined cells for (111) M × N surface slabs for each stripe coverage ratio; similarly, we created bulk cells by stacking six (111) layers of M × N platinum atoms. Cell dimensions and parameters used for these slabs and bulk cells are listed in Table S.1 in the ESI.† Specifically, each unit cell is defined as having a 2 × N-60° translational surface symmetry, and lattice vectors (including the additional lattice vector in the bulk) run parallel to shortest-distance atom pair vectors. The k point samples along each lattice vector are obtained from gamma-centered (24/M) × (24/N) × 1 grids for surface slabs, and gamma-centered (24/M) × (24/N) × 4 grids for bulk crystal, respectively; 24 points were chosen per reciprocal atom for that density provides a sufficient balance between computational efficiency and convergence of the formation energy.
Within the constraints posed by the surface slab cells, we created one M × N surface for each slab cell defined in Table S.1 (ESI†), which we subsequently relaxed below a maximum atomic force of 0.01 eV Å−1. We generated simulation cells containing on-surface adsorbed O* configurations for 0.25 ML, 0.33 ML, and 1.0 ML coverages, using 4 × 4, 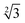 ×
× 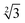 and 4 × 4 unit cells respectively. For these on-surface O* configurations, all oxygen atoms are placed strictly above the top layer of uncorrugated Pt(111) surfaces, and distributed as equidistantly as possible. In these cells, no Pt atoms were lifted from the top layer of the Pt(111) surface.
and 4 × 4 unit cells respectively. For these on-surface O* configurations, all oxygen atoms are placed strictly above the top layer of uncorrugated Pt(111) surfaces, and distributed as equidistantly as possible. In these cells, no Pt atoms were lifted from the top layer of the Pt(111) surface.
We generated initial PtO2 stripe supercells (1 ML) from the 2 × 4 slab cell by lifting one surface row or a grid consisting of eight atom-wide triangles, respectively, and suspending them using oxygen atoms following the suggestions by Van Spronsen et al.17 From these structures we created cells containing dilated stripes (stripe/surface ratios: 2/3, 3/4, 4/5, 5/6, 6/7, 5/8, 7/8, 8/9, 9/10) by removing one PtO2 unit from each stripe supercell, and scaling the remaining PtO2 segments along the long surface vector to close the gap left behind. For the stripe cells, Pt (in the oxide)-to-Pt (in the surface) ratios vary from 2/3 to 9/10. To more broadly sample low-energy stripe structures, platinum and oxygen coordinates in initial PtO2 stripes were either shifted systematically relative to the surface (by either half or a quarter of bulk interatomic spacing) or randomly displaced, and oxygen atoms were selectively moved to obtain geometries containing low-coordinated Pt sites in specific stripe segments. This process is illustrated in Fig. 2.
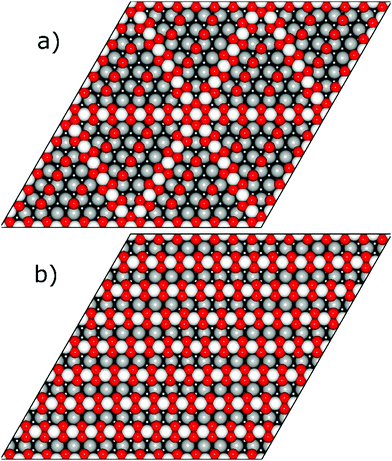
Resulting stripe structures and on-surface O* configurations were relaxed, and vibrational analysis was performed on the lowest DFT energy configurations pertaining to individual stripe PtO2/Pt(displaced) ratios. These computations are detailed in the ESI.† Relaxed geometries of the 2/3, 3/4, 7/8, and 1/1 dilated PtO2 stripes are shown in Fig. 3. We calculated Helmholtz free energies for Pt(111) and oxidized Pt(111) surface slabs using the methods listed in Section 1 of the ESI.†
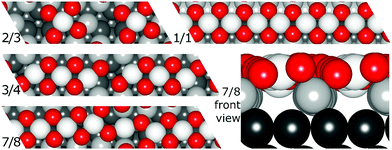 | ||
| Fig. 3 Relaxed PtO2 stripe structures in top and front views. Platinum atoms are gray (darker grey is deeper into the slab), and oxygen atoms are red and relatively smaller. | ||
3. Results and discussion
3.1 Results without vibrational energy
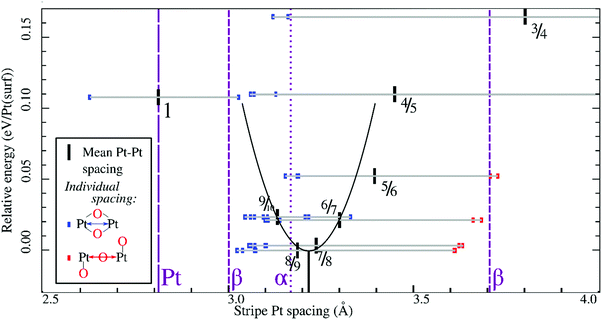
In all geometry optimizations (both in- and excluding vibrational energy), the most stable PtO2 stripes contain stretches of nearly rectangular planar 4-coordinated stripe Pt atoms with surrounding oxygen atoms slightly misaligned with respect to the surface vectors, alternating with single 2-coordinated stripe Pt atoms as shown for the 7/8 structure in Fig. 3. This holds for all structures ranging from 4/5 to 8/9. Fig. 4 plots stripe energies against individual and mean Pt–Pt spacing (excluding stripe vibrations), and shows that the formation energies are directly related to the degree of lattice mismatch. This assumption is reasonable given there are no apparent phase changes in either the PtO2 stripes or in respective decorated surfaces. Excluding vibrations, the optimum PtO2/Pt(displaced) ratio lies between 7/8 and 8/9, judging from a least-squares quadratic fit of the four lowest-energy points (see Fig. 4). In general, the shorter Pt–Pt distances in the four most stable stripes cluster between the Pt–Pt distance in bulk α-PtO2 and that of the shorter Pt–Pt spacing in bulk β-PtO2, while the longer Pt–Pt distances are close to that of longer Pt–Pt spacing in bulk β-PtO2. The optimum Pt–Pt spacing appears to be 3.20 Å, while for 7/8 and for 8/9, they are 3.22 Å and 3.17 Å, respectively (R2 = 0.930). The average Pt–Pt distances in the 7/8 and 8/9 stripes are relatively close to those in bulk α-PtO2, which is the most stable bulk PtO2 phase. The relation between PtO2/Pt(displaced) ratios and stripe thermodynamics including vibrational energies will be discussed later in this paper.The most stable stripe structures found in our calculations, i.e. the 6/7, 7/8, and 8/9 stripes, correspond closely to the spokewheel structures observed by Van Spronsen et al. There is a close correlation between the Pt–Pt atom spacing in the stripe and the formation energy. The correspondence of most stable Pt–Pt spacing with those in most stable bulk structures indicates the physics underlying Pt–O bulk and stripe oxide interactions are remarkably similar; hence, such structures may aid bulk formation. Taken together, both observations suggest that the degree to which Pt–Pt or Pt–O bonds can relax dominates stripe thermodynamics, and suggests that removal of platinum from the stripe relative to the density of Pt in the underlying surface is favorable, allowing the stripe to dilate.
Energies of formation for each individual stripe – excluding vibrational free energies of the PtO2 units and the underlying surfaces – are plotted against the O2 chemical potential and the electrochemical potential relative to the computational hydrogen electrode (E0–ESHE) in Fig. 5. The plot includes on-surface O* configurations, in which no platinum is lifted from the surface as described previously. For a Pt (in stripe)–Pt (in surface) ratio of 1, all original surface atoms lifted from the surface remain in the stripe. For other PtO2/Pt(displaced) ratios, some platinum atoms are instead expelled from the area in which a stripe is being formed, and migrate on top of the original surface. Hence, a plot of the free energy of formation against the chemical potential of the expelled Pt atom(s) is included in Figure S.2 in the ESI.†
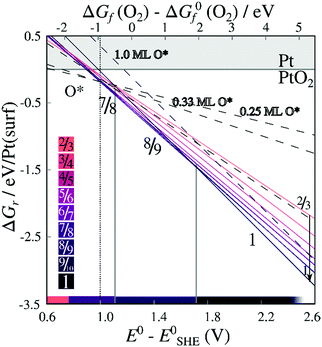 | ||
| Fig. 5 Energies of formation, excluding the contribution of the vibrational modes, for oxygenated Pt surfaces with respect to the O2 chemical potential and the electrochemical potentials. Lines are labeled by the corresponding stripe PtO2/Pt(displaced) ratios M/N or coverages x ML O*. Contiguous lines refer to PtO2 stripes; colors correspond to PtO2/Pt(displaced) ratios as defined in the color bars (bottom-left inset). Dashed lines refer to on-surface O*. Both figures are based on DFT binding energies for Pt bulk (see Table S.5 in the ESI†). | ||
We can infer from Fig. 5 that forming non-dilated stripes, i.e. surface oxidation without emitting Pt atoms from the surface, is stable only at high oxygen chemical potential or high electrochemical potential. In contrast, 5/6, 6/7, 7/8, 8/9 dilated stripes are significantly more stable than either the Pt(111) surface or stripes with other PtO2/Pt(displaced) ratios at 1 bar O2 pressure and standard temperature. This means there is a clear (electronic) driving force towards lower PtO2/Pt(displaced) ratios in general. Stripe formation is also more favorable than high-coverage (1 ML) on-surface oxygen adsorption, as shown in Fig. 5.
3.2 Results with vibrational energy
As the internal energy difference between 7/8 and 8/9 stripes is ∼2 meV/Pt(surf), and the difference between 6/7 or 9/10 and the 8/9 stripe is ∼20 meV/Pt(surf), vibrational energies might influence the trend as for which stripe is most stable.Our oxygen coverages are high, entire rows of Pt atoms are lifted out of the surface, there are strong adsorbate–surface interactions, and minute energy differences between individual configurations. A traditional adsorbate-only vibrational analysis (where the surface vibrational modes are assumed un-perturbed by the adsorbate) may hence lead to incorrect approximations of vibrational enthalpies and entropies. Hence we attempt to subsume standard adsorbate-only vibrational analysis into a adsorbate-bulk vibrational analysis. This methodology is based on the assumption that the amplitudes of forces exerted between two atoms in a lattice decay quickly enough with increasing distance between them. This enables us to describe their vibrational modes using only short-range interactions where necessary, including between different simulation models.
Using this method, we may stack bulk layers under the surface of interest, aiming to converge to a vibrational energy which accurately represents both surface, bulk, and surface–bulk interactions. While selecting the atoms taking part in this vibrational analysis, one must take into account to which degree the vibrational data correctly represents the atoms affected by the chemical reaction under study. In the context of the stripe-oxygenated Pt surfaces we are studying, four categories of atoms can be defined: stripe atoms, the (remaining) top surface atoms, the first underlying layer and the underlying layers or bulk. For pristine surfaces, the former two correspond to the top surface layer, while the second corresponds to the first subsurface layer.
We decided to analyze 5/6, 6/7, 7/8, and 8/9 stripes as their internal energies are closest to the optimum and, hence, they are the structures of which the relative energies may be affected most by vibrational energy contributions (see Table S.6, ESI†). In calculating the vibrational contribution to the free energy, all vibrational modes were calculated by ±0.02 Å single atom displacements along Cartesian unit vectors, of which one is parallel to the short edge of the surface, and the other is perpendicular to the surface. The forces exerted by these stripe/surface/subsurface atoms on each other and on the first two underlying layers are compiled into a group of Hessian matrix elements – note that we only have information on stripe-to-underlying layer coupling rather than the other way around – which is combined with a large Hessian matrix describing the force gradients of a set of bulk layers with the two underlying layers mentioned above and (if applicable) two layers above and below the current bulk layer. This matrix is illustrated in Fig. S.1 in the ESI;† some further practical details are listed in ESI Section 4.†
When including only the first (corrugated) platinum layer and the oxygen atoms, vibrational contributions destabilize stable stripes by ∼0.35 eV per Pt(surf) relative to their respective pristine surfaces. Including three bulk layers, for which the vibrational energy converges while remaining computationally reliable as shown in ESI Section 4,† causes a further increase of vibrational free energy for less dilated structures, and a decrease in energy for the more dilated structures. Adding two additional bulk layers beyond the first layer results in vibrational free energy changes ranging from 10–40 meV per Pt(surf), depending on the stripe PtO2/Pt(displaced) ratio (see Table S.4 in the ESI†). The resulting vibrational energies depend monotonously on PtO2/Pt(displaced) ratios, indicating that stripes with PtO2/Pt(displaced) ratios between those investigated have intermediate vibrational energies. After adding the vibrational contributions, Fig. 6 shows that the 6/7 stripe is more stable than the 7/8 stripe by 9 meV per Pt(surf), while the 7/8 stripe is more stable than the 8/9 stripe by 13 meV per Pt(surf). This suggests the most stable PtO2/Pt(displaced) ratio to be close to 6/7 or 7/8, which still corresponds closely to the experimentally observed data.
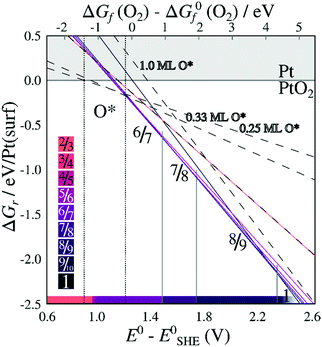 | ||
| Fig. 6 Energies of formation, including the contribution of vibrational modes, for PtO2 superstructures with respect to O2 chemical potentials (a) and electrochemical potentials relative to CHE (b), labeled by PtO2/Pt(displaced) ratios M/N. Dashed lines refer to on-surface O*. Shades correspond to PtO2/Pt(displaced) ratios as defined in the color bars. All energies are based on DFT binding energies for Pt bulk (see Table S.5, ESI†). | ||
Similarly, Fig. 7 shows that the minimum of the quadratic fit of the stripe energies versus the Pt–Pt spacing when including vibrations, shifts from 3.20 Å at 3.28 Å, close to the 6/7 structure spacing, while maintaining a clear relation between energies and Pt–Pt spacing (R2 = 0.997). Although the 6/7 stripe is most stable in our calculations including vibrational energy corrections, the 7/8 structure is less than 0.5 kBT/Pt(surf) higher in energy, suggesting that even if there are no additional entropy terms favoring 7/8 stripes, significant populations of 7/8 stripe structure domains can be found on an oxidized Pt(111) surface. Note that the spokewheel structures include nodes and non-reconstructed domains adjacent to stripe segments, which may affect the optimal Pt–Pt spacing. The total vibrational correction raises the predicted onset potentials for 0.25 ML oxygen adsorption to 0.9 V, while shifting the onset potential for stripe formation to ∼1.2 V. This onset potential lies within the expected range for initial oxide formation as discussed above.
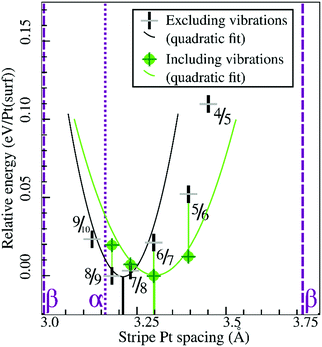 | ||
| Fig. 7 Comparison of selected stripe energies with and without vibrational energy corrections and their respective quadratic fits; legend in inset. | ||
The model defined above does not take into account repulsion between adjacent stripes. Leaving out every second stripe in a double-spaced unit cell stabilizes each individual stripe by 0.248 eV per Pt(surf) or less (see Table S.6, ESI†). Repulsion between stripes appears to be significant, but is smaller than the binding energy of adjacent stripes. This means the adjacent stripe model is representative of real stripe coverages.
The onset (electro)chemical potential for the formation of atomic oxygen and surface oxide stripes compares well with oxygen adsorption/oxide formation observed experimentally. Before the formation of the PtO2 film, and in the absence of specific adsorption of Pt(111) (i.e. in perchloric acid), there is a voltammetric peak at 1.10 V (with an onset at ∼1.05 V) typically attributed to surface atomic oxygen (but see studies by Huang et al.28,29).30 Importantly, the formation of this surface species does not involve any major structural rearrangement of the platinum surface atoms. Using in situ X-ray spectroscopy, Liu et al. have shown that higher densities of on-surface O* on a Pt(111) electrode, which they find near 0.8 to 1.0 V, lead to partial perpendicular displacement of Pt atoms from the top surface layer. This suggests that higher coverages may cause Pt atoms to be lifted from the surface, which is a first step towards reconstruction into PtO2 stripes. Further oxidation of Pt(111) leads to a new voltammetric feature with an onset at ca. 1.25 V. In situ Raman spectroscopic measurements of Pt(111) by Huang et al. have shown that this feature is accompanied by the formation of an α-PtO2 film.28 Once this film is formed and subsequently reduced, the Pt(111) structure changes and develops defect sites,11 in agreement with the idea that the formation of the oxide film (or oxide stripes) leads to an expulsion of Pt atoms, which do not return to their original position after oxide reduction. These observations are in excellent agreement with the predictions of Fig. 5 and 6. The relative stability of stripe structures also corresponds well with the findings by Van Spronsen et al. mentioned in the Introduction,17 who observed 7/8 dilated spokewheel segments in SEM images. Van Spronsen's stripes were created at 2.2 bar and 535 K, which is equivalent to an oxygen potential shift of −0.488 eV or an electrode potential at 300 K of 1.11 V. The PtO2/Pt(displaced) ratio of the stripes determines the number of Pt atoms expelled from the Pt surface during a single oxidation–reduction cycle (this number is larger with a smaller PtO2/Pt(displaced) ratio). The larger this number, the faster the surface will roughen during multiple oxidation–reduction cycles (for a detailed model of this surface roughening, see Rost et al.31). Pt from the platinum oxide may also dissolve into the electrolyte during the reductive scan, leading to platinum corrosion; however, this Pt dissolution is expected to be more dominant when a thicker oxide is formed.6,32
When comparing the stripe model and our corresponding results to the electrochemical place-exchange studies, we find that oxide chains are plausible products of Pt(111) oxidation under electrochemical conditions, compatible with X-ray diffraction analysis by Drnec et al.4 Although the structures we studied exhibit long-range order, which runs contrary to the conclusions of Drnec et al., the observation of disordered and isolated spokewheels by Van Spronsen et al. in early Pt(111) oxidation is consistent with both our dilated stripe structures and findings by Drnec et al.4,17 Pt atoms are suspended by more than one oxygen atom; in fact, two oxygen atoms per Pt atom are adsorbed above surface platinum atoms. This agrees with electron distributions found by Drnec et al.,4 yet contradicts their assumed place exchange model in which one O atom displaces one Pt atom and is incorporated into the surface.4,22 Additionally, even though they consider their data based on the traditional concept of place-exchange, their observation of two discrete zones of oxygen atoms between two layers of Pt atoms, rather than being embedded within a surface Pt layer,4 suggests no oxygen is incorporated into the surface during place exchange, and that no oxygen is found above the Pt atoms. This contradicts the alternatingly buckled stripe model as proposed by Holby et al.15 The stripes found through our relaxation had O atoms and lifted Pt atoms elevated roughly the same amount above the original Pt(111) surface, which seems to disagree with the Pt(surf)–O–Pt layering found by Drnec et al.; however, we did not include dipole stabilization, which does happen in aqueous environments and may provide a driving force for lifted Pt atoms to pucker out of the stripe. Altogether, we find that non-buckled stripe – or spokewheel – formation is a more likely process of electrochemical oxidation of Pt(111) than either buckled stripes or traditional place exchange.
4. Conclusion
Understanding the driving forces for stripe structure formation allows us to better understand Pt catalyst structure evolution under oxidative and electrochemical conditions. We have found a clear correlation between increasingly oxidative potentials and the surface phase transition from adsorbed oxygen to the PtO2 stripes, and the thermodynamics of stripe formation suggests that the optimum average Pt–Pt spacing, and the spacing observed in spokewheel PtO2 structures by Van Spronsen et al., is close to that of both bulk PtO2 species. This results in expulsion of platinum atoms relative to the Pt density in the surface layer, allowing the dilation of the stripe to occur. Formation of these PtO2 stripes is plausible at electrochemical potentials similar to those suggested in literature for oxygen adsorption and surface oxide formation. This indicates we have found a plausible early oxidation structure which not only closely corresponds to the stripe hypothesis by van Spronsen et al. and their observations in gas phase, but also provide a good description of the electrochemical oxidation of the Pt(111) surface. The platinum oxide structures we have found are a key towards understanding the roughening observed during oxidation–reduction cycles, as well as to the formation of thicker oxide layers on Pt(111).Our findings show that accurate computational modeling of electrochemical oxidation reactions on Pt(111) is possible, including active sites specific to PtO2 stripes. This knowledge is equally applicable to Pt(111) surfaces under elevated O2 pressure. Hence, future computational work may aid the design of more active real-life industrial platinum(-like) catalysts.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by the Netherlands Organization for Scientific Research (NWO) in the framework of the Solar Fuels Graduate Program. Additionally this project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 707404. Supercomputing facilities (Cartesius at surfSARA) used in this project were sponsored by NWO Physical Sciences, with financial support from NWO.References
- B. L. M. Hendriksen and J. W. M. Frenken, Phys. Rev. Lett., 2002, 89, 046101 CrossRef CAS.
- M. D. Ackermann, T. M. Pedersen, B. L. M. Hendriksen, O. Robach, S. C. Bobaru, I. Popa, C. Quiros, H. Kim, B. Hammer, S. Ferrer and J. W. M. Frenken, Phys. Rev. Lett., 2005, 95, 255505 CrossRef CAS.
- I. Langmuir, Trans. Faraday Soc., 1922, 17, 621–654 RSC.
- J. Drnec, M. Ruge, F. Reikowski, B. Rahn, F. Carla, R. Felici, J. Stettner, O. M. Magnussen and D. A. Harrington, Electrochim. Acta, 2017, 224, 220–227 CrossRef CAS.
- Y. Furuya, T. Mashio, A. Ohma, M. Tian, F. Kaveh, D. Beauchemin and G. Jerkiewicz, ACS Catal., 2015, 5, 2605–2614 CrossRef CAS.
- A. A. Topalov, I. Katsounaros, M. Auinger, S. Cherevko, J. C. Meier, S. O. Klemm and K. J. J. Mayrhofer, Angew. Chem., Int. Ed., 2012, 51, 12613–12615 CrossRef CAS.
- V. Komanicky, K. C. Chang, A. Menzel, N. M. Markovic, H. You, X. Wang and D. Myers, J. Electrochem. Soc., 2006, 153, B446–B451 CrossRef CAS.
- M. Matsumoto, T. Miyazaki and H. Imai, J. Phys. Chem. C, 2011, 115, 11163–11169 CrossRef CAS.
- T. M. Pedersen, W. X. Li and B. Hammer, Phys. Chem. Chem. Phys., 2006, 8, 1566–1574 RSC.
- P. P. Lopes, D. Tripkovic, P. F. B. D. Martins, D. Strmcnik, E. A. Ticianelli, V. R. Stamenkovic and N. M. Markovic, J. Electroanal. Chem., 2018, 819, 123–129 CrossRef CAS.
- L. Jacobse, Y. F. Huang, M. T. M. Koper and M. J. Rost, Nat. Mater., 2018, 17, 277–282 CrossRef CAS.
- S. P. Devarajan, J. A. Hinojosa and J. F. Weaver, Surf. Sci., 2008, 602, 3116–3124 CrossRef CAS.
- J. M. Hawkins, J. F. Weaver and A. Asthagiri, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 125434 CrossRef.
- A. Farkas, D. Fantauzzi, J. E. Mueller, T. W. Zhu, C. Papp, H. P. Steinruck and T. Jacob, J. Electron Spectrosc., 2017, 221, 44–57 CrossRef.
- E. F. Holby, J. Greeley and D. Morgan, J. Phys. Chem. C, 2012, 116, 9942–9946 CrossRef CAS.
- H. Luo, S. Park, H. Y. H. Chan and M. J. Weaver, J. Phys. Chem. B, 2000, 104, 8250–8258 CrossRef CAS.
- M. A. van Spronsen, J. W. M. Frenken and I. M. N. Groot, Nat. Commun., 2017, 8, 429 CrossRef.
- A. K. N. Reddy, M. A. Genshaw and J. O. Bockris, J. Chem. Phys., 1968, 48, 671–674 CrossRef CAS.
- H. You, D. J. Zurawski, Z. Nagy and R. M. Yonco, J. Chem. Phys., 1994, 100, 4699–4702 CrossRef CAS.
- B. E. Conway, B. Barnett, H. Angerstein-Kozlowska and B. V. Tilak, J. Chem. Phys., 1990, 93, 8361–8373 CrossRef CAS.
- B. E. Conway, Prog. Surf. Sci., 1995, 49, 331–452 CrossRef CAS.
- M. Ruge, J. Drnec, B. Rahn, F. Reikowski, D. A. Harrington, F. Carla, R. Felici, J. Stettner and O. M. Magnussen, J. Am. Chem. Soc., 2017, 139, 4532–4539 CrossRef CAS.
- Y. H. Liu, A. Barbour, V. Komanicky and H. You, J. Phys. Chem. C, 2016, 120, 16174–16178 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed.
- S. Hanselman, M. T. M. Koper and F. Calle-Vallejo, ACS Energy Lett., 2018, 3, 1062–1067 CrossRef CAS.
- Y. F. Huang, P. J. Kooyman and M. T. M. Koper, Nat. Commun., 2016, 7, 12440 CrossRef CAS.
- Y. F. Huang and M. T. M. Koper, J. Phys. Chem. Lett., 2017, 8, 1152–1156 CrossRef CAS.
- A. M. Gomez-Marin and J. M. Feliu, Electrochim. Acta, 2012, 82, 558–569 CrossRef CAS.
- M. J. Rost, L. Jacobse and M. T. M. Koper, Nat. Commun., 2019 DOI:10.1038/s41467-019-13188-0.
- X. Deng, F. Galli and M. T. M. Koper, J. Am. Chem. Soc., 2018, 140, 13285–13291 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Thermodynamics of stripe formation and free molecules, computational details of DFT calculations and stripe geometries, DFT formation energies and corrections for free molecules, surface and stripe vibrational analysis including bulk modes, formation energies of PtO2 structures under standard conditions, and stripe formation energies with respect to Pt binding energies. All calculations are performed at 300 K, and simulations were performed using the PBE exchange–correlation functional through VASP. All structural images were rendered using VESTA.33 See DOI: 10.1039/c9cp05107d |
| This journal is © the Owner Societies 2020 |