Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combined density functional theory and molecular dynamics study of Sm0.75A0.25Co1−xMnxO2.88 (A = Ca, Sr; x = 0.125, 0.25) cathode material for next generation solid oxide fuel cell†
Emilia
Olsson
 a,
Jonathon
Cottom
a,
Jonathon
Cottom
 b,
Xavier
Aparicio-Anglès
a and
Nora H.
de Leeuw
b,
Xavier
Aparicio-Anglès
a and
Nora H.
de Leeuw
 *ac
*ac
aDepartment of Chemistry, University College London, WC1H 0AJ, London, UK
bDepartment of Physics and Astronomy, University College London, WC1E 6BT, London, UK
cSchool of Chemistry, Cardiff University, Main Building, Park Place, CF10 3AT, Cardiff, UK. E-mail: deLeeuwN@cardiff.ac.uk
First published on 12th December 2019
Abstract
One of the main challenges facing solid oxide fuel cell (SOFC) technology is the need to develop materials capable of functioning at intermediate temperatures (500–800 °C), thereby reducing the costs associated with SOFCs. Here, Sm0.75A0.25MnxCo1−xO2.88 (A = Ca, or Sr) is investigated as a potential new cathode material to substitute the traditional lanthanum–strontium manganate for intermediate temperature SOFCs. Using a combination of density functional theory calculations and molecular dynamics simulations, the crucial parameters for SOFC performance, such as the electronic structure, electronic and ionic conductivity, and thermal expansion coefficient, were evaluated. An evaluation of the results illustrates that the conductivity and thermal match of the materials with the electrolyte is dramatically improved with respect to the existing state-of-the-art.
1. Introduction
Solid oxide fuel cells (SOFC) are devices that are used to efficiently convert chemical energy into electrical energy.1 As the name indicates, the electrolyte material is a solid oxide, in which oxygen anions are driven from the cathode to the anode by means of an oxygen vacancy hopping mechanism.2,3 However, high operating temperatures are required in order to ensure maximum oxygen conversion and high oxygen diffusion rates through the materials. These high operating temperatures are known to involve serious drawbacks that directly affect the long-term stability of the device.2,3 On the one hand, they favor the reactivity between cell components, and on the other hand, the device is subject to additional mechanical stress derived from the different thermal expansion of the materials.4 Hence, the costs of SOFC are inflated due to short cell lifetimes, in addition to the intrinsic high cost of the materials, making improving SOFC durability a key objective before the potential of these devices can be realized.5Logically, durability can be improved by reducing the energetic budget available to breakdown processes, as such one of the main goals is to reduce the operating temperature. With the current cathode material of choice La1−xSrxMnO3−d (LSM), the oxygen reduction becomes inefficient and the cathode is no longer able to support efficient oxygen diffusion with a reduced thermal budget.2,6–9 As a result, alternative cathode materials have been extensively investigated, among these SmCoO3-based perovskites have gained increasing attention as potential substitutes for LSM. At intermediate temperatures (500–800 °C), SmCoO3-based perovskites have higher oxygen reduction efficiency and, unlike LSM, they support rapid oxygen diffusion, thus showing SmCoO3 to be an efficient mixed ionic and electronic conductor (MIEC).1 The balance between both types of conductivity is important, and they are inversely related to the oxygen content.10 Hence, high oxygen content benefits electronic conduction (σe) but lowers the ionic conductivity (σO), consequently leading to lower oxygen-surface exchange and high cell polarization resistance.10 It is also important to highlight that electronic conduction is typically at least two orders of magnitude larger than the ionic conductivity, therefore, the ionic conductivity is the performance limiting factor for SOFC.10 Efficient SOFC cathode materials should also have good oxygen reduction kinetics at the cathode surface, especially efficient O2 dissociation kinetics. Previous work on O2 dissociation on cathode surfaces have shown that this reaction is commonly facilitated by surface oxygen vacancies.11
Atomistic level characterization of SmCoO3-based perovskites has remained relatively scarce, and hence systematic study of the effect of different dopants on the oxygen diffusion and electronic properties is useful for guiding and understanding experimentally observed trends. Doping SmCoO3 has proven to be an efficient means of balancing both conduction schemes to obtain the best possible performance. From our previous work, we have demonstrated that A-site doping with Ca2+ and Sr2+ significantly enhances oxygen diffusion,12 and that B-site doping with Mn3+ allows increasing electronic conductivity (σe) and decreasing thermal expansion coefficient (TEC),13 improving compatibility with IT-SOFC electrolyte materials such as gadolinium-doped ceria (GDC). Previous work on related perovskites has shown that the interaction between the divalent dopants and oxygen vacancies (which are formed to charge compensate upon divalent ion doping) can result in the formation of dopant-vacancy clusters. These clusters could act as oxygen vacancy traps, hence limiting the ionic conductivity. Ca has generally been seen to have a stronger binding to oxygen vacancies than Sr, but this binding energy is in many cases negligible at IT-SOFC operating conditions.14–17 Hence both Sr and Ca are investigated as dopants in this study. Furthermore, both Ca and Sr are commonly used in La-based perovskites to increase oxygen ion conduction.18,19 In this work, we show that the combination of dopants at both the Sm- and Co-sites leads to a cathode material with both high oxygen and electron conduction, guiding the way towards the next generation of cathode materials.
2. Computational methods
To investigate the influence of Ca, Sr, and Mn doping on the electronic and ionic conductivities, the electronic structure of the different systems was studied using density functional theory (DFT) calculations in the Vienna ab initio simulation package, VASP.20–23 The projector-augmented wave method (PAW) was applied to describe the ion–electron interaction,24 and the kinetic energy cut-off was set to 500 eV. All calculations were spin-polarized with the Perdew–Burke–Ernzerhof (PBE)25 functional and ran until electronic and ionic self-consistence, with a convergence criteria of 10−5 eV and 10−3 eV Å−1, respectively. For each atomic species, we considered the following valence electrons: Sm (5s25p66s2), Ca (3s23p64s2), Sr (4s24p65s2), Mn (3p63d64s1), Co (4s23d7), and O (2s22p4). The tetrahedron method with Blöchl corrections for smearing26 was applied with a 4 × 4 × 4 Γ-centered Monkhorst–Pack grid,27 and Bader AIM (Atoms in Molecules) charges were calculated using the Henkelman algorithm.28,29 All DFT calculations were performed in the 40 atoms 2 × 2 × 2 Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m pseudo-cubic simulation cell. We have used the On-site coulombic interaction (DFT+U) for the Co and Mn 3d-electrons to account for the self-interaction error,30–32 by means of Dudarev's approach,33 with Hubbard parameters (Ueff) for Mn and Co of 4 and 3 eV respectively.13,34,35 To evaluate σe, the electronic transport properties was calculated using the BoltzTrap code (version 2),36 which calculates electronic transport properties in terms of constant relaxation time (τ) from the Boltzmann transport equation. Due to the lack of experimental data for τ for the here investigated materials, we present both σe/τ, and σe with an approximated τ from previous literature studies.
m pseudo-cubic simulation cell. We have used the On-site coulombic interaction (DFT+U) for the Co and Mn 3d-electrons to account for the self-interaction error,30–32 by means of Dudarev's approach,33 with Hubbard parameters (Ueff) for Mn and Co of 4 and 3 eV respectively.13,34,35 To evaluate σe, the electronic transport properties was calculated using the BoltzTrap code (version 2),36 which calculates electronic transport properties in terms of constant relaxation time (τ) from the Boltzmann transport equation. Due to the lack of experimental data for τ for the here investigated materials, we present both σe/τ, and σe with an approximated τ from previous literature studies.
In tandem with the DFT+U calculations, molecular dynamics (MD) simulations were conducted to evaluate the ion diffusion and the thermal response of the bulk material, employing the DL_POLY 4.07 code37 to simulate a 20 × 20 × 20 supercell (39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms) under NPT conditions with a Nosé–Hoover thermostat.38 With a timestep of 0.5 fs and an equilibration period of 11 ps, statistics were collected after a production run of 100 ps. The Ewald summation was employed to account for electrostatic interactions, with the Verlet algorithm evaluating the atomic motions. Short-range interatomic interactions were simulated using the Buckingham potential, within the Born model for ionic solids.39–41 Electronic polarization was included through the shell model, where ions are modeled as cores with a harmonic spring (k) connected to a massless shell with charge Y. The interatomic potentials used here (ESI† Table S1) are primarily obtained from Olsson et al., and Cherry et al., which have previously been used to model ionic conductivity (σO) in perovskites.12,19,42–44
000 atoms) under NPT conditions with a Nosé–Hoover thermostat.38 With a timestep of 0.5 fs and an equilibration period of 11 ps, statistics were collected after a production run of 100 ps. The Ewald summation was employed to account for electrostatic interactions, with the Verlet algorithm evaluating the atomic motions. Short-range interatomic interactions were simulated using the Buckingham potential, within the Born model for ionic solids.39–41 Electronic polarization was included through the shell model, where ions are modeled as cores with a harmonic spring (k) connected to a massless shell with charge Y. The interatomic potentials used here (ESI† Table S1) are primarily obtained from Olsson et al., and Cherry et al., which have previously been used to model ionic conductivity (σO) in perovskites.12,19,42–44
3. Results and discussion
3.1 Dopant configuration
To evaluate the effect of the mixed doping scheme on electronic, thermal expansion, and conduction properties of SmCoO3, the energetically most stable dopant configurations need to be explored and identified. To achieve this all the non-equivalent dopant and oxygen vacancy distributions in the SmCoO3 lattice are identified using the Site-Occupancy Disorder (SOD) program.45 SOD uses bulk symmetry operations to determine all the inequivalent lattice position, thus limiting consideration of the dopant configurations to the non-equivalent substitutions only. Sr and Ca concentrations of 0.25 were considered, based on our previous work.12 According to the Kröger–Vink notation for this dopant scheme (ESI† eqn (S.1)), one oxygen vacancy (VO) is required to ensure the charge neutrality of the system. For Mn, we have considered two different concentrations, 0.125 and 0.25, based on our previous study on Co-site doping in these materials.13 This resulted in 3 different configurations for x = 0.125, and 23 for x = 0.25.After bulk optimization using DFT+U, we calculated the relative abundance of each configuration at intermediate working temperatures using Boltzmann distributions,45 showing that only the most stable configuration for each x is expected to be found. This was evident for both concentrations and dopant combinations, although more so for x = 0.125, where the difference in energy between the different configurations was higher than that found between the three most stable configurations for x = 0.25 (a full list is available in Table S2 in the ESI†). Hence, only the most stable configuration per concentration was considered to evaluate the electronic structure of the system.
3.2 Electronic and magnetic structures
From projected density of states plots (PDOS), it can be seen that Sm0.75A0.25MnxCo1−xO2.88 is half-metallic with electronic conduction being only possible through the α-channel. The effect of Ca and Sr on the electronic structure is similar, whereas the major difference between the systems lay in the Mn concentration. For x = 0.125 this α-channel is mainly described by an overlapping of O(2p) and Co t2g and eg states, but without any contribution from the Mn(3d) orbitals, whereas for x = 0.25 Mn(3d), both t2g and eg are also present. The overlap of the t2g and eg orbitals in all electronic structures (Fig. 1), is a result of the loss of the Co octahedral environment that is necessary for an effective octahedral crystal field splitting of the orbitals, evidenced by the distortion of the Co–O bonds relative to the non-doped SCO matrix (Table 1).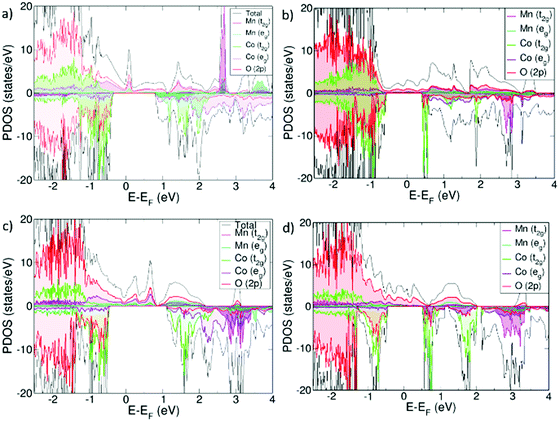 | ||
| Fig. 1 Projected Density of States (PDOS) for (a) Sm0.75Ca0.25Mn0.125Co0.875O2.88, (b) Sm0.75Sr0.25Mn0.125Co0.875O2.88, (c) Sm0.75Ca0.25Mn0.25Co0.75O2.88 and (d) Sm0.75Sr0.25Mn0.25Co0.75O2.88. | ||
| Ca | Sr | |||
|---|---|---|---|---|
| x = 0.125 | x = 0.25 | x = 0.125 | x = 0.25 | |
| μ Mn (μB) | 3.29 | 3.48 | 3.38 | 3.49 |
| μ Co (μB) | 0.19, 0.25, 1.89, 2.01, 2.04, 2.41, 2.96 | 2.03, 2.20, 2.27 | 0.02, 0.12, 0.14, 0.28, 1.86, 2.49, 2.94 | 2.31, 2.32, 2.92 |
| q A | 1.55 | 1.55 | 1.58 | 1.59 |
| q Sm | 2.10 | 2.12 | 2.10 | 2.13 |
| q Co | 1.23, 1.25, 1.31, 1.34 | 1.28, 1.29, 1.18, 1.19 | 1.26, 1.22, 1.18, 1.49 | 1.26, 1.27, 1.33 |
| q Mn | 1.71 | 1.67 | 1.77 | 1.74 |
| q O | −1.15 | −1.16 | −1.15 | −1.18 |
| Co–O (Å) | 1.86, 1.87, 1.89, 1.90, 1.91, 1.93, 1.94, 1.95, 1.96, 1.97 | 1.87, 1.88, 1.91, 1.94, 1.96 | 1.83, 1.84, 1.87, 1.88, 1.89, 1.91, 1.92, 1.93, 1.94, 1.95, 1.96, 1.97 | 1.85, 1.86, 1.88, 1.89, 1.91, 1.94, 1.95 |
| Mn–O (Å) | 1.87, 1.90, 1.91, 1.98 | 1.95, 1.96, 1.98, 1.99 | 1.89, 1.93, 1.94, 1.97 | 1.91, 1.93, 1.94, 1.95, 1.97, 2.00 |
Consequently, this enables different Co d-orbital occupations from the expected t62ge0g, thus leading to low-to-intermediate spin states (LS/IS), intermediate (IS), and intermediate-to-high (IS/HS) spin states (see ESI† for a full description of the different spin states), as deduced from Co magnetizations (Table 1). From a non-distorted octahedral environment, cobalt magnetic moments (μCo) are expected to be 0 (low spin state), but under the presence of distortions, μCo increase. In the ideal case, IS gives μCo = 2, and HS μCo = 4, whereas the combined IS/HS will have μCo with values in between 2 and 4. For x = 0.125, μCo ranges from 0.19 to 2.96 for the Ca-containing system, and from 0.02–2.94 for the Sr-containing one. Hence, LS/IS, IS, and IS/HS spin states are observed for Co in both materials. For x = 0.25, all Co in both systems show an IS state of around 2. Distortions in the Co–O bond distances, compared to pristine SmCoO3, is unequivocally related to the Co magnetic moments, where the more distorted the system is, the more uniform are μCo values. Distortion, however, does not seem to influence μMn as it is high for both concentrations; the Mn–O distortions are therefore more likely to be an effect of Mn being a Jahn–Teller center. Moreover, different magnetic orderings were calculated, with the ferromagnetic found to be the most stable ordering for all cases studied. Finally, according to the calculated Bader charges, Table 1, there is no evidence of charge transfer between any of the metallic species, as was also seen in previous studies.13
3.3 Electronic conductivity
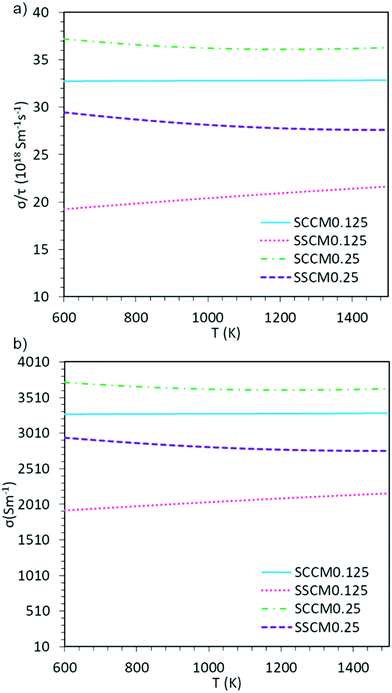
The subtle differences observed in the electronic structure of these materials could have a direct impact on their respective electronic transport properties, which could also vary with temperature. To evaluate the electronic transport properties of these materials at IT-SOFC conditions, the electronic conductivity as a function of temperature (600–1500 K) is presented in Fig. 2. It is important to note here, that due to a lack of experimental values of τ for these systems, we present both the electronic conductivity over relaxation time (σe/τ), and σe with an approximate τ of 10−16 s. τ in this range has previously been used for other cobaltate, manganate, and calcium systems.46–48 Regardless of the chosen τ, these results are useful for comparing the different dopant schemes and trends therein.The calculated σe (Fig. 2) show greater conductivity for x = 0.25 than for x = 0.125, indicating that a higher portion of manganese in these perovskite systems is beneficial for electronic conduction, regardless of A-site dopant. This difference in electronic conductivity between the two concentrations is directly associated with the fact that for x = 0.125 there is no contribution from either Co or Mn at the Fermi level, whereas they do contribute for x = 0.25, making the conduction more effective. Moreover, the Ca-containing systems show higher σe, both as a function of constant relaxation time (Fig. 2a), and when explicitly setting the relaxation time (Fig. 2b). Finally, the trends regarding temperature and dopant concentration seen in Fig. 2 is in line with previous experimental results.5,49–53 At IT-SOFC operating temperatures the limiting factor to IT-SOFC cathode efficiency lies in the ionic and not the electronic conductivity, and hence it is of utmost importance that one also evaluates a material's ionic conductivity.
3.4 Ionic conduction
Thus, it becomes also necessary to study the ionic conductivity (σO). Computationally, σO can be calculated from oxygen diffusion coefficients (DO), which are obtainable from the mean square displacement (MSD) of oxygen atoms, calculated using MD simulations, through| 〈r2(t)〉 = 6DOt + BO | (1) |
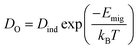 | (2) |
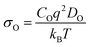 | (3) |
| T (K) | Ca | Sr | ||
|---|---|---|---|---|
| D O, x = 0.125 | D O, x = 0.25 | D O, x = 0.125 | D O, x = 0.25 | |
| 600 | 0.759 | 2.45 | 2.17 | 2.11 |
| 800 | 2.93 | 4.09 | 4.33 | 4.58 |
| 1000 | 7.69 | 9.04 | 7.83 | 8.91 |
| 1200 | 23.0 | 23.8 | 22.5 | 18.5 |
| 1500 | 75.9 | 80.7 | 74.2 | 65.7 |
| E mig (eV) | 0.42 | 0.44 | 0.42 | 0.38 |
| TEC (×106 K−1) | 19.5 | 14.6 | 19.7 | 16.7 |
Sm0.75A0.25MnxCo1−xO2.88 show very high DO (Table 2), for the whole range of temperatures. As a result, oxygen diffusion is markedly more efficient in these materials than in LSM, regardless of Mn-concentration. Furthermore, Emig for the oxygen diffusion remains mostly unchanged with increasing x, at around 0.42 eV, which is ≈40% lower than LSM,41 thus confirming these materials as excellent oxygen conductors.54 Furthermore, these four systems show similar Emig to La0.9Sr0.1ScO3−d (0.47 eV),55 Sr-doped LaFeO3 (0.44 eV),16 La0.5Sr0.5Co0.75Fe0.25O3−d (0.44 eV),56 Ba0.5Sr0.5Co0.75Fe0.25O2.88 (0.42, and 0.46 eV),57 and Ba0.5Sr0.5CoO2.88 (0.40, and 0.43 eV).57 From these results it is clear that Sm0.75A0.25MnxCo1−xO2.88 material presents a distinct improvement on LSM, both in terms of Emig and DO, and shows oxygen migration energies in line with previously reported good IT-SOFC cathode candidates.41 Additionally, from comparison with experimental LSM (DO = 3 × 10−12 cm2 s−1 at 900 °C (1173 K)58), it is clear that DO is much higher in Sm0.75A0.25MnxCo1−xO2.88. The calculated σO (Fig. 2), derived from DO according to the formula shown in the ESI,† shows the same trend as observed for DO, with Mn-doping not providing any genuine advantage on σO. However, it is clearly seen that at low temperatures, Mn-doping at x = 0.25 is most advantageous as it produces the highest σO. As the ionic conduction is the rate-limiting process (and orders of magnitudes lower than σe) for IT-SOFC MIEC cathodes, a higher σO is more beneficial for the application investigated here. Furthermore, comparing the Sm-site dopants, Sr has lower Emig, but comparable DO to the Ca-doped system. Hence, in agreement with studies on related lanthanide perovskites, both Sr and Ca dopants are highly beneficial for generating high oxygen ion conductivity, and more importantly higher than the traditional SOFC cathode LSM (Fig. 3).9,18,59
3.5 Thermal expansion
The suitability of these materials as IT-SOFC cathodes is further determined by their electrolyte compatibility. An IT-SOFC cathode should have a TEC of the same order as the electrolyte, too large a difference in thermal expansion responses will lead to cell failure. Hence, the final part of this study deals with the thermal expansion of Sm0.75A0.25Co1−xMnxO2.88. The TEC (αT) is related to the supercell volume, assuming a linear dependence, through eqn (4), and was obtained from MD simulations.60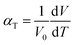 | (4) |
For Sm0.75A0.25Co1−xMnxO2.88 to be a viable candidate material for SOFC cathodes, its TEC needs to be close to that of SOFC electrolyte materials. Common SOFC electrolytes include YSZ, LSGM, and GDC, which have TEC of 10–13 × 10−6 K−1, and it is generally accepted that cathodes with TEC smaller than 15 × 10−6 K−1 are suitable.61,62 TEC for x = 0.125 is calculated to be 19.5 × 10−6 K−1, and 19.7 × 10−6 K−1 for Ca- and Sr-doped, respectively. A larger difference in the thermal expansion behavior is observed at x = 0.25, where Ca-doped has a TEC of 14.6 × 10−6 K−1, and Sr-doped 16.7 × 10−6 K−1, which shows that these materials should be suitable for IT-SOFC cathodes.
4. Conclusion
In this work, a systematic DFT and MD study of Sm0.75A0.25Co1−xMnxO2.88 has been conducted to elucidate these materials’ suitability as next-generation IT-SOFC cathodes. Sm0.75Ca0.25Co0.75Mn0.25O2.88 showed the most promising electronic conductivity occurring via both Co and Mn d-orbitals that overlap at the Fermi level. This overlap is a consequence of the distortion induced by the dopants, which at the same time facilitates a different electron occupation in the metal-d orbitals, which overall results in a ferromagnetic arrangement of the different magnetic moments. Improvement, as compared to SmCoO3 and LSM, was also observed in the ionic conduction, which is the limiting factor for the efficiency of the material at operating temperatures. In fact, Sm0.75Ca0.25MnxCo1−xO2.88 has much higher ionic conductivity and a lower activation energy for oxygen migration than LSM, with fast oxygen diffusion even at lower temperatures. Finally, the last bit of the IT-SOFC cathode puzzle is the mechanical coupling between electrolyte and cathode, described in terms of TEC. We show here, that introducing manganese into the lattice, at x = 0.25, dramatically decreases TEC, reducing it to a value close to IT-SOFC electrolytes. Comparing in between the Sm-site dopants, Ca doping gives slightly lower TEC than Sr, in conjunction with previous studies. The combination of all these properties suggests that Sm0.75A0.25Mn0.25Co0.75O2.88 would combine the optimum bulk properties desirable for IT-SOFC cathode material. These results further justify an investigation into the surface properties of this material, especially into the oxygen reduction reaction kinetics, and will be the topic of a future report.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors acknowledge the Engineering and Physical Sciences Research Council (EPSRC) for financial support (Grants references EP/K016288/1 and EP/K001329/1), the UCL Grace High Performance Computing Facility (Grace@UCL), and the Hartree Centre resources in this work. Finally, via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202, EP/R029431), this work made use of the facilities of ARCHER, the UK's national high-performance computing service. N. H. D. L. thanks the Royal Society for an Industry Fellowship. E. O. gratefully acknowledges EPSRC funding from the Centre for Doctoral Training in Molecular Modelling and Materials Science (EP/G036675/1). Information on the data underpinning the results presented here, including how to access them, can be found in the Cardiff University data catalogue at http://doi.org/10.17035/d.2019.0086840493.References
- I. Fullarton, J. Jacobs and H. Van Benthem, Study of oxygen ion transport in acceptor doped samarium cobalt oxide, Ionics, 1995, 1, 51–58 CrossRef CAS.
- R. M. Ormerod, Solid oxide fuel cells, Chem. Soc. Rev., 2003, 32, 17–28 RSC.
- B. C. Steele and A. Heinzel, Materials for fuel-cell technologies, Nature, 2001, 414, 345–352 CrossRef CAS.
- C. Yu and S. B. Adler, Thermal and Chemical Expansion of Sr-Doped Lanthanum Cobalt Oxide (La1−xSrxCoO3−δ), Chem. Mater., 2005, 17, 4537–4546 CrossRef.
- Y. Wang, X. Zhao, S. Lü, X. Meng, Y. Zhang, B. Yu, X. Li, Y. Sui, J. Yang, C. Fu and Y. Ji, Synthesis and characterization of SmSrCo2−xMnxO5+δ (x = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0) cathode materials for intermediate-temperature solid-oxide fuel cells, Ceram. Int., 2014, 40, 11343–11350 CrossRef CAS.
- S. M. Haile, Fuel cell materials and components. The Golden Jubilee Issue—Selected topics in Materials Science and Engineering: Past, Present and Future, Acta Mater., ed. S. Suresh, 2003, vol. 51, pp. 5981–6000 Search PubMed.
- S. J. Skinner, Recent advances in Perovskite-type materials for solid oxide fuel cell cathodes, Int. J. Inorg. Mater., 2001, 3, 113–121 CrossRef CAS.
- J. Van Herle, A. J. J. McEvoy and K. Ravindranathan Thampi, A study on the La1−xSrxMnO3 oxygen cathode, Electrochim. Acta, 1996, 41, 1447–1454 CrossRef CAS.
- R. A. De Souza, J. A. Kilner and J. F. Walker, A SIMS study of oxygen tracer diffusion and surface exchange in La0.8Sr0.2MnO3+δ, Mater. Lett., 2000, 43, 43–52 CrossRef CAS.
- R. Pelosato, G. Cordaro, D. Stucchi, C. Cristiani and G. Dotelli, Cobalt based layered perovskites as cathode material for intermediate temperature Solid Oxide Fuel Cells: A brief review, J. Power Sources, 2015, 298, 46–67 CrossRef CAS.
- Y. Cao, M. J. Gadre, A. T. Ngo, S. B. Adler and D. D. Morgan, Factors controlling surface oxygen exchange in oxides, Nat. Commun., 2019, 10, 1346 CrossRef PubMed.
- E. Olsson, X. Aparicio-Anglès and N. H. de Leeuw, A computational study of the electronic properties, ionic conduction, and thermal expansion of Sm1−xAxCoO3 and Sm1−xAxCoO3−x/2 (A = Ba2+, Ca2+, Sr2+, and x = 0.25, 0.5) as intermediate temperature SOFC cathodes, Phys. Chem. Chem. Phys., 2017, 19, 13960–13969 RSC.
- E. Olsson, J. Cottom, X. Aparicio-Anglès and N. H. de Leeuw, Computational study of the mixed B-site perovskite SmBxCo1−xO3−d (B = Mn, Fe, Ni, Cu) for next generation solid oxide fuel cell cathodes, Phys. Chem. Chem. Phys., 2019, 21, 9407–9418 RSC.
- M. S. Islam, P. R. Slater, J. R. Tolchard and T. Dinges, Doping and defect association in AZrO(3) (A = Ca, Ba) and LaMO(3) (M = Sc, Ga) perovskite-type ionic conductors, Dalton Trans., 2004, 3061–3066 RSC.
- J. Okasinski, J. B. Cohen, J. Hwang, T. O. Mason, Z. Ding, O. Warschkow and D. E. Ellis, Defect and electronic structures of calcium-doped lanthanum cuprate, J. Am. Ceram. Soc., 1999, 82, 2451–2459 CrossRef CAS.
- A. Jones and M. S. Islam, Atomic-scale insight into LaFeO3 perovskite: Defect nanoclusters and ion migration, J. Phys. Chem. C, 2008, 112, 4455–4462 CrossRef CAS.
- M. S. Islam, Computer modelling of defects and transport in perovskite oxides, Solid State Ionics, 2002, 154–155, 75–85 CrossRef CAS.
- M. Islam and M. Cherry, Protons in LaMO3: atomistic modelling and ab initio studies, Solid State Ionics, 1997, 97, 33–37 CrossRef CAS.
- M. S. D. Read, M. S. Islam, G. W. Watson, F. King and F. E. Hancock, Defect chemistry and surface properties of LaCoO3, J. Mater. Chem., 2000, 10, 2298–2305 RSC.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. Perdew, K. Burke and M. Ernzerhof, Errata: Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 77, 1396 CrossRef.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- T. Geng, Z. Han and S. Zhuang, Effective Coulomb interaction in LaMnO3, Phys. B, 2010, 405, 3714–3716 CrossRef CAS.
- P. Ravindran, A. Kjekshus, H. Fjellvåg, A. Delin and O. Eriksson, Ground-state and excited-state properties of LaMnO3 from full-potential calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 064445 CrossRef.
- P. Ravindran, R. Vidya, H. Fjellvåg and A. Kjekshus, Electronic Structure and Excited-state Properties of Perovskite-like Oxides, J. Cryst. Growth, 2004, 268, 554–559 CrossRef CAS.
- S. Dudarev, G. Botton and S. Savrasov, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- Y.-L. Lee, J. Kleis, J. Rossmeisl and D. Morgan, Ab initio energetics of LaBO3 (001) (B = Mn, Fe, Co, and Ni) for solid oxide fuel cell cathodes, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 224101 CrossRef.
- E. Olsson, X. Aparicio-Anglès and N. H. de Leeuw, Ab initio study of vacancy formation in cubic LaMnO3 and SmCoO3 as cathode materials in solid oxide fuel cells, J. Chem. Phys., 2016, 145, 014703 CrossRef PubMed.
- G. K. H. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, DL_POLY, J. Mater. Chem., 2006, 16, 1911–1918 RSC.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- M. Born and J. Mayer, Lattice theory of ionic solids, Phys. B, 1932, 75, 1–18 CAS.
- J. E. Mayer, Dispersion and Polarizability and the van der Waals Potential in the Alkali Halides, J. Chem. Phys., 1933, 1, 270–279 CrossRef CAS.
- M. S. Islam, M. Cherry and C. R. A. Catlow, Oxygen Diffusion in LaMnO3 and LaCoO3 Perovskite-Type Oxides: A Molecular Dynamics Study, J. Solid State Chem., 1996, 124, 230–237 CrossRef CAS.
- M. Cherry, M. S. Islam and C. R. A. Catlow, Oxygen ion migration in perovskite-type oxides, J. Solid State Chem., 1995, 118, 125–132 CrossRef CAS.
- T. S. Bush, J. D. Gale, C. R. A. Catlow and P. D. Battle, Self-consistent interatomic potentials for the simulation of binary and ternary oxides, J. Mater. Chem., 1994, 4, 831 RSC.
- G. V. Lewis and C. R. A. Catlow, Potential models for ionic oxides, J. Phys. C: Solid State Phys., 1985, 18, 1149–1161 CrossRef CAS.
- R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. de Leeuw, Symmetry-adapted configurational modelling of fractional site occupancy in solids, J. Phys.: Condens. Matter, 2007, 19, 256201 CrossRef.
- J. D. Baran, M. Molinari, N. Kulwongwit, F. Azough, R. Freer, D. Kepaptsoglou, Q. M. Ramasse and S. C. Parker, Tuning Thermoelectric Properties of Misfit Layered Cobaltites by Chemically Induced Strain, J. Phys. Chem. C, 2015, 119, 21818–21827 CrossRef CAS.
- M. Molinari, D. a. Tompsett, S. C. Parker, F. Azough and R. Freer, Structural, electronic and thermoelectric behaviour of CaMnO3 and CaMnO(3−δ), J. Mater. Chem. A, 2014, 2, 14109 RSC.
- J. D. Baran, C. Eames, K. Takahashi, M. Molinari, M. S. Islam and S. C. Parker, Structural, Electronic, and Transport Properties of Hybrid SrTiO3-Graphene and Carbon Nanoribbon Interfaces, Chem. Mater., 2017, 29, 7364–7370 CrossRef CAS.
- H. Kozuka, K. Ohbayashi and K. Koumoto, LaCo1−xNixO3 with Improved Electrical Conductivity, Inorg. Chem., 2012, 51, 9259–9264 CrossRef CAS.
- H. Kozuka, H. Yamada, T. Hishida, K. Ohbayashi and K. Koumoto, SrxLa1−xMnO3: N-type oxides with phase stability at high temperatures in air, J. Mater. Chem. A, 2013, 1, 3249–3253 RSC.
- H. Kozuka, K. Ohbayashi and K. Koumoto, Electronic conduction in La-based perovskite-type oxides, Sci. Technol. Adv. Mater., 2015, 16, 026001 CrossRef PubMed.
- H. Kozuka, H. Yamada, T. Hishida, K. Yamagiwa, K. Ohbayashi and K. Koumoto, Electronic transport properties of the perovskite-type oxides La1−xSrxCoO3 ± delta, J. Mater. Chem., 2012, 22, 20217 RSC.
- K. Cvejin, L. Manjakkal, J. Kulawik, K. Zaraska and D. Szwagierczak, Characterization and applicability of Sm0.9Sr0.1CoO3−δ in oxygen sensors, Microelectron. Int., 2014, 31, 154–157 CrossRef CAS.
- T. C. Yeh, J. L. Routbort and T. O. Mason, Oxygen transport and surface exchange properties of Sr0.5Sm0.5CoO3−δ, Solid State Ionics, 2013, 232, 138–143 CrossRef CAS.
- T. T. Mayeshiba and D. D. Morgan, Factors controlling oxygen migration barriers in perovskites, Solid State Ionics, 2016, 296, 71–77 CrossRef CAS.
- Y. A. Mastrikov, R. Merkle, E. A. Kotomin, M. M. Kuklja and J. Maier, Formation and migration of oxygen vacancies in La(1−x)Sr(x)Co(1−y)Fe(y)O(3−δ) perovskites: insight from ab initio calculations and comparison with Ba(1−x)Sr(x)Co(1−y)Fe(y)O(3−δ), Phys. Chem. Chem. Phys., 2013, 15, 911–918 RSC.
- M. M. Kuklja, E. A. Kotomin, R. Merkle, Y. A. Mastrikov and J. Maier, Combined theoretical and experimental analysis of processes determining cathode performance in solid oxide fuel cells, Phys. Chem. Chem. Phys., 2013, 15, 5443–5471 RSC.
- S. P. Jiang, Development of lanthanum strontium manganite perovskite cathode materials of solid oxide fuel cells: a review, J. Mater. Sci., 2008, 43, 6799–6833 CrossRef CAS.
- C. Tealdi, L. Malavasi, C. A. J. Fisher and M. S. Islam, Disproportionation, dopant incorporation, and defect clustering in perovskite-structured NdCoO3, J. Phys. Chem. B, 2006, 110, 5395–5402 CrossRef CAS PubMed.
- N. Orlovskaya, M. Lugovy, S. Pathak, D. Steinmetz, J. Lloyd, L. Fegely, M. Radovic, E. A. Payzant, E. Lara-curzio, L. F. Allard and J. Kuebler, Thermal and mechanical properties of LaCoO3 and La0.8Ca0.2CoO3 perovskites, J. Power Sources, 2008, 182, 230–239 CrossRef CAS.
- Z. Gao, L. V. Mogni, E. C. Miller, G. Railsback, S. A. Barnett, J. G. Railsback and S. A. Barnett, A perspective on low-temperature solid oxide fuel cells, Energy Environ. Sci., 2016, 9, 1602–1644 RSC.
- J. A. Kilner and M. Burriel, Materials for Intermediate-Temperature Solid-Oxide Fuel Cells, Annu. Rev. Mater. Res., 2014, 44, 365–393 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Interatomic potential set used for the molecular dynamics simulations, the oxygen vacancy compensation scheme equation, dopant configuration selection and Boltzmann distributions, and a graphic description of the cobalt spin state. See DOI: 10.1039/c9cp04892h |
| This journal is © the Owner Societies 2020 |