Mechanism of highly enhanced hydrogen storage by two-dimensional 1T′ MoS2†
Abstract
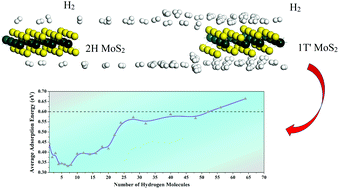
Hydrogen energy is a high-efficiency and clean energy, but the problem of storage still prevents its extensive use. Large-surface-area, two-dimensional (2D) layered materials have an advantage in hydrogen storage applications. Monolayer MoS2 is a typical 2D material that has been widely studied recently. And the 1T′ phase of MoS2 is a focus especially for studies concerning hydrogen. Here, first-principles calculations are carried out to investigate the adsorption behaviors of hydrogen molecules on 1T′ MoS2. Comparing with other MoS2-based materials, such as doped or decorated 2H-MoS2, 1T′ MoS2 has even better performance in hydrogen adsorption, and its preparation is easier. In multiple hydrogen molecule adsorption, the material shows good stability and appropriate adsorption energy while adsorbing hydrogen molecules. With the researches in this paper, the connection between the adsorption energy and hydrogen mass fraction was set up. This can provide a reference for further studies on hydrogen storage applications.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...