2D-Coordination polymers based on 1H-indazole-4-carboxylic acid and transition metal ions: magnetic, luminescence and biological properties

Abstract

We report the formation of five novel multifunctional coordination polymers based on 1H-indazole-4-carboxylic acid (HL). To the best of our knowledge, these complexes are the first examples of coordination compounds constructed with this interesting ligand. These materials were synthesized by solvothermal routes, possess different 2D-structures and show interesting magnetic properties due to the copper compound showing an unusual spin-canted effect while the anisotropic cobalt material behaves as a field-induced single molecule magnet. MTT assays performed on human embryonic kidney (HEK293) and mouse skin melanoma (B16-F10) cell lines indicated that the Cd-based compound was the only one exhibiting dose-dependent toxicity on B16-F10 cells, most likely due to the release of toxic Cd(II). Cadmium and zinc polymers exhibit interesting luminescence properties. The fact that zinc polymers did not exhibit inherent toxicity against both cancer and non-cancerous cells make this new family an excellent candidate for further investigation in the field of luminescent materials with biomedical applications.

---

Introduction

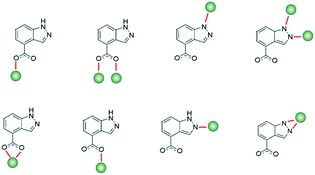
Interest in coordination polymers (CPs), also known as metal–organic frameworks (MOFs), has been remarkably increasing,¹ due to their multiple types of verified industrial applications,² such as gas storage and purification, catalysis, luminescence and magnetism, as well as the great possibilities they offer in design and their great synthetic reproducibility. Of particular interest is the fact that their metal–organic hybrid nature offers potentially limitless arrangement types and topological architectures,³ reinforcing the versatility of use. In particular, the study of transition metal ion-based MOFs has evolved enormously in a great quantity of areas, and considering the advantage that ions have fairly predictable coordination spheres, it allows us to design materials with application for virtually all fields. In this sense, in recent years, our group and others have worked on the design of novel MOFs to study their properties in luminescence,⁴ gas adsorption,⁵ catalysis,⁶ magnetism,⁷ biology as drug-delivery systems,⁸ cytotoxic agents⁹ and sensing.¹⁰ Bearing in mind the interest of our group in the study of MOFs based on nitrogen linkers with carboxylate groups, we decided to study the properties of this type of materials with the interesting 1H-indazole-4-carboxylic acid because, as far as we know, there are no coordination compounds synthesized with it. This ligand is an ideal candidate for forming CPs because of its multiple coordination possibilities derived not only from its carboxylate group but also from its indazole ring,¹¹ being able to show some interesting coordination modes (Scheme 1).

Scheme 1 Plausible coordination modes of 1H-indazole-4-carboxylic acid.

In addition, the study of the properties of these materials can be very interesting, not only it can enable promising photoluminescence performance resulting from aromatic rings, but also it has been seen in some recent studies that they can have very interesting anti-cancer properties, turning these CPs into interesting multifunctional materials.

Considering all of the above, in this work, we present a new family of 2D-coordination polymers, [Co(L)₂(H₂O)₂]_n (1), [Ni(L)₂(H₂O)₂]_n (2), [Cu(L)₂(H₂O)]_n (3), [Zn(L)₂]_n (4) and [Cd(L)₂]_n (5), based on 1H-indazole-4-carboxylic acid and transition metal ions, which have been fully characterized from a structural, luminescence and cytotoxic point of view, highlighting the magnetic properties.

Results and discussion

A solvothermal reaction between 1H-indazole-4-carboxylic acid and the corresponding metal salts in DMF : H₂O (1 : 1) for 24 h produces five new MOF coordination polymers based on two-dimensional systems with interesting properties.

Description of the structures

Compounds 1 and 2 crystallize in the monoclinic P2₁/c space group and are isostructural materials; therefore, only the structure of 1 is described in detail. The Co(II) ion is located in an inverted position, so that the asymmetric unit contains a half cobalt ion, one deprotonated ligand and a coordination water molecule (Fig. 1a). The Co1 ion has a well-defined octahedral CoN₂O₄ coordination environment according to SHAPE values (Table S4†). The coordinating heteroatoms are all placed in trans positions according to their nature (imine N atoms, carboxylate O atoms and water O atoms). Due to the negative charge of the carboxylate oxygen atoms, the shortest bond distance corresponds to Co1–O1 (2.0913(9) Å), while Co1–O1W and Co1–N1 distances appear to be somewhat longer (2.1266(9) and 2.1539(11) Å, respectively).

Fig. 1 a) Building unit of compound 1 with atom labels for the coordination sphere. Dashed blue lines represent the intramolecular hydrogen bonds. b) View along the b axis of the packing of three 2D layers, each of them with a different colour. The same structure was obtained for compound 2.

The structure is extended in two directions from each single Co(II) atom. Firstly, the indazole derivatives that are coordinated from N1 are inversely oriented so that the carboxylate groups are located in the opposite sites (Fig. 1a). Thus, these carboxylate groups coordinate in a monodentate mode to other metallic centers in a zigzag fashion (Fig. 1b). Secondly, the carboxylate groups coming from other two main ligands are nearly perpendicular to imine coordinated indazole derivatives (an angle of 72.68° is formed between the two ligands growing in different directions), expanding the structure in a plane. The structures grow in independent 2D layers (Fig. 1b), but intermolecular hydrogen bonds play an essential role in stabilizing the structure (Fig. S1†). The trans water molecules act as a donor and acceptor of these bonds. In fact, they form intramolecular hydrogen bonds with the non-coordinating carboxylate O2 atom, forming a distorted six membered ring (Co1–O1W–H1W1⋯O2–C8–O1) and an intermolecular bond with O1 (O1W⋯O1). O1W accepts an additional intermolecular hydrogen bond from a neighbouring imine group (N2⋯O1W). The ionic Co(II) centres are well isolated within the same chain with a distance of 9.104 Å, whereas the intermolecular distances are much shorter (5.301 Å).

Compound 3 crystallizes in the monoclinic system and the P2₁/c space group. Although it is similar to 1 and 2, in this case, the asymmetric unit is comprised of a single Cu(II) ion coordinated to two crystallographically independent monoanionic ligands (labelled A and B) and one coordination water molecule (Fig. 2). The Cu1 ion possesses a CuN₂O₃ coordination environment (Fig. 2a), forming a slightly distorted polyhedron between a square pyramid and vacant octahedron according to the SHAPE measurements (Table S5†). The two nitrogen atoms N1A and N1B in opposite positions along with two monodentate carboxylate oxygen atoms belonging to two other main ligands (O1A(i) and O1B(i)) are nearly coplanar and form the base of the pyramid. The remaining oxygen atom O1W from the water molecule is coordinated in the apical position, completing the polyhedron. The Cu–O_carboxylate bonds are the shortest ones (1.948(3) and 1.972(3) Å), whereas the Cu–N bonds are slightly longer (1.993(4) and 2.013(4) Å) and Cu–O1W shows the longest distance with 2.361(4) Å.

Fig. 2 a) Building unit of compound 3 with atom labels for the coordination sphere. Dashed blue lines represent the intramolecular hydrogen bonds. b) View along the b axis of the packing of three 2D layers, each of them coloured by a different colour.

Similar to 1 and 2, the structure is extended in two directions from each Cu(II) atom. The inversely oriented indazole derivatives are responsible for the zigzag expansion of the structure. In this case, the intrachain adjacent Cu(II) polyhedra form an angle of 80.71° between the square bases. In addition to the hydrogen bonds, intermolecular π⋯π interactions among indazole rings significantly influence the crystal packing of the structure and the stabilization of the independent 2D layers (Fig. 2b and S2†). In regard to H bonds, the apical water molecule acts again as a donor (with O1A and O2B atoms) and an acceptor (with an N2A atom). It establishes an intramolecular H bond between O1W⋯O2B (forming an even more distorted six membered ring due to the longer Cu1–O1W distance), whereas an intermolecular one is formed between O1W⋯O1A. At the same time, it accepts an intermolecular H bond from N2A.

Because there is not another water molecule trans to O1W, the non-coordinating oxygen atom from the other carboxylate group is stabilized by a N2B⋯O2A hydrogen bond. Moreover, in this case, the neighbouring molecules form additional intermolecular π⋯π interactions between C1A⋯C5B, C1A⋯C6B and C2A⋯C5B that contribute to the long ordering organization of the structure (Fig. S2†). Finally, it is worth mentioning that the shortest Cu⋯Cu distance arose from the intermolecular ones is 4.743 A, while the intramolecular Cu⋯Cu distances are almost double of this value (8.803 and 8.904 Å).

Relative to compound 4, single crystals could not be isolated for XR diffraction. However, according to infrared spectroscopy and elemental analyses, it may be confirmed that it is probably an isostructural compound to the cadmium based compound 5.

Compound 5 crystallizes in the orthorhombic system and the Pccn space group. The asymmetric unit contains a half Cd(II) ion and a single 1H-indazole-4-carboxylate ligand. Different from the previous structures, in this compound, water molecules are absent and the CdN₂O₄ coordination sphere is bonded to four different indazole derivatives (Fig. 3a). Two of them are coordinated through the imine nitrogen atoms and the others via bidentate carboxylate groups. Thus, the environment of the metal ion is far from an ideal geometry, as all the SHAPE values clearly deviate from zero (Table S4†). Alternatively, when considering the second coordination sphere for the carboxylate units and assuming C8 and C8(i) as the vertices of the polyhedron, a slightly distorted tetrahedral shaped fragment is obtained (Table S6†). Concerning the bond distances, the Cd1–N1 distance is short (2.267(10) Å), whereas the Cd1–O_carboxylate bonds vary from shorter (2.291(9) Å) to longer distances (2.448(10) Å).

Fig. 3 a) Building unit of compound 5 with atom labels for the coordination sphere. b) View along the a axis of the packing of three 2D layers, each of them coloured by a different colour.

The structure grows in 2D layers due to the orientation of the four indazole derivatives coordinated to Cd1. Similar to a propeller, the planes formed by C1–N1–N2 and O1–C8–O2 create open angles in the range of 45.11–78.63°, allowing the structure to extend all over the ab plane (Fig. 3b). In terms of 3D packing, intermolecular hydrogen bonds and π⋯π interactions are fundamental to stabilize the system. Hydrogen bonds are formed between O2⋯N2 of adjacent layers growing in opposite directions. In addition, the indazole rings create π⋯π stacking interactions among them (Fig. S4†). As it occurs with the other structures, the shortest Cd⋯Cd interactions are the ones between different molecules (6.194 Å), although the intramolecular distances are shorter than those in the cobalt, nickel and copper compounds (7.950 Å).

Magnetic properties

Static magnetic measurements. The temperature dependence of the χ_MT product for complexes 1–3 (χ_M being the molar paramagnetic susceptibility of the compound) under a constant magnetic field of 0.1 T in the 2–300 K range is displayed in Fig. 4, 6 and 7, respectively. All the measurements were carried out on the powdered samples.

Fig. 4 Temperature dependence of the χ_MT product for 1 in the 2–300 K range. The red solid line is generated from the best fit to the Hamiltonian in eqn (1).

The χ_MT data for compound 1 is characteristic of anisotropic Co(II) ions. The room temperature value for 1 (3.07 cm³ K mol⁻¹) is much larger than the spin-only value for a high-spin Co(II) ion (S = 3/2, 1.875 cm³ K mol⁻¹ with g = 2). This high value indicates a significant orbital contribution to the magnetic moment. When lowering the temperature, the χ_MT product decreases gradually reaching a minimum of 1.58 cm³ K mol⁻¹ (Fig. 4). The monotonous decrease is mainly associated to spin–orbit coupling (SOC) effects.¹² However, due to the considerably short (5.301 Å) intermolecular interactions between Co(II) ions, weak antiferromagnetic interactions could be also involved. To further analyse the magnetic behaviour of 1, the T state to P state isomorphism (T–P) in the Hamiltonian in eqn (1) is an appropriate option, since the magnetic behaviour of octahedral Co(II) complexes is usually induced by first-order spin–orbital coupling.¹³

Ĥ = σλL̂Ŝ + Δ[L̂_z² − L̂(L̂ + 1/3)] + μ_BH(−σL̂ + g_iŜ) (1)

In this equation, λ is the SOC parameter, σ = −Aκ is a combination of the covalence and orbital reduction factors, and Δ is the axial orbital splitting of the T₁ term. The data were fitted using the software PHI¹⁴ and the following set of parameters was obtained: λ = −183 cm⁻¹, σ = 1.09, Δ = 640 cm⁻¹, and g = 2.06 with R = 6.7 × 10⁻¹.

The field-dependent magnetization curves at different temperatures that are shown in Fig. 5 confirm the presence of significant magnetic anisotropy, since they are not superimposable. In order to gain information about the magnitude and sign of the anisotropy parameter (D), all the isofield magnetization curves were simultaneously fitted using the PHI program based on the following spin Hamiltonian:

Ĥ = gμ_BŜ·B + D(Ŝ_z² − Ŝ²/3) + E(Ŝ_x² − Ŝ_y²) (2)

where S is the spin ground state, D and E are the axial and transverse magnetic anisotropies, respectively, μ_B is the Bohr magneton, and H is the applied magnetic field. The best fit of the data led to the following set of parameters: D = 50.0 cm⁻¹, E = 10.0 cm⁻¹, g_x = g_y = 2.31, g_z = 2.60, and R = 2.52 × 10⁻¹. It is worth mentioning that an unreasonable set of parameters was obtained by changing the sign of D. The influence of intra and intermolecular interactions was neglected in the treatment of the magnetic data due to the results that were obtained from the DFT calculations carried out with the broken-symmetry methodology. A dinuclear fragment of 1 was cut from the crystal structure in order to represent the superexchange pathway. The calculation suggests a negligible coupling with very weak ferromagnetism (J ∼ 0.004 cm⁻¹, Fig. S5†).

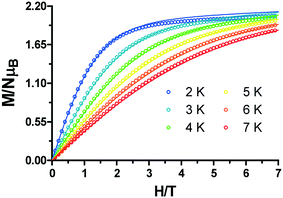Fig. 5 Field dependence of the magnetization for 1. The solid lines are generated from the best fit to the magnetic parameters.

At room temperature, the χ_MT value of 1.04 cm³ K mol⁻¹ for complex 2 is in good agreement with the expected value of 1.00 cm³ K mol⁻¹ for an isolated Ni(II) ion with g = 2.0 (Fig. 6). Upon cooling, the χ_MT value remains nearly constant up to 10 K and then abruptly decreases, reaching a minimum value of 0.69 cm³ K mol⁻¹. This behaviour is the first evidence of zero-field splitting (ZFS) in Ni(II) compounds.⁷ In addition, the magnetization curve at 2 K saturates below 2μ_B, which definitely confirms the presence of this effect (Fig. 6, inset).¹⁵ We assume that the long (9.045 Å) intramolecular distances will cause negligible interactions (as it was confirmed for 1 by DFT calculations) in comparison to the mentioned ZFS. Therefore, the dc magnetic susceptibility data and magnetization curves at different temperatures were simultaneously analysed with the PHI software and the Hamiltonian in eqn (2).

Fig. 6 Temperature dependence of the χ_MT product for 2 in the 2–300 K range. Inset: Field dependence of the magnetization for 2. The solid lines are generated from the best fit to the magnetic parameters.

The best fit of the experimental data was obtained with the following set of parameters: g = 2.04, D = −10.58 cm⁻¹, and E = +0.29 cm⁻¹, with R = 2.49 × 10⁻². In view of the short intermolecular distances (5.305 Å) between Ni(II) ions provided by hydrogen bonds, intermolecular interactions were considered in the Hamiltonian. However, the fit to the magnetic data afforded nearly the same values, so they were discarded in order to be coherent with the previous fit of 1.

The temperature dependence of the magnetic susceptibility for 3 in the 2–300 K temperature range under an applied field of 0.1 T is displayed in Fig. 7. At room temperature, the χ_MT value of 0.436 cm³ K mol⁻¹ is higher than the spin only value expected for an isolated Cu(II) center (0.375 cm³ K mol⁻¹ with S = 1/2 and g = 2.0). This occurs when the orbital angular moment is not completely quenched, leading to higher g values and, inherently, to higher χ_MT.¹⁶ Upon cooling, the χ_MT decreases gradually from room temperature, reaching the lowest value of 0.355 cm³ K mol⁻¹ at 10 K. Below this temperature, the signal sharply increases to a maximum of 0.467 cm³ K mol⁻¹ at 5 K before it drops rapidly to 0.398 cm³ K mol⁻¹ at 2 K. The maximum displayed at the low temperature could be associated to spontaneous magnetization indicating spin-canted antiferromagnetism that leads, at the same time, to ferromagnetic ordering.¹⁷ The last drop in χ_MT could be explained by the zero-field-splitting (ZFS) of the ground state.¹⁸

Fig. 7 Temperature dependence of the χ_MT product for 3 in the 2–300 K range. Inset: Temperature dependence of the χ_MT product at the indicated fields in the 2–30 K range.

The proposed spin-canted effect can be verified by studying the field-dependence of the χ_MT in the temperature region where the maximum appears. In the inset of Fig. 7, it is evidenced that the χ_MT value is field-dependent. When intensifying the magnitude of the external magnetic field from 4.5 Oe to 500 Oe, the maximum value at 5 K becomes nearly one order of magnitude smaller. This suggests that the high fields are quenching the effect of the weak antiferromagnetism, which confirms the spin canting behaviour.

Moreover, zero-field-cooled (ZFC) and field-cooled (FC) measurements were carried out to continue investigating the aforementioned effect. As shown in Fig. 8a, both curves show a divergence at 6 K, which can be indicative of a possible phase transition.¹⁹ Finally, a hysteresis loop was recorded at 2.0 K in the ±7 T range. Although not obvious, an open loop is seen with a coercive field of 220 Oe and a remnant magnetization of 0.0035μ_B (Fig. 8b, inset)_. The reason for having a small hysteresis loop could arise from a small spin canted effect.

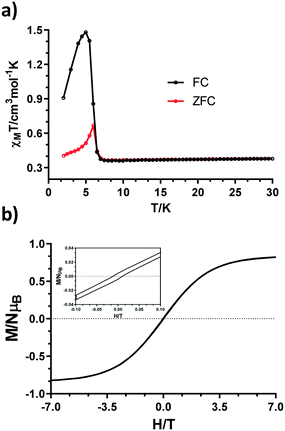Fig. 8 a) ZFC and FC curves under H = 100 Oe. b) Hysteresis loop measured at 2 K in the ±7 T range (bottom).

It has been reported that the origin of such a spin canted effect might arise from single ion anisotropy or from antisymmetric exchange coupling.²⁰ In our case, since the metal ion is Cu(II), which is normally considered isotropic, the second hypothesis was considered. In fact, we performed the same DFT calculations such as the ones that were carried out for 1, but as shown in Fig. S5† and as it could be expected from long intramolecular Cu⋯Cu distances, the interaction appears to be negligible (J ≃ 0.09 cm⁻¹). However, as it was mentioned in the crystal structure description, the intermolecular Cu⋯Cu distances are shorter than the intramolecular ones and this could play an essential role when considering antisymmetric exchange interactions.

Dynamic magnetic measurements. With the aim to find out whether compounds 1 and 2 display slow relaxation of the magnetization or not, dynamic magnetic properties were studied by susceptibility by applying an alternating current (ac) as a function of both temperature and frequency. In the case of 2, there was no signal in the χ_M′′(T) plot even when applying an external static magnetic field, which confirms that there is no SIM behaviour. In contrast, the strong spin-orbit coupling of the Co(II) ion makes compound 1 a more promising candidate for behaving as a SIM. Indeed, even though maxima could not be observed above 2.0 K due to the fast quantum tunnelling of the magnetization (QTM) in the absence of an external magnetic field, when repeating the measurements under an external static field of 1 kOe, frequency dependent maxima could be observed in the χ_M′′(T) plot up to 9.0 K. This behaviour is common in octahedral Co(II) compounds, since they have positive D values as confirmed by the static magnetic measurements and an external magnetic field is required in order to observe slow magnetic relaxation.²¹

In the low frequency (60–1000 Hz) and temperature regions, the presence of two overlapping maxima is observed, which can be attributed to the presence of two thermally activated relaxation processes. When increasing the temperature and the frequency of the oscillating field, the intensity of the first maximum is lowered, although the broadness and the low-symmetry shaped maxima indicate the presence of both processes (Fig. 9).

Fig. 9 Temperature dependence of the molar out-of-phase ac magnetic susceptibility (χ_M′′) for 2 under an applied field of H_dc = 1000 Oe at different frequencies. Inset: Arrhenius plot (blue and red lines) for the relaxation times.

This can be also seen in the Argand diagram (Cole–Cole plot, Fig. S7†), where the sum of two semicircles is observed in the 3.6–6.0 K temperature range, confirming the coexistence of fast and slow relaxation processes (FR and SR, respectively).

In view of this, the relaxation times were extracted for each process, fitting the data in the 2.5–8.0 K range by using a sum of two modified Debye functions with the CCFIT software.²² It is worth mentioning that the software provides τ and α values for the two processes in the whole temperature range. Nonetheless, taking into account that each process operates or predominates in a certain temperature range, Arrhenius plots were constructed individually in the 2.5–5.5 K and 5.5–8.0 K temperature ranges for SR and FR, respectively. In the case of the slow relaxation process, the non-linearity of the relaxation times along with the relatively wide distribution of the α values (0.22(2.5 K)–0.19(5.5 K)) is indicative of the presence of simultaneous relaxation mechanisms. Therefore, the data were fitted to the following equation:

τ⁻¹ = τ₀⁻¹ exp(−U_eff/k_Bt) + AT (3)

where the first term accounts for the Orbach mechanism, while the second one accounts for the direct process. The fit afforded the next set of parameters: A = 710.3 s⁻¹ K⁻¹, τ₀ = 1.73 × 10⁻⁶ s and U_eff = 22.6 K. In contrast, the relaxation times of the FR, which were fitted to the Orbach mechanism, are in agreement with the α values (∼0(5.5 K)–∼0(8.0 K)), which suggest the presence of a unique relaxation mode. The fit afforded the following parameters: τ₀ = 3.88 × 10⁻⁸ s and U_eff = 56.6 K. The occurrence of two independent relaxations could be explained by the presence of short intermolecular distances between Co(II) centers.²³ Although the paramagnetic ions are well isolated within the 2D layers, the hydrogen bonds connecting these layers provoke short interionic distances that could provide weak, but not negligible, interactions. Therefore, one of the processes could be attributed to an exchange coupled system and the other one could arise from each single ion. However, it is worth mentioning that there are other systems in the literature that show the same behaviour even though the paramagnetic ions are well isolated in the structure.²⁴

Photoluminescence studies

Due to its extended aromaticity, the 1H-indazole-4-carboxylic acid ligand is a good candidate for enhancing emissive properties. For this reason, we decided to carry out an experimental–theoretical study of the luminescence properties of the ligand and d¹⁰ compounds in the solid state and at room temperature (Fig. 10). Moreover, recent studies have shown that CPs containing d¹⁰ metal ions enable the stabilization of long-lasting phosphorescence (LLP) or afterglow phenomena.²⁵ Under excitation at 340 nm, compounds 4 and 5 showed an intense emission at 388 nm and 403 nm, respectively. These emission bands are significantly blue shifted with respect to the free ligand (415 nm). Emission bands for these types of aromatic ligands generally originate from π* → σ and/or π* → π photon relaxation; this energy gap generally decreases (red shifted emission or bathochromic emission) upon ligand coordination to metals due to the increased rigidity provided to the system.²⁶ The mentioned hypsochromic emission of these materials must therefore arise from either structural and/or electronic features resulting from events other than metal coordination; such events can cause an increase in the n → π* and/or π → π* energy gap of the light emitting ligand.²⁷ The existence of π–π stacking interaction between rings of neighboring ligands (3.39 Å) (Fig. 3) could explain this effect.

Fig. 10 Room temperature solid-state emission spectra of the ligand (blue), 4 (green) and 5 (red) upon sample excitation at λ_ex = 340 nm.

Cytotoxicity of the coordination polymers

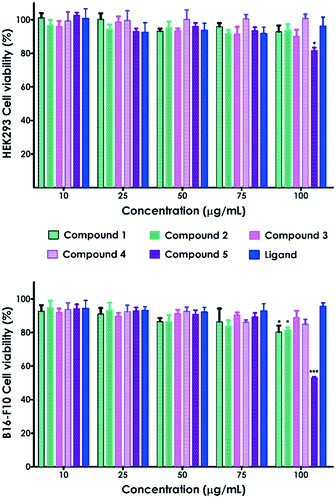
We have also evaluated the biological response of the complexes and the ligand through in vitro cell viability assays on HEK293 human embryonic kidney and B16-F10 skin melanoma cell lines (Fig. 11). The CPs 1–5 and the ligand exhibited no significant toxicity on HEK-293 cells in the analyzed range of concentrations (10–100 μg mL^–1, Fig. 11). Only compound 5 at the highest concentration (100 μg mL⁻¹) prompted a decrease of HEK293 cell viability up to 81.6%. B16-F10 cell viability was also reduced up to 80.2% and 81.4% in contact with 100 μg mL⁻¹ of compounds 1 and 2, respectively (Fig. 11).

Fig. 11 Viability of HEK-293 and B16-F10 cells in contact with compounds 1–5 and the ligand at increasing concentrations (10, 25, 50, 75 and 100 μg mL⁻¹). Data are shown as the mean ± SEM (n = 3). *p < 0.05 and ***p < 0.001 are compared to those of untreated cells using one-way ANOVA followed by a Bonferroni comparison test.

Nonetheless, all these values are above the accepted cytocompatibility cut-off (70%, ISO 10993-5:2009).²⁸ On the other hand, compound 5 showed significant cytotoxicity on melanoma cells (B16-F10), reducing the viability up to 53% at the highest concentration (100 μg mL⁻¹). This toxicity was not observed on embryonic cells, indicating that compound 5 selectively kills B16-F10 skin melanoma cells. Indeed, it has been previously reported that cell lines can differ in their sensitivity to external stimuli.²⁹ The large size of the MOFs, at the micro–millimetric scale, dismisses the uptake in cells as the mechanism of toxicity. Thus, the observed toxicity is most likely due to the release of Cd(II) from the MOFs. In fact, previous studies demonstrated that Cd exhibits dose-dependent toxicity on different cell lines.³⁰ However, these preliminary in vitro results should be complemented with further experiments to further evaluate the observed cell-type specificity.

Conclusion

In summary, a new family of transition metal coordination polymers, with bidimensional structures, have been synthesized with 1H-indazole-4-carboxylic acid: [Co(L)₂(H₂O)₂]_n (1), [Ni(L)₂(H₂O)₂]_n (2), [Cu(L)₂(H₂O)]_n (3), [Zn(L)₂]_n (4) and [Cd(L)₂]_n (5). Static magnetic measurements and DFT calculations performed on 1–3 indicate that the 1H-indazole-4-carboxylate ligand provides almost negligible intrachain exchange interactions. However, the quite unusual spin-canted effect in compound 3, which is normally attributed to anisotropic ions, shows that the shorter intramolecular Cu⋯Cu distances that arise from the packing of the structure could affect the bulk magnetic properties of the material. The more anisotropic Co based compound 1, which behaves as a field-induced single molecule magnet, displays two characteristic maxima in the out-of-phase susceptibility data. These two maxima are defined by thermally activated SR and FR, but having different origins of each process. As occurs in 3, the intermolecular Co⋯Co distances are shorter than the intramolecular ones and this provokes a relaxation that is attributed to a weak exchange coupled system, whereas the other one appears to be of single ion in origin. On the other hand, CPs 4 and 5 exhibit hypsochromic emission with respect to the free ligand, arising from either structural and/or electronic features resulting from events other than metal coordination. Cell viability tests on HEK-293 and B16-F10 cell lines showed non cytotoxic effects with compounds 1–4. However, compound 5 exhibited toxicity on the melanoma B16-F10 cell line. With these studies, we have shown the great versatility of the 1H-indazole-4-carboxylic acid to form coordination polymers with multifunctional applications. Currently, more work is being developed in our laboratory to obtain other systems with different dimensionalities using lanthanide ions.

Experimental

Preparation of complexes

All the reagents were purchased commercially and used without any further purification.

Synthesis of [M(L)₂(H₂O)₂]_n for {M = Co(1), Ni(2)}. Single orange (1) and green (2) crystals were obtained by following the next synthesis method. 0.047 mmol 1H-indazole-4-carboxylic acid was dissolved in 0.5 mL of DMF and 0.5 mL of distilled water. On the other hand, 0.095 mmol MCl₂·6H₂O was dissolved in 0.5 mL of distilled water and 0.5 mL of DMF. Both solutions were mixed in a closed glass vessel and introduced in an oven at 100 °C for 24 h. The crystals were washed with water/methanol. Anal calcd for CoC₁₆H₁₄N₄O₆ (1): C, 46.06; H, 3.38; N, 13.43. Found: C, 46.03; H, 3.36; N, 13.46. Anal calcd for NiC₁₆H₁₄N₄O₆ (2): C, 46.08; H, 3.38; N, 13.44. Found: C, 46.05; H, 3.35; N, 13.47.

Synthesis of [Cu(L)₂(H₂O)]_n (3). The general procedure described for 1 was followed but using CuCl₂·2H₂O as the metal source, which led to green single crystals (3). Yield: 55% based on Cu. Anal calcd for CuC₁₆H₁₂N₄O₅ (3): C, 47.59; H, 2.99; N, 13.87. Found: C, 47.54; H, 2.96; N, 13.90.

Synthesis of [M(L)₂]_n for {M = Zn(4), Cd(5)}. The general procedure described for 1 was followed but using M(C₂H₃O₂)₂·2H₂O as the metal source, which led to white single crystals (4 and 5). Yield: 56% based on metal. Anal calcd for ZnC₁₆H₁₀N₄O₄ (4): C, 49.57; H, 2.60; N, 14.45. Found: C, 49.62; H, 2.56; N, 14.51. Anal calcd for CdC₁₆H₁₀N₄O₄ (5): C, 44.21; H, 2.32; N, 12.89. Found: C, 44.18; H, 2.30; N, 12.91.

In addition to elemental analyses, all the samples were examined by FT-IR spectroscopy (Fig. S9, ESI†).

Physical measurements

Elemental analyses (C, H and N) were carried out at the Centro de Instrumentación Científica (University of Granada) on a Fisons-Carlo Erba analyzer model EA 1108 (Thermo Scientific, Waltham, MA, USA). Infrared (IR) spectra (400–4000 cm⁻¹) were recorded on a Nicolet FT-IR 6700 spectrometer in KBr pellets. Photoluminescence (PL) measurements were carried out on the crystalline samples at room temperature using a Varian Cary-Eclipse fluorescence spectrofluorometer equipped with a Xe discharge lamp (peak power equivalent to 75 kW), Czerny–Turner monochromators, and an R-928 photomultiplier tube. For the fluorescence measurements, the photomultiplier detector voltage was fixed at 600 V, and the excitation and emission slits were set at 5 and 2.5 nm, respectively. Phosphorescence spectra were recorded with a total decay time of 20 ms, a delay time of 0.2 ms and a gate time of 5.0 ms. The photomultiplier detector voltage was set at 800 V, and both excitation and emission slits were open at 10 nm. Alternating current magnetic measurements were performed under zero and 1000 Oe applied static fields on a Quantum Design SQUID MPMS XL-5 device by using an oscillating ac field of 3.5 G and ac frequencies ranging from 600 to 10 000 Hz.

Cell viability assays

Human embryonic kidney (HEK293, ECACC 85120602) and mouse skin melanoma (B16-F10, ATCC® CRL-6322) cell lines were supplied by the Cell Bank of the Scientific Research Center of the University of Granada (Spain). HEK293 cells were cultured in a standard tissue culture flask and maintained in Eagle's minimum essential medium (EMEM with EBSS) supplemented with 2 mM glutamine, 1% non essential amino acids (NEAA), 1 mM sodium pyruvate (NaP) and 10% foetal bovine serum (FBS) at 37 °C with 5% CO₂. B16-F10 cells were cultured in EMEM with EBSS supplemented with 2 mM glutamine and 10% FBS.

The cells were detached from the culture flasks by trypsinization, centrifuged and resuspended. The cells were cultured into a 96-well flat transparent plate (10⁴ cells per well) for 48 hours. Then, the cells were exposed to different concentrations (10, 25, 50, 75 and 100 μg mL⁻¹) of compounds 1, 2, 3, 4 and 5 and the corresponding ligand. All the experiments were performed in triplicate. After 48 hours of culture, cell viability was assessed by MTS assay using the CellTiter 96® AQueous One Solution Reagent (Promega, Madison, WI) according to the manufacturer's instructions. Twenty microliters of the AQueous One Solution Reagent was added to each well and the absorbance at 490 nm was measured with a spectrophotometer (Infinite® 200 PRO NanoQuant) after 2 hours of incubation. This absorbance is proportional to the number of metabolically active cells. The relative cell viability (%) was calculated with respect to the non-treated cells. Results are expressed as the average ± standard error of the mean (S.E.M., as error bars). One-way ANOVA with Bonferroni's post-test was performed using GraphPad Prism software (version 6.0).

Single-crystal structure determination

Single crystals of suitable dimensions were used for data collection. For compounds 1–3 and 5, the diffraction intensities were collected on a Bruker X8 APEX II and Bruker D8 Venture equipped with a photon detector with graphite monochromated MoKα radiation (λ = 0.71073 Å). The data reduction was performed with the APEX2 (ref. 31) software and corrected for absorption using SADABS.³² In all cases, the structures were solved by the direct methods and refined by full-matrix least squares with SHELXL-2018.³³ Details of the selected bond lengths and angles are given in Tables S1–S3.† CCDC reference numbers for the structures are 1940509–1940512 (Table 1).

Table 1 Crystallographic data and structural refinement details for the compounds

Compounds	1	2	3	5
a S = [∑w(F0^2 − Fc^2)^2/(Nobs − Nparam)]^1/2. b R 1 = ∑||F0| − |Fc||/∑|F0|. c Values in parentheses for reflections with I > 2s(I). d wR2 = [∑w(F0^2 − Fc^2)^2/∑wF0^2]^1/2; w = 1/[σ^2(F0^2) + (aP)^2] where P = (max(F0^2, 0) + 2Fc^2)/3 with a = 5.9161.
Formula	C16H14CoN4O6	C16H14NiN4O6	C16H12CuN4O5	C16H10CdN4O4
M r	417.24	417.02	403.84	434.68
Crystal system	Monoclinic	Monoclinic	Monoclinic	Orthorhombic
Space group (no.)	P21/c (14)	P21/c (14)	P21/c (14)	Pccn (56)
a (Å)	5.3010(2)	5.3050(3)	10.1061(8)	12.3609(15)
b (Å)	10.0099(3)	9.9880(4)	9.8617(7)	9.9856(11)
c (Å)	15.2097(6)	15.0820(7)	14.7053(8)	12.3887(14)
α (°)	90	90	90	90
β (°)	96.8820(10)	97.362(2)	94.716(2)	90
γ (°)	90	90	90	90
V (Å^3)	801.25(5)	792.55(7)	1460.62(17)	1529.1(3)
Z	2	2	4	4
D c (g cm^−3)	1.729	1.747	1.836	1.888
μ(MoKα) (mm^−1)	1.117	1.271	1.537	1.459
T (K)	100	100	100	100
Observed reflections	2068 (1890)	2056 (1869)	3769 (2769)	2010 (1829)
R int	0.0464	0.0400	0.1496	0.0683
Parameters	124	124	225	114
GOF^a	0.989	1.057	1.201	1.496
R 1 ^,	0.0284 (0.0246)	0.0254 (0.0223)	0.1269 (0.0868)	0.1192 (0.1130)
wR2^d	0.0662 (0.0642)	0.0571 (0.0558)	0.1355 (0.1254)	0.2917 (0.2890)
Largest difference in peak and hole (e Å^−3)	0.421 and −0.671	0.394 and −0.430	0.663 and −1.303	1.640 and −2.878

---

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support was given by the Junta de Andalucía (Spain) (FQM-394 and FQM-1484), the Red Guipuzcoana de Ciencia, Tecnología e Innovación (OF218/2018), the University of the Basque Country (GIU 17/13), the Gobierno Vasco/Eusko Jaurlaritza (IT1005-16), the Spanish Ministry of Science, Innovation and Universities (MCIU/AEI/FEDER, UE) (PGC2018-102052-A-C22, PGC2018-102052-B-C21), and Junta de Andalucía (FQM-394 and FQM-1484). The authors thank the technical and human support provided by the SGIker of UPV/EHU and European funding (ERDF and ESF). A. Z.-L. is grateful to the Government of the Basque Country for the predoctoral fellowship. J. M. D.-L and G. B. R.-R. acknowledge the FEDER/MCIU/AEI for their Ramón y Cajal (RYC-2016-21042) and Juan de la Cierva (JdC-2017) fellowships, respectively.

Notes and references

1. (a) K. Otsubo, T. Haraguchi and H. Kitagawa, Coord. Chem. Rev., 2017, 346, 123–138; (b) S. Furukawa, J. Reboul, S. Diring, K. Sumida and S. Kitagawa, Chem. Soc. Rev., 2014, 43, 5700–5734; (c) F. X. Xamena, I. Llabres and J. Gascon, RSC Catal. Ser., 2013, 12, 406–424.
2. (a) A. Dhakshinamoorthy and H. Garcia, Chem. Soc. Rev., 2014, 43, 5750–5765; (b) L. Ma, C. Abney and W. Lin, Chem. Soc. Rev., 2009, 38, 1248–1256; (c) P. Horcajada, R. Gref, T. Baati, P. K. Allan, G. Maurin, P. Couvreur, G. Ferey, R. E. Morris and C. Serre, Chem. Rev., 2012, 112, 1232–1268; (d) P. Ramaswamy, N. E. Wong and G. K. H. Shimizu, Chem. Soc. Rev., 2014, 43, 5913–5932; (e) K. Fujie, R. Ikeda, K. Otsubo, T. Yamada and S. Kitagawa, Chem. Mater., 2015, 27, 7355–7361; (f) S. Lee, E. A. Kapustin and O. M. Yaghi, Science, 2016, 353, 808–811; (g) Y. Inokuma, S. Yoshioka, J. Ariyoshi, T. Arai, Y. Hitora, K. Takada, S. Matsunaga, K. Rissanen and M. Fujita, Nature, 2013, 495, 461–466; (h) V. Stavila, A. A. Talin and M. D. Allendorf, Chem. Soc. Rev., 2014, 43, 5994–6010; (i) J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491; (j) G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147; (k) H. S. Quah, W. Chen, M. K. Schreyer, H. Yang, M. W. Wong, W. Ji and J. J. Vital, Nat. Commun., 2015, 6, 7954–7961; (l) A. Dhakshinamoorthy, M. Alvaro and H. Garcia, Chem. Commun., 2012, 48, 11275–11288.
3. W. Lu, Z. Wei, Z.-Y. Gu, T.-F. Liu, J. Park, J. Park, J. Tian, M. Zhang, Q. Zhang, T. Gentle, M. Boscha and H.-C. Zhou, Chem. Soc. Rev., 2014, 43, 5561–5593.
4. J. M. Seco, S. Pérez-Yáñez, D. Briones, J. Á. García, J. Cepeda and A. Rodríguez-Diéguez, Cryst. Growth Des., 2017, 17, 3893–3906.
5. (a) J. M. Seco, D. Fairen-Jimenez, A. J. Calahorro, L. Méndez-Liñán, M. Pérez-Mendoza, N. Casati, E. Colacio and A. Rodríguez-Diéguez, Chem. Commun., 2013, 49, 11329–11331; (b) J. Cepeda, M. Pérez-Mendoza, A. J. Calahorro, N. Casati, J. M. Seco, M. Aragones-Anglada, P. Z. Moghadam, D. Fairen-Jimenez and A. Rodríguez-Diéguez, J. Mater. Chem. A, 2018, 6, 17409–17416.
6. (a) M. Cabrero-Antonino, S. Remiro-Buenamañana, M. Souto, A. A. García-Valdivia, D. Choquesillo-Lazarte, S. Navalón, A. Rodríguez-Diéguez, G. Mínguez Espallargas and H. García, Chem. Commun., 2019, 55, 10932–10935; (b) X. Sang, R. Tao, Y. Zhang, H. Zhu and D. Wang, ChemPlusChem, 2020, 85, 123–129; (c) X. Hu, H. Zhu, X. Sang and D. Wang, Adv. Synth. Catal., 2018, 22, 4293–4300.
7. A. A. García-Valdivia, J. M. Seco, J. Cepeda and A. Rodríguez-Diéguez, Inorg. Chem., 2017, 56, 13897–13912.
8. D. Briones, B. Fernández, A. J. Calahorro, D. Fairen-Jimenez, R. Sanz, F. Martínez, G. Orcajo, E. San Sebastián, J. M. Seco, C. S. González, J. Llopis and A. Rodríguez-Diéguez, Cryst. Growth Des., 2016, 16, 537–540.
9. B. Fernández, I. Oyarzabal, E. Fischer-Fodor, S. Macavei, I. Sánchez, J. M. Seco, S. Gómez-Ruiz and A. Rodríguez-Diéguez, CrystEngComm, 2016, 18, 8718–8721.
10. J. M. Seco, E. San Sebastián, J. Cepeda, B. Biel, A. Salinas-Castillo, B. Fernández, D. P. Morales, M. Bobinger, S. Gómez-Ruiz, F. C. Loghin, A. Rivadeneyra and A. Rodríguez-Diéguez, Sci. Rep., 2018, 8, 14414.
11. C. Ge, X. Sang, L. Zhang and D. Wang, Green Chem., 2018, 20, 1805–1812.
12. E. Colacio, J. Ruiz, E. Ruiz, E. Cremades, J. Krzystek, S. Carretta, J. Cano, T. Guidi, W. Wernsdorfer and E. K. Brechin, Angew. Chem., Int. Ed., 2013, 52, 9130–9134.
13. F. Lloret, M. Julve, J. Cano and E. Pardo, Inorg. Chim. Acta, 2008, 361, 3432.
14. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164.
15. J. Titiš and R. Boča, Inorg. Chem., 2010, 49, 3971.
16. M. Zhu, S.-Q. Su, X.-Z. Song, Z.-M. Hao, S.-Y. Song and H.-J. Zhang, Dalton Trans., 2012, 41, 13267–13270.
17. M. Hernández-Molina, F. Lloret, C. Ruiz-Pérez and M. Julve, Inorg. Chem., 1998, 37, 4131.
18. (a) C. D. Zhang, S. X. Liu, C. Y. Sun, F. J. Ma and Z. M. Su, Cryst. Growth Des., 2009, 9, 3655; (b) S. Z. Li, P. T. Ma, H. Z. Niu, J. W. Zhao and J. Y. Niu, Inorg. Chem. Commun., 2010, 13, 805; (c) J. W. Zhao, D. Y. Shi, L. J. Chen, X. M. Cai, Z. Q. Wang, P. T. Ma, J. P. Wang and J. Y. Niu, CrystEngComm, 2012, 14, 2797.
19. Q. Chen, M. H. Zeng, L. Q. Wei and M. Kurmoo, Chem. Mater., 2010, 22, 4328.
20. T. Moriya, Phys. Rev., 1960, 120, 91.
21. R. Herchel, L. Váhovská, I. Potočňák and Z. Trávníček, Inorg. Chem., 2014, 53, 5896.
22. N. F. Chilton, CCFIT program, The Chilton Group, Manchester, U.K., 2014, http://www.nfchilton.com/software.html.
23. (a) E. A. Buvaylo, V. N. Kokozay, O. Y. Vassilyeva, B. W. Skelton, A. Ozarowski, J. Titiš, B. Vranovičová and R. Boča, Inorg. Chem., 2017, 56, 6999; (b) C. Rajnák, F. Varga, J. Titiš, J. Moncoľ and R. Boča, Eur. J. Inorg. Chem., 2017, 1915; (c) C. Rajnák, J. Titiš, O. Fuhr, M. Ruben and R. Boča, Inorg. Chem., 2014, 53, 8200.
24. R. Boča, J. Miklovič and J. Titiš, Inorg. Chem., 2014, 53, 2367.
25. J. Cepeda and A. Rodríguez-Diéguez, CrystEngComm, 2016, 18, 8556–8573.
26. H.-Y. Ren, C.-Y. Han, M. Qu and X.-M. Zhang, RSC Adv., 2014, 4, 49090.
27. (a) S. S. S. Raj, H. K. Fun, J. Zhang, R. G. Xiong and X. Z. You, Polyhedron, 2006, 25, 635–644; (b) A. J. Calahorro, E. San Sebastián, A. Salinas-Castillo, J. M. Seco, C. Mendicute-Fierro, B. Fernández and A. Rodríguez-Diéguez, CrystEngComm, 2015, 17, 3659–3666.
28. X. Liu, D. P. Rodeheaver, J. C. White, A. M. Wright, L. M. Walker, F. Zhang and S. Shannon, Regul. Toxicol. Pharmacol., 2018, 97, 24–32.
29. (a) M. Khan, A. Mohammad, G. Patil, S. A. Naqvi, L. K. Chauhan and I. Ahmad, Biomaterials, 2012, 33, 1477–1488; (b) B. Fernández, I. Fernández, J. Cepeda, M. Medina-O'Donnell, E. E. Rufino-Palomares, A. Raya-Barón, S. Gómez-Ruiz, A. Pérez-Jiménez, J. A. Lupiáñez, F. J. Reyes-Zurita and A. Rodríguez-Diéguez, Cryst. Growth Des., 2018, 18, 969–978.
30. G. Ravindran, D. Chakrabarty and A. Sarkar, Anim. Cells Syst., 2017, 21, 23–30.
31. Bruker Apex2, Bruker AXS Inc., Madison, Wisconsin, USA, 2004.
32. G. M. Sheldrick, SADABS, Program for Empirical Adsorption Correction, Institute for Inorganic Chemistry, University of Gottingen, Germany, 1996.
33. G. M. Sheldrick, SHELXTL Version 2014/7, http://shelx.uni-ac.gwdg.de/SHELX/index.

---

Footnote

† Electronic supplementary information (ESI) available. Crystallographic tables, continuous shape measurements, figures of the supramolecular structures, magnetic measurements and infrared spectra. CCDC numbers: 1940509–1940512. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ce00544d

---