Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solution and calorimetric thermodynamic study of a new 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) 1 sulfamethazine–3-methylsalicylic acid co-crystal†
1 sulfamethazine–3-methylsalicylic acid co-crystal†
Dipali
Ahuja
 a,
Michael
Svärd
a,
Michael
Svärd
 *b,
Matteo
Lusi
*b,
Matteo
Lusi
 a and
Åke C.
Rasmuson
ab
a and
Åke C.
Rasmuson
ab
aSSPC, the SFI Research Centre for Pharmaceuticals, Bernal Institute, Department of Chemical Sciences, University of Limerick, Co. Limerick, Ireland
bDepartment of Chemical Engineering, KTH Royal Institute of Technology, Teknikringen 42, SE-10044 Stockholm, Sweden. E-mail: micsva@kth.se
First published on 4th May 2020
Abstract
A new 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal of sulfamethazine (API, SMT) and 3-methylsalicylic acid (coformer, 3mSA) has been synthesized and its crystal structure solved by single crystal X-ray diffraction (XRD). The co-crystal has been thoroughly characterized by powder XRD, thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC). The pure co-crystal could be synthesized by solvent drop grinding, cooling crystallization and slurry conversion co-crystallization. Ternary phase diagrams have been constructed in methanol and acetonitrile at 30 °C. The co-crystal exhibits incongruent dissolution in both solvents. The thermodynamics of co-crystal formation have been estimated from solubility data and calorimetric data, respectively, showing that formation of the SMT–3mSA co-crystal from its solid components is spontaneous and entropy-driven. The co-crystal formation is associated with a 5% increase in molecular volume. A relationship between the size of the region where the co-crystal is the most stable solid phase and the relative solubility of the co-crystal components has been uncovered. The co-crystal region becomes smaller as the solubility ratio increases.
1 co-crystal of sulfamethazine (API, SMT) and 3-methylsalicylic acid (coformer, 3mSA) has been synthesized and its crystal structure solved by single crystal X-ray diffraction (XRD). The co-crystal has been thoroughly characterized by powder XRD, thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC). The pure co-crystal could be synthesized by solvent drop grinding, cooling crystallization and slurry conversion co-crystallization. Ternary phase diagrams have been constructed in methanol and acetonitrile at 30 °C. The co-crystal exhibits incongruent dissolution in both solvents. The thermodynamics of co-crystal formation have been estimated from solubility data and calorimetric data, respectively, showing that formation of the SMT–3mSA co-crystal from its solid components is spontaneous and entropy-driven. The co-crystal formation is associated with a 5% increase in molecular volume. A relationship between the size of the region where the co-crystal is the most stable solid phase and the relative solubility of the co-crystal components has been uncovered. The co-crystal region becomes smaller as the solubility ratio increases.
Introduction
Many active pharmaceutical ingredients (APIs) fall in the Biopharmaceutics Classification System (BCS) class II category, signifying a high permeability but low solubility.1 Hence, development of new opportunities and techniques to improve and control the pharmacological properties of APIs is vital.2 Both crystalline and amorphous solid forms can be exploited, but the former is preferable for meeting specifications related to stability, purity and processing.3 Modification of crystal packing and intermolecular interactions of molecules directly affects the physicochemical properties. This approach is called crystal engineering3 and has facilitated tailoring of solid forms with enhanced desirable properties such as solubility,4 hygroscopicity,5 stability,6,7 and bioavailability.8Co-crystals are single-phase crystalline solids composed of two or more different components in a specific stoichiometric ratio.9 Molecules of any shape or size possessing complementary bonding functionalities can lead to co-crystal formation. They are held together by non-covalent interactions, the most important being hydrogen bonding because of its directional nature. The “pKa rule” is often used to predict whether an acid–base pair of compounds will crystallise as a salt or a co-crystal. The rule states that salt formation generally requires a difference of about 3.0 pKa units between the conjugate acid form of the base (protonated form) and the acid, i.e. ΔpKa = [pKa (base) − pKa (acid) ≥ 3.0]. If the pKa of acid is greater than that of the protonated base leading to a negative ΔpKa value, this most likely leads to the formation of a co-crystal. The prediction is not very accurate for ΔpKa values between 0 and 3, for which either a salt or a co-crystal could form.10,11
A number of co-crystals have been reported in the literature for different APIs, and the number is continuously increasing. For the API in this study, sulfamethazine (SMT), which exists as a single polymorphic form, the number of co-crystals reported in the literature is around 33.12 A few solvates for SMT are also reported in the literature.13 SMT is an antimicrobial and anti-infective agent, used as a veterinary medicine and for treatment of malaria, rheumatoid fever and toxoplasmosis in humans. The coformer, 3-methylsalicylic acid (3mSA), also known as 2,3-cresotinic acid, o-cresotinic acid and hydroxytoluic acid, is a derivative of salicylic acid. There are no polymorphs known for 3mSA in the open literature. It has a marked fibrinolytic activity in human plasma. The chemical structures of the API, SMT and the coformer, 3mSA are shown in Fig. 1.
For robust industrial manufacturing of co-crystals, the size, shape and location of the co-crystal region in the phase diagram is of importance. The appearance and symmetry of the phase diagram depends on the components as well as the solvent. A co-crystal can show congruent or incongruent dissolution, leading to symmetric or asymmetric phase diagrams. However, the factors that cause and control the co-crystal dissolution behaviour are not clear. In previous work, we have shown that the solubility ratio between the pure co-crystal components cannot be used to reliably predict the co-crystal dissolution behaviour.14 However, it has also been shown that pure co-crystal can still be isolated regardless of whether the system is congruent or incongruent.14
In the literature, a few co-crystals have resulted in an improved bioavailability of the poorly soluble API.15–17 The co-crystal solubility is an important parameter, indicative of bioavailability, but for incongruent systems measurement of solubility by traditional methods is not possible. Co-crystal solubility can be represented in terms of the solubility product, which includes the concentration of both solid components.18 The true indicator of co-crystal stability is the Gibbs energy, but there are few studies in the literature dedicated to the thermodynamics of co-crystal formation.19
In this work, a new 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal between SMT and 3mSA has been manufactured, and the crystal structure solved and characterized using X-ray diffraction (XRD), thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC). The ternary phase diagrams of this 1
1 co-crystal between SMT and 3mSA has been manufactured, and the crystal structure solved and characterized using X-ray diffraction (XRD), thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC). The ternary phase diagrams of this 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal system have been constructed in two solvents, methanol and acetonitrile, at 30 °C. The thermodynamic functions of co-crystal formation have been estimated using solubility and calorimetric data. A relationship between the size of the region in the ternary phase diagram where the co-crystal is the stable solid phase and the coformer to API solubility ratio is shown in the present work.
1 co-crystal system have been constructed in two solvents, methanol and acetonitrile, at 30 °C. The thermodynamic functions of co-crystal formation have been estimated using solubility and calorimetric data. A relationship between the size of the region in the ternary phase diagram where the co-crystal is the stable solid phase and the coformer to API solubility ratio is shown in the present work.
Experimental work
Materials
Sulfamethazine (CAS Registry Number 57-68-1), purity >99%, 3-methylsalicylic acid (CAS Registry Number 83-40-9), purity >97% and methanol (CAS Registry Number 67-56-1, HPLC grade, purity >99.9%) were purchased from Sigma-Aldrich. Acetonitrile (CAS Registry Number 75-05-8, HPLC grade, purity >99.9%) was purchased from Fisher Chemicals. All the chemicals were used as received.Solid state analysis
Single-crystal X-ray diffraction measurements for structural determination of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 SMT–3mSA co-crystal were collected at 104 K using a Bruker Quest D8 diffractometer with Mo Kα (λ = 0.7093 Å) radiation. The diffractometer was equipped with CMOS photon detector. Data were corrected for absorption using empirical methods (SADABS) based upon symmetry-equivalent reflections combined with measurements at different azimuthal angles. The structure was solved with the SHELX structure solution program using direct methods and refined with the Olex2 refinement package using Gauss–Newton minimisation. Non-hydrogen atoms were refined anisotropically and hydrogen atoms were placed in calculated positions refined using idealized geometries (riding model) and assigned fixed isotropic displacement parameters.
1 SMT–3mSA co-crystal were collected at 104 K using a Bruker Quest D8 diffractometer with Mo Kα (λ = 0.7093 Å) radiation. The diffractometer was equipped with CMOS photon detector. Data were corrected for absorption using empirical methods (SADABS) based upon symmetry-equivalent reflections combined with measurements at different azimuthal angles. The structure was solved with the SHELX structure solution program using direct methods and refined with the Olex2 refinement package using Gauss–Newton minimisation. Non-hydrogen atoms were refined anisotropically and hydrogen atoms were placed in calculated positions refined using idealized geometries (riding model) and assigned fixed isotropic displacement parameters.
Powder X-ray diffraction (PXRD) data were collected in reflectance mode using an Empyrean diffractometer (PANalytical, Philips) equipped with Cu Kα1,2 radiation (γ = 1.5406 Å) operating at 40 kV and 40 mA at room temperature. Samples were scanned between 2θ values of 5 and 40° at a step size of 0.01313° 2θ with step time 73 s per step on a spinning silicon holder.
An Agilent Technologies 1260 Infinity Series setup comprising a 1260 Quat solvent delivery pump, auto injector, absorbance UV spectrophotometric detector (275 nm) and Agilent ChemStation software was used for HPLC analysis. A Macherey-Nagel EC 100/4.6 Nucleodur C18 column was used. Methanol and 2% (v/v) acetic acid in water in the volume ratio 88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 were used as the mobile phase.
12 were used as the mobile phase.
A TA Instruments Q50 V20.13 Build 39 under nitrogen environment was used to perform thermogravimetric analysis (TGA) experiments. Samples were placed on open platinum pans and heated up to 773 K at a ramp rate of 20 K min−1.
Melting temperatures and associated enthalpies of fusion were determined using a TA Instruments Q2000 differential scanning calorimeter, at a constant heating rate of 3 K min−1. In all DSC experiments, evenly distributed powder samples of approx. 5 mg were encapsulated in Tzero aluminum pans, the furnace was purged with nitrogen gas at 50 mL min−1, and the instrument was calibrated against the melting properties of indium. The heat capacity signal was calibrated using a linear function of temperature against a sapphire sample. Sample weights were re-measured after each run to verify that no mass loss due to sublimation, evaporation or degradation had occurred.
Preparation of co-crystal
The co-crystal was initially synthesized using the solvent drop grinding method. Equimolar amounts of sulfamethazine (SMT) and 3-methylsalicylic acid (3mSA) were weighed. The mix was finely ground with a few drops of acetonitrile for about 15–20 minutes by hand using a pestle and mortar. The resulting white powder was characterized by PXRD and DSC. Slurry conversion co-crystallization (explained below) was employed for the co-crystal synthesis for ternary phase diagram investigations.Measurement of solubility
Solubility of SMT and 3mSA in acetonitrile and methanol at 30 °C was determined by a gravimetric technique explained previously.14 An OHAUS Explorer analytical balance with a resolution of 10−4 g was used for weighing of chemicals. The experiments were carried out in 30 mL glass vials with magnetic stirrer bars. The water bath setup comprised a Grant ST26 stainless steel thermostatic water bath; 26 L, 505 × 300 × 200 mm; equipped with a Grant C2G cooling unit and a Grant GR150 control unit; stability ±0.01 °C and uniformity ±0.05 °C with a serial submersible 60 points magnetic stirrer plate (2Mag) placed on the base and a submersible water pump (1400 L h−1) to enhance circulation in the bath. For each solute, an amount of solid material in excess of solubility was added to 5 mL solvent at 30 °C and allowed to reach equilibrium under stirring. After 24 hours, the agitation was stopped and the solids allowed to settle for a period of 15–20 minutes. 1 mL of the clear, saturated liquid above the solid was pipetted out using a pre-heated syringe and filtered through a 0.2 μm PTFE syringe filter into a pre-weighed pre-heated glass vial (m1). The vial was then weighed immediately and the mass recorded as m2. The solvent was then allowed to evaporate by placing the vial for a sufficient time (usually overnight) in the fume hood until visually dry and the mass recorded. The mass at the point where no further decrease could be observed was considered to be the mass of the dry vial (m3). The solubility was then calculated using (m3 − m1)/(m2 − m3) as g of solute per g of solvent. In each case, three repeats were performed. To confirm the identity of the solid form, the solid material in the equilibrium slurry was sampled and analysed by PXRD.Construction of the ternary phase diagram and determination of invariant points
Phase diagrams for this co-crystal system were constructed in two solvents (methanol and acetonitrile) at 30 °C. Slurry conversion was employed to determine the invariant points by equilibrating several mixtures of the two solid co-crystal components with the solvent. The solid and the solution phases were then analysed. At 30 °C, SMT and 3mSA were mixed with the solvent and stirred for 72 hours, a time sufficient to reach equilibrium. Preliminary experiments were performed to establish the equilibration time. Slurry experiments were run for different times, starting from 24 hours and gradually increasing the time until constant concentrations of SMT and 3mSA were reached at 48 hours. The suspension was left to stand to allow sedimentation of the solid material. The saturated solution was withdrawn and filtered into two aliquots. The solid material was analyzed by PXRD. One aliquot of the liquid was diluted by pure solvent and examined by HPLC. The concentration of SMT and 3mSA was determined from calibration curves in the pure solvent. The second aliquot of the liquid phase was evaporated to dryness to determine the total dissolved solute in the liquid phase by gravimetry. The solubility of the pure components and the composition of the invariant points were converted to mass fraction on a total mass basis and plotted using the Prosim Ternary Diagram software.20Single crystal preparation
The ternary phase diagram was used as guidance to identify a composition where the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal was the most stable solid phase. SMT, 3mSA and acetonitrile were mixed in the corresponding ratio and the mixture was allowed to stir at 30 °C. The saturated solution was withdrawn with a pre-heated syringe, filtered into a preheated glass vials, and heated to 30 °C for 30 minutes. The solution was then allowed to stand at 20 °C in a temperature-controlled water bath until single crystals were obtained. The crystals were isolated, surface dried on Whatman filter paper before PXRD analysis was carried out.
1 co-crystal was the most stable solid phase. SMT, 3mSA and acetonitrile were mixed in the corresponding ratio and the mixture was allowed to stir at 30 °C. The saturated solution was withdrawn with a pre-heated syringe, filtered into a preheated glass vials, and heated to 30 °C for 30 minutes. The solution was then allowed to stand at 20 °C in a temperature-controlled water bath until single crystals were obtained. The crystals were isolated, surface dried on Whatman filter paper before PXRD analysis was carried out.
Results and discussion
Solid phase and crystal structure analysis
The crystallographic data obtained for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal between SMT and 3mSA is summarized in Table 1.
1 co-crystal between SMT and 3mSA is summarized in Table 1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 SMT–3mSA co-crystal
1 SMT–3mSA co-crystal
| SMT–3mSA co-crystal | |
|---|---|
| Stoichiometry | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
| Empirical formula | C20H22N4O5S |
| Formula mass | 430.48 |
| Temperature (K) | 104 |
| Crystal system | Orthorhombic |
| Space group | Pbca |
| a (Å) | 11.0926 (6) |
| b (Å) | 14.8423 (8) |
| c (Å) | 25.6676 (14) |
| α (°) | 90 |
| β (°) | 90 |
| γ (°) | 90 |
| V (Å3) | 4225.9 (4) |
| Z | 8 |
| P calc (g cm−3) | 1.353 |
| R-factor (%) | 5.35 |
| μ (mm−1) | 0.192 |
| θ (max) | 28.456 |
| N ref | 5330 |
| N par | 274 |
| Goodness-of-fit (GOF) | 1.159 |
The crystal structure belongs to the Pbca space group (orthorhombic). Fig. 2 depicts the molecular packing and hydrogen bond pattern present in the co-crystal. The asymmetric unit of the SMT–3mSA co-crystal comprising one molecule of SMT and one molecule of 3mSA is held by a R22(8) hydrogen bond motif between the 3mSA carboxylic acid and the amide tautomer of SMT. The N–H---O bond between SMT sulfonamide and 3mSA carbonyl, and the O–H---N bond between 3mSA hydroxyl and SMT pyrimidine nitrogen, are key components of the crystal structure. The phenyl ring of 3mSA shows π–π interactions with both the pyrimidine (parallel displacement) and phenyl ring (T-shaped) of SMT. Two SMT molecules are held together by hydrogen bonds of the type N–H---O. Each SMT molecule is bonded to two other SMT molecules and one 3mSA molecule. The dihedral angle between the two rings (phenyl and pyrimidine) in SMT of the co-crystal, 72.11° is close to the corresponding angle, 75.55° in pure SMT, which is a monomorphic system.21 The angles around the trigonal carbon in 3mSA of the co-crystal, 115.83° and 121.60°, are similar to those observed in pure 3mSA.22 The central ‘S’ atom in the SMT molecule, both in single and multicomponent crystal structures, shows tetrahedral geometry. The angle in pure SMT is ∼108.2°, and that in the co-crystal is ∼107.8°.
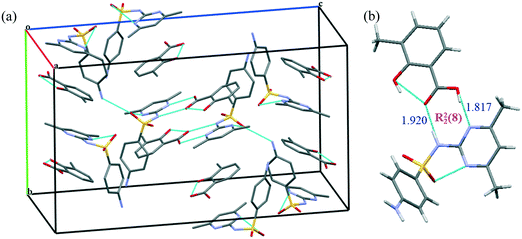 | ||
Fig. 2 Unit cell of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 SMT–3mSA co-crystal depicting the crystal packing and bonding pattern (a), hydrogen bonding forming a R22(8) moiety in the SMT–3mSA co-crystal, distances in Å (b). 1 SMT–3mSA co-crystal depicting the crystal packing and bonding pattern (a), hydrogen bonding forming a R22(8) moiety in the SMT–3mSA co-crystal, distances in Å (b). | ||
The optical micrograph of the co-crystal single crystal shows a plate-like crystal habit as seen in Fig. 3.
The experimental PXRD pattern recorded for the co-crystal matches well with the that calculated (using the software Mercury) from the crystal structure determined by the single crystal-XRD (Fig. 4a). In addition, the co-crystal pattern is unique as compared to the pure components, indicating the formation of a new solid phase (Fig. 4b).
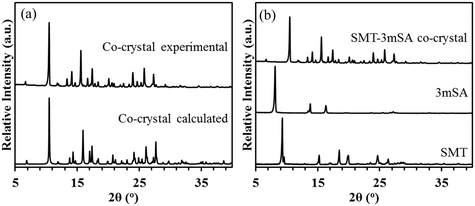 | ||
Fig. 4 Experimental and simulated PXRD patterns for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 SMT–3mSA co-crystal (a); comparison of PXRD patterns between the SMT–3mSA co-crystal with SMT and 3mSA (b). 1 SMT–3mSA co-crystal (a); comparison of PXRD patterns between the SMT–3mSA co-crystal with SMT and 3mSA (b). | ||
The crystal structure determination suggests that the solid is a co-crystal as opposed to a salt. The two C–O bond lengths for the carboxylate group of the coformer, 3mSA are 1.242 and 1.302 Å, bringing the difference to 0.06 Å. This is similar to the case of the SMT–salicylic acid co-crystal, where the difference between the two C–O bond lengths is 0.049 Å (GEYSAE).23 For salts, this difference is usually less than 0.03 Å as the carboxylate ion, formed after proton loss goes into resonance.24 Using 2.6525 as pK1 value for the conjugate acid form of the basic SMT and 2.9526 as pK1 value for 3mSA, ΔpKa becomes −0.3, which according to the pKa rule also suggests that SMT–3mSA should form a co-crystal as opposed to a salt.27 These pKa values correspond to the amino functional group of the basic API and to the carboxylic group of the acidic coformer. The interactions in the co-crystal occur through the sulfonamide group of the API and the carboxylic group of the coformer. It is interesting to note that the amino group, based on which the pKa rule is applied does not interact with the coformer. The geometric and steric factors ensure that the system assembles in a way to minimize the free energy. This indicates that, although the pKa rule can act as a guide in predicting whether a salt or co-crystal will form, it is not completely reliable.
Thermal analysis and solid phase thermodynamics
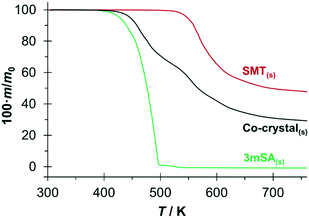
TGA curves for the three pure solid phases SMT, 3mSA and co-crystal are presented in Fig. 5. There is no indication of any bound solvent in either of the solids. For 3mSA, the mass starts to decrease at around 420 K, and at 500 K virtually all the 3mSA has been lost, due to sublimation, evaporation and/or degradation. The co-crystal curve exhibits a similar tendency, with an onset of mass loss at approximately 440 K. At 520 K, there is a slight change in the slope of the co-crystal TGA curve, and by then 35% of the initial mass has been lost, corresponding to the loss of a stoichiometric amount of 3mSA from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal; the molar masses of SMT and 3mSA being 278.33 g mol−1 and 152.15 g mol−1, respectively. This temperature value corresponds well to the point where the TGA curve for pure SMT begins to decrease. Both the SMT and the co-crystal curves then proceed to decay further in a similar fashion.
1 co-crystal; the molar masses of SMT and 3mSA being 278.33 g mol−1 and 152.15 g mol−1, respectively. This temperature value corresponds well to the point where the TGA curve for pure SMT begins to decrease. Both the SMT and the co-crystal curves then proceed to decay further in a similar fashion.
The DSC traces for the pure co-crystal and for the two respective pure components each show a single endothermic melting peak; Fig. 6. The extrapolated onset melting temperatures and the associated enthalpies of fusion of the co-crystal and 3mSA were determined as averages of either 4 or 5 repeat DSC runs. The data is given in Table 2 together with data for SMT from previous work.28 The melting point of the co-crystal (453.0 K) is intermediate between that of pure SMT (469.7 K) and pure 3mSA (436.5 K). Notably, the molar values of the enthalpy and entropy of fusion for the co-crystal are significantly higher than for the pure components, but the sum of the values of the pure components exceeds the value for the co-crystal, both with respect to enthalpy (5.1 kJ mol−1) and entropy (10.5 J mol−1 K−1) (please note that one mole of co-crystal consists of one mole each of API and coformer). This suggests that the co-crystal has a higher, less favourable enthalpy than the sum of its components, but also a higher, more favourable entropy. However, since these phase transitions occur at different temperatures, an exact comparison cannot be done without making temperature corrections using heat capacity data.
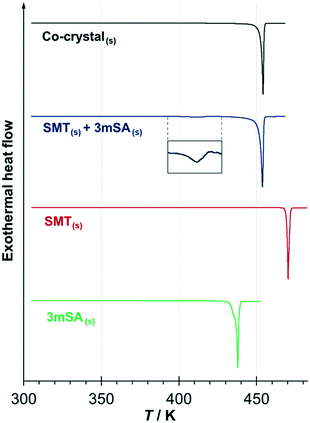 | ||
Fig. 6 DSC thermograms of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 SMT–3mSA co-crystal, the pure components (SMT and 3mSA) and an equimolar physical mixture of the solid components. 1 SMT–3mSA co-crystal, the pure components (SMT and 3mSA) and an equimolar physical mixture of the solid components. | ||
| Sulfamethazine28 | 3-Methylsalicylic acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystala 1 co-crystala |
|
|---|---|---|---|
| a 1 mole co-crystal = 1 mol API + 1 mol coformer. | |||
| T m/K [N] | 469.66 ± 0.03 [4] | 436.5 ± 0.21 [4] | 453.04 ± 0.09 [5] |
| ΔfusH (Tm)/kJ mol−1 | 36.0 ± 0.14 | 25.71 ± 0.09 | 56.6 ± 0.19 |
| ΔfusH (Tm)/kJ g−1 | 0.129 ± 0.0005 | 0.169 ± 0.0006 | 0.132 ± 0.0004 |
| ΔfusS (Tm)/J K−1 mol−1 | 76.7 ± 0.30 | 58.9 ± 0.22 | 125.0 ± 0.42 |
| ΔfusS (Tm)/J K−1 g−1 | 0.275 ± 0.0011 | 0.387 ± 0.0015 | 0.290 ± 0.0010 |
The DSC thermogram for the equimolar physical mixture of API and coformer (Fig. 6) exhibits two discrete endothermic peaks. The first is a faint endothermic event (shown in inset) with an onset at 406 K (standard error = 1.3 K) and an enthalpy of 6.6 kJ mol−1 (standard error = 0.11 kJ mol−1), as averaged over four repeat scans. This is followed by a melting peak that matches the melting peak of the co-crystal with respect to both onset temperature and enthalpy to within the levels of experimental uncertainty. From this, it may be concluded that the endotherm at 406 K corresponds to the spontaneous, solid–solid transformation of the equimolar mechanical mixture into the co-crystal.
The Gibbs energy of formation of a solid co-crystal (AB), ΔformABG at temperature T in relation to the solid components (A and B) in the solid state can be written as:
| ΔformABG = ΔformABH − TΔformABS = GsAB − GsA − GsB | (1) |
Occasionally,33 notably including the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal between SMT and salicylic acid (SA),14 the reverse relationship is observed, meaning the process of co-crystal formation is endothermic, and an increase in entropy drives the process. As can be directly observed, cf. the thermograms in Fig. 6, formation of the 1
1 co-crystal between SMT and salicylic acid (SA),14 the reverse relationship is observed, meaning the process of co-crystal formation is endothermic, and an increase in entropy drives the process. As can be directly observed, cf. the thermograms in Fig. 6, formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 SMT–3mSA co-crystal from an equimolar mixture of API and coformer is endothermic at elevated temperatures (6.6 kJ mol−1 at 406 K). However, the co-crystal formation still occurs spontaneously at 406 K. This shows that the Gibbs energy of co-crystal formation is negative, and that the process accordingly has to be driven by a favourable entropy increase, similarly as for the 1
1 SMT–3mSA co-crystal from an equimolar mixture of API and coformer is endothermic at elevated temperatures (6.6 kJ mol−1 at 406 K). However, the co-crystal formation still occurs spontaneously at 406 K. This shows that the Gibbs energy of co-crystal formation is negative, and that the process accordingly has to be driven by a favourable entropy increase, similarly as for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 SMT–SA co-crystal.14
1 SMT–SA co-crystal.14
The entropy increase occasionally observed in co-crystal formation has been proposed to be associated with a volume increase.29,34 If one molecule of co-crystal (AB) is defined as one molecule of each component (A and B), the increase in molecular volume can be calculated as:
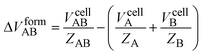 | (2) |
Solubility and phase diagrams
The solubility data for SMT and 3mSA in acetonitrile and methanol at 30 °C are listed in Table 3. In both solvents, the order of solubility is same, the coformer 3mSA being is significantly more soluble than the API, SMT. The solubility ratio of 3mSA to SMT in methanol (41.7) is notably higher than in acetonitrile (6.2).| Solvent | Solubility (mol L−1) | Solubility ratio (3mSA/SMT) | Dissolution behaviour | |
|---|---|---|---|---|
| SMT | 3mSA | |||
| Acetonitrile | 0.0592 | 0.3675 | 6.2 | Incongruent |
| Methanol | 0.0650 | 2.7121 | 41.7 | Incongruent |
The ternary phase diagrams for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
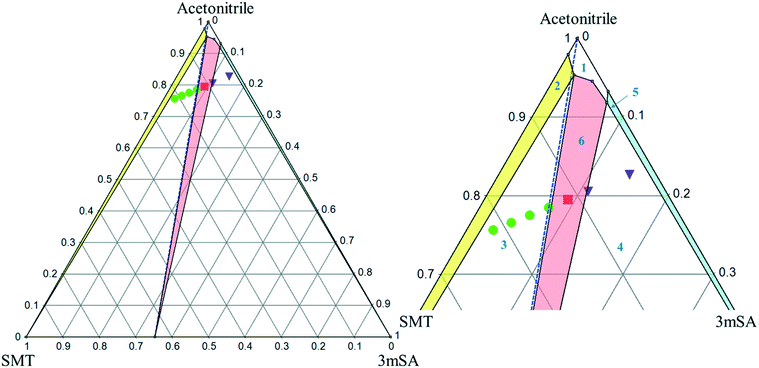
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 SMT–3mSA co-crystal in acetonitrile and methanol are depicted in Fig. 7 and 8, respectively. The choice of mass fraction over mole fraction was made to enhance the visibility of the solubility curves in the ternary phase diagrams. The 1
1 SMT–3mSA co-crystal in acetonitrile and methanol are depicted in Fig. 7 and 8, respectively. The choice of mass fraction over mole fraction was made to enhance the visibility of the solubility curves in the ternary phase diagrams. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric line does not intersect the co-crystal solubility curve and accordingly the co-crystal shows incongruent dissolution in both solvents. Additional slurry experiments confirmed the nature of incongruent dissolution for the SMT–3mSA co-crystal. In both solvents, excess of pure co-crystal, transformed to a mixture of SMT and co-crystal. In methanol, with a higher solubility ratio of coformer to API, the co-crystal region in the ternary phase diagram is skewed more towards the more soluble component 3mSA side, and is very narrow. In acetonitrile, the co-crystal region is broader, although still skewed towards the coformer side.
1 stoichiometric line does not intersect the co-crystal solubility curve and accordingly the co-crystal shows incongruent dissolution in both solvents. Additional slurry experiments confirmed the nature of incongruent dissolution for the SMT–3mSA co-crystal. In both solvents, excess of pure co-crystal, transformed to a mixture of SMT and co-crystal. In methanol, with a higher solubility ratio of coformer to API, the co-crystal region in the ternary phase diagram is skewed more towards the more soluble component 3mSA side, and is very narrow. In acetonitrile, the co-crystal region is broader, although still skewed towards the coformer side.
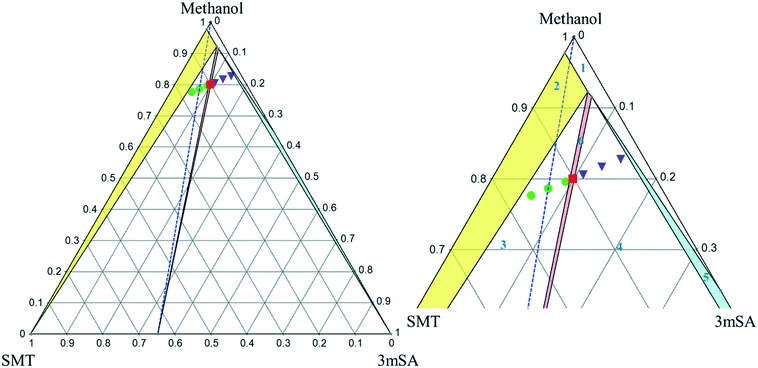 | ||
Fig. 8 Full scale (left) and zoom-in view of ternary phase diagram of SMT–3mSA co-crystal system in methanol at 30 °C. Values are in mass fractions. The blue dotted line is the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar stoichiometric line. Regions and various points are same as marked in Fig. 7. 1 molar stoichiometric line. Regions and various points are same as marked in Fig. 7. | ||
The invariant points are the solution concentrations at which two solid phases are stable and simultaneously in equilibrium with the solution. The compositions in mole fractions are given in Table 4. The phase diagrams in Fig. 9 show the incongruent nature in the two solvents and highlight the contrast in the sizes of regions where the co-crystal is stable. Dissolution of the pure 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal in either solvent is thermodynamically expected to lead to the formation of solid SMT or a mixture of SMT and co-crystal depending on the quantity of solvent and extent of dissolution. Likewise, evaporation of a solution at 30 °C containing a stoichiometric 1
1 co-crystal in either solvent is thermodynamically expected to lead to the formation of solid SMT or a mixture of SMT and co-crystal depending on the quantity of solvent and extent of dissolution. Likewise, evaporation of a solution at 30 °C containing a stoichiometric 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of SMT and 3mSA in methanol or acetonitrile would not (from a thermodynamic point of view) lead to the formation of pure co-crystal. This can be analysed by following the 1
1 mixture of SMT and 3mSA in methanol or acetonitrile would not (from a thermodynamic point of view) lead to the formation of pure co-crystal. This can be analysed by following the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric line joining the solvent vertex and the 1
1 stoichiometric line joining the solvent vertex and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal composition point on the SMT–3mSA axis. Since in both solvents the stoichiometric line crosses through regions ‘2’ and ‘3’, formation of either solid SMT or a mixture of SMT and co-crystal is to be expected, depending on the evaporation end point.
1 co-crystal composition point on the SMT–3mSA axis. Since in both solvents the stoichiometric line crosses through regions ‘2’ and ‘3’, formation of either solid SMT or a mixture of SMT and co-crystal is to be expected, depending on the evaporation end point.
| Solvent | Solid phase at equilibrium | Invariant points (mole fraction) | K sp (M2) | ||
|---|---|---|---|---|---|
| SMT | 3mSA | Solvent | |||
| Acetonitrile | SMT + co-crystal | 0.0041 | 0.0055 | 0.9903 | 8.0 × 10−3 |
| 3mSA + co-crystal | 0.0013 | 0.0211 | 0.9775 | 1.1 × 10−2 | |
| Co-crystal | 0.0016 | 0.0122 | 0.9861 | 7.6 × 10−3 | |
| Methanol | SMT + co-crystal | 0.0027 | 0.0125 | 0.9848 | 2.1 × 10−2 |
| 3mSA + co-crystal | 0.0025 | 0.0144 | 0.9730 | 2.3 × 10−2 | |
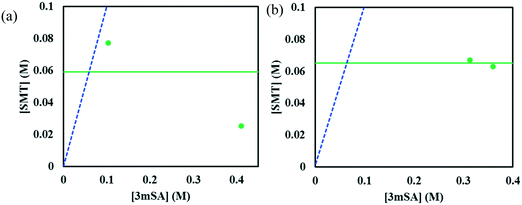
Since in both solvents the co-crystal dissolves incongruently, co-crystal solubility determination via traditional techniques such as gravimetry is not possible as it relies on establishment of thermodynamic equilibrium between the solution and the co-crystal. However, in both solvents, we observe from Fig. 9, that the SMT solution concentration at the invariant point with solid SMT and co-crystal is higher than the SMT concentration in a binary system of solvent and solid SMT. Accordingly, dissolution of the pure 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal in either solvent will lead to a solution having a higher SMT concentration than that obtained by dissolving pure solid SMT. Accordingly, from a pharmaceutical preformulation point of view, the co-crystal will potentially lead to a higher dissolution rate and thus potentially a higher bioavailability.
1 co-crystal in either solvent will lead to a solution having a higher SMT concentration than that obtained by dissolving pure solid SMT. Accordingly, from a pharmaceutical preformulation point of view, the co-crystal will potentially lead to a higher dissolution rate and thus potentially a higher bioavailability.
From a co-crystal manufacturing point of view, the pure SMT–3mSA co-crystal, in spite of the incongruency, can still be obtained by slurry conversion crystallization from a physical mixture of the two solid components in the solvent, if the overall composition is in the co-crystal region (region 6) of the phase diagram (Fig. 7 and 8). This requires an initial excess addition of the more soluble 3mSA than SMT, to place the conditions on the solubility curve of the co-crystal, then followed by addition of a suitable stoichiometric amount of each of the two pure solid components. The co-crystal formation can be initiated by addition of a smaller amount of co-crystal seeds.
In solution, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal (AB) dissolves into API (A) and coformer (B) (eqn (3)) and the co-crystal solubility product (Ksp) is the product of activities of the API and the coformer in the solution at equilibrium (eqn (4)). If the activity coefficients are neglected, Ksp simplifies to the product of concentrations of A and B. This is analogous to ionic compounds, for which the constant Ksp refers to the product of ionic concentrations in the saturated solution and is proportional to the solubility.37,38 The Ksp values in methanol and acetonitrile are given in Table 4 as calculated from the data of the invariant points. Notably, it is higher in methanol than in acetonitrile, signifying a higher co-crystal solubility in methanol. The difference in the Ksp values calculated from concentrations at the two invariant points, respectively, in the same solvent stems from the neglect of solution activity coefficients. If activity coefficients are accounted for, the Ksp should be equal in the two invariant points and in fact be independent of the solvent. Using eqn (5), and from the average Ksp, the values obtained for the co-crystal intrinsic solubility in acetonitrile and methanol are 0.094 mol L−1 and 0.148 mol L−1, respectively.
1 co-crystal (AB) dissolves into API (A) and coformer (B) (eqn (3)) and the co-crystal solubility product (Ksp) is the product of activities of the API and the coformer in the solution at equilibrium (eqn (4)). If the activity coefficients are neglected, Ksp simplifies to the product of concentrations of A and B. This is analogous to ionic compounds, for which the constant Ksp refers to the product of ionic concentrations in the saturated solution and is proportional to the solubility.37,38 The Ksp values in methanol and acetonitrile are given in Table 4 as calculated from the data of the invariant points. Notably, it is higher in methanol than in acetonitrile, signifying a higher co-crystal solubility in methanol. The difference in the Ksp values calculated from concentrations at the two invariant points, respectively, in the same solvent stems from the neglect of solution activity coefficients. If activity coefficients are accounted for, the Ksp should be equal in the two invariant points and in fact be independent of the solvent. Using eqn (5), and from the average Ksp, the values obtained for the co-crystal intrinsic solubility in acetonitrile and methanol are 0.094 mol L−1 and 0.148 mol L−1, respectively.
| AB ↔ Aliq + Bliq | (3) |
| Ksp = aA,liqaB,liq = γA[A]γB[B] ≈ [A][B] | (4) |
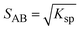 | (5) |
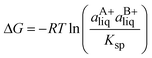 | (6) |
As is shown in Table 5, the solubility ratio of the pure co-crystal components, i.e. coformer to API solubility, cannot be used to predict whether the co-crystal will dissolve congruently or incongruently. The data for the solubility ratio and dissolution behaviour of the SMT–salicylic system has been taken from previous work.14
| Co-crystal | Stoichiometry | Solvent | Solubility ratio (r) | Dissolution behaviour |
|---|---|---|---|---|
| a Data taken from ref. 14. | ||||
| Sulfamethazine–3-methylsalicylic acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Acetonitrile | 6.2 | Incongruent |
| Methanol | 41.7 | Incongruent | ||
| Sulfamethazine–salicylic acida | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Acetonitrile | 11.5 | Congruent |
| Methanol | 61.8 | Incongruent | ||
| DMSO–methanol | 2.9 | Incongruent | ||
With the change in solvent, the size of the region where co-crystal is the most stable solid phase changes appreciably. The size of this region can be estimated in terms of the area of a triangle, given by Heron's formula (eqn (7)). In Fig. 10b, the three vertices of the triangle in the ternary phase diagram are the stoichiometric point (R) and the two invariant points (P and Q); the coordinates represented as x, y, and z. Using the 3D-distance equation (eqn (8)), the lengths (d) of the edges ‘PQ’, ‘QR’, and ‘PR’ denoted as ‘da’, ‘db’, and ‘dc’ respectively can be determined, which in turn can be used to determine the area ‘A’ represented by the purple region in Fig. 10b. Notably, the curvature of the co-crystal solubility line between the two invariant points, is neglected. Solubility ratio, denoted as ‘r’ refers to the coformer to API solubility ratio. The linear best fit between log (A) and log (r) is shown in the schematic in Fig. 10a. The regression coefficient, 0.94 depicts the linearity of the data. In Fig. 10a, data from an additional system, SMT–salicylic acid in methanol, acetonitrile and DMSO–methanol is included.14 The three coordinates required for the calculation of the area (invariant points and co-crystal stoichiometric point) were extracted. An inverse relationship between ‘r’ and ‘A’, meaning a high coformer to API solubility ratio leads to a small co-crystal region and a low solubility ratio leads to a big co-crystal region in the ternary phase diagram.
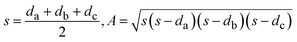 | (7) |
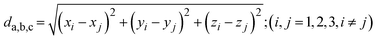 | (8) |
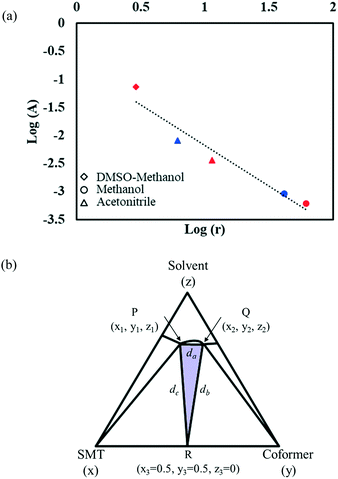 | ||
Fig. 10 Plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A (area of region in ternary phase diagram where co-crystal is the stable solid phase) vs. log A (area of region in ternary phase diagram where co-crystal is the stable solid phase) vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r (ratio of coformer to API solubility). Red symbols correspond to the SMT–salicylic acid co-crystal;14 blue symbols correspond to the SMT–3mSA co-crystal; different shapes represent different solvents (a); schematic representing the three vertices of the triangle P, Q, R; purple coloured region represents the area of the triangle (b). r (ratio of coformer to API solubility). Red symbols correspond to the SMT–salicylic acid co-crystal;14 blue symbols correspond to the SMT–3mSA co-crystal; different shapes represent different solvents (a); schematic representing the three vertices of the triangle P, Q, R; purple coloured region represents the area of the triangle (b). | ||
Conclusions
A new 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal between sulfamethazine and 3-methylsalicylic acid has been synthesized. The crystal structure has been solved and the co-crystal characterized by several techniques. The ternary phase diagram has been constructed in methanol and acetonitrile. The co-crystal exhibits incongruent dissolution in both solvents. Co-crystal formation from its solid components is shown to be spontaneous, with a negative Gibbs energy change, and endothermic, and hence driven by entropy increase. It is accompanied by an increase in molecular volume of at least 5%. The melting point of the co-crystal is 453.0 K, which is between the melting points of the pure API and coformer. The enthalpy of melting of the co-crystal is 56.6 kJ mol−1, higher than that of both the API and coformer. The size of the region where co-crystal is stable, is inversely proportional to the solubility ratio of the coformer to API.
1 co-crystal between sulfamethazine and 3-methylsalicylic acid has been synthesized. The crystal structure has been solved and the co-crystal characterized by several techniques. The ternary phase diagram has been constructed in methanol and acetonitrile. The co-crystal exhibits incongruent dissolution in both solvents. Co-crystal formation from its solid components is shown to be spontaneous, with a negative Gibbs energy change, and endothermic, and hence driven by entropy increase. It is accompanied by an increase in molecular volume of at least 5%. The melting point of the co-crystal is 453.0 K, which is between the melting points of the pure API and coformer. The enthalpy of melting of the co-crystal is 56.6 kJ mol−1, higher than that of both the API and coformer. The size of the region where co-crystal is stable, is inversely proportional to the solubility ratio of the coformer to API.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication has emanated from research conducted with the financial support of the Swedish Research Council (Grant Number 2019-5059), the SSPC, the SFI Centre for Pharmaceuticals funded by Science Foundation Ireland (SFI), co-funded under the European Regional Development Fund under Grant Number 12/RC/2275, as well as support from the Bernal Institute and the Department of Chemical Sciences, both at the University of Limerick. The authors would like to acknowledge Peraka Krishna Sumanth for collecting single crystal XRD data.References
- R. Savla, J. Browne, V. Plassat, K. M. Wasan and E. K. Wasan, Drug Dev. Ind. Pharm., 2017, 43, 1743–1758 CrossRef CAS PubMed.
- B. M. Couillaud, P. Espeau, N. Mignet and Y. Corvis, ChemMedChem, 2019, 14, 8–23 CrossRef CAS PubMed.
- N. K. Duggirala, M. L. Perry, Ö. Almarsson and M. J. Zaworotko, Chem. Commun., 2016, 52, 640–655 RSC.
- C. B. Aakeröy, S. Forbes and J. Desper, J. Am. Chem. Soc., 2009, 131, 17048–17049 CrossRef PubMed.
- S. F. Chow, M. Chen, L. Shi, A. H. Chow and C. C. Sun, Pharm. Res., 2012, 29, 1854–1865 CrossRef CAS PubMed.
- A. V. Trask, W. D. S. Motherwell and W. Jones, Int. J. Pharm., 2006, 320, 114–123 CrossRef CAS PubMed.
- Y. Corvis, P. Négrier, M. Lazerges, S. Massip, J.-M. Léger and P. Espeau, J. Phys. Chem. B, 2010, 114, 5420–5426 CrossRef CAS PubMed.
- A. J. Smith, P. Kavuru, L. Wojtas, M. J. Zaworotko and R. D. Shytle, Mol. Pharmaceutics, 2011, 8, 1867–1876 CrossRef CAS PubMed.
- S. Aitipamula, R. Banerjee, A. K. Bansal, K. Biradha, M. L. Cheney, A. R. Choudhury, G. R. Desiraju, A. G. Dikundwar, R. Dubey, N. Duggirala, P. P. Ghogale, S. Ghosh, P. K. Goswami, N. R. Goud, R. K. R. Jetti, P. Karpinski, P. Kaushik, D. Kumar, V. Kumar, B. Moulton, A. Mukherjee, G. Mukherjee, A. S. Myerson, V. Puri, A. Ramanan, T. Rajamannar, C. M. Reddy, N. Rodriguez-Hornedo, R. D. Rogers, T. N. G. Row, P. Sanphui, N. Shan, G. Shete, A. Singh, C. C. Sun, J. A. Swift, R. Thaimattam, T. S. Thakur, R. Kumar Thaper, S. P. Thomas, S. Tothadi, V. R. Vangala, P. Vishweshwar, D. R. Weyna and M. J. Zaworotko, Cryst. Growth Des., 2012, 12, 4290–4291 CrossRef CAS.
- S. L. Childs, G. P. Stahly and A. Park, Mol. Pharmaceutics, 2007, 4, 323–338 CrossRef CAS PubMed.
- S. Kumar, Indian J. Pharm. Sci., 2018, 79, 858–871 Search PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- D. Ahuja, P. Bannigan and A. C. Rasmuson, CrystEngComm, 2017, 19, 6481–6488 RSC.
- D. Ahuja, M. Svärd and Å. C. Rasmuson, CrystEngComm, 2019, 21, 2863–2874 RSC.
- M. B. Hickey, M. L. Peterson, L. A. Scoppettuolo, S. L. Morrisette, A. Vetter, H. Guzmán, J. F. Remenar, Z. Zhang, M. D. Tawa and S. Haley, Eur. J. Pharm. Biopharm., 2007, 67, 112–119 CrossRef CAS PubMed.
- M. S. Jung, J. S. Kim, M. S. Kim, A. Alhalaweh, W. Cho, S. J. Hwang and S. P. Velaga, J. Pharm. Pharmacol., 2010, 62, 1560–1568 CrossRef CAS PubMed.
- D. P. McNamara, S. L. Childs, J. Giordano, A. Iarriccio, J. Cassidy, M. S. Shet, R. Mannion, E. O'Donnell and A. Park, Pharm. Res., 2006, 23, 1888–1897 CrossRef CAS PubMed.
- S. J. Nehm, B. Rodríguez-Spong and N. Rodríguez-Hornedo, Cryst. Growth Des., 2006, 6, 592–600 CrossRef CAS.
- G. L. Perlovich, CrystEngComm, 2017, 19, 2870–2883 RSC.
- www.prosim.net .
- A. K. Basak, S. K. Mazumdar and S. Chaudhuri, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 492–494 CrossRef.
- M. P. Gupta and S. M. Prasad, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1971, 27, 713–717 CrossRef CAS.
- U. Patel, M. Haridas and T. Singh, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1988, 44, 1264–1267 CrossRef.
- P. C. Vioglio, M. R. Chierotti and R. Gobetto, Adv. Drug Delivery Rev., 2017, 117, 86–110 CrossRef PubMed.
- J. Tolls, Environ. Sci. Technol., 2001, 35, 3397–3406 CrossRef CAS PubMed.
- J. Buckingham, Dictionary of organic compounds, CRC Press, 1996 Search PubMed.
- A. J. Cruz-Cabeza, CrystEngComm, 2012, 14, 6362–6365 RSC.
- M. Svärd, D. Ahuja and Å. C. Rasmuson, Cryst. Growth Des., 2020 Search PubMed , Manuscript under revision.
- G. L. Perlovich, CrystEngComm, 2018, 20, 3634–3637 RSC.
- M. A. Oliveira, M. L. Peterson and R. J. Davey, Cryst. Growth Des., 2011, 11, 449–457 CrossRef CAS.
- A. O. Surov, K. A. Solanko, A. D. Bond, A. Bauer-Brandl and G. L. Perlovich, CrystEngComm, 2016, 18, 4818–4829 RSC.
- H. S. Chan, J. Kendrick, M. A. Neumann and F. J. Leusen, CrystEngComm, 2013, 15, 3799–3807 RSC.
- S.-W. Zhang, A. P. J. Brunskill, E. Schwartz and S. Sun, Cryst. Growth Des., 2017, 17, 2836–2843 CrossRef CAS.
- S.-W. Zhang, A. P. Brunskill, E. Schwartz and S. Sun, Cryst. Growth Des., 2017, 17, 2836–2843 CrossRef CAS.
- R. K. Tiwari, M. Haridas and T. P. Singh, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1984, 40, 655–657 CrossRef.
- G. R. Desiraju, Cryst. Growth Des., 2011, 11, 896–898 CrossRef CAS.
- S. N. Bhattachar, L. A. Deschenes and J. A. Wesley, Drug Discovery Today, 2006, 11, 1012–1018 CrossRef CAS PubMed.
- D. J. Good and N. Rodríguez-Hornedo, Cryst. Growth Des., 2009, 9, 2252–2264 CrossRef CAS.
- S. Zhang and Å. C. Rasmuson, CrystEngComm, 2012, 14, 4644–4655 RSC.
Footnote |
| † CCDC 1991374. For crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ce00498g |
| This journal is © The Royal Society of Chemistry 2020 |