Open Access Article
Open Access ArticleChirality and stereoisomerism of organic multicomponent crystals in the CSD†
Eline
Grothe
 ,
Hugo
Meekes
,
Hugo
Meekes
 and
René
de Gelder
and
René
de Gelder
 *
*
Institute for Molecules and Materials, Radboud University, Nijmegen, The Netherlands. E-mail: r.degelder@science.ru.nl
First published on 6th May 2020
Abstract
With the current interest in multicomponent crystals containing chiral residues, a wide variety of studies could benefit from a comprehensive inventory of chirality in multicomponent crystals. We combined computational approaches for identifying chiral carbon atoms and methods for identifying residue types in order to make such an inventory for all organic multicomponent entries in the Cambridge Structural Database (CSD). [Groom et al., Acta Cryst. B, 2016, 72, 171–179] This inventory provides a new and extended view on multicomponent classification by including chirality. We classified 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355 multicomponent CSD-entries into one of seven multicomponent classes and one of seven stereoisomerism classes, based on the residue type and the presence of chirality in each entry. We present refcode lists of the 49 resulting subclasses, and examples of applications of the combined classification.
355 multicomponent CSD-entries into one of seven multicomponent classes and one of seven stereoisomerism classes, based on the residue type and the presence of chirality in each entry. We present refcode lists of the 49 resulting subclasses, and examples of applications of the combined classification.
1 Introduction
A variety of studies report the influence of chirality and the type of multicomponent system on properties like crystallographic symmetry and enantioselectivity.1–5 For example, the crystallization behaviour of racemic mixtures in multicomponent systems has been shown to vary greatly between different types of multicomponent systems, as well as between multicomponent and unary systems. Springuel et al. compared the cocrystallization behaviour of racemic mixtures combined with enantiopure coformers to that of diastereomeric salts.6 Crystallization of salts is known to result in diastereomeric salt formation, where the enantiopure counterion crystallizes with both enantiomers at different solubilities. Springuel et al. showed that 38 out of 44 of these cocrystals found in the Cambridge Structural Database (CSD),6,7 show enantiospecificity, meaning that the enantiopure coformer only cocrystallizes with one of the enantiomers in the racemic mixture. A subsequent experimental screening on new systems affirmed this finding: 13 out of 15 cocrystal systems showed enantiospecificity.6In another study, Cruz Cabeza et al. investigated 3921 binary solvates of chiral and achiral molecules in a data mining study in 2007, and revealed that the space group occurrence of solvates greatly varies with the solvent.4 Space group choice is an important issue in crystal structure prediction (CSP), where crystal structures are usually generated for only a selection of space groups. Often, about ten of the most common space groups are used,8–10 which corresponds to 88% of the crystal structures in the CSD.11 By determining the space group distribution in solvates, Cruz Cabeza et al. showed that CSP of some solvates can be performed on less than ten space groups without reducing the confidence of including the correct space group.
As part of a database study into the stability of binary cocrystals Gavezzotti et al. found that the frequency of Sohncke space groups in binary cocrystals is much lower than in unary crystals.12 As Pidcock determined that over 50% of chiral compounds found in the CSD crystallize in a Sohncke space group, in contrast to 10% of achiral entries,5 Gavezzotti et al. hypothesized that there may be a low fraction of chiral molecules in the binary cocrystal set. However, they had no means to directly determine the fraction of chiral molecules in their set. With an inventory of all chiral molecules in binary cocrystals we would be able to verify or falsify their hypothesis.
About half of all active pharmaceutical ingredients (APIs) are chiral compounds, most of which have been marketed as racemic compounds, such as ibuprofen (a nonsteroidal anti-inflammatory drug), or propranolol (a β-blocker).13 Owing to technological advances in chiral separation and asymmetric syntheses, the US Food and Drug Administration (FDA) officially promotes the development of new chiral drugs as enantiopure compounds since 1992.14 The separation of enantiomers from a racemic mixture (chiral resolution) can be achieved by a variety of methods, such as chiral chromatography, diastereomeric salt formation, and conglomerate crystallization.15–17 Enantiospecific cocrystallization3 and conglomerate cocrystallization18 have been reported as possible alternatives for chiral resolution of racemic compounds that do not easily form salts or racemic conglomerates. These enantiopure cocrystals of APIs are also attractive from a crystal-engineering point of view, because multicomponent crystals can be designed to improve physicochemical properties of the deliverable without modifying the API.19 This again underlines the importance of understanding the influence and occurrence of chirality in multicomponent crystals.
In this contribution, we will make a comprehensive inventory of chirality in multicomponent crystals through data mining. We identify carbon stereocenters and determine the relative configuration of residues to distinguish opposite enantiomers and configurational diastereomers; other types of chirality are excluded (e.g. P or S stereocenters, and axial chirality). Our combined stereoisomeric and multicomponent classification leads to 49 subclasses that are provided as lists of CSD refcodes. We will show how the results can serve various goals: e.g. the study of enantiospecific behaviour of cocrystals and space group choice in CSP. Additionally, we will determine both the fraction of chiral molecules in binary cocrystals in the CSD and in Gavezzotti's cocrystal dataset, to verify the hypothesis on the lack of Sohncke space groups in this set.
2 Nomenclature
2.1 Multicomponent classification
A residue is considered to be a complete set of covalently bonded elements. In this contribution, covalent bonds will be defined by the connectivity records of the datafile used. Two residues are considered different when the connectivity, elements or relative configuration is different. The latter qualification occurs when two residues with otherwise identical connectivity have chiral centres whose configuration is non-identical, non-opposite. This means that for the multicomponent classification configurational diastereomers are considered different residues, but enantiomers are not. In our search for diastereomers we have only focussed on cases that have one or more different stereocenters; we did not include geometric (E/Z or cis/trans) isomers.Now we can define multicomponent crystals as crystals with two or more different residues. We refer to the number of different residues in the crystal as ZR such that ZR > 1 for multicomponent crystals and ZR = 1 for single-component (or ‘unary’) crystals.
We adhere to the classification system as defined by Grothe et al. in 2016,20 by defining three types of residues – ions, solvents, and coformers – as follows:
Ion residue with a nonzero formal charge.
Solvent neutral residue, liquid at ambient conditions.
Coformer neutral residue that is not a solvent.
We use the atomic charges in the data file to determine the net charge of each residue and to identify ions. Zwitterions have no net charge and are not considered ions. We use a list of 100 known solvents to identify solvents and thereby solvates. This list includes the most common solvents used for the crystallization of organic and organometallic compounds.21
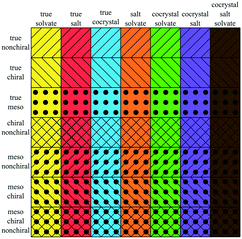
With this definition of residue and residue type we can distinguish seven different types of multicomponent crystals, outlined in Table 1 and Fig. 1(a).20 Crystals comprised of only solvents are not included in this classification.
| Ion | Solvent | Coformer | |
|---|---|---|---|
| Unary | 0 | 0 | 1 |
| True solvate | 0 | ≥1 | 1 |
| True salt | ≥2 | 0 | 0 |
| True cocrystal | 0 | 0 | ≥2 |
| Salt solvate | ≥2 | ≥1 | 0 |
| Cocrystal solvate | 0 | ≥1 | ≥2 |
| Cocrystal salt | ≥2 | 0 | ≥1 |
| Cocrystal salt solvate | ≥2 | ≥1 | ≥1 |
 | ||
| Fig. 1 Three overlapping classes (a) multi-component classes* and (b) stereoisomeric classes, visualized as circles. Each color represents one multicomponent class from Table 1, each filling represents one stereoisomeric class from Table 2. *Reprint of multicomponent classification as presented in ref. 20. | ||
2.2 Stereoisomeric classification
The chirality of sp3 carbon atoms is determined by the covalent connectivity and atomic number of its four substituents.22 If none of the substituents are identical the carbon is chiral.In terms of chirality we can distinguish between chiral and achiral residues; the latter can be mesoisomeric or nonchiral:
Chiral non-superposable with its mirror image.
Achiral superposable with its mirror image.
Nonchiralachiral residue without chiral centres.
Mesoisomerachiral residue with chiral centres.
Our algorithms identify chiral residues with chiral carbons. If for each chiral centre an equivalent centre of opposite chirality is found, then the structure will be identified as a mesoisomer.
With this definition of mesoisomers, chiral and nonchiral residues, we can distinguish seven different types of stereoisomeric crystals, as follows:
True nonchiral only nonchiral residues.
True chiral only chiral residues.
True meso only meso residues.
Chiral nonchiral both chiral and nonchiral residues.
Meso nonchiral both meso and nonchiral residues.
Meso chiral both meso and chiral residues.
Meso chiral nonchiral meso, chiral and nonchiral residues.
This is summarized in Table 2 and visualized in Fig. 1(b).
| Nonchiral | Meso | Chiral | |
|---|---|---|---|
| True nonchiral | ≥1 | 0 | 0 |
| True meso | 0 | ≥1 | 0 |
| True chiral | 0 | 0 | ≥1 |
| Meso nonchiral | ≥1 | ≥1 | 0 |
| Chiral nonchiral | ≥1 | 0 | ≥1 |
| Meso chiral | 0 | ≥1 | ≥1 |
| Meso chiral nonchiral | ≥1 | ≥1 | ≥1 |
2.3 Stereoisomeric multicomponent classification
Table 2 presents seven mutually exclusive classes of stereoisomerism in crystals. When we combine the stereoisomeric with the multicomponent classification we can distinguish 49 subclasses of multicomponent crystals based on their stereoisomerism and residue types, as in Fig. 2.As examples of this classification, Fig. 3 shows three different crystal structures found in the CSD. CSD-entry ZULCIU23 in Fig. 3(a) is a true meso cocrystal: it contains two coformers both of which are mesoisomers. Interestingly, the two mesoisomers differ from one another only by relative configuration and are therefore diastereomers. Remember that in terms of classifying multicomponent crystals, diastereomers are considered different residues.
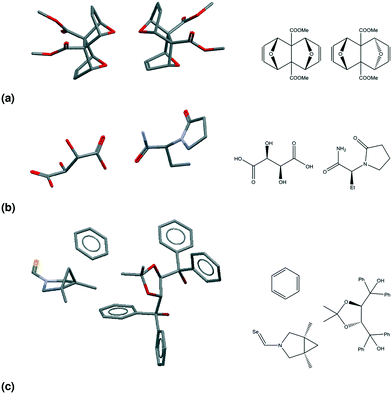 | ||
| Fig. 3 The asymmetric units (left) and structural formulae (right) for three CSD-entries. (a) ZULCIU:23 a true meso cocrystal. Both coformers are mesoisomers and form a diastereomeric pair. (b) YASGEG:24 a true chiral cocrystal. Both coformers are chiral residues. (c) MAXBET:25 a meso chiral nonchiral cocrystal solvate. Both coformers have chiral centres, but only one is chiral; the solvent is nonchiral. | ||
CSD-entry YASGEG24 in Fig. 3(b) is a true chiral cocrystal: it contains two coformers, both of which are chiral. This crystal of levetiracetam ((S)-2-(2-oxopyrrolidin-1-yl)butanamide) and D-tartaric acid was obtained by Springuel et al.,24 and is an example of enantiospecific cocrystallization, meaning that the levetiracetam L-tartaric acid cocrystal does not form.3
CSD-entry MAXBET25 in Fig. 3(c) is a meso chiral nonchiral cocrystal solvate: it contains two coformers and one solvent; one of the coformers is chiral, the other is a mesoisomer, the solvent – benzene – is a nonchiral residue.
2.4 List of terms
Besides the classification terms defined above, we also use several terms in our analysis, that might be worth defining in advance:Sohncke space group space group containing no mirror nor inversion symmetry operations.
Racemate equimolar mixture of a pair of enantiomers (in any state).
Conglomerate crystal enantiopure crystal formed from a racemate.
Conglomerate cocrystal enantiopure cocrystal formed from a racemic mixture of enantiomers and a coformer.
3 Methods
ConQuest 2.03 was used to search the CSD 5.40 database (including updates up to and including May 2019) for entries with the following flags: “3D-coordinates determined”, “Not disordered”, “No errors”, “Not polymeric”, “Organics”. We exported the entries to files with pdb and mol2 format and for repeated refcodes discarded all but the highest sequential number, and passed these files to our in-house program ChiChi.26 The majority of the discarded refcodes are redeterminations, however, some polymorphs will inevitably also be discarded with this selection.27The multicomponent classification is based on the types of residue in an entry: ion, solvent molecule, or coformer, and follows the rules outlined in Table 1. In earlier work, only ions and non-ions were identified automatically by Maruchi (a separate algorithm), and we would identify solvents separately by generating a hit list in ConQuest for each known solvent.20 However, we now incorporated determination of residue types in the latest version of ChiChi. Given an input file of atom and bond records of known solvents ChiChi distinguishes solvents from coformers automatically. A list of 100 known solvents used in this research is available as ESI.† Water is identified by checking for neutral residues consisting of one sp3 oxygen atom and two hydrogen atoms. Some hydrates will not be classified as solvates in case the water molecule in the model is incomplete, e.g. FUPBUN.28
ChiChi determines the stereoisomerism of entries by first finding chiral carbons in the entry's residues, and then comparing all the entry's chiral residues. Its methods have been described in detail previously.26 The algorithm is limited to carbon stereocenters; other types of chirality (e.g. P or S stereocenters and axial chirality) are not considered. A key step involves ranking the atoms by atom type and topology, which allows for sorting the atoms and thereby for the comparison of two residues or two substituents. Hydrogen atoms are not included in topology as determined by ChiChi. For the ranking procedure, atom numbers are used as atom type descriptors and atomic walk count sequences are used as descriptors of atom topology. After sorting the atoms by their ranks, two residues in an entry or two substituents of a potentially chiral carbon can be compared by sorted atom types and sorted atomic walk count arrays. For chiral carbons, the sign of chirality is determined by determining the coordinates of the three heaviest ranked substituents. This algorithm distinguishes two enantiomers, but does not reproduce R–S-labels often used in nomenclature.
In addition to the algorithm described previously20 we let ChiChi also read the “SYBYL atom types” from the atom records in the mol2 file. These types are used as a last step in ranking the atoms and as a last step in comparing residues before comparing their chirality. SYBYL types are also relevant for distinguishing between solvents (and small molecules in general) such as cyclohexane and benzene, which cannot be distinguished based on atom types and topology alone.
Some data inconsistencies are known to occur in the CSD. Entries with erroneous or incomplete records or inconsistent bond types might be misclassified by ChiChi. To prevent misclassifications based on charge, entries with a net charge are flagged by ChiChi.
To prevent misclassifications based on SYBYL types, ChiChi only uses the following SYBYL types: sp, sp2, sp3, ar, pl3, Du, and the remainder is classified as unknown. ChiChi converts N.4, N.am, S.o, and S.o2 to sp3, C.cat to sp2, and pairs of O.co2 to sp2 and sp3. Additionally, nitrogen atoms in contrast to other atom types, are not ranked by SYBYL type, because the N.pl3 type is very inconsistently assigned and can refer to sp2, sp3, or aromatic nitrogen (DIMPEW,29 YUZXUO,30 ACINOP31 respectively). When comparing two residues pl3 nitrogen is a wildcard for pl3, sp2, sp3 and ar nitrogen.
ChiChi analyzed and classified 309![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588 entries after which we rejected 6932 entries. Most of the rejected entries had a net charge in the asymmetric unit. A summary of entry rejections can be found in the ESI.† For 2 entries the space group was manually added, as the given space group is not recognized by ChiChi: “B2/c” in ZZZIYE06 (ref. 32) and “I2/m11” in NIYBOM01 (ref. 33) (ChiChi recognizes all settings available in the ConQuest space group query). The results in the following section are based on the remaining 302
588 entries after which we rejected 6932 entries. Most of the rejected entries had a net charge in the asymmetric unit. A summary of entry rejections can be found in the ESI.† For 2 entries the space group was manually added, as the given space group is not recognized by ChiChi: “B2/c” in ZZZIYE06 (ref. 32) and “I2/m11” in NIYBOM01 (ref. 33) (ChiChi recognizes all settings available in the ConQuest space group query). The results in the following section are based on the remaining 302![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 656 entries.
656 entries.
4 Results and discussion
Table 3 shows the classification of the 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355 multicomponent entries in our dataset, a subset we will refer to in this paper as MULTI. Not all 49 subclasses (Fig. 2) are populated. For example, the only true meso crystals we found are true cocrystals; none of the other multicomponent classes contain a true meso entry. One of these true meso crystals, ZULCIU23 is shown in Fig. 3(a). Some other subclasses are existent, but rare, such as meso chiral true salts (5 entries in MULTI), meso chiral nonchiral salt solvates (2 entries). One entry, KOTNEO,34 was classified as a true chiral cocrystal salt, however, the supposed coformer was actually a solvent that is not included in our list of solvents known to the algorithm (pentan-2-ol). For clarity, the entry was manually reclassified in the ESI† and in Table 3 as a true chiral salt solvate, the only entry in its class. The crystal structure of KOTNEO is shown in Fig. 4(a).
355 multicomponent entries in our dataset, a subset we will refer to in this paper as MULTI. Not all 49 subclasses (Fig. 2) are populated. For example, the only true meso crystals we found are true cocrystals; none of the other multicomponent classes contain a true meso entry. One of these true meso crystals, ZULCIU23 is shown in Fig. 3(a). Some other subclasses are existent, but rare, such as meso chiral true salts (5 entries in MULTI), meso chiral nonchiral salt solvates (2 entries). One entry, KOTNEO,34 was classified as a true chiral cocrystal salt, however, the supposed coformer was actually a solvent that is not included in our list of solvents known to the algorithm (pentan-2-ol). For clarity, the entry was manually reclassified in the ESI† and in Table 3 as a true chiral salt solvate, the only entry in its class. The crystal structure of KOTNEO is shown in Fig. 4(a).
| True solvate | True salt | True cocrystal | Salt solvate | Cocrystal solvate | Cocrystal salt | Cocrystal salt solvate | Subtotal | |
|---|---|---|---|---|---|---|---|---|
| True nonchiral | 151![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231 231 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 658 658 |
6805 | 5654 | 1012 | 1738 | 609 | 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 599 599 |
| True chiral | 13 | 584 | 444 | 1 | 0 | 0 | 0 | 1042 |
| True meso | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 8 |
| Chiral nonchiral | 8919 | 4549 | 903 | 1714 | 183 | 213 | 82 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563 563 |
| Meso nonchiral | 599 | 209 | 161 | 75 | 26 | 36 | 9 | 1115 |
| Meso chiral | 0 | 5 | 17 | 0 | 0 | 2 | 0 | 24 |
| Meso chiral nonchiral | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 4 |
| Subtotal | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654 654 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005 005 |
8338 | 7446 | 1223 | 1989 | 700 | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355 355 |
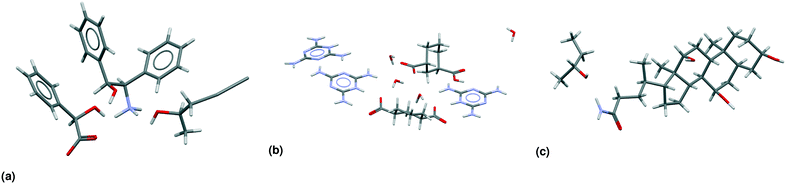 | ||
| Fig. 4 Asymmetric units of CSD-entries in the MULTI set. (a) KOTNEO34 is the only entry in its subclass: a true chiral salt solvate. It was initially classified as a cocrystal salt, because the solvent (pentan-2-ol) is not included in our list of solvents. (b) JUMYIB35 is a meso chiral nonchiral salt solvate. (c) TEHPO36 is a true chiral true solvate. | ||
There are only four cases of meso chiral nonchiral crystals in the MULTI set of 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355 entries. Fig. 3(c) already showed an example of a meso chiral nonchiral cocrystal solvate; Fig. 4(b) shows another crystal structure, this one a salt solvate, JUMYIB.35 None of the other multicomponent classes contain entries that have meso, chiral, as well as nonchiral residues. Fig. 4(c) shows a true chiral true solvate, TEHPOL;36 only 13 true solvates out of 24
355 entries. Fig. 3(c) already showed an example of a meso chiral nonchiral cocrystal solvate; Fig. 4(b) shows another crystal structure, this one a salt solvate, JUMYIB.35 None of the other multicomponent classes contain entries that have meso, chiral, as well as nonchiral residues. Fig. 4(c) shows a true chiral true solvate, TEHPOL;36 only 13 true solvates out of 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654 are true chiral.
654 are true chiral.
In the ESI† refcode lists for all of the 31 populated subclasses can be found. In the following sections, we will discuss application of this classification system to studies of space group frequency, enantiospecificity and kryptoracemates. In earlier work, we published a list of kryptoracemates, which is an interesting subset of enantiomers that crystallize in a Sohncke space group.26 In section 4.3 this subset will be discussed once more, and a refcode list of multicomponent kryptoracemates is supplied in the ESI† as well.
4.1 Multicomponent stereoisomeric classification
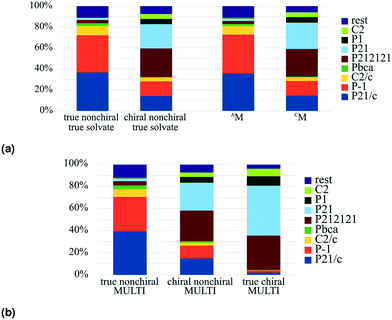
The trend was initially observed by Cruz-Cabeza et al. in solvates; when we plot a similar graph for the whole MULTI set, we can see that this trend is in fact present for multicomponent crystals in general, see Fig. 5(b). The trend continues for true chiral entries (Fig. 5(b)), with P21 becoming the most prevalent space group and 94.5% of the crystals occupying a Sohncke space group.
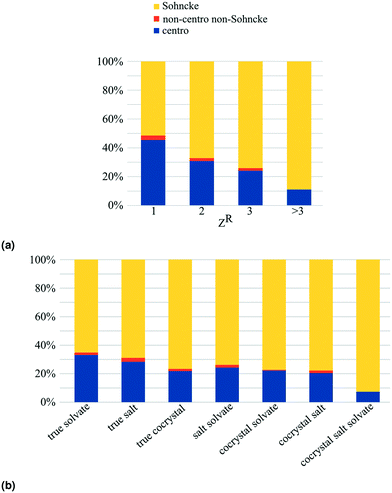
In the MULTI set the chiral compounds are indeed underrepresented in the true cocrystal class, but what about the NOCOR set? We can determine the representation of chiral compounds in the NOCOR set using the refcodes provided by Gavezzotti et al.: most of the NOCOR set is present in our MULTI set (1758 of 1941) of which ChiChi identified 152 entries with a chiral residue (9%). We can confirm Gavezzotti's hypothesis of underrepresentation of chiral compounds in the NOCOR set. Moreover, we can also add to the idea that this underrepresentation causes a reduced frequency of Sohncke space groups by looking at the space group types occupied by chiral versus achiral entries in each of the compared subsets. This is done in Table 4 for the NOCOR subset, as well as the true cocrystals and unary crystals in our dataset, where each set is separated into crystals with and without chiral residues. We can see that the space group type frequency is strongly dependent on the chirality of the residues in the set: in the achiral sets the vast majority is centrosymmetric, whereas the chiral sets are mostly Sohncke. While 42% of all unary crystals contain a chiral residue, only 16% of true cocrystals, and 9% of the NOCOR subset does. Therefore, we can confirm Gavezzotti's suspicion that Sohncke space groups are less frequent in cocrystals due to a lower fraction of chiral compounds.
| Centro | Non-centro | Sohncke | |
|---|---|---|---|
| Unary crystals | |||
| Achiral | 85% | 7% | 9% |
| Chiral | 45% | 3% | 51% |
| True cocrystals | |||
| Achiral | 90% | 4% | 5% |
| Chiral | 22% | 2% | 77% |
| True chiral | 8% | 2% | 91% |
| NOCOR | |||
| Achiral | 90% | 5% | 5% |
| Chiral | 31% | 0% | 69% |
| True chiral | 0% | 0% | 100% |
Interestingly, the frequency of Sohncke crystals of chiral residues is much higher in true cocrystals than it is in unary crystals. This may be at least partially explained by the type of studies that yield multicomponent crystals. More often than unary crystals, cocrystals are designed with a specific purpose, which in the case of chiral residues could be chiral resolution. The high frequency of true chirality in true cocrystals (5%) is especially interesting given the underrepresentation of chiral residues in this set. This overrepresentation of true chiral entries in cocrystals could be caused by scientific interest in enantioselective or diastereomeric behaviour of cocrystals, because these systems contain multiple chiral residues.
True chiral multicomponent crystals contain only chiral residues. In Table 3 we can see that true chirality is less frequent in true solvates (<1%) than in true salts and true cocrystals. This can be explained because true chiral true solvates must contain a chiral solvent, and most solvents are achiral.‡
4.2 Enantiospecificity and conglomerates
One way to obtain enantiopurity is through spontaneous resolution, i.e. conglomerate crystallization. In case a chiral compound of interest does not form unary conglomerate crystals, multicomponent crystallization could provide an alternative route to spontaneous resolution. The numerous possible counterions, coformers and solvents are encouraging for the odds of finding a conglomerate system, but at the same time it is not feasible to test all systems experimentally. This is where the CSD can be of help. The enantiopure multicomponent entries containing the racemic compound of interest, could indicate as candidate systems, or one can look at the type of counterions, coformers and solvents that tend to crystallize with the racemic compound.Only Sohncke space groups, having no inversion or mirror symmetry operations, allow for enantiopure crystals. To get an idea of how common enantiopurity is in multicomponent crystals, we can look at Fig. 6. The Sohncke frequency directly translates into frequency of enantiopurity, because the number of kryptoracemates is negligible (≤1% for all subsets). The frequency of enantiopure crystals increases with the number of residues: from 51% of unary crystals, to 88% of quaternary and higher order crystals.
Even though enantiopure crystals are more common for multicomponent systems, we cannot draw any conclusions on the frequency of conglomerates, because there is no way of telling whether an enantiopure entry is a conglomerate or was crystallized starting from enantiopure material, other than consulting the corresponding literature.
Another way to resolve a racemate is using an enantiospecific coformer. This is different from diastereomeric and from conglomerate crystallization in that only one of the enantiomers forms a crystal with the resolving agent. In contrast, in diastereomeric and conglomerate systems both enantiomers form crystals with the resolving agent, where in the case of diastereomeric systems, the crystals have different physical properties such as solubility. Springuel et al., who studied the differences between true chiral binary cocrystals and true chiral binary salts, found that while the salts usually form diastereomeric pairs of crystals, the cocrystal systems are often enantiospecific.6 To estimate the frequency of enantiospecificity, they consulted the literature for 52 cocrystals with two or more chiral residues in order to determine whether the systems are enantiospecific or “diastereomeric”. The results of their literature study indicate that as much as 86% ± 13% of cocrystals with multiple chiral residues are enantiospecific, and the rest are diastereomeric systems. This estimate can be improved by studying more crystals. The subclass of true chiral true cocrystals would be very suitable for this end: because true chiral entries consist of only chiral residues, these entries consist of multiple chiral residues similar to the 52 studied by Springuel et al. With our classification we have identified 444 true chiral true cocrystal entries in the MULTI set, all of which are binary cocrystals (ZR = 2). This set could be used in a literature study to improve the certainty of the enantiospecificity estimate calculated by Springuel et al., as this high percentage is promising for the use of resolution methods.
4.3 Curiosities
In Table 5, the space group frequencies of all Sohncke crystals are compared to those of unary and multicomponent kryptoracemates. Mind, the size of the latter is only 90 entries. P212121 is the most populated Sohncke space group, and P21 as the second most populated Sohncke space group. The frequency of P212121 drops from 49% for all Sohncke crystals to 26% for unary kryptoracemates and 16% for multicomponent kryptoracemates, while the frequencies of P21 and P1 space groups increase.
| Entries | P212121 | P21 | P1 | |
|---|---|---|---|---|
| Sohncke | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 202 202 |
49% | 35% | 5% |
| Unary k.rac. | 462 | 26% | 50% | 18% |
| Multi k.rac. | 90 | 16% | 60% | 16% |
We would like to highlight CSD-entry YUBTEW38 in Fig. 7, perhaps the most exotic multicomponent kryptoracemate in the CSD: a chiral nonchiral kryptoracemic cocrystal salt solvate. Da Silva et al.38 obtained this crystal from a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio between lamivudine and racemic mandelic acid in a solvent mixture of water and ethyl alcohol. The crystal structure shows proton transfer only between the R-enantiomer of mandelic acid and lamivudine, forming a very robust ionic pair of lamivudine and R-mandelate, while the S-enantiomer acts as a neutral coformer. Three water molecules contribute to stabilizing the crystal structure.
2 molar ratio between lamivudine and racemic mandelic acid in a solvent mixture of water and ethyl alcohol. The crystal structure shows proton transfer only between the R-enantiomer of mandelic acid and lamivudine, forming a very robust ionic pair of lamivudine and R-mandelate, while the S-enantiomer acts as a neutral coformer. Three water molecules contribute to stabilizing the crystal structure.
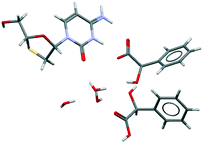 | ||
| Fig. 7 The asymmetric unit of CSD-entry YUBTEW38 shows an ionic pair of lamivudine and R-mandelate, a S-mandelic acid coformer, and three water molecules. Lamivudine and the mandelic acid residues are chiral residues. The space group is C2. | ||
In Table 6 the space group frequencies of true chiral diastereomers are compared to those of all true chiral multicomponent crystals. P21 is the most populated space group for the complete set of true chiral multicomponent crystals (45%) as well as being the most populated space group for the subset of true chiral diastereomeric crystals (48%). P212121 and P1 are at position two or three. Space group P212121 ranks second for the complete true chiral multicomponent set with 31%, however, only 8% of the diastereomeric subset occupies this space group. Reversely, P1 is occupied by 9% of true chiral multicomponent crystals, which is increased to 23% for the diastereomeric subset. This emphasizes how the nature of the residues strongly affects space group frequency.
| Entries | P21 | P212121 | P1 | Other | |
|---|---|---|---|---|---|
| True chiral multi | 1042 | 45% | 31% | 9% | 15% |
| True chiral dias. | 130 | 48% | 8% | 23% | 22% |
5 Conclusions
We combined computational approaches for identifying chiral carbons and residue types in order to make an inventory for all organic multicomponent entries in the CSD. 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355 multicomponent CSD-entries were classified into 49 subclasses; 31 of which are actually populated. We provided refcode lists for the 49 subclasses, as well as refcode lists of multicomponent kryptoracemates and diastereomeric crystals.
355 multicomponent CSD-entries were classified into 49 subclasses; 31 of which are actually populated. We provided refcode lists for the 49 subclasses, as well as refcode lists of multicomponent kryptoracemates and diastereomeric crystals.
The classification shows some interesting features, such as the underrepresentation of some subclasses (e.g. true chiral true solvates) and complete absence of others (e.g. true chiral salt solvates). While some of this is explained by the rarity of certain residues (e.g. chiral solvents), we have not been able to explain all numbers yet.
22% of true cocrystals is in one of the chiral subclasses (i.e. true chiral, chiral nonchiral, meso chiral and meso chiral nonchiral) which is below average. At the same time as much as 5% of true cocrystals is true chiral, which is far above average. Decomposing all subsets is beyond the scope of this contribution, however, we identified several curiosities, including multicomponent kryptoracemates and diastereomeric cocrystals. It turns out that these diastereomeric entries greatly contribute to the high number of true chiral true cocrystals: 130 out of 444 true chiral true cocrystals consist of diastereomeric pairs.
The extended multicomponent classification with a classification based on chirality provides a more detailed picture of multicomponent crystals, and discloses the interplay between chirality and type of multicomponent system. Following the results of Cruz Cabeza et al. regarding space group frequencies of data sets with and without chiral coformers, we could confirm that true nonchiral true solvates occupy different space groups than chiral nonchiral true solvates. We showed the same difference is found for all true nonchiral multicomponent systems versus all chiral nonchiral multicomponent systems. We were also able to verify the hypothesis of Gavezzotti et al. that chirality is underrepresented in true cocrystals.
This study illustrates the enormous diversity in crystal structures found in the CSD. Studies that draw statistics from the CSD can benefit from larger data sets which can easily be created using the here presented classification and refcode lists.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is supported by the Dutch Technology Foundation STW, which is part of the Netherlands Organization for Scientific Research (NWO), and which is partly funded by the Ministry of Economic Affairs.Notes and references
- T. Rekis, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76 DOI:10.1107/S2052520620003601.
- I. J. Scowen, T. S. Alomar, T. Munshi and C. C. Seaton, CrystEngComm, 2020 10.1039/D0CE00301H.
- G. Springuel and T. Leyssens, Cryst. Growth Des., 2012, 12, 3374–3378 CrossRef CAS.
- A. J. Cruz Cabeza, E. Pidcock, G. M. Day, W. D. S. Motherwell and W. Jones, CrystEngComm, 2007, 9, 556–560 RSC.
- E. Pidcock, Chem. Commun., 2005, 3457–3459 RSC.
- G. Springuel, K. Robeyns, B. Norberg, J. Wouters and T. Leyssens, Cryst. Growth Des., 2014, 14, 3996–4004 CrossRef CAS.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- J. Dunitz, G. Filippini and A. Gavezzotti, Helv. Chim. Acta, 2000, 83, 2317–2335 CrossRef CAS.
- J. P. M. Lommerse, W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, W. T. M. Mooij, S. L. Price, B. Schweizer, M. U. Schmidt, B. P. van Eijck, P. Verwer and D. E. Williams, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 697–714 CrossRef CAS PubMed.
- G. M. Day, W. D. S. Motherwell and W. Jones, Phys. Chem. Chem. Phys., 2007, 9, 1693–1704 RSC.
- Cambridge Structural Database, CSD Space Group Statistics - Space Group Frequency Ordering, 2017 Search PubMed.
- A. Gavezzotti, V. Colombo and L. Lo Presti, Cryst. Growth Des., 2016, 16, 6095–6104 CrossRef CAS.
- L. A. Nguyen, H. He and C. Pham-Huy, Int. J. Biomed. Sci., 2006, 2, 85 CAS.
- Development of New Stereoisomeric Drugs, 1992, https://www.fda.gov/regulatory-information/search-fda-guidance-documents/development-new-stereoisomeric-drugs Search PubMed.
- T. Ward, Anal. Chem., 2002, 74, 2863–2872 CrossRef CAS PubMed.
- L. Pasteur, C. R. Hebd. Seances Acad. Sci., 1853, 162–166 Search PubMed.
- L. Pasteur, Ann. Chim. Phys., 1848, XXIV, 442–459 Search PubMed.
- E. Elacqua, Supramolecular chemistry of molecular concepts: tautomers, chirality, protecting groups, trisubstituted olefins, cyclophanes, and their impact on the organic solid state, PhD thesis, University of Iowa, 2012 Search PubMed.
- P. Vishweshwar, J. McMahon, J. Bis and M. J. Zaworotko, J. Pharm. Sci., 2006, 95, 499–516 CrossRef CAS PubMed.
- E. Grothe, H. Meekes, E. Vlieg, J. H. ter Horst and R. de Gelder, Cryst. Growth Des., 2016, 16, 3043–3554 CrossRef.
- C. Görbitz and H. Hersleth, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56(Pt 3), 526–534 CrossRef PubMed.
- G. M. Crippen, Curr. Comput.-Aided Drug Des., 2008, 4, 259–264 CrossRef CAS.
- R. A. Valiulin, T. M. Arisco and A. G. Kutateladze, J. Org. Chem., 2012, 78, 2012–2025 CrossRef PubMed.
- G. Springuel, B. Norberg, K. Robeyns, J. Wouters and T. Leyssens, Cryst. Growth Des., 2012, 12, 475–484 CrossRef CAS.
- T. Olszewska, A. Pyszno, M. J. Milewska, M. Gdaniec and T. Połoński, Tetrahedron: Asymmetry, 2005, 16, 3711–3717 CrossRef CAS.
- E. Grothe, H. Meekes and R. de Gelder, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 453–465 CrossRef CAS PubMed.
- A. Cruz-Cabeza, S. Reutzel-Edens and J. Bernstein, Chem. Soc. Rev., 2015, 44, 8619–8635 RSC.
- D. M. Zimmerman, B. E. Cantrell, J. K. Swartzendruber, N. D. Jones, L. G. Mendelsohn, J. D. Leander and R. C. Nickander, J. Med. Chem., 1988, 31, 555–560 CrossRef CAS PubMed.
- G. L. Perlovich, A. M. Ryzhakov, V. V. Tkachev, L. K. Hansen and O. A. Raevsky, Cryst. Growth Des., 2013, 13, 4002–4016 CrossRef CAS.
- T. Sun, CSD Communication (Private Communication), 2015 Search PubMed.
- S. Kiviniemi, M. Nissinen, T. Alaviuhkola, K. Rissanen and J. Pursiainen, J. Chem. Soc., Perkin Trans. 2, 2001, 2364–2369 RSC.
- A. Rae and A. Willis, Z. Kristallogr. - Cryst. Mater., 2003, 218, 221–230 CAS.
- B. Narymbetov, S. Khasanov, L. Zorina, L. Rozenberg, R. Shibaeva, D. Konarev and R. Lyubovskaya, Kristallografiya, 1997, 42, 851 CAS.
- K. Kodama, H. Shitara and T. Hirose, Cryst. Growth Des., 2014, 14, 3549–3556 CrossRef CAS.
- L. Giri and V. Pedireddi, J. Mol. Struct., 2015, 1100, 455–463 CrossRef CAS.
- P. Briozzo, T. Kondo, K. Sada, M. Miyata and K. Miki, Acta Crystallogr., Sect. B: Struct. Sci., 1996, 52, 728–733 CrossRef.
- L. Fábián and C. Brock, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 94–103 CrossRef PubMed.
- C. C. da Silva and F. T. Martins, RSC Adv., 2015, 5, 20486–20490 RSC.
- S. P. Kelley, L. Fábián and C. P. Brock, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 79–93 CrossRef CAS PubMed.
- T.-C. Chou, S.-Y. Chen and C. Yie-Hsung, Tetrahedron, 2003, 59, 9939–9950 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: 31 CSD-refcode lists of subsets resulting from the classification; one CSD-refcode list of 90 multicomponent kryptoracemates; one CSD-refcode list of 165 cocrystals containing diastereomeric pairs; a list of solvents known to the algorithm used; a summary of rejected entries. All are supplied as txt files. See DOI: 10.1039/d0ce00403k |
| ‡ Chiral solvents in our list include butane-2-ol, and 2-methylpiperidine. |
| This journal is © The Royal Society of Chemistry 2020 |