 Open Access Article
Open Access ArticleHydrogen atoms in bridging positions from quantum crystallographic refinements: influence of hydrogen atom displacement parameters on geometry and electron density†
Lorraine A.
Malaspina
 a,
Anna A.
Hoser
a,
Anna A.
Hoser
 b,
Alison J.
Edwards
b,
Alison J.
Edwards
 c,
Magdalena
Woińska
c,
Magdalena
Woińska
 b,
Michael J.
Turner
d,
Jason R.
Price
b,
Michael J.
Turner
d,
Jason R.
Price
 e,
Kunihisa
Sugimoto
e,
Kunihisa
Sugimoto
 fg,
Eiji
Nishibori
fg,
Eiji
Nishibori
 h,
Hans-Beat
Bürgi
h,
Hans-Beat
Bürgi
 ij,
Dylan
Jayatilaka
ij,
Dylan
Jayatilaka
 d and
Simon
Grabowsky
d and
Simon
Grabowsky
 *ai
*ai
aInstitute for Inorganic Chemistry and Crystallography, University of Bremen, Leobener Str. 3, 28359 Bremen, Germany
bBiological and Chemical Research Centre, Chemistry Department, University of Warsaw, Zwirki i Wigury 101, 02-089 Warsaw, Poland
cAustralian Centre for Neutron Scattering, ANSTO, New Illawarra Road, Lucas Heights NSW 2234, Australia
dSchool of Molecular Sciences, Chemistry M313, The University of Western Australia, 35 Stirling Highway, Perth WA 6009, Australia
eAustralian Synchrotron, ANSTO, 800 Blackburn Rd, Clayton VIC 3168, Australia
fJapan Synchrotron Radiation Research Institute (JASRI), 1-1-1 Kouto, Sayo-cho, Sayo-gun, Hyogo 679-5198, Japan
gInstitute for Integrated Cell-Material Sciences (iCeMS), Kyoto University, Yoshida-Ushinomiya-cho, Sakyo-ku, Kyoto 606-8501, Japan
hDivision of Physics, Faculty of Pure and Applied Sciences, Tsukuba Research Center for Energy Materials Science (TREMS), University of Tsukuba, Japan
iDepartment of Chemistry and Biochemistry, University of Bern, Freiestrasse 3, 3012 Bern, Switzerland. E-mail: simon.grabowsky@dcb.unibe.ch
jDepartment of Chemistry, University of Zürich, Winterthurerstrasse 190, 8057 Zürich, Switzerland
First published on 15th June 2020
Abstract
Resonance-assisted hydrogen bonds (RAHBs) are exploited in chemical synthesis or serve as models for biologically relevant proton-transfer reactions [K. T. Mahmudov and A. J. L. Pombeiro, Chem. – Eur. J., 2016, 22, 16356–16398]. Their properties depend on the position of the hydrogen atom between donor and acceptor atoms. In the intramolecular RAHB of hydrogen maleate salts, this position is strongly influenced by the counter cation and varies from highly asymmetric to perfectly symmetric. This compound class is therefore ideally suited to investigate the factors determining geometry and electron density of intramolecular RAHBs. Here, it is shown that Hirshfeld atom refinements (HARs) of X-ray diffraction data of different hydrogen maleate salts can accurately and precisely match the hydrogen atom positions obtained from neutron diffraction and are independent of the model used for the hydrogen atom displacement parameters. Thus, the simplest, i.e. isotropic, HAR model can be used to locate hydrogen atoms also in bridging positions. In contrast, the determination of electron-density parameters with X-ray constrained wavefunction (XCW) fitting requires anisotropic, highly accurate hydrogen atom displacement parameters.
1 Introduction
The accurate and precise determination of the coordinates and the displacement parameters of hydrogen atoms from X-ray diffraction data is still a challenge. There are two main reasons for this:i) X-rays are diffracted mainly by the electrons in the crystal. The single electron of a hydrogen atom contributes very little to the total diffraction signal. In addition, the information about hydrogen atoms is mainly in the low-order region because the hydrogen atom scattering factor decays rapidly with scattering angle. However, accurate high-order data are also important to avoid distortion of hydrogen electron density arising from inaccurate modeling of the heavier elements.
ii) The hydrogen atom does not have a core, but only a single valence electron. In a covalent X–H bond, its electron density is shifted away from the proton towards X. The independent atom model (IAM),1 the most widely used model for X-ray crystal structure refinement, does not account for this effect, because it uses spherical electron densities corresponding to non-interacting atoms. Consequently, hydrogen atom positions derived from X-ray IAM are questionable and X–H bond lengths are usually too short by about 0.1 Å on average.2
There are several different strategies to handle hydrogen atom positions in IAM-based X-ray structure determinations:3 free refinement of hydrogen atom positions leading to the bias discussed in the previous paragraph, geometric placement and riding model according to the Shelx philosophy,4 constraining the X–H bond lengths to values of the same or similar compounds obtained from neutron-diffraction experiments5 or from theoretical calculations,6 or normalization based on correlations.3,7
In alternative approaches, more reliable hydrogen atom positions are obtained by replacing the spherical IAM scattering factors with non-spherical ones. Stewart et al. were the first to use a scattering factor for a polarized hydrogen atom.8,9 Their approach produces more reliable X–H bond distances.10,11 In a further step of sophistication, scattering factors are expressed in terms of tabulated multipole parameters. This procedure produces X–H bond distances in good agreement with those derived from neutron-diffraction experiments.12 In this study, the non-spherical atomic scattering factors are obtained in a different way: the electron density is calculated ab initio, partitioned into atomic electron densities with Hirshfeld's stockholder method, and the latter are Fourier-transformed. This procedure is called Hirshfeld atom refinement (HAR).13,14 It determines hydrogen atom positions accurately and precisely from X-ray diffraction data with resolutions as low as 0.8 Å.15–17
All the methods mentioned in the previous paragraph use theoretically calculated atomic scattering factors in the structural least-squares refinement against the experimental structure factors. They produce atomic coordinates and non-hydrogen anisotropic displacement parameters (ADPs) of high quality. Hydrogen atom displacement parameters are usually not refined anisotropically. Although this is possible in HAR, it sometimes leads to skewed or even non-positive definite (NPD) ADPs for hydrogen atoms. Hence, HAR should not be considered a standard procedure to derive experimental hydrogen ADPs.18 Given this shortcoming, the question arises whether and how the treatment of the hydrogen displacement parameters influences the accuracy and precision of the X–H bond lengths and the electron density in the neighborhood of the hydrogen atoms. It was stated in an earlier HAR study that freely refined hydrogen atom ADPs are needed to obtain hydrogen atom positions in strong hydrogen bonds that agree with results from neutron diffraction.17 In a more extended study, it was found that freely refined hydrogen ADPs lead to improved statistical agreement of X–H bond distances with neutron-diffraction-derived values, even when the ADPs become NPD,16i.e. unphysical.19
Alternatively, hydrogen atom ADPs can be estimated using, e.g., the SHADE method (simple hydrogen anisotropic displacement estimator, http://shade.ki.ku.dk)20 by combining the external rigid-body, i.e. TLS (translation/libration/screw coupling),21 contributions with internal mode contributions calculated theoretically or taken from spectroscopy or neutron diffraction. ADPs of typical covalently bonded hydrogen atoms obtained from SHADE220 are usually in good agreement with those obtained from neutron diffraction.15 Here, we prefer the more advanced SHADE3 version which is better suited for hydrogen atoms in strong hydrogen bonds because their internal mean square displacements (MSDs) are different from those of typical covalently bonded hydrogen atoms, on which the SHADE2 library is based.22 SHADE3 offers two different ways to include the internal mode contributions for hydrogen atoms in hydrogen bonds:22 1) transfer of experimental internal MSDs from neutron diffraction measurements of related compounds; or 2) use of internal MSDs calculated from high-frequency intramolecular vibrations. The latter can be obtained from spectroscopy or from periodic calculations in the program CRYSTAL;23 both possibilities were used in this study. In any case, results from SHADE3 strongly depend on the input – the quality of the calculations or the quality of the spectroscopic measurements. Moreover, hydrogen atom displacements in such RAHBs as discussed here have a significant anharmonic component, whereas all CRYSTAL calculations were conducted in the harmonic approximation.
In the first part of this study, we investigate how four different ways of treating hydrogen atom displacement parameters affect the accuracy and precision of the hydrogen atom coordinates: a) HAR_aniso, freely refined ADPs from HAR; b) HAR_iso, freely refined isotropic displacement parameters from HAR; c) HAR_neutron, HAR with fixed ADPs derived from neutron diffraction; d) HAR_shade3, HAR with fixed ADPs estimated with SHADE3.
An accurate description of ADPs is not only important for the determination of atomic coordinates, but also for the experimental determination of electron-density parameters. Although it is widely recognized that “no reasonable estimate of the charge density parameters can be obtained without an adequate description of the thermal motion”,24 80% of the experimental charge density studies published between 1999 and 2007, which involved hydrogen atoms, used isotropic hydrogen displacement parameters.25,26 Only a few papers report that for hydrogen atoms in strong hydrogen bonds, the best topological electron-density parameters are obtained with anisotropic hydrogen atom treatment.27–29
In the second part of this study, we further investigate the dependence of the electron density on the treatment of the hydrogen atom displacement parameters with X-ray constrained wavefunction (XCW) fitting30–32 using all four different kinds of displacement parameters (XCW_aniso, XCW_iso, XCW_neutron, XCW_shade3). XCW fitting is an alternative to multipole modeling of the charge density.33 It derives molecular orbitals and thus charge densities that are not only eigenfunctions of an electronic operator, but are also fitted to the experimental structure factors.
The analysis presented here is performed for a very challenging case, namely a series of hydrogen maleate salts (HM, see Scheme 1) with a very short and strong resonance-assisted intramolecular [O⋯H⋯O]− hydrogen bond (RAHB).34,35 Neutron diffraction experiments established O–H distances between 1.072(4) and 1.2135(4) Å depending on the counter cation, i.e. spanning a range from highly asymmetric to perfectly symmetric cases.3,36–38 Due to the high variability of the O–H bond length in the intramolecular hydrogen bond, this class of compounds is ideal for the aims of this study.
The chemical formulae of the HM salts analyzed in this work, together with the abbreviations used throughout the manuscript, and the references to previous X-ray and neutron structure determinations are:
• 4-Aminopyridinium hydrogen maleate (4AP HM, [C5H7N2][C4H3O4], Fig. S1a to d,†3,39);
• 8-Hydroxyquinolinium hydrogen maleate (8HQ HM, [C9H8NO][C4H3O4], Fig. 1e–h and S1e–h,†3,40).
 | ||
| Fig. 1 HAR-refined structures of the asymmetric units of Mg and 8HQ HM (light blue colored water molecules are symmetry-generated) in all four different HAR models. These two compounds serve as two representative examples; the remaining compounds are shown in the ESI,† Fig. S1–S4. ADPs are shown at a 50% probability level. Pictures are drawn with the software Mercury. | ||
• Potassium hydrogen maleate (K HM, K[C4H3O4], Fig. S2a–d,†3,37,38,41–44);
• Lithium hydrogen maleate dihydrate (Li HM, Li(H2O)2[C4H3O4], Fig. S2e–h,†3,45,46);
• Magnesium bis(hydrogen maleate) hexahydrate (Mg HM, Mg(H2O)6[C4H3O4]2, Fig. 1a–d and S3a–d,†3,47,48);
• Sodium hydrogen maleate trihydrate (Na HM, Na(H2O)3[C4H3O4], Fig. S3e–h,†3,36,49–52);
• L-Phenylalaninium hydrogen maleate (PhAla HM, [C9H12NO2][C4H3O4], Fig. S4a–d,†3,17,53).
The hydrogen atom positions and electron-density distributions are determined with different choices of hydrogen atom displacement parameters as described above using high-resolution X-ray diffraction data sets measured at 15 K at the synchrotron SPring-8. The results will be compared with those of a Laue-neutron-diffraction study of the same compounds at 12 K.3
Overall, the aim of this paper is to test the impact of different models of hydrogen atom displacement parameters on quantum-crystallographic refinements. In a first step, their impact on the hydrogen atom positions is evaluated by using HAR. In a second step, their impact on electron-density parameters is investigated by using XCW fitting.
2 Experimental details and methodology
2.1 Crystallization
All compounds were crystallized using the slow-evaporation method in covered embryo dishes. Solvents, reagents, size and color of the crystals used in the X-ray diffraction measurements are listed for each compound in Table S1 in the ESI.†2.2 Data collection and refinement
All high-resolution X-ray diffraction experiments except that for Li HM were carried out at the SPring-8 beamline BL02B1 of the Japan Synchrotron Radiation Research Institute. The crystals were mounted on a glass pin using a drop of perfluorinated oil and flash-cooled to temperatures between 15 and 25 K using a helium gas-flow low-temperature device.54 The measurements were carried out at a wavelength of 0.353(1) Å reaching high resolutions in the range from 0.38 to 0.45 Å, with redundancies usually above 10 and an average completeness of close to 100% in triclinic, monoclinic and orthorhombic space groups. Reflections were recorded using a cylindrical image-plate camera.54 Integrated intensities of all Bragg reflections were obtained with the software RAPID-AUTO55 which was also used for data scaling and the application of absorption correction whenever applicable. Table 1 summarizes details of the measurements and subsequent refinements. Except for PhAla HM,17 these synchrotron X-ray data have not been published before.| Compound | 4AP HM | 8HQ HM | K HM | Li HM |
|---|---|---|---|---|
| a Detailed refinement statistics for all different models (HAR_aniso, HAR_iso, HAR_neutron, HAR_shade3 and IAM_tonto) can be found in Table S2 in the ESI.† Here, averaged values for all HAR models relative to the IAM carried out in the software Tonto by using the same number of reflections, weighting scheme and least-squares routine are shown. | ||||
| Crystal system | Monoclinic | Orthorhombic | Orthorhombic | Monoclinic |
| Space group | P21 | P212121 | Pbcm | P21/n |
| Formula | C9H10N2O4 | C13H11NO5 | C4H3KO4 | C4H7LiO6 |
| Formula Z | 2 | 4 | 4 | 4 |
| a (Å) | 7.85280(10) | 5.33860(10) | 4.50760(10) | 5.83310(10) |
| b (Å) | 5.54510(10) | 9.9878(2) | 7.70270(10) | 5.94390(10) |
| c (Å) | 10.9223(2) | 22.3493(4) | 15.9229(3) | 18.7920(4) |
| α (°) | ||||
| β (°) | 96.394(7) | 91.3050(10) | ||
| γ (°) | ||||
| Volume (Å3) | 472.648(14) | 1191.68(4) | 552.854(18) | 651.38(2) |
| Crystal dimensions (μm3) | 110 × 90 × 80 | 119 × 92 × 66 | 150 × 150 × 50 | 215 × 213 × 171 |
| Temperature (K) | 16.5(10) | 15(2) | 15(2) | 100(2) |
| Reflections measured | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 399 399 |
80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 044 044 |
86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584 584 |
99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 272 272 |
| Unique refl. | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565 565 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 641 641 |
5366 | 7520 |
| Observed refl. (F > 4σ(F)) | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 813 813 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 569 569 |
4972 | 6436 |
| Max. resolution (Å) | 0.40 | 0.43 | 0.38 | 0.45 |
| Completeness | 0.973 | 0.997 | 1 | 0.998 |
| Wavelength (Å) | 0.3532 | 0.35307 | 0.3531 | 0.71073 |
| R int | 0.0243 | 0.0522 | 0.0422 | 0.0302 |
| R(F > 4σ(F)) IAM/HARa | 0.028/0.019 | 0.045/0.033 | 0.026/0.021 | 0.028/0.019 |
| ρ min (e Å−3) IAM/HARa | −0.57/−0.28 | −0.56/−0.30 | −0.39/−0.37 | −0.32/−0.23 |
| ρ max (e Å−3) IAM/HARa | 0.67/0.32 | 0.64/0.31 | 0.51/0.48 | 0.43/0.16 |
| Deposition number | CCDC-1989500 | CCDC-1987762 | CCDC-1989533 | CCDC-1989516 |
| Compound | Mg HM | Na HM | PhAla HM (ref.17) | |
|---|---|---|---|---|
| Crystal system | Monoclinic | Triclinic | Monoclinic | |
| Space group | P21/c |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21 | |
| Formula | C8H18MgO14 | C4H9NaO7 | C13H15N1O6 | |
| Formula Z | 2 | 2 | 2 | |
| a (Å) | 10.195(2) | 5.9224(4) | 10.905(2) | |
| b (Å) | 11.759(2) | 6.2512(3) | 5.2338(10) | |
| c (Å) | 6.6206(13) | 11.2141(7) | 11.439(2) | |
| α (Å) | 103.935(7) | |||
| β (Å) | 103.66(3) | 91.490(6) | 101.36(3) | |
| γ (Å) | 99.823(7) | |||
| Volume (Å3) | 771.2(3) | 396.07(4) | 640.1(2) | |
| Crystal dimensions (μm3) | 150 × 130 × 100 | 130 × 130 × 70 | 200 × 100 × 30 | |
| Temperature (K) | 14.9(2) | 15(2) | 25.0(2) | |
| Reflections measured | 155![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 955 955 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 649 649 |
124![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185 185 |
|
| Unique refl. | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589 589 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 183 183 |
7820 | |
| Observed refl. (F > 4σ(F)) | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 643 643 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 038 038 |
7564 | |
| Max. resolution (Å) | 0.40 | 0.40 | 0.45 | |
| Completeness | 0.997 | 0.939 | 0.998 | |
| Wavelength (Å) | 0.3532 | 0.3531 | 0.354 | |
| R int | 0.0265 | 0.0175 | 0.022 | |
| R(F > 4σ(F)) IAM/HARa | 0.023/0.016 | 0.026/0.019 | 0.029/0.020 | |
| ρ min (e Å−3) IAM/HARa | −0.27/−0.32 | −0.46/−0.48 | −0.40/−0.23 | |
| ρ max (e Å−3) IAM/HARa | 0.41/0.41 | 0.69/0.34 | 0.31/0.21 | |
| Deposition number | CCDC-1989534 | CCDC-1989518 | CCDC-1989535 | |
The lithium hydrogen maleate data set is the only one which was collected at 100 K on a Bruker D8 Venture single-crystal diffractometer fitted with an IμS microfocus radiation source using Mo-Kα radiation and a Photon-100 CMOS detector. Data integration and reduction were carried out using the APEX3 software package.56 Pertinent details about measurement, data reduction and refinement are given in Table 1.
The crystal structures were solved with SHELXT57 and the initial IAM refinements were performed with SHELXL4 within the WinGX software package.58 Hydrogen atoms were located from difference Fourier maps and refined isotropically. ADPs were refined only for non-hydrogen atoms. This provided the starting model which was then submitted to the software Tonto59 for an additional IAM in Tonto and subsequent HARs. Within Tonto, the IAM refinement and the HARs were based on |F| with weight = 1/σ(|F|) using merged reflections, whereby negative |F|2 reflections, |F| < 4.0 sigma(|F|) and all systematic absences were pruned. The level of theory for the HARs was HF/def2-TZVP. The crystal environment was simulated using a self-consistent cluster of point charges and dipoles up to a radius of 8 Å around the central formula unit calculated from the Hirshfeld partitioning. The R-values and residual density values in Table 1 show that HAR significantly improves the modelling of the experimental structure factors compared to IAM. The crystallographic information files that reside with the Cambridge Structural Database (see Table 1 for CCDC deposition numbers) contain only the HARs with hydrogen ADPs from neutron diffraction (including X-ray structure factors). They can be downloaded free of charge from https://summary.ccdc.cam.ac.uk/structure-summary-form. Methodological differences between the different HAR models are discussed in the next section, and CIFs for all models are deposited with this paper.
The XCW fittings based on the fixed HAR geometries and ADPs were also carried out with Tonto at HF/def2-TZVP. Note that in the XCW fitting step no self-consistent field of point charges and dipoles was used since it is expected that the crystal field effects are absorbed by the wavefunction during the fitting procedure. This point is further discussed in Ernst et al.60 and Grabowsky et al.61 The figures of merit after XCW fitting and the maximum value of the manually adjusted perturbation parameter λ determining the degree of influence of the experimental structure factors on the wavefunction are collected in Tables S5 and S6 in the ESI.†
2.3 HAR and XCW models
All the input files for HAR and subsequent XCW fitting were generated with the shell script lamaGOET, which serves as a graphical user interface to Tonto.62 The following HARs were performed:• HAR_aniso: refinement of all coordinates and ADPs with HAR, including those for hydrogen atoms.
• HAR_iso: refinement of all parameters except for hydrogen atoms which were refined isotropically.
• HAR_neutron: refinement of all parameters for non-hydrogen atoms and hydrogen atom positions; the hydrogen atom ADPs were constrained to the values obtained from the corresponding neutron-diffraction experiments at nearly the same temperatures as described above. For Li HM, X-ray and neutron diffraction experiments were conducted at different temperatures (12 K vs. 100 K). Therefore, the hydrogen atom ADPs of the neutron diffraction experiment at 12 K were scaled to those at 100 K with the program UIJXN63 (section 7 in the ESI†).
• HAR_shade3: refinement of all parameters for non-hydrogen atoms within HAR. Only hydrogen atom positions were refined, but the hydrogen atom ADPs were constrained to the values obtained from the SHADE3 procedure. To estimate ADPs from SHADE3, first periodic DFT calculations with the program Crystal1423 were conducted. Frequencies and normal mode vectors were calculated at the gamma point of the Brillouin zone at the B3LYP/pob-TZVP level of theory within the harmonic approximation. Before frequency calculations, geometry optimizations were carried out upon fixing the lattice constants. The resulting frequencies at the minimum-energy geometries were read by the SHADE3 server at http://shade.ki.ku.dk to derive the internal MSDs needed for the hydrogen ADP estimation. This procedure was adopted for 4AP, Mg, Li and Na HMs. However, the O–H distances in the intramolecular hydrogen bond in question after optimization did not necessarily accurately coincide with the experimental neutron-diffraction derived O–H distances anymore, which biases the obtained MSDs (see Table S4 in the ESI†). Therefore, for the two symmetric compounds K and PhAla HM we tested an alternative strategy, namely extracting the MSDs from experimental infra-red spectra of the K HM salt.64 For 8HQ HM, there are no experimental spectra available. Since the O–H distances in 8HQ HM are very similar to those in Na HM, we used the MSDs derived from the geometry optimization of Na HM for 8HQ HM.
The XCW fittings were performed with the geometries and ADPs obtained from or used in the above HAR refinements, leading to the four models XCW_aniso, XCW_iso, XCW_neutron, XCW_shade3.
2.4 Symmetrization of the Hirshfeld atom density
For optimal HAR results, the fragment wavefunction chosen to represent the crystal should be as realistic as possible.15E.g., results for oxalic acid dihydrate obtained for fragments which obeyed the point group symmetry were better than those which did not.31,32 K HM forms a polymeric chain with symmetry operations leading to half a HM anion and half a K cation in the asymmetric unit. Thus, it was not possible to select a representative fragment of the periodic crystal such that the non-spherical Hirshfeld atom scattering factors for the hydrogen atom on the mirror plane and for the K cation on a 2-fold axis had the required site symmetries. In this case, the HAR failed. Therefore, the symmetries of the non-spherical scattering factors of atoms in special positions were restored by averaging over the site symmetry operators. This simple procedure allows HAR even for choices of the fragment that are inconsistent with the space-group symmetry. Details of the efficient implementation of this important procedure in Tonto will be reported elsewhere in due course.For structures which are not network compounds, the cluster of point charges and dipoles simulating the crystal environment should always consist of complete molecules with at least one atom within 8 Å of any atom of the central molecule. In Tonto, the default is to always auto-complete the molecules in the cluster. However, if the structure being refined is a network compound such as Li and K HM, this would lead to the generation of an infinite set of point charges which the software cannot handle. Thus, we have added the option to avoid the auto-completion of the molecules at the edge of the cluster in the Tonto code (called the defrag option). It was used here for the Li and K HM refinements.
3 Results and discussion
In the main text, results are illustrated for the Mg and 8HQ HM compounds only, the ones that show the best and the worst quality indicators, respectively (Table 1). Fig. 1 shows their HAR-refined structures in all four models (for the other compounds see Fig. S1–S4 in the ESI†). The intramolecular hydrogen bond in Mg HM determined from neutron diffraction is nearly symmetric with the shorter O–H distance being 1.1874(16) Å, whereas in 8HQ HM it is clearly asymmetric with d(O–H) = 1.072(3) Å. All four HAR models recover these two different bonding scenarios with d(O–H) ranging from 1.180(5) to 1.185(4) Å for Mg HM (two O–H bonds drawn by the software Mercury based on distance criteria, Fig. 1) and 1.066(8) to 1.080(9) Å for 8HQ HM (only one O–H bond drawn by the software Mercury based on distance criteria, Fig. 1). The same level of agreement of around one X-ray standard uncertainty is found for all compounds in all HAR models (Table 3).Discrepancies occur for the ADPs of the hydrogen atoms midway between donor and acceptor atoms in the short and strong intramolecular RAHBs (Fig. 1). For Mg HM, the HAR_aniso ADP is much smaller than the neutron-derived one, and its main direction of extension is perpendicular to the O–H–O bond axis, in contrast to the neutron-derived one. In turn, the hydrogen atom ADP from the SHADE3 model is oblique relative to the O–H–O bond axis, also in contrast to the neutron-derived one. In 8HQ HM, the corresponding HAR_aniso hydrogen ADP is NPD (depicted by a box of arbitrary size). The SHADE3-derived and neutron ADPs also show some dissimilarities in terms of shape, magnitude and direction.
The SHADE- and neutron-derived ADPs of the hydrogen atoms not involved in an intramolecular hydrogen bond are very similar to each other; overall, the freely refined ADPs in the HAR_aniso model are similar to the neutron-derived ADPs as well, at least visually (Fig. 1). There are a few slightly skewed hydrogen ADPs in the 8HQ cation, whereas the ADPs in the water molecules of Mg HM are modelled very accurately in HAR_aniso.
One may ask whether HAR-derived ADPs are needed to obtain accurate HAR-derived X–H bond distances as preempted by Fig. 6 in Woińska et al.17 for PhAla HM. More specifically, one may want to know whether anisotropic displacement parameters are needed for the derivation of accurate and precise hydrogen atom positions irrespective of how they were refined or estimated, or whether isotropic ones derived from HAR are sufficient.19 In an attempt to answer these questions, subsection 3.1 discusses the differences between the hydrogen ADPs in much more detail using statistics. In subsections 3.2 and 3.3, the impact of these differences on the O–H bond distances and on the electron-density distributions will be analyzed.
3.1 ADP statistics
Table 2 compares the HAR-derived hydrogen atom ADPs and the SHADE3-estimated ones with the neutron-derived ADPs for all compounds in terms of mean ratios and mean absolute differences. For hydrogen atom H1 in the RAHB, nearly all indicators are less favourable than those for the other hydrogen atoms. Note that in all cases the Uii values for H1 are underestimated in the HAR_aniso refinements and overestimated in SHADE3 relative to the neutron values. This indicates that modeling the ADPs of H1 is most challenging both for the free HAR refinement and the SHADE3 estimation, because it is displaced from its usual position near a donor atom towards the acceptor atom and anharmonic contributions were neglected.| Cation | Method | All H atoms 〈UiiX/UiiN〉 | All but H1 | H1 | All H atoms 〈|UijX − UijN|〉 | All but H1 | H1 | All H atoms 〈|UiiX − UiiN|〉 | All but H1 | H1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 4AP | HAR | 1.16(38) | 1.19(34) | 0.95(76) | 0.0044(38) | 0.0041(35) | 0.0070(56) | 0.0061(43) | 0.0056(40) | 0.0109(53) |
| SHADE3 | 1.07(17) | 1.07(17) | 1.16(8) | 0.0022(15) | 0.0022(16) | 0.0019(12) | 0.0023(17) | 0.0023(18) | 0.0028(9) | |
| 8HQ | HAR | 1.39(50) | 1.45(42) | 0.83(94) | 0.0076(62) | 0.0076(61) | 0.0082(70) | 0.0108(68) | 0.0105(70) | 0.0139(37) |
| SHADE3 | 1.23(19) | 1.23(16) | 1.27(47) | 0.0031(27) | 0.0031(27) | 0.0034(34) | 0.0048(28) | 0.0048(28) | 0.0055(38) | |
| K | HAR | 0.94(59) | 1.15(15) | 0.73(85) | 0.0051(63) | 0.0026(23) | 0.0076(82) | 0.0086(74) | 0.0037(29) | 0.0135(75) |
| SHADE3 | 1.12(27) | 0.97(4) | 1.27(34) | 0.0023(39) | 0.0009(8) | 0.0036(54) | 0.0032(53) | 0.0008(8) | 0.0055(73) | |
| Li | HAR | 0.74(25) | 0.79(22) | 0.45(26) | 0.0069(66) | 0.0067(62) | 0.0084(90) | 0.0111(67) | 0.0104(66) | 0.0156(67) |
| SHADE3 | 0.69(24) | 0.70(26) | 0.62(10) | 0.0070(70) | 0.0072(73) | 0.0060(57) | 0.0121(67) | 0.0123(72) | 0.0109(28) | |
| Mg | HAR | 1.10(29) | 1.16(25) | 0.67(32) | 0.0035(30) | 0.0034(26) | 0.0045(50) | 0.0043(32) | 0.0041(27) | 0.0065(67) |
| SHADE3 | 1.12(17) | 1.14(16) | 1.00(22) | 0.0033(31) | 0.0034(32) | 0.0024(17) | 0.0037(38) | 0.0038(40) | 0.0032(17) | |
| Na | HAR | 1.09(26) | 1.12(23) | 0.89(40) | 0.0035(25) | 0.0034(25) | 0.0043(26) | 0.0038(29) | 0.0037(28) | 0.0046(41) |
| SHADE3 | 0.99(13) | 0.98(13) | 1.02(12) | 0.0018(17) | 0.0018(18) | 0.0013(6) | 0.0023(21) | 0.0023(22) | 0.0017(2) | |
| PhAla | HAR | 1.22(32) | 1.26(29) | 0.70(36) | 0.0050(45) | 0.0050(45) | 0.0044(36) | 0.0061(47) | 0.0061(47) | 0.0061(43) |
| SHADE3 | 1.19(23) | 1.16(21) | 1.52(21) | 0.0026(25) | 0.0023(20) | 0.0059(55) | 0.0036(30) | 0.0032(23) | 0.0102(44) |
The SHADE3-derived ADPs for all atoms but H1 are nearly always closer to the neutron-derived ones than the HAR-refined values (Table 2). The mean absolute differences 〈|UijX − UijN|〉 vary in the range 0.0009(8) to 0.0072(73) Å2 for SHADE3 and 0.0026(23) to 0.0076(61) Å2 for HAR_aniso. Although the closer similarity of the SHADE3 results to the neutron-derived results is expected since SHADE3 partially uses neutron-diffraction-derived information as explained above, the differences between the HAR and the SHADE3 results are not large; they are always within a single sample standard deviation. For covalently bonded hydrogen atoms in two related compounds studied earlier, the 〈|UijX − UijN|〉 values are in the range 0.0023(19) to 0.0045(51) Å2 estimated with SHADE2 and 0.0045(32) to 0.0089(76) Å2 for HAR.15
PEANUT plots show the nature of HAR_aniso- and SHADE3-derived differences UijN − UijX (Fig. 2 for compounds Mg and 8HQ HM; Fig. S5–S7† for all other compounds).65 Both methods tend to underestimate the ADPs of the atom H1 along the O–H–O bond axis and overestimate them perpendicular to the O–H–O axis. The ADPs for the two hydrogen atoms in the hydrogen maleate C–H bonds (Fig. 2 and S5–S7†) tend to be systematically overestimated by both HAR and SHADE3 models perpendicular to the C–H axis.
 | ||
| Fig. 2 PEANUT65 representation of differences between neutron ADPs and those from anisotropic HAR refinements (HAR_aniso) or SHADE3 estimation (HAR_shade3) for the two representative compounds Mg and 8HQ HM. For all other compounds, see Fig. S5–S7.† The plots show positive (blue) and negative (red) differences between root-mean square displacements, scaled by factors of 4.62 (a and b) and 3.08 (c and d). | ||
Table S3 in the ESI† compares the isotropic hydrogen displacement parameters from HAR and IAM with the equivalent hydrogen ADPs (Ueq) from neutron diffraction. The isotropic displacement parameters from HAR are significantly closer to the neutron-derived Ueq values than those from IAM. This suggests that if isotropic hydrogen atom displacement parameters are used to derive X–H bond lengths (see subsection 3.2), they should be refined in HAR simultaneously with the coordinates, not taken from a preceding IAM.
From a statistical point of view we conclude that on the whole the HAR-derived ADPs are not unreasonable or unphysical, but they are less accurate than neutron-derived or SHADE-estimated ones (Table 2).
3.2 O–H bond lengths
We have previously derived the functional relationship between the O–H distances in hydrogen maleate compounds and the corresponding O⋯O distances.3 Here, the range of O⋯O distances is 2.404 to 2.444 Å and the range of O–H distances is 1.080 to 1.215 Å (model HAR_neutron, Table 3). As mentioned above, the HAR-derived O–H bond distances are in excellent agreement with the neutron-derived values, mostly within one X-ray standard uncertainty, whereas the IAM-derived O–H bond distances scatter, being accurate for 8HQ and K HM, but very inaccurate for, e.g., 4AP or PhAla HM (Table 3). Note that the HAR-derived O–H distances are not systematically too short as normally observed for X-ray-refined IAM X–H bond distances, but show minor fluctuations around the neutron reference values.| Cation | HAR_aniso | HAR_iso | HAR_neutron | HAR_shade3 | Tonto_IAM | Neutron |
|---|---|---|---|---|---|---|
| 4AP | 1.200(8) | 1.196(8) | 1.196(9) | 1.195(9) | 1.049(15) | 1.194(3) |
| 0.006 | 0.002 | 0.002 | 0.001 | −0.145 | ||
| 1.005 | 1.002 | 1.002 | 1.001 | 0.879 | ||
| 8HQ | 1.066(8) | 1.072(8) | 1.080(9) | 1.080(9) | 1.084(13) | 1.072(3) |
| −0.006 | 0.000 | 0.008 | 0.008 | 0.012 | ||
| 0.994 | 1.000 | 1.007 | 1.007 | 1.011 | ||
| K | 1.2145(3) | 1.2145(3) | 1.2146(3) | 1.2147(4) | 1.2151(8) | 1.2135(4) |
| 0.0010 | 0.0010 | 0.0011 | 0.0012 | 0.0016 | ||
| 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | ||
| Li | 1.100(4) | 1.100(5) | 1.101(6) | 1.099(5) | 1.074(9) | 1.109(3) |
| −0.009 | −0.009 | −0.008 | −0.010 | −0.035 | ||
| 0.992 | 0.992 | 0.993 | 0.991 | 0.968 | ||
| Mg | 1.182(4) | 1.185(4) | 1.181(5) | 1.180(5) | 1.209(7) | 1.1874(16) |
| −0.005 | −0.002 | −0.006 | −0.007 | 0.022 | ||
| 0.995 | 0.998 | 0.995 | 0.994 | 1.018 | ||
| Na | 1.089(5) | 1.091(5) | 1.099(5) | 1.098(5) | 0.999(7) | 1.0813(12) |
| 0.008 | 0.010 | 0.018 | 0.017 | −0.082 | ||
| 1.007 | 1.009 | 1.016 | 1.015 | 0.924 | ||
| PhAla | 1.201(17) | 1.188(16) | 1.196(18) | 1.20(2) | 1.07(2) | 1.208(3) |
| −0.007 | −0.020 | −0.012 | −0.008 | −0.138 | ||
| 0.994 | 0.983 | 0.990 | 0.993 | 0.886 |
The O–H bond distances resulting from the four HAR models are very similar. There is no systematic dependence on the source of the hydrogen ADPs, not even if isotropic displacement parameters from HAR are used (visualized in Fig. 3). In all but one case, the accuracy of the four HAR models, including HAR_iso, is nearly the same; all of them reproduce the neutron-derived O–H bond lengths. In general, the precision from HAR (represented by the lengths of the bars in Fig. 3) is also excellent, and there is no difference between the different HAR models, including HAR_iso. PhAla HM shows to be the least precise measurement. In addition, the HAR_iso model of PhAla HM appears to be an outlier in terms of accuracy; here, HAR_aniso matches the HAR_neutron reference bond length much better than the isotropic model. This led Woińska et al.17 to conclude that freely refined hydrogen atom ADPs are needed to obtain good hydrogen positions from HAR, which disagrees with the general conclusions from this study and from Dittrich et al.19
 | ||
| Fig. 3 O1–H1 distances with standard uncertainties (colored bars) obtained from all four HAR models and from the neutron diffraction experiment. | ||
Here, we conclude that accurate and precise hydrogen atom positions in short symmetric and asymmetric O–H–O hydrogen bonds can be obtained with isotropic and anisotropic ADPs from HAR as well as with SHADE3-estimated ADPs. This holds even if the refined ADP is NPD as in the case of 8HQ HM. However, this does not necessarily imply that the use of an isotropic or NPD ADP is justified if properties are to be derived from a crystallographic model, as for example in an experimental electron-density study. This point is discussed in the next section.
3.3 XCW fitting
The results of an electron-density investigation via XCW fitting depend on many parameters such as the choice of the quantum-mechanical Hamiltonian and basis set, the atomic positions and displacement parameters as well as the weight of the quantum-mechanical energy relative to the diffraction information. The interpretation of the fitting results is concerned with the physical meaning of the differences between the fitted and unperturbed wavefunction ansatz (crystal-field effect, electron correlation).60,66 In this subsection, we only discuss the influence of the four different models of hydrogen atom displacement parameters on the electron-density distribution obtained via XCW fitting to the experimental structure factors. In XCW fitting, the forms of the displacement parameters are taken into account in the wavefunction calculation via the thermal-smearing model, so their imprint on the derived electron density is directly visible. The thermal-smearing model used here is the same as used in HAR, namely the atom-centered one based on Hirshfeld's stockholder partitioning.13 It is compared to two-center thermal-smearing models in detail in Bučinský et al.67XCW fittings were carried out with the four different sets of anisotropic and isotropic hydrogen atom displacement parameters and the atomic positions fixed at their values obtained from HAR. XCW fitting statistics are given in Tables S5 and S6 in the ESI.†R-Values and minimum/maximum residual electron density values do not differ between the different models. This means that the type of displacement parameter has no influence on the overall performance measured with these numbers. Note, however, that the R-values are slightly higher than those from HAR indicating that the present XCW fitting results do not account for the crystal field in the same way as the perturbation with cluster charges used in HAR.
As mentioned in the introduction, for the case of the multipole model several studies show that the use of ADPs for hydrogen atoms as opposed to isotropic displacement parameters crucially affects the topological description of strong hydrogen bonds.27–29 Here, we find that bond-topological electron-density properties and integrated atomic charges are not affected by the differences in the ADP models (Table S7 in the ESI†). Therefore, we turn to the analysis of the three-dimensional electron-density distributions and their differences between different models.
Fig. 4 shows the residual electron density distributions for both compounds Mg and 8HQ HM based on the model XCW_neutron (for corresponding plots of the other compounds, see ESI† Fig. S8 and S9; for two-dimensional contour plots for Mg and 8HQ HM in all four models, see Fig. S10 and S11†). The features of the residual electron density for Mg HM are significantly smaller (note that the isovalue is smaller for Mg HM) and more randomly distributed than for 8HQ HM, where some of the features are located inside the C–O bonds and around the oxygen atoms. These differences in the distributions indicate the difference in the quality of the two data sets (Table 1). However, in both cases the hydrogen atom positions and their direct vicinity are free of residual electron density showing that the ADPs and electron density models used are adequate for their description. For the subsequent comparisons of residual electron density differences it should be kept in mind that the isolevels in Fig. 4 are 0.10 and 0.12 e Å−3, respectively, with maximum values being 0.28 and 0.29 e Å−3 (Tables S5 and S6†).
 | ||
| Fig. 4 Residual electron density distribution in the XCW_neutron models. Blue = positive, red = negative. a) Isovalue = 0.10 e Å−3; b) isovalue = 0.12 e Å−3. The corresponding plots for the other compounds are shown in Fig. S8 and S9.† | ||
Fig. 5 and 6 show the differences in the residual XCW electron-density distributions for Mg and 8HQ HM using different ADP models. The influence of the ADP model is estimated to be about 10% of the total residual density, the estimate being based on the selection of a meaningful isovalue of 0.012 e Å−3 for the differences. Corresponding figures for the other compounds as well as difference plots of the total electron densities for all compounds are collected in the ESI† (Fig. S12–S16 and S17–S23, respectively).
 | ||
| Fig. 5 Residual electron density differences between XCW fittings with different ADP models for Mg HM. Isovalue = 0.012 e Å−3, yellow = positive, blue = negative. The corresponding plots for the other compounds are shown in Fig. S12–S16.† | ||
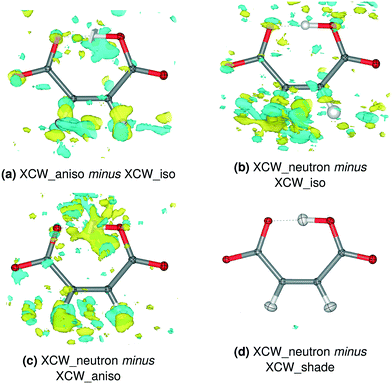 | ||
| Fig. 6 Residual electron density differences between XCW fittings with different ADP models for 8HQ HM. Isovalue = 0.012 e Å−3, yellow = positive, blue = negative. The corresponding plots for the other compounds are shown in Fig. S12–S16.† | ||
In some previous studies that used XCW fitting, results were based on hydrogen atom ADPs freely refined in a preceding HAR under the assumption that this procedure is superior to XCW fitting with isotropic hydrogen displacement parameters.68–70 In these studies, the hydrogen atom ADPs appeared to be physically reasonable, but the underlying assumption was, to the best of our knowledge, never tested. Here, we compare the residual densities between XCW_aniso and XCW_iso models for Mg and 8HQ HM that bear both physically reasonable and unreasonable hydrogen atom ADPs. Both Fig. 5a) and 6a) show a significant accumulation of residual electron density around the O–H–O and C–H hydrogen atoms, reflecting the change of the ADP model for these atoms from HAR-refined isotropic to anisotropic. However, it is unclear if these differences imply an improvement of the electron-density description on going from the anisotropic to the isotropic model, especially in view of the ADP of H1 which is too small in Mg HM and NPD in 8HQ HM (Fig. 1 and 2).
The question can be answered if the XCW_neutron model is taken as a trustworthy reference model: Fig. 5b) and c) and 6b) and c) show the inadequacy of both the HAR-refined isotropic and anisotropic displacement parameters, especially for H1. In contrast, there is practically no difference residual density feature if the SHADE3-estimated ADPs are used instead of the neutron-derived ones [Fig. 5d) and 6d)]. This implies that for electron-density studies of hydrogen bonds, the HAR-refined isotropic and anisotropic displacement parameters should not be used, whereas the SHADE-estimated ones seem more adequate. This contrasts with the results in section 3.2 for the hydrogen atom positions, which are largely independent of the model used for the hydrogen atom displacement parameters.
The shape of the residual-density differences for the C–H bonds in Mg HM is as expected for the difference between models with anisotropic and isotropic displacement parameters, i.e. models carrying a spherical versus an ellipsoidal object [Fig. 5a) and b)]. The loss of difference residual density features around the C–H bonds in Fig. 5c) thus implies that at least for Mg HM, the refined hydrogen ADPs in the C–H bonds are adequate for a charge-density study. Hence, we conclude that the above assumption, namely that hydrogen anisotropic displacement parameters from HAR are preferable over isotropic ones in XCW fitting, may be justified for some regular covalently bonded hydrogen atoms, but not for others [as in 8HQ HM, cf.Fig. 6c)] and certainly not for hydrogen atoms in strong hydrogen bonds.
4 Conclusions
This study has focussed on a series of hydrogen maleate salts with strong and short intramolecular resonance-assisted O–H–O hydrogen bonds (RAHBs) in which the hydrogen atom position varies from strongly asymmetric to perfectly symmetric depending on the nature of the cation and the crystal packing.In the first part (section 3.1), we compared isotropic and anisotropic hydrogen atom displacement parameters obtained with Hirshfeld atom refinement (HAR) from high-resolution low-temperature synchrotron X-ray diffraction data, derived from neutron-diffraction studies of the same compounds at the same temperatures or estimated with the SHADE3 approach. Their similarities and differences were analyzed statistically. On average, HAR-refined hydrogen ADPs are not significantly less accurate than those estimated with the SHADE3 procedure. However, they can become skewed or non-positive definite indicating some kind of overfitting, especially for hydrogen atom H1 in the RAHB. In these cases, limited or no physical meaning can be assigned to the HAR-refined hydrogen ADPs.
In the second part (section 3.2), the influence of the four different hydrogen displacement parameter models on the refined hydrogen atom positions and the associated bond distances was investigated. It was found that HAR produces highly accurate and precise O–H bond lengths irrespective of the displacement parameter model used. This means that a HAR_iso model, which is the simplest and most widely applicable model, is sufficient to obtain reliable X–H bond distances. This result confirms earlier studies that showed that HAR refinements can produce accurate and precise X–H bond distances not only for classical X–H covalent bonds, but also for three-center–four-electron bonds. Note, however, that the isotropic displacement parameters must come from HAR as described here, not from a preceding IAM refinement. Moreover, concomitant HAR refinement of the isotropic displacement parameters together with positions leads to slightly better distances compared to a model where the isotropic displacement parameters are kept fixed during the refinement of the positions.
In the third part (section 3.3), we studied the influence of the model for the hydrogen atom displacement parameter on the electron-density distribution resulting from X-ray constrained wavefunction (XCW) fitting against the experimental structure factors. If one considers residual electron densities obtained with neutron-derived ADPs as a trustworthy reference, XCW fitting with SHADE3-estimated ADPs yields comparable information, whereas fitting with HAR-refined isotropic or anisotropic hydrogen atom displacement parameters yields inferior results. Although the overall impact of the hydrogen displacement parameter model amounts to only about 10% of the overall residual density, the use of HAR-refined hydrogen atom displacement parameters in an experimental electron-density study is not recommended. In the near future, we will extend this study toward the evaluation of crystal- and electric-field effects in hydrogen maleate compounds – an aspect explicitly excluded from this study. What has been found here is that it is important to use the most accurate ADPs available for hydrogen atoms for an evaluation of the experimentally determined electron densities and associated crystal electric fields.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. Grabowsky thanks the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) for funding of an Emmy Noether project (GR 4451/1-1) and an Individual Research Grant (GR 4451/2-1) as well as the Australian Research Council (ARC) for a Discovery project (DP110105347) and a Discovery Early Career Researcher Award (DE140101330). The synchrotron measurements at SPring-8 were carried out under proposal nos. 2013B1056 and 2014A1078.References
- A. H. Compton, Nature, 1915, 95, 343–344 CrossRef CAS.
- R. I. Cooper, A. L. Thompson and D. J. Watkin, J. Appl. Crystallogr., 2010, 43, 1100–1107 CrossRef CAS.
- L. A. Malaspina, A. J. Edwards, M. Woińska, D. Jayatilaka, M. J. Turner, J. R. Price, R. Herbst-Irmer, K. Sugimoto, E. Nishibori and S. Grabowsky, Cryst. Growth Des., 2017, 17, 3812–3825 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- F. H. Allen and I. J. Bruno, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 380–386 CrossRef CAS.
- V. L. Deringer, V. Hoepfner and R. Dronskowski, Cryst. Growth Des., 2012, 12, 1014–1021 CrossRef CAS.
- M. Lusi and L. J. Barbour, Cryst. Growth Des., 2011, 11, 5515–5521 CrossRef CAS.
- J. Bentley and R. F. Stewart, J. Comput. Phys., 1973, 11, 127–145 CrossRef.
- R. F. Stewart, J. Bentley and B. Goodman, J. Chem. Phys., 1975, 63, 3786–3793 CrossRef CAS.
- R. Destro, R. E. Marsh and R. Bianchi, J. Phys. Chem., 1988, 92, 966–973 CrossRef CAS.
- C. Gatti, E. May, R. Destro and F. Cargnoni, J. Phys. Chem. A, 2002, 106, 2707–2720 CrossRef CAS.
- K. K. Jha, B. Gruza, P. Kumar, M. L. Chodkiewicz and P. M. Dominiak, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 296–306 CrossRef CAS.
- D. Jayatilaka and B. Dittrich, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 383–393 CrossRef CAS.
- S. C. Capelli, H.-B. Bürgi, B. Dittrich, S. Grabowsky and D. Jayatilaka, IUCrJ, 2014, 1, 361–379 CrossRef CAS.
- M. Fugel, D. Jayatilaka, E. Hupf, J. Overgaard, V. R. Hathwar, P. Macchi, M. J. Turner, J. A. K. Howard, O. V. Dolomanov, H. Puschmann, B. B. Iversen, H.-B. Bürgi and S. Grabowsky, IUCrJ, 2018, 5, 32–44 CrossRef CAS.
- M. Woińska, S. Grabowsky, P. M. Dominiak, K. Woźniak and D. Jayatilaka, Sci. Adv., 2016, 2, e1600192 CrossRef.
- M. Woińska, D. Jayatilaka, M. A. Spackman, A. J. Edwards, P. M. Dominiak, K. Woźniak, E. Nishibori, K. Sugimoto and S. Grabowsky, Acta Crystallogr., Sect. A: Found. Adv., 2014, 70, 483–498 CrossRef PubMed.
- C. Köhler, J. Lübben, L. Krause, C. Hoffmann, R. Herbst-Irmer and D. Stalke, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 434–441 CrossRef.
- B. Dittrich, J. Lübben, S. Mebs, A. Wagner, P. Luger and R. Flaig, Chem. – Eur. J., 2017, 23, 4605–4614 CrossRef CAS.
- A. Ø. Madsen, J. Appl. Crystallogr., 2006, 39, 757–758 CrossRef CAS.
- V. Schomaker and K. N. Trueblood, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1968, 24, 63–76 CrossRef CAS.
- A. Ø. Madsen and A. A. Hoser, J. Appl. Crystallogr., 2014, 47, 2100–2104 CrossRef CAS.
- R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. d'Arco, Y. Noël, M. Causá, M. Rérat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317 CrossRef CAS.
- T. S. Koritsanszky and P. Coppens, Chem. Rev., 2001, 101, 1583–1628 CrossRef CAS PubMed.
- A. E. Whitten and M. A. Spackman, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 875–888 CrossRef PubMed.
- P. Munshi, A. Ø. Madsen, M. A. Spackman, S. Larsen and R. Destro, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 465–475 CrossRef CAS PubMed.
- A. A. Hoser, P. M. Dominiak and K. Woźniak, Acta Crystallogr., Sect. A: Found. Crystallogr., 2009, 65, 300–311 CrossRef CAS PubMed.
- P. Roversi and R. Destro, Chem. Phys. Lett., 2004, 386, 472–478 CrossRef CAS.
- A. Ø. Madsen, H. O. Sørensen, C. Flensburg, R. F. Stewart and S. Larsen, Acta Crystallogr., Sect. A: Found. Crystallogr., 2004, 60, 550–561 CrossRef PubMed.
- D. Jayatilaka, Phys. Rev. Lett., 1998, 80, 798–801 CrossRef CAS.
- D. Jayatilaka and D. J. Grimwood, Acta Crystallogr., Sect. A: Found. Crystallogr., 2001, 57, 76–86 CrossRef CAS PubMed.
- D. J. Grimwood and D. Jayatilaka, Acta Crystallogr., Sect. A: Found. Crystallogr., 2001, 57, 87–100 CrossRef CAS PubMed.
- S. Grabowsky, A. Genoni and H.-B. Bürgi, Chem. Sci., 2017, 8, 4159–4176 RSC.
- G. Gilli and P. Gilli, J. Mol. Struct., 2000, 552, 1–15 CrossRef CAS.
- K. T. Mahmudov and A. J. L. Pombeiro, Chem. – Eur. J., 2016, 22, 16356–16398 CrossRef CAS PubMed.
- G. Olovsson, I. Olovsson and M. Lehmann, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1984, 40, 1521–1526 CrossRef.
- F. Fillaux, N. Leygue, J. Tomkinson, A. Cousson and W. Paulus, Chem. Phys., 1999, 244, 387–403 CrossRef CAS.
- C. C. Wilson, L. H. Thomas and C. A. Morrison, Chem. Phys. Lett., 2003, 381, 102–108 CrossRef CAS.
- N. Lah and I. Leban, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2003, 59, o537–o538 CrossRef PubMed.
- S. Franklin and T. Balasubramanian, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2009, 65, o58–o61 CrossRef CAS PubMed.
- S. F. Darlow and W. Cochran, Acta Crystallogr., 1961, 14, 1250–1257 CrossRef CAS.
- S. F. Darlow, Acta Crystallogr., 1961, 14, 1257–1259 CrossRef.
- S. Peterson and H. A. Levy, J. Chem. Phys., 1958, 29, 948–949 CrossRef CAS.
- M. Fleck and L. Bohatý, Z. Naturforsch., B: J. Chem. Sci., 2009, 64, 517–524 CAS.
- M. Gupta, S. Prasad and T. Gupta, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1975, 31, 37–40 CrossRef.
- P. Popelier, A. Lenstra and H. Geise, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1989, 45, 1024–1028 CrossRef.
- M. Gupta, C. Van Alsenoy and A. Lenstra, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1984, 40, 1526–1529 CrossRef.
- F. Vanhouteghem, A. Lenstra and P. Schweiss, Acta Crystallogr., Sect. B: Struct. Sci., 1987, 43, 523–528 CrossRef.
- M. Gupta and B. Yadav, Cryst. Struct. Commun., 1974, 3, 595–597 CAS.
- Y. Zheng, Z. Kong and J. Lin, Z. Kristallogr. - New Cryst. Struct., 2001, 216, 355–356 CAS.
- J.-X. Yuan, M.-L. HU, D.-M. Chen and L.-C. Chen, Chem. Res. Chin. Univ., 2002, 18, 249–251 CAS.
- M. Pajtasova, J. Maroszová, M. Koman and M. Melnik, Main Group Met. Chem., 2007, 30, 245–252 CAS.
- M. Alagar, R. Krishnakumar and S. Natarajan, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2001, 57, o968–o970 CrossRef CAS.
- K. Sugimoto, H. Ohsumi, S. Aoyagi, E. Nishibori, C. Moriyoshi, Y. Kuroiwa, H. Sawa and M. Takata, AIP Conference Proceedings, 2010, pp. 887–890 Search PubMed.
- Rigaku Corporation, RAPID AUTO version 2.41, Tokyo, Japan, 2004 Search PubMed.
- Bruker AXS Inc., APEX3, Wisconsin, USA, 2016 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849–854 CrossRef CAS.
- D. Jayatilaka and D. J. Grimwood, International Conference on Computational Science, 2003, pp. 142–151 Search PubMed.
- M. Ernst, A. Genoni and P. Macchi, J. Mol. Struct., 2020, 1209, 127975 CrossRef CAS.
- S. Grabowsky, A. Genoni, S. P. Thomas and D. Jayatilaka, The advent of quantum crystallography: form and structure factors from quantum mechanics for advanced structure refinement and wavefunction fitting, in 21st Century Challenges in Chemical Crystallography, Structure and Bonding, ed. D. M. P. Mingos and P. R. Raithby, Springer, 2020 Search PubMed.
- L. A. Malaspina, A. Genoni and S. Grabowsky, J. Appl. Crystallogr., 2020 Search PubMed , under revision.
- R. H. Blessing, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 816–823 CrossRef PubMed.
- M. V. Vener, A. V. Manaev and V. G. Tsirelson, J. Phys. Chem. A, 2008, 112, 13628–13632 CrossRef CAS PubMed.
- W. Hummel, J. Hauser and H.-B. Bürgi, J. Mol. Graphics, 1990, 8, 214–220 CrossRef CAS PubMed.
- A. Genoni, L. H. Dos Santos, B. Meyer and P. Macchi, IUCrJ, 2017, 4, 136–146 CrossRef CAS PubMed.
- L. Bučinský, D. Jayatilaka and S. Grabowsky, Acta Crystallogr., Sect. A: Found. Adv., 2019, 75, 705–717 CrossRef PubMed.
- M. Fugel, M. V. Ponomarenko, M. F. Hesse, L. A. Malaspina, F. Kleemiss, K. Sugimoto, A. Genoni, G.-V. Röschenthaler and S. Grabowsky, Dalton Trans., 2019, 48, 16330–16339 RSC.
- M. Fugel, L. A. Malaspina, R. Pal, S. P. Thomas, M. W. Shi, M. A. Spackman, K. Sugimoto and S. Grabowsky, Chem. – Eur. J., 2019, 25, 6523–6532 CrossRef CAS PubMed.
- H. Yanai, T. Suzuki, F. Kleemiss, H. Fukaya, Y. Dobashi, L. A. Malaspina, S. Grabowsky and T. Matsumoto, Angew. Chem., Int. Ed., 2019, 58, 8839–8844 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of crystallization, refinements, molecular structures, isotropic displacement parameter comparisons, PEANUT plots, quantum-mechanically optimized geometries, X-ray constrained wavefunction fittings, topological analyses, and the use of the UIJXN scaling procedure. CCDC 1987762, 1989500, 1989516, 1989518, 1989533–1989535. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ce00378f |
| This journal is © The Royal Society of Chemistry 2020 |

