Relevant π-hole tetrel bonding interactions in ethyl 2-triazolyl-2-oxoacetate derivatives: Hirshfeld surface analysis and DFT calculations†
Abstract
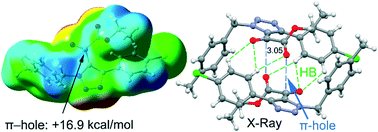
This manuscript reports the synthesis, spectroscopic and X-ray characterization of four triazole derivatives that include an α-ketoester functionality and two phenyl substituents. In particular, ethyl 2-(4-(4-chlorophenyl)-1-(4-methylbenzyl)-1H-1,2,3-triazol-5-yl)-2-oxoacetate (1), ethyl 2-(1-(4-methylbenzyl)-4-phenyl-1H-1,2,3-triazol-5-yl)-2-oxoacetate (2), ethyl 2-(1-benzyl-4-(3-fluorophenyl)-1H-1,2,3-triazol-5-yl)-2-oxoacetate (3) and ethyl 2-(1-benzyl-4-(4-methoxyphenyl-1H-1,2,3-triazol-5-yl))-2-oxoacetate (4) were synthesized in good yields. All the compounds form self-assembled dimers in the solid state establishing two symmetrically equivalent O⋯π-hole tetrel bonding interactions. These interactions have been analyzed using Hirshfeld surface analysis, DFT calculations and Bader's theory of atoms-in-molecules and further rationalized using molecular electrostatic potential (MEP) surface calculations. We have studied how the nucleophilic/electrophilic nature of the –COOEt and –CO– groups is affected by the substituents of the rings and, consequently, influences the interaction energy of the C⋯O tetrel bond.


 Please wait while we load your content...
Please wait while we load your content...